Study of the Characteristics of Second-Order Underdamped Unsaturated Stochastic Resonance System Driven by OFDM Signals
Abstract
1. Introduction
- A method for enhancing and demodulating OFDM signals based on SUUBSR is proposed.
- OFDM signals are divided into in-phase and quadrature components, which are processed separately by stochastic resonance, addressing the limitation that stochastic resonance systems cannot directly process OFDM signals.
- Analytical expressions for the transient and steady-state responses, as well as time-resolved expressions, of the OFDM signal enhancement and demodulation system based on SUUBSR are theoretically derived. The influence of various parameters on the transient and steady-state responses of the system is analyzed.
- The potential energy loss of OFDM signals during enhancement processing by stochastic resonance is theoretically analyzed.
- The enhancement and demodulation system based on SUUBSR is implemented for OFDM signals with different subcarrier modulation schemes.
2. Model of Second-Order Underdamped Unsaturated Bistable Stochastic Resonance System Driven by OFDM Signals
2.1. Potential Function Model
2.2. OFDM Baseband Complex Signal Model and the SUUBSR System Model
OFDM Baseband Complex Signal Model
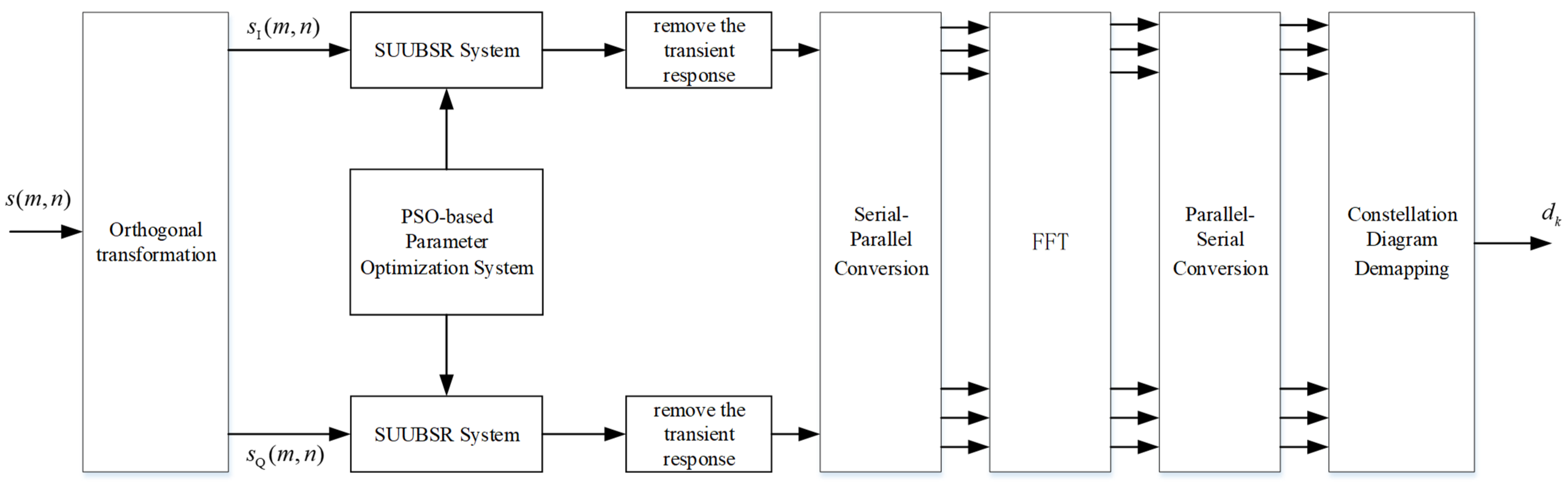
2.3. OFDM Signal Enhancement and Demodulation Model Based on Second-Order Underdamped Unsaturated Stochastic Resonance System
3. Transient Response Analysis of Second-Order Underdamped Stochastic Resonance System Excited by OFDM Signals
3.1. First Passage Time Analysis of System Response
3.2. Transient Steady-State Response Analysis of Underdamped Stochastic Resonance System
3.2.1. Transient Response Theory Derivation
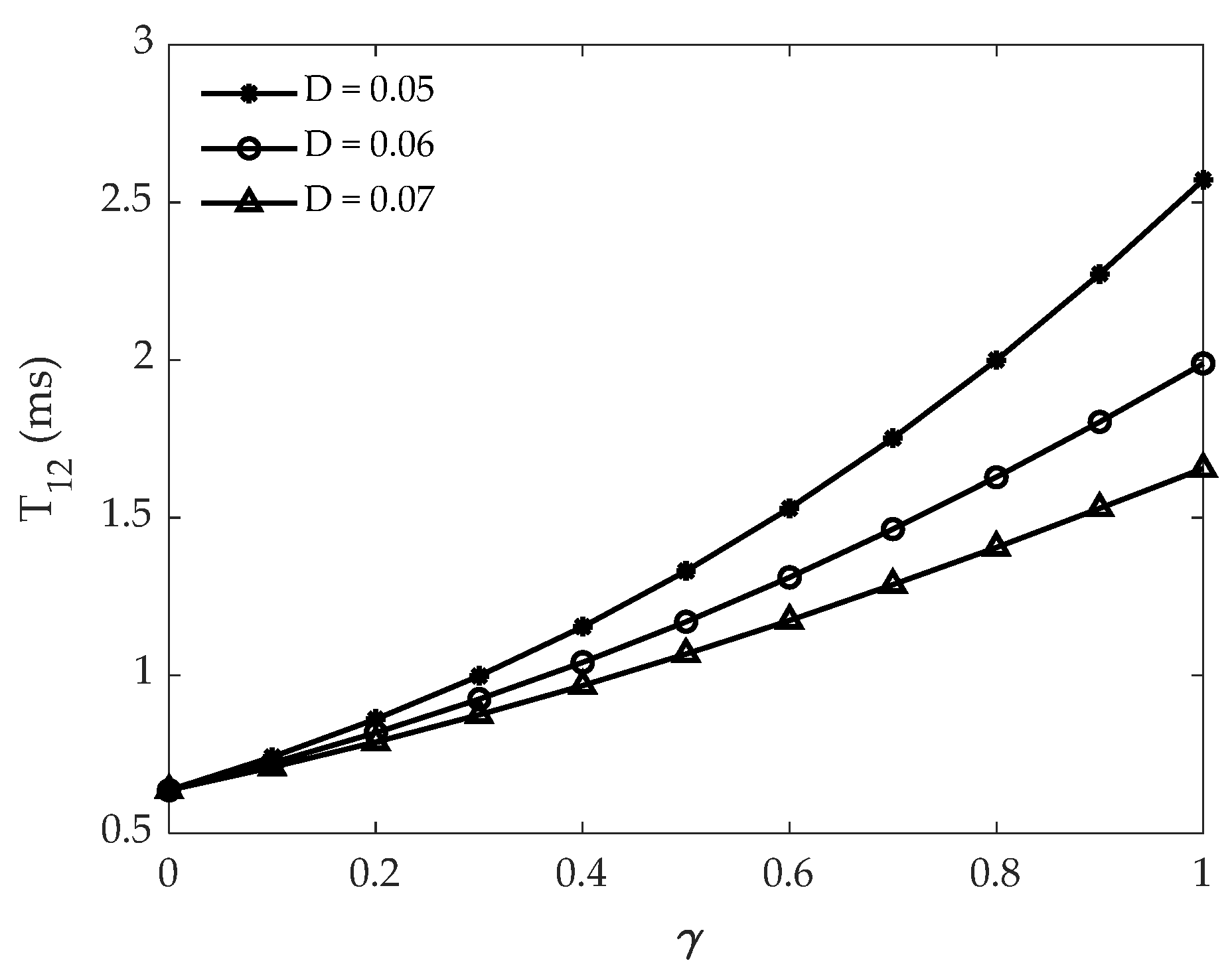
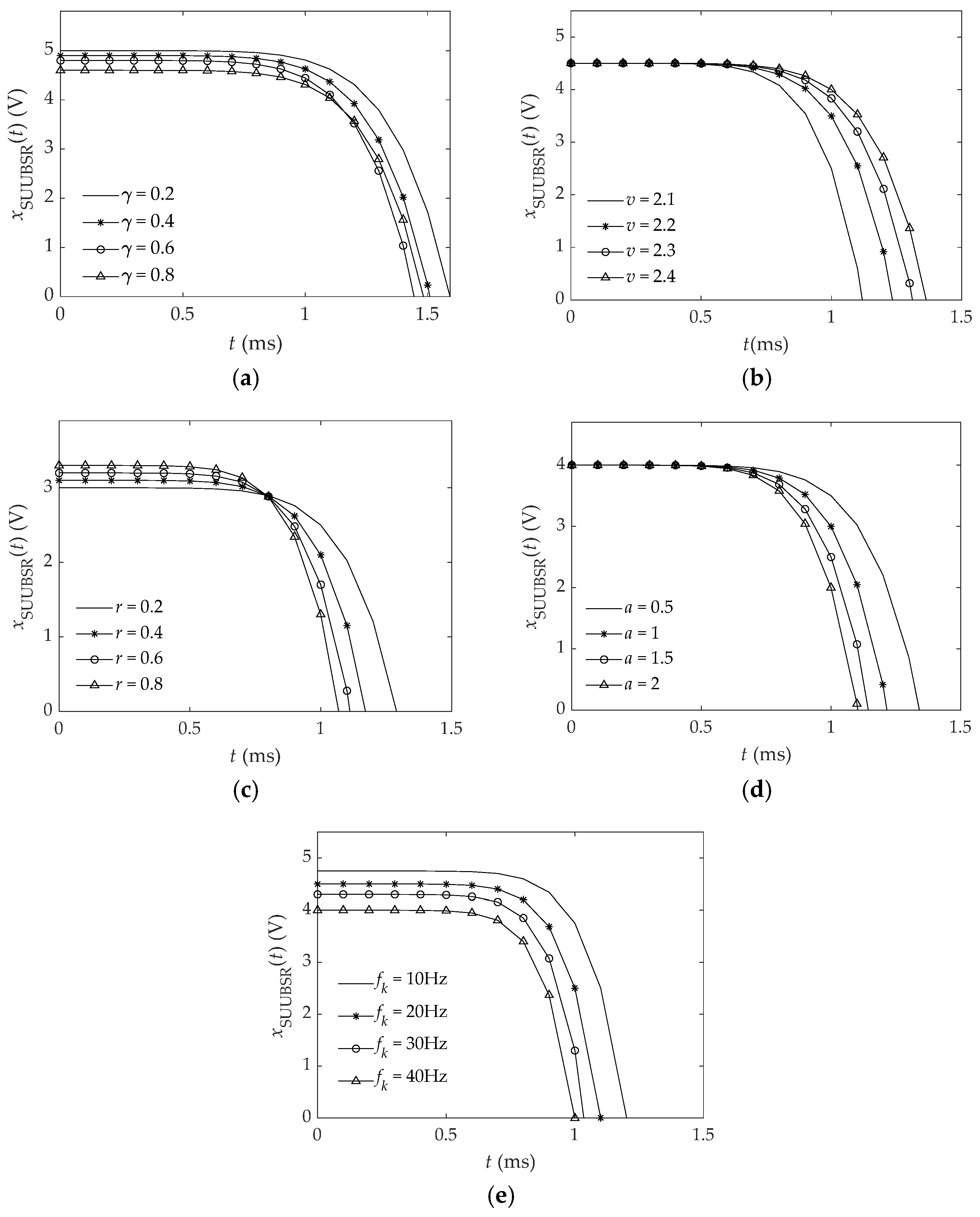
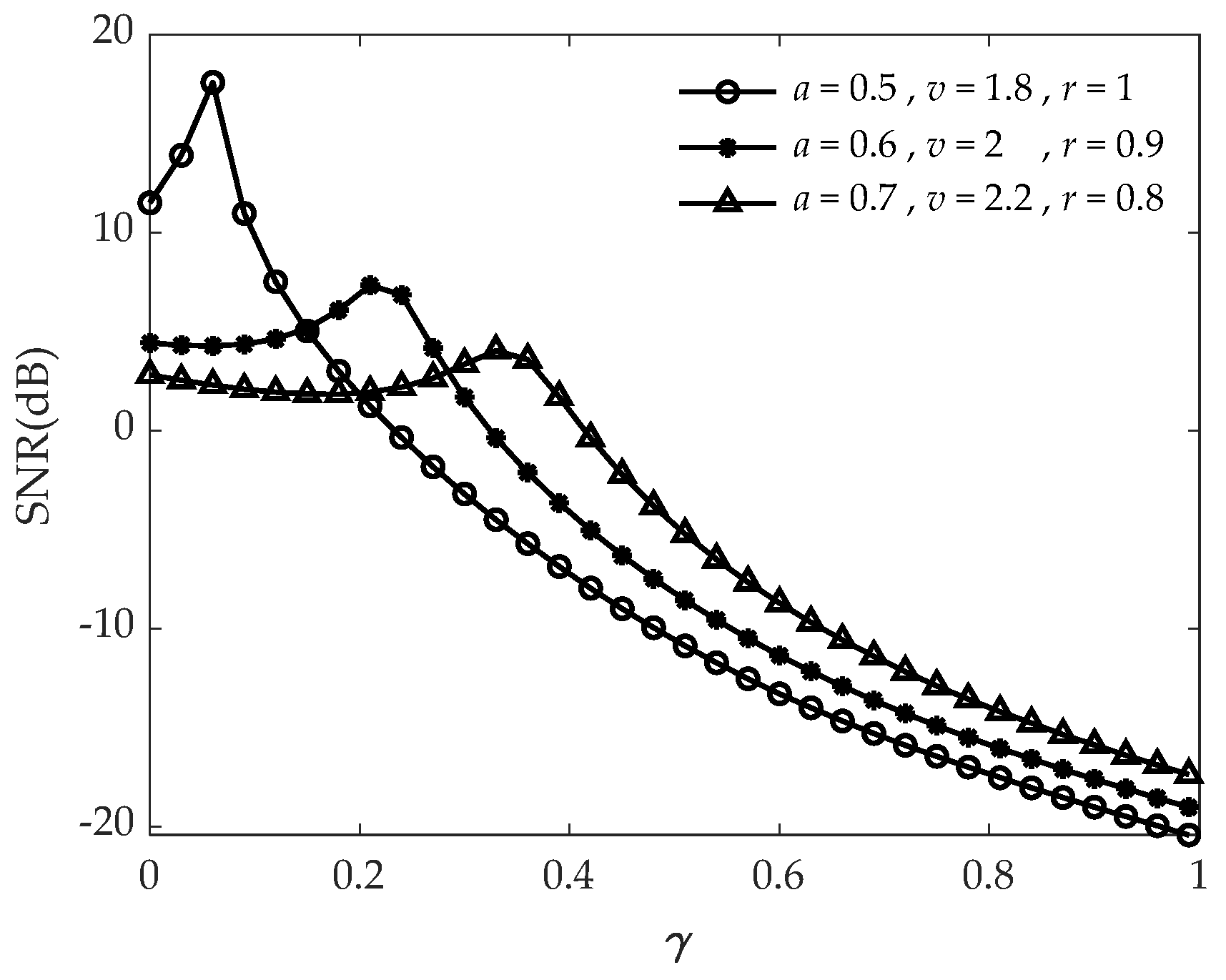
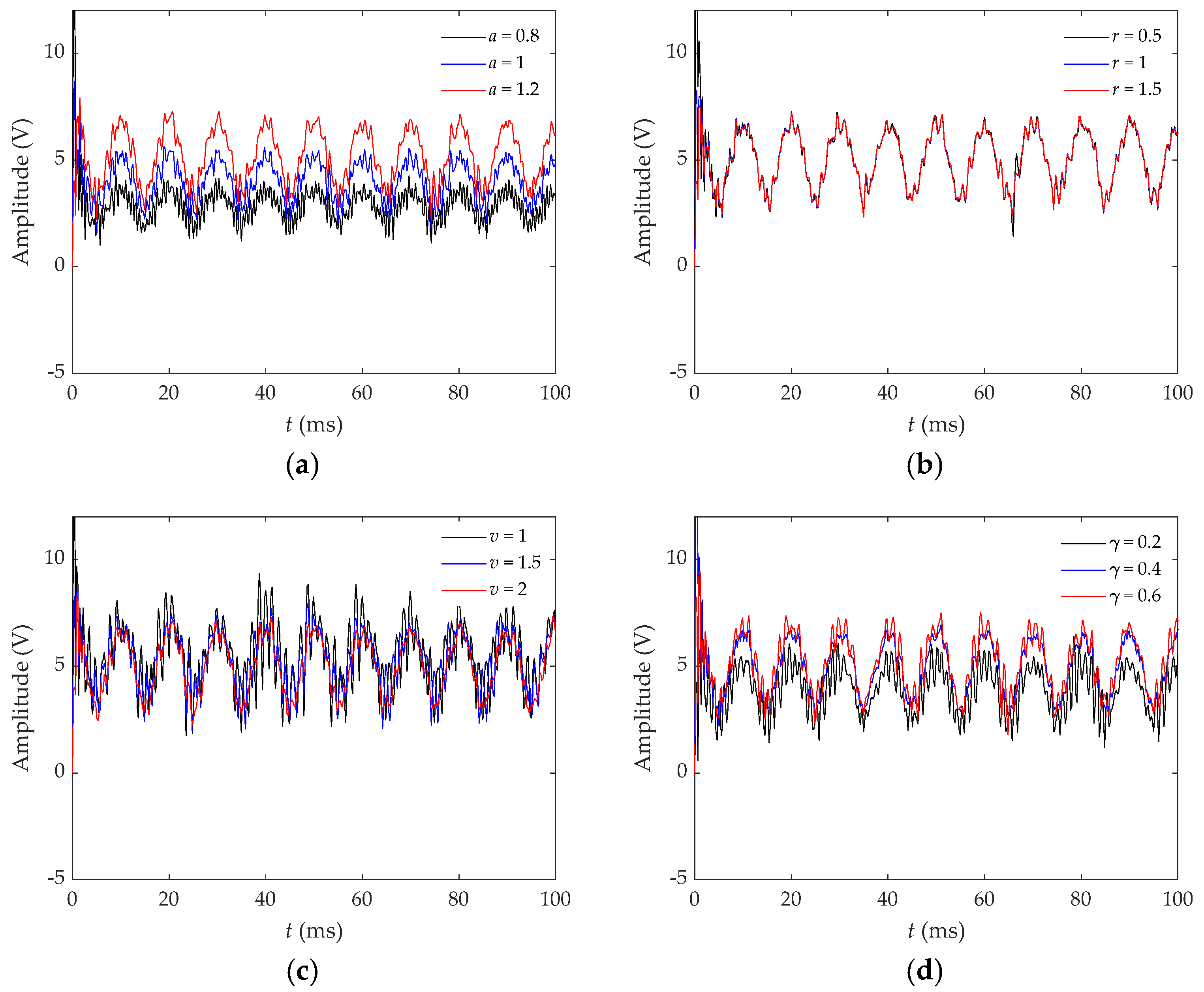
3.2.2. Influence of System Parameters and Input Signal Frequency on the System Response Speed
3.3. Steady-State Response Analysis
4. Experimental Simulation
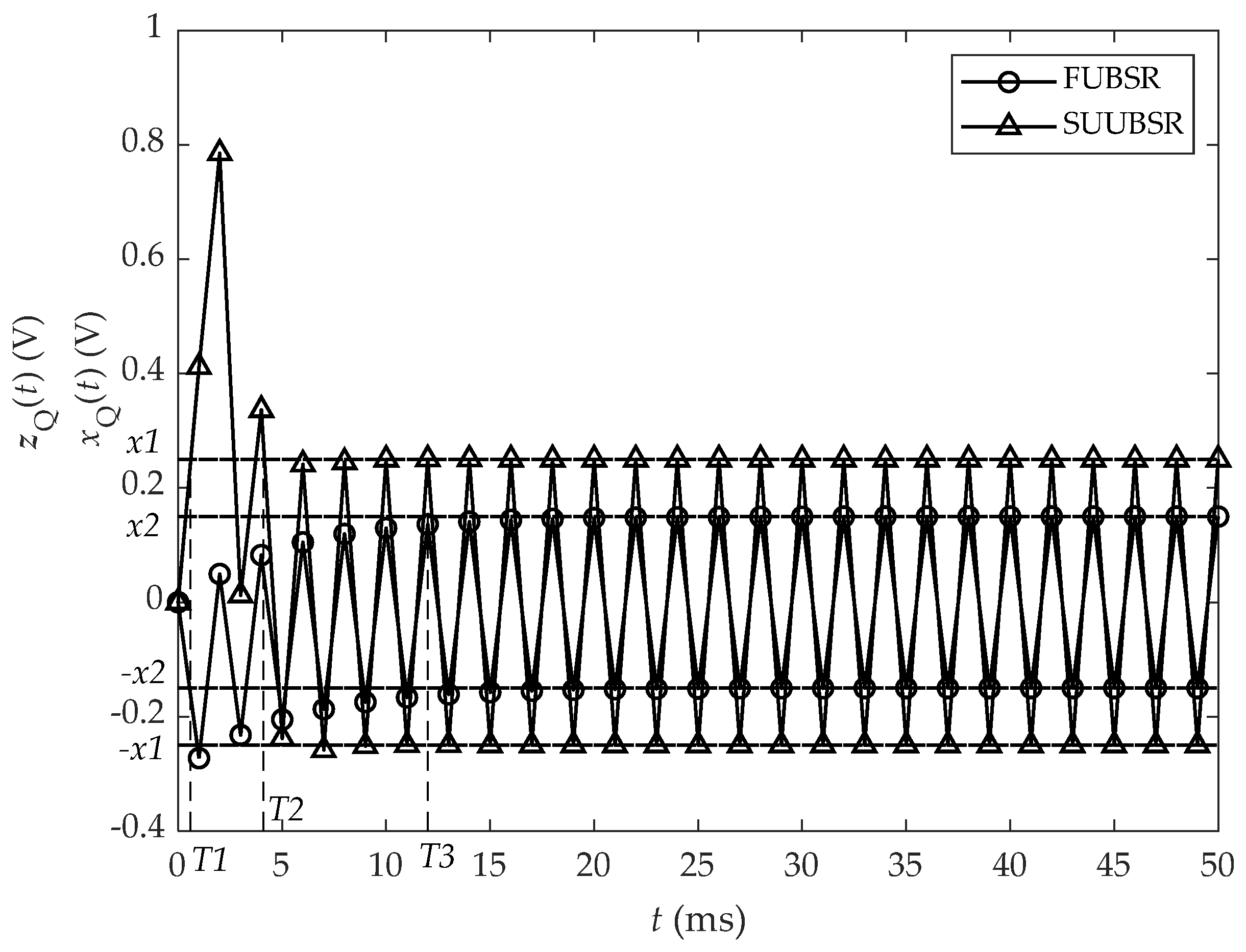
4.1. Detection Simulation of Communication Signal Waveform by FUBSR and SUUBSR
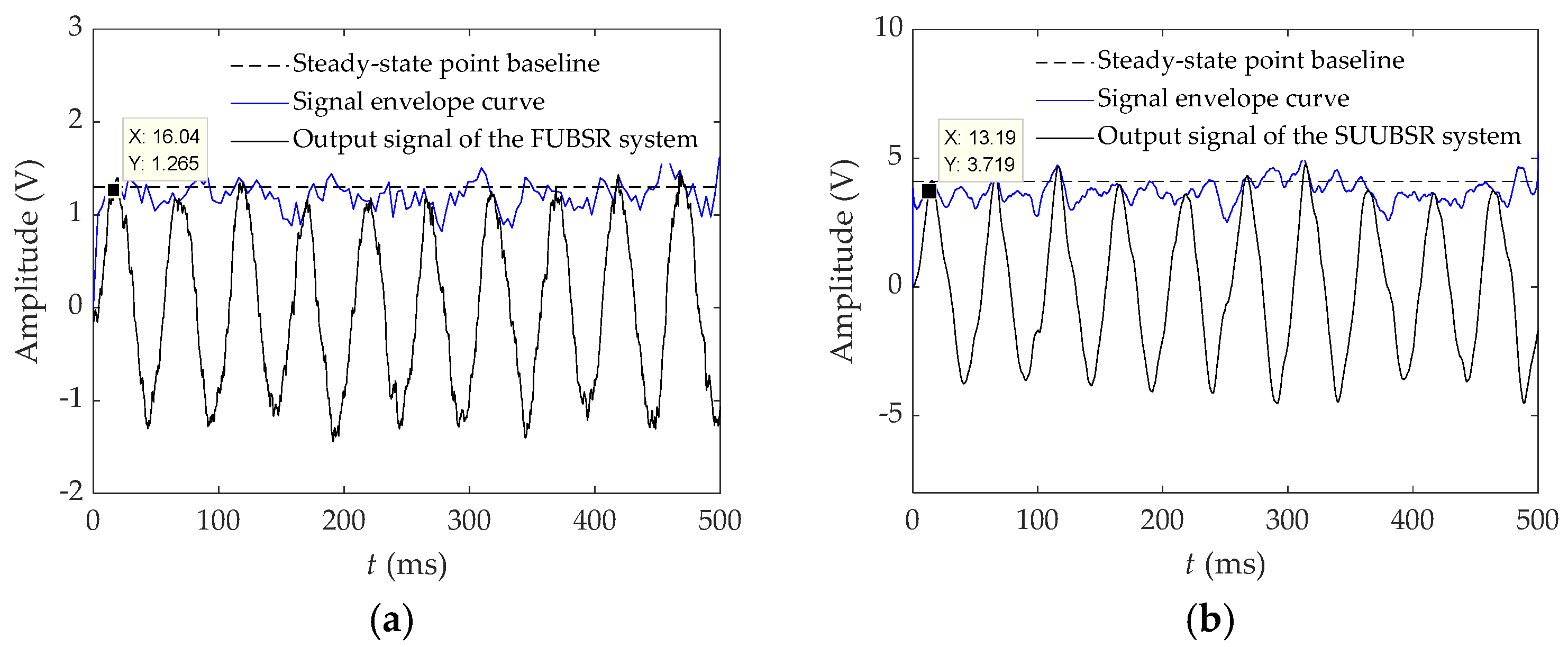
4.1.1. Detection Simulation of Single-Carrier Signal Waveform by FUBSR and SUUBSR
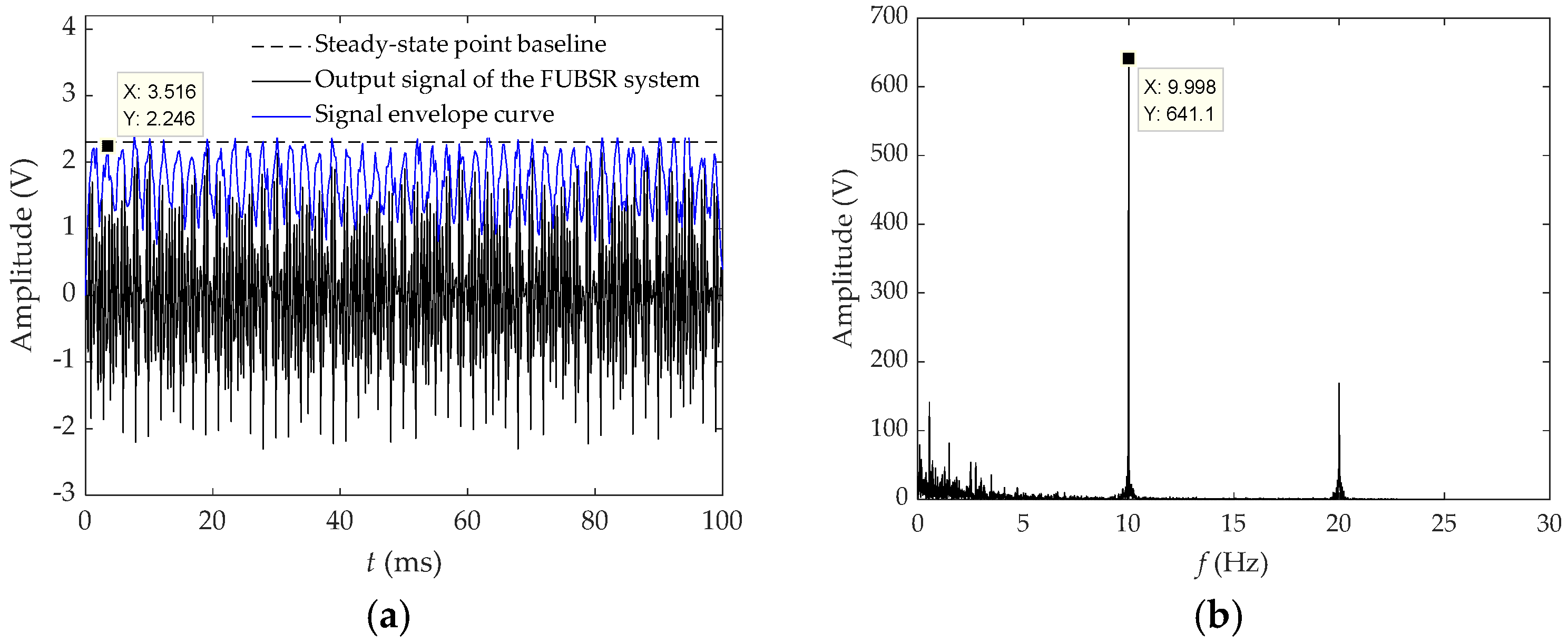
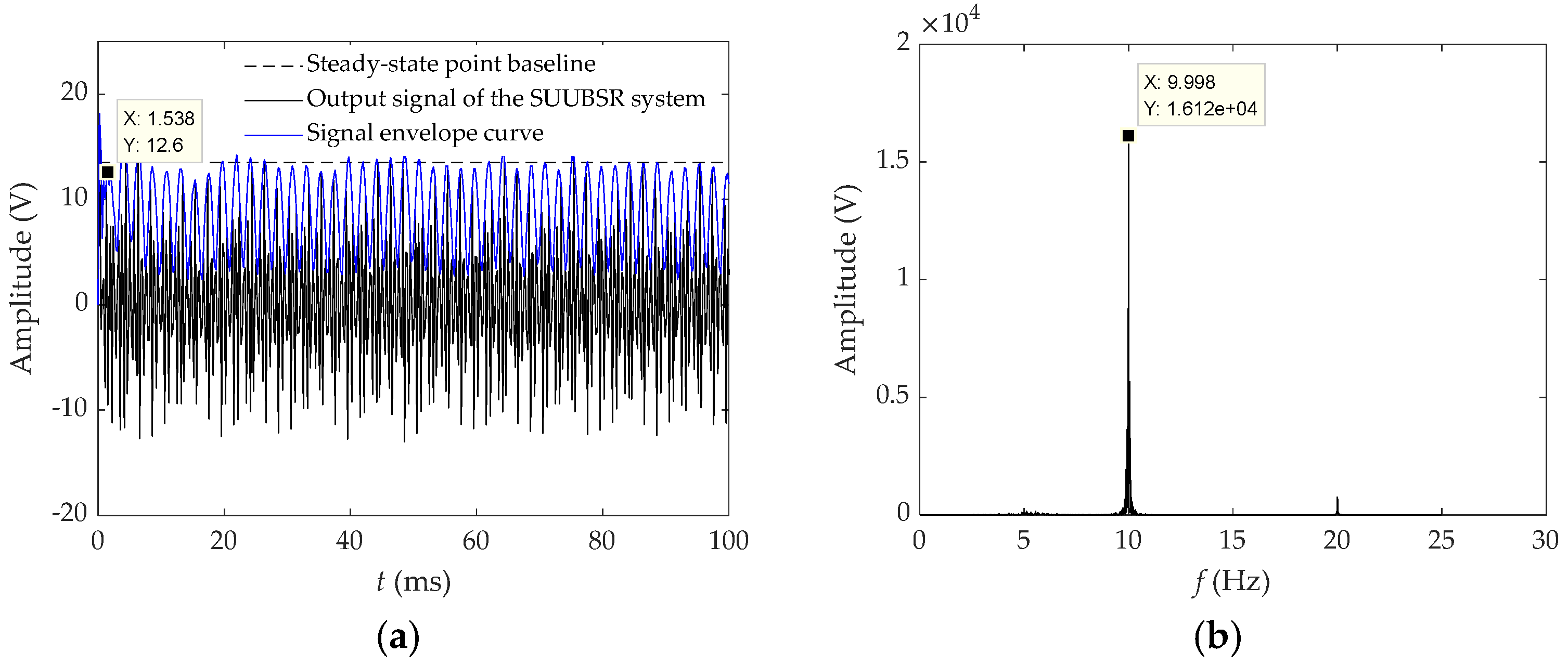
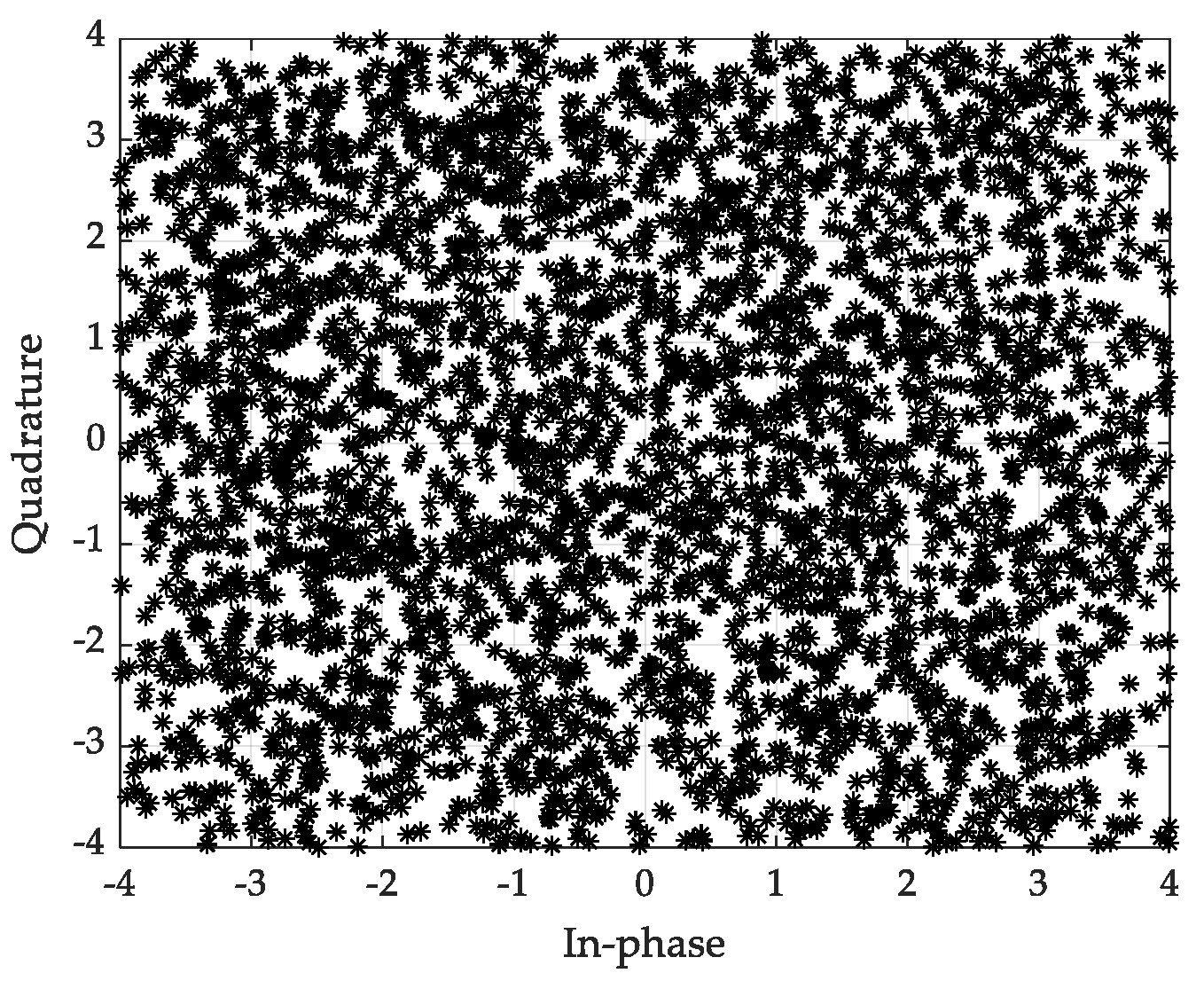
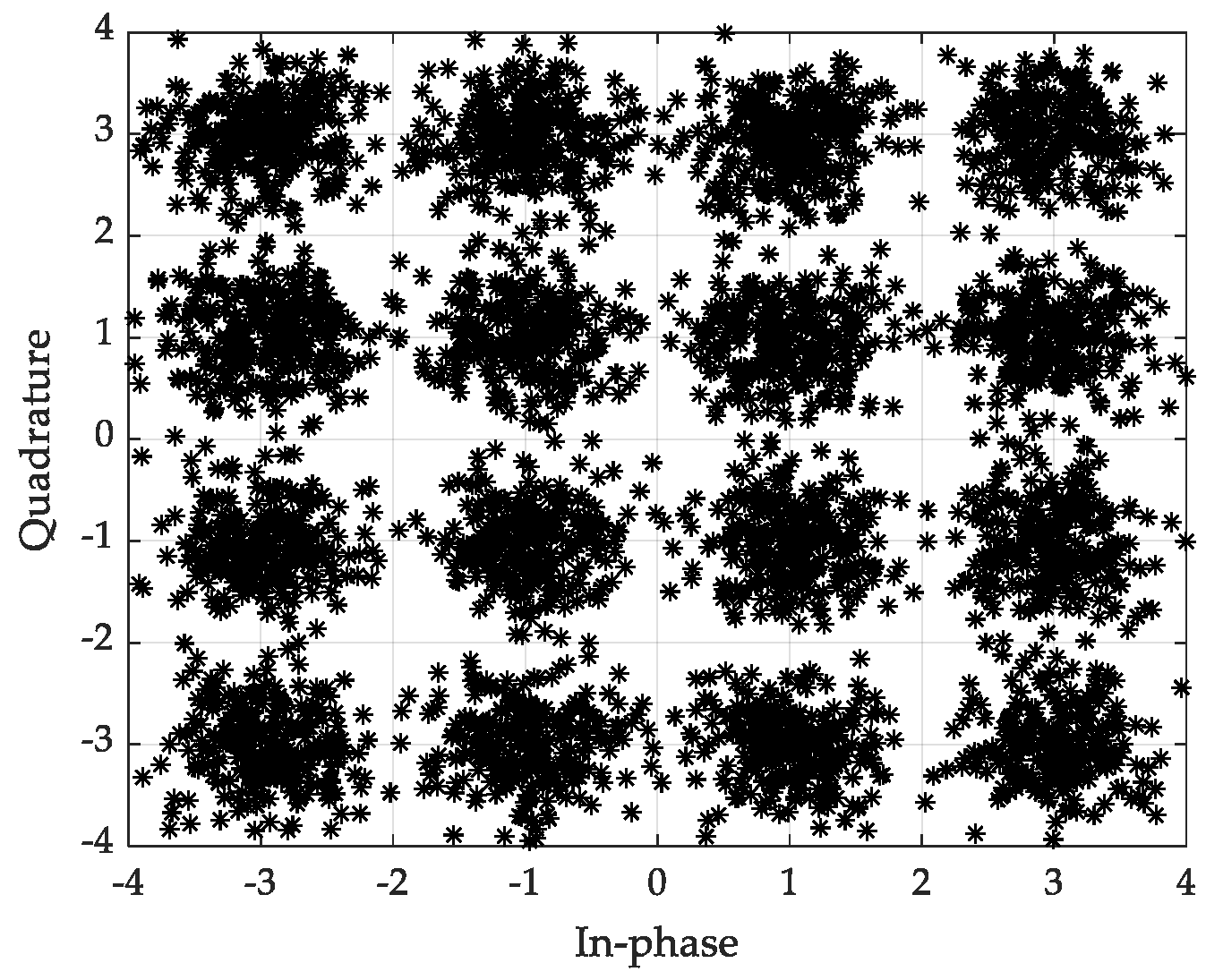
4.1.2. Simulation of Detection of OFDM Signal Waveforms by FUBSR Stochastic Resonance and SUUBSR Systems
4.2. Performance Analysis of OFDM Signal Demodulation
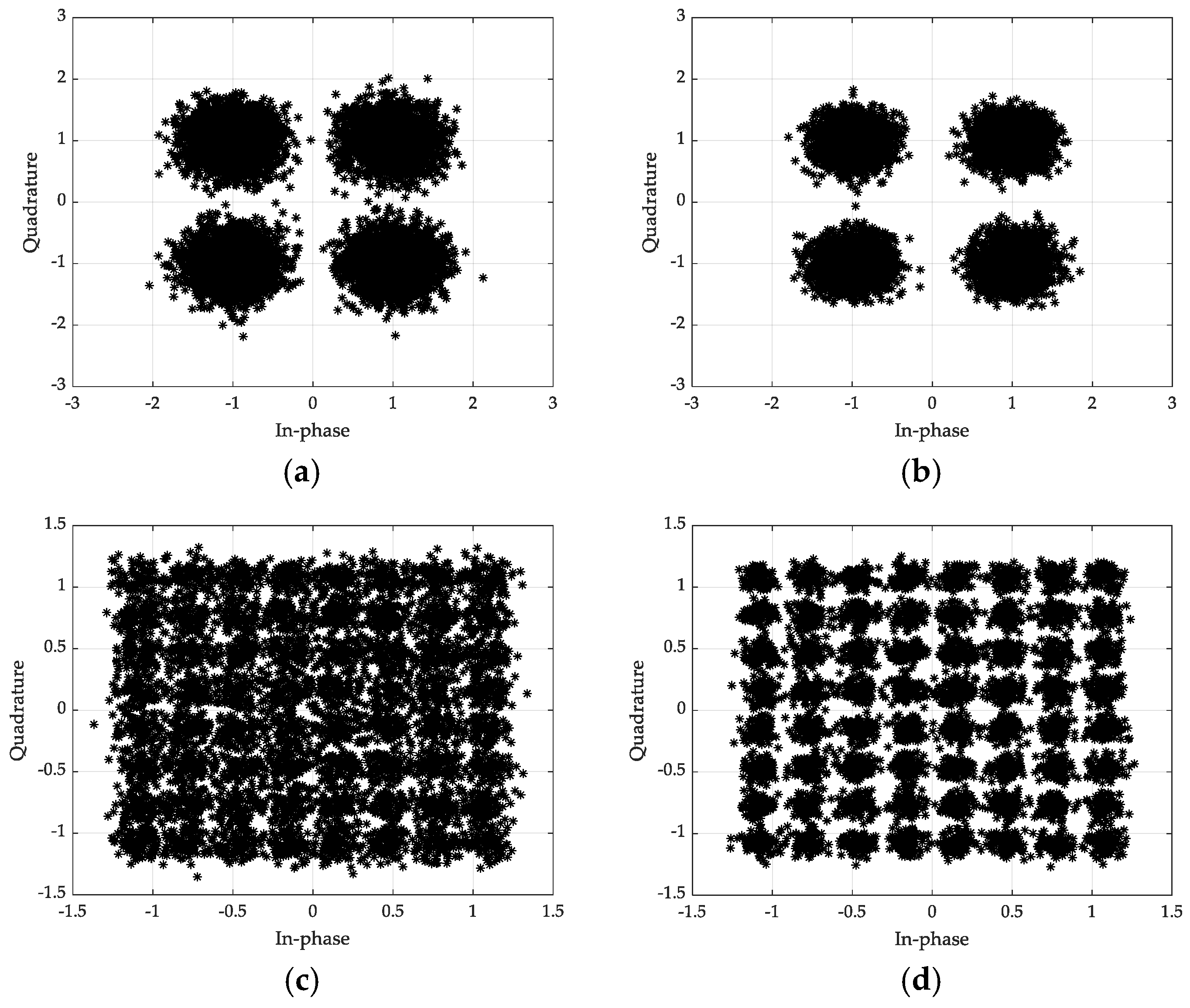
4.2.1. Simulation of Demodulation Process of OFDM Signals by FUBSR and SUUBSR Systems
4.2.2. Demodulation Effect of OFDM Signals in Different Stochastic Resonance Systems
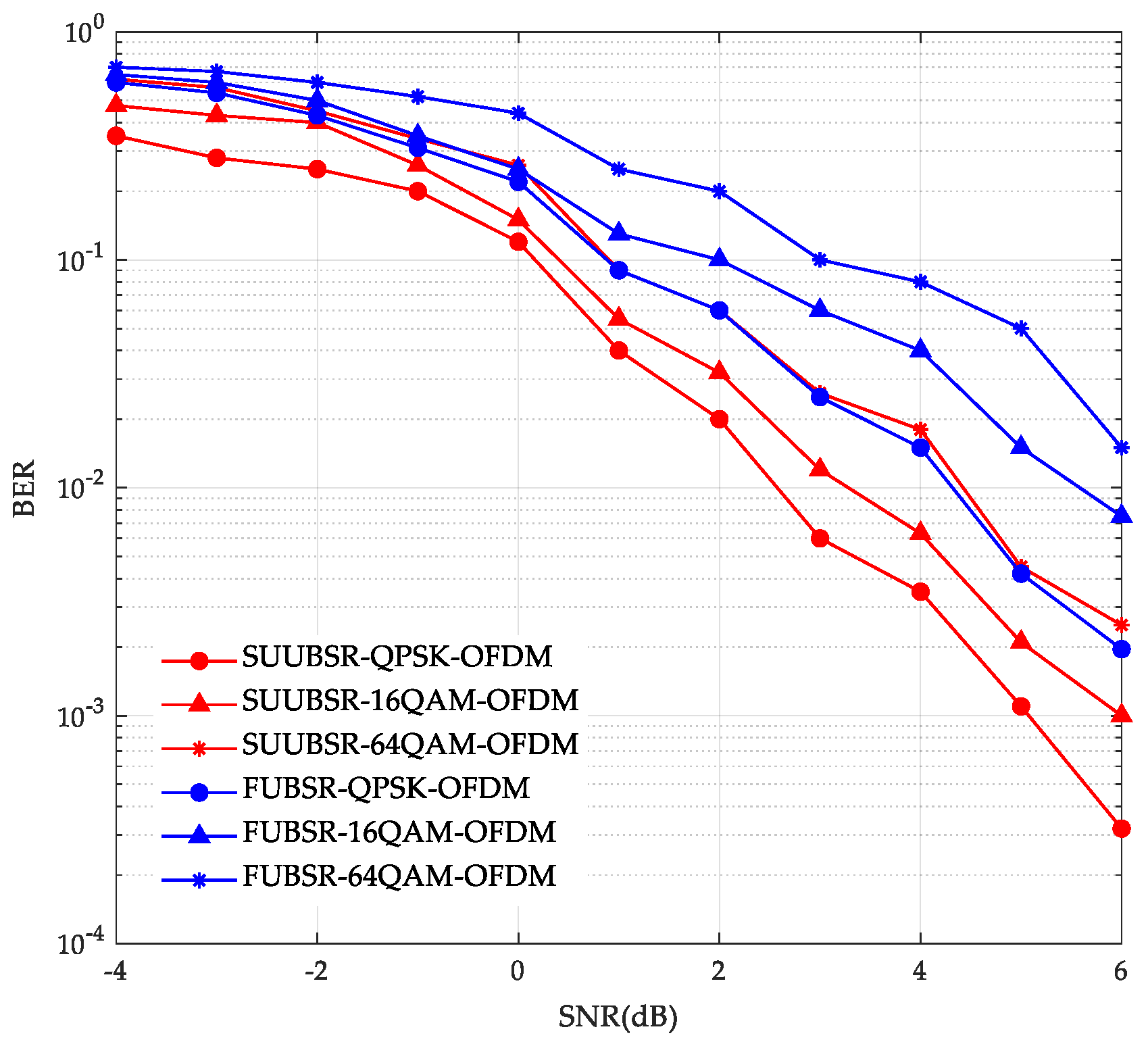
4.3. System Bit Error Rate Analysis
4.4. Algorithm Complexity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Full English Name |
| OFDM | Orthogonal frequency division multiplexing |
| SR | Stochastic resonance |
| MPFT | The mean first passage time |
| SUUBSR | Second-order underdamped unsaturated bistable stochastic resonance |
| FUBSR | First-order unsaturated bistable stochastic resonance |
| SNR | Signal–noise ratio |
| BER | Bit error rate |
References
- Ji, C.; Zhao, Q.; Yu, Y.; Dai, W. Detection of Weak Signals Under Low SNR Stochastic Resonance System. IEEE Access 2023, 11, 101881–101889. [Google Scholar] [CrossRef]
- Gao, R.; Jiao, S.; Xue, Q. Research and application of composite stochastic resonance in enhancement detection. Chin. Phys. B 2024, 33, 37–46. [Google Scholar] [CrossRef]
- Ma, Z.; Jin, Y. Stochastic resonance in periodic potential driven by dichotomous noise. Acta Phys. Sin. 2015, 64, 84–90. [Google Scholar] [CrossRef]
- Ding, J.; Guo, Y.; Mi, L. The transient characteristics of an underdamped periodic potential system excited by two different kinds of noise. Probabilistic Eng. Mech. 2023, 72, 103450. [Google Scholar] [CrossRef]
- Zhang, C.; Lai, Z.; Tu, Z.; Liu, H. Stochastic resonance induced weak signal enhancement in a second-order tri-stable system with single-parameter adjusting. Appl. Acoust. 2024, 216, 109753. [Google Scholar] [CrossRef]
- Zhai, Y.; Fu, Y.; Kang, Y. Incipient Bearing Fault Diagnosis Based on the Two-State Theory for Stochastic Resonance Systems. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Jin, Y.; An, Y. Weak Bearing Fault Diagnosis Based on Improved Stochastic Resonance of the Multi-Stable System. Trans. Beijing Inst. Technol. 2024, 44, 447–457. [Google Scholar] [CrossRef]
- Li, M.; Shi, P.; Zhang, W.; Han, D. A novel underdamped continuous unsaturation bistable stochastic resonance method and its application. Chaos Solitons Fractals 2021, 151, 111228. [Google Scholar] [CrossRef]
- Liu, G.; Peng, L. Research on the Application of Random Resonance in Three Stable Traps in Weak OFDM Signal Detection. Acta Metrol. Sin. 2023, 44, 1872–1881. [Google Scholar]
- Liu, G.; Liang, Y. Research on OFDM signal detection method based on random resonance in bistable well. J. Syst. Simul. 2022, 34, 2046–2055. [Google Scholar] [CrossRef]
- Wang, X.; Xiong, X.; Li, C.; Wu, B.; Niu, L. Impact of potential function asymmetry on the performance of a novel stochastic resonance system. Chin. J. Phys. 2024, 91, 11–24. [Google Scholar] [CrossRef]
- Shu, Y.; Shen, J.; Lin, Y. Early Weak Fault Signal Enhancement and Recognition Method of Rudder Paddle Bearings Based on Parameter Adaptive Stochastic Resonance. IEEE Access 2024, 12, 9458–9467. [Google Scholar] [CrossRef]
- Fu, Y.; Kang, Y.; Liu, R. Novel Bearing Fault Diagnosis Algorithm Based on the Method of Moments for Stochastic Resonant Systems. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Zhang, D.; Ma, Q. Time-delayed feedback bistable stochastic resonance system and its application in the estimation of the Polyester Filament Yarn tension in the spinning process. Chaos Solitons Fractals 2023, 168, 1113133. [Google Scholar] [CrossRef]
- Hu, G. Time-dependent solution of multidimensional Fokker–Planck equations in the weak noise limit. J. Phys. A—Math. Gen. 1989, 22, 365–377. [Google Scholar]
- Ding, Y.; Kang, Y.; Zhai, Y. Rolling Bearing Fault Diagnosis Based on Exact Moment Dynamics for Underdamped Periodic Potential Systems. IEEE Trans. Instrum. Meas. 2023, 72, 1–12. [Google Scholar] [CrossRef]
- Gong, X.; Xu, P. Stochastic resonance of multi-stable energy harvesting system with high-order stiffness from rotational environment. Chaos Solitons Fractals 2023, 172, 113534. [Google Scholar] [CrossRef]
- Mcnamara, B.; Wiesenfeld, K. Theory of stochastic resonance. Phys. Rev. A 1989, 39, 48544869. [Google Scholar] [CrossRef]
- Xu, H.; Zhou, S. Periodicity-assist double delay-controlled stochastic resonance for the fault detection of bearings. Measurement 2024, 225, 114018. [Google Scholar] [CrossRef]


| System | Number of Multiplications | Number of Additions |
|---|---|---|
| FUBSR | ||
| SUUBSR |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Wang, D. Study of the Characteristics of Second-Order Underdamped Unsaturated Stochastic Resonance System Driven by OFDM Signals. Appl. Sci. 2024, 14, 11324. https://doi.org/10.3390/app142311324
Liu G, Wang D. Study of the Characteristics of Second-Order Underdamped Unsaturated Stochastic Resonance System Driven by OFDM Signals. Applied Sciences. 2024; 14(23):11324. https://doi.org/10.3390/app142311324
Chicago/Turabian StyleLiu, Gaohui, and Dekang Wang. 2024. "Study of the Characteristics of Second-Order Underdamped Unsaturated Stochastic Resonance System Driven by OFDM Signals" Applied Sciences 14, no. 23: 11324. https://doi.org/10.3390/app142311324
APA StyleLiu, G., & Wang, D. (2024). Study of the Characteristics of Second-Order Underdamped Unsaturated Stochastic Resonance System Driven by OFDM Signals. Applied Sciences, 14(23), 11324. https://doi.org/10.3390/app142311324





