Intelligent End-Edge Computation Offloading Based on Lyapunov-Guided Deep Reinforcement Learning

Abstract

To address the end-edge computation offloading challenge in the multi-terminal and multi-server environment, this paper proposes an intelligent computation offloading algorithm based on Lyapunov optimization and deep reinforcement learning. We formulate a network computation rate maximization problem while balancing constraints including offloading time, CPU frequency, energy consumption, transmission power, and data queue stability. Due to the fact that the problem is mixed integer nonlinear programming, we transform it into a deterministic problem based on Lyapunov optimization theory, and then model it as a Markov decision process. Then, we employ deep reinforcement learning algorithm, i.e., asynchronous advantage actor-critic (A3C), and propose Lyapunov-guided A3C algorithm named LyA3C to approximate the optimal computation offloading policy. Experiments show that the LyA3C algorithm can converge stably and effectively improve the long-term network computation rate by 2.8% and 5.7% in comparison to the A2C-based and TD3-based algorithms.

1. Introduction

In the context of the fourth industrial revolution represented by “Industry 4.0”, communication technology and manufacturing technology are deeply integrated, enhancing networking and intelligence industrial of production process [1]. Thus, it is necessary to establish an interconnected, intelligent and stable industrial wireless network [2]. Industrial wireless technology, an innovation of this century, has become a hot spot after the field bus. Industrial wireless changes the information transfer of the existing control system. It boasts robust anti-interference capabilities, low power consumption, high reliability, and numerous other technical virtues [3]. In the future, industrial control technology will necessitate stringent requirements for reliability, low latency, and high-speed performance, further underscoring the significance of these advancements.

The industrial production process involves a large number of industrial tasks and the rapid increase of CPU-bound applications and delay-sensitive applications has added new challenges to the development of industrial wireless networks. Confronted with this deluge of industrial tasks, the conventional cloud computing model encounters limitations in addressing data processing and computational demands. Mobile edge computing (MEC) has emerged to enhance data processing efficiency.

By strategically deploying edge servers at the network’s periphery, the MEC system effectively brings the computing prowess of the cloud center closer to the edge, satisfying the escalating demand for computational augmentation at industrial terminals while fostering proximity between industrial terminals and edge servers. This arrangement curtails transmission time for industrial tasks, mitigating the latency in cloud computing. Nonetheless, when large-scale industrial tasks migrate to these edge servers concurrently, network congestion occurs, escalating task processing time delays and reducing computational throughput. Consequently, computation offloading in industrial wireless networks confronts the following pivotal challenges. Firstly, devising offloading strategies that are prudently calibrated to performance metrics. Secondly, dynamically allocating industrial tasks according to actual demand, ensuring optimal resource utilization. Enhancing resource utilization and optimizing performance metrics like energy consumption, time delay, and computation rate are essential to address these challenges.

When tackling dynamic challenges in the computation offloading strategies, ensuring system stability is very important. The Lyapunov optimization theory, originating from control theory, emerges as a robust approach to validate system stability and has been ingeniously adapted to construct queuing models for dynamic systems. Incorporating queue size into the objective function resolution, it fosters a relatively stable system state, thereby achieving the desired optimization objectives. Solving dynamic problems such as mixed-integer nonlinear programming (MINLP) requires high computation complexity, especially in large networks. The Lyapunov optimization theory excels in dynamically adapting to the ever-changing network conditions at every instant of system evolution, negating the need for manual intervention in adjusting control variables [4]. It is adaptable to real-time control of dynamically changing systems. Also, it ensures relatively low computation complexity, which is more straightforward than the direct solution of other algorithms [5]. Therefore, the application of Lyapunov optimization can transform the MINLP problem into continuous deterministic sub-problems while providing theoretical guarantee for the long-term stability of the system.

Traditional model-driven computation offloading and resource allocation strategies rely on exhaustive system information to construct accurate system models. Nevertheless, the inherent dynamism and randomness of industrial wireless networks pose significant challenges in gathering comprehensive system information necessary for accurate modeling [6]. This becomes particularly problematic in large-scale industrial settings, where a vast amount of intricately coupled system data results in an unwieldy state space, significantly impeding the efficiency of reinforcement learning. To overcome this bottleneck, data-driven deep reinforcement learning (DRL), as an innovative scheme, opens up new avenues for the computation offloading problems. DRL skillfully combines deep learning and reinforcement learning, using deep neural networks (DNN) to directly map from the environment state to the optimal action in order to maximize the long-term reward. This process is done automatically through continuous interaction with the environment. This integration not only alleviates the computational complexity of the problem but also endows the approach with the capability to autonomously learn from past experiences, bypassing the need for manually labeled training data, thus greatly facilitating the feasibility of its real-time online application. This is significant for efficiently generating computation offloading strategies in dynamic environments.

However, existing works have given limited consideration to the long-term network computation rate problem under long-term stability of the system. To this end, this paper proposes an intelligent computation offloading algorithm based on Lyapunov optimization and DRL for the end-edge task offloading problem under long-term stability constraints to maximize the long-term network computation rate. In the case of rapidly changing channel conditions and dynamic task arrivals, our algorithm can maximize the long-term network computation rate and guarantee long-term stability of the system.

The main contributions of this paper are summarized as follows.

• Firstly, we construct an edge computing-enhanced industrial wireless network, where each industrial terminal can choose an industrial base station for binary computation offloading. In this scenario, we formulate a network computation rate maximization problem while balancing constraints including offloading time, CPU frequency, energy consumption, transmit power, and data queue stability.
• Secondly, to maintain system stability, we define two dynamic queues, which are task queue and virtual energy queue. Based on these two dynamic queues, we minimize the upper bound of the drift-penalty function by using Lyapunov optimization, and transform the long-term MINLP problem into deterministic sub-problems. As the Lyapunov optimization problem is still non-convex, we further solve the problem with DRL.
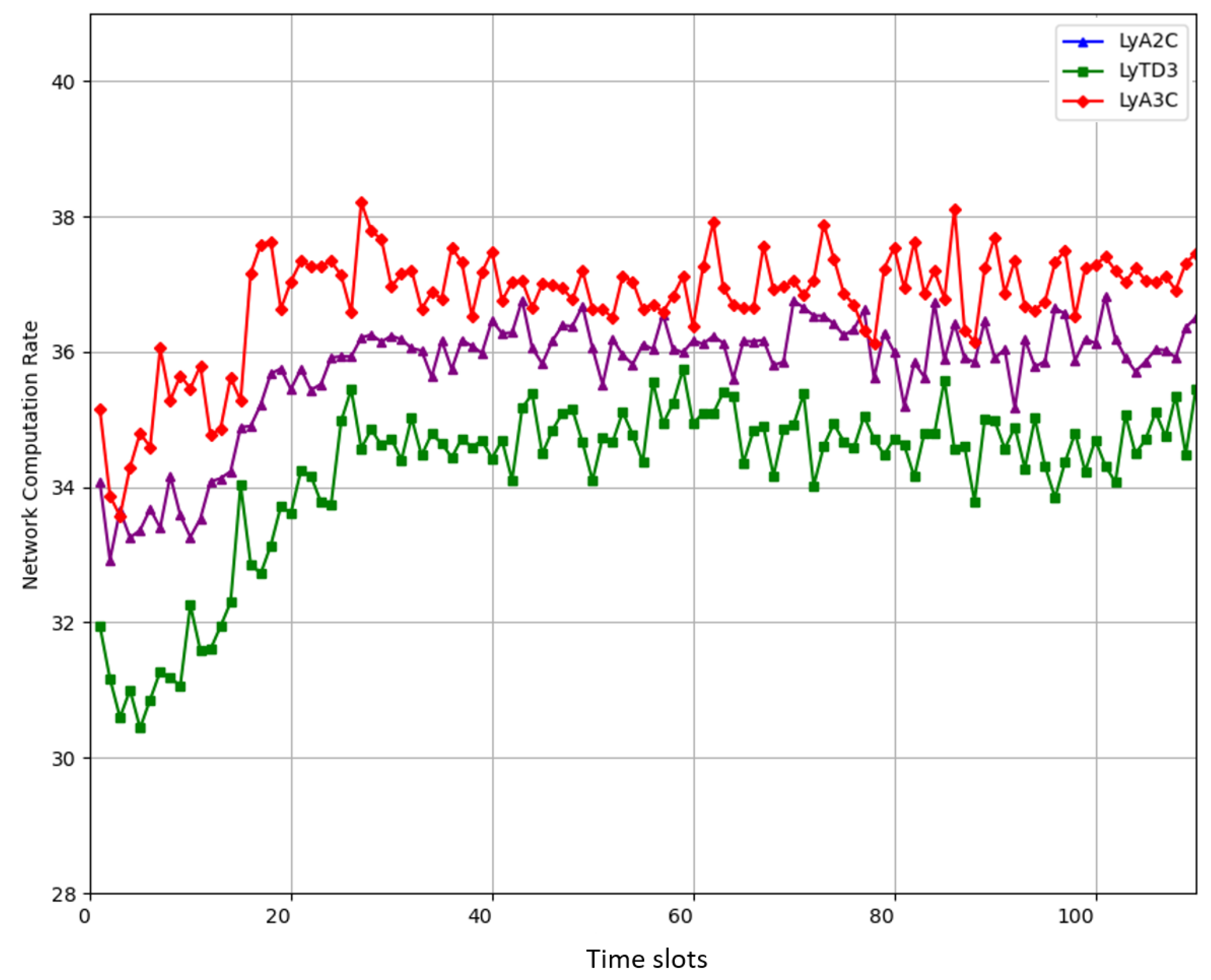
• Thirdly, we employ asynchronous advantage actor-critic (A3C) and propose Lyapunov-guided A3C algorithm named LyA3C for solution. Experiment results show that the LyA3C algorithm can converge stably and effectively improve the long-term network computation rate by comparing it with A2C-based and TD3-based algorithms.

The rest of this paper is organized as follows. Section 2 discusses related works. Section 3 describes the system model. Then, Section 4 presents the proposed LyA3C algorithm. Next, Section 5 evaluates LyA3C through extensive experiments. Finally, Section 6 concludes the whole work.

2. Related Work

For industrial tasks, different algorithms were proposed to balance the computation offloading and resource allocation in different scenarios.

Most existing works take delay or energy consumption minimization as the optimization objective. For example, Ref. [7] employed the double and dueling architectures on the basis of deep Q-network, and proposed the D3QN-based multi-priority computation offloading scheme to minimize overall task delay. Ref. [8] used Lyapunov optimization to decompose the multi-layer multi-timescale resource allocation problem into three sub-problems, and employed a deep actor-critic algorithm to minimize the total queuing delay of all devices. Ref. [9] proposed a multi-agent deep reinforcement learning (MADRL)-based scheduling algorithm, which actor-critic (AC) framework with estimation and target networks is designed for policy and value iterations to minimize delay. Similarly, Ref. [10] proposed multi-agent double actor-critic algorithm to reduce the task processing delay while improving the blockchain transaction throughput. Ref. [11] designed a joint communication and computation resource allocation mechanism based on Q-learning to minimize the total task delay cost. On the other hand, Ref. [12] incorporated a data fusion system in the architecture and designed a joint computation offloading and resource allocation scheme to minimize the overall queuing delay of the system. Ref. [13] designed an algorithm that decomposes the problem into task offloading and channel allocation sub-problems, and proposed a low-complexity heuristic algorithm to solve the sub-problem efficiently for total weighted task processing latency minimization. Ref. [14] developed a novel online SBS peer offloading framework by leveraging the Lyapunov technique, in order to maximize the long-term system performance while keeping the energy consumption of SBSs below individual long-term constraints. Ref. [15] aimed to optimize the average energy consumption by using non-orthogonal multiple access (NOMA) technique to improve the spectral efficiency and access, which is solved using successive convex approximation. Ref. [16] combined NOMA technique and frequency division multiple access and used long short-term memory network to optimize the objective. Ref. [17] used the air-ground integrated computing networks multi-agent deep deterministic policy gradient algorithm to minimize the average energy consumption by jointly optimizing the computation task allocation and wireless resource allocation.

Furthermore, there are also many works that combined time delay and energy consumption as optimization objectives. For example, Ref. [18] added a greedy algorithm to multi-intelligence depth determination of policy gradients to minimize the weighted sum of delay and energy consumption. Ref. [19] established a dual queue model containing data and computation queues, used the proximal policy optimization algorithm to minimize the weighted sum of average time delay and system energy consumption. Ref. [20] proposed an online joint offloading and resource allocation framework under the long-term MEC energy constraint, aimed at guaranteeing the users’ QoE. Ref. [21] aimed to minimize the task expected cost, which includes the task execution time delay and energy consumption, and applied the time division multiple access technique to optimize the objective function.

In addition, there are also some works that used other variables as the optimization objectives. For example, Ref. [22] considered the computation rate and energy consumption in computation offloading, proposed a deep deterministic policy gradient-based multiple continuous variable decision model to make the optimal offloading decision in edge computing. Ref. [23] proposed a computation offloading algorithm based on deep Q-Learing and used asynchronous federated deep Q-Learing to offload task. Ref. [24] proposed a multi-agent soft-actor-critic-discrete for task offloading and resurce allocation to maximize throughput while minimizing power consumption on the remote side. Ref. [25] proposed a low-complexity online computation offloading and trajectory scheduling algorithm to minimize the system energy efficiency by using Lyapunov optimization methods, where the system energy efficiency is defined as the ratio of the system’s total long-term energy consumption. Ref. [26] took the same variables as the optimization objective and used convex decomposition methods.

3. System Model

3.1. Network Model

In this paper, we propose an end-edge industrial wireless network system with edge computation capability, which consists of an edge layer and an end layer. As depicted in Figure 1, the industrial wireless network is composed of M industrial base stations and N industrial terminals to support industrial production and manufacturing in factories. We define $\mathcal{M}=\{1,2,\dots ,M\}$ as the set of M industrial base stations and $\mathcal{N}=\{1,2,\dots ,N\}$ as the set of N industrial terminals.

Figure 1. System model.

In this scenario, the industrial base station is equipped with an edge computing server, which is designed to supply computation resources for multiple industrial terminals. It also facilitates the scheduling of industrial terminals within its service area. The end layer comprises numerous industrial terminals with sensing, computing, communication and control capabilities, each of which generates an indivisible task that necessitates processing. Initially, each industrial terminal endeavors to process the task data using its own resources. However, when the task’s computation requirements, in terms of cycles, are substantial, the industrial terminal may find itself unable to meet the designated deadline due to resource limitations. In such case, the industrial terminal must offload the task to a proximate industrial base station to ensure timely completion.

In t-th time slot, the channel gain between m-th industrial base station and n-th industrial terminal is denoted as $h_{n,m}$, where $h_{n,m}$ remains constant during the time slot, but it varies independently from time slot to time slot.

3.2. Task Model

For n-th industrial terminal, its computation task is denoted as $D_n$. The data arriving at the data queue of n-th industrial terminal is denoted as $A_n$ and it is assumed that $\mathbb{E}\left[{\left(A_n\right)}^2\right]={\eta }_n<\infty$, $n=1,\dots ,N$.

When $d_{n,m}=1$, n-th industrial terminal offloads all task $D_n$ to m-th industrial base station. When $d_{n,m}=0$, n-th industrial terminal does not offload any task to m-th industrial base station. According to the execution location of the computation task and the size of the offloading data, the offloading decision is binary with two cases: end computing and edge computing.

Correspondingly, each industrial terminal has a task buffer, the queue length of the buffer in t-th time slot is denoted as $Q_n\left(t\right)$. Thus, the queue length can be updated as

$$Q_n(t+1)=max\{Q_n\left(t\right)-D_n,0\}+A_n,$$

(1)

3.3. End Computing Model

When n-th industrial terminal processes data locally, the local CPU frequency is $f_n$ is bounded by an upper limit value $f_n^{max}$, namely $f_n\le f_n^{max}$. Thus, the computation size of the offloaded task in t-th time slot is calculated as

$$D_n^{end}=f_n{\tau }_{n}T/\varphi ,$$

(2)

where ${\tau }_n\in [0,1]$ is the computation offloading time ratio and T is the length of a frame. Obviously, ${\tau }_{n}T$ is denoted as the amount of time allocated to the industrial terminal for computation offloading, and there should be ${\sum }_{n=1}^N{\tau }_n\le 1$.

Furthermore, the energy consumption in t-th time slot is calculated as

$$E_n^{end}=\kappa {\left(f_n\right)}^3{\tau }_{n}T,\forall d_{n,m}=0,$$

(3)

where $\varphi >0$ represents the number of computation cycles required to process one bit of data, $\kappa >0$ represents the computation energy efficiency parameter.

3.4. Edge Computing Model

When n-th industrial terminal decides to offload data on the end layer, we define transmit power as $P_n$ with an upper limit $P_n^{max}$, namely $P_n\le P_n^{max}$. Note that n-th industrial terminal evaluates the computation resources of each candidate industrial base station, and only chooses one of the multiple industrial base stations for computation offloading at one time.

The energy consumption for computation offloading is calculated as $e_n=P_n{\tau }_{n}T$, where $P_n$ is the transmit power. At this time, we neglect the delay on edge computing and result downloading. Thus, according to Shannon’s theorem, the computation size of the offloaded task on the end layer is given by

$$\begin{array}{c}{D}_{n,m}^{edge}=W{log}_2\left(1+{\displaystyle \frac{P_n{h}_{n,m}}{N_0}}\right){\tau }_{n}T\hfill \\ =W{log}_2\left(1+{\displaystyle \frac{e_n{h}_{n,m}}{{\tau }_{n}T{N}_0}}\right){\tau }_{n}T,\forall d_{n,m}=1,\hfill \end{array}$$

(4)

where W is bandwidth, $h_{n,m}$ is the channel gain between m-th industrial base station and n-th industrial terminal, and $N_0$ denotes the noise power.

In this way, the total computation task by end computing or edge computing is calculated as $D_{n,m}=(1-d_{n,m})D_n^{end}+d_{n,m}{D}_{n,m}^{edge}$, namely

$$D_{n,m}={\displaystyle \frac{(1-d_{n,m})f_n{\tau }_{n}T}{\varphi }}+d_{n,m}W{log}_2\left(1+{\displaystyle \frac{e_n{h}_{n,m}}{{\tau }_n{N}_0}}\right){\tau }_{n}T$$

(5)

Correspondingly, the network computation rate given by $z_{n,m}=D_{n,m}/T$ is calculated as

$$z_{n,m}={\displaystyle \frac{(1-d_{n,m})f_n{\tau }_n}{\varphi }}+d_{n,m}W{log}_2\left(1+{\displaystyle \frac{e_n{h}_{n,m}}{{\tau }_{n}T{N}_0}}\right){\tau }_n,$$

(6)

As the industrial base stations are powered by constant energy, we ignore the computing energy consumption and only consider the offloading energy consumption. Thus, the energy consumption for edge computing is calculated as $E_n^{edge}=e_n$. Furthermore, the total energy consumption is calculated as $E_{n,m}=(1-d_{n,m})E_n^{end}+d_{n,m}{E}_n^{edge}$, namely

$$e_{n,m}=(1-d_{n,m})\kappa {(f_n)}^3{\tau }_{n}T+d_{n,m}{e}_n,$$

(7)

where $\kappa$ denotes the computing energy efficiency.

4. End-Edge Computation Offloading Based on Lyapunov-Guided DRL

In this section, we first explicitly formulate the network computation rate maximization problem, then decouple the problem by Lyapunov optimization and finally propose the intelligent computation offloading algorithm based on Lyapunov-guided DRL.

4.1. Problem Formulation

In order to achieve end-edge computation offloading for complex industrial tasks, we formulate the network computation rate maximization problem, assuming that each industrial terminal generates only one indivisible real-time task $S_n$. The set of tasks is represented as $S=\{S_1,S_2,\dots ,S_N\}$, where each task is denoted as $S_n=\{d,\tau ,f,e\}$. In detail, $d_m=\{d_{n,1},d_{n,2},\dots ,d_{n,M}\}$, $\tau =\{{\tau }_1,{\tau }_2,\dots ,{\tau }_N\}$, $f=\{f_1,f_2,\dots ,f_N\}$, $e=\{e_1,e_2,\dots ,e_N\}$.

Then, we formulate the network computation rate maximization problem $P_1$ as

$$\begin{array}{c}{\displaystyle \underset{d,\tau ,f,e}{max}}{\displaystyle \underset{K\to \infty }{lim}}{\displaystyle \frac{1}{K}}{\displaystyle \sum _{t=1}^K}{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{m=1}^M}{\beta }_n{z}_{n,m}\hfill \\ \mathrm{s}.\mathrm{t}.C_1:{\displaystyle \sum _{n=1}^N}{\tau }_n\le 1,\hfill \\ C_2:d_{n,m}\in \{0,1\},\hfill \\ C_3:f_n\le f_n^{max},\forall n,\hfill \\ C_4:P_n\le P_n^{max},\forall n,\hfill \\ C_5:e_n\le P_n^{max}{\tau }_n,\forall n,\hfill \\ C_6:{\displaystyle \sum _{m=1}^M}\left({\displaystyle \frac{(1-d_{n,m})f_n{\tau }_{n}T}{\varphi }}+d_{n,m}W{log}_2\left(1+{\displaystyle \frac{e_n{h}_{n,m}}{{\tau }_n{N}_0}}\right){\tau }_{n}T\right)\le Q_n\left(t\right),\forall n,\hfill \\ C_7:{\displaystyle \underset{K\to \infty }{lim}}{\displaystyle \frac{1}{K}}{\displaystyle \sum _{t=1}^K}\mathbb{E}\left[Q_n\left(t\right)\right]<\infty ,\forall n,\hfill \\ C_8:{\displaystyle \underset{K\to \infty }{lim}}{\displaystyle \frac{1}{K}}{\displaystyle \sum _{t=1}^K}\mathbb{E}[(1-d_{n,m})\kappa {\left(f_n\right)}^3{\tau }_n+d_{n,m}{e}_n]<{\xi }_n,\forall n,\hfill \end{array}$$

(8)

where ${\beta }_n$ is the weight for n-th industrial terminal, ${\xi }_n$ is power threshold. $C_1$ is the computation offloading time ratio constraint, which means the ratio sum of computation offloading time should not exceed one. $C_2$ is the binary computation offloading decision constraint. $C_3$ is local CPU frequency constraint, which means there is a maximum value $f_n^{max}$ for the local CPU frequency. $C_4$ is the transmit power constraint, which means there is a maximum value $P_n^{max}$ for the transmit power. $C_5$ is the energy consumption constraint used for data offloading, which means there is a maximum value $P_n^{max}{\tau }_n$ for the energy consumption. $C_6$ is the data causality constraint. $C_7$ is the data queue stability constraint, which means time queue is strongly stable if the average queue length is limited. $C_8$ is the average energy consumption constraint, which means there is a maximum value ${\xi }_n$ for the average energy consumption.

4.2. Problem Transformation by Lyapunov Optimization

As the problem $P_1$ is a MINLP problem, its direct solution process is complicated, the Lyapunov optimization theory is introduced to model the dynamic queue, and this strategy decomposes the MINLP problem into deterministic sub-problems through the construction of mathematical models under the premise of ensuring the stability of the system.

In order to satisfy the average power consumption constraint $C_8$ in $P_1$, we introduce N virtual energy queues ${\left\{Y_{n,m}\left(t\right)\right\}}_{N\times M}$ for industrial terminals. Let $Y_{n,m}\left(1\right)=0$, the queue length can be updated as

$$Y_{n,m}(t+1)=max(Y_{n,m}\left(t\right)+e_{n,m}-{\xi }_n,0),$$

(9)

When the virtual energy queue is stabilized, the average energy consumption satisfies $e_{n,m}\le {\xi }_n$.

After establishing dynamic queues, we define $F\left(t\right)=\left\{Q\right(t),Y(t\left)\right\}$ as the total queue backlog, then we employ quadratic Lyapunov function

$$L\left(F\left(t\right)\right)={\displaystyle \frac{1}{2}}{\displaystyle \sum _{n=1}^N}{Q}_n{\left(t\right)}^2+{\displaystyle \frac{1}{2}}{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{m=1}^M}{Y}_{n,m}{\left(t\right)}^2,$$

(10)

to represent the stability of the queues.

Correspondingly, the Lyapunov drift function of the total queue backlog is defined as

$$\mathrm{\Delta } L\left(F\left(t\right)\right)=\mathbb{E}\left[\right(L\left(F(t+1)\right)-L\left(F\left(t\right)\right)\left|F\left(t\right)\}\right.,$$

(11)

which demonstrates the improvement from t-th time slot to ($t+1$)-th time slot. That is to say, the Lyapunov drift can reflect the system dynamics between two continuous states. From the perspective of system stability, the smaller the Lyapunov drift, the more stable the system is.

However, the Lyapunov drift still depends on the system information of the next time slot. Thus, we further derive the Lyapunov drift.

According to [27], for nonnegative real numbers A, B, C, and D satisfying $A\le max\left(B-C,0\right)+D$, there should be $A^2\le B^2+C^2+D^2-2B\left(C-D\right)$, so we have

$$\begin{array}{cc}{Q}_n{\left(t+1\right)}^2\hfill & ={\left[\left[Q_n\left(t\right)-D_n\right]+A_n\right]}^2\hfill \\ & \le Q_n{\left(t\right)}^2+{\left(D_n\right)}^2+{\left(A_n\right)}^2+2Q_n\left(t\right)\left(A_n-D_n\right),\hfill \end{array}$$

(12)

In this way, we can drive the upper bound of the Lyapunov drift function for data queue as

$$\begin{array}{cc}\mathrm{\Delta }L\left(Q_n\left(t\right)\right)\hfill & =\mathbb{E}\left[{\displaystyle \frac{1}{2}}{\displaystyle \sum _{n=1}^N}{Q}_n{(t+1)}^2-{\displaystyle \frac{1}{2}}{\displaystyle \sum _{n=1}^N}{Q}_n{\left(t\right)}^2\left|Q_n\left(t\right)\right.\right]\hfill \\ & \le \mathbb{E}\left[{\displaystyle \sum _{n=1}^N}\left({\displaystyle \frac{1}{2}}\left({\left(D_n\right)}^2+{\left(A_n\right)}^2\right)+Q_n\left(t\right)\left(A_n-D_n\right)\right)\left|Q_n\left(t\right)\right.\right]\hfill \\ & =B_1+\mathbb{E}\left[{\displaystyle \sum _{n=1}^N}\left(Q_n\left(t\right)\left(A_n-D_n\right)\right)\left|Q_n\left(t\right)\right.\right],\hfill \end{array}$$

(13)

where $B_1={\displaystyle \sum _{n=1}^N}{\displaystyle \frac{{\left(D_n\right)}^2+{\left(A_n\right)}^2}{2}}$.

At the same time, we can have the upper bound of the Lyapunov drift function for virtual energy queue as

$$\mathrm{\Delta }L\left(Y_{n,m}\left(t\right)\right)\le B_2+\mathbb{E}\left[{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{m=1}^M}{Y}_{n,m}\left(t\right)\left(e_{n,m}-{\xi }_n\right)\left|Y_{n,m}\left(t\right)\right.\right],$$

(14)

where $B_2={\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{m=1}^M}{\displaystyle \frac{{\left(e_{n,m}\right)}^2+{\left({\xi }_n\right)}^2}{2}}$.

Through the above process, the upper bound of the Lyapunov drift function for total queue backlog is given by

$$\mathrm{\Delta }L\left(F\left(t\right)\right)\le B+{\displaystyle \sum _{n=1}^N}{Q}_n\left(t\right)\mathbb{E}\left[\left(A_n-D_n\right)\left|F\left(t\right)\right.\right]+{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{m=1}^M}{Y}_{n,m}\left(t\right)\mathbb{E}\left[\left(e_{n,m}-{\xi }_n\right)\left|F\left(t\right)\right.\right],$$

(15)

where $B=B_1+B_2$.

At the same time, it is obvious that the upper bound of the Lyapunov drift function is no longer decided by the system information of the next time slot. Then, the Lyapunov drift-plus-penalty approach is used to maximize the network computation rate while satisfying queue stability, that is to say minimizing the drift-plus-penalty expression within each time slot, we have

$$\mathrm{\Delta }\left(F\left(t\right)\right)\triangleq \mathrm{\Delta }L\left(F\left(t\right)\right)-V{\displaystyle \sum _{n=1}^N}\mathbb{E}\left[{\beta }_n{z}_{n,m}\left|F\left(t\right)\right.\right],$$

(16)

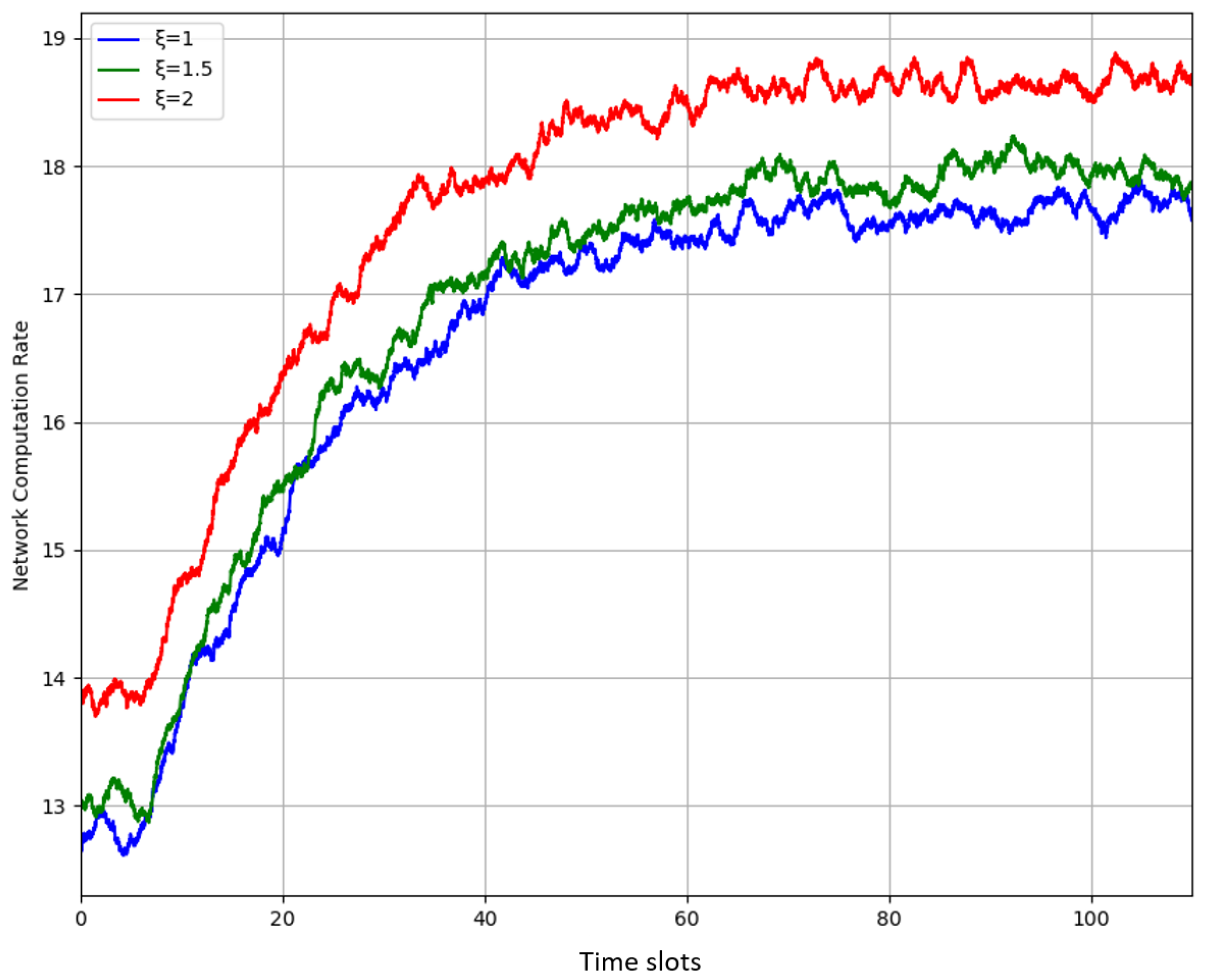
where $V>0$ is penalty weight that controls the significance of system data and virtual energy queue backlog.

Then the upper bound of the Lyapunov drift-plus-penalty is given by

$$\begin{array}{cc}\mathrm{\Delta }\left(F\left(t\right)\right)\hfill & =B+{\displaystyle \sum _{n=1}^N}{Q}_n\left(t\right)\mathbb{E}\left[\left(A_n-D_n\right)\left|F\left(t\right)\right.\right]\hfill \\ & +{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{m=1}^M}{Y}_{n,m}\left(t\right)\mathbb{E}\left[\left(e_{n,m}-{\xi }_n\right)\left|F\left(t\right)\right.\right]-V\mathbb{E}\left[{\beta }_n{z}_{n,m}\left|F\left(t\right)\right.\right],\hfill \end{array}$$

(17)

By removing the constant terms from observation at the beginning of t-th time slot, the algorithm decides the actions by maximizing the following

$${\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{m=1}^M}\left(\left(Q_n\left(t\right)+V{\beta }_n\right)z_{n,m}-Y_{n,m}\left(t\right)e_{n,m}\right),$$

(18)

Then the problem $P_1$ can be decoupled into deterministic sub-problems $P_2$, we formulate the problem $P_2$ as

$$\begin{array}{c}{\displaystyle \underset{d,\tau ,f,e}{max}}{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{m=1}^M}\left(\left(Q_n\left(t\right)+V{\beta }_n\right)z_{n,m}-Y_{n,m}\left(t\right)e_{n,m}\right)\hfill \\ \mathrm{s}.\mathrm{t}.C_1:{\displaystyle \sum _{n=1}^N}{\tau }_n\le 1,\hfill \\ C_2:d_{n,m}\in \{0,1\},\hfill \\ C_3:f_n\le f_n^{max},\forall n,\hfill \\ C_4:P_n\le P_n^{max},\forall n,\hfill \\ C_5:e_n\le P_n^{max}{\tau }_n,\forall n,\hfill \\ C_6:{\displaystyle \sum _{m=1}^M}\left({\displaystyle \frac{(1-d_{n,m})f_n{\tau }_{n}T}{\varphi }}+d_{n,m}W{log}_2\left(1+{\displaystyle \frac{e_n{h}_{n,m}}{{\tau }_n{N}_0}}\right){\tau }_{n}T\right)\le Q_n\left(t\right),\forall n,\hfill \end{array}$$

(19)

At this time, $P_1$ has been decoupled into deterministic sub-problems within each time slot, the next step is to apply DRL algorithm to solve $P_2$ in each time slot.

4.3. MDP Modeling

However, the transformed problem $P_2$ is still difficult to solve as the variables are still coupled with each other. Thus, we first transform it into a MDP and then employ DRL to approximate the optimal solution.

For MDP modeling, there are state space, action space and reward space for DRL.

• State space: In t-th time slot, the state $s\left(t\right)$ consisting of the channel gain and the system queue is defined as

  $$s\left(t\right)=\{\mathbf{h}\left(t\right),\mathbf{Q}\left(t\right),\mathbf{Y}\left(t\right)\},$$

  (20)

  where $\mathbf{h}\left(t\right)={\left\{h_{n,m}\left(t\right)\right\}}_{N\times M}$ is the channel gain among industrial base stations and industrial terminals, $\mathbf{Q}\left(t\right)={\left\{Q_n\left(t\right)\right\}}_N$ is the set of data queue length, and $\mathbf{Y}\left(t\right)={\left\{Y_{n,m}\left(t\right)\right\}}_{N\times M}$ is the set of virtual energy queue length.
• Action space: In t-th time slot, the action $a\left(t\right)$ consists of an optimal offloading action, the computation offloading time ratio, the local CPU frequency and the total energy consumption, defined as

  $$a\left(t\right)=\left\{\mathbf{d}\left(t\right),\tau \left(t\right),\mathbf{f}\left(t\right),\mathbf{e}\left(t\right)\right\},$$

  (21)

  where $\mathbf{d}\left(t\right)={\left\{d_{n,m}\left(t\right)\right\}}_{N\times M}$ is the set of optimal offloading action, and $\tau \left(t\right)={\left\{{\tau }_n\left(t\right)\right\}}_N$ is the set of computation offloading time ratio, $\mathbf{f}\left(t\right)={\left\{f_n\left(t\right)\right\}}_N$ is the set of local CPU frequency, $\mathbf{e}\left(t\right)={\left\{e_{n,m}\left(t\right)\right\}}_{N\times M}$ is the set of energy consumption.
• Reward space: The reward $r\left(t\right)$ denotes the action reward generated when taking action $a\left(t\right)$ in the current state $s\left(t\right)$. According to the objective function, the reward $r_n\left(t\right)$ for n-th industrial terminal and m-th industrial base station in t-th time slot is defined as

  $$r_{n,m}\left(t\right)=(Q_n\left(t\right)+V{\beta }_n)z_{n,m}-Y_{n,m}\left(t\right)e_{n,m}\left(t\right).$$

  (22)
  Based on this, the sum of incentives received by all industrial terminals is calculated as

  $$r\left(t\right)={\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{m=1}^M}{r}_{n,m}\left(t\right),$$

  (23)
  Obviously, the larger the reward, the larger the network computation rate of the industrial terminal. Furthermore, the cumulative reward is defined as

  $$R\left(t\right)={\displaystyle \sum _{t=0}^K}{\gamma }^{t}r\left(t\right),$$

  (24)

  where $\gamma \in [0,1]$ is the discount factor indicating how the previous reward impacts the current reward.

Through the above process, we model the transformed problem into an MDP. As such, we can maximize the network computation rate by maximizing the long-term accumulative reward while satisfying all constraints, during which an effective policy can be obtained.

4.4. Lyapunov-Guided A3C Algorithm

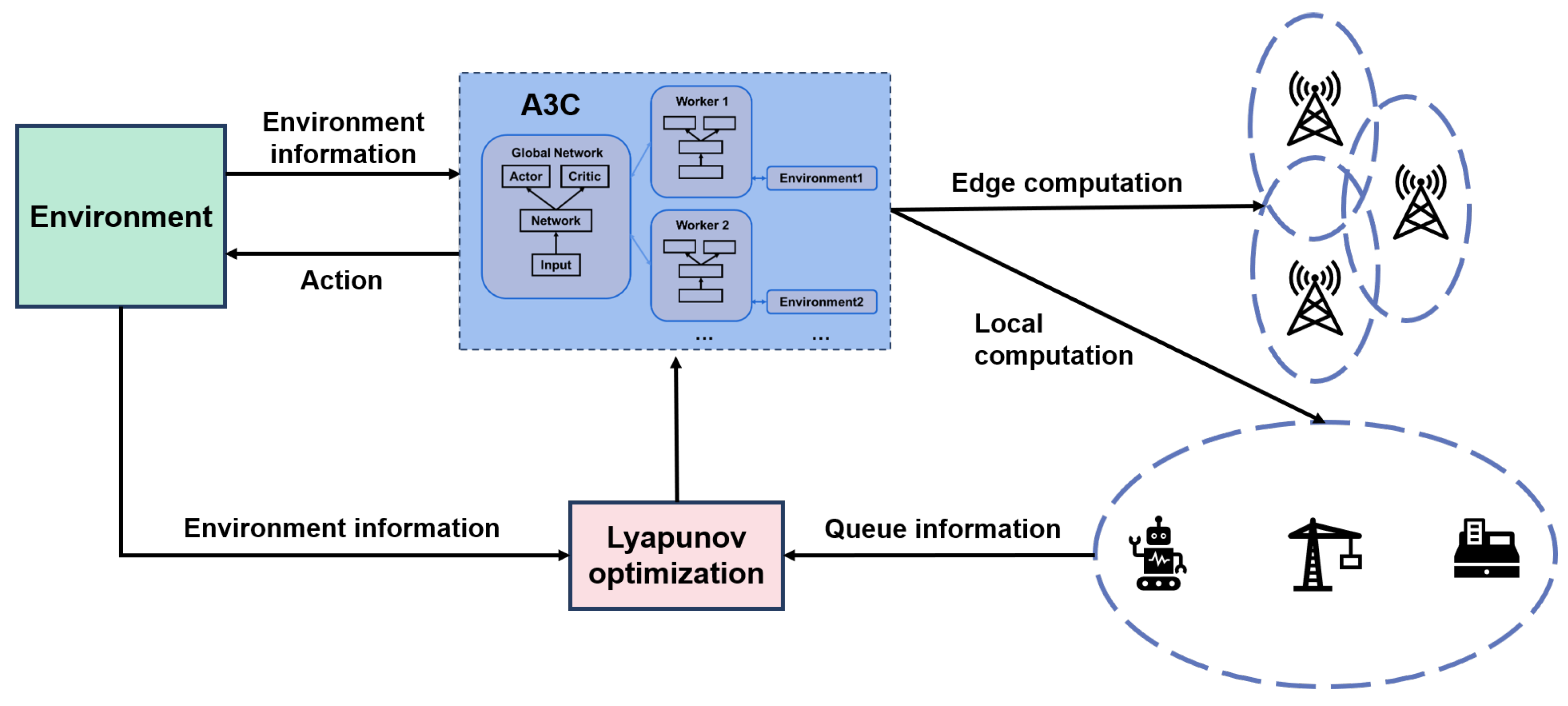
With the formulated MDP model, we further propose the LyA3C algorithm based on the A3C algorithm. The structure of our proposed algorithm is depicted in Figure 2. There are a global network and several worker agents, where the globe network and the worker agents are set in the same actor-critic structure.

Figure 2. Algorithm structure.

Taking one of the worker agents as an example, it includes two modules: the actor module and the critic module. The two modules accept the state and output the state value as well as the corresponding policy. Specifically, $a\left(t\right)=\pi \left(s\left(t\right)\left|\theta \right.\right)$ denotes the policy learned from the current state, where $\pi \left(s\left(t\right)\left|\theta \right.\right)$ is the explored offloading policy. The network parameter of actor network is denoted as $\theta$. The gradient of the expected cumulative discounted reward is

$$\nabla \theta {\mathbb{E}}_{\pi }\left[{\displaystyle \sum _{t=0}^{\infty }}{\gamma }^{t}r\left(t\right)\right]={\mathbb{E}}_{\pi }\left[{\nabla }_{\theta }log\pi \left(s\left(t\right)\left|\theta \right.\right)A\left(s,a\right)\right],$$

(25)

where $A\left(s,a\right)$ is the advantage function. $A\left(s,a\right)$ is used to measure the dominance of the state $s\left(t\right)$ when the agent selects action $a\left(t\right)$ and executes the policy $\pi$ compared to executing an arbitrary action. According to the current strategy, the value of $A\left(s,a\right)$ is obtained from the value $V\left(s\left(t\right)\right)$ and is calculated as

$$A\left(s,a\right)=r\left(t\right)+\gamma V\left(s\left(t+1\right)\right)-V\left(s\left(t\right)\right),$$

(26)

where $\gamma$ is discount factor.

The parameter $\theta$ is updated based on

$$\theta =\theta +\alpha {\displaystyle \sum _t}{\nabla }_{\theta }log\pi \left(s\left(t\right)\left|\theta \right.\right)A\left(s,a\right),$$

(27)

where $\alpha$ is the learning rate of the actor network.

In contrast, the parameter of the critic network $\phi$ is updated as

$$\phi =\phi +\chi {{\displaystyle \sum _t}{\nabla }_{\theta }\left(r\left(t\right)+\gamma V\left(s\left(t+1\right)\right)-V\left(s\left(t\right)\right)\right)}^2,$$

(28)

where $\chi$ is the learning rate of the critic network.

Through the above process, each worker agent will send the accumulated updates to the global network, then the global network asynchronously updates $\theta$ and $\phi$.

To sum up, the overall flowchart of the LyA3C algorithm is shown in Figure 3.

Figure 3. Flowchart of the LyA3C algorithm.

The algorithm is summarized as Algorithm 1.

Algorithm 1 The LyA3C Algorithm

1: Initialize number of industrial terminals N; number of industrial base stations M; Lyapunov drift-plus-penalty parameter V; 2: Initialize the A3C network with actor $\pi \left(s\right)$ and critic $V\left(s\right)$; 3: repeat 4: Collect a set of trajectories {$s\left(t\right)$, $a\left(t\right)$, $r\left(t\right)$, $s\left(t+1\right)$}; 5: for each time slot $t=1$ to K do 6:     Actor step sample action $a\left(t\right)\sim \pi \left(s\left(t\right)\right)$; 7:     Critic step compute value estimate $V\left(s\left(t\right)\right)$; 8:     Compute advantage function using Equation (25); 9:     Each worker agent update $\theta$ and $\phi$ using Equations (27) and (28); 10:   Global network update $\theta$ and $\phi$; 11: end for

4.5. Complexity Analysis

The complexity analysis of the proposed LyA3C algorithm is based on the structure of the neural network used for the critic network and actor network. The critic network contains the input layer $K_i$, the hidden layer $K_h$ and the output layer $K_o$. The complexity of the critic network is calculated as $\mathcal{O}(K_i{K}_h+K_i{K}_o)$. Similarly, the actor network also contains the input layer $K_i$, the hidden layer $K_h$, and the output layer $K_o$. The complexity of the actor network is calculated as $\mathcal{O}(K_i{K}_h+K_i)$. For each agent, the overall complexity is the sum of the complexity of the critic network and the actor network: $\mathcal{O}\left(2K_i{K}_h+K_i{K}_o+K_i\right)=\mathcal{O}\left(K_i\left(2K_h+K_o+1\right)\right)$.

5. Experimental Results and Analysis

5.1. Experimental Setup

In this section, we evaluate the performance of the proposed algorithm. All experiments are evaluated on a platform equipped with Intel Core i7-11700 2.5GHz CPU and Pytorch. During the experiments, we choose two benchmark DRL algorithms for comparison, including A2C-based and TD3-based algorithms.

During experiments, it is assumed that the channel gain $h_{n,m}$ follows the path loss model as $\overline{h_{n,m}}=A_d{\left({\displaystyle \frac{3\times {10}^8}{4\pi f_c{d}_{n,m}}}\right)}^{d_e}$, where $d_{n,m}$ denotes the distance between n-th industrial terminal and m-th industrial base station and is measured in meters. The noise power is denoted by $N_0=W{\upsilon }_0$, indicates that the task arrivals of all industrial terminals obey an exponential distribution with equal average rates $\mathbb{E}\left[{\left(A_n\right)}^2\right]={\eta }_n<\infty ,n=1,\dots ,N$. The number of industrial base stations is set to 3 and the number of industrial terminals is set to 10, and all industrial terminals are identical industrial terminals with the specific parameter values shown in Table 1.

Table 1. Simulation Parameters.

Parameter	Symbols	Value
Antenna gain	$A_d$	3
Carrier frequency	$f_c$	915 MHz
Path loss exponent	$d_e$	3
Noise power spectral density	${\upsilon }_0$	−174 dBm/Hz
Bandwidth	W	2 MHz
Maximum local CPU	$f_n^{max}$	0.3 GHz
Maximum Transmit Power	$P_n^{max}$	0.1 watt
Communication overhead	${\upsilon }_u$	1.1
Computation energy efficiency	$\kappa$	${10}^{-26}$
Computation cycles per one bit	$\varphi$	100
Memory capacity	q	1024
Energy consumption threshold	${\xi }_n$	0.04 watt
Lyapunov control parameter	V	20
Data arrival rate	${\lambda }_n$	2.7 Mbps

5.2. Experiments and Analysis

Figure 4 presents a comparative analysis of the network computation rates across various algorithms under identical model conditions. The network computation rates of all algorithms oscillate within a defined range, signifying that each algorithm achieves a relatively stable rate over time. Specifically, TD3-based and A2C-based algorithms record lower long-term network computation rates. Although a temporary intersection exists between the LyA3C and A2C-based algorithms at a specific time, the LyA3C algorithm ultimately outperforms the rest by attaining the highest optimal network computation rate. This superiority is attributed to the LyA3C algorithm’s deployment of multiple parallel agents, which enhances the network computation rate during operation. As time progresses, the fluctuation range diminishes, steadily converging toward the optimal network computation rate.

Figure 4. Network computation rate for different algorithms.

In Figure 5, Figure 6 and Figure 7, we evaluate the performance of the three algorithms in terms of network computation rate, average data queue length and average energy consumption under different data arrival rates. Note that the experimental values are the average of multiple experiments in which we fixed the other parameter settings and gradually increased the data arrival rate from 0 to 5 Mbps. Note that LyA3C performs the best in all three experiments.

Figure 5. Relationship between data arrival rate and network computation rate for different algorithms.

Figure 6. Relationship between data arrival rate and average data queue length for different algorithms.

Figure 7. Relationship between data arrival rate and average energy consumption for different algorithms.

From Figure 5, Obviously, as the data arrival rate ${\eta }_n$ increases, the network computation rate exhibits an upward trend. This is because when the data arrival rate is low, the queue is stable in the long term. At this point, the network computation rate is directly proportional to ${\eta }_n$. However, when the data arrival rate is very high, conflicts among resources increase, causing the network computation rate to stop increasing or even decrease.

Figure 6 shows that the average data queue length tends to rise with the increase in ${\eta }_n$. This is because a large amount of data is constantly entering the queue. Although an increase in the network computation rate can accelerate the data leaving the queue, the amount of data leaving the queue is still less than the amount of data arriving. Consequently, the average data queue length grows until it reaches maximum capacity.

In Figure 7, the average energy consumption is positively correlated with the data arrival rate. Hence the average energy consumption gradually increases as ${\eta }_n$ grows, leveling off when ${\eta }_n$ is relatively large.

Figure 8 presents the trend of network computation rates over time under various energy consumption threshold constraints ${\xi }_n$ for all industrial terminals. It is observable that the larger the value of ${\xi }_n$, the higher the network computation rate. The primary reason is that as ${\xi }_n$ increases, the available energy for computation also increases, which in turn enhances the network computation rate, and ensures the long-term stability of the system. Specifically, when ${\xi }_n=2$, the network computation rate gradually increases with time and ultimately converges to a higher value. When ${\xi }_n=1.5$ and ${\xi }_n=1$, although the network computation rate also increases, it eventually falls short of the value observed when ${\xi }_n=2$.

Figure 8. Effect of different energy consumption thresholds on network computation rate.

Figure 9 evaluates the changes in task queue length of the three algorithms with different energy thresholds. The figure shows that the task queue of the three algorithms decreases with the increase of the energy consumption threshold. This is because when the energy consumption threshold increases, the energy available to the industrial terminal for computation offloading increases, more tasks are processed on time, and the length of the task queue decreases. When the energy consumption threshold reaches a specific value, the industrial terminal is no longer affected by energy consumption, tasks can be freely scheduled, and the task queue length converges to a specific value. When the energy consumption threshold is small, the LyA3C algorithm is affected by the energy consumption threshold, and the length of the task queue is relatively long. As the energy consumption threshold increases, the number of tasks in the queue continues to decrease, reaching the optimum among the three algorithms, and eventually reaching stability.

Figure 9. Relationship between energy consumption thresholds and data queue length for different algorithms.

6. Conclusions

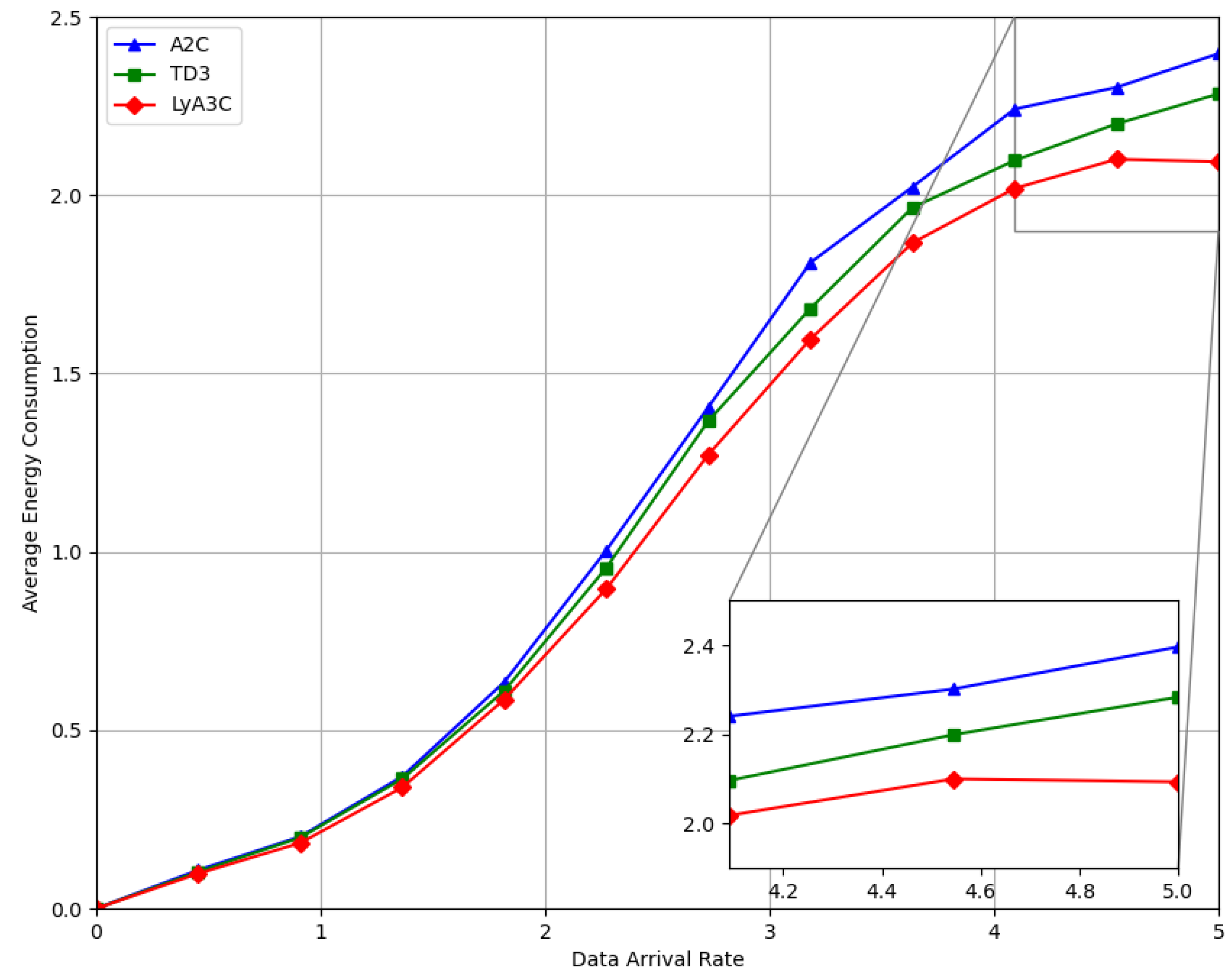
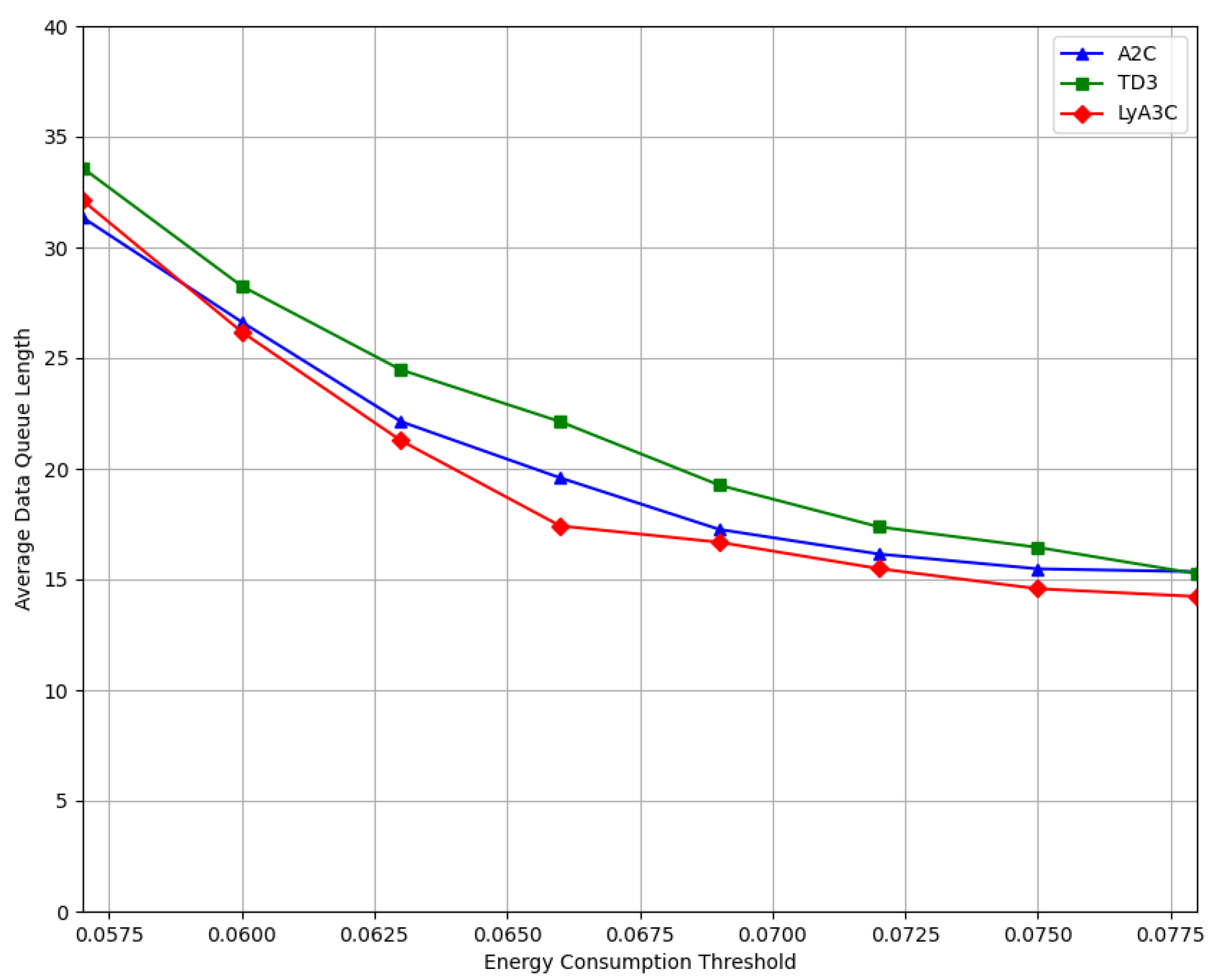
In this paper, we proposed an intelligent computation offloading algorithm based on Lyapunov optimization and DRL. With full consideration of the offloading time, data causality, local CPU frequency, energy consumption, transmit power, and data queue stability, the long-term network computation rate maximization problem was formulated. To solve this problem, we designed the data queue and virtual energy queue backlog, derived the upper bound of the Lyapunov drift based on the Lyapunov optimization theory, and decoupled the complex MINLP problem into deterministic sub-problems. Then, we reformulated the transformed problem into MDP, and approximated the optimal solution using the proposed LyA3C algorithm. Experimental results showed that compared with two benchmark algorithms, including A2C-based and TD3-based algorithms, the proposed LyA3C algorithm could converge stably and effectively improve the long-term network computation rate by 2.8% and 5.7% while satisfying various constraints.

In the future, in addition to the binary offloading adopted in the paper, we will consider dividing the computation task into multiple independent sub-tasks for multi-destination computation offloading. Moreover, different from the fact that all industrial base stations are homogeneous providing the same computation resource, i.e., CPU, we will consider the case that, different industrial base stations provide different kinds of computation resources including CPU, GPU and NPU.