1. Introduction
Morchella (morel mushrooms) holds significant economic value, primarily due to its rich nutritional content, remarkable medicinal properties, and strong market demand. As a rare edible fungus, Morchella is widely used in high-end cuisine, health products, and pharmaceuticals. Its abundance of proteins, amino acids, vitamins, and minerals gives it a prominent position in the health food market. Moreover, advances in artificial cultivation techniques and the growing demand in international markets have created substantial economic benefits and promising commercial prospects for the Morchella industry. Known for its unique flavor and rich nutrients, Morchella is recognized globally as a rare edible fungus [
1]. With the advent and continuous innovation of exogenous nutrient bag technology [
2], the cultivation area of Morchella in China has rapidly expanded, making it one of the most popular cultivated fungi [
3,
4]. China has now become the world’s largest outdoor cultivation base for Morchella [
5]. Currently, Morchella sowing is mainly performed manually, highlighting the importance of developing intelligent machinery specifically designed for Morchella sowing to meet the growing demand.
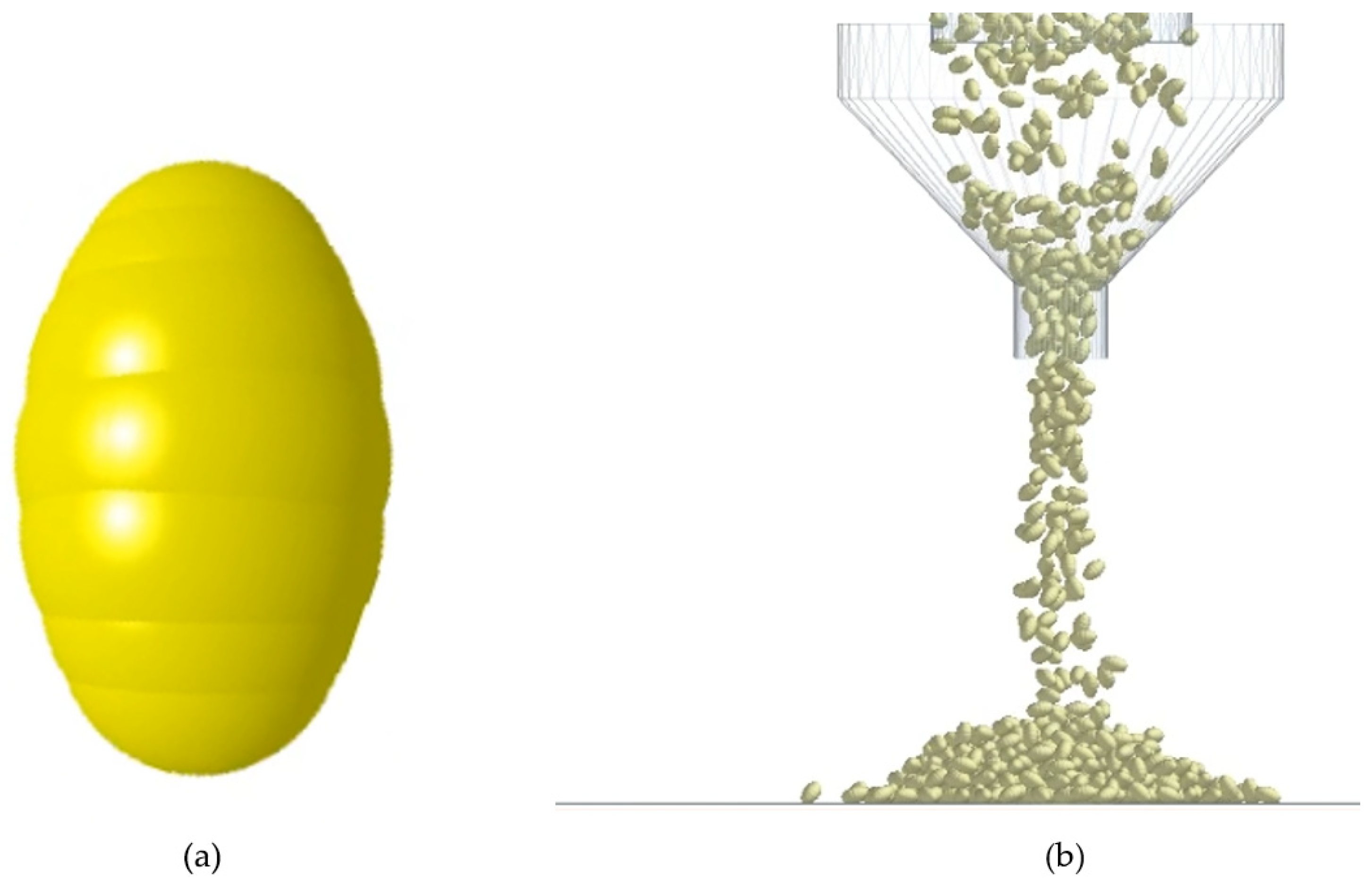
Morchella seeds, as a type of low-temperature fermentation fungus, exhibit cohesive particle behavior due to moisture and particle stickiness, forming agglomerated structures, which are characteristic of bulk materials. Currently, there is limited research on the contact parameters of cohesive particulate materials. With advancements in computer technology, the discrete element method (DEM) has been widely applied in agricultural equipment research [
6,
7]. DEM is a method for analyzing the contact interactions between particles and between particles and boundaries, as well as their different physical and mechanical properties [
8]. Since DEM simulation was first applied to material parameter calibration, it has been introduced by many scholars into various particle calibration models, providing a valuable reference for the design and optimization of seeding machinery [
9]. This approach effectively enhances production efficiency and reduces costs. In the production and processing of Morchella, accurately calibrating the DEM parameters of Morchella seeds is of great significance. Through DEM simulation, characteristics such as seed flowability and piling behavior can be optimized, which helps improve the efficiency of equipment design, streamline production processes, and reduce experimental costs and time. Parameter calibration not only enhances simulation accuracy but also provides data support for automated production and planting systems, promoting the scale and modernization of the Morchella industry.
In countries such as the United States and France, many scholars have conducted calibration studies on DEM parameters for various agricultural materials. Adilet et al. [
10] and his team used a rotating drum apparatus to calibrate the particle-to-particle and particle-to-material interactions of wheat seeds, successfully measuring static and rolling friction coefficients, which were effectively applied in DEM simulations of wheat. However, this method has limitations when applied to the calibration of Morchella seeds. The morphology, softness, and adhesiveness of Morchella spores are significantly different from those of wheat seeds, making it difficult for the rotating drum to accurately capture their interactions. Additionally, Morchella cultivation requires strict control over environmental factors such as temperature and humidity, which the rotating drum cannot accommodate. Benjamin et al. [
11] and his team developed a near-infrared reflectance spectroscopy (NIRS) calibration method to estimate fiber content in rapeseed, revealing significant genetic differences across genotypes. While this NIRS-based calibration method succeeded in measuring fiber content, it may not be suitable for Morchella seed calibration. Firstly, the physical properties of Morchella seeds, including their shape, adhesiveness, and softness, differ greatly from rapeseed, making it challenging for NIRS to capture the complex interaction characteristics. Secondly, the dynamic environmental conditions required for Morchella growth cannot be adequately assessed by NIRS calibration, making it difficult to reflect its actual growth and interaction dynamics. Jan et al. [
12] and his team proposed the differential evolution (DE) algorithm, which improved the calibration accuracy of soil models. However, its application to Morchella seed calibration may be limited. The growth of Morchella involves complex biological traits and dynamic environmental conditions, while DE algorithms are better suited for optimizing continuous physical parameters and are less effective in handling multivariable biological systems and environmental fluctuations. On the other hand, Salavat Mudarisov et al. [
13] and his team’s Hertz–Mindlin with JKR model calibration method proved promising for Morchella seed calibration. This method accurately describes the adhesion and contact behavior between seeds and substrate, while optimizing substrate particle size to ensure aeration and drainage, better simulating the growth environment of Morchella.
Domestic scholars have proposed a “virtual calibration” method using the DEM to address the challenge of timely and accurate acquisition of contact parameters for small cohesive particles with high moisture content. Yu et al. and Jun et al. [
14,
15], among others, used DEM to study the interactions between key components of seeders and seeds, providing valuable insights for the calibration of Morchella seeds. Firstly, their research emphasized the mechanical properties during the contact process between mechanical components and seeds, offering a reference for modeling the movement and interaction behavior of Morchella seeds within the substrate. Secondly, the precise seed positioning and seeding control strategies in seeder design can help optimize the distribution and nutrient absorption of Morchella seeds in the substrate. By applying similar DEM techniques, it is possible to better simulate the complex interactions between Morchella seeds and the substrate. The JKR (Johnson–Kendall–Roberts) sphere adhesion model proposed by Wang et al., Yi et al. [
16,
17], and others has been widely applied in DEM simulations and has successfully completed material calibration experiments. This model, which accounts for the adhesive forces and contact behaviors between particles, is particularly suited for materials with high surface energy and adhesion properties. This method provides important insights for the calibration of Morchella seeds. Firstly, the JKR model can accurately describe the adhesive behavior between particles, which is similar to the adhesive interactions between Morchella seeds and the substrate during cultivation. Therefore, the application of this model can help precisely simulate the complex contact processes between Morchella seeds and the substrate. Secondly, the model allows for the study of the impact of particle surface energy on their mechanical behavior, which is crucial for optimizing the growth conditions of Morchella seeds in various substrates. By adjusting the contact parameters and surface characteristics between particles, the accuracy of Morchella seed calibration can be improved, enabling a more accurate simulation of its growth behavior in real environments. Liu et al. [
18], Wang et al. [
19], Zhao et al. [
20], Yuan et al. [
21], and Bai et al. [
22] conducted DEM parameter calibration studies on grains, soil, and organic fertilizers, providing references for the calibration of Morchella seeds. Their research methods can be used to measure the physical parameters of Morchella seeds and simulate their interactions with the substrate, particularly in terms of aeration and drainage, which are key for optimizing the growth environment of Morchella seeds. In Lin et al. and Luo et al. [
23,
24], the rolling friction coefficient of earthworm casting particles was studied at different moisture contents, indicating that moisture content has a significant impact on the rolling friction coefficient of particles. This has important implications for the calibration of Morchella seeds. Changes in moisture content may similarly affect the adhesiveness and flowability of Morchella seeds in the substrate, making it essential to consider the mechanical behavior and flow characteristics under different humidity conditions during the calibration process to study simulations that more accurately reflect the actual growth environment.
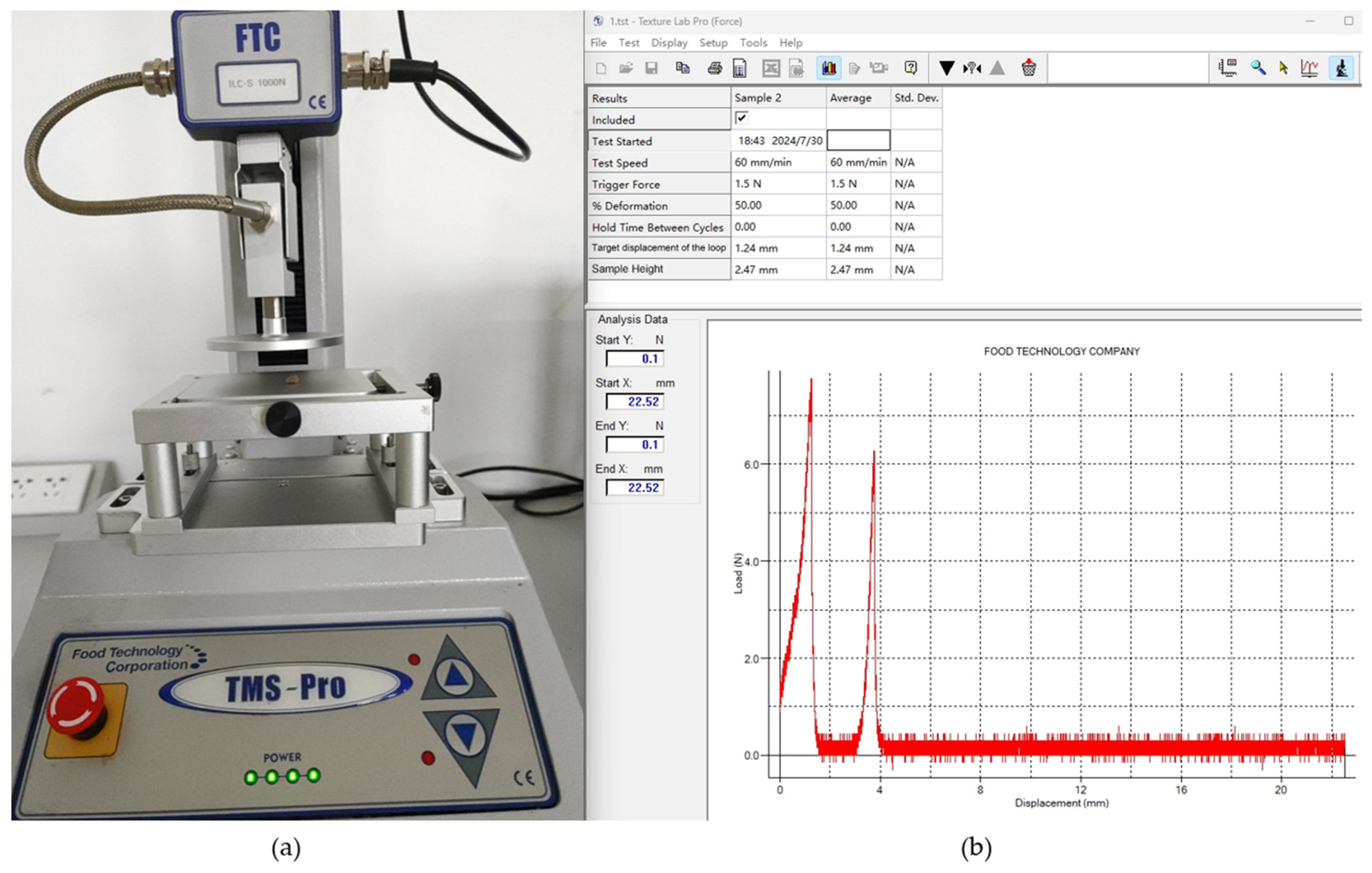
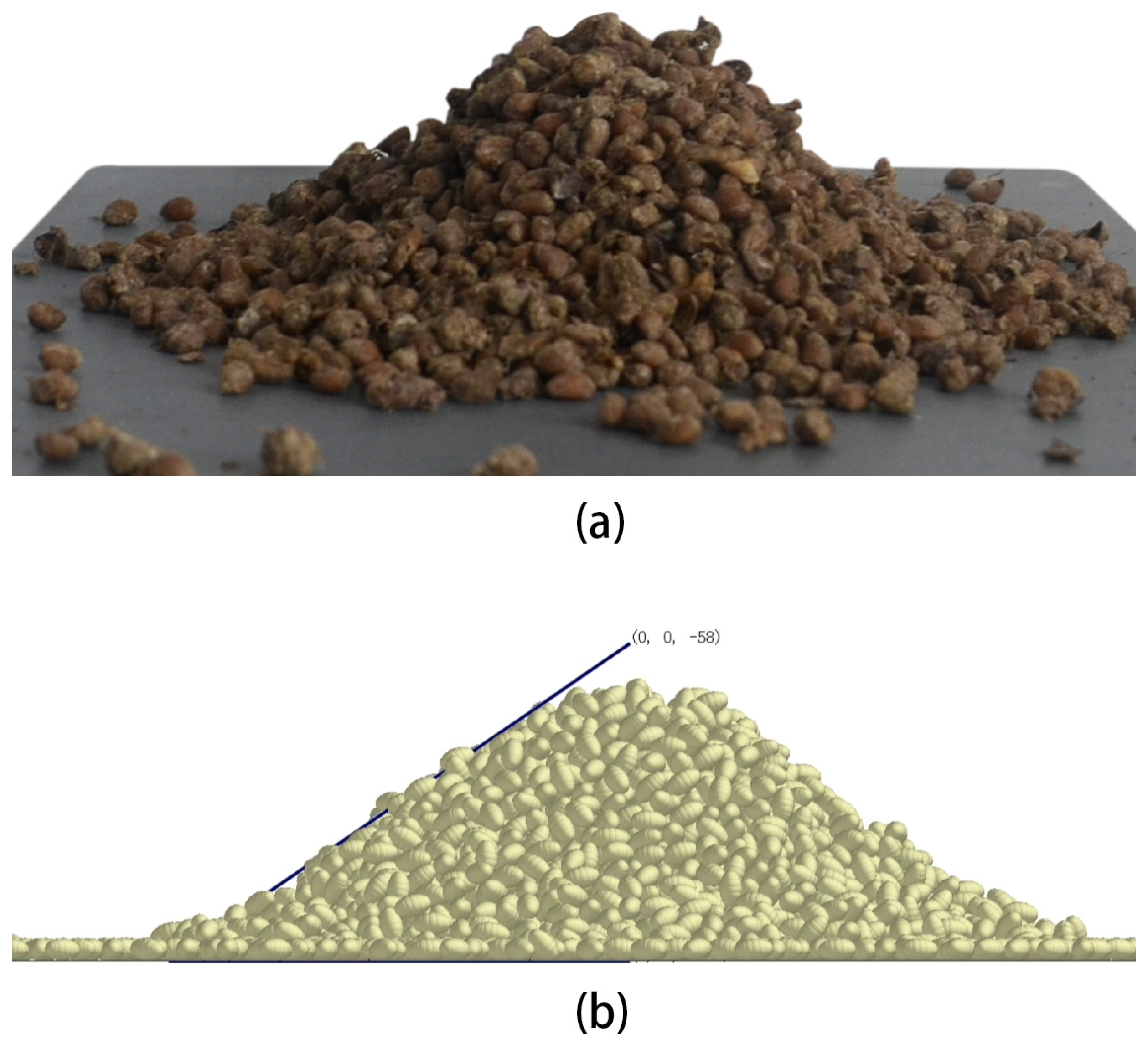
In summary, this study aims to calibrate the contact parameters of Morchella seeds as cohesive particulate materials under high moisture content. By measuring the repose angle of the seeds and optimizing the parameters using the DEM simulation, a regression model was established to describe the relationship between the contact parameters and the repose angle using experimental design methods. The optimal parameter combination was then obtained. Finally, by comparing the simulation results with the physical experimental values in order to verify the reliability of the calibration parameters, this study provides fundamental data support for the design and simulation optimization of key components in Morchella seeding machinery.