Computational Methodology for the Development of Wrinkled Tubes by Plastic Deformation
Abstract
:1. Introduction
2. State-of-the-Art: Wrinkled Tube in Metal Sheets by Forming
3. Materials and Methods
3.1. Mathematical Model
3.1.1. Pre-Processing
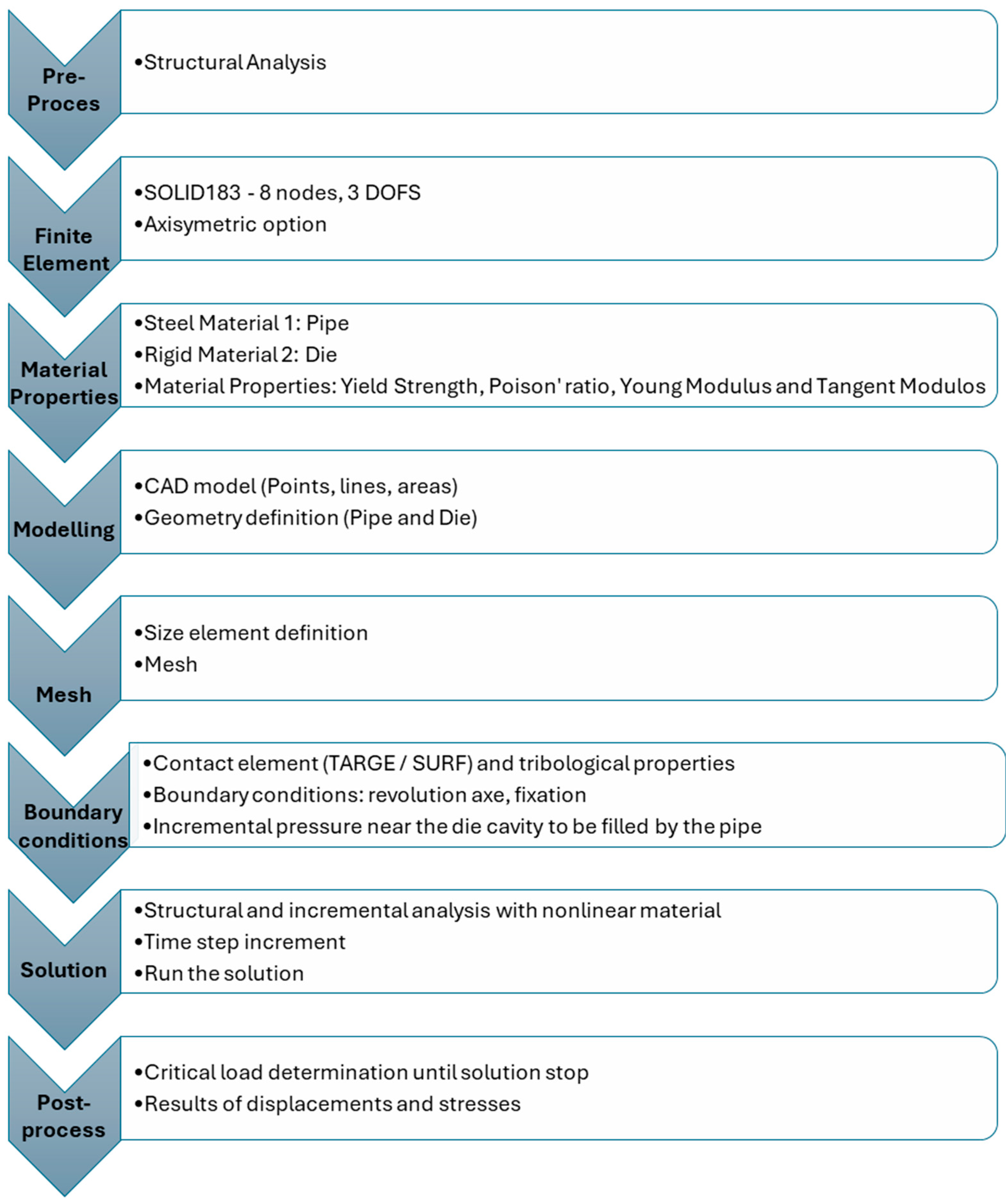
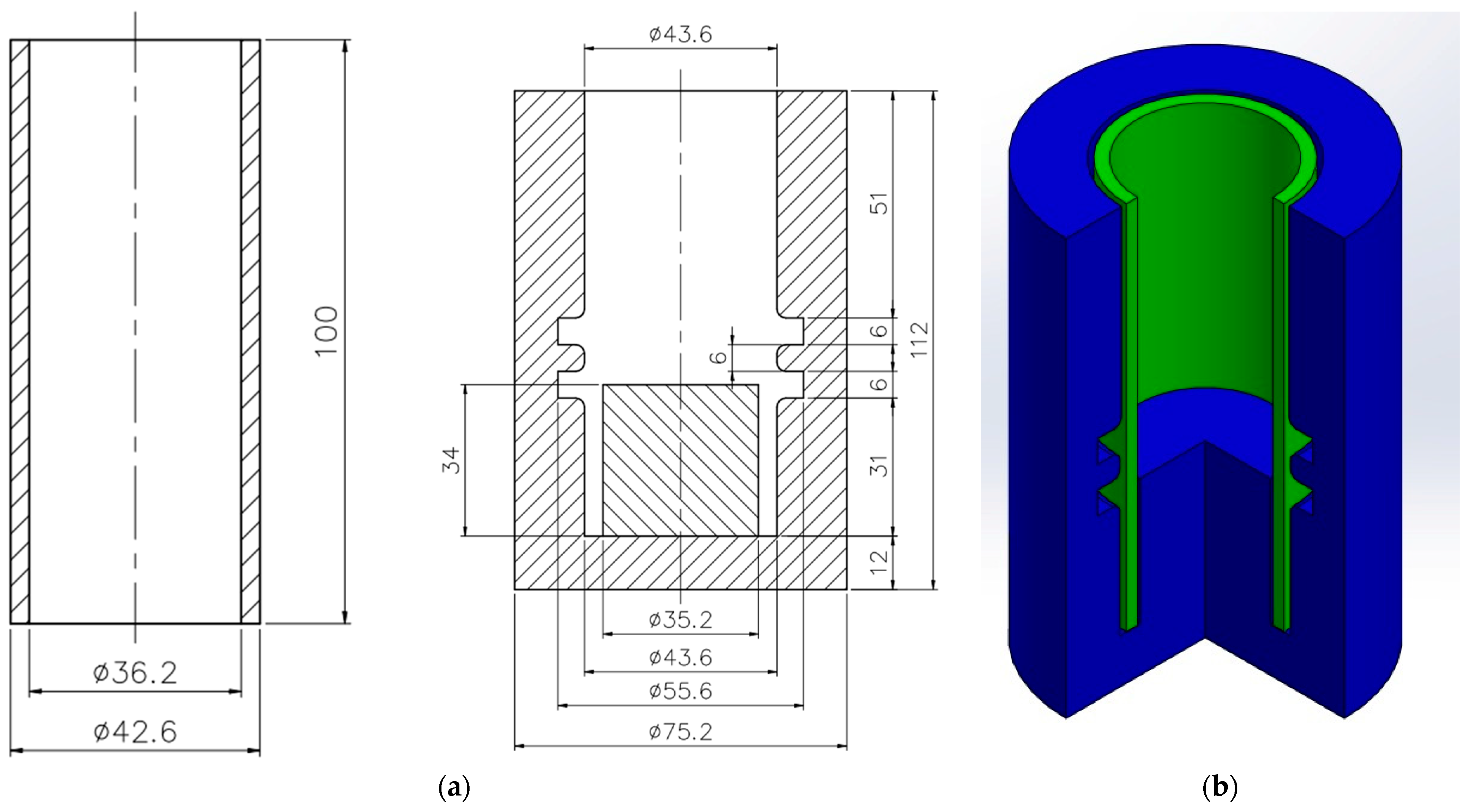
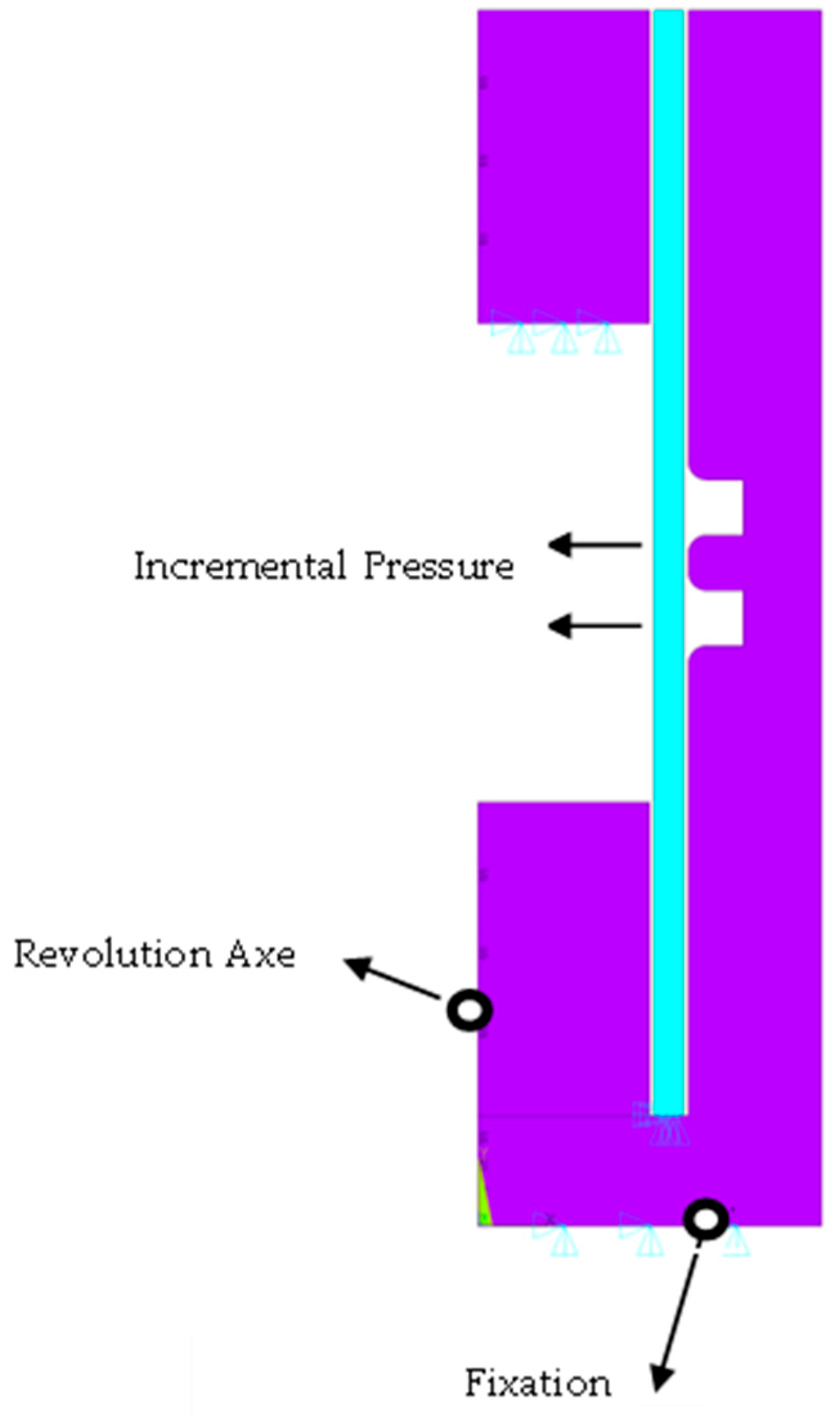
3.1.2. Boundary Conditions
- (a)
- Contact Lines
- (b)
- Axis of Symmetry, Fixation, and Applied Loads
4. Results and Discussion
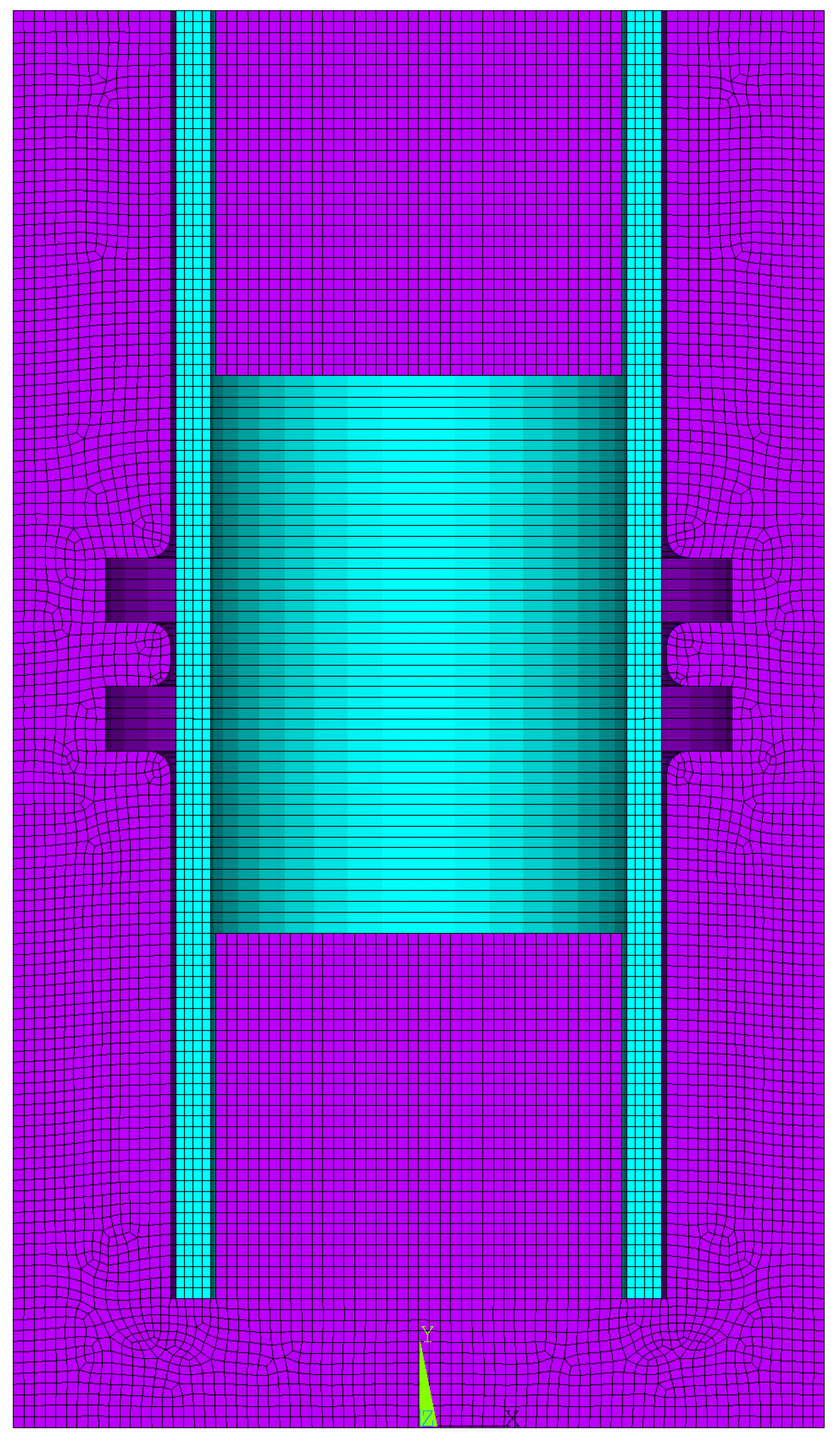
4.1. Die Geometry Convergence
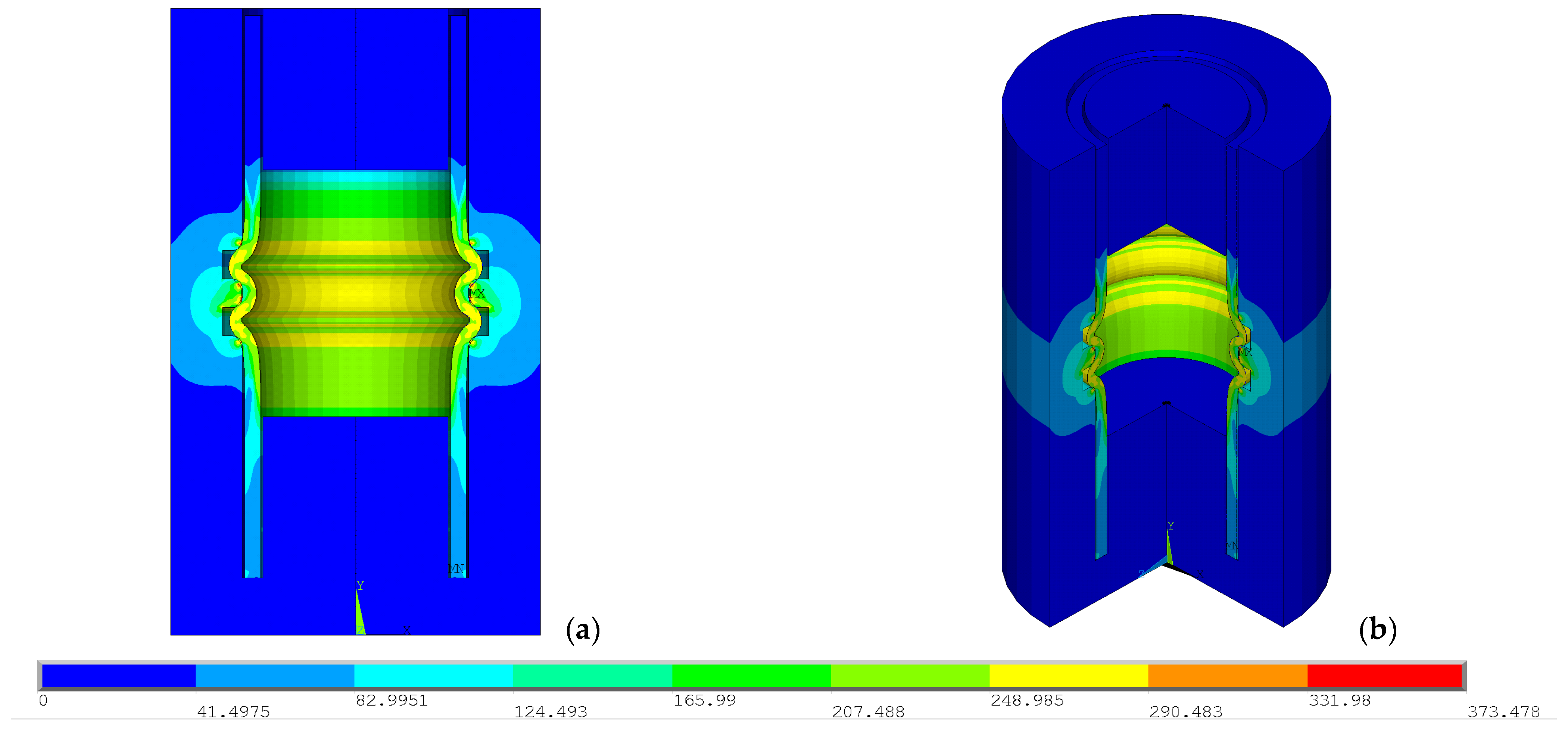
4.2. Results of Von Mises Stresses
4.3. Maximum Pressure and Displacements of the Tube
4.4. Applications and Experimental Tests
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bell, C.; Corney, J.; Zuelli, N.; Savings, D. A state-of-the-art review of hydroforming technology. Int. J. Mater. Form. 2020, 13, 789–828. [Google Scholar] [CrossRef]
- Liu, Y.X.; Qiu, X.; Wang, W.; Yu, T.X. An improved two-arcs deformational theoretical model of the expansion tubes. Int. J. Mech. Sci. 2017, 133, 240–250. [Google Scholar] [CrossRef]
- Meraz, M.; Kumar, M.; Singh, R.P. Experimental Study of Hydroformed Al6061T4 Elliptical Tube Samples under Different Internal Pressures. EMITTER Int. J. Eng. Technol. 2022, 10, 351–369. [Google Scholar] [CrossRef]
- Vyas, H.D.; Mehta, K.P.; Badheka, V.; Doshi, B. Friction welding of dissimilar joints copper-stainless steel pipe consist of 0.06 wall thickness to pipe diameter ratio. J. Manuf. Process 2021, 68, 1176–1190. [Google Scholar] [CrossRef]
- Alves, L.M.; Dias, E.J.; Martins, P.A.F. Joining sheet panels to thin-walled tubular profiles by tube end forming. J. Clean. Prod. 2011, 19, 712–719. [Google Scholar] [CrossRef]
- Huang, J.; Liu, J.; Gong, H.; Deng, X. A comprehensive review of loosening detection methods for threaded fasteners. Mech. Syst. Signal Process 2022, 168, 108652. [Google Scholar] [CrossRef]
- Yuan, S.J.; Cui, X.-L.; Wang, X.S. Investigation into wrinkling behavior of thin-walled 5A02 aluminum alloy tubes under internal and external pressure. Int. J. Mech. Sci. 2015, 92, 245–258. [Google Scholar] [CrossRef]
- Budynas, R.G.; Nisbett, J.K. Shigley’s Mechanical Engineering Design; McGraw Hill: New York, NY, USA, 2008; ISBN 0071268960. [Google Scholar]
- Miller, G.G. Tube Forming Processes: A Comprehensive Guide; Society of Manufacturing Engineers: Southfield, MI, USA, 2003; ISBN 9780872636330. [Google Scholar]
- Wang, X.S.; Cui, X.L.; Yuan, S.J. Research on flattening behavior of wrinkled 5A02 aluminum alloy tubes under internal pressure. Int. J. Adv. Manuf. Technol. 2016, 87, 1159–1167. [Google Scholar] [CrossRef]
- Buffa, G.; Fratini, L.; La Commare, U.; Römisch, D.; Wiesenmayer, S.; Wituschek, S.; Merklein, M. Joining by forming technologies: Current solutions and future trends. Int. J. Mater. Form. 2022, 15, 27. [Google Scholar] [CrossRef]
- Alves, L.M.; Afonso, R.M.; Martins, P.A.F. Double-sided self-pierce riveting. Int. J. Adv. Manuf. Technol. 2020, 108, 1541–1549. [Google Scholar] [CrossRef]
- Gupta, P.K. Numerical Investigation of Process Parameters on External Inversion of Thin-Walled Tubes. J. Mater. Eng. Perform. 2014, 23, 2905–2917. [Google Scholar] [CrossRef]
- Hwang, Y.-M.; Pham, H.-N.; Tsui, H.-S.R. Investigation of Punch Shape and Loading Path Design in Hydro-Flanging Processes of Aluminum Alloy Tubes. Metals 2021, 11, 636. [Google Scholar] [CrossRef]
- Cao, B.; Sun, Q.; Iwamoto, T. Bending fracture strength of the pipe joint using iron-based shape memory alloy (Fe-SMA) subjected to different expansion methods at various deformation rates. Eng. Struct. 2022, 267, 114669. [Google Scholar] [CrossRef]
- Zhu, Q.-Q.; Huang, S.; Wang, D.-X.; Li, J.-P.; Hua, F.-A.; Yang, P. Numerical simulation and experimental study of warm hydro-forming of magnesium alloy sheet. J. Manuf. Process 2022, 80, 43–53. [Google Scholar] [CrossRef]
- Kovács, P.Z. Joining of EN AW 6060 Pipes by Plastic Forming. Period. Polytech. Mech. Eng. 2024, 68, 31–37. [Google Scholar] [CrossRef]
- Du, B.; Zhao, C.; Dong, G.; Bi, J. FEM-DEM coupling analysis for solid granule medium forming new technology. J. Mater. Process. Technol. 2017, 249, 108–117. [Google Scholar] [CrossRef]
- Le, T.-K.; Bui, T.-A. Cold Forging Effect on the Microstructure of Motorbike Shock Absorbers Fabricated by Tube Forming in a Closed Die. Appl. Sci. 2021, 11, 2142. [Google Scholar] [CrossRef]
- Silva, G.C.; Soares, S.C.R.; Vieira, A.L. Pipe joining by mechanical conformation in thin sheets with rotary locking via a notch. Eng. Struct. 2021, 249, 113151. [Google Scholar] [CrossRef]
- Falk, T.; Jakel, M. Increasing flexibility of self-pierce riveting using numerical and statistical methods. Procedia Manuf. 2019, 29, 264–270. [Google Scholar] [CrossRef]
- Ghosh, S.; Kikuchi, N. Finite element formulation for the simulation of hot sheet metal forming processes. Int. J. Eng. Sci. 1988, 26, 143–161. [Google Scholar] [CrossRef]
- Antônio, A.C.; Sam, C.; Matteo, S. Optimization and inverse analysis in metal forming: Scientific state-of-the-art and recent trends. Int. J. Mater. Form. 2022, 15, 44. [Google Scholar] [CrossRef]
- Pepelnjak, T.; Gantar, G.; Kuzman, K. Numerical simulations in optimisation of product and forming process. J. Mater. Proc. Technol. 2011, 115, 122–126. [Google Scholar] [CrossRef]
- Starman, G.; Cafuta, G.; Mole, N. A Method for Simultaneous Optimization of Blank Shape and Forming Tool Geometry in Sheet Metal Forming Simulations. Metals 2021, 11, 544. [Google Scholar] [CrossRef]
- Van, D.D.; Vu, D.Q. Investigation on Billets and Tools Geometry in Cold Forging of the Straight Bevel Gear. Int. J. Adv. Sci. Eng. Inform. Technol. 2022, 12, 867–872. [Google Scholar] [CrossRef]
- Wu, W.; Zeng, T.; Hao, W.; Jiang, S. Microstructure and Mechanical Properties of Aluminum Matrix Composites Reinforced with In-Situ TiB2 Particles. Front. Mater. 2022, 9, 817376. [Google Scholar] [CrossRef]
- Alves, L.M.; Afonso, R.M.; Martins, P.A.F. A new deformation assisted tube-to-tubesheet joining process. Thin-Walled Struct. 2021, 163, 107784. [Google Scholar] [CrossRef]
- Memon, S.; Nikhare, C.P. Investigation of tube sheet joining through hydroforging process. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition (IMECE) (Advanced Manufacturing Article V02AT02A052), Columbus, OH, USA, 30 October–3 November 2022; American Society of Mechanical Engineers (ASME): New York, NY, USA, 2022; Volume 2. [Google Scholar] [CrossRef]
- Geier, M.; Paese, E.; dos Santos, T.; Homrich, R.P.; Rosa, P.; Rossi, R. Joining by electromagnetic forming. Compr. Mater. Process. 2023, 3, 316–333. [Google Scholar] [CrossRef]
- Wang, P.; Jin, J.; Afonso, R.M.; Wang, Y.; Zhang, C.; Xiang, N.; Wang, X.; Zhao, X. A novel mechanical joining method for sheet-tube structures by annular ring compression. Thin-Walled Struct. 2023, 191, 111031. [Google Scholar] [CrossRef]
- Geier, M.; José, M.M.; Rossi, R.; Rosa, P.A.R.; Martins, P.A.F. Interference-fit joining of aluminium tubes by electromagnetic forming. Adv. Mater. Res. 2013, 853, 488–493. [Google Scholar] [CrossRef]
- Kim, C.; Lee, J.; Barlat, F.; Lee, M. Frictional Behaviors of a Mild Steel and a TRIP780 Steel Under a Wide Range of Contact Stress and Sliding Speed. J. Tribol. 2014, 136, 021606. [Google Scholar] [CrossRef]
- Geier, M.; Paese, E.; Rossi, R.; Rosa, P.A.R.; Homrich, R.P. Experimental Analysis of Interference-Fit Joining of Aluminum Tubes by Electromagnetic Forming. IEEE Trans. App. Supercond. 2020, 30, 1–6. [Google Scholar] [CrossRef]
- Resk, H.; Delannay, L.; Bernacki, M.; Coupez, T.; Logé, R. Adaptive mesh refinement and automatic remeshing in crystal plasticity finite element simulations. Model. Simul. Mater. Sci. Eng. 2009, 17, 75012. [Google Scholar] [CrossRef]
- Dixit, U.S.; Raj, A.; Petrov, P.A.; Matveev, A.G. Numerical simulations for studying the influence of friction in forging. Adv. Mater. Process Technol. 2022, 8, 2752–2774. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.; Su, D.; Su, D.; Jin, J.; Jin, J.; Zhou, Z.; Zhou, Z.; Xue, Z.; Xue, Z.; et al. Numerical Simulation on Optimization of Process Parameters for Free Bending of Metal Tubes. Math. Probl. Eng. 2022, 2022, 4173457. [Google Scholar] [CrossRef]
- Phan, T.H.L.; Luyen, T.T.; Nguyen, D.T. A Study Utilizing Numerical Simulation and Experimental Analysis to Predict and Optimize Flange-Forming Force in Open-Die Forging of C45 Billet Tubes. Appl. Sci. 2023, 13, 9063. [Google Scholar] [CrossRef]
- Reynolds, J.; Zhang, H.; Rasmussen, K.J.R. Investigation of U-head rotational stiffness in formwork supporting scaffold systems. Eng. Struct. 2017, 136, 1–11. [Google Scholar] [CrossRef]

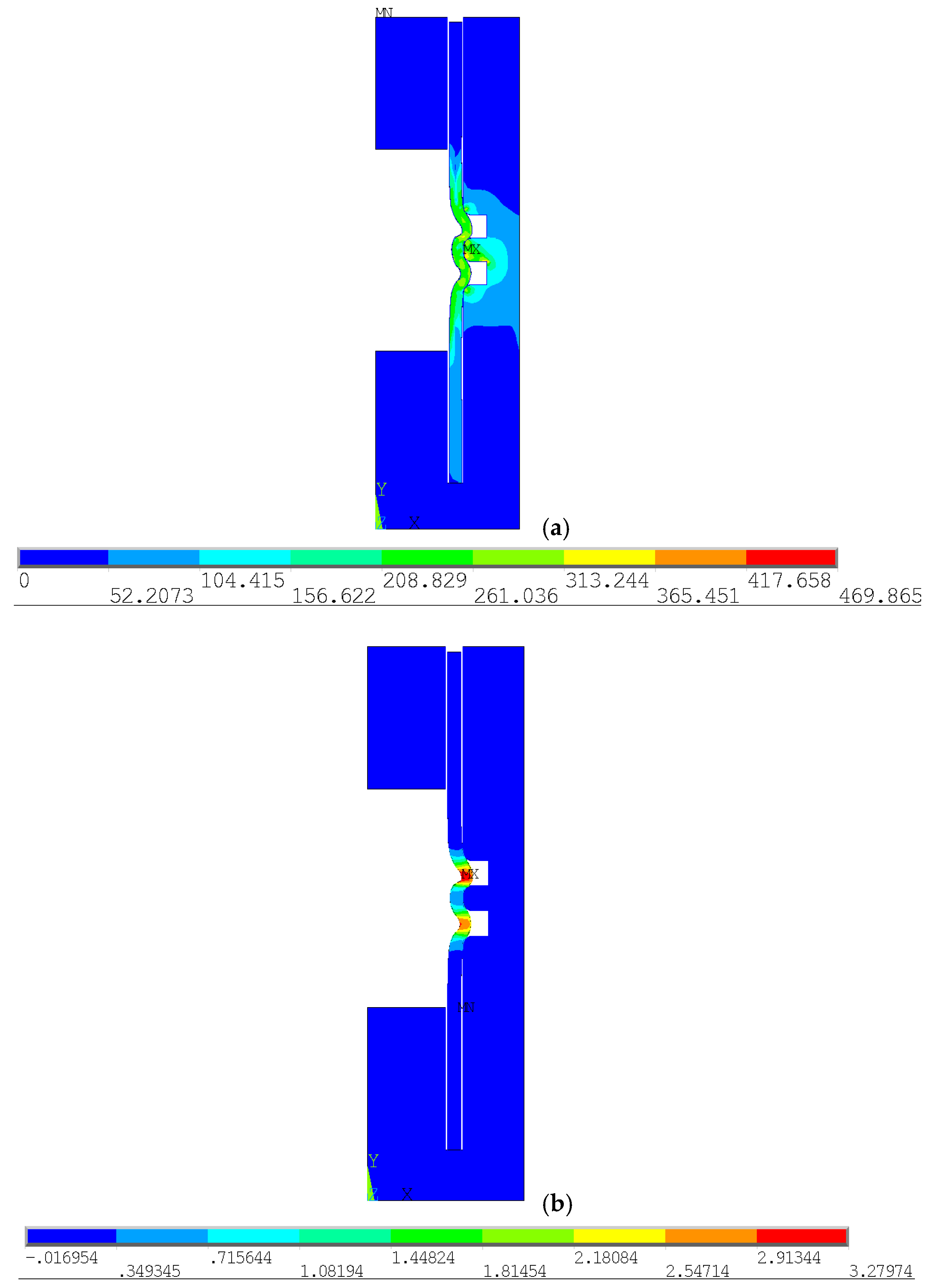

| Displacement in X | Displacement in Y |
|---|---|
| X-axis, Upper cavity node 11,238: +2.937 mm | Y-axis, Upper cavity node 11,592: −1.2645 mm |
| X-axis, Lower cavity node 11,215: +3.2797 mm | |
| Maximum pressure applied: 301.02 N/mm2 |
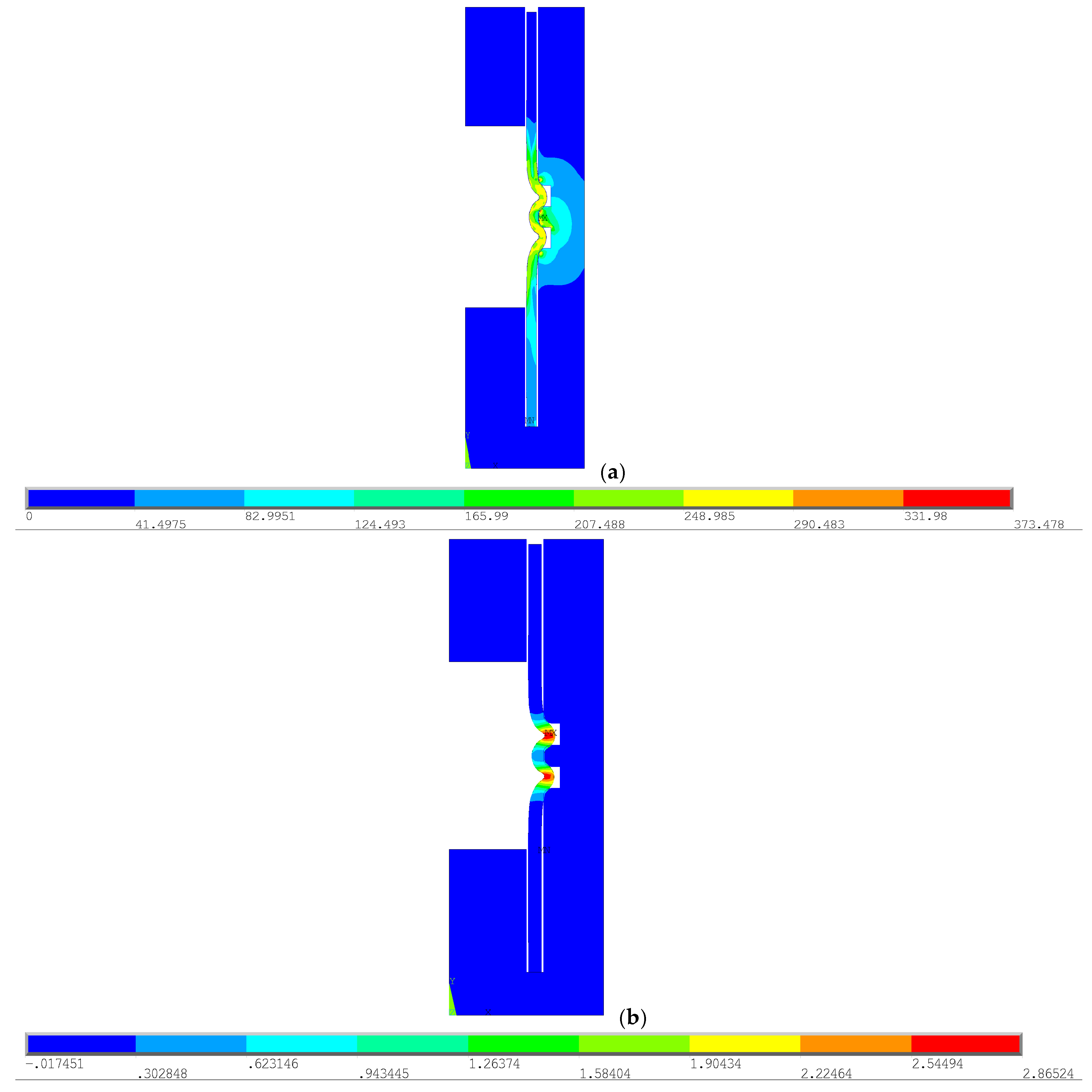
| Displacement in X | Displacement in Y |
|---|---|
| X-axis, Upper cavity node 11,177: +2.8590 mm | Y-axis, Upper cavity node 11,036: −1.1929 mm |
| X-axis, Lower cavity node 11,151: +2.848 mm | |
| Maximum Pressure Applied: 373.478 N/mm2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soares, S.C.R.; Silva, G.C.; Fonseca, E.M.M. Computational Methodology for the Development of Wrinkled Tubes by Plastic Deformation. Appl. Sci. 2024, 14, 11126. https://doi.org/10.3390/app142311126
Soares SCR, Silva GC, Fonseca EMM. Computational Methodology for the Development of Wrinkled Tubes by Plastic Deformation. Applied Sciences. 2024; 14(23):11126. https://doi.org/10.3390/app142311126
Chicago/Turabian StyleSoares, Samara C. R., Gilmar C. Silva, and Elza M. M. Fonseca. 2024. "Computational Methodology for the Development of Wrinkled Tubes by Plastic Deformation" Applied Sciences 14, no. 23: 11126. https://doi.org/10.3390/app142311126
APA StyleSoares, S. C. R., Silva, G. C., & Fonseca, E. M. M. (2024). Computational Methodology for the Development of Wrinkled Tubes by Plastic Deformation. Applied Sciences, 14(23), 11126. https://doi.org/10.3390/app142311126







