A New Approach to Characterize Superplastic Materials from Free-Forming Test and Inverse Analysis

Featured Application

The presented approach may be applied in manufacturing firms that use superplastic materials to have information on the adopted materials.

Abstract

For about 60 years, the aerospace industry has been strongly interested in superplastic forming processes to produce extremely light and complex-shaped components. Superplastic characteristics are found in lightweight metallic materials such as titanium-based, aluminum-based, and, more recently, magnesium-based alloys. Since the high ductility exhibited by superplastic materials is two orders of magnitude higher than that of conventional materials, complex-shaped components can be obtained. If made with conventional materials, they require expensive assembly operations. The behaviour of superplastic materials is summarized by a constitutive equation commonly obtained via tensile testing that subjects the tested material to a one-dimensional stress state. On the contrary, free-forming tests allows us to test the material by subjecting it to a stress state similar to that determined during a real superplastic-forming process. The aim of this work is to define the characteristic parameters of superplastic materials by free-forming tests. The behaviour of superplastic materials is commonly modelled using a power law which puts the material into a stress-to-strain-rate relationship. This law needs to identify two parameters characterizing superplastic materials: the strain rate sensitivity index and the strength coefficient. In this work, a new procedure is presented that implies the two material parameters vary with strain. It allows for a reduction in the number of constants needed to determine the material constitutive equation, thus requiring low simulation time compared to models that adopt the multiple-objective optimization based on genetic algorithms (GAs). It is more suitable to be used in the industrial field. Furthermore, the proposed procedure is compared with a conventional procedure which is also based on the inverse analysis carried out through the use of a finite element analysis. The results of the conventional procedure, based on the inverse analysis, which is conducted through the use of a finite element analysis, are used to calculate the material constants, and are compared with those coming from the procedure proposed in this work. The proposed procedure appears equally simple and gives more accurate results compared to the conventional procedure. In fact, the maximum percentage error, regarding the prediction of the forming times of a free-forming process, was reduced from 20% to 8%. The development of the proposed procedure, as well as the comparison of the results with a conventional procedure, required the development of an experimental activity. This activity consists of free-forming tests conducted at a constant pressure (the pressures employed vary from 0.2 to 0.4 MPa), at a temperature of 753 K, and on circular sheets (thickness 1.0 mm and radius 40 mm) in superplastic magnesium alloy AZ31.

1. Introduction

Forming processes are becoming more and more complex to satisfy the client requirements of personalization and accuracy. The development of digital twin tools [1] or neural networks [2] may help to optimize these processes under these requirements.

The phenomenon of superplasticity allows some metal alloys to reach high tensile elongations if they are worked in particular forming conditions. Such conditions require a fine and stable-grain structure at the process temperature, a high and constant process temperatures (above half the melting temperature of the material), and very low strain rates that are typically between 10⁻³ and 10⁻⁵ s⁻¹. Information on the microstructure of superplastic materials is widely discussed in [3,4,5].

The superplastic forming process (SPF) requires the use of a pressurized gas instead of the punch used in the traditional forming process. As shown in Figure 1, the pressurized gas pushes the superplastic sheet to adhere to the surfaces of the die by copying its internal geometry. The superplastic sheet, clamped on the die using a blank holder, is (i) indirectly heated until it reaches the optimum value of the process temperature [6] and is (ii) subjected to the action of a load curve (pressure–time) that guarantees the optimal superplastic conditions. Finite element modelling (FEM) of the forming process is relied upon to accurately design the optimal load curve [7,8,9,10,11].

The main superplastic materials of industrial interest are titanium-based alloys, which are used in the aerospace industry, biomedical sector, and architectural applications, and aluminum-based alloys, which are mainly used in the aircraft industry [4]. Superplastic materials decrease the weight of the aircraft, thereby consuming less fuel. Thus, the manufacturing processes connected with this class of materials may be considered green technologies to provide an answer to environmental requirements.

To take advantage of the high formability and high strength-to-weight ratio as evidence in superplastic aluminum alloy sheets, superplastic forming (SPF) processes have been employed in the automotive industry. In a single forming step, parts of complex shapes can be manufactured by decreasing the assembly operations and the weight of the parts. Recently, magnesium-based alloys have been studied in superplastic conditions due to the decrease in material cost and an interesting strength/weight ratio [12,13,14,15,16], even when they present more critical issues [17,18].

In recent years, quick plastic forming processes have been introduced to speed up hot forming processes, which do not fully exploit the high superplastic properties of aluminum- and magnesium-based alloys [4,19,20,21,22,23]. Moreover, since the superplastic forming processes involve sheet metal stretching [24,25], to better control the thickness distribution of a manufactured part, multiphase forming processes have been used [26,27,28], or alternatively, forming processes on a sheet of variable thickness have been proved [6,22,29,30,31].

To describe the behaviour of superplastic materials, several constitutive models [4,32,33,34,35,36] have been proposed; they require the identification of different constants by characterizing the material through several experimental tensile tests. However, it has been demonstrated that the results of the tensile test are not accurate enough to be introduced into the simulation of superplastic forming processes [37,38,39,40]. On the contrary, the free-forming test is rapid and accurate since it involves a deformation condition similar to that of industrial forming processes. The free-forming tests require using a die with a simple geometry that allows for the manufacturing of hemispheres.

The novelty of this work is due to the use of a numerical-experimental approach based on inverse analysis to identify the characteristic parameters of sheets in AZ31 superplastic magnesium alloy that varies with strain. The reference constitutive equation, widely used in the scientific literature, which describes the behaviour of superplastic materials [3,4,5,37,41,42,43,44], is used in this study. In a previous work, the authors introduced the general procedure for the characterization of magnesium alloy AZ31 [45], the new approach is deeply discussed and compared with the conventional procedure for the characterization of materials (based on the free-forming and inverse analysis). The procedure proposed in this paper allows for a reduction in the number of constants needed to determine the material constitutive equation, thereby requiring low simulation time. It is more suitable for use in the industrial field. Furthermore, the proposed procedure appears equally simple and gives more accurate results than the conventional procedure. The forming times of free-forming processes are predicted more accurately (the maximum achieved error is 8%).

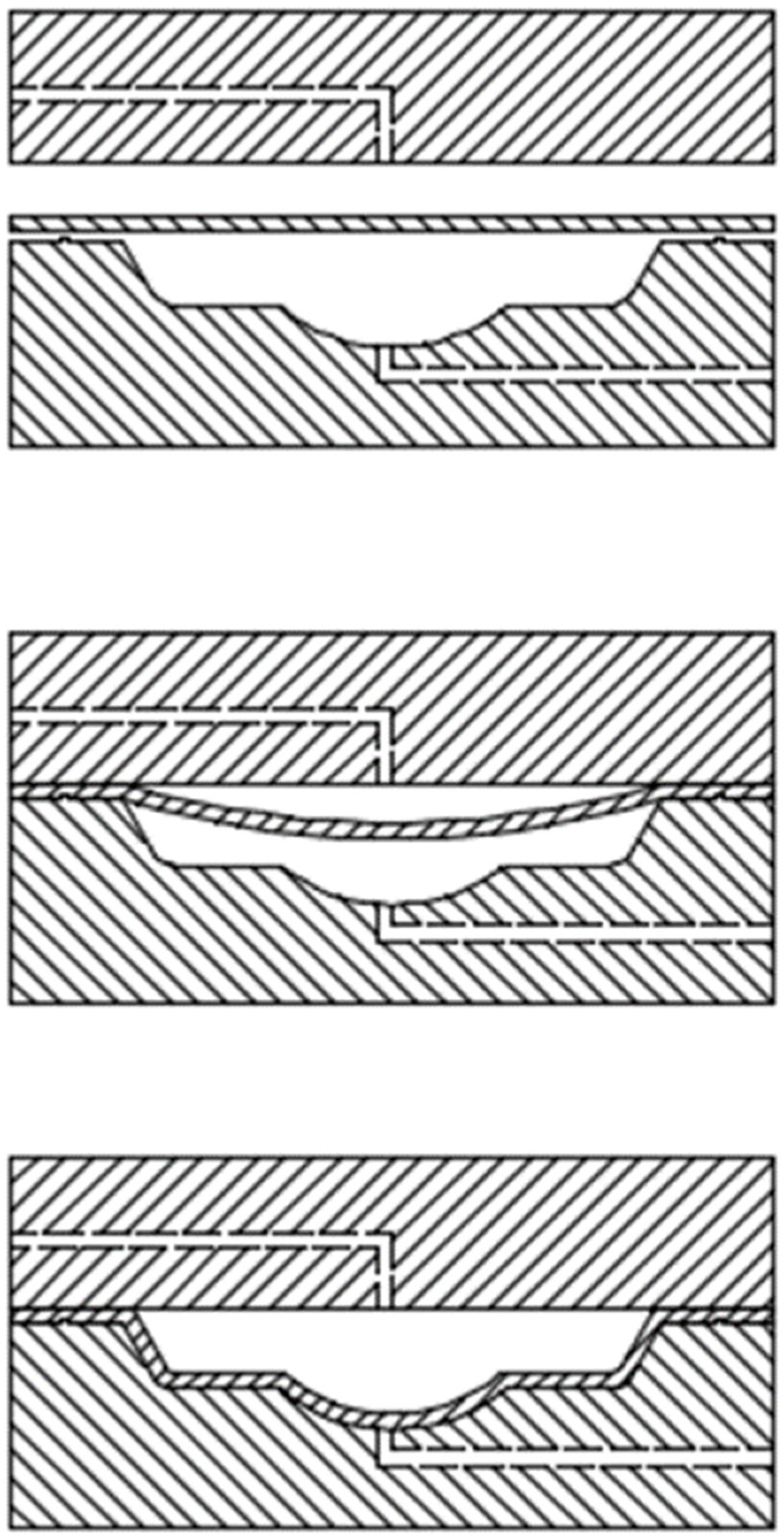
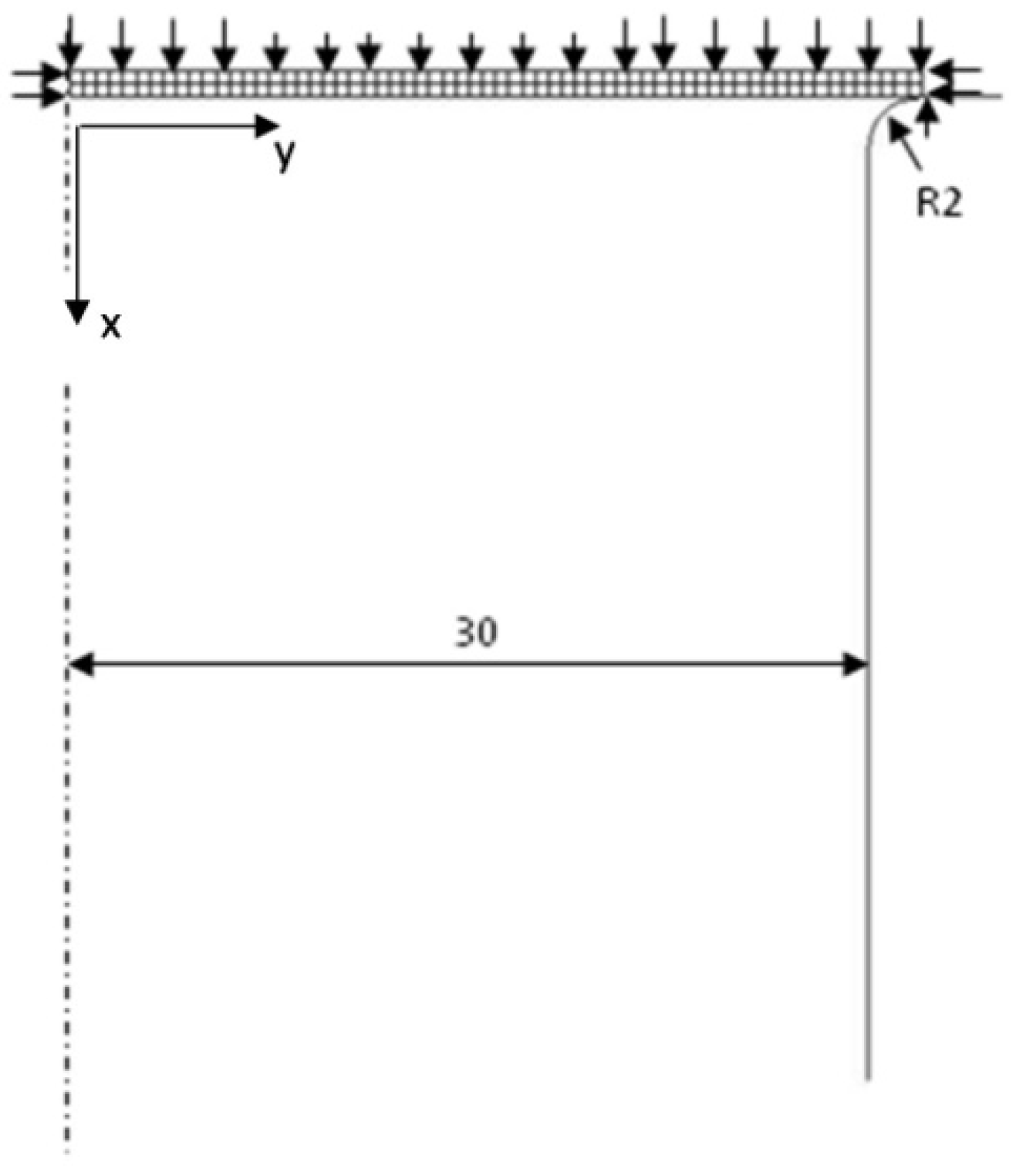
2. Materials and Methods

In this work, a circular sheet with a thickness of 1 mm and a radius of 40 mm in AZ31 superplastic magnesium alloy AZ31 (average grain size 10 µm) was used to evaluate the parameters characterizing the material using a new characterization procedure. This alloy, whose chemical composition by weight is Mg-3%Al1%Zn, is widely used for industrial applications [4]. It was submitted to the free-forming test at constant pressure with two pressure values (p₁ = 0.2 MPa and p₂ = 0.4 MPa) at a temperature of 753 K.

The equipment used to perform the free-forming test is composed of two semi-dies with a cylindrical shape (one inside the other) and wrapped with an electrical resistance [46]. Once the sheet was placed between the two half-dies, the electrical resistance heated it up to the process temperature that is controlled by an automatic system to supply electricity. At this point, gas was introduced into the die at constant pressure, p₁ or p₂. The height h reached at the apex of the dome was measured independent of the forming time, t, through a measuring laser put above the die. This height was usually dimensionless with respect to the radius of the cylindrical die, a. In this way, the dimensionless height H was evaluated using the formula below.

$$\mathrm{H}=\mathrm{h}/\mathrm{a},$$

(1)

Finite element modelling used the commercial software MSC.Marc^® (version 2024.1) and was based on the rigid-plastic flow formulation. The numerical simulation used an axisymmetric model characterized by 128 elements with four nodes [47]. A FEM scheme of the free-forming test is shown in Figure 2 where a datum reference frame was introduced with x-axis oriented as the symmetry axis. The boundary conditions are as follows:

-

For the node in contact with the die and placed on the external edge of the metal sheet, ux = 0 and uy = 0 (where u is the displacement of the node);

-

For the nodes on the external edge (not in contact with the die) uy = 0;

-

For all the nodes on the axis of symmetry (condition of axisymmetry) uy = 0;

-

The upper edges of the metal sheet are subjected to a uniform pressure (in one case p = 0.2 MPa and in the other case p = 0.4 MPa).

It was possible to identify two bodies: the metal sheet (i.e., a deformable body that is discretized in finite elements) and the die (i.e., a rigid body). The presence of a blank holder was simulated by introducing appropriate boundary conditions at the nodes located on the outer edge of the sheet. In particular, the node in contact with the die had zero displacement along the x and y directions. The nodes on the edge that were not in contact with the die and were constrained not to move along the y-direction. For the conditions of axisymmetry, the nodes on the symmetry axis had a zero displacement along the y direction (that is, along the direction orthogonal to the symmetry axis). The pressure of the forming gas was applied uniformly to the top face of the sheet. The value of the forming pressure as well as the constitutive equation of the material was introduced through the adoption of a subroutine.

3. Theory

A superplastic material is generally characterized by the power law below.

$$\overline{\mathsf{\sigma }}=\mathrm{K}{\mathsf{\epsilon }}^{\mathrm{n}}{\mathsf{\delta }}^{\mathrm{m}},$$

(2)

This law puts into relationship the equivalent stress, σ, to the equivalent strain, ε, and to the strain rate, δ, through the strain rate sensitivity index, m, the strain hardening index, n, and the strength coefficient, K.

To determine the constants of Equation (2), the conventional procedure [38,47], which is used to characterize the behaviour of superplastic materials, requires the calculation of the strain rate sensitivity index through two free-forming experimental tests that are carried out at two values of pressure (p₁ and p₂) that are kept constant. The tests must be carried out until a unitary value of the dimensionless displacement, H, is reached. In this way, it is possible to calculate m using the following expression [4,37,43,48,49]:

$$\mathrm{m}=\ln \left({\mathrm{p}}_1/{\mathrm{p}}_2\right)/\ln \left({\mathrm{t}}_2/{\mathrm{t}}_1\right),$$

(3)

where t₁ and t₂ are the times to reach the unit value of the dimensionless displacement, H, under the action of a constant pressure equal to p₁ and p₂, respectively.

To evaluate the n and K constants, the finite element modelling of the free-forming process is commonly used [38,47]. The normalized time, τ, is defined as follows:

$$\mathsf{\tau }={\mathrm{t}}_{\mathrm{H}=1}/{\mathrm{t}}_{\mathrm{H}=0.5},$$

(4)

where t_H=1 and t_H=0.5 are the times needed to reach the dimensionless displacements H = 1 and H = 0.5, respectively. Therefore, once an arbitrary value is assigned to K and the constant m is known, numerical simulations are carried out by varying the n constant. The value of the strain hardening index n is found by minimizing the following function Q(n):

$$\begin{gathered} \mathrm{Q}\left(\mathrm{n}\right)={\left({\displaystyle \frac{{\left(\ln \mathsf{\tau }\right)}^{\mathrm{F}\mathrm{E}\mathrm{M}}-{\left(\ln \mathsf{\tau }\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}{{\left(\ln \mathsf{\tau }\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}}\right)}_{{\mathrm{p}}_1}^2+{\left({\displaystyle \frac{{\left(\ln \mathsf{\tau }\right)}^{\mathrm{F}\mathrm{E}\mathrm{M}}-{\left(\ln \mathsf{\tau }\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}{{\left(\ln \mathsf{\tau }\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}}\right)}_{{\mathrm{p}}_2}^2+{\left({\displaystyle \frac{{\left(\mathsf{\epsilon }\right)}^{\mathrm{F}\mathrm{E}\mathrm{M}}-{\left(\mathsf{\epsilon }\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}{{\left(\mathsf{\epsilon }\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}}\right)}_{{\mathrm{p}}_1}^2+ \\ {\left({\displaystyle \frac{{\left(\mathsf{\epsilon }\right)}^{\mathrm{F}\mathrm{E}\mathrm{M}}-{\left(\mathsf{\epsilon }\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}{{\left(\mathsf{\epsilon }\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}}\right)}_{{\mathrm{p}}_2}^2, \end{gathered}$$

(5)

which is constituted by quantities, such as normalized time, τ, and equivalent strain, ε, of FEM numerical simulations and experimental tests.

Similarly, once the value of the hardening index, n, is determined, further numerical simulations of the free-forming test allow for the evaluation of the strength coefficient, K, by minimizing the function F(K) given by the following formula:

$$\mathrm{F}\left(\mathrm{K}\right)={\left({\displaystyle \frac{{\left({\mathrm{t}}_{\mathrm{H}}\right)}^{\mathrm{F}\mathrm{E}\mathrm{M}}-{\left({\mathrm{t}}_{\mathrm{H}}\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}{{\left({\mathrm{t}}_{\mathrm{H}}\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}}\right)}_{{\mathrm{p}}_1}^2+{\left({\displaystyle \frac{{\left({\mathrm{t}}_{\mathrm{H}}\right)}^{\mathrm{F}\mathrm{E}\mathrm{M}}-{\left({\mathrm{t}}_{\mathrm{H}}\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}{{\left({\mathrm{t}}_{\mathrm{H}}\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}}\right)}_{{\mathrm{p}}_2}^2,$$

(6)

where t is the time required to reach the unit dimensionless displacement, through FEM numerical simulations and experimental tests, under the action of the constant pressure p₁ or p₂.

In this work, the procedure proposed for the characterization of superplastic materials involves a reduction in the material parameters. In fact, the reference power law is no longer given by Equation (2) but by the following formula:

$$\overline{\mathsf{\sigma }}=\mathrm{C}{\mathsf{\delta }}^{\mathrm{m}},$$

(7)

where m and C are parameters that depend on the equivalent strain, ε. The variability of m with strain is determined experimentally by dividing the dimensionless height, H, into five ranges (0 ≤ H ≤ 0.2; 0.2 < H ≤ 0.4; 0.4 < H ≤ 0.6; 0.6 < H ≤ 0.8; 0.8 < H ≤ 1.0). For each range the parameter m can be determined using the following equation:

$$\mathrm{m}=\ln \left({\mathrm{p}}_1/{\mathrm{p}}_2\right)/\ln \left(\mathsf{\Delta }{\mathrm{t}}_2/\mathsf{\Delta }{\mathrm{t}}_1\right),$$

(8)

in Equation (8), Δt₁ and Δt₂ are the times needed to fill the single range of H under the action of the pressure p₁ and p₂, respectively.

The value of the C constant is determined, for each range of H through minimization via finite element analysis of the function F(C):

$$\mathrm{F}\left(\mathrm{C}\right)={\left({\displaystyle \frac{{\left({\mathrm{t}}_{\mathrm{H}}\right)}^{\mathrm{F}\mathrm{E}\mathrm{M}}-{\left({\mathrm{t}}_{\mathrm{H}}\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}{{\left({\mathrm{t}}_{\mathrm{H}}\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}}\right)}_{{\mathrm{p}}_1}^2+{\left({\displaystyle \frac{{\left({\mathrm{t}}_{\mathrm{H}}\right)}^{\mathrm{F}\mathrm{E}\mathrm{M}}-{\left({\mathrm{t}}_{\mathrm{H}}\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}{{\left({\mathrm{t}}_{\mathrm{H}}\right)}^{\mathrm{E}\mathrm{X}\mathrm{P}}}}\right)}_{{\mathrm{p}}_2}^2,$$

(9)

in which, t is the time connected to the single sub-interval of H, both in FEM numerical simulation and experimental approach, under the action of the constant pressure p₁ or p₂.

To estimate the constants of the constitutive models that were proposed in [4,32,33,34,35,36], the multiple-objective optimization based on genetic algorithms (GA) was adopted. It involved many numerical simulations and, therefore, a very high simulation time. The procedure proposed in this paper allows for a reduction in the number of constants to determine the material constitutive equation, thereby requiring low simulation time. It is more suitable for being used in the industrial field.

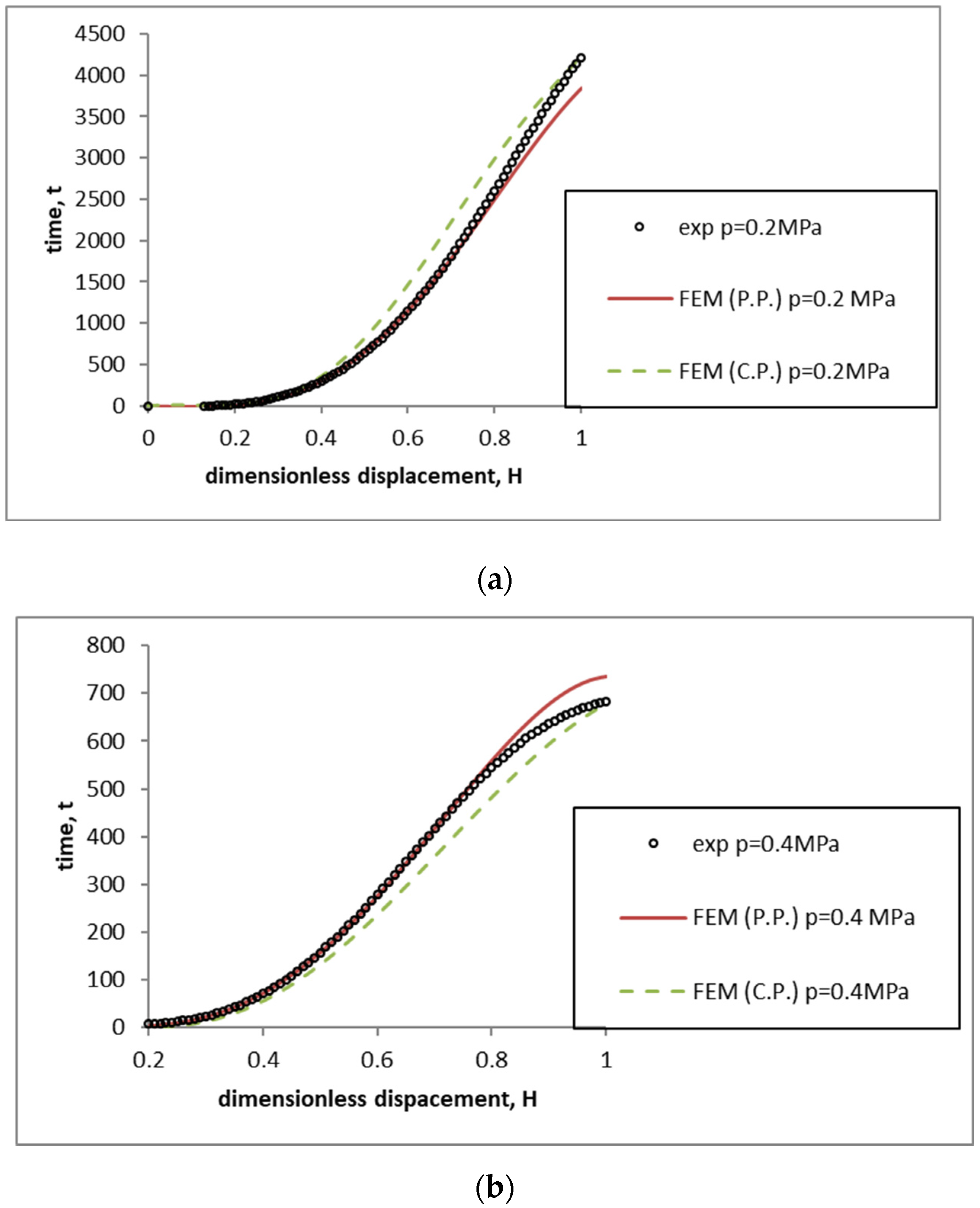
4. Results and Discussion

The experimental activity consisted of submitting a disc in AZ31 superplastic magnesium alloy to the free-forming test carried out at a temperature of 753 K and a constant pressure of 0.2 and 0.4 MPa, respectively. Each test was repeated three times for a total of six tests.

Table 1. Evaluation of the strain rate sensitivity index, m, of the conventional and proposed procedures.

Dimensionless Displacement H	Strain Rate Sensitivity Index, m, of Conventional Procedure	Strain Rate Sensitivity Index, m, of Proposed Procedure
0 ≤ H ≤ 1	0.381	/
0 ≤ H ≤ 0.2	/	0.703
0.2 ≤ H ≤ 0.4	/	0.465
0.4 ≤ H ≤ 0.6	/	0.495
0.6 ≤ H ≤ 0.8	/	0.406
0.8 ≤ H ≤ 1	/	0.284

shows the value of the m parameter that was measured through the conventional procedure (Equation (3)) proposed in this work for which the m parameter varies inside each range of H (Equation (8)).

Table 2. Evaluation of the hardening index, n, and the strength coefficients, K and C.

Dimensionless Displacement H	Strain Hardening Index, n, of Conventional Procedure	Strength Coefficient, K, of Conventional Procedure	Strength Coefficient, C, of Proposed Procedure
0 ≤ H ≤ 1	0.1	163.24	/
0 ≤ H ≤ 0.2	/	/	862.875
0.2 ≤ H ≤ 0.4	/	/	241.357
0.4 ≤ H ≤ 0.6	/	/	346.950
0.6 ≤ H ≤ 0.8	/	/	198.300

shows the values of n and K obtained using the conventional procedure and the values of parameter C for each range of H obtained using the proposed procedure.

The reliability of the parameters characterizing the magnesium-based alloy AZ31 (identified through the conventional procedure and the procedure proposed in this work) was estimated by comparing the results of the FEM simulation of free-forming processes with those coming from the experimental activity.

In particular, the comparison results are represented by the forming times achieved at each configuration of the deformed metal sheet. The metal sheet configuration is associated with the dimensionless displacement achieved at the apex of the same metal sheet, H. Figure 3a,b show the forming times associated with each dimensionless displacement achieved in two free-forming processes conducted at the constant pressures (p₁ = 0.2 MPa and p₂ = 0.4 MPa) by a sequence of small circles. At the same time, Figure 3a,b show the results of the simulations conducted using the following as parameters characterizing the material:

-

The parameters coming from the conventional procedure (C.P.) adopted to identify them (dotted line—FEM C.P.);

-

The parameters coming from the proposed procedure (P.P.) adopted to identify them (solid line—FEM P.P.).

Figure 3 shows a qualitative comparison between the obtained results. It can be seen that the use of the m and C parameters, which vary with H, allows for the obtaining of t-H curves via FEM nearer to the experimental ones than the constants m, n, and K do. It was quantified that the comparison between the numerical and experimental results through the parameter ∆.

$$∆={\displaystyle \frac{t_{FEM}-t_{EXP}}{t_{EXP}}}\ast 100,$$

(10)

The maximum value of the percentage difference between numerical and experimental approaches, ∆, decreases from about 20%, when the constants obtained from the conventional procedure in the interval 0.2 ≤ H ≤ 1 are used, to about 8%, when the m and C parameters are obtained from the proposed procedure.

In this last case, the maximum value of the percentage difference, ∆, is reached in the last range of H which is used to evaluate m and C. It can be due to the fact that in this last range, the function F(C) reaches 0.016 as the minimum value, while in the previous range, it reaches 0 as the minimum. The function F(C) has been shown in Section 3, concerning the theory of the proposed procedure to identify the parameters characterizing the material (Equation (9)). The function F(C) is representative of the adaptability of the experimental results to the FEM results. The more it tends to zero, the greater is the adaptability between the FEM and experimental results. Moreover, in the range 0.8 < H ≤ 1, the metal sheet is close to the breaking point which may involve a larger difference between numerical and experimental results due to an unsuitability of the use of the power law model.

5. Conclusions

In this work, the behaviour of superplastic materials was modelled using the power law which puts into relationship stress and strain rate. The free-forming test was used to evaluate the two characteristic parameters of a sheet in AZ31 magnesium-based superplastic alloy. For this purpose, it was necessary to perform a numerical-experimental procedure consisting of free-forming experimental tests and an inverse analysis through FEM. The proposed procedure was performed and the results, in terms of the H-t curve, were compared with those coming from a conventional procedure to calculate the material constants. The obtained results highlight the following:

• The proposed procedure turned out to be more effective than the conventional procedure, since it involves a reduction in the percentage difference from the experimental results;
• The predicted forming time envisaged by the FEM differs from the experimental value at most by 20% for the conventional procedure and 8% for the proposed procedure;
• The procedure proposed in this paper allows for a reduction in the number of constants needed to determine the material constitutive equation, thereby requiring low simulation time;
• The proposed procedure is more suitable for being used in the industrial field.