Performance Comparison of Vertex Block Descent and Position Based Dynamics Algorithms Using Cloth Simulation in Unity

Abstract

This paper presents a comparative study of the Vertex Block Descent (VBD) and Position-Based Dynamics (PBD) algorithms, focusing on their performance in physical simulation tasks. Unity, a versatile physics engine, served as the simulation platform for the experiments. Among various types of physical simulations of deformable objects, fluids, and cloth dynamics, cloth simulations were chosen for implementation with both algorithms. The experimental setup ensured identical parameters, including time steps and movement behavior, for both algorithms across scenarios involving hanging, object-to-object collisions, and self-collisions. The results indicate that while the performance difference in frames per second (fps) between the two algorithms is negligible for simulations with a small number of nodes, the VBD algorithm consistently outperforms the PBD algorithm as the node count increases. Furthermore, this study provides practical guidelines for maintaining real-time performance, detailing the maximum node count each algorithm can support, while sustaining a minimum threshold of 30 fps, which is necessary for real-time applications. The comparison was conducted using CPU-based computation to establish a baseline for future studies in GPU-accelerated environments, where parallel processing is expected to further highlight the performance advantages of VBD. Future work will extend this research by evaluating additional physical simulation models, including the Mass-Spring System and Extended Position-Based Dynamics (XPBD), and developing optimizations to enhance the efficiency and scalability of these algorithms.

1. Introduction

Physics-based simulation methods are increasingly studied to realistically represent virtual objects, thus enabling their physical properties to resemble those of real-world entities. Since realistic motion representation plays a crucial role in enhancing visual realism, the simulation of deformable objects has become a central focus of computer graphics research. Recently, such simulations have gained prominence in applications like medical simulations and education, facilitated by the use of diverse physics engines such as Unity, Unreal, and CryEngine [1]. In this study, simulations were implemented using the Unity engine, a versatile platform that supports various operating system environments, including Windows, Linux, and iOS, and finds application across multiple domains [2,3,4].

Among physics-based simulations, cloth simulation represents a vital research area to achieve realistic visual depictions of objects like clothing, curtains, and flags [5]. Cloth simulations demand accurate physical modeling along with high computational performance to support real-time interaction. However, increased complexity, particularly with numerous nodes, leads to elevated computational costs and potential performance degradation [6,7,8,9]. Since the 1980s, numerous researchers, including Terzopoulos et al. and Desbrun et al., have explored the Mass-Spring System approach for deformable object simulation, particularly in the context of cloth simulation algorithms. The Mass-Spring System represents deformable materials using a network of mass nodes connected by springs, providing a relatively straightforward structural model; however, it presents inherent limitations in physical accuracy [10,11,12,13]. Conversely, the Finite Element Method (FEM), which simulates the elastic deformability of objects, excels in accurately modeling complex physical properties, especially for 3D deformable objects. Nevertheless, FEM is predominantly used in high-quality rendering scenarios due to its intensive computational demands, making it less suitable for real-time applications [14,15,16]. More recently, a range of algorithms has emerged to enhance the accuracy and efficiency of real-time simulations. Among these, Vertex Block Descent (VBD) and Position-Based Dynamics (PBD), which this study examines, are notable for their respective strengths and weaknesses. PBD is widely recognized for its robust and intuitive handling of object positions, yielding stable and visually coherent results across various simulations, while supporting real-time performance. It is particularly effective in handling inter-object and self-collisions [17,18]. However, PBD’s frame-by-frame computational approach can lead to inaccuracies in object representation during larger time-step simulations [19]. On the other hand, VBD leverages block-based parallel processing to enable stable and efficient performance, even with high-resolution meshes and increased node counts. However, the block-wise processing nature of VBD may introduce accuracy challenges in more complex simulation scenarios [20]. Real-time simulation plays a crucial role in interactive content, such as games, VR, and AR. Maintaining a stable frame rate (fps) is essential to achieve real-time responsiveness, with minimum fps requirements differing by application: 30 fps for animations, 60 fps for games, and 90 fps for VR and AR environments [21,22,23]. In this study, we implemented real-time cloth simulation using two algorithms (VBD and PBD) and compared their performance. The simulations were evaluated under identical conditions in terms of node count and time steps, and the scenarios included hanging, object-to-object collision, and self-collision to assess fps consistency for each algorithm.

Table 1. Comparing the advantages and disadvantages of algorithm.

Algorithm	Advantages	Disadvantages
Mass-Spring System	- Simple and intuitive implementation - Lightweight and efficient calculations - Suitable for small-scale simulations	- May produce unrealistic deformations (lack of physical accuracy) - Can be unstable in complex simulations
FEM	- Physically accurate and realistic deformations - Can account for various material properties	- Computationally expensive and slow - Challenging to implement parallelization
PBD	- Stable and fast calculations - Well suited for parallelization - Excellent performance in real-time simulations	- Focuses on stability over accuracy (less physically accurate) - Performance may degrade with high node density
VBD	- High stability and accuracy - Better performance in complex simulations compared to PBD - Suitable for parallelization	- High implementation complexity - May not show significant performance gains in small-scale simulations

below compares the advantages and disadvantages of each algorithm.

In this paper, we implement and compare cloth simulations using both the VBD and PBD algorithms. The comparative analysis focuses on three scenarios—hanging, object-to-object collisions, and self-collisions—under identical conditions involving node counts and time-lapse-based fps measurements. Our results demonstrate that VBD achieves superior fps, outperforming PBD by up to 82.9% in hanging scenarios, 31.1% in object-to-object collision scenarios, and 8.8% in self-collision scenarios when operating with a large number of nodes. This performance comparison is based on CPU-only computations, while future work will involve optimization via GPU-based parallel processing using compute shaders, with the expectation of further enhancing performance.

2. Related Works

2.1. Cloth Simulation

Deformable object simulation is a critical area in computer graphics and physics-based animation. Deformable objects are characterized by their ability to change shape in response to external forces, unlike rigid bodies in conventional modeling. Examples of such objects are cloth, water, and rubber. Algorithms based on physical principles are employed to realistically simulate the behavior and deformability of these objects [24,25,26]. Cloth simulation, which began with simple modeling techniques, has evolved into one of the most sophisticated forms of variational object simulation that incorporates complex physical laws. Due to its thin, flexible nature, cloth exhibits diverse deformable states in various environments, necessitating the application of intricate physical models [27,28,29].

The primary objective of cloth simulation is to replicate realistic cloth movement, and numerous algorithms have been proposed to capture cloth elasticity, collision, and interaction with external forces, such as wind. Early research focused on force–object relationships, leading to the development of models such as the Mass-Spring System [30], Finite Element Method [31], and Rigid Body Dynamics [32]. However, these models have limitations, including performance degradation, lack of real-time capability, and unrealistic motion as simulation complexity increases. PBD was introduced to address these limitations. Initially developed by Jakobsen [33], PBD provides a stable and efficient approach by applying wedge-based constraints instead of force-based methods. Macklin et al. [34]. further refined and optimized PBD for real-time interaction.

More recently, the VBD algorithm that has been proposed provides an efficient approach to parallelize large-scale computations. By processing nodes in block units, VBD significantly enhances performance, particularly in simulations involving a high number of nodes [35]. In this paper, we implement cloth simulation using both the Position-Based Dynamics and Vertex Block Descent algorithms, both of which are known for their suitability in real-time simulations, and analytically compare their performance.

2.2. Position-Based Dynamics

2.2.1. Key Characteristics of Position-Based Dynamics

The PBD algorithm offers a method for controlling deformable objects by directly manipulating their positions rather than computing acceleration through forces. By bypassing the intermediate step of velocity calculation, this approach ensures computational stability and provides significant advantages in collision handling, particularly in resolving penetration issues between objects. The key characteristics of the PBD algorithm are as follows:

• Position-Based Approach: The PBD algorithm enforces physical constraints by directly adjusting the positions of objects, rather than utilizing a force-based approach. This allows for physical simulation to be achieved through direct positional modifications.
• Stability: PBD prevents excessive energy accumulation due to external forces by directly correcting position values without the need for velocity calculations. This approach effectively reduces instability in the system.
• Efficiency: The PBD algorithm is notably efficient, especially in collision handling. At each time step, collision constraints are introduced to prevent object penetration. Bender [36] demonstrated that in scenarios involving self-collision, such as cloth movement and overlap, PBD ensures real-time performance, compared to traditional force-based methods.

2.2.2. Key Formula of Position-Based Dynamics Algorithm

The main formula of the PBD algorithm is related to how to solve constraints based on location.

• Update location to meet constraints
  The position of the object in the PBD algorithm is updated according to the following equation:

  $$\mathsf{\Delta }Pi=-\lambda \nabla C\left(Pi\right)$$

  (1)

  where $Pi$ is the position of vertex $i$, $C\left(Pi\right)$ is the position-based constraint, $\nabla$ is the gradient of the constraint, and $\lambda$ is the Lagrange multiplier that regulates the strength of the constraint. This equation is a method of adjusting the position of an object to satisfy the constraint and calculates the final position by repeatedly projecting the constraint.
• Distance constraint
  The distance constraint between the two vertices $i$ and $j$ is defined as

  $$C\left(Pi,Pj\right)=\parallel Pi-Pj\parallel -d$$

  (2)

  where $d$ is the desired distance. To satisfy the corresponding constraints, each vertex is updated as follows:

  $$\mathsf{\Delta }Pi=-{\displaystyle \frac{wi}{wi+wj}}\left(\parallel Pi-Pj\parallel -d\right){\displaystyle \frac{Pi-Pj}{\parallel Pi-Pj\parallel }}$$

  (3)

  $$\mathsf{\Delta }Pj=-{\displaystyle \frac{wj}{wi+wj}}\left(\parallel Pi-Pj\parallel -d\right){\displaystyle \frac{Pi-Pj}{\parallel Pi-Pj\parallel }}$$

  (4)

  where $wi$ and $wj$ are the weights of each vertex.

2.3. Vertex Block Descent

2.3.1. Key Characteristics of Vertex Block Descent

The VBD algorithm provides an efficient approach to solving the dynamics of deformable objects in physically based simulations by employing a position-based update mechanism akin to PBD. Unlike traditional methods, VBD incorporates a modified Implicit Euler integration scheme to enhance stability during time integration [35]. Central to VBD is the Block Coordinate Descent approach, which iteratively updates the position of each vertex using a Gauss–Seidel-like process across the mesh of the object, significantly reducing the computational cost. The key characteristics of the VBD algorithm are as follows:

• Block Coordinate Descent: This method performs vertex-level parallel computation, independently calculating and updating each node of the mesh to maximize parallelism. In particular, mesh coloring techniques are employed to minimize task handling bottlenecks, thereby improving computational efficiency.
• Stability: VBD ensures high stability even under large time steps, making it well suited for real-time simulations. This stability is particularly advantageous when computational resources are constrained, enabling robust results without compromising accuracy.
• Efficiency: By using a localized linear system, VBD achieves relatively low computational cost, thus demonstrating high efficiency in its calculations.
• Optimization for Large-Scale Simulations: The VBD algorithm is adept at handling common optimization challenges inherent in large-scale simulations. It can efficiently manage complex physical interactions, such as object-to-object collisions and self-collisions, even in scenarios involving a substantial number of nodes.

2.3.2. Key Formula of Vertex Block Descent Algorithm

The VBD algorithm works by optimizing the position of each vertex individually to minimize the energy of the entire system. At this time, we solve the local system for each vertex, and proceed with global optimization:

• Minimize global energy
  The purpose of the VBD algorithm is to minimize the energy $G\left(x\right)$ of the entire system. $G\left(x\right)$ is defined as follows:

  $$G\left(x\right)={\displaystyle \frac{1}{2h^2}}{\parallel x-y\parallel }_M^2+E\left(x\right)$$

  (5)

  where $h$ is the time step; $y$ is the predicted position, including the external acceleration; and $E\left(x\right)$ is the deformable energy.
• Minimize local energy
  The VBD algorithm locally minimizes the energy for each vertex $i$. The local energy $G_i\left(x\right)$ of each vertex is defined as

  $$G_i\left(x\right)={\displaystyle \frac{m_i}{2h^2}}{\parallel x_i-y_i\parallel }^2+{\displaystyle \sum }_{j\in F_i}{E}_j\left(x\right)$$

  (6)

  where $F_i$ is the set of all force elements acting on vertex $i$.
• Update the vertex location
  To update the position of each vertex, we define a linear system using the Hessian matrix and Newton’s method:

  $$H_i\mathsf{\Delta }{x}_i=f_i$$

  (7)

  where $H_i$ is the Hessian matrix of vertex $i$, $f_i$ is the total force acting on the vertex, and $\mathsf{\Delta }{x}_i$ is the position change.

The VBD algorithm performs this process repeatedly several times, gradually reducing the energy in the system and converging to the optimal state.

2.4. Unity Engine

Game engines are comprehensive software frameworks that integrate essential technologies for game development, including graphics rendering, physics simulation, audio processing, artificial intelligence, and networking. Core features of game engines include 3D model and texture rendering, lighting effects and shadow generation, physics-based simulations, animation handling, and support for interactive function. By offering these capabilities within a unified framework, game engines enable seamless development of content across diverse platforms, such as VR, AR, XR, and games. Among the available game engines, Unity stands out as one of the most widely used, finding applications not only in game development but also in various simulation domains. For instance, Xu et al. [37] utilized Unity and the PhysX engine to construct a model to simulate the backdraft phenomena model, while Mohan et al. [38] implemented VR-based surgical simulations using Unity, effectively applying deformable object algorithms to simulate human organs and animal models. These examples demonstrate the versatility of game engines, highlighting their potential for facilitating the implementation of deformable object algorithms across a wide range of fields.

3. Method

In the Unity environment implemented in this paper, the PBD algorithm and VBD algorithm derive results with different fps values, depending on the performance of the PC and the number of nodes of the model being simulated.

Table 2. Environment for tests.

Name	Specification
CPU	Intel i7-13700, 2.1 GHz
GPU	Nvidia GeForce RTX 4070 Ti, 12 GB VRAM
Memory	64 GB
Dev Tool	Unity 2022.3.30f1

shows the use environment of the computer for testing the simulation:

3.1. Position-Based Dynamics Progression

Algorithm 1 shows the flow of cloth simulation using the Unity version of the PBD algorithm implemented in this study as a pseudocode:

Algorithm 1: Position-Based Dynamics for Cloth Simulation

1: Initialize cloth mesh, rest positions, and parameters

2: For each time step:

3:  PredictPositions()

4:  // PBD core loop

5:  For iteration = 1 to solverIterations:

6:    SolveDistanceConstraints()

7:    SolveBendingConstraints()

8:  UpdateVelocitiesAndPositions()

9:  HandleExternalCollisions()

10:  HandleSelfCollisions()

11: Function PredictPositions():

12:  For each vertex v:

13:    If v is not pinned:

14:     v.predictedPosition = v.position + timeStep * v.velocity + gravity * timeStep^2 / 2

15: Function SolveDistanceConstraints():

16:  For each edge (v1, v2):

17:    restLength = initialLength(v1, v2)

18:    currentVector = v2.predictedPosition - v1.predictedPosition

19:    currentLength = length(currentVector)

20:    correction = (currentLength - restLength) * currentVector / currentLength

21:    If v1 is not pinned:

22:     v1.predictedPosition += 0.5 * stiffness * correction

23:    If v2 is not pinned:

24:     v2.predictedPosition -= 0.5 * stiffness * correction

25: Function SolveBendingConstraints():

26:  For each triangle pair (t1, t2):

27:    Calculate dihedral angle

28:    Calculate bending force

29:    Apply force to vertices of t1 and t2

30: Function UpdateVelocitiesAndPositions():

31:  For each vertex v:

32:    If v is not pinned:

33:     v.velocity = (v.predictedPosition - v.position) / timeStep

34:     v.velocity *= (1 - damping)

35:     v.position = v.predictedPosition

36: Function HandleExternalCollisions():

37:  For each vertex v:

38:    If v collides with external object:

39:     Move v to collision surface

40:     Update v.velocity (reflect or absorb)

41: Function HandleSelfCollisions():

42:  For each vertex pair (v1, v2):

43:    If distance(v1, v2) < collisionThreshold:

44:     Separate v1 and v2

45:     Update velocities of v1 and v2

The algorithm begins by representing the cloth as a mesh structure that is composed of interconnected vertices. Each vertex holds position and velocity data, and is linked to neighboring vertices, establishing the structural integrity of the cloth. Each simulation step consists of the following sequential processes:

• Prediction of Vertex Positions: The algorithm first predicts the subsequent position of each vertex by factoring in its current position, velocity, and gravitational forces. This prediction accounts for the time step, ensuring that pinned vertices remain fixed.
• Constraint Resolution: Physical constraints on the cloth are resolved through multiple iterations. The two primary constraints are the distance constraint and the bending constraint. The distance constraint prevents overstretching or compression by maintaining the original distance between connected vertices, with the stiffness parameter controlling the cloth’s stretch and crumple response. The bending constraint, which manages the extent of bending, is addressed by calculating the angle between adjacent triangles.
• Velocity and Position Update: The new velocity and position of each vertex are then updated based on the predicted positions. A damping parameter is applied in this stage to simulate kinetic energy loss, allowing for the cloth to naturally come to rest, rather than moving indefinitely.
• Collision Handling: Two types of collisions are managed: external collisions (between the cloth and another object) and self-collisions (within the cloth itself). For external collisions, the impacted vertex is repositioned on the collision surface, and its velocity is appropriately adjusted. For self-collisions, when different parts of the cloth come too close, the collision is detected, and the vertices are separated accordingly.

These stages ensure realistic cloth behavior, balancing physical accuracy and computational efficiency for real-time simulation applications.

3.2. Vertex Block Descent Progression

Algorithm 2 shows the flow of cloth simulation using the Unity version of the VBD algorithm implemented in this study as a pseudocode.

Algorithm 2: Vertex Block Descent for Cloth Simulation

1: Initialize cloth mesh, rest positions, and parameters

2: For each time step:

3:  AdaptiveInitialization()

4:  // VBD core loop

5:  For iteration = 1 to maxIterations:

6:   For each color in vertexColors:

7:     For each vertex v with current color:

8:     If v is not pinned:

9:      constraint_energy = ComputeConstraintEnergy(v)

10:      hessian = ComputeLocalHessian(v)

11:      deltaX = Solve(hessian, force)

12:      v.position += deltaX

13:    HandleExternalCollisions()

14:    HandleSelfCollisions()

15:  ApplyVelocityUpdate()

16: Function AdaptiveInitialization():

17:  For each vertex v: 25 Estimate acceleration

18:    v.predicted_position = v.position + timeStep * v.velocity + estimated_acceleration * timeStep^2 / 2

19: Function ComputeConstraintEnergy(v):

20:  energy = ComputeInertiaEnergy(v)

21:  For each neighbor n of v:

22:    energy += ComputeSpringEnergy(v, n)

23:  Return energy

24: Function ComputeLocalHessian(v):

25:  Compute Hessian matrix based on local deformation

26: Function Solve(hessian, gradient):

27:  Return hessian^(-1) * gradient

28: Function HandleExternalCollisions():

29:  Detect and resolve collisions for each vertex

30: Function HandleSelfCollisions():

31:  For each vertex v:

32:    For each other vertex u:

33:     If distance(v, u) < collisionThreshold:

34:      Apply repulsion force between v and u

35:      Update v.position and u.position

36:   // Optional: Continuous Collision Detection (CCD)

37:   For each edge e1:

38:    For each edge e2:

39:     If e1 and e2 intersect:

40:       Resolve edge–edge collision

The algorithm for cloth simulation initializes with a mesh structure, where each vertex has a set position, velocity, and connectivity to neighboring vertices, forming the cloth structure. The simulation process iterates through time steps, with each step composed of sequential stages that ensure realistic cloth behavior. These stages are as follows:

• Mesh Initialization: The algorithm initializes the cloth mesh, setting up the initial positions of each vertex and defining necessary parameters, such as stiffness and damping factors.
• Adaptive Initialization: At each time step, the algorithm starts with Adaptive Initialization, where it estimates the acceleration of each vertex, and predicts its next position. This is calculated by integrating the velocity and the estimated acceleration over the time step, with the following formula:

  v.predicted_position = v.position + timeStep × v.velocity + estimated_acceleration × timeStep²/2

  (8)
• Iterative Optimization: The algorithm then enters the core iterative loop, which runs for a specified maximum number of iterations. Within each iteration, the vertices are processed based on their assigned color group, where vertices in each color can be optimized independently. This vertex-coloring technique groups vertices to allow for parallel processing. For each vertex v in the current color group:
  • Compute Constraint Energy: The algorithm calculates the constraint energy for the vertex, which includes both the inertial energy and the spring energy relative to neighboring vertices. The spring energy helps maintain the original distances between connected vertices, preventing excessive stretching or compression.
  • Compute Local Hessian Matrix: The local Hessian matrix is then calculated to capture the local deformable of the vertex. This matrix helps in solving for the position update by approximating the local stiffness of the vertex.
  • Solve for Position Update: Using the Hessian and the energy gradient, a linear system is solved to compute the position variation Δx, which is then applied to the position of the vertex.
  • Velocity and Damping Update: After all iterations, the algorithm updates the velocity of each vertex based on the changes in position, applying a damping factor to simulate energy loss. This damping allows for the cloth to settle into a resting state, preventing perpetual motion.
• Collision Handling: After updating the positions within each iteration, collision handling takes place:
  • External Collisions: For each vertex, collisions with external objects are detected and resolved by repositioning the vertex onto the collision surface, adjusting its velocity accordingly.
  • Self-Collisions: For internal cloth collisions, the algorithm checks the distance between vertices. If two vertices come closer than a set collision threshold, a repulsive force is applied to separate them. Edge-to-edge collisions are also managed using Continuous Collision Detection (CCD) to resolve intersections between edges within the cloth.

These steps in the VBD algorithm in Unity ensure a balance of physical accuracy and computational efficiency, making it suitable for real-time cloth simulations that handle complex interactions while preserving the structural integrity of the cloth.

4. Results

The following is the result of comparing the average fps after executing cloth simulation of PBD and VBD for each situation of hanging, object-to-object collision, and self-collision. Equation (9) shows how the results are compared:

Comparison(%) = [(VBD fps − PBD fps) / PBD fps] × 100

(9)

4.1. Hanging Cloth Simulation

In the case of the hanging simulation, mesh monitoring was conducted using the wind function in Unity to observe the state of the mesh. Figure 1 shows the result for a 64 × 64 node configuration. The simulations were performed under identical parameter settings, and it was confirmed that the visual outcomes were almost identical. Figure 2 and

Table 3. Average fps for each node in the hanging cloth simulation.

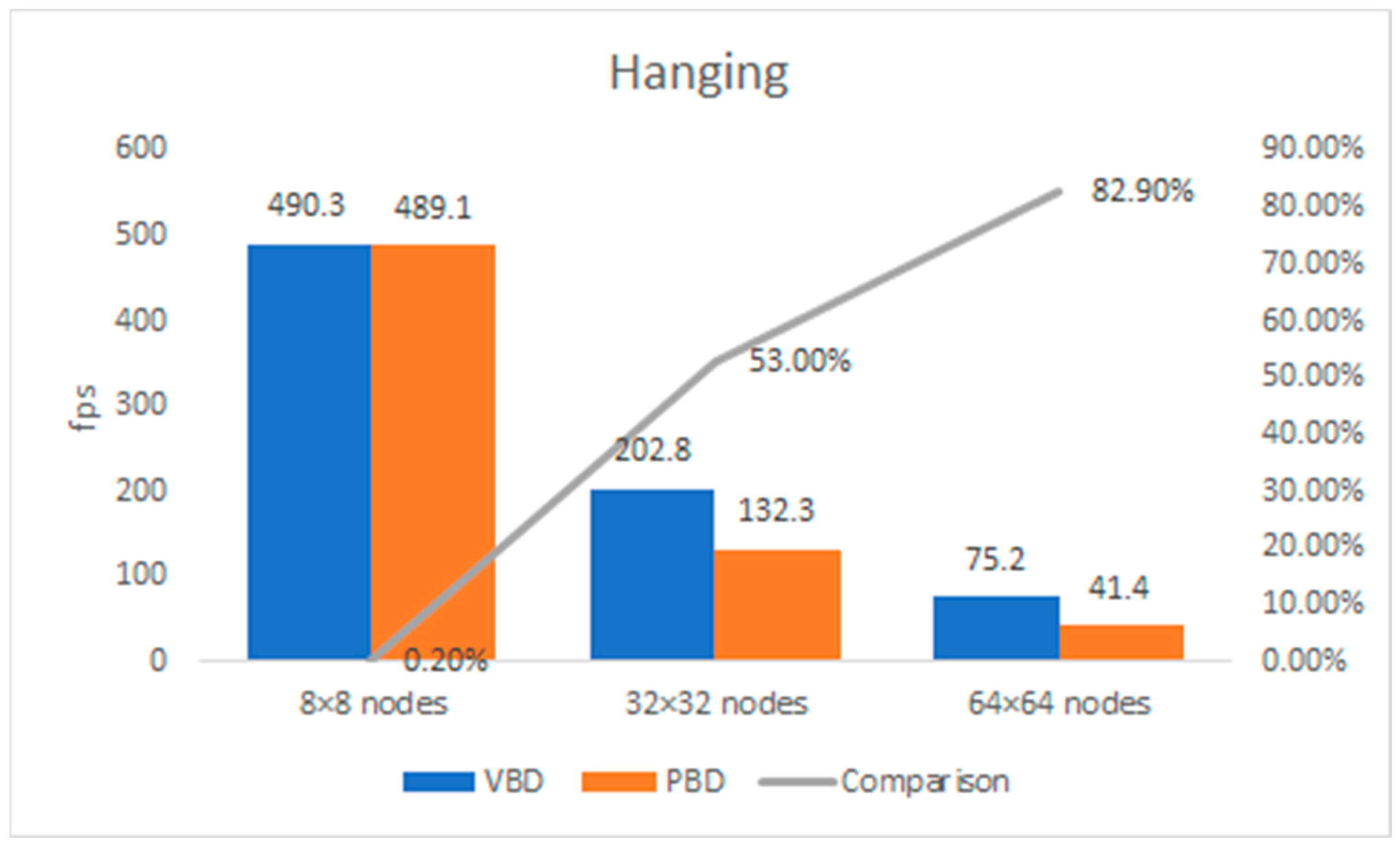
Hanging	8 × 8 Nodes	64 × 64 Nodes	128 × 128 Nodes
VBD	490.3 fps	202.8 fps	75.2 fps
PBD	489.1 fps	132.3 fps	41.4 fps
Comparison	0.20%	53.0%	82.9%

presents the cloth simulation results for both PBD and VBD. All simulation parameters were kept consistent, with the time step set to 0.01 s.

4.2. Object-to-Object Collision Cloth Simulation

In the object-to-object collision simulation, a red sphere collided with a cloth. The simulation was conducted by gradually increasing the number of nodes to the maximum level that still ensured real-time performance. Node configurations of 8 × 8, 32 × 32, and 64 × 64 were tested, and Figure 3 shows the collision result for the 64 × 64 node configuration. A slight difference was observed in the friction behavior of the sphere due to differences in the collision calculation processes between the PBD and VBD algorithms. However, both simulations demonstrated realistic expressive power. Figure 4 and

Table 4. Average fps for each node in the object-to-object collision simulation.

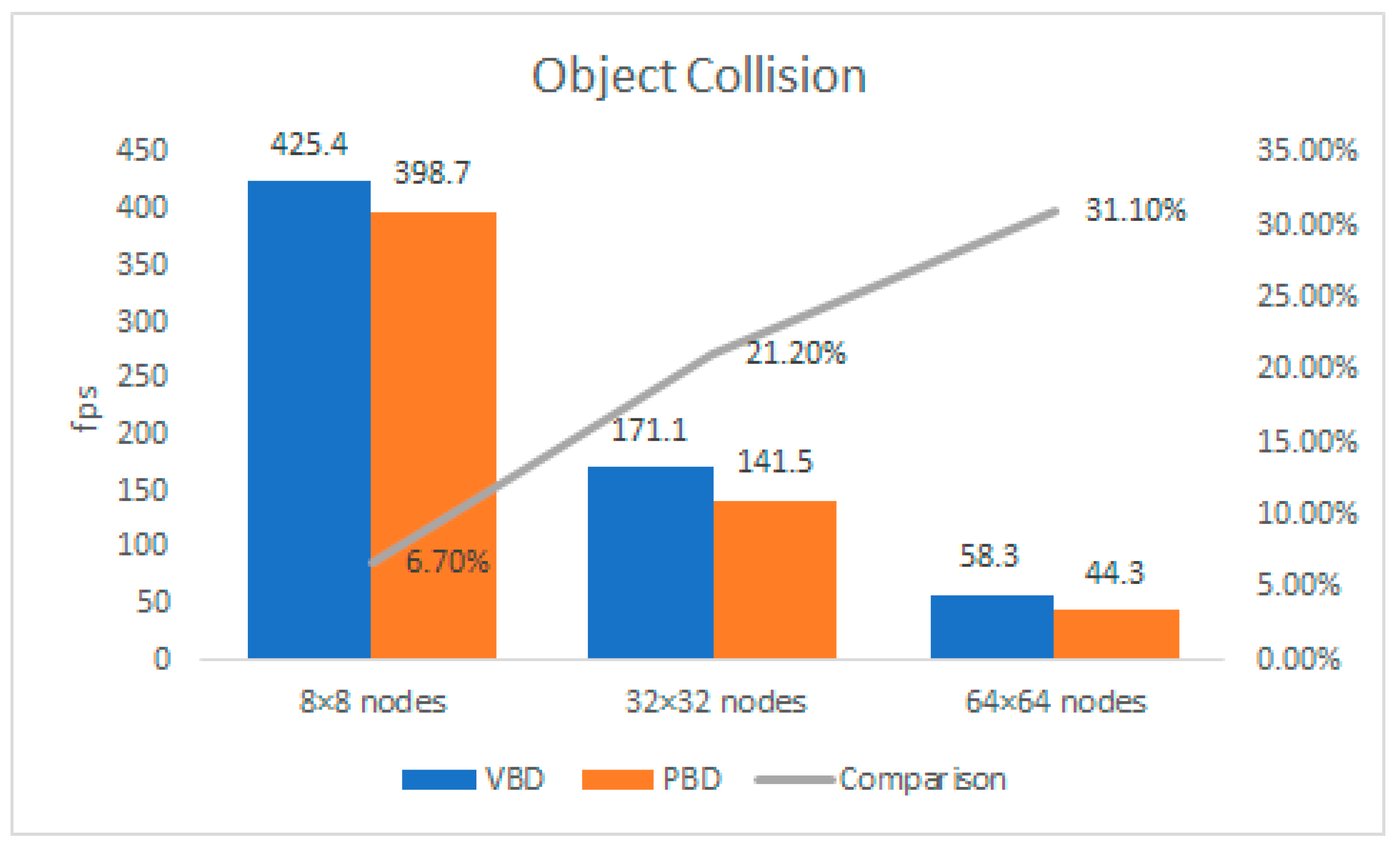
Object Collision	8 × 8 Nodes	32 × 32 Nodes	64 × 64 Nodes
VBD	425.4 fps	171.1 fps	58.3 fps
PBD	398.7 fps	141.5 fps	44.3 fps
Comparison	6.7%	21.2%	31.1%

presents the results of the object-to-object collision simulation. All simulation parameters were kept identical, with the time step set to 0.01 s.

4.3. Self-Collision Cloth Simulation

In the self-collision simulation, textures were added to the previously implemented simulation to observe folding patterns, with textures applied to both the front and back sides. As the number of nodes increased to the maximum level ensuring real-time performance, the simulation maintained real-time fps at 8 × 8 and 16 × 16 node configurations. However, as the computational complexity increased exponentially from 32 × 32 nodes, the fps dropped significantly. Figure 5 shows the result of the collision at the 16 × 16 node configuration. Both simulations reproduced realistic wrinkle effects similar to actual cloth, but differences in wrinkle direction were observed due to variations in their calculation methods. Figure 6 and

Table 5. Average fps for each node in the self-collision simulation.

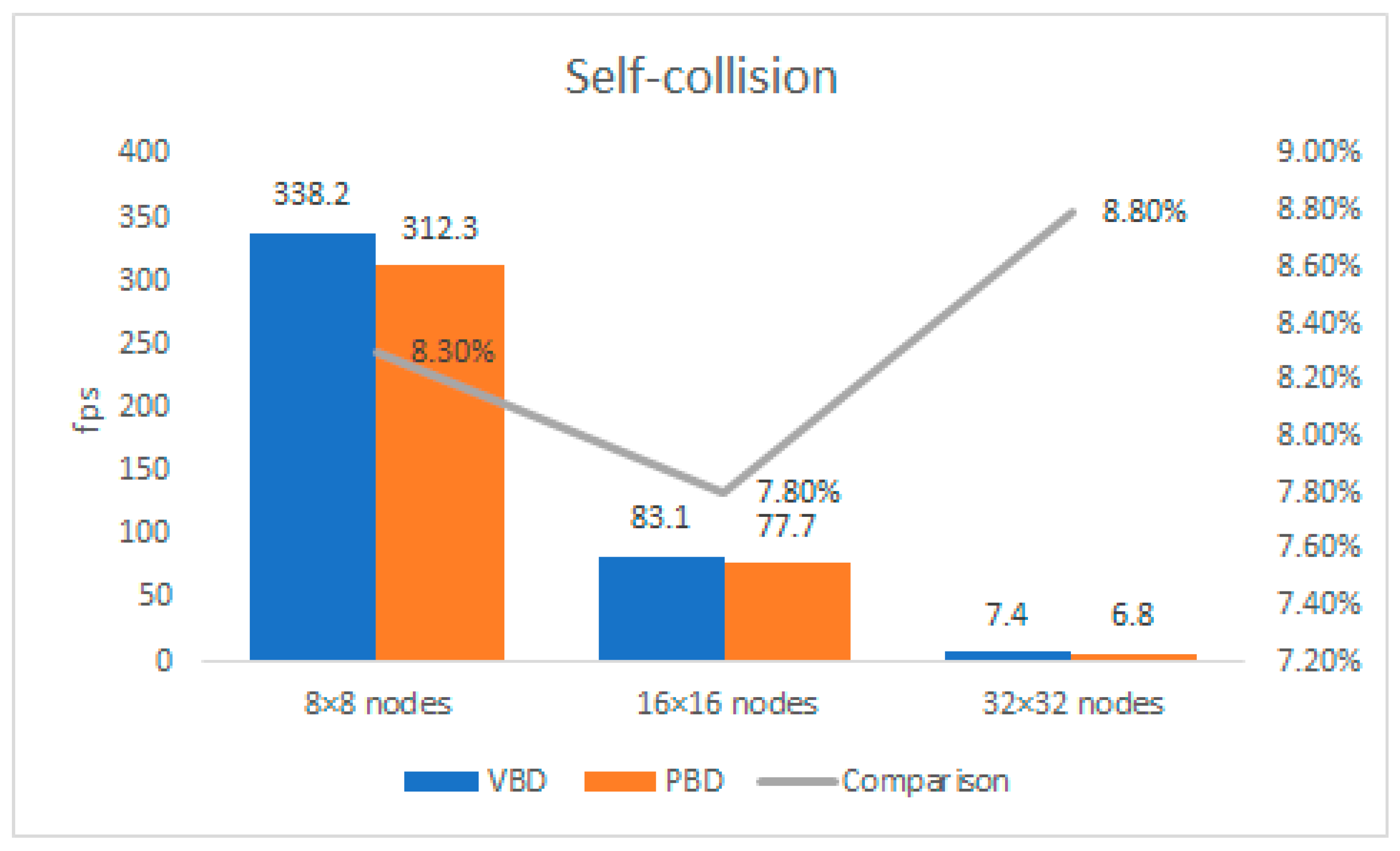
Self-Collision	8 × 8 Nodes	16 × 16 Nodes	32 × 32 Nodes
VBD	338.2 fps	83.1 fps	7.4 fps
PBD	312.3 fps	77.7 fps	6.8 fps
Comparison	8.3%	7.8%	8.8%

present the simulation results for self-collisions using PBD and VBD. All simulation parameters were kept identical, with the time step set to 0.01 s.

4.4. Guidelines for Maintaining Real-Time Performance

As discussed above, the difference in fps was compared based on the number of nodes where both simulations yielded comparable results. The findings indicate that under the same node configurations, VBD achieved better performance than PBD. Based on these results, we evaluated the maximum number of nodes each simulation could handle while maintaining a stable 30 fps, ensuring real-time performance.

Table 6. Maximum number of nodes for each simulation.

	Node × Node (Total Nodes)	fps
Hanging
VBD	120 × 120 (14,400)	30.1
PBD	93 × 93 (8649)	30.6
Object-to-object collision
VBD	92 × 92 (8464)	30.2
PBD	80 × 80 (6400)	30.1
Self-collision
VBD	23 × 23(529)	30.1
PBD	21 × 21(441)	31.5

presents the maximum number of nodes each simulation could support, and the corresponding average fps using these configurations:

5. Discussion

So far, we have compared and measured the difference in fps and the maximum number of nodes that can be expressed in the same time step environment. Following this, the time step was increased to check when the cloth object became abnormal, to check the maximum calculation section limit of PBD and VBD.

In the hanging simulation, the fps of each algorithm was compared using the standard 0.01 s time step. However, when the time step was increased to 0.02 s, the cloth simulated with the PBD algorithm exhibited sagging, as highlighted by the red circle in Figure 7. A similar sagging phenomenon was also observed in the object-to-object collision scenario, further increasing the inaccuracy of the algorithm’s physical calculations. This inaccuracy resulted in abnormal energy accumulation and dissipation, which negatively affected the stability of the simulation.

Table 7. Changes in hanging cloth area by time step.

Time Step	0.01 s	0.02 s
VBD	100–101.5%	100–101.8%
PBD	100–101.1%	100–107.4%

presents the variation in the cloth’s area during the hanging simulation for each algorithm. A larger increase in the cloth’s area indicates reduced computational accuracy.

In the self-collision simulation, while significant sagging did not occur, errors were observed in the collision process itself. When the time step was increased to 0.1, it was noted that PBD produced artifacts, with many objects penetrating the overlapping parts of the cloth, as Figure 8 shows. In contrast, VBD demonstrated relatively stable collision results, even with the same 0.1 time step. The red circle in Figure 8 shows where the mesh is broken. This indicates that the calculation accuracy of PBD was lower than that of VBD, as the inaccuracy in the physical simulation increased with the larger time step. Therefore, this test confirms that VBD can simulate larger time steps more stably compared to PBD.

6. Conclusions and Future Works

VBD, which was introduced in 2024, is an improved algorithm over the previously published methods. In this study, the existing VBD algorithm, originally implemented in C++, was integrated into Unity, a physics engine, for simulation. Despite being conducted in a CPU-only environment without GPU acceleration, VBD demonstrated better fps performance than PBD. In the hanging scenario, as the number of nodes increased, VBD achieved up to 82.9% better fps, showing a clear performance advantage over PBD. In the object-to-object collision scenario, VBD provided up to 31.1% higher fps with the same number of nodes. As node counts increased, the computational load grew rapidly, and the performance gap between VBD and PBD widened further than in the hanging scenario. In the self-collision scenario, the difference in performance between VBD and PBD was smaller than in the previous cases, likely due to the increased computational complexity, which limited performance in the CPU-only environment. These results are based on identical parameters, time steps, and node counts for both algorithms. Additionally, the maximum number of nodes that could sustain real-time performance was measured for each scenario. In this study, 30 fps was established as the minimum standard for real-time performance, representing the lowest frame rate at which games and animations can maintain real-time responsiveness across various graphic content types. However, studies by Lee, S. et al. [39] suggest that lower frame rates in VR and AR environments can lead to motion sickness. Therefore, a minimum frame rate of 60 fps is recommended for VR and AR content to ensure a smoother and more comfortable user experience. In the hanging simulation, PBD could maintain real-time performance with up to 93 × 93 nodes, while VBD supported up to 120 × 120 nodes. For object-to-object collisions, the limits were 92 × 92 nodes for PBD and 80 × 80 nodes for VBD. In self-collision simulations, PBD and VBD could sustain real-time performance with up to 21 × 21 and 23 × 23 nodes, respectively. As expected, as the operations became more complex, the limitations in the CPU-based simulations became more noticeable. This study proposed a simulation design methodology utilizing only CPU resources, excluding compute shaders, implemented in C# within Unity. This approach may demonstrate improved results on devices relying solely on CPU computation, particularly if advancements in memory or CPU performance are achieved. Furthermore, since VBD is optimized for parallel processing, it is expected to achieve significantly better performance with GPU acceleration through compute shaders. Future research will focus on improving computational processes and implementing a variety of physical simulation algorithms, including VBD, PBD, the Mass-Spring System, and Extended Position-Based Dynamics (XPBD), on GPU platforms. Comparative studies will further optimize these algorithms. Future work will also explore real-time simulations for augmented reality (AR), virtual reality (VR), and resource-constrained platforms, such as mobile and web environments, using optimized algorithms tailored for these platforms.