Proactive Production Scheduling Approach for Off-Site Construction with Due Date Uncertainty
Abstract
1. Introduction
2. Relevant Studies on PC Production Scheduling Under Uncertain Environments
2.1. Reactive Approach
2.2. Proactive Approach
3. Proactive PC Production Scheduling Model with Contractor Schedule Uncertainty
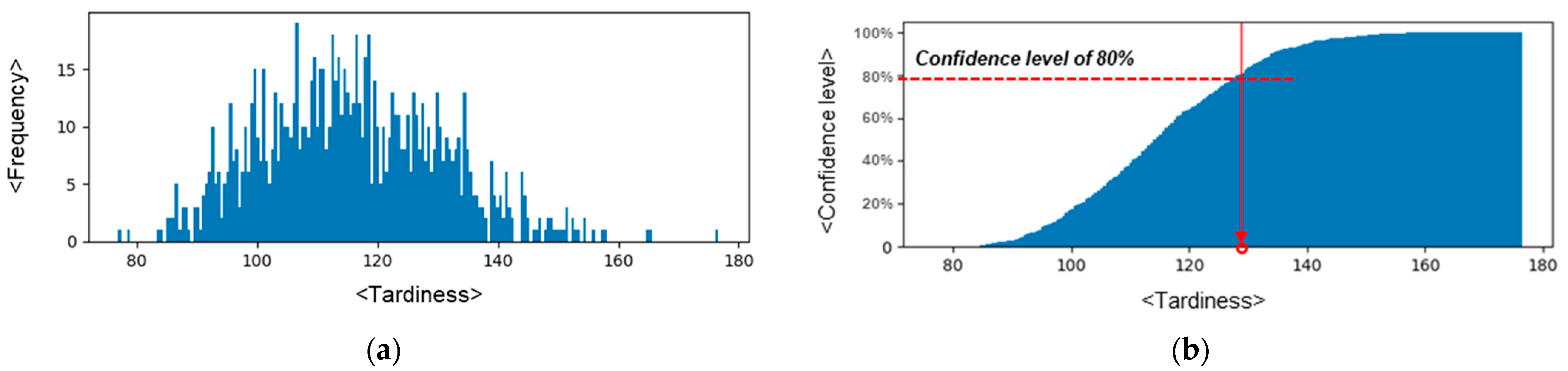
3.1. MC-Method-Based PC Production Simulation Module
| Algorithm 1: MC-method-based PC production simulation module | |
| Input: | job sequence, contractor’s due date reliability, confidence level (, # of simulations (S), processing time ( |
| Output: | tardiness at the confidence level ( |
| 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16: 17: 18: 19: 20: 21: 22: | FOR simulation in 1 to S DO Generate the changed due date dataset () based on the contractor’s due date reliability FOR process in 1 to 6 DO FOR each in job sequence DO IF Set the start time of job in process () as the finish time of job in previous process () ELSE Set the start time of job in process () as the finish time of previous job () Calculate the finish time () by adding to the processing time of PC type t in process p () IF the finish time of the process () is out of the working hour, IF Skip the next day and add it to the processing time corresponding to the job ELSE IF , Set it to the next day ELSE Add non-working hours to it END FOR END FOR Calculate tardiness END FOR Find tardiness at the confidence level ( RETURN tardiness at the confidence level ( |
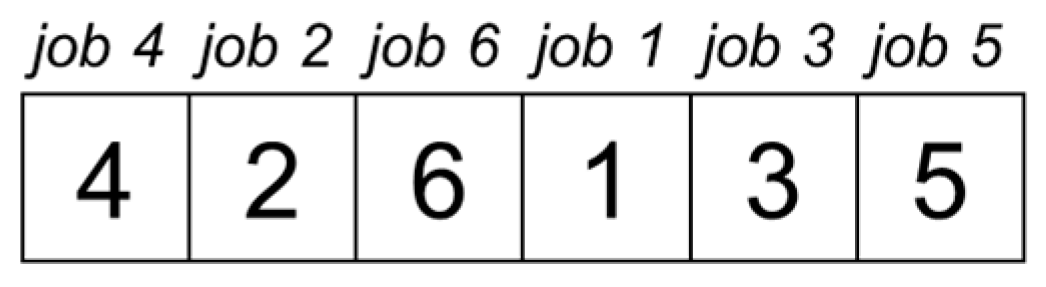
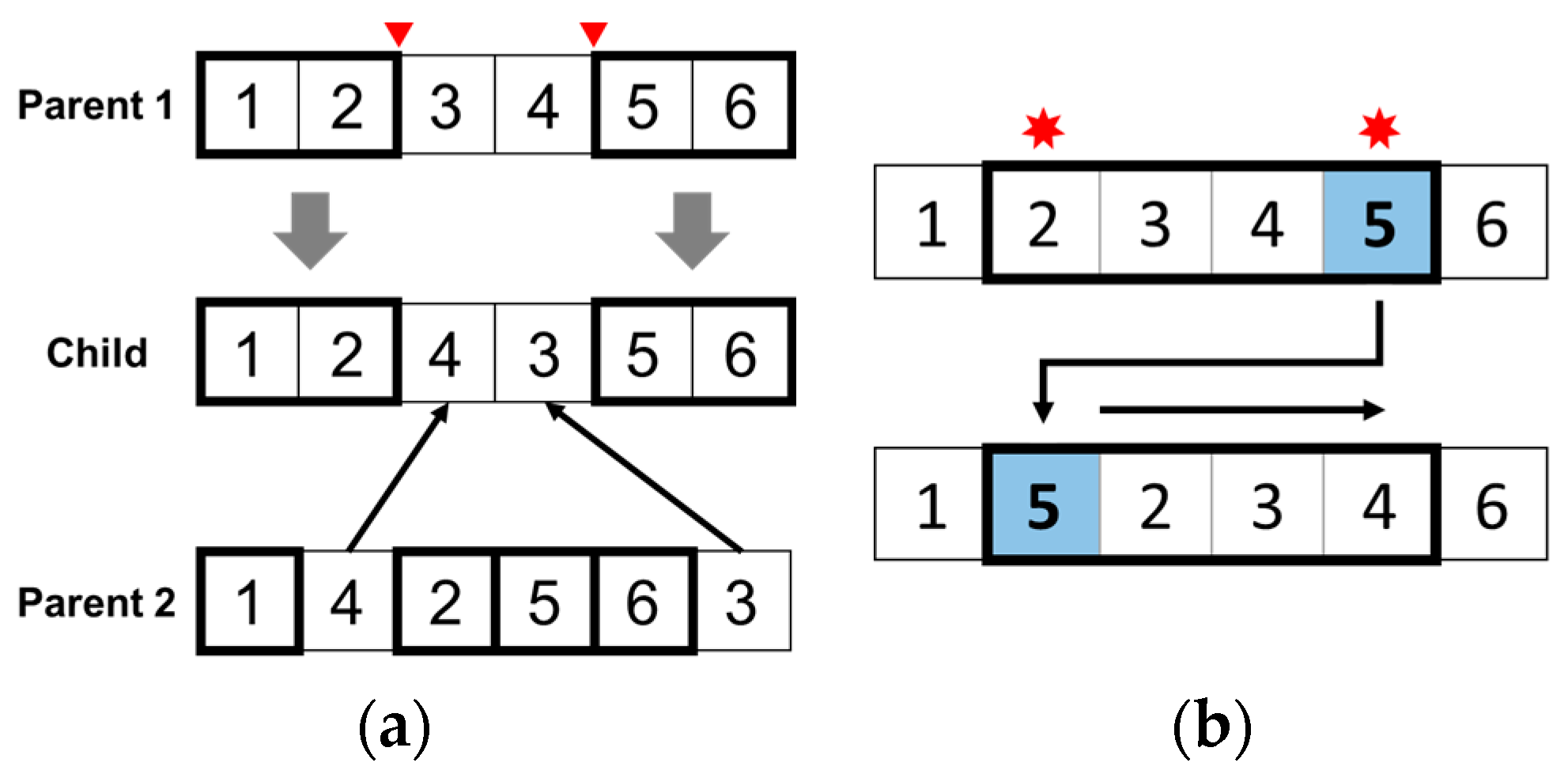
3.2. GA-Based PC Production Schedule Optimization Module
| Algorithm 2: GA-based PC production schedule optimization module | |
| Input: | population size, crossover rate, mutation rate, elite number, stopping criteria |
| Output: | the best individual in a population |
| 1: 2: 3: 4: 5: 6: 7: 8: 9: | Generate an initial population of candidate solutions to the problem Evaluate the objective function of the individual in the population by Algorithm 1 WHILE NOT stopping criteria DO Perform selection of parents from the population Produce offspring by crossover between selected parents Perform mutation on offspring Evaluate the objective function of offspring by Algorithm 1 Make a new population by replacing the worst individual in offspring with the elite individual in the population RETURN best individual in the population |
4. Experimental Study
4.1. Overview
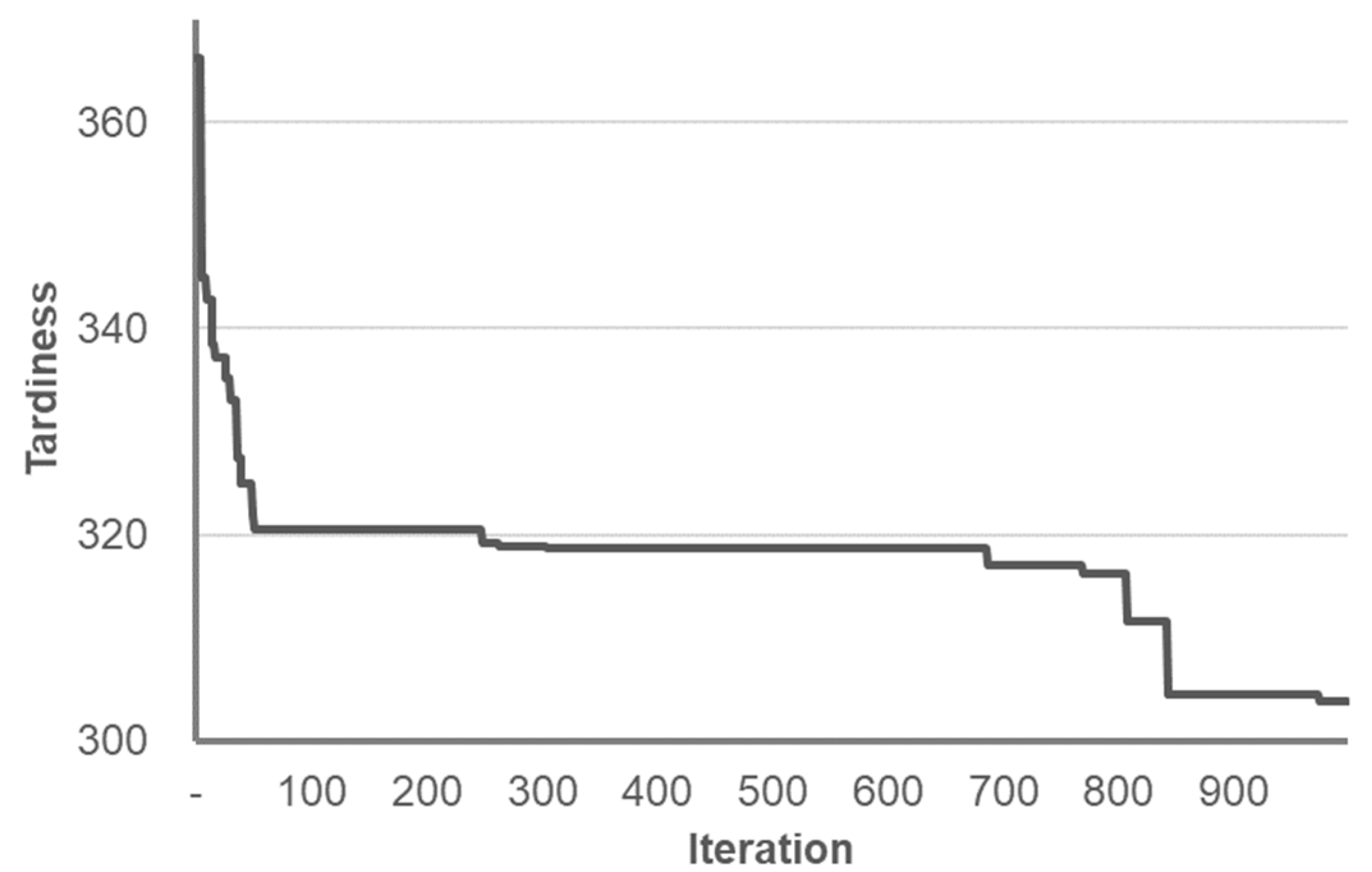
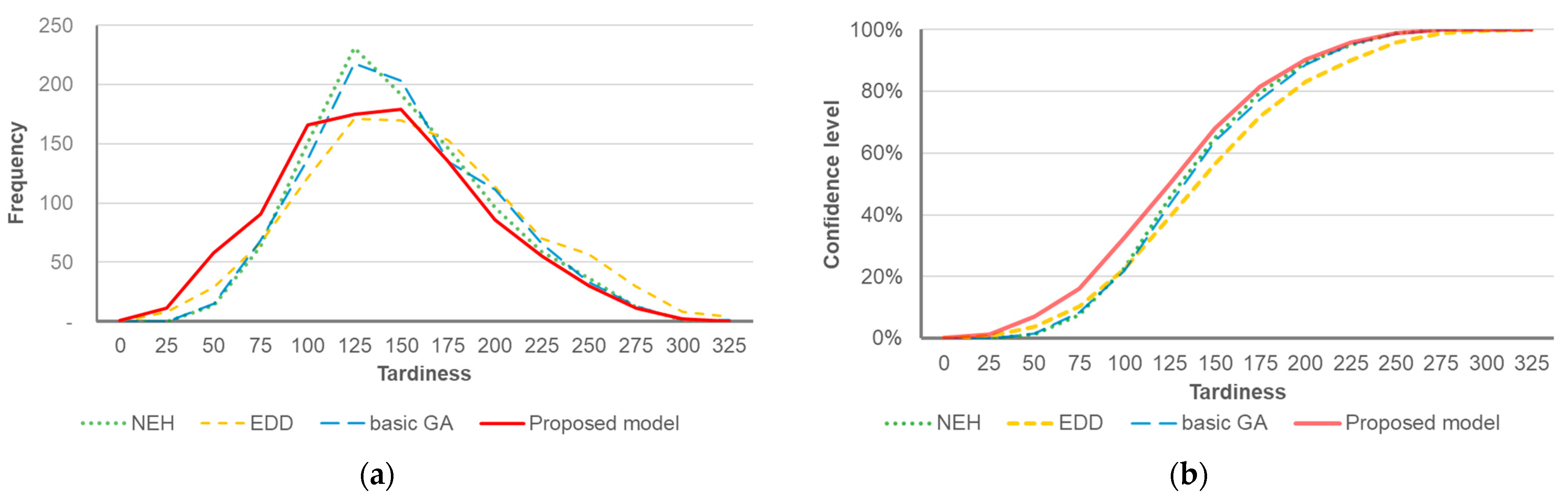
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jang, J.; Ahn, S.; Cha, S.H.; Cho, K.; Koo, C.; Kim, T.W. Toward productivity in future construction: Mapping knowledge and finding insights for achieving successful off-site construction projects. J. Comput. Des. Eng. 2021, 8, 1–14. [Google Scholar] [CrossRef]
- Kim, T.; Kim, Y.W.; Cho, H. Dynamic production scheduling model under due date uncertainty in precast concrete construction. J. Clean. Prod. 2020, 257, 120527. [Google Scholar] [CrossRef]
- Kim, T.; Kim, Y.W.; Lee, D.; Kim, M. Reinforcement learning approach to scheduling of precast concrete production. J. Clean. Prod. 2022, 336, 130419. [Google Scholar] [CrossRef]
- Goren, S.; Sabuncuoglu, I. Robustness and stability measures for scheduling: Single-machine environment. Iie Trans. 2008, 40, 66–83. [Google Scholar] [CrossRef]
- Herroelen, W.; Leus, R. Robust and reactive project scheduling: A review and classification of procedures. Int. J. Prod. Res. 2004, 42, 1599–1620. [Google Scholar] [CrossRef]
- Bonfill, A.; Espuna, A.; Puigjaner, L. Proactive approach to address the uncertainty in short-term scheduling. Comput. Chem. Eng. 2008, 32, 1689–1706. [Google Scholar] [CrossRef]
- Novas, J.M.; Henning, G.P. A reactive scheduling approach based on domain-knowledge. Comput. Aided Chem. Eng. 2009, 27, 765–770. [Google Scholar]
- Baohua, W.; Shiwei, H.E. Robust optimization model and algorithm for logistics center location and allocation under uncertain environment. J. Transp. Syst. Eng. Inf. Technol. 2009, 9, 69–74. [Google Scholar]
- Chan, W.T.; Wee, T.H. A multi-heuristic GA for schedule repair in precast plant production. In Proceedings of the 13th International Conference on Automated Planning and Scheduling (ICAPS), Trento, Italy, 9–13 June 2003; pp. 236–245. [Google Scholar]
- Ko, C.H.; Wang, S.F. GA-based decision support systems for precast production planning. Autom. Constr. 2010, 19, 907–916. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, H. Dynamic response to demand variability for precast production rescheduling with multiple lines. Int. J. Prod. Res. 2018, 56, 5386–5401. [Google Scholar] [CrossRef]
- Ma, Z.; Yang, Z.; Liu, S.; Wu, S. Optimized rescheduling of multiple production lines for flowshop production of reinforced precast concrete components. Autom. Const. 2018, 95, 86–97. [Google Scholar] [CrossRef]
- Du, J.; Dong, P.; Sugumaran, V. Dynamic production scheduling for prefabricated components considering the demand fluctuation. Intell. Autom. Soft Comput. 2020, 26, 715–723. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Hu, H.; Dai, L. Hybrid rescheduling optimization model under disruptions in precast production considering real-world environment. J. Constr. Eng. Manag. 2021, 147, 04021012. [Google Scholar] [CrossRef]
- Zhang, R.; Feng, X.; Mou, Z.; Zhang, Y. Green optimization for precast production rescheduling based on disruption management. J. Clean. Prod. 2023, 420, 138406. [Google Scholar] [CrossRef]
- Chen, J.; Liu, X. GEP algorithm-based optimization method for PCs production scheduling under due date variation. In Proceedings of the 2023 4th International Conference on Computer Engineering and Application (ICCEA), Hangzhou, China, 7–9 April 2023; pp. 347–352. [Google Scholar]
- Wang, Z.; Hu, H.; Gong, J. Framework for modeling operational uncertainty to optimize off-site production scheduling of precast components. Autom. Constr. 2018, 86, 69–80. [Google Scholar] [CrossRef]
- Benjaoran, V.; Dawood, N.; Hobbs, B. Flowshop scheduling model for bespoke precast concrete production planning. Constr. Manag. Econ. 2005, 23, 93–105. [Google Scholar] [CrossRef]
- Ghasemi, A.; Farajzadeh, F.; Heavey, C.; Fowler, J.; Papadopoulos, C.T. Simulation optimization applied to production scheduling in the era of industry 4.0: A review and future roadmap. J. Ind. Inf. Integr. 2024, 39, 100599. [Google Scholar] [CrossRef]
- Wanke, P.; Ewbank, H.; Leiva, V.; Rojas, F. Inventory management for new products with triangularly distributed demand and lead-time. Comput. Oper. Res. 2016, 69, 97–108. [Google Scholar] [CrossRef]
- Liang, T.F. Application of interactive possibilistic linear programming to aggregate production planning with multiple imprecise objectives. Prod. Plan. Contr. 2007, 18, 548–560. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Reeves, C.R. A genetic algorithm for flowshop sequencing. Comput. Oper. Res. 1995, 22, 5–13. [Google Scholar] [CrossRef]
- Murata, T.; Ishibuchi, H.; Tanaka, H. Genetic algorithms for flowshop scheduling problems. Comput. Ind. Eng. 1996, 30, 1061–1071. [Google Scholar] [CrossRef]
- Kim, Y.D. Heuristics for flowshop scheduling problems minimizing mean tardiness. J. Oper. Res. Soc. 1993, 44, 19–28. [Google Scholar] [CrossRef]

| Product Type | Processing Time (h) | |||||
|---|---|---|---|---|---|---|
| p1 | p2 | p3 | p4 | p5 | p6 | |
| P1 | 2.0 | 3.6 | 2.5 | 10 | 1.0 | 1.1 |
| P2 | 3.1 | 3.2 | 1.0 | 10 | 1.5 | 2.1 |
| P3 | 2.2 | 2.8 | 1.7 | 10 | 1.0 | 0.8 |
| P4 | 0.8 | 1.9 | 1.2 | 10 | 1.0 | 1.2 |
| P5 | 1.2 | 2.0 | 2.6 | 10 | 0.8 | 0.9 |
| P6 | 3.0 | 4.0 | 1.1 | 10 | 1.6 | 2.5 |
| P7 | 1.1 | 2.2 | 1.6 | 10 | 1.0 | 2.1 |
| Contractor | Product Type | Due Date (Most Pessimistic, Most Likely, Most Optimistic Value) |
|---|---|---|
| C1 | P1 | (24, 24, 24) |
| P2 | (24, 24, 24) | |
| C2 | P2 | (0, 24, 72) |
| P3 | (0, 24, 72) | |
| C3 | P3 | (0, 48, 120) |
| P4 | (0, 48, 120) | |
| C4 | P4 | (0, 48, 132) |
| P5 | (0, 48, 132) | |
| C5 | P5 | (0, 72, 168) |
| P6 | (0, 72, 168) | |
| C6 | P6 | (12, 96, 204) |
| P7 | (12, 96, 204) |
| Solver | Production Sequence | w/Due Date Uncertainty | w/o Due Date Uncertainty | ||
|---|---|---|---|---|---|
| Tardiness (h) | Confidence Level (%) | Tardiness (h) | Confidence Level (%) | ||
| EDD | [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12] | 335.8 | 100 | 148.6 | 39 |
| NEHedd | [6, 1, 3, 8, 5, 4, 7, 9, 2, 10, 12, 11] | 324.7 | 100 | 115.5 | 16 |
| basic GA | [6, 4, 2, 8, 5, 7, 3, 9, 1, 10, 12, 11] | 328.5 | 100 | 114.5 | 15 |
| Proposed model | [6, 1, 2, 4, 7, 3, 9, 8, 5, 10, 12, 11] | 303.8 | 100 | 134.4 | 31 |
| Solver | Production Sequence | Tardiness Based on a Confidence Level (h) | |||||
|---|---|---|---|---|---|---|---|
| 50% | 60% | 70% | 80% | 90% | 100% | ||
| EDD | [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12] | 155.6 | 169.4 | 183.9 | 202.1 | 228.7 | 324.7 |
| NEHedd | [6, 1, 3, 8, 5, 4, 7, 9, 2, 10, 12, 11] | 165.4 | 179.6 | 195.8 | 216.0 | 249.0 | 335.8 |
| basic GA | [6, 4, 2, 8, 5, 7, 3, 9, 1, 10, 12, 11] | 159.0 | 170.5 | 184.1 | 204.9 | 227.9 | 328.5 |
| Proposed model with 50% | [7, 1, 2, 4, 8, 6, 3, 9, 5, 10, 12, 11] | 138.8 | 155.2 | 171.8 | 185.9 | 213.5 | 343.1 |
| ‘’ with 60% | [7, 1, 2, 4, 8, 6, 3, 5, 9, 10, 12, 11] | 139.2 | 155.0 | 171.6 | 185.8 | 213.0 | 343.3 |
| ‘’ with 70% | [6, 1, 2, 4, 8, 3, 7, 5, 9, 10, 12, 11] | 142.0 | 156.1 | 169.8 | 190.4 | 216.4 | 316.5 |
| ‘’ with 80% | [7, 1, 2, 4, 6, 8, 3, 5, 9, 10, 12, 11] | 139.6 | 155.3 | 171.3 | 185.4 | 213.5 | 342.5 |
| ‘’ with 90% | [7, 1, 2, 4, 8, 6, 3, 5, 9, 10, 12, 11] | 139.2 | 155.0 | 171.6 | 185.8 | 213.0 | 343.3 |
| ‘’ with 100% | [6, 1, 2, 4, 7, 3, 9, 8, 5, 10, 12, 11] | 149.3 | 161.5 | 177.9 | 194.5 | 224.7 | 303.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, T.; Kim, Y.-W. Proactive Production Scheduling Approach for Off-Site Construction with Due Date Uncertainty. Appl. Sci. 2024, 14, 11017. https://doi.org/10.3390/app142311017
Kim T, Kim Y-W. Proactive Production Scheduling Approach for Off-Site Construction with Due Date Uncertainty. Applied Sciences. 2024; 14(23):11017. https://doi.org/10.3390/app142311017
Chicago/Turabian StyleKim, Taehoon, and Yong-Woo Kim. 2024. "Proactive Production Scheduling Approach for Off-Site Construction with Due Date Uncertainty" Applied Sciences 14, no. 23: 11017. https://doi.org/10.3390/app142311017
APA StyleKim, T., & Kim, Y.-W. (2024). Proactive Production Scheduling Approach for Off-Site Construction with Due Date Uncertainty. Applied Sciences, 14(23), 11017. https://doi.org/10.3390/app142311017







