Time-Varying Preference Bandits for Robot Behavior Personalization

Abstract

Robots are increasingly employed in diverse services, from room cleaning to coffee preparation, necessitating an accurate understanding of user preferences. Traditional preference-based learning allows robots to learn these preferences through iterative queries about desired behaviors. However, these methods typically assume static human preferences. In this paper, we challenge this static assumption by considering the dynamic nature of human preferences and introduce the discounted preference bandit method to manage these changes. This algorithm adapts to evolving human preferences and supports seamless human–robot interaction through effective query selection. Our approach outperforms existing methods in time-varying scenarios across three key performance metrics.

1. Introduction

Recent advancements in machine learning have facilitated the interaction between robots and humans, enabling robots to offer adept services in diverse applications, such as autonomous driving systems [1] and collaborative assembly in smart factories [2]. Given these developments, it is crucial that robotic systems dynamically adapt to the preferences of users involved in these interactions. Recent approaches in robotics have employed preference-based learning (PBL) to learn user preference [3,4,5,6,7,8,9]. In PBL, human preferences are modeled as a reward function, learned by presenting users with diverse robot behaviors and having them select preferred ones. The robot’s behavior can be tailored to align with the user’s preference by maximizing the learned reward model.

While most existing methods [3,4,5,6,7,8,9] have successfully captured user preferences in an online manner, a clear limitation arises from the presumption of a stationary reward function to model user preference. Notably, user preference might evolve while interacting with robotic systems [10,11]. Hence, robots must adeptly adjust to evolving preferences to maintain appropriate behavior. For instance, initial encounters with service robots may prompt users to favor cautious behavior due to unfamiliarity, but as users grow accustomed to the robot’s presence, preferences often shift towards more task-specific behaviors, as depicted in Figure 1. Beyond this scenario, user preferences can evolve due to diverse factors, encompassing trends, emotions, and age. To address these dynamic preferences, we present a method capable of adapting to evolving user inclinations.

The challenge of adapting to dynamic user preferences can be addressed by using a non-stationary bandit framework [12]. The bandit framework [13] is extensively utilized to optimize decision-making processes under uncertain and unknown rewards, where an agent selects from a set of options, each providing stochastic rewards. The primary goal of this framework is to maximize the cumulative reward over time, thereby finding an optimal option even without the explicit knowledge of the rewards. This framework strategically balances the selection of high-potential queries against those already known to align with user preferences, enabling efficient and adaptive query selection to acquire time-varying reward functions.

In this paper, we propose a novel preference-based learning method, called discounted preference bandits (DPBs), to address time-varying preferences. First, our algorithm is inherently adaptive to time-varying environments by updating parameters based on penalized likelihood. Second, we theoretically demonstrate a no-regret convergence for the proposed method. In the simulation, the proposed method outperforms existing methods [3,5,6,7] in terms of cosine similarity, simple regret, and cumulative regret in time-varying scenarios. Finally, simulation and real-world user studies confirm that the proposed method successfully adapts to time-varying scenarios, especially with respect to robot behavior adaptation and environmental changes.

2. Related Work

2.1. Active Preference-Based Learning

Preference-based learning facilitates learning reward functions by asking queries as a form of comparison. Active learning techniques [4,5,6] have been studied concurrently to address data inefficiency problems. However, prior studies on preference-based learning [3,4,5,6,7,8,9] have always considered static reward functions. Attempts have been made to address non-stationary preferences [11], but a limitation remains in the form of multiple different reward functions defined and the time-varying property represented as a transition among the reward functions. Therefore, in this paper, we mainly consider a time-varying reward function.

2.2. Bandits for Preference-Based Learning

Our research concentrates on developing algorithms for service robots in passive scenarios, adapting to individuals’ changing preferences while providing services. Prior bandit studies [14,15,16] for time-varying preference focus on collaborative tasks where humans are actively engaged in tasks, especially in scenarios where human preference changes based on task understanding and robot dynamics. Hence, we contemplate a framework that learns solely from preference labels provided by humans, rather than relying on data where people explicitly indicate preferred actions [14] or reveal sequences of their behaviors [15]. We consider the contextual bandit framework studied to address drifting environments with time-varying parameters [17,18]. Particularly, in [18], the estimator is studied based on the time-varying generalized linear model by using a discount factor $\gamma$ to penalize old actions and rewards. We extend these ideas [17,18] to preference-based learning by applying them to the time-varying logistic bandit. While our convergence analysis techniques are similar to [17,18], we introduce a different design matrix and query selection rules.

2.3. Batch Selection

Extended query generation times can impair the reward learning process during human–robot interactions. Batch query selections have been developed alongside active learning methods to expedite query generation times. In [5], diversifying batch samples has been investigated, while a subsequent study in [7] used determinantal point processes (DPPs) to enhance both the quality and diversity of the queries. Inspired by [5,7,19], we address computational delays by selecting top-k queries at each iteration.

3. Problem Statement

3.1. Preliminaries

We consider the robot in a fully observable dynamical system. Let $s\in \mathcal{S}$ denote the continuous state of the dynamical system and $a\in \mathcal{A}$ denote the robot’s action, where $\mathcal{S}$ and $\mathcal{A}$ are state and action space, respectively. Then, we define a trajectory $\xi ={\left((s_h,a_h)\right)}_{h=0}^H\in \mathrm{\Xi }$ as a finite sequence of pairs of continuous state and action where H is the time horizon of the trajectory and $\mathrm{\Xi }$ is the set of all feasible trajectories. We assume that the user’s preference can be represented as a reward function $r:\mathrm{\Xi }\to \mathbb{R}$. Similar to prior works [4,6], a reward function is modeled as a linear function with respect to the feature vector over the trajectory, which can be written as

$$\begin{array}{c}\hfill r(\xi ;\theta ):=\theta ·\mathrm{\Phi }\left(\xi \right)=\theta ·\sum _{h=0}^H\varphi (s_h,a_h),\end{array}$$

(1)

where $\varphi$ is a feature map from $\mathcal{S}\times \mathcal{A}$ to ${\mathbb{R}}^d$, $\mathrm{\Phi }\left(\xi \right):={\sum }_{h=0}^H\varphi (s_h,a_h)$, d is a dimension of features, and $\theta$ is the parameter that encodes a user’s preference.

3.2. Problem Formulation

In general, preference-based learning (PBL) assumes that there exists an optimal parameter ${\theta }^{*}$ that best represents the user preference. Unlike the general assumption, since our goal is to model a time-varying preference, we assume that the optimal parameter ${\theta }_t^{*}$ can be changed through time t and the deviation of parameter change is not arbitrary but bounded. The more formal definition of time-varying property is explained in Section 5. Our goal is to learn the time-varying parameter ${\theta }_t^{*}$ using preference feedback collected by pairwise comparisons in an online manner.

We consider a general PBL protocol: For each iteration, the robot demonstrates a query consisting of two trajectories, ${\xi }_t^A$ and ${\xi }_t^B$, and the user provides binary feedback $R_t\in \{0,1\}$. $R_t=1$ indicates that the user prefers ${\xi }_t^A$ over ${\xi }_t^B$; otherwise, $R_t=0$ is given. From the assumption on user preference and reward model, the preference of ${\xi }_t^A$ over ${\xi }_t^B$ is equivalent to $r_t\left({\xi }_t^A\right)>r_t\left({\xi }_t^B\right)$. While the inequality between $r_t\left({\xi }_t^A\right)$ and $r_t\left({\xi }_t^B\right)$ is deterministic given a reward function, the user response can be noisy and uncertain [4,5]. Hence, the user’s noisy response is usually modeled as a probabilistic distribution [19].

$$\begin{array}{cc}\hfill P& \left(R_t\mid {\xi }_t^A,{\xi }_t^B;{\theta }_t^{*}\right)={\displaystyle \frac{e^{\left(R_{t}r\left({\xi }_t^A,{\theta }_t^{*}\right)+(1-R_t)r\left({\xi }_t^B,{\theta }_t^{*}\right)\right)}}{e^{r\left({\xi }_t^A,{\theta }_t^{*}\right)}+e^{r\left({\xi }_t^B,{\theta }_t^{*}\right)}}},\hfill \end{array}$$

(2)

4. Methods

We present a novel discounted preference bandit (DPB) to estimate the time-varying preference with the minimum number of queries. First, we newly define a context vector as the difference of feature vectors between two trajectories, i.e., $X:=\mathrm{\Phi }\left({\xi }^A\right)-\mathrm{\Phi }\left({\xi }^B\right)$, which represents the information of comparison. Let $\mathcal{X}$ be a set of possible context vectors that are converted from all trajectory pairs. Then, the query selection problem is converted to choosing a proper query vector in $\mathcal{X}$. Furthermore, based on X, the probabilistic model in (2) can be converted into the following logistic distribution,

$$\begin{array}{cc}\hfill P& \left(R_t\mid {\xi }_t^A,{\xi }_t^B;{\theta }_t^{*}\right)=e^{R_t{X}_t^{⊺}{\theta }_t^{*}}/\left(1+e^{X_t^{⊺}{\theta }_t^{*}}\right),\hfill \end{array}$$

(3)

where $X_t$ indicates a context vector of $({\xi }_t^A,{\xi }_t^B)$ that are compared at round t. By introducing a context vector $X_t$, PBL can be reduced to the online learning problem. Algorithm 1 demonstrates the online learning process of DPB to acquire time-varying reward functions. In each round t, DPB selects a batch of queries as outlined in line 4. The human then observes these queries and provides preference labels for each query as described in line 5. Finally, the parameter is updated with the collected preference data as shown in line 6.

Algorithm 1 Discounted Preference Bandits (DPBs)

Require:  $c_{\mu },\delta ,\lambda ,\gamma ,d,T,D,S,b,\mathcal{X}$ Ensure:  ${\widehat{\theta }}_T$   1: $t\leftarrow 0$, $N\left(\gamma \right)\leftarrow ln(1/(1-\gamma \left)\right)/(1-\gamma )$, and $V_0\leftarrow \lambda I_d$   2: while$t<T$  do   3:     Set ${\alpha }_t$ in Theorem 1   4:     Select top-b queries ${\left\{X_{t+i}\right\}}_{i=0}^{b-1}\in \mathcal{X}$ from (4)   5:     Demonstrate ${\left\{X_{t+i}\right\}}_{i=0}^{b-1}$ and collect ${\left\{R_{t+i}\right\}}_{i=0}^{b-1}$   6:     Estimate ${\widehat{\theta }}_t$ by solving (5) and $t\leftarrow t+b$   7: end while

4.1. Absolute Upper Confidence Bound

Suppose that the parameter ${\widehat{\theta }}_t$ is estimated, which will be explained later. At round t, DPB chooses an action based on the following action selection rule

$$\begin{array}{c}\hfill X_t:=arg\underset{X\in \mathcal{X}}{max}|X^{⊺}{\widehat{\theta }}_{t-1}| + {\alpha }_{t-1}{\parallel X\parallel }_{V_{t-1}^{-1}},\end{array}$$

(4)

where $V_{t-1}:={\sum }_{s=1}^{t-1}{\gamma }^{t-1-s}{X}_s{X}_s^{⊺}+\lambda I_d$, $X_s$ is a past query vector from $s=1$ to $t-1$, $\lambda$ is a regularization coefficient, $I_d$ is an identity matrix, and ${\alpha }_t$ is a scale parameter that controls the importance between the first and second term.

The first term indicates the absolute difference of the estimated rewards between two trajectories. Since we construct a context vector from two trajectories, X and $-X$ contain the same information, i.e., $X=\mathrm{\Phi }\left({\xi }_A\right)-\mathrm{\Phi }\left({\xi }_B\right)$ and $-X=\mathrm{\Phi }\left({\xi }_B\right)-\mathrm{\Phi }\left({\xi }_A\right)$. Hence, computing the reward via the absolute value ensures the equivalence between selecting X and $-X$. Based on this trick, the query selection method (4) employs the upper confidence bound (UCB) [20]. The second term in (4) represents the confidence bound that magnifies the amount of the uncertainty of the first term $|X^{⊺}{\widehat{\theta }}_{t-1}|$. Particularly, $V_t$, called a design matrix, embodies the empirical covariance of X, and the parameter $\gamma$ of $V_t$ is a discount factor in $(0,1]$ which penalizes an effect of past data. Intuitively, as t grows, additional query vectors are added into $V_t$, thereby augmenting the minimum eigenvalue of $V_t$ and, thus, diminishing the term ${\alpha }_t{\parallel X\parallel }_{V_{t-1}^{-1}}$. Consequently, the confidence bound eventually decreases.

Our proposed query selection method simultaneously considers two key factors by leveraging UCB. The first factor evaluates how much the chosen query contributes to learning the relevant parameters. The second factor considers how much the user will like the query when presented as a demonstration. While conventional approaches focus on the first factor [4,5,6,7], the proposed approach incorporates the second factor by applying the UCB method. The consideration of the quality of queries experienced by the user [5] is vital because it may help build user familiarity and trust with the robot. If users consistently encounter undesirable queries, it might lead to mistrust in the robot’s behavior. Therefore, our approach carefully balances these factors, adjusting the trade-off between two factors via ${\alpha }_t$, which will be further examined in Section 5.

While the query selection rule selects a single query, choosing a batch of queries is more efficient in practice. In PBL, extended durations for query generation and parameter updates can challenge users, particularly those who are less patient. Thus, we adopt a simple batched version by selecting the top b queries based on the UCB score (4), where b is the number of queries in a single batch. To approximate the solution for (4), we prepare a finite set of trajectory pairs by randomly generating and selecting two trajectories. The feature vectors derived from this set are used to compute (4) and to select the top-b queries among the finite set.

4.2. Discounted Parameter Estimation

After selecting a query and receiving its label, the parameter of the user preference is estimated considering changes over time. Let $m\left(x\right)$ denote $m\left(x\right):=ln(1+exp(x\left)\right)$. Suppose t data points are given, i.e., $(X_1,R_1),\cdots ,(X_t,R_t)$. We can estimate ${\theta }_t^{*}$ by using the discounted maximum log-likelihood scheme [12] as follows,

$$\begin{array}{c}\hfill {\widehat{\theta }}_t=\underset{{\parallel \theta \parallel }_2\le S}{argmin}\sum _{s=1}^t{\gamma }^{t-s}\left[m\left(X_s^{⊺}\theta \right)-R_s{X}_s^{⊺}\theta \right]+{\displaystyle \frac{\lambda }{2}}{\parallel \theta \parallel }_2^2,\end{array}$$

(5)

where $\gamma$ is a discount factor in $(0,1)$. This discounted negative log-likelihood (5) intuitively shows that the parameter ${\widehat{\theta }}_t$ is about to be learned as the most recent optimal parameter ${\theta }_t^{*}$ that changes over time. Note that the minimizer of (5) satisfies ${\sum }_{s=1}^t{\gamma }^{t-s}\left[\mu \left(X_s^{⊺}\theta \right)X_s-X_s{R}_s\right]+\lambda \theta =0$, which makes the gradient of (5) be equal to zero.

5. Theoretical Analysis

In this section, we analyze the cumulative regret of the proposed method. The cumulative regret is defined as

$$\begin{array}{c}\hfill {\mathcal{R}}_T:=\sum _{t=1}^T\mu \left(\right|{\left(X_t^{*}\right)}^{⊺}{\theta }_t^{*}\left|\right)-\mu \left(\right|X_t^{⊺}{\theta }_t^{*}\left|\right),\end{array}$$

(6)

where $\mu \left(x\right)$ is a logistic function, i.e., $\mu \left(x\right):={(1+e^{-x})}^{-1}$, $X_t^{*}:=arg{max}_{X\in \mathcal{X}}\mu \left(\right|X^{⊺}{\theta }_t^{*}\left|\right)$, and T is the number of iterations. $X_t^{*}$ indicates the optimal query that contains the optimal trajectory such that ${max}_{\xi }\mathrm{\Phi }{\left(\xi \right)}^{⊺}{\theta }_t^{*}$. The cumulative regret is widely employed in bandit settings as a measure to assess the efficiency of exploration methods [13]. Then, we prove that our method has the sub-linear regret under the mild assumption on ${\theta }_t^{*}$. In other words, our theoretical results tell us that the proposed method efficiently adapts to the time-varying parameters. First, we introduce the assumptions.

Assumption 1.

For $\forall t$, $\forall X\in \mathcal{X}$, and $\forall {\theta }_t^{*}$, there exist D and S such that ${\parallel X\parallel }_2\le D$ holds and $\parallel {\theta }_t^{*}{\parallel }_2\le S$ holds.

Assumption 2.

Let $B_T$ be the number of changing points. Assume that ${\theta }_t^{*}$ is changed up to $B_T$ times during T rounds.

Initially, we make Assumption 1 that both feature vectors and the parameters are bounded. Assumption 2 tells us that the user parameter is changed discretely $B_T$ times. Note that $B_T=T$ indicates the most volatile user, and $B_T=0$ indicates a stationary user. Furthermore, we define the lower bound of the derivative of the logistic function.

Definition 1.

For the logistic function μ, there exists a positive constant $c_{\mu }$ such that $c_{\mu }:={inf}_{{\parallel \theta \parallel }_2\le S,{\parallel x\parallel }_2\le D}\dot{\mu }\left(x^{⊺}\theta \right)>0$. Note that $c_{\mu }$ always exists for bounded θ and x.

Now, the set of time indices used for analysis is defined.

Definition 2.

For fixed γ, let us define $N\left(\gamma \right):=\lceil ln(1/(1-\gamma \left)\right)/(1-\gamma )\rceil$ and define an index set as $\mathcal{T}\left(\gamma \right):=\{t\in \mathbb{N}|t\le T and {\theta }_s^{*}={\theta }_t^{*} holds for \forall s\in (t-N\left(\gamma \right),t]\}$.

For t in $\mathcal{T}\left(\gamma \right)$, we can find the interval $[t-N(\gamma ),t]$ where ${\theta }_s^{*}$ does not change. In other words, ${\theta }_s^{*}$ is fixed for $N\left(\gamma \right)$ rounds. Then, we prove that the proposed method can adapt ${\theta }_s^{*}$ in at least $N\left(\gamma \right)$ rounds and, hence, the proposed method is no regret. Now, we first derive the confidence bound of the estimated parameter ${\widehat{\theta }}_t$ as follows.

Theorem 1.

Suppose that Assumptions 1–2 hold. Consider the gap between ${\widehat{\theta }}_t$ and ${\theta }_t^{*}$. For all $t\in \mathcal{T}\left(\gamma \right)$, the following inequality holds with probability at least $1-\delta$,

$$\begin{array}{c}\hfill \left|X^{⊺}({\widehat{\theta }}_t-{\theta }_t^{*})\right|\le \parallel {\widehat{\theta }}_t-{\theta }_t^{*}{\parallel }_{V_t}{\parallel X\parallel }_{V_t^{-1}}\le {\alpha }_t{\parallel X\parallel }_{V_t^{-1}}\end{array}$$

(7)

where ${\alpha }_t:={\displaystyle \frac{1}{c_{\mu }}}\sqrt{2ln\left({\displaystyle \frac{1}{\delta }}\right)+dln\left(1+{\displaystyle \frac{D^2(1-{\gamma }^t)}{d\lambda (1-\gamma )}}\right)}+{\displaystyle \frac{\sqrt{\lambda }S}{c_{\mu }}}+{\displaystyle \frac{S{D}^2{\gamma }^{N\left(\gamma \right)}}{c_{\mu }\sqrt{\lambda }(1-\gamma )}}$.

${\alpha }_t$ is used to compute the confidence bound of the estimated parameter. By using Theorem 1, we can derive the regret bound of the proposed DPB. The detailed proofs of Theorem 1 can be found in Appendix A.

Theorem 2.

Suppose that Assumptions 1–2 hold; then, for fixed $\delta \in (0,1)$, with probability at least $1-\delta$, the regret of DPB is bounded as follows: ${\mathcal{R}}_{\mathcal{T}}\le \tilde{O}\left(B_T{d}^{1/2}{T}^{1/2}\right)$.

If $\tilde{O}\left(B_T{d}^{1/2}{T}^{1/2}\right)$ is sub-linear with respect to T, then, the proposed DPB is called no-regret. However, the sub-linearity of DPB depends on $B_T$. In particular, if $B_T=O\left(T^{1/2-ϵ}\right)$ holds for $ϵ>0$, then, the DPB finally converges to the time-varying user preferences. This result shows some theoretical limitations of the proposed method since it cannot overcome the time-varying tendency of ${\theta }_t^{*}$ if $B_T$ grows faster than $\sqrt{T}$. This regret bound is the first result in preference-based learning for time-varying settings.

6. Experimental Settings

Simulation Setup. We validate our work in three simulation environments: Driver [1], Tosser [21], and Avoiding. The Driver environment aims to drive while aware of the other vehicle and the Tosser environment learns to put the ball in a certain basket with diverse trajectories. The features utilized are identical to [5], distance to the closest lane, speed, heading angle, and distance to the other vehicles for Driver and maximum horizontal range, maximum altitude, the sum of angular displacements at each timestep, and final distance to the closest basket for Tosser. We newly created an Avoiding environment where the robot moves the object over the laptop to place the final target pose, similarly to [22]. Four-dimensional hand-coded features: The height of the end-effector from the table, the distance between the end-effector and the laptop, the moving distance, and the distance between the end-effector and the user, are utilized in Avoiding. Optimal parameters were randomly generated for each seed.

Dataset. To discretize a trajectory space, a query set $\mathcal{X}$ is predefined in Driver and Tosser by sampling K trajectories with uniformly random controls. In Avoiding, RRT* is used to create trajectories after randomly sampling the passing midpoint through the fixed start and target point. We set K to 20,000 for Driver and Tosser, and to 5000 for Avoiding.

Evaluation Metrics. In our experiments, we use the following three suitable metrics: the cosine similarity $m_{CS}$, the simple regret $m_{SR}$, and the cumulative regret $m_{CR}$. First, cosine similarity $m_{CS}={\left({\widehat{\theta }}_t\right)}^{⊺}{\theta }_t^{*}/{\parallel {\widehat{\theta }}_t\parallel }_2{\parallel {\theta }_t^{*}\parallel }_2$ is measured as the alignment metric leveraged in most existing research [4,5,6]. Simple regret is defined as $m_{SR}=\mathrm{\Phi }{\left({\xi }_t^{*}\right)}^{⊺}{\theta }_t^{*}-\mathrm{\Phi }{\left({\widehat{\xi }}_t^{*}\right)}^{⊺}{\theta }_t^{*}$, where ${\widehat{\xi }}_t^{*}$ is an optimal trajectory of learned parameter, i.e., ${\widehat{\xi }}_t^{*}:=arg{max}_{\xi \in \mathrm{\Xi }}\mathrm{\Phi }{\left(\xi \right)}^{⊺}{\widehat{\theta }}_t$. The quality of the optimized trajectory can be measured by the simple regret, with smaller values indicating better performance. Cumulative regret $m_{CR}$, defined in Section 5, illustrates how much reward will be lost by exploration. Minimizing cumulative regret is often the object of the bandit framework.

Baselines. We compare the performance of DPB with other methods using different criteria for query selection, such as batch active learning [5,7], information gain [6], and maximum regret [3]. All these baseline algorithms were adapted into batch selection versions to select the top-b queries to ensure fair comparisons.

• Greedy: This method selects top-b queries based on conditional entropy in a greedy way [5].
• Medoid: This method first selects top-B queries based on conditional entropy where $B>b$. B samples are clustered into b subsets via k-medoids [23] and selects b representative queries from the subsets.
• DPP: This method naturally considers diversity and informativeness simultaneously by using k-DPP [24].
• Information: A query is selected with the highest information gain for easy labeling by the user [6].
• Max Regret: A query is selected with the highest regret over the solution space. Note that regret in [3] uses the same terminology but does not adhere to the conventional notion of regret like (6).
• Random: We select uniformly random b queries.

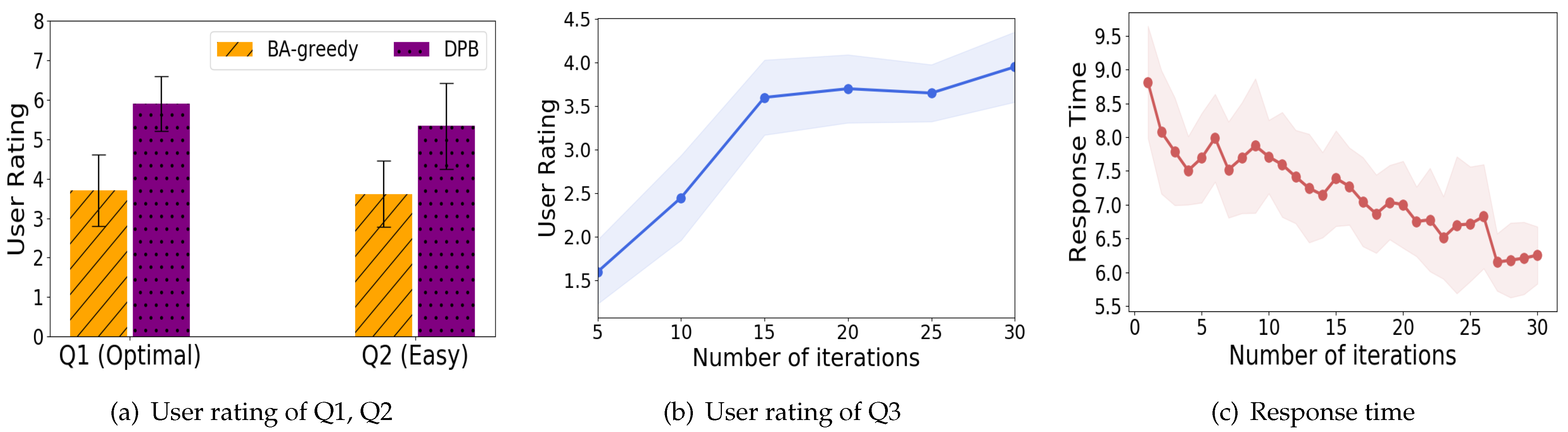
7. Simulation Results

We validated the superiority of DPB in three different preference changing scenarios: smooth preference changes in Section 7.1, abrupt preference changes in Section 7.2, and static preferences in Section 7.3. The experiments in this section were conducted using synthetic data, and the results from real-world scenarios involving users and physical robots will be presented in Section 8.

7.1. Performance on Smooth Preference Changes

To simulate smooth preference changes, we randomly select two parameters, ${\theta }_1^{*},{\theta }_2^{*}$, within a proper range and linearly interpolate them by dividing the interval into 10 points. ${\theta }_t^{*}$ is changed every 30 rounds, making a total of nine changes. After reaching ${\theta }_2^{*}$, 120 additional rounds are executed; hence, 390 rounds are conducted in total.

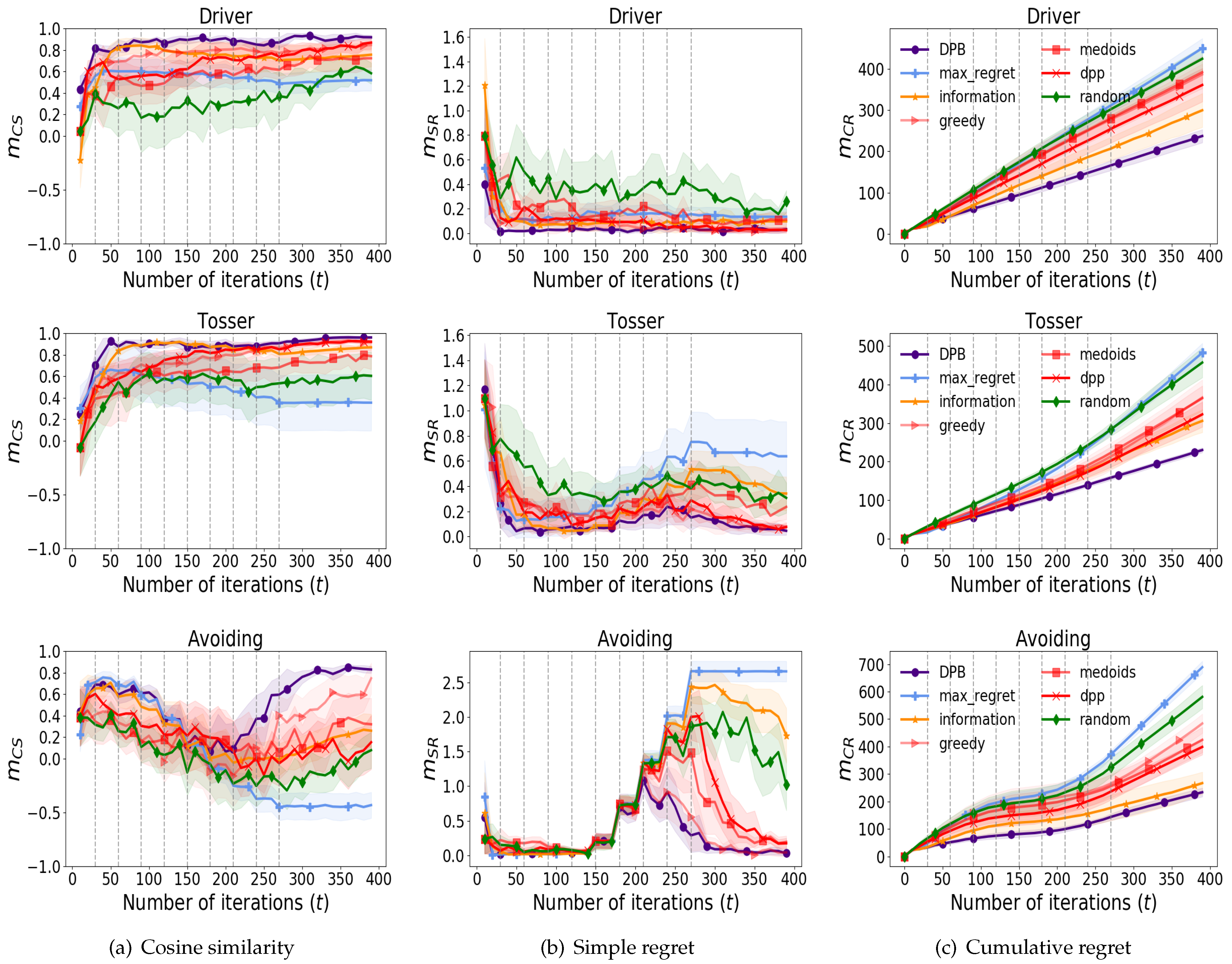
Each row in Figure 2 shows the performances of each algorithm in $Driver$, $Tosser$, and $Avoiding$, respectively. For Figure 2c, DPB clearly outperforms the baselines on $m_{CR}$ since other baselines cannot consider $m_{CR}$. Lower values of $m_{CR}$ indicate that the proposed query selection rule effectively balances the trade-off between the user’s preference for the presented trajectories and their associated uncertainties, as discussed in Section 4.1. This balance enables the generation of high-quality queries, which are well suited for eliciting meaningful user feedback in real-world scenarios with smooth preference changes. Regarding $m_{CS}$ in Figure 2a, it can be observed that DPB adapts to smooth parameter changes faster than other algorithms in terms of parameter estimation. We presume that the superior performance of DPB is derived from the effect of discounts on the past data. Finally, the DPB algorithm also outperforms with respect to $m_{SR}$ as demonstrated in Figure 2b. Thus, in scenarios characterized by smoothly varying preferences, the DPB method demonstrates the capability to generate well-suited queries, facilitating superior estimation of reward parameters and optimal trajectories compared to baseline approaches.

Interestingly, baseline algorithms adopt poorly in $Avoiding$. We believe that this effect is correlated with the abruptness at which the parameters are changed. As the optimal parameters are linearly interpolated, the deviation ${\parallel \Delta {\theta }_t^{*}\parallel }_2$ is consistent with every parameter changes. The average deviation ${\parallel \Delta {\theta }_t^{*}\parallel }_2$ over the seeds is computed as $0.087$, $0.094$, and $0.184$ for $Driver$, $Tosser$, and $Avoiding$, respectively. For Avoiding, the optimal parameter changes comparatively drastically, resulting in a bad performance for the baseline algorithms. Furthermore, the limited adaptability in time-varying scenarios for the maximum regret algorithm might stem from its query selection rule over the solution space. This algorithm tends to converge towards local optima due to its greedy selection that restricts the trajectories to be compared, wherein it selects two trajectories exhibiting the highest estimated regret based on parameter obtained from Markov chain Monte Carlo. However, the results of all simulations support that DPB adapts to the smooth preference changes faster than baselines.

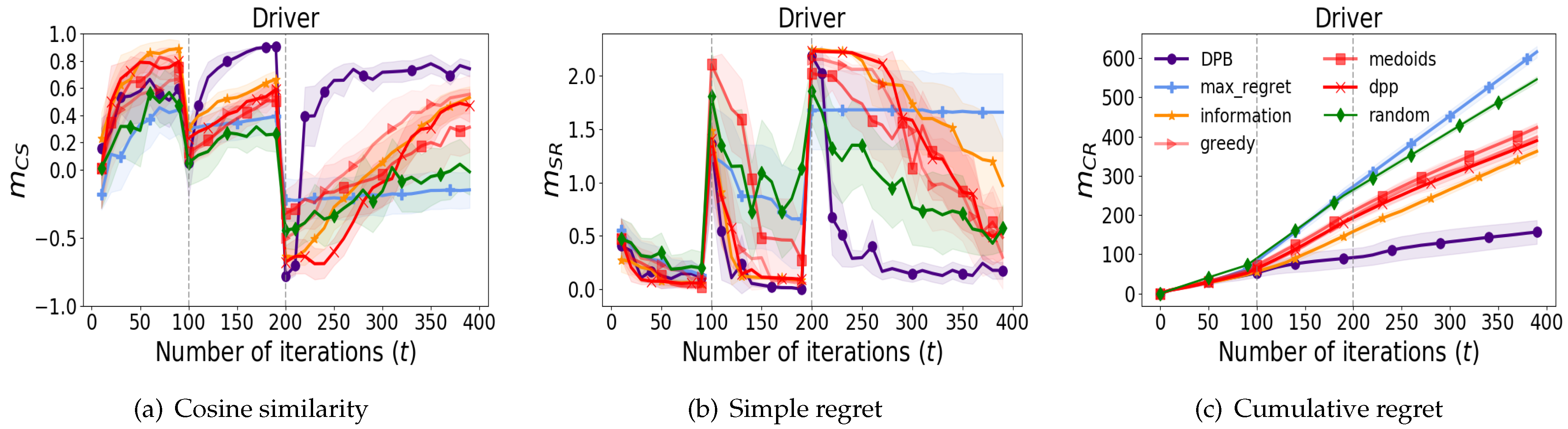
7.2. Performance on Abrupt Preference Changes

To analyze scenarios involving more realistic changes in human preferences, which are not likely to be smooth, simulations are designed to accommodate abrupt changes in preference. For abrupt preference changes, we conducted experiments in Driver involving two significant alterations at 100 and 200 rounds, resulting in ${\parallel \Delta {\theta }_1^{*}\parallel }_2$ and ${\parallel \Delta {\theta }_2^{*}\parallel }_2$ values of $1.267$ and $1.775$, respectively. Figure 3c similarly demonstrates that DPB achieves sub-linear convergence in cumulative regret. While other algorithms do not adapt well to sudden changes in preference, Figure 3a,b show that DPB adapts to abrupt changes in preference. A comparative analysis of the results presented in Figure 2 and Figure 3 reveals that the DPB method consistently outperforms baseline approaches, particularly in scenarios involving abrupt and realistic changes in human preferences. These findings underscore the effectiveness of DPB in addressing dynamic preference scenarios.

In the case of the max regret algorithm, metrics such as $m_{CS}$ and $m_{CR}$ struggle to adapt to changing parameters. They exhibit consistent behavior even when user preferences shift. This issue strongly aligns with the findings from the Avoiding task illustrated in Figure 2. We attribute this limitation to the inherent characteristics of the max regret algorithm, which has difficulty adjusting to abrupt changes in preferences and tends to converge to local optima.

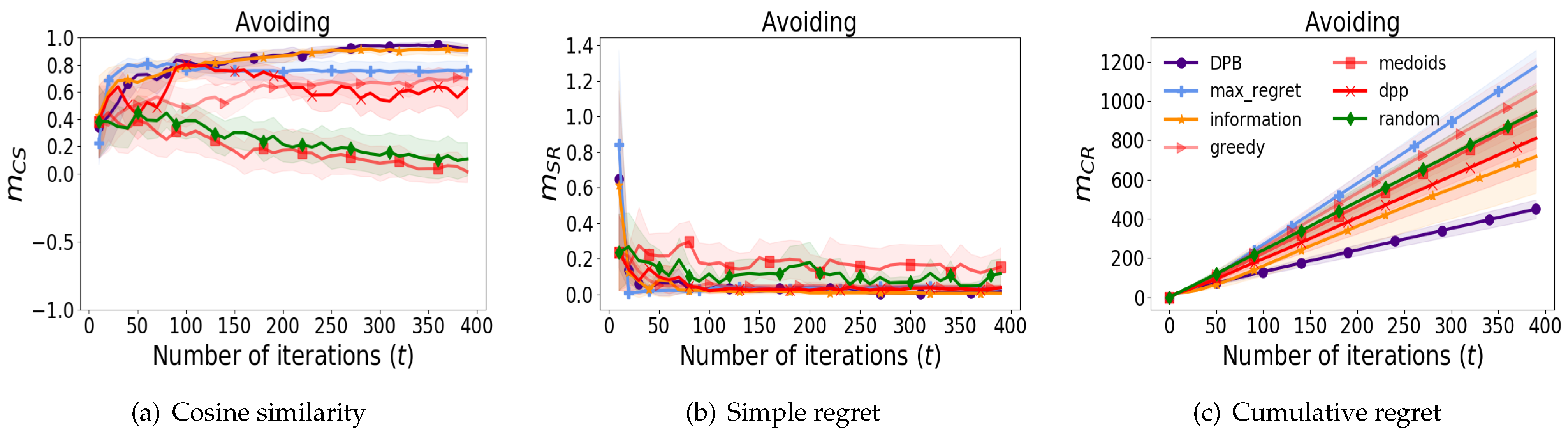
7.3. Sanity Check on Static Preferences

To ensure the performance of baseline algorithms, Figure 4 presents the results of Avoiding in conventional static human preference scenarios; i.e., parameter ${\theta }_1^{*}$ does not change over time. We opted for the Avoiding environment due to its relatively inferior performance compared to the environments discussed in Section 7.1 and Section 7.2. The optimal parameter ${\theta }_1^{*}$ is identical to the simulation experiments in Section 7.1. In Figure 4a,b, we can observe that DPB converges faster than other baselines except for the information gain method that shows a similar convergence speed. The results indicate that DPB demonstrates strong performance even in scenarios involving conventional static preferences. The algorithm effectively estimates preference parameters while identifying optimal trajectories that align with user preferences. Its adaptability to both time-varying and static preferences highlights the practical capability of DPB to accurately estimate preference parameters and generate user-preferred trajectories, reinforcing its applicability in diverse real-world scenarios. Moreover, Figure 4c also supports that DPB guarantees to minimize the cumulative regret. The generated queries also demonstrate superior quality in scenarios with static preferences. It is noteworthy that the maximum regret algorithm in Figure 4 shows reasonable performance in a static setting unlike in the time-varying setting shown in Figure 2 and Figure 3.

8. User Studies

8.1. Real-World User Study

We extended our validation beyond simulations by conducting experiments using the Doosan A0912 manipulator [25] with real users. The experiments focused on evaluating the practical applicability of our DPB algorithm in addressing time-varying user preferences driven by environmental changes. By leveraging real-world setups, the study ensures that DPB can effectively adapt to dynamic preferences while maintaining consistent performance. The results demonstrate the practical effectiveness of DPB in real-world applications, showcasing its capacity to provide personalized and context-aware robotic behavior. Our user study was conducted with the following details.

8.1.1. Objective

The primary objective of the user study was to evaluate the effectiveness of the DPB algorithm in addressing time-varying user preferences influenced by environmental changes. By focusing on preference adaptation in dynamically shifting environments, the study sought to demonstrate the algorithm’s capability to enhance the flexibility and usability of collaborative robotic systems in practical settings.

8.1.2. User Study Setup

We conducted the real-world Avoiding experiment. The total number of iterations and batches for each algorithm was eight and two, respectively. To prevent bias, the queries generated at each batch step were shuffled randomly before displaying the robot’s behavior. Additionally, we introduced a fragile object, such as a wine glass, halfway through the experiment to prompt changes in user preferences in response to environmental variations. We believe that changing surrounding environments can induce changes in user preferences over time.

8.1.3. Doosan A0912 Specifications

The Doosan A0912 robotic manipulator is a lightweight (9 kg), 6-DOF (degrees of freedom) collaborative robot, designed for precise tasks with a repeatability of ±0.03 mm (Doosan Robotics, Plano, TX, USA). With a working radius of 1200 mm, it is suitable for applications requiring extended reach and dexterity. The 6-DOF configuration allows it to perform complex movements, making it ideal for tasks such as assembly, inspection, and material handling in constrained spaces. Its compact design and high precision enhance its usability in various industrial applications.

8.1.4. Subjects

We recruited nine participants. The participants were aged between their 20s and 30s, comprising nine males. Four participants had prior experience interacting with robots, while the remaining participants had no experience with physical robots.

8.1.5. Independent Variables

We conducted a comparative analysis of the DPB algorithm and the Greedy algorithm [5], which serves as the best-performing baseline in our simulation experiments. This comparison was aimed at evaluating the effectiveness of DPB in addressing both static and time-varying user preferences. By benchmarking DPB against a well-established algorithm known for its strong performance, we sought to demonstrate the advantages of our method in achieving user-aligned optimal trajectories. The results of this comparison offer valuable insights into the robustness and adaptability of DPB in scenarios where conventional algorithms may encounter challenges.

8.1.6. Hypotheses

We set up the following two hypotheses to verify the DPB algorithm. (H1) DPB adapts faster in time-varying parameters than the Greedy method. (H2) Participants find DPB queries to be easier to answer than the Greedy method. Note that our method is not directly designed for H2. However, it can be hypothesized that our batch selection rule has potentially synthesized easy questions for the user to respond to, since our algorithm finally tries to maximize $|X_t^{⊺}\widehat{\theta }|$, which leads to choosing two trajectories with a significant difference between their expected rewards. In PBL, since producing easy questions is very important [6], we would like to test not only H1 but also H2.

8.1.7. Dependent Measures

To evaluate the user study, we designed the following two questions, Q1 and Q2, using 7-point Likert scale responses from participants. (Q1) "The robot behavior matched how I wanted the task to be done." (7—Strongly agree; 1—Strongly disagree), and (Q2) "It was easy to choose a preferred trajectory in the comparison query." (7—Strongly agree; 1—Strongly disagree). Q1 was designed to evaluate how closely the algorithm estimates a user preference-aligned trajectory. For Q2, if the user gave a high score in the answer to Q2 and the user’s preferred option among the comparison query was clearly set, the user did not hesitate to select a preferred trajectory. Therefore, the high score of Q2 is the basis for supporting H2, meaning that the comparison query is easy to answer. Additionally, we added (Q3) Is there any change in your optimal trajectory while interacting with the robot? (7—Strongly agree; 1—Strongly disagree) to demonstrate whether the placement of the wine glass induced preference changes. In other words, if the moment we added the wine glass to the environment and the moment the Q3 response value increases matched, it means that we were able to change the user’s preference as we intended. The participants were asked Q1 after watching the optimal trajectory determined by the learned parameters after all queries. Additionally, they were asked Q2 after responding to each query and Q3 after responding to the batch size query.

8.1.8. Time-Varying Scenario with Environmental Changes

Figure 5 shows the results of the real-world user study with time-varying preferences regarding environmental changes. The Q1 result in Figure 5b demonstrates that DPB better captures the user’s recent preferences than the greedy algorithm. We also verified the significance of the experiment through a two-sample t-test $(p<0.05)$, supporting H1. The Q2 ratings in Figure 5b indicate that users find DPB easier to respond to queries than the baseline algorithm $(p<0.05)$, supporting H2. Finally, Figure 5c shows that environmental changes, such as the placement of wine glasses, create time-varying user preferences. Consequently, from Figure 5b,c, DPB effectively adapts to time-varying preferences and outperforms other existing methods [5,7]. Moreover, to further validate our findings, we performed a Bonferroni correction on the results of Q1 and Q2. The adjusted p-values, which remained statistically significant with $p<0.05$, further corroborate the effectiveness and robustness of the results, providing additional confidence in the validity of our approach.

8.2. Simulation User Study

We also conducted a simulation user study to validate the adaptability of DPB in time-varying scenarios, especially regarding robot behavior adaptation over repeated interactions. We believe that human preferences may evolve to repeated interactions with robot behaviors over time. The simulation user study proceeded with two major modifications from the real-world user study. First, algorithms were deployed in Tosser with 10 participants. Furthermore, 30 iterations with five batches for each algorithm were executed to induce participants’ robot behavior adaptation over repeated interactions. Response times were measured at every iteration without the participants’ awareness. Anticipating that participants would gradually adapt to the robot’s behavior, we hypothesized that their decision-making process to give feedback accelerates and thereby response times would exhibit a decrease.

Time-Varying Scenario with Robot Behavior Adaptation over Repeated Interactions

Figure 6 demonstrates the result of the simulation user study in the time-varying scenario with robot behavior adaptation over repeated interactions. Figure 6a illustrates the outcomes of Q1 and Q2, indicating that DPB exhibits better performance over the greedy algorithm in adapting to time-varying scenarios involving robot behavior adaptation $(p<0.001)$ and in the ability to generate easy queries to respond $(p<0.001)$, supporting H1 and H2. Moreover, Figure 6c shows that response time decreases as the iteration proceeds, implying that participants tend to adapt to robot behaviors. The simulation user study results validate the practical adaptability of DPB in time-varying scenarios with robot behavior adaptation over repeated interactions. Additionally, we also conducted a Bonferroni correction in simulation user study to the results of Q1 and Q2. The adjusted p-values, which remained highly significant at $(p<0.001)$, indicate strong support for the effectiveness of the proposed approach.

9. Conclusions

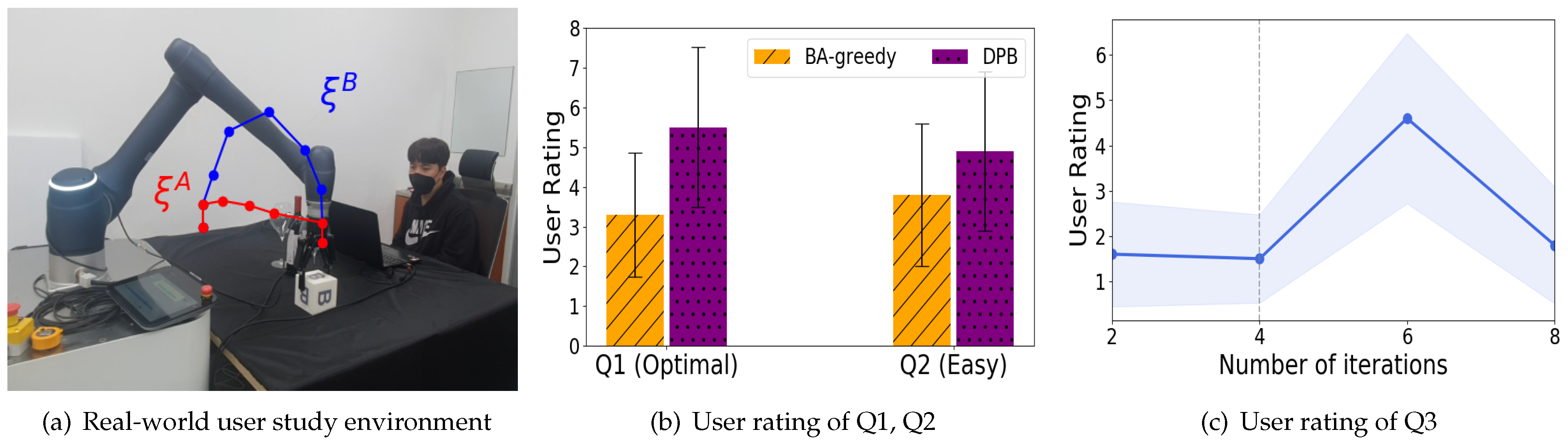
Our proposed algorithm introduces a novel approach to address time-varying preferences using discounted likelihood. Then, our theoretical analysis establishes that DPB demonstrates sub-linear cumulative regret under preference changes occurring less than $O\left(T^{1/2}\right)$ times. Experimental outcomes highlight the adaptiveness of our framework compared to previous methods in handling time-varying user preferences. Particularly, our DPB method effectively minimizes cumulative regret, while other approaches struggle in this regard. User studies further validate the competitiveness of DPB in time-varying environments with environmental changes and robot behavior adaptation over repeated interactions.

In robotics, addressing the time-varying preferences of users is crucial, as their expectations can shift depending on the context or environment. Robotic systems are required to perform a wide range of actions across diverse scenarios, adapting their behavior to evolving human needs. For instance, in autonomous driving systems, the DPB method enables vehicles to modify their driving styles—such as acceleration, braking, or lane-changing. Passengers preferring a smoother, more conservative ride may find the vehicle adjusting its behavior accordingly, while those prioritizing efficiency could benefit from optimized travel times. This continuous learning and adaptation enhance the personalization and comfort of autonomous systems. It would be interesting to consider additional factors such as emotions or social contexts that influence preference changes. Exploring these aspects and developing a unified model capable of perceiving user states and learning preferences across diverse users represent promising directions for future research.