Abstract
Studying the factors affecting machining accuracy, surface quality, and machining efficiency in the powerful honing machining process system, analyzing the basic law between various errors and machining quality, exploring the method of evaluating the quality of honing, and improving the machining quality and transmission performance of hardened gears has important engineering application value. Firstly, this paper establishes an effective abrasive grains micro-edge honing quality evaluation model, proposes a method based on the Trapezoidal Fuzzy Analytic Hierarchy Process (Tra-FAHP) and Set Pair Analysis (SPA) to comprehensively evaluate the quality of the honing process, and obtains the influence weights of each factor on the quality of honing. Secondly, the paper analyzes the influence rules of three types of abrasive grain sizes on helix error, tooth pitch error, tooth profile error, surface roughness, and honing efficiency. Finally, the correctness of the established comprehensive evaluation model of honing quality was verified with the threshold method and weights. The research results show that the model can correctly evaluate the quality of hardened gear honing and can be applied to studying the influence of abrasive grain micro-edge honing on machining characteristics.
1. Introduction
Gear honing, a key finishing process in gear manufacturing, has the advantages of high tooth precision, high load-carrying capacity, low transmission noise, and regular tooth texture, etc. [,], These characteristics make it particularly suitable for gear processing in the production of new energy vehicle drivetrains [,,]. The quality of honed teeth plays a crucial role in gear life, transmission noise, and load-carrying capacity. However, the factors affecting the quality of honed teeth are characterized by randomness, complexity, and unpredictability, making a detailed analysis of honing machining characteristics challenging. Compared to traditional grinding methods, the quality of honing is further improved [].
Honing as a gear finishing method, which uses a pair of staggered-axis cylindrical gears for forced meshing into a movement through the honing wheel on the abrasive grains sliding friction workpiece tooth surface, removes a thin layer of material. Some scholars evaluated the quality improvement of gears with grinding wheels from different perspectives. Sandro Pereira da Silva [] established the relationship between five input parameters such as spindle speed, machining time, X- and Z-direction feed rate, and spark out time with total profile deviation (fα), total helix deviation (fβ), and total cumulative pitch deviation (fp) by using a grain swarm algorithm. Yuan Bin [] has optimized and actively controlled the spindle speed, axial feed speed, and radial feed speed of the honing process parameters at a constant cutting speed to minimize the total tooth shape error. The above literature focuses on the effect of various factors on the accuracy of the tooth surface.
Xin Li [] compared five gear finishing processes and comprehensively evaluated the tooth surface quality with parameters such as surface roughness, surface morphology, surface residual stress, surface texture roughness, and peak radius of curvature after machining, The Author highlighted the synergistic optimization of factors such as abrasive grain size and shape as an effective method to improve both machining efficiency and surface quality. W. Liu [] designed an orthogonal test of a diamond abrasive grain grinding wheel on silicon carbide grinding to analyze the effects of the processes such as grain size, grinding wheel speed, workpiece speed, and grinding depth on surface roughness, surface topography, and grinding force. The grinding quality was comprehensively analyzed, and the process parameters were optimized based on these factors. The above literature focuses on the effects of various factors on surface quality.
Silva, SP [] studied the effect of honing process parameters such as speed of pinion, speed of the grinding wheel, feed rate, spark out, and cycle time. The experimental results showed that the helix form error and the evolvent profile error were affected by the cycle time and feed rate. Sergey Riabchenko [] evaluated the working efficiency of disc circles through parameters such as grinding power, surface roughness, involute tooth shape accuracy, and wear of the disc circles. The experimental results show that the dimensional wear of the grinding wheel is the main factor affecting the accuracy of grinding processing, and the grinding efficiency is correlated with the depth of cut and the grinding time of a single tooth. Fuwei Wang [] proposed a specific energy model for quantitatively evaluating the material removal rate of honed teeth. Experimentally, it was observed that a larger honing depth resulted in an increase in material removal rate. In addition, at the same workpiece speed and honing depth, an increase in both the cross-axis angle and axial feed rate resulted in an increase in specific honing energy and a decrease in material removal rate. The above studies focus on the effects of various factors on processing efficiency.
Based on controlling systematic errors in the honing process and external disturbances, the honing process and the parameters that characterize the properties of the honing wheel are considered key elements affecting honing quality. Based on the above literature and existing research foundation [,,,], the honing process parameters mainly include honing speed, honing depth, feed rate, and cross-axis angle, and the main factors characterizing the surface morphology of the honing wheel are abrasive grain size, shape of abrasive grain, effective number of abrasive grain, clearance between abrasive grains, and grinding cutting angle. Some studies showed that the dimensional wear of grinding wheels is the main factor affecting the accuracy of gear machining. Honing of teeth is a generative machining process that requires high dimensional accuracy of honing wheel surfaces. The critical factors affecting the dimensional wear [,] of grinding wheels include abrasive grain shedding, abrasive grain fracturing, and abrasive grain abrasion. The 12 parameters listed above were selected as key factors affecting the quality of honed teeth.
At present, research on honing quality is primarily evaluated from the aspects of tooth shape accuracy, tooth surface quality, and honing efficiency. Tooth shape accuracy includes helix error, tooth pitch error, and tooth profile error. Surface roughness affects tooth wear resistance, fit stability, corrosion resistance, etc., which is often used to evaluate surface quality. Compared with other gear finishing processes, the unique surface texture of honing can reduce transmission noise and vibration [], and the surface residual stresses can significantly increase service life []. Therefore, the research on the quality of honed tooth surfaces focuses on three factors: surface roughness, residual stresses, and tooth texture. Honing efficiency is characterized by the ratio of material removal rate to machining time. Existing studies on the quality of honed teeth mostly analyze individual factors without considering a comprehensive evaluation of multiple factors. Based on the above shortcomings, the study introduces a comprehensive evaluation method for multiple factors.
2. Related Work
Fuzzy Hierarchical Analysis (FHA) is a multi-objective decision-making method that is widely used for comprehensive evaluation in the field of machining. In order to solve the complex problem of machinability of titanium alloy, which has low density, high hardness, low thermal conductivity, and low modulus of elasticity. K. Fuse [] applied a combination of FHA and ideal similarity ranking preferred fuzzy technology for multi-objective decision-making on the wire-cutting machining process, combined with experiments to optimize a set of optimal process parameters. For the complexity of laser melting coating, there is no practical method to evaluate the quality of the coating. W.X. Liang [] proposed a fuzzy comprehensive model for evaluating the quality of plating from the macroscopic profile, microstructure, and mechanical properties, using FHA to rank the evaluation indexes in terms of weights and optimizing the process parameters. A.S. Patil [] modeled and evaluated the milling quality of Ti6AI4V in terms of Surface integrity, Flank, and Crater wear. FHA and prioritization were used to determine the better process parameters. Trapezoidal fuzzy numbers, a type of fuzzy mathematics, can also be used for multi-factor evaluation of honing quality.
However, a single evaluation method has a large deviation between the theoretical calculation results and the actual value, unable to address the ambiguities, uncertainties, and issues related to quantification among multiple factors. SPA is a mathematical method for dealing with the interaction of determinism and uncertainty in a system. Y.H. Liu [] combined FAH and SPA to carry out a comprehensive evaluation of regional comprehensive energy consumption, through the measured data, the reliability of the comprehensive evaluation method and results was verified.
G.Z. Huang [] combined the fuzzy comprehensive analysis method and SPA for construction safety evaluation and found that combining the two methods could simultaneously handle the uncertainty and fuzziness of information in construction safety and achieve better evaluation results. J.W. Wang [] compared the evaluation results of traditional FAH, entropy weighting, fuzzy comprehensive evaluation, gray correlation analysis, and ideal solution similarity preference ranking method and proposed an environmental risk synthesis method based on the combination of intuitive FAH and SPA. According to the results, the evaluation model is more objective and reasonable for addressing the ambiguities and uncertainties in environmental risks.
In this paper, for the factors affecting the quality of honed teeth, which are characterized by randomness, complexity, and unpredictability, an effective abrasive grains micro-edge honing characteristic evaluation model is established to solve the problem of unsystematic and incomplete evaluation of honing quality and provide a decision-making basis for the manufacture of high-performance hard gears.
3. Evaluation Methodology and Factor Analysis
3.1. Evaluation Methodology
In this study, a combination of Tra-FAHP and SPA was used to evaluate the quality of the Cubic Boron Nitride (CBN) grit micro-edge honing process, and the evaluation process is shown in Figure 1.
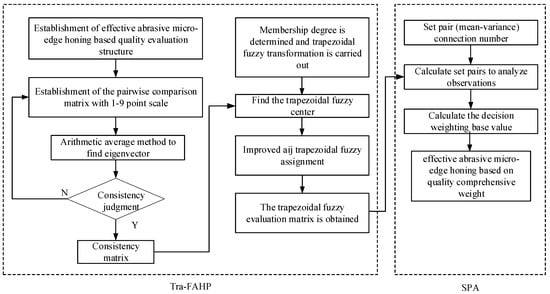
Figure 1.
Flow chart of the integrated, comprehensive evaluation method.
Firstly, analyze and identify the honing quality indexes and establish an effective abrasive grains micro-edge honing quality evaluation system based on AHP. Then, obtain the consistency matrix. Secondly, the trapezoidal fuzzy evaluation matrix is obtained by trapezoidal fuzzification of the consistency matrix elements through the trapezoidal fuzzy center inverse formula. Finally, the transformation of fuzzy numbers to linkage numbers is achieved through ean-variance, which introduces SPA to determine the final quality evaluation composite weights.
3.2. Establishing a Three-Stage and Four-Level Indicator System
Based on the analysis of the factors affecting the honing process quality and the relationships between the indicators mentioned above, a three-level and a four-level indicator system, as illustrated in Figure 2, has been established to comprehensively evaluate the honing quality.
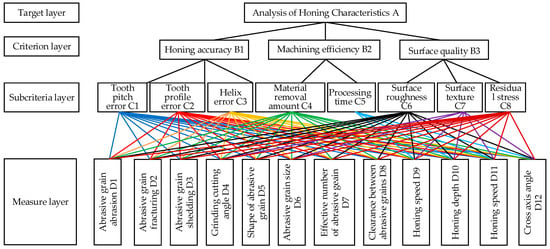
Figure 2.
Evaluation index system of honing quality gears based on Tra-FAHP.
4. Evaluation Procedure
4.1. AHP Determines the Consistency Matrix
AHP is a subjective assignment method that can clearly identify evaluation models for complex, cross-cutting decision-making problems. By making pairwise comparisons between two factors at the same level, it can derive the importance of each factor relative to the elements of the previous level. The specific process is as follows:
- (1)
- Build hierarchy
In Figure 2, a logical hierarchy is constructed based on the factors associated with the enhancement of quality. “It’s an indicator system composed of three tiers and four levels, with the top-level objective (A) serving as the overarching evaluation. This is then followed by the criterion level (B), which encompasses observation B for objective A. The sub-criterion level (C) then follows, with observation C for B forming its basis. Finally, the element level (D) addresses the factors affecting the top-level objective (A).
- (2)
- Constructing the Pairwise Comparison Matrix
The relative importance of the two elements is evaluated using the “1–9 point scale”, as illustrated in Table 1 []. An pairwise comparison judgment matrix regarding is established.

Table 1.
Satie’s 1–9 point scale and corresponding definitions.
According to the hierarchical structure of the evaluation model, created , , , …, among other paired comparison matrices totaling twelve.
In the formula, represents the judgment matrix, where n denotes the total number of elements. The value of element indicates the degree of importance of the i-th element relative to the j-th element within the same level in terms of their influence on the upper-level element. It holds that and are reciprocals, that is, , and .
- (3)
- Check consistency
Consistency testing CR is calculated according to Equation (2), and a CR value of less than 0.1 indicates that the consistency test has been passed. The consistency index RI is shown in Table 2, and the consistency index (CI) is computed as per Equation (3).

Table 2.
Random index values for different scales.
In this context, refers to the maximum eigenvalue of the judgment matrix, and n represents the number of columns or rows of the judgment matrix.
The matrices that pass the consistency test are deemed to exhibit satisfactory consistency and can be used for trapezoidal fuzzy transformation.
4.2. Determine the Trapezoidal Fuzzy Evaluation Matrix
The concept of trapezoidal fuzzy numbers was proposed by Zadeh in 1965. It utilizes trapezoidal membership functions to address problems in uncertain environments.
- (1)
- Constructing a fuzzy judgment matrix
Assuming , where are real numbers in the set , and . Here, and represent the lower and upper bounds of the trapezoidal fuzzy number , respectively, while and are the median values of the trapezoidal fuzzy number. The formula for the trapezoidal membership function is given as (4) [].
Considering the subjectivity, ambiguity, and uncertainty in the scoring provided by experts in the direction of honing, the trapezoidal fuzzy numbers are calculated using the trapezoidal centroid formula. This process transforms the general judgment matrix into a fuzzy judgment matrix. In order to better reflect the experts’ thought processes, as shown in Table 3, an improved valuation method is applied to the traditional “1–9 point scale” method [].

Table 3.
‘1–9 point scale‘ method and improved trapezoidal fuzzy number.
In order to facilitate subsequent calculations, a brief introduction to the arithmetic rules of trapezoidal fuzzy numbers is provided. Let two trapezoidal fuzzy numbers be and , and let l be any constant. The arithmetic rules are as follows in Table 4:

Table 4.
Trapezoidal Fuzzy Number Arithmetic Rules.
By using the data from Table 4 to replace the elements in the simplified matrix with trapezoidal fuzzy numbers, ensuring consistency, the fuzzy judgment matrix U expressed in terms of trapezoidal fuzzy numbers can be obtained. The simplified matrix must satisfy the consistency requirement, and the improved trapezoidal fuzzy number judgment matrix also meets the consistency requirement [].
Assuming that n (n > 1) experts with equal status are invited to score at the same time, the reduced matrix after the consistency test is performed, and trapezoidal fuzzy processing is performed. The matrix after fuzzification of the nth expert data is recorded as:
In Formula (6), , K = 1, 2, ⋯, n.
Based on the preferences of n experts, calculate the average of as the evaluation fuzzy matrix using the formula:
- (2)
- Index weight calculation.
In order to reduce the influence of extreme data on the overall weight, the paper uses the geometric average method to ascertain the fuzzy evaluation value of the factor layer , and the weight of the evaluation index is:
In Formula (8), is the weight of the index , and the values of , , and are calculated by Formula (9), and , , , .
Normalize the calculation of fuzzy evaluation index weights .
In Formula (10), is the expectation of the weight of the evaluation index. By combining Formulas (5)–(7), the Tra-FAHP weight and normalized weight of each evaluation index can be obtained.
4.3. SPA Evaluation Model
SPA is a systematic method proposed by scholar Zhao Keqin in 1989, which utilizes the dialectical unity of opposites to analyze the relationships between determinacy and indeterminacy, with a focus on the connectivity function []. Based on the dialectical unity thought, it analyzes the identity, opposition, and differences of set pairs, reflecting the interconnection between the determinacy and indeterminacy of things.
4.3.1. Establishment of a SPA Evaluation Model
Let the sub-criteria layer C of the criterion layer have the attribute weights relative to the target layer A denoted by , and the attribute values of the criterion layer be represented as . The weighted comprehensive value of uncertain multi-attribute decision-making is given by:
Equation (11) represents the weighted comprehensive optimization decision value for the quality evaluation scheme of effective abrasive grains micro-edge honing process using CBN coated internal gear honing wheels.
The SPA evaluation matrix is constituted as a 12-row by 8-column matrix, with the factor layer D represented as row vectors and the sub-criterion layer C as column vectors, where the composite value serves as the individual elements.
4.3.2. SPA Analysis
Let the set pair H be constituted by sets A and B, denoted as . The relationship between set A and set B, as well as the degree of their superiority and inferiority, can be represented by the connectivity degree .
In Equation (12), a, b and c are identity degree, difference degree, and opposition degree, respectively, , and In reference [], it was proposed that the mean and variance of sample characteristic parameters in statistics can be represented by trapezoidal fuzzy number characteristic parameters based on the uncertainty system theory of SPA. The characteristics of the ‘mean + variance’ combination are represented by the connective . The utilization of this feature, the connection number , establishes a coupling between trapezoidal fuzzy number and SPA.
For trapezoidal fuzzy numbers , if are considered as four observations of the same object U, then the average value of is:
The variance s of trapezoidal fuzzy number is:
represents the certainty of fuzzy numbers, and the variances are the description of the uncertainty of fuzzy numbers, illustrating the centralized (certainty) and discrete (un-certainty) nature of the trapezoidal fuzzy numbers in a statistical context.
Then the mean-variance connection number is:
The mean and variance s can be mapped to the two-dimensional deterministic-uncertain plane of SPA, and the mean and variance s are expressed as the deterministic-uncertain weight in the “modulus” value of the set pair plane vector, which is calculated by Formula (16):
The overall weight is obtained by normalizing the “model”.
5. Verification of Comprehensive Evaluation Model for Honing Processing Quality
5.1. Determining the Weight of Influencing Factors of Honing Machining Quality
According to the gear honing quality evaluation hierarchy shown in Figure 2, the questionnaire was designed to hire five experts of equal status with relevant industry backgrounds to score the factors affecting machining quality. After consistency adjustment and testing, an improved trapezoidal fuzzy number assignment calculation method was applied. It determines the quality of the internal gear honing wheel’s CBN coating, the effectiveness of abrasive grains, and the micro-edge honing processing quality. The hierarchical structure of the factors under the relative evaluation index and the corresponding Tra-FAHP weights are shown in Table 5.

Table 5.
The Tra-FAHP weights of the relative evaluation indicators of factors.
The data in Table 5 are passed through the algorithm in Table 3, which could obtain the weights of each attribute of the sub-criteria layer C with respect to the top layer A, as shown in Table 6 The weights are normalized to obtain .

Table 6.
The weight of sub-criterion C relative to top-level A.
Firstly, the SPA matrix is processed using “mean + variance”. Secondly, the “mode” of the plane vector set is calculated and normalized, and finally, the integral weights of elements at each layer are obtained, as shown in Figure 3.
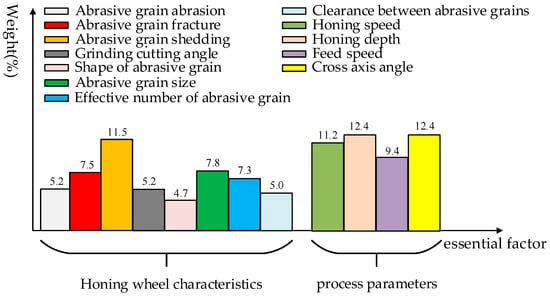
Figure 3.
Honing processing quality influence factor weight value.
From the data in Figure 3, it can be concluded that the honing speed, honing depth, feed rate, and cross-axis angle are controllable parameters in the actual machining process. The honing speed has a weight value of 45.4% in the overall evaluation of micro-edge honing characteristics, which significantly impacts the quality of honing operations. Additionally, abrasive grain fracturing (7.5%), abrasive grain shedding (11.5%), and abrasive grain size (7.3%) are affected by the honing wheel life and the hardness of the workpiece. In different honing conditions, only by choosing reasonable characteristic process parameters can the honing ability of the honing wheel be brought into full play and good honing effect be obtained. To further confirm the significance of the factors, sensitivity analyses were performed through the trapezoidal fuzzy set-pair analysis method.
5.2. Analyze the Sensitivity of the Key Factor of the Machining Quality
In order to clarify the research objectives, it is first assumed that the importance of criterion layer B will change, followed by the calculation of the trapezoidal fuzzy set for a single criterion. The sensitivity results of key factors are shown in Figure 4. As can be seen from the size of the weighting value, the effect of abrasive grain shedding on honing accuracy and machining efficiency is the most significant, while the effect of abrasive grain size on surface quality is also considerable.
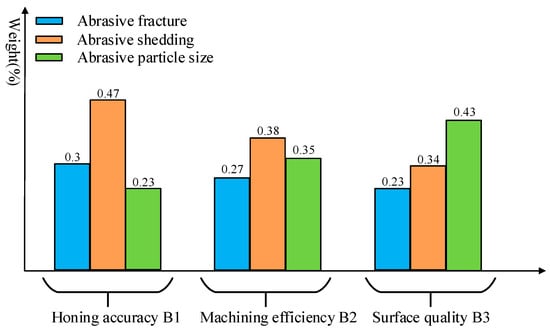
Figure 4.
Tra-FAHP- SPA analysis results.
On the one hand, the hardness of abrasive particles present on the CBN honing wheel is much higher than the hardness of the workpiece tooth surface. In addition, the cutting force and cutting heat of abrasive particles in the gear honing process are low, so the abrasive particles rarely break off, maintaining the integrity of the honing wheel. On the other hand, because the honing wheel’s characteristics wear very little during the initial and normal wear stages, the impact of abrasive breakage and falling off on the machining quality of the workpiece can be negligible.
In the stage of rapid wear, the honing force and temperature rise sharply, resulting in grinding wheel blockage and insufficient coating retention. As a result, the abrasive particles break or fall off, forming a self-sharpening phenomenon and keeping the grinding wheel continuously honing. At the same time, a large number of axial shedding is easy to cause helix errors and pitch errors. A large number of radial drops are easy to cause tooth profile errors and pitch errors. The falling off and breaking of abrasive particles affect the integrity of the polishing wheel and reduce the quality of the honing process. To sum up, we have analyzed the whole cutting process, as shown in Figure 4, and the analysis results are consistent with reality.
5.3. CBN Abrasive Grain Micro-Edge Honing Processing Experiment
In order to verify the accuracy of the comprehensive evaluation model, taking the key factor of abrasive grain size as an example, the influence experiment of different abrasive mesh sizes on honing quality is designed.
5.3.1. Specimen Requirements
Take the high-speed gear in the gearbox of a new energy vehicle as an example. The design parameters of the process requirements adopted are shown in Table 7, and the processing quality of the gear is evaluated and analyzed.

Table 7.
Transmission gear parameters.
5.3.2. Processing Conditions
According to GB/T10095.1-2008 cylindrical gear precision system, GB/T 131-2006 [] product geometry series specifications and design parameters requirements, select YK4825 power gear honing machine, and use the experimental parameters shown in Table 8, and then honing the gear.

Table 8.
Honing gear experimental parameters.
In the Table 8, # denotes the mesh size, and 100# denotes the abrasive mesh size of 100.
As shown in Figure 5. The gear honing accuracy test was completed in the 3903T gear measuring Center of Harbin Measuring Tool Factory. The screw error, tooth profile error, and tooth spacing error can be measured simultaneously in this experiment. The VHX-7000 Ultra depth of field microscope from KEYENCE (Osaka, Japan) was used to measure the roughness of the top of the tooth surface, the indexing circle, and the root of the tooth, and then the average roughness was calculated. In addition, the material removal rate is calculated by the weight change of the gear before and after the honing process.
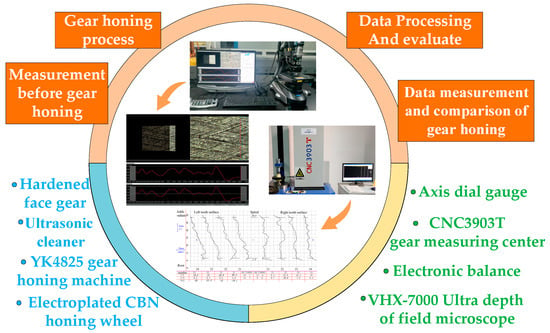
Figure 5.
Gear honing quality test instrument and method.
5.4. Effect of CBN Grain Size on Honing Quality
5.4.1. The Relationship Between Grain Size and Honing Precision
- (1)
- Total deviation between grain size and helix
As shown in Figure 6, As the abrasive mesh size increases, the size of the abrasive decreases. After honing, the average value of the spiral deviation of 300# and 540# abrasive particles decreases successively, and the difference between them is very small. The smaller the abrasive grain size, the more concentrated the helical total deviation distribution of the workpiece tooth surface after honing so that the minimum helical error of 540# is smaller than the corresponding value of 300#.
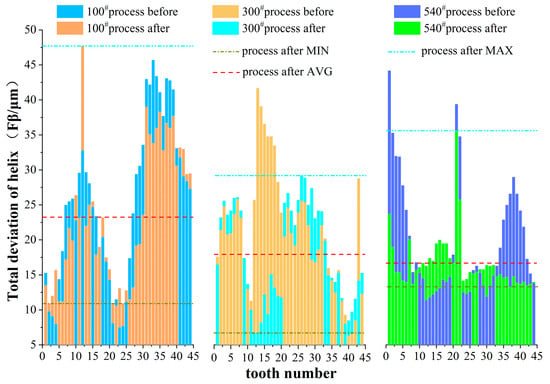
Figure 6.
CBN grain size and total deviation of tooth surface helix.
After machining with 100#, 300#, and 540# grinding wheels, the total screw deviation of the workpiece tooth surface is improved in different degrees, and the improvement degree is affected by the error accumulation and error recurrence before honing. Under the machining of the 540# honing wheel, the maximum error of the tooth line of No. 21 gear did not decrease significantly. In actual production, by increasing the number of honing operations, the error replication coefficient and the maximum error of the helix of the workpiece tooth surface can be effectively reduced. The honing precision can be improved to meet the design requirements.
- (2)
- Grain size and single pitch deviation.
In the electronic gearbox, the workpiece gear and the honing wheel are forced to engage according to the theoretical transmission ratio, which plays a significant role in correcting the pitch deviation. In Figure 7, with the increase in abrasive mesh size, the algebraic difference between the measured tooth pitch and the theoretical tooth pitch decreases progressively. The distribution of pitch deviation is also gradually approaching the zero line, which indicates that the ability to correct the change of common normal length is enhanced, so the machining accuracy of honing teeth is improved. The pitch error of the workpiece shows an obvious sinusoidal distribution after 540# abrasive honing, which reflects the circular run-out error between the honing wheel and the workpiece. It is a random error generated by the previous process. After honing, the pitch error is obviously reduced. Due to error accumulation, the pitch error of the workpiece is still approximately sinusoidal. In the subsequent work, the error recurrence coefficient can be effectively reduced by increasing the number of honing operations.
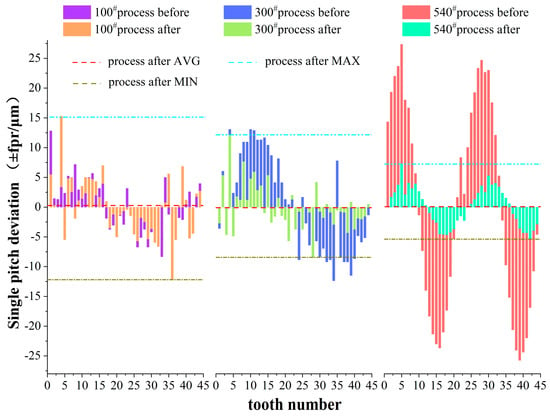
Figure 7.
Comparison of single pitch deviation before and after honing.
- (3)
- Cumulative total deviation of grain size and tooth profile
As shown in Figure 8, the average value of the cumulative total deviation of the tooth profile decreases with the increase of abrasive mesh size, which indicates that the accuracy of the workpiece is gradually improved after honing. For the wheel with a large prehoned tooth profile deviation, the tooth profile deviation curve of the honed wheel after precision reshaping is closer to the theoretical value. After the secondary enveloping cutting process of the workpiece tooth profile, the involute tooth profile deviation of the workpiece gear is reduced.
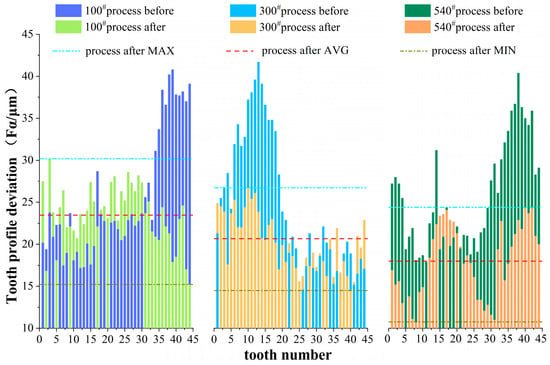
Figure 8.
Comparison of total deviation of tooth profile before and after honing.
100# abrasive particles are used in roughing operations to remove process residues with high throughput and efficiency. The use of 300# and 540# abrasive particles for finishing can effectively reduce the tooth profile error, installation error, and short cycle error in the machine tool transmission chain. The error between the actual and designed tooth shapes is reduced while the machining precision is improved. It is also found that the small abrasive mesh size leads to the uniform distribution of the spacing, and the high precision of the honing wheel tooth shape reduces the tooth shape deviation, both of which improve the precision of the honing workpiece.
5.4.2. The Relationship Between Surface Roughness
It can be seen from Figure 9 that the average, maximum, and minimum values of workpiece tooth surface roughness decrease with the increase of abrasive mesh size when other process conditions remain unchanged, thus improving the honing tooth surface quality. The reason can be revealed according to the Ra expression of honing surface roughness.
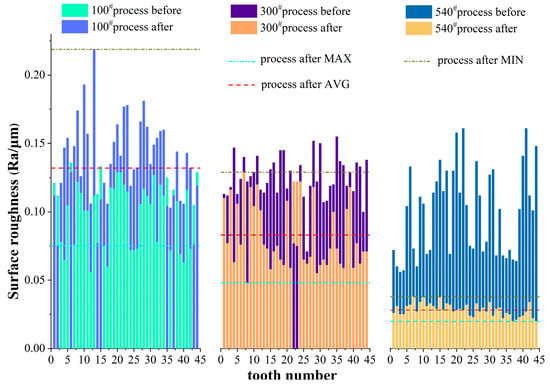

Figure 9.
Relationship between abrasive grain size and surface roughness with honing gear.
In Equation (18) c curl compensation coefficient, workpiece rotational speed, t honing machining time, and the maximum valley height of the workpiece surface after honing are:
In Equation (19), abrasive grain top cone angle, workpiece contact point velocity, honing wheel contact point velocity, the radius of curvature of the workpiece tooth surface , the radius of curvature of the abrasive grain wheel tooth surface , and the average abrasive grain spacing are simplified as:
is the honing wheel grit size, is the organization number. The combined analysis of the above equations shows the surface roughness , and the maximum height of the valley on the surface of the workpiece after honing . And because of the average interval of abrasive grain , therefore , . That is, as the grain mesh size increases, the abrasive grain size decreases, and the average spacing of the abrasive grain decreases, resulting in a decrease in the maximum valley height , which in turn decreases the surface roughness value and the surface roughness quality improves.
5.4.3. The Relationship Between Grain Size and Processing Efficiency
As shown in Figure 10, with the reduction in grain mesh size of the CBN honing wheel, cutting performance and honing processing efficiency are significantly improved. On the one hand, the size of abrasive particles increases with the decrease of grain mesh size. At the same time, the surface width of the abrasive particles and the nominal width of the abrasive chip cutting layer in front of the tool is increased, resulting in more material being cut off from the workpiece surface per unit time, which improves the honing efficiency. On the other hand, when the grain mesh size is small, the contact area between the abrasive particle and the binder is larger, and the height of the abrasive edge is also larger, which makes the chip space and lubricating cooling effect of the honing wheel better, thus enhancing the ability to resist external intrusion. The abrasive particles are less likely to fall off, and the low wear rate of the honing wheel improves the life and processing efficiency of the honing wheel.
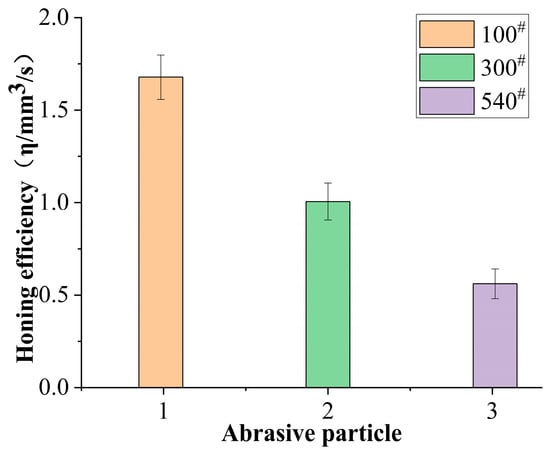
Figure 10.
Relationship between abrasive grain size and material removal rate with honing gear.
In addition, it is found that the honing state of clogging and surface passivation is likely easy to occur when the honing wheel is machined with large grain mesh size CBN. This phenomenon leads to a decrease in honing efficiency because the large grain mesh size will cause the pore volume and the nominal cross-sectional area of the debris of the honing wheel to be reduced. In addition, the number of effective abrasive cutting edges and abrasive chips increases. Therefore, in the range of small cut times, a part of the grinding chips is taken away by the cutting fluid, and the other part is retained in the pore volume. This results in a lower actual cutting depth of abrasive particles and a lower effective material removal rate per unit of time compared to the theoretical material removal rate.
With the increase in honing times, the probability of abrasive cutting-edge wear increases. The effective cutting depth of the 100# honing wheel is greater than that of the 540# honing wheel. The chip fusion in the pore of the honing wheel increases with the increase in temperature. After a certain number of honing cycles, the amount of abrasive plugging increases with the increase of the grain mesh size of the CBN honing wheel. Therefore, the honing wheel with a large grain mesh size should be selected in semi-fine honing and fine honing. On the contrary, the honing wheel with a small grain mesh size has a large penetration depth of abrasive particles, high honing temperature, and large material removal. At the same time, there are more grinding chips and fused caking materials blocked in the gap between abrasive particles, so the mesh number of small particles is more suitable for coarse honing.
5.5. Analysis of Comprehensive Evaluation Result of Gear Honing Processing Quality
The experiments mainly measured the experimental values of different abrasive grain size D6 on the five factors of sub-criterion layer indexes C1, C2, C3, C4, and C6. Based on the characteristics that the unit, order of magnitude, and trend of each index’s influence on honing quality are not uniform and cannot be measured, the threshold method is adopted to conduct dimensionless processing of experimental data [] to ensure the reliability of the evaluation.
The greater the indicator value, the better the honing quality. The material removal rate indicator value falls into the category of “the larger, the better”. The formula for dimensionless processing is as follows:
If the index value of the sub-criterion layer increases, the quality of honing teeth will deteriorate. Parameters such as surface roughness, single pitch deviation, total tooth profile deviation, and total helix deviation all follow the principle of “the smaller, the better.” The dimensionless processing formula is as follows:
In this context, represents the normalized value of the i-th factor in the k-th group of experiments, while denotes the honed experimental value of the i-th factor in the k-th group.
By incorporating the aforementioned experimental values into the sub-criteria layer C, we can evaluate the quality differences of CBN grinding with varying granularity. The comprehensive evaluation model can be derived from Equation (23).
In the equation, represents the evaluation weight matrix of factors, with specific values obtained for the weight matrix of sub-criteria layer C referenced in Table 6 as . denotes the evaluation weight of experimental data.
is a dimensionless matrix of ,,, The calculation result is:
Bring the results of and into Formula (23), obtained . The comprehensive evaluation of the honing quality corresponding to the three-grain sizes was ranked 0.53 > 0.47 > 0.34. This indicates that 300# CBN grit has the best honing quality, 540# CBN grit has the worst honing quality, and 100# is in between. In the matrix, the weights of 100# and 300# abrasive grits are in good agreement, and the difference in the evaluation of machining efficiency between the two in the matrix is 0.23, and the difference in the evaluation of surface roughness is 0.52, which is larger than that of the evaluation of the individual tooth pitch deviation, the cumulative total deviation of the tooth profile, and the total deviation of the helix. This indicates that the abrasive grain size has a greater impact on machining efficiency and surface roughness and a smaller impact on honing accuracy. The conclusion is consistent with the conclusion of the comprehensive evaluation sensitivity in Figure 4, which verifies the correctness of the established comprehensive evaluation model of honing machining quality and can provide a decision-making basis for the manufacture of high-performance hardened gears.
6. Conclusions
- (1)
- Based on Tra-FAHP and SPA, a comprehensive evaluation model for CBN micro-edge honing quality is established, which eliminates the subjective influence of AHP and ensures that the evaluation results are more reasonable and objective. The established evaluation model can quantitatively and effectively identify and evaluate the quality of the honing process with certainty and uncertainty factors, guiding the honing process of high-performance hardened gears.
- (2)
- With increasing grain size, the mean value of total helix deviation sequentially decreases. The distribution of tooth pitch deviation gradually approaches the zero line; the correction ability of the change of the length of the common normal line increases; the average value of the total profile deviation decreases, making the accuracy of the honed workpiece gradually improve. However, affected by the phenomenon of error reenactment, the maximum error reduction of the helix of the tooth surface after honing with large-sized abrasive grain is not obvious. Increasing the number of honing operations and reducing the error reflection coefficient can effectively reduce the maximum error of the workpiece tooth surface helix and improve the honing machining accuracy.
- (3)
- With abrasive grain size decreasing, the average spacing of abrasive grain decreases, resulting in decreased maximum valley height , which makes the surface roughness value smaller. Improvement of surface quality after honing.
- (4)
- With the increase of abrasive grain size, the cutting performance improves, and the honing machining efficiency obviously improves, which is applied to rough honing machining.
The article evaluates the effect of abrasive grain size on the quality of the honing process. The established comprehensive evaluation model can also be applied to the evaluation of other 11 key factors on the quality of the honing process. The study provides a theoretical basis for the comprehensive evaluation of honing quality and the optimization of process parameters. In the future, we will focus on studying the influence of key factors, such as abrasive grain and process parameters, on honing quality by improving the comprehensive evaluation model of honing characteristics and proposing a more scientific control strategy to guide the development of honing wheels and the honing process. of the manuscript.
Author Contributions
Conceptualization, J.S. and Y.L.; methodology, J.Z., Y.G., J.S. and F.W.; software, J.S.; validation, Y.Y. and J.Z.; formal analysis, Y.G.; investigation, Y.Y., J.Z. and J.S.; resources, Y.G.; data curation, J.S.; writing—original draft preparation, J.S. and Y.Y.; writing—review and editing, Y.G., F.W. and L.L.; visualization, F.W., L.L. and Y.G.; supervision, Y.Y.; project administration, Y.G.; funding acquisition, Y.L. and Y.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [the Young Talent Cultivation Programme of North Minzu University] grant number [No. 2023QNPY13], [the Ningxia Natural Science Foundation] grant number [No. 2023AAC02047], [the Ningxia Engineering Research Center for Hybrid Manufacturing System Foundation] grant number [No. 2023GCJS008], and [Key research and development projects of North Minzu University] grant number [No. FHZL20240731].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, G.H.; Han, J.; Tian, X.Q.; Tang, J.P.; You, T.F.; Xia, L. Prediction of honing force based on kinematic-geometric simulation. J. Manuf. Process. 2023, 101, 1136–1146. [Google Scholar] [CrossRef]
- An, I.H.; Ahn, M.J.; Xu, Z.; Lyu, S.K. A Study on the Effect of the Honing in SCM420H Planetary Gear. J. Korean Soc. Manuf. Process Eng. 2011, 10, 13–18. [Google Scholar]
- Zhang, L.Y.; Zheng, T.L.; Li, T.J.; Wang, J.; Wang, C.L.; Jiang, Y.H.; Li, C.Y.; Yuan, F.X.; Yao, Z.H. Precision Forming Process Analysis and Forming Process Simulation of Integrated Structural Gear for New Energy Vehicles. Manuf. Technol. 2023, 23, 958–966. [Google Scholar] [CrossRef]
- Liu, Y.H.; Huang, X.H.; Cao, H.J.; Wang, J.C.; Xiao, H.P. Model of Surface Texture for Honed Gear Considering Motion Path and Geometrical Shape of Abrasive Particle. Chin. J. Mech. Eng. 2023, 36, 96. [Google Scholar] [CrossRef]
- Wang, B.; Guo, X.; Zhang, W.; Chen, Z. A study of an electric parking brake system for emergency braking. Int. J. Veh. Des. 2015, 67, 315–346. [Google Scholar] [CrossRef]
- Klocke, F.; Brumm, M.; Kampka, M. Process model for honing larger gears. In Proceedings of the International Gear Conference 2014, Lyon, France, 26–28 August 2014; Velex, P., Ed.; Chandos Publishing: Oxford, UK, 2014; pp. 118–128. [Google Scholar] [CrossRef]
- da Silva, S.P.; Ribeiro, S.L.M.; Brandao, L.C. Particle swarm optimization for achieving the minimum profile error in honing process. Precis. Eng.-J. Int. Soc. Precis. Eng. Nanotechnol. 2014, 38, 759–768. [Google Scholar] [CrossRef]
- Yuan, B.; Han, J.; Tian, X.Q.; Xia, L. Optimization and active control of internal gearing power honing process parameters for better gear precision. Mech. Sci. 2022, 13, 449–458. [Google Scholar] [CrossRef]
- Li, X.; Shao, W.; Tang, J.Y.; Zhang, D.; Chen, J.L.; Zhao, J.Y.; Wen, Y.Q. Multi-physics field coupling interface lubrication contact analysis for gear transmission under various finishing processes. Eng. Fail. Anal. 2024, 165, 108742. [Google Scholar] [CrossRef]
- Liu, W.; Deng, Z.; Shang, Y.; Wan, L. Effects of grinding parameters on surface quality in silicon nitride grinding. Ceram. Int. 2017, 43, 1571–1577. [Google Scholar] [CrossRef]
- Silva, S.P.; Brandao, L.C.; Pereira, R.F.P. Evaluation of Quality of Steering Systems Using the Honing Process and Surface Response Methodology. In Proceedings of the 13th CIRP Conference on Modelling of Machining Operations, Sintra, Portugal, 12–13 May 2011; pp. 821–825. [Google Scholar]
- Riabchenko, S.; Krivosheja, A.; Burykin, V.; Najdenko, A.; Bandurenko, M. Gear Grinding by Superhard Materials Wheels. In Proceedings of the Advanced Manufacturing Processes: Selected Papers from the Grabchenko’s International Conference on Advanced Manufacturing Processes (InterPartner-2019), Odessa, Ukraine, 10–13 September 2019; Tonkonogyi, V., Ed.; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Wang, F.W.; Chen, Y.L.; Gao, Y.; Liang, Y.; Wang, R.M.; Zhao, D.F. Modeling of Specific Energy in the Gear Honing Process. Energies 2023, 16, 5744. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, F.W.; Liang, Y.; Han, J.; Su, J.; Tong, Y.; Liu, L. Cutting Performance of Randomly Distributed Active Abrasive Grains in Gear Honing Process. Micromachines 2021, 12, 1119. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Ren, X.Q.; Han, J.; Wang, F.W.; Liang, Y.; Liu, L. Simulation to Microtopography Formation of CBN Active Abrasives on a Honing Wheel Surface. Coatings 2021, 11, 0540. [Google Scholar] [CrossRef]
- Wang, F.W.; Chen, Y.L.; Gao, Y.; Liang, Y.; Su, J.; Liu, L. Peridynamic Simulation to Fracture Mechanism of CBN Grain in the Honing Wheel Dressing Process. Micromachines 2021, 12, 1186. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.F.; Li, G.H.; Hu, B.W.; Miao, W.C. Impact-abrasive Wear Behavior of ZTA and NbC Reinforced Fe60 Matrix Composites. J. Wuhan Univ. Technol.-Mater. Sci. Ed. 2023, 38, 1426–1433. [Google Scholar] [CrossRef]
- Ma, W.; Lu, D.H.; Tang, L.; Gong, W.H.; Yan, Q.H. Effect of matrix hardness on the impact abrasive wear performance of ZTAp/steel architecture composite. Mater. Res. Express 2021, 8, 026507. [Google Scholar] [CrossRef]
- Tang, J.P.; Han, J.; Tian, X.Q.; Li, Z.F.; You, T.F.; Li, G.H.; Xia, L. Flexible modification and texture prediction and control method of internal gearing power honing tooth surface. Adv. Manuf. 2024, 1–15. [Google Scholar] [CrossRef]
- Wang, J.C.; Cao, H.J.; Liu, Y.H.; Huang, X.H. Simulation and experimental research on residual stress of honed gear based on scratch test. Int. J. Adv. Manuf. Technol. 2022, 123, 985–998. [Google Scholar] [CrossRef]
- Fuse, K.; Dalsaniya, A.; Modi, D.; Vora, J.; Pimenov, D.Y.; Giasin, K.; Prajapati, P.; Chaudhari, R.; Wojciechowski, S. Integration of Fuzzy AHP and Fuzzy TOPSIS Methods for Wire Electric Discharge Machining of Titanium (Ti6Al4V) Alloy Using RSM. Materials 2021, 14, 7408. [Google Scholar] [CrossRef]
- Patil, A.S.; Sunnapwar, V.K.; Bhole, K.S.; Oza, A.D.; Shinde, S.M.; Ramesh, R. Effective machining parameter selection through fuzzy AHP-TOPSIS for 3D finish milling of Ti6Al4V. Int. J. Interact. Des. Manuf.-IJIDEM 2022, 1–25. [Google Scholar] [CrossRef]
- Liu, Y.H.; Liu, W.; Meng, X.L.; Zhang, X.H.; Ge, S.Y.; Liu, H. Comprehensive Evaluation of Regional Integrated Energy System Using the Fuzzy Analytic Hierarchy Process Based on Set Pair Analysis. In Proceedings of the 58th IEEE/IAS Industrial and Commercial Power Systems Technical Conference Asia (IEEE I and CPS Asia), Shanghai, China, 8–11 July 2022; pp. 2019–2024. [Google Scholar]
- Huang, G.Z.; Wu, Z.G.; Yang, C.S.; Liu, H. Research on construction safety evaluation based on Fuzzy-Set Pair Analysis model. In Proceedings of the International Conference on Manufacturing Science and Technology (ICMST 2011), Singapore, 16–18 September 2011; pp. 6587–6593. [Google Scholar]
- Wang, J.W.; Liu, S.; Song, Y.H.; Wang, J.; Wu, H. Environmental Risk Assessment of Subway Station Construction to Achieve Sustainability Using the Intuitionistic Fuzzy Analytic Hierarchy Process and Set Pair Analysis. Discret. Dyn. Nat. Soc. 2021, 2021, 5541493. [Google Scholar] [CrossRef]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Abdullah, L.; Najib, L. A new type-2 fuzzy set of linguistic variables for the fuzzy analytic hierarchy process. Expert Syst. Appl. 2014, 41, 3297–3305. [Google Scholar] [CrossRef]
- Liu, Y. Application research of index weight determination method based on trapezoidal fuzzy number. J. Nanjing Univ. Inf. Sci. Technol. (Nat. Sci. Ed.) 2009, 1, 369–372. [Google Scholar] [CrossRef]
- Jin, D.T.; Zhou, T.; Yang, X.H.; Lu, Y.; Wang, K.W. Assessment of Regional Water Resource Carrying Capacity by the Connection Number of Set Pair Analysis. Therm. Sci. 2024, 28, 2287–2294. [Google Scholar] [CrossRef]
- Wu, W. Application of relation number to multi-attribute decision making of ladder fuzzy number. Pract. Underst. Math. 2013, 43, 160–166. [Google Scholar]
- GB/T10095.1-2008; Cylindrical Gears—Precision Systems—Part 1: Definition and Allowable Values of Tooth Surface Deviation on the Same Side of the Gear Teeth. National Standard of the People’s Republic of China: Beijing, China, 2008.
- GB/T 131-2006; Geometric Product Specification (GPS). The Representation of Surface Structure in Technical Product Documents. National Standard of the People’s Republic of China: Beijing, China, 2006.
- Li, Y.L.; Han, K.X.; Wu, J.W. The Applicability Analysis and Improvement of Several Index Dimensionless Methods. In Proceedings of the 13th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Guilin, China, 29–31 July 2017; pp. 3084–3088. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).