Abstract
Returning pruned branches into the field is a key procedure in kiwifruit cultivation. It utilizes discarded branches and aids in orchard management. Shearing and bending behaviors dominate the mechanized process of branch return; however, current research lacks appropriate modeling methods for these processes. In this study, we developed a discrete element method (DEM) model to simulate the shearing and bending behaviors of kiwifruit branches. Initially, laboratory experiments determined the shear strength and elastic modulus of branch samples to be 31.38 MPa and 1.21 GPa, respectively. An annular kiwifruit branch DEM model was constructed. A Plackett–Burman design test identified significant influencing factors: effective modulus of bond, bond cohesion, effective modulus between ball and wall, and the normal-to-shear stiffness ratio. Utilizing the response surface method, we derived relationships between DEM parameters and mechanical responses. Optimal parameter combinations were found: an effective modulus of bond at 2.2 × 109 Pa, bond cohesion at 2.56 × 108 Pa, effective modulus between ball and wall at 1.27 × 108 Pa, and a normal-to-shear stiffness ratio of 1.16. Finally, simulations of the shearing and bending processes were conducted. The optimal parameter combination was verified with a relative error of 4.5%. Displacement–force curves showed general consistency, indicating reliability in the modeling approach.
1. Introduction
The forestry and fruit industries are integral components of the agricultural production system. In China, orchard areas have expanded rapidly, from 1657 thousand hectares in 1978 to 13,010 thousand hectares in 2022. In fruit production, pruning is essential for bearing fruit the following year. This practice generates substantial quantities of pruned branches, estimated at 3750 kg per hectare annually [1,2,3]. A significant portion of these pruned branches is either discarded arbitrarily or burned in the open air. Such practices create serious safety hazards and environmental pollution, representing a major waste of resources. Multiple approaches have been developed to harness these pruned branches effectively. In China, they are primarily used as fertilizer, raw materials, or energy resources [4].
China leads global kiwifruit production, with an annual yield of up to 3 billion tons [5,6]. Nearly half of this production comes from Shaanxi Province. Kiwifruit, a vine plant, matures its fruit on the branches during autumn. In winter, long kiwifruit branches are commonly pruned and discarded in orchards. Farmers in Shaanxi Province predominantly use direct branch returning as fertilizer. This practice involves smashing or chopping long branches into smaller pieces with straw-returning machines or dedicated fruit branch shredders. This accelerates decomposition and enhances soil fertility. Increased yields and reduced fertilizer applications lead to higher incomes for farmers. Additionally, avoiding branch burning improves the agricultural ecological environment.
During the mechanized branch returning operation, shearing and bending behaviors dominate the branch chopping and smashing processes. Thus, shear and bending properties are extremely important for understanding kiwifruit branch mechanics. Previous research has employed universal testing machines to investigate the bending, shear, and compression characteristics of crops such as corn, wheat, and rice [7,8,9]. Physical properties of apple branches and vine branches, along with other fruit branches, have also been determined [10,11,12]. However, little research has been conducted on the smashing process of fruit branches. The study of the bending and shearing process could help to understand the failure mechanism of maximum breaking force, destructional form, and deformation extent, and then help to design high-quality branch-returning machines to improve branch-returning quality, but little research has been conducted to deeply investigate the processes. This is due to a lack of proper methods. Moreover, the bending and shearing behavior were not easily observed in detail in traditional field and laboratory experiments.
The finite element method (FEM) and discrete element method (DEM) are two main numerical analysis methods that have been applied in agricultural processes to address certain limitations [13,14,15,16]. The FEM is able to study material failure and large-scale deformation and requires mathematical continuity, while the DEM shows an advantage in the research of discrete objects. When a fruit branch or crop straw breaks in the bending or shearing process, the branch will transition from a continuous medium to a discontinuous medium. With the bonding model of the DEM, bonds break and particles separate when the stress surpasses the predefined thresholds of tensile strength or cohesion; thus, the branch’s breaking behavior could be simulated with high accuracy [17]. The visual similarity is better with the DEM than the FEM, as can been found in the previous literature, especially that referring to the simulation of failure and fracture behaviors [18]. In addition, it is more convenient to quantitatively analyze the fracture and deformation characteristics with the bonding keys built into the DEM model [19]. In recent studies, the tensile behavior of plant fiber, the bending behavior of wheat straw, and the shearing behavior of banana straw have been studied [20,21]. However, most of these models are established with one single type of experiment, such as cutting force, bending force, or repose angle, which makes the model unreliable when it is utilized in a different process. For kiwifruit branches, only one DEM model with high moisture content was established based on a three-point bending test [12]. However, shearing simulation was not conducted and the influence of DEM parameters on the mechanical and dynamic behavior of kiwifruit branches was not revealed. Despite these advancements, there remains a lack of suitable modeling methods for the bending and shearing processes of kiwifruit branches.
The overall goal of this study is to develop a DEM model establishment methodology based on more than one type of experiment and to investigate the failure characteristics of kiwifruit branches with the established model. Specific objectives of this study are as follows: (1) determine the shearing and bending properties of kiwifruit branches; (2) establish a kiwifruit branch model with the DEM and simulate its bending and shearing behavior; and (3) calibrate the key DEM parameters of the model with simulation and laboratory tests and verify the calibrated parameters.
2. Materials and Methods
The DEM was employed to develop a model of kiwifruit branches and simulate their bending and shearing behaviors. The model establishment process included a mechanical property test of kiwifruit branches, the establishment of the DEM model, parameter calibration of the DEM model, and model reliability verification [22,23].
2.1. Description of Kiwifruit Branch Samples
The kiwifruit branch samples were collected in April from the experimental orchard of Northwest A&F University, situated in Wugong County, Xianyang City, Shaanxi Province (108°2′ E, 34°27′ N). The selected variety for sampling was “Cuixiang”, the predominant cultivar widely cultivated in the Shaanxi region. As shown in Figure 1a, the kiwifruit branch is macroscopically composed of the rind, pith, and marrow cavity. The average water content of the branch sample was measured at 9.1% using a rapid moisture meter, while the density was determined to be 0.577 g/cm3 using a densimeter with the water draining method. The cross-sectional external diameter measured 10.5 ± 2.3 mm, while the inner diameter was 3.0 ± 1.2 mm, both determined using a vernier caliper. Each sample was then cut into 10 mm segments for experiment, as illustrated in Figure 1b.

Figure 1.
Branch samples used for mechanical property tests: (a) The cross-sectional image of kiwifruit branch and (b) branch samples for experiment.
2.2. Mechanical Property Test of Kiwifruit Branch
A 10 kN electronic universal testing machine (Figure 2), located in the biomechanics lab of the College of Mechanical and Electronic Engineering, Northwest A&F University (CMT6104, Meister Industrial System Co., Ltd., Shenzhen, China), was used to conduct the shearing test and three-point bending test. The elastic modulus and shear strength of the kiwifruit branches were determined using these measurements. Each test was replicated 20 times.
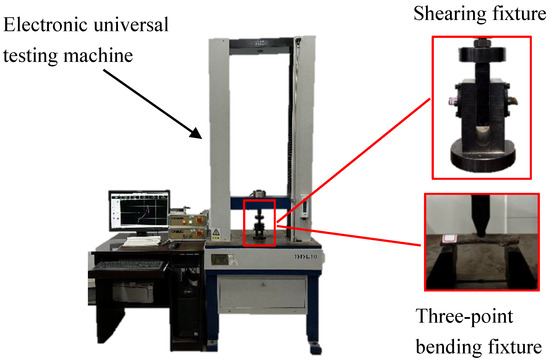
Figure 2.
Kiwifruit branch mechanical property test.
For the shearing test, a shearing fixture was utilized as shown in Figure 2. The branch was positioned across the apertures of the stationary and moving blades prior to each test. The moving blade then descended to shear the branch at a loading rate of 20 mm/min. The test was terminated once the branch broke.
A force–displacement curve can be obtained from each test. Peak shear force can be easily recognized from the force–displacement curve. The shear strength τ was calculated according to Equations (1) and (2) [24]:
where Fsmax is the peak shear force (N), A is the cross-sectional area of the branch (mm2), D is the external diameter (mm), and d is the inner diameter of the branch (mm).
For the three-point bending test (Figure 2), the two ends of the branch were placed on a steel support. A cylindrical indenter was then used to apply load at a displacement rate of 20 mm/min. The elastic modulus Eb was determined using Equation (3) [24]:
where Fb is the load of the cylinder indenter (N), L is the distance between the two supports (70 mm), S is the deflection (mm), and I is the inertia moment of the branch.
Since the cross-sectional geometry of the kiwifruit branch is approximately annular, the moment of inertia was calculated using Equation (4):
2.3. Discrete Element Modeling of Kiwifruit Branch
The kiwifruit branch model was constructed using the DEM software PFC3D 6.0 (Itasca Consulting Group, Inc., Minneapolis, MN, USA). This software employs two primary elements—balls and walls—to simulate the mechanical and dynamic behavior of materials. Agricultural materials are represented by individual balls or ball clusters, while agricultural machinery or its components are modeled by wall assemblies.
Previous studies have utilized the DEM to create branch model with small particles. The parallel bond model is composed of linear model, dashpot, and parallel bond (Figure 3). It allows adjacent particles to bond together when their distance falls within a certain range and was employed to simulate the cohesion within the kiwifruit branch tissues. Parallel bonds are capable of transmitting both force and moment between the balls. The force–displacement law for the parallel bond model updates the contact force and moment as detailed in Equation (5):
where Fc is contact force, Mc is contact moment, Fl is linear force, Fd is dashpot force, F is the parallel bond force, and M is the parallel bond moment.
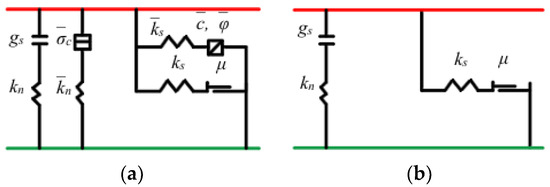
Figure 3.
Behavior and components of parallel bond model: (a) bonded (b) unbonded.
The parallel bond force is resolved into normal and shear forces, and the parallel bond moment is resolved into twisting and bending moments according to Equation (6):
where Fn is the normal force, Ft is the shear force, Mt is the twisting moment, and Mb is the bending moment.
Parallel bond provides mechanical behavior of a finite-sized piece of cement-like material deposited between the two contacting balls. Relative motion between the balls could cause force and moment to develop within the bond material. This force and moment then act on the two contacting balls. Bonds break and particles separate when the stress surpasses the predefined thresholds of tensile strength or cohesion and the bond material is removed from the model, thus simulating the branch’s breaking behavior. The unbonded parallel bond model is equivalent to the linear model [17].
Considering the complexity of kiwifruit branches, modeling their actual structure is challenging. In this study, to facilitate the establishment of the DEM model, the rind, which has a relatively minor impact on mechanical properties, was disregarded, and the branch was simplified to an annular structure composed of a cluster of particles.
Initially, a box with dimensions of 100 mm in length, 14 mm in width, and 14 mm in height was created and filled with balls. The diameter of these balls was uniformly distributed, ranging from 0.6 to 0.8 mm. Subsequently, a cylindrical assembly of balls with a diameter of 10.5 mm was formed by selectively removing particles located outside the cylindrical region. The medullary space was then simulated by removing a central cylindrical volume of particles with a diameter of 3.0 mm. The final branch model is depicted in Figure 4a, with the bonding keys of the parallel bond model between particles illustrated in Figure 4b.

Figure 4.
Schematic diagram of the kiwifruit branch model: (a) branch model consisting of particles and (b) bonding keys of the model.
The fundamental parameters of the DEM model are listed in Table 1. The friction coefficient between the ball and wall and the ball local damping coefficient friction angle and bond gap were derived from prior studies [12,25]. The other 6 parameters, which are likely to affect the mechanical properties of the kiwifruit branch, are currently undergoing calibration and will be discussed in the subsequent section.

Table 1.
Parameters of the DEM model.
2.4. Calibration for DEM Model Parameters
The calibration of the DEM model parameters was achieved through simulations of shearing and three-point bending tests, with the objective of identifying the optimal parameters that minimize the discrepancy with laboratory experimental data. The fixture’s outline was measured and precisely replicated in CAD software SolidWorks 2018 at a 1:1 scale. Subsequently, the fixture model was exported to the DEM software PFC3D 6.0 for simulation purposes. As depicted in Figure 5, models of the kiwifruit branch and bonding keys were specifically created for the three-point bending and shearing tests, respectively.
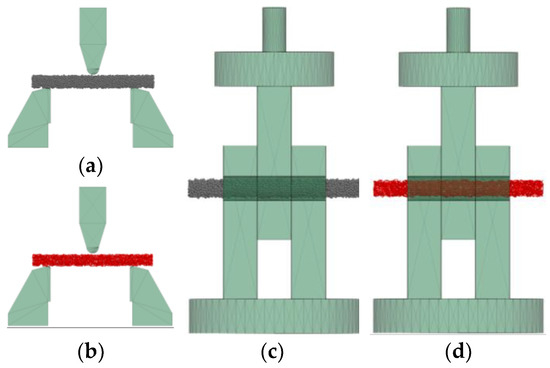
Figure 5.
DEM simulation of three-point bending test and shearing test: (a) three-point bending test simulation for branch model, (b) three-point bending test simulation for bonding keys, (c) shearing test simulation for branch model, and (d) shearing test simulation for bonding keys.
The calibration process consists of three stages: First, a Plackett–Burman design screening test is conducted to identify the significant parameters affecting the mechanical response of the DEM model, with the factor levels detailed in Table 2. Second, a steepest ascent test is employed to refine the value range of these significant parameters. Finally, a response surface methodology test is utilized to develop a predictive model correlating the DEM parameters with mechanical response, with the goal of determining the optimal parameter set that minimizes the deviation from laboratory experimental results.

Table 2.
Factors and levels of Plackett–Burman design test.
3. Results and Discussion
3.1. Experimental Result
The mechanical properties of the kiwifruit branch, derived from shearing and three-point bending tests, are summarized in Table 3. The branch’s average external and internal diameters were determined to be 10.5 mm and 3.0 mm, respectively. The average elastic modulus was found to be 1.21 GPa, and the shear strength was 31.38 MPa. While the diameter and shear strength closely align with the values reported by Fu [12], there is a notable discrepancy in the elastic modulus. This discrepancy may be attributed to differences in moisture content, as well as the omission of the marrow cavity in Fu’s study.

Table 3.
Mechanical properties of kiwifruit branch.
3.2. Screening Out Significant Parameters
The scheme and results of the Plackett–Burman test are shown in Table 4. Six blank columns were created for error analysis, and a total of 12 tests were performed. As we can see from the results, the elastic modulus and shear strength varied in a wide range under different parameter combinations. The range of shear strength ranged from 12.17 to 66.15 MPa, while the elastic modulus ranged from 1.06 to 2.00 GPa.

Table 4.
Scheme and results of Plackett–Burman design test.
The results, as listed in Table 5, were analyzed using Design-Expert software 10 (Stat Ease Ltd., Godward St NE, Minneapolis, MN, USA). Both models demonstrated significance with p-values lower than 0.05. In terms of shear strength, the cohesion of the bond and the effective modulus between the ball and the wall were found to be significant factors. This relation between cohesion and shear strength was also found in an experiment on frozen unsaturated silt [26]. Study [27] reported a significant effect of cohesion on tensile strength, indicating the importance of cohesion on the DEM model. Similarly, the effective modulus of the bond, the effective modulus between the ball and the wall, and the normal-to-shear stiffness ratio were identified as influential on the elastic modulus. However, the effective modulus of the ball and the tensile strength of the bond did not exhibit a significant impact on either of the mechanical properties assessed.

Table 5.
ANOVA of Plackett–Burman design test.
3.3. Determination of the Optimal Ranges of Significant Parameters
Based on the results of the Plackett–Burman test, four parameters were identified to have significant effect on the mechanical properties: effective modulus of bond, cohesion of bond, effective modulus between ball and wall, and normal-to-shear stiffness ratio. These parameters were selected to do the steepest ascent test, which was set uniformly in six steps, as listed in Table 6. In total, six simulations were required to refine the parameter ranges and find out the optimal values. Meanwhile, the remaining parameters were assigned with intermediate values: the effective modulus of the ball at 7.5 × 107 Pa and the tensile strength of the bond at 2.5 ×108 Pa. The relative error between simulated and experimental mechanical responses was utilized to ascertain the optimal parameter range, as defined by Equation (7).
where RE is the relative error, Sss is the shear strength of the simulation test, Lss is the shear strength of the laboratory test, Sem is the elastic modulus of the simulation test, and Lem is the elastic modulus of the laboratory test.

Table 6.
Scheme and results of steepest ascent test.
The results from Table 6 indicate that Test No. 2 achieved the lowest relative error at 7.2%. It is observed that as the test factors increased, both shear strength and elastic modulus also increased. The relative error initially decreased but then started to rise after Test No. 2. Based on these findings, the optimal range for the four significant parameters is likely to be close to the values observed in Test No. 2. Consequently, the parameter values from the first to the third test were selected as the initial range for conducting the response surface test.
3.4. Determination of Optimal Values for the DEM Parameters
In the response surface test, the range identified during the steepest ascent experiment was employed. To estimate experimental error, five tests were conducted at the central point, totaling 21 tests. The scheme and outcomes of the test are presented in Table 7. The shear strength values ranged from 13.45 to 72.02 MPa, while the elastic modulus values varied from 1.03 to 1.53 GPa.

Table 7.
Scheme and results of response surface test.
Analysis of variance (ANOVA) of the models is shown in Table 8. Both models were highly significant with p-value smaller than 0.01. All four factors under examination significantly influenced the elastic modulus. The cohesion of the bond and the effective modulus between the ball and the wall significantly affected shear strength. Regarding interaction effects, only factors D2 and E2 were found to significantly impact shear strength. Based on these results, the models for shear strength and elastic modulus were formulated, as presented in Equations (8) and (9), respectively. In these equations, only significant factors were retained; non-significant factors were omitted.
y1 = 4.06118 − 1.24953 × B + 0.328864 × D + 0.301449 × E − 4.27666 × F − 0.0942861 × D2 − 0.0587426 × E2
R2 = 0.98
R2 = 0.98
y2 = −47.57 − 7.26 × D + 4.45 × E
R2 = 0.97
R2 = 0.97

Table 8.
Variance analysis of response surface test.
The examined models for elastic modulus y1 and shear strength y2 exhibited very high coefficients of determination (R2), with values of 0.98 and 0.97, respectively. The R2 value indicated how much variability in the values of the mechanical response can be explained by the experimental variables.
The analysis of the F-value of each factor presented in Table 8 revealed the order of importance of the four factors on shear strength as E > B > F > D and for elastic modulus as E > D > B > F. According to the developed optimization regression model of each index, and considering the significance and importance order of the factors, we have selected the two most influential factors for each index to investigate their impact on elastic modulus and shear strength (Figure 6).
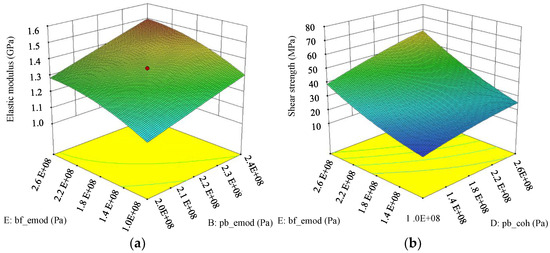
Figure 6.
Response surface of the two significant factors on mechanical response: (a) response surface on elastic modulus and (b) response surface on shear strength.
Figure 6a illustrates that the elastic modulus obviously increased with the simultaneous increase in effective modulus between ball and wall and effective modulus of bond. Whereas a more modest increase was observed when either the effective modulus between the ball and wall or the effective modulus of the bond was increased.
As shown in Figure 6b, with the increase in the effective modulus between the ball and wall and cohesion, the shear strength increased. This is similar to the findings of a DEM maize straw model study [28], where the maximum shear force was found to increase with the increase in stiffness between ball and wall. Additionally, the positive effect of cohesion was also found on tensile strength [29]. The curve for the effect of the effective modulus between the ball and wall was steeper than that for cohesion, indicating that the former has a greater influence on shear strength than the latter.
3.5. Parameter Verification and Simulation of Shearing and Bending Process
Based on the above response surface test analysis, a multi-objective variable optimization method facilitated by Design-Expert software was employed to identify the optimal values that minimize the relative error for both indices. By setting the experimental outcomes as the benchmark, the analysis revealed that the optimal values were 2.2 × 109 Pa for the effective modulus of the bond, 2.56 × 108 Pa for the cohesion of the bond, 1.27 × 108 Pa for the effective modulus between the ball and the wall, and 1.16 for the normal-to-shear stiffness ratio. Subsequently, these optimal combinations were integrated into the DEM model to verify the results.
With the derived values, a verification simulation test was performed. The simulation result of the shear strength was 29.57 MPa and the elastic modulus was 1.17 GPa. The discrepancies between these results and the experimental data were 5.8% and 3.3%, respectively. The relative error was calculated to be 4.5%, which is lower than the previous result. According to previous DEM model establishment studies, an error within 10% is acceptable [30,31]. Therefore, the calibrated parameters for the kiwifruit branch model were deemed reliable. As depicted in Figure 7a, the force–displacement curves from both the experimental shear tests and the simulations were found to be largely consistent. The shear force increased initially, reaching a peak at about 6 mm of displacement. It then slightly decreased before increasing again with minor fluctuations until it reached the maximum shear force. Subsequently, the force dropped sharply, aligning with the behavior observed in shearing tests of banana straw, Chinese cabbage root, and safflower [32,33,34]. However, two peak points were found in the shearing simulation of Chinese cabbage simulation due to the lower density of the model. Additionally, the shear force of safflower slowly decreased after the peak point because it is more flexible than the kiwifruit branch.
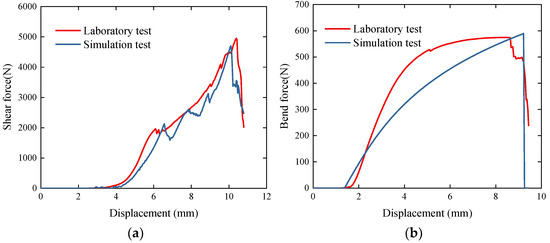
Figure 7.
Displacement–force curve comparison of laboratory and simulation test: (a) displacement–force curve on shearing test, (b) displacement–force curve on three-point bending test.
In the simulation of the shearing process (Figure 8), at first, the central part of the branch, positioned within the upper blade of the shearing fixture, underwent extrusion, and the junction between the central section and the two ends was subjected to tensile forces (Figure 8a). As the load increased, the right junction experienced failure, causing the branch to separate into two segments (Figure 8b). Subsequently, with the ongoing application of load, the left junction also failed, ultimately resulting in the branch breaking into three distinct pieces (Figure 8c). These outcomes displayed high resemblance with those observed during the experiment (Figure 8d), indicating the visual simulation ability of the DEM. This kind of ability was also found in the simulation of a series of agricultural materials, such as wheat plants, maize straw, Chinese cabbage, and tobacco leaf [32,35,36,37].
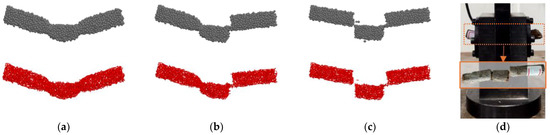
Figure 8.
Verification of branch shearing behaviors of simulation and experiment: (a) first stage of branch shearing simulation, (b) second stage of branch shearing simulation, (c) last stage of branch shearing simulation, and (d) shearing experiment results.
As observed in Figure 7b, the force–displacement curves from both the experimental and simulated three-point bending tests closely resembled each other. At the initial stage, with a low load, the branch sample and the DEM model exhibited elastic behavior, characterized by a rapid increase in bending force. As the loading cylindrical indenter continued to move, the rate of force increase diminished, and the curve’s slope decreased, indicating the onset of plastic behavior—a phenomenon also observed in wheat straw [21,38]. During the bending process, as illustrated in Figure 9a, the bottom section of the branch experienced tensile stress, while the upper section was under compressive stress. The greatest displacement occurred in the middle and bottom sections of the branch, leading to initial fracture at the bottom (Figure 9b). With the sustained application of load, the crack quickly propagated to the upper section (Figure 9c). The peak force coincided with the complete fracture of the branch, displaying characteristics of brittle fracture. The simulation results closely matched the experimental observations (Figure 9d), thereby confirming the accuracy of the simulation.
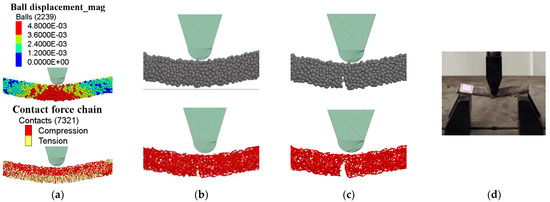
Figure 9.
Verification of branch bending behaviors of simulation and experiment: (a) stress–strain state of branch bending simulation, (b) fracture first appeared, (c) fracture extended to the top, and (d) bending experiment results.
4. Conclusions
In this study, a DEM model of the kiwifruit branch was developed. The model could simulate the bending and shearing processes of kiwifruit branches with high reliability. With this model, failure characteristics such as the breaking force and fracture development were observed. The results could provide reference for the investigation of the bending and shearing process of flexible materials and the failure mechanism of agricultural materials.
- (1)
- The shear modulus and elastic modulus of the kiwifruit branch samples were determined to be 31.38 MPa and 1.21 GPa, respectively, through shearing and three-point bending tests.
- (2)
- Four DEM parameters were identified as having a significant impact on the mechanical response of the kiwifruit branch model: effective modulus of bond, cohesion of bond, effective modulus between ball and wall, and normal-to-shear stiffness ratio.
- (3)
- Through response surface methodology, the functions relating DEM parameters to the mechanical response of the kiwifruit branch model were established. The optimum parameter combination of the effective modulus of bond, cohesion of bond, effective modulus between ball and wall, and normal-to-shear stiffness ratio was determined to be 2.2 × 109 Pa, 2.56 × 108 Pa, 1.27 × 108 Pa, and 1.6.
- (4)
- The verification tests conducted with the optimal parameter combination revealed a relative error of 4.5% between the simulation and experimental results. The displacement–force curves demonstrated a high degree of congruence, affirming the reliability of the developed model.
Author Contributions
Conceptualization: H.Z. and W.L.; H.Z. reviewed the literature and wrote the initial draft of the paper with assistance from Z.Z. (Zhiqi Zheng). Z.Z. (Zhiqiang Zhang) and R.T. contributed to revising the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 32101630), the Key Research and Development Program of Shaanxi Province, China (No. 2023-YBNY-226), and a grant from the China Postdoctoral Science Foundation (No. 2020M683578).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sun, X.Y.; Wei, X.F.; Zhang, J.X.; Ge, Q.; Liang, Y.Y.; Ju, Y.L.; Zhang, A.; Ma, T.T.; Fang, Y.L. Biomass estimation and physicochemical characterization of winter vine prunings in the Chinese and global grape and wine industries. Waste Manag. 2020, 104, 119–129. [Google Scholar] [CrossRef] [PubMed]
- Jing, W.T.; Zhao, J.H.; Zhuang, T.F.; Liu, Z.J.; Yang, X.J.; Liu, L.J. Review on theory and equipment of mechanical vibration picking of forest fruits. Trans. Chin. Soc. Agric. Mach. 2023, 54 (Suppl. S1), 144–160. [Google Scholar]
- Yuan, Y.W.; Bai, S.H.; Niu, K.; Zhou, L.M.; Zhao, B.; Wei, L.G.; Xiong, S.; Liu, L.J. Research progress on mechanized harvesting technology and equipment for forest fruit. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2022, 38, 53–63. [Google Scholar]
- Cai, Z.Y.; Mao, B.Q.; Ao, C.L.; Liu, B.Q. Public preferences and willingness to pay for environmental benefits of straw return: Empirical evidence from Northeast China. J. Environ. Manag. 2024, 371, 123078. [Google Scholar] [CrossRef] [PubMed]
- Xie, X.; Rahman, M.M.; Pang, R.L.; Qiao, C.K.; Guo, L.L.; Xie, H.Z.; Pang, R.L.; Tian, F.J. Effect of forchlorfenuron (CPPU) on fruits quality and residue analysis in kiwifruits. J. Food Compos. Anal. 2024, 133, 106383. [Google Scholar] [CrossRef]
- Yan, Y.C.; Hao, S.H.; Gao, Y.L.; Xin, D.; Niu, Z.J. Design of kiwifruit orchard disease and pest detection system based on aerial and ground multi-source information. Trans. Chin. Soc. Agric. Mach. 2023, 54, 291–300. [Google Scholar]
- Chen, Z.G.; Wang, D.F.; Li, L.Q.; Shan, R.X. Experiment on tensile and shearing characteristics of rind of corn stalk. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2012, 28, 59–65. [Google Scholar]
- Shi, N.; Guo, K.Q.; Fan, Y.J.; Liu, B.X.; Yuan, X.L. Peeling and shearing mechanical performance test of cotton stalks in extrusion state. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2017, 33, 51–58. [Google Scholar]
- Yang, H.W.; Zhang, L.Y.; Tang, Z.Q.; Yu, F.H.; Xu, T.Y. Effects of mechanical and physicochemical properties on the lodging resistance of hybrid japonica rice. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2024, 40, 44–52. [Google Scholar]
- Kang, F.; Tong, S.Y.; Zhang, H.S.; Li, W.B.; Chen, Z.J.; Zheng, Y.J. Analysis and experiments of reciprocating cutting parameters for apple tree branches. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2020, 36, 9–16. [Google Scholar]
- Bu, L.X.; Chen, C.K.; Hu, G.R.; Zhou, J.G.; Sugirbay, A.; Chen, J. Investigating the dynamic behavior of an apple branch-stemfruit model using experimental and simulation analysis. Comput. Electron. Agric. 2021, 186, 106224. [Google Scholar] [CrossRef]
- Fu, S.K. Design and Experiment of Organic Fertilizer Application Machine for Kiwi Orchard. Master’s Thesis, Northwest A&F University, Yangling, China, 2021. [Google Scholar]
- Gao, X.J.; Xie, G.F.; Xu, Y. Application of a staggered symmetrical spiral groove wheel on a quantitative feeding device and investigation of particle motion characteristics based on DEM. Powder Technol. 2022, 407, 117650. [Google Scholar] [CrossRef]
- Gong, H.; Chen, Y.; Wu, S.L.; Tang, Z.Y.; Liu, C.; Wang, Z.Q.; Fu, D.B.; Zhou, Y.H.; Qi, L. Simulation of canola seedling emergence dynamics under different soil compaction levels using the discrete element method (DEM). Soil Tillage Res. 2022, 223, 105461. [Google Scholar] [CrossRef]
- László, P.; Bence, S.; Kornél, T. Measuring and modelling of soil displacement from a horizontal penetrometer and a sweep using an IMU sensor fusion and DEM. Soil Tillage Res. 2024, 244, 106207. [Google Scholar] [CrossRef]
- Mak, J.; Chen, Y.; Sadek, M.A. Determining parameters of a discrete element model for soil–tool interaction. Soil Tillage Res. 2012, 118, 117–122. [Google Scholar] [CrossRef]
- Itasca. User’s Manual for PFC3D Version PFC5.0; Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 2017. [Google Scholar]
- Li, M.; Xu, S.; Yang, Y.W.; Guo, L.; Tong, J. A 3D simulation model of corn stubble cutting using finite element method. Soil Tillage Res. 2017, 166, 43–51. [Google Scholar] [CrossRef]
- Shi, L.R.; Zhao, W.Y.; Sun, W. Parameter calibration of soil particles contact model of farmland soil in northwest arid region based on discrete element method. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2017, 33, 181–187. [Google Scholar]
- Zhao, H.B.; Huang, Y.X.; Liu, Z.D.; Liu, W.Z.; Zheng, Z.Q. Applications of discrete element method in the research of agricultural machinery: A review. Agriculture 2021, 11, 425. [Google Scholar] [CrossRef]
- Shi, Y.Y.; Jiang, Y.; Wang, X.C.; Thuy, N.T.D.; Yu, H.M. A mechanical model of single wheat straw with failure characteristics based on discrete element method. Biosyst. Eng. 2023, 230, 1–15. [Google Scholar] [CrossRef]
- Liu, Y.G.; Zhao, J.G.; Yin, B.Z.; Ma, Z.K.; Hao, J.J.; Yang, X.; Feng, X.J.; Ma, Y.J. Discrete element modelling of the yam root-soil complex and its verification. Biosyst. Eng. 2022, 220, 55–72. [Google Scholar] [CrossRef]
- Xie, K.T.; Zhang, Z.G.; Wang, F.A.; Jiang, S.F.; Wang, C.L. Mathematical model construction and verification of soil and Panax Notoginseng root adhesion. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2022, 38, 131–141. [Google Scholar]
- Zhang, Y.Q.; Cui, Q.L.; Li, H.B. Study on biomechanical properties of oat straw. Farm Prod. Process. 2021, 539, 24–27. [Google Scholar]
- Gong, H.; Chen, Y.; Zheng, W.H.; Zeng, Z.W.; Li, S.; Qi, L. Measurements and DEM modelling of soybean seed expansion. Comput. Electron. Agric. 2023, 208, 107786. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Huang, W.H.; Vanapalli, S.K. Experimental investigations of the shear strength and deformation behavior of a frozen unsaturated silt. Cold Reg. Sci. Technol. 2024, 12, 104332. [Google Scholar] [CrossRef]
- Wang, M.; Cao, P. Calibrating the micromechanical parameters of the PFC2D 3D models using the improved simulated annealing algorithm. Math. Probl. Eng. Theory Methods Appl. 2017, 2017, 6401835. [Google Scholar] [CrossRef]
- Zheng, Z.Q.; Zhao, H.B.; Liu, P.; He, J. Maize straw cutting process modelling and parameter calibration based on discrete element Method (DEM). INMATEH-Agric. Eng. 2021, 63, 461–468. [Google Scholar] [CrossRef]
- Vahid, S.; Chen, Y. Simulation of tensile behavior of plant fibers using the Discrete Element Method (DEM). Compos. Part A Appl. Sci. Manuf. 2018, 114, 196–203. [Google Scholar] [CrossRef]
- Su, Y.; Xu, Y.; Cui, T.; Gao, X.J.; Xia, G.Y.; Li, Y.B.; Qiao, M.M. Determination and interpretation of bonded particle model parameters for simulation of maize kernels. Biosyst. Eng. 2021, 210, 193–205. [Google Scholar] [CrossRef]
- Islam, M.S.; Larpruenrudee, P.; Rahman, M.M.; Li, G.L.; Husain, S.; Munir, A.; Zhao, M.; Sauret, E.; Gu, Y.T. Pharmaceutical aerosol transport in airways: A combined machine learning (ML) and discrete element model (DEM) approach. Powder Technol. 2024, 448, 120271. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Du, D.D.; Long, S.F.; Wang, Y.W.; Han, C.J.; Xu, Y. Optimization and validation of root-cutting device for Chinese cabbage harvester based on discrete element method. Comput. Electron. Agric. 2023, 214, 108314. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Zeng, C.; Xing, Z.Y.; Xu, P.; Guo, Q.F.; Shi, R.M.; Wang, Y.Z. Discrete element modelling and parameter calibration of safflower biomechanical properties. Int. J. Agric. Biol. Eng. 2024, 17, 37–46. [Google Scholar]
- Zhang, X.R.; Hu, X.H.; Liu, J.X.; Yang, Y.M.; Li, Y. Calibration and verification of bonding parameters of banana straw simulation model based on discrete element method. Trans. Chin. Soc. Agric. Mach. 2023, 54, 121–130. [Google Scholar]
- Schramm, M.; Tekeste, M.Z.; Plouffe, C.; Harby, D. Estimating bond damping and bond Young’s modulus for a flexible wheat straw discrete element method model. Biosyst. Eng. 2019, 186, 349–355. [Google Scholar] [CrossRef]
- Zhang, F.W.; Song, X.F.; Zhang, X.K.; Zhang, F.Y.; Wei, W.C.; Dai, F. Simulation and experiment on mechanical characteristics of kneading and crushing process of corn straw. Trans. Chin. Soc. Agric. Eng. 2019, 35, 58–65. [Google Scholar]
- Tian, Y.Y.; Zeng, Z.W.; Gong, H.; Zhou, Y.H.; Qi, L.; Zhen, W.B. Simulation of tensile behavior of tobacco leaf using the discrete element method (DEM). Comput. Electron. Agric. 2023, 205, 107570. [Google Scholar] [CrossRef]
- Sun, K.; Yu, J.Q.; Zhao, J.W.; Liang, L.S.; Wang, Y.; Yu, Y.J. A DEM-based general modeling method and experimental verification for wheat plants in the mature period. Comput. Electron. Agric. 2023, 214, 108283. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).