Spectral Separation of Up-Conversion Luminescence Processes

Abstract

Here, we present a novel method for the separation of overlapping emission spectral lines corresponding to nonlinear processes, which differ by effective nonlinearity with respect to the pump field power. The method exploits the factorization of wavelength and pumping power dependencies of the components processes contributions to the total luminescence. The advantage of our method is an ability to be self-testing and robust with respect to noise and experimental imperfections. We successfully demonstrate functionality of the method in the experiment with up-conversion luminescence of the fluorophosphate glass doped with rare-earth ions Yb³⁺ and Tm³⁺ pumped by 975 nm CW diode laser.

1. Introduction

Separation of complex emission spectra into individual components, corresponding to different emission processes, is of utmost importance for analyzing the emitting media. It had arisen at the very early age of spectroscopy, and continues to be relevant up to this day. The nature of the problem is simple: the registered signal at a given frequency is a sum of signals, corresponding to different emission lines or bands. It is not possible to distinguish components of the emission signal, corresponding to different processes, without using some additional information about these processes. The whole variety of existing and widely applied spectra separation methods can be divided into two major branches: one either fits the spectrum with known shapes, or exploits a chemometry-like approach, changing the respective contribution of different processes and measuring the total signal for each setting. The first approach is extensively discussed and used. Powerful numerical methods have been developed to deal with noise and inference of large number of spectral components. Nowadays, commercial (such as PeakFit by Systat Software Inc. US or Peak Resolve by OMNIC, US) and even free software packages are available, allowing us to perform fitting with a plethora of basic shapes (Gaussian, Lorentzian, etc.) [1,2]. The first approach is very versatile, and continues to be actively discussed and improved. One can infer spectral derivatives of several orders [3], or use the Fourier transform of the compound spectrum to provide more info for the fitting procedure [4]. Statistical inference techniques, such as maximum likelihood [5] and Bayesian estimation [6,7], have been applied for the task. The recent vogue of deep learning also found its way to spectral separation [8].

The second approach also boasts quite a long history. It was pioneered by Lawton and Sylvestre [9], and Alentsev and Fock [10]. The second approach does not require any a priori knowledge of component spectra. Registering compound spectra for a sufficient number of different weight settings allows one inferring all the components. The works [9,10] also birthed an extensive and already well matured field of research. In particular, a plethora of chemometric methods has stemmed from it [11,12].

The most common way to perform spectral separation by the second approach is to change respective quantities of the emitting agents; for example, the concentrations of different chemicals in the mixture. To our knowledge, not much attention was paid to the possibility of distinguishing spectral components by different effective nonlinearities of the incoherent emission processes associated with these components (here we can only mention a recent work [13]).

Separating the incoherent nonlinear processes by pump power dependence means that the spectral components inference can be carried on without a priori assumptions and/or some preliminary modeling with just a single sample by pump power variation. This possibility can be quite useful when researching nonlinear media aiming for properties necessary for particular applications in sensing/imaging, multi-photon absorption, metrology, etc.

Here, we present such an approach to spectral separation, and apply it to a particular kind of highly nonlinear media, which commonly demonstrates several nonlinear processes occurring simultaneously [14]. These media are the up-conversing (UC) ones, transforming longer wavelength pump into shorter wavelength luminescence; remarkably, UC processes might not require high pump power to occur. Spectral components of such up-conversion luminescence (UCL) processes are known to exhibit quite versatile dependencies on the pump power [15,16]. Also, spectral overlapping of UC processes is quite common for media with rather different nature of nonlinearity [17,18,19,20,21,22,23,24,25] UCL processes are widely implemented in modern optical and biomedical technologies. They are actively used for lasers [26,27,28,29,30] (and micro-lasers, in particular [31]), photoelectric devices (such as temperature sensors [32]), and solar cells [33,34,35,36,37]. Remarkable success was achieved with UC nanoparticles in optogenetics, bio-imaging, for optical control of the neural activity, i.e., in the widest field of so-called “theranostics”, combining therapy with sensing [38,39,40]. In a majority of these applications, UC processes are realized with optically active media, doped with rare-earth ions (REIs), which are also the staple for modern lasing/amplifying optical systems, optical communication and quantum memories for long-range quantum communication networks, etc. [14,30,41,42,43,44,45]. Of particular note is the use of up-conversion nanoparticles for reaching high nonlinearity (with up to a 26th power of pump energy density) and super-resolution imaging with up to 12 nm spatial resolution as well [46,47,48].

The remarkable feature of our approach is its self-testing. In particular, the validity is manifested by coincidence of obtained components spectra for different regions of the pump power variation. The possibility of such self-testing is very important for the spectral separation method, because it is able to work even for the case when power dependence of the spectral component changes with pump power (which is rather common for UCL processes with REIs).

Also, self-testing allows us to observe the emergence of processes, breaking factorization of the spectral, and the pump power dependencies underlying our method (such as, for example, cross-relaxation [15,16]).

We demonstrate our approach in the experiment using fluorophosphate glass doped with rare-earth ions Yb³⁺ and Tm³⁺ pumped by 975 nm CW diode laser.

The outline of this paper is as follows: In Section 2, we discuss our spectral separation method. In Section 3, we describe the experiment and the up-conversion processes occurring in our experiment. In Section 4, the spectral separation procedure is carried on for several spectral regions, in which we observed UCL of ions Tm³⁺, sensitized by Yb³⁺ ions. There, we also illustrate the self-testing procedure.

2. Spectrum Separation Method

Our spectral separation problem can be formulated in the following generic way. The compound wavelength and pump-dependent measured signal $\mathrm{J}(\lambda ,\mathrm{I})$ is represented as a sum of N components,

$$\begin{array}{c}\hfill \mathrm{J}(\lambda ,\mathrm{I})=\sum _{j=1}^N{\mathrm{J}}_j(\lambda ,\mathrm{I}),\end{array}$$

(1)

where the function ${\mathrm{J}}_j(\lambda ,\mathrm{I})$ describe a contribution of j-th process to the registered signal. We assume that finding each ${\mathrm{J}}_j(\lambda ,\mathrm{I})$ constitutes the solution of the spectral separation problem, providing sufficient information about the underlying processes. The key assumption of our separation method is factorization of the spectral and power dependence for each component process

$${\mathrm{J}}_j(\lambda ,\mathrm{I})=f_j\left(\lambda \right)g_j\left(\mathrm{I}\right),$$

(2)

where the power parts $g_j\left(\mathrm{I}\right)$ are assumed to be known, and the spectral parts $f_j\left(\lambda \right)$ are to be found.

When, for any given ${\lambda }_l$, one can make measurements for a set of $M\ge N$ powers $\left\{{\mathrm{I}}_k\right\}$, satisfying the condition (2), and the rank of the matrix $g_j\left({\mathrm{I}}_k\right)$ is N, the solution of the spectral separation problem for the vector $f_j\left({\lambda }_l\right)$ is a standard linear inversion with semipositivity constraints (i.e., $f_j\left(\lambda \right)\ge 0$). One can implement a plethora of numerical methods for it, starting, for example, with linearly constrained least squares estimation [11,12]. Repeating the procedure for a necessary set of wavelength one, thus would perform the spectral separation.

However, practical realization of this seemingly simple procedure faces two major difficulties (here, we are not addressing any possible conditions on the spectral functions $f_j\left(\lambda \right)$, making it necessary to perform inference for a set of wavelength values together, and not for each one separately). Firstly, for a given sample of a nonlinear medium to be analyzed, one generally does not know the functions $g_j\left({\mathrm{I}}_k\right)$ beforehand. Secondly, fulfillment of the factorization condition (2) should also be verified.

Let us demonstrate ways to deal with these problems with an example of up-conversion processes involving rare-earth ions. For them, it is quite common, exhibiting a UCL proportional to

$$g\left({\mathrm{I}}_j\right)\propto {\mathrm{I}}^{n_j},$$

(3)

where the number $n_j$ is commonly referred as the “photonity” of the j-th process (or, more conveniently, the “effective nonlinearity”, EN) [15,16]. Dependence (3) seems intuitive and straightforward. At least when there is no saturation, one expects this EN to correspond to the number of absorbed photons per emitted photon at a given wavelength, just like it is, for example, for frequency doubling by three-wave mixing. However, for complicated multi-level systems, such as rare-earth ions (Figure 1 gives an example of such a system; it will be discussed in more detail in the next section), this simple rule does not generally hold, even if the pump power dependence can be well described by Equation (3). EN might not even be an integer. To add, interaction between ions in the media (for UCL, it is cross-relaxation that can cause such phenomena such as, for example, the “photon avalanche” [49,50,51,52]) can break factorization (2), for instance, leading to the component signals of the following form [15,16]:

$${\mathrm{J}}_j(\lambda ,\mathrm{I})={\displaystyle \frac{f_j\left(\lambda \right){\mathrm{I}}^{n_j}}{1+c_j\left(\lambda \right){\mathrm{I}}^{k_j}}},$$

(4)

where the spectral function $c_j\left(\lambda \right)$ and EN $k_j$ describes contribution of the cross-relaxation process to j-th component signal (such an expression was actually used in the recent work [13] for fitting the component signal). As Equation (4) shows, one might have both factorization and power scaling (3), even for larger intensities when the cross-relaxation influence is strong.

Thus, we have devised the following practical procedure. We introduce EN for the compound signal as

$$n(\lambda ,\mathrm{I})\equiv {\displaystyle \frac{d}{dln\mathrm{I}}}ln\left(\mathrm{J}(\lambda ,\mathrm{I})\right).$$

(5)

Then, for some particular values of pump power $\mathrm{I}$ we look for spectral regions of weakly changing $n(\lambda ,\mathrm{I})$, aiming to attribute it to some particular UC process (or, to be precise, the sum of processes with the same EN). Then, we check found values of EN against measurements for the set of pump power values close to the initially chosen $\mathrm{I}$. If our suggestion of the processes with the same EN in the considered spectral intervals is asserted, we assign $n(\lambda ,\mathrm{I})\approx n_j$ for the j-th region, and proceed approximating $n(\lambda ,\mathrm{I})$ in all the wavelength range of our interest with the following expression obtained from Equations (1)–(3):

$$n(\lambda ,\mathrm{I})=\sum _{j=1}^N{n}_j{\displaystyle \frac{{\mathrm{J}}_j(\lambda ,\mathrm{I})}{\mathrm{J}(\lambda ,\mathrm{I})}}.$$

(6)

Taking some $M\ge N$ values of pump power, one can infer spectral functions $f_j\left(\lambda \right)$ from Equation (6).

For separation of just the two spectral components ${\mathrm{J}}_{1,2}(\lambda ,\mathrm{I})$, the approach in (6) is especially simple and illustrative. For this case, one can obtain the following equations from Equation (6):

$${\mathrm{J}}_1(\lambda ,\mathrm{I})=\mathrm{J}(\lambda ,\mathrm{I}){\displaystyle \frac{n_2-n(\lambda ,\mathrm{I})}{n_2-n_1}},{\mathrm{J}}_2(\lambda ,\mathrm{I})=\mathrm{J}(\lambda ,\mathrm{I}){\displaystyle \frac{n_1-n(\lambda ,\mathrm{I})}{n_1-n_2}},$$

(7)

It is important to note that our method is actually self-testing in different ways. Firstly, and the most obviously, coincidence of the inferred $f_j\left(\lambda \right)$ for different pump power values would justify the approach (5). Even if $n_j$ actually depends on the pump power (which is often the case, as will be seen in Section 4), the factorization approximation (2) might still work, providing for satisfactory self-testing and validity of the method. Other self-testing features can be discerned from Equation (7). For $n_2>n_1$, semi-positive definiteness of the inference results holds for

$$n_2\ge n(\lambda ,\mathrm{I})\ge n_1.$$

(8)

If assumptions (2, 3) are valid, Condition (8) is satisfied.

Notice also that experimental imperfections and noise might lead to such point-to-point variations in the measured UC luminescence power as to make it necessary to apply smoothing procedures to the measured data to consistently estimate log-log derivatives [53].

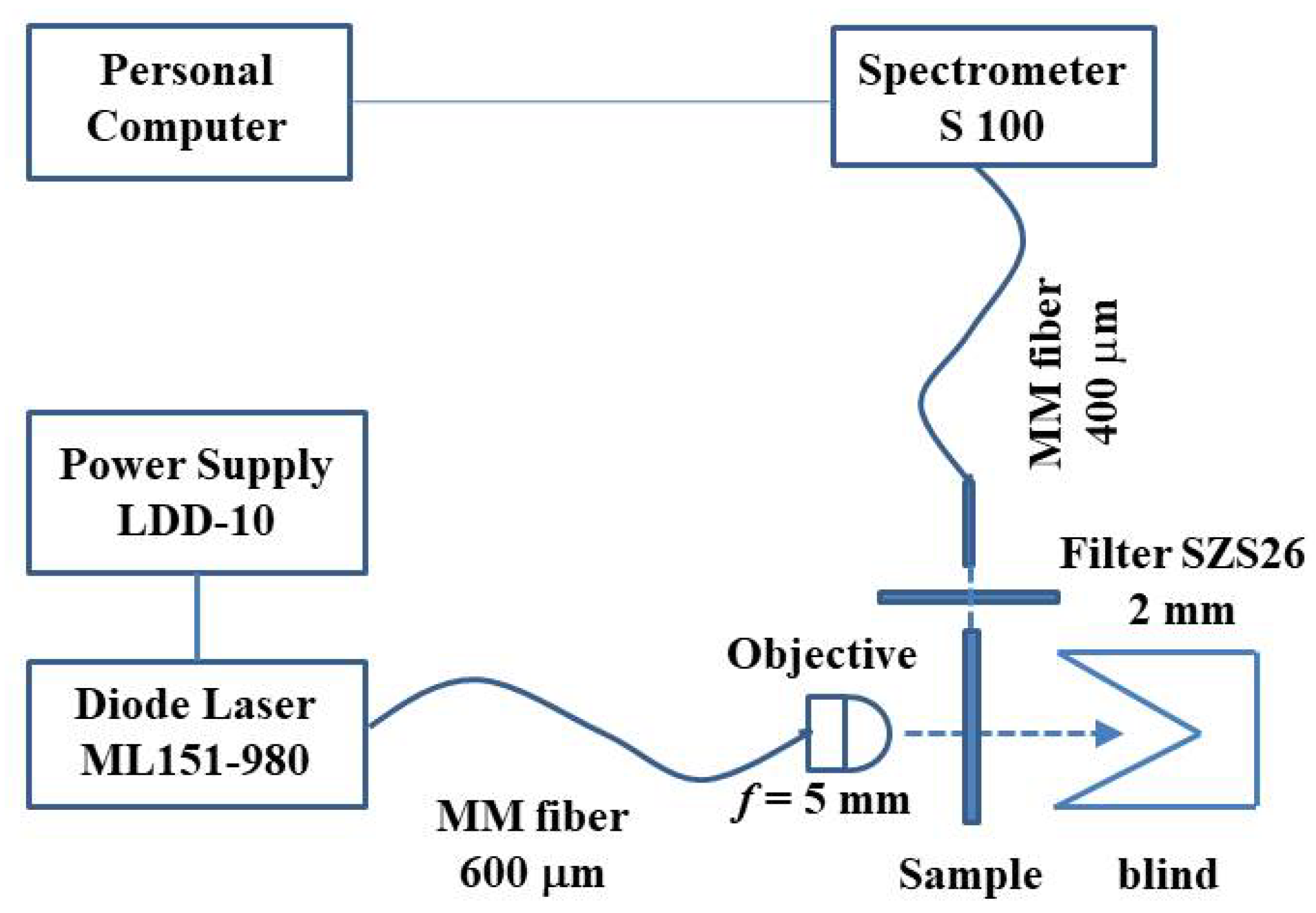
3. Experiment

We have performed measurements of UCL on a sample of the fluorophosphate glass, doped with rare-earth Yb³⁺ and Tm³⁺ ions at concentrations of 10% and 0.1%, respectively. The chemical composition of the glass samples was 5Ba(PO₃)₂–84.9(AlF₃–CaF₂–MgF₂–BaF₂–SrF₂)–10YbF₃-0.1TmF₃. The sample of the fluorophosphate glass was fabricated at the ITMO University, St. Petersburg, Russia [19]. This sample was also used in our recent work for line verification in luminescence spectra of up-conversion processes [18]. The measurement scheme is depicted in Figure 2. UCL was excited by the CW diode laser ML151-980 (“Milon Laser”Co Ltd., St. Petersburg, Russia) with a power of up to 2 W at the near-infrared region ${\lambda }_{pump}\approx 975$ nm. The UCL radiation was recorded with the spectrometer S-100 (“Solar LS”, Minsk, Belarus). UCL was collected from the lateral face of the sample to simplify filtering of the pump. Each spectral point was determined as a result of averaging over 10 measurements; each measurement was carried on during 7 ms.

In our scheme, the UCL was sensitized. The laser excited ions Yb³⁺. Then, one has the upconverting energy transferred from the sensitizer Yb³⁺ to the acceptor ion Tm³⁺. Such an excitation scheme is typical for this sensitizer–acceptor ion pair, and allows for an efficient cascaded energy transfer through a sequence of Tm³⁺ levels (the scheme of the participating levels is shown in Figure 1) [18,20,54]. For our consideration, we used the following observed UCL processes excited by the laser at 975 nm in the wavelength range of 300–900 nm (for the state notations see Figure 1).

1.

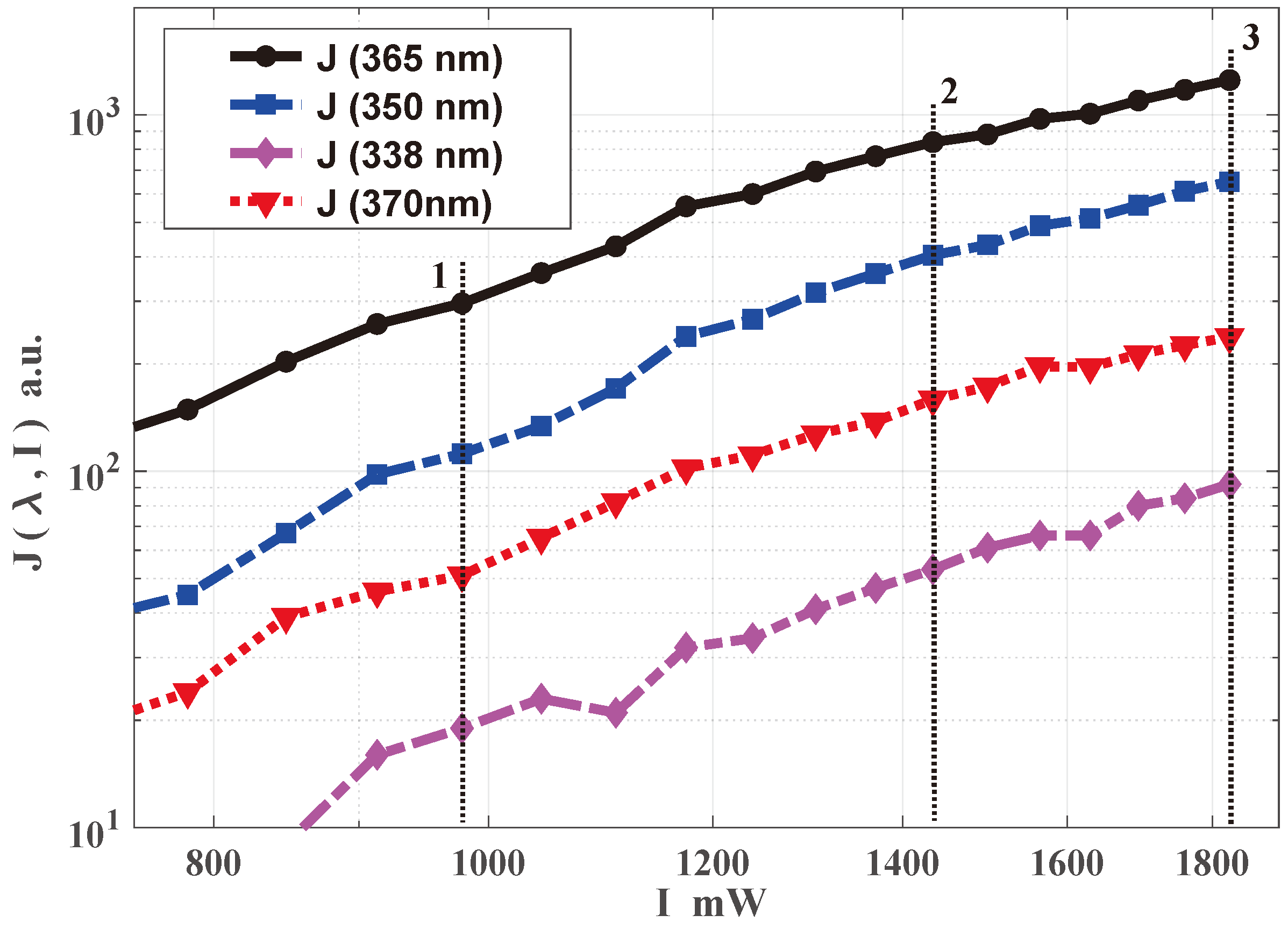
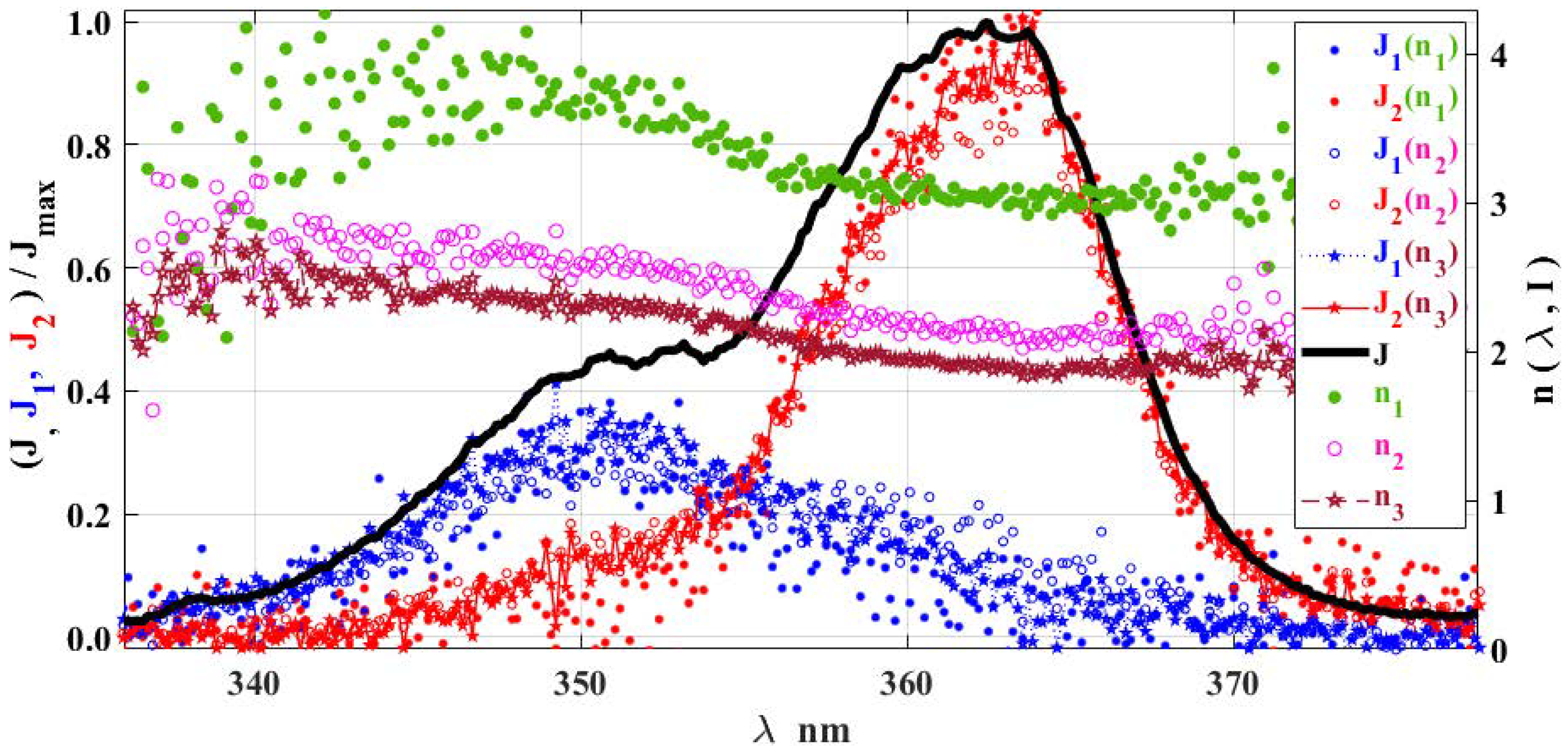
In the region of 335–380 nm with a sufficiently strong excitation power (700–2000 mW), one detects UCL from two different levels, ${}^{1}I_6\to {}^{3}F_4$ at 350 nm and ${}^{1}D_2\to {}^{3}H_6$ at 365 nm, corresponding to the processes with different ENs. The third UCL process ${}^{3}P_0\to {}^{3}F_4$ is quite weak, and left only negligible trace at 337 nm. Also notice that the processes ${}^{1}I_6\to {}^{3}F_4$ and ${}^{3}P_0\to {}^{3}F_4$ have a very close EN, and could hardly be separated by our method in (6) and (7) for the considered range of pump powers. These processes can still be separated using a stronger pump and larger Tm³⁺ ions concentrations such that cross-relaxation processes strongly impact the observed ENs. However, for such pump powers, the validity of the factorization (2) is questionable. So, we are not considering this possibility in the current work. Here, we considering only UCL from two different levels ${}^{1}I_6\to {}^{3}F_4$ at 350 nm and ${}^{1}D_2\to {}^{3}H_6$ at 365 nm, corresponding to the processes with different ENs.

2.

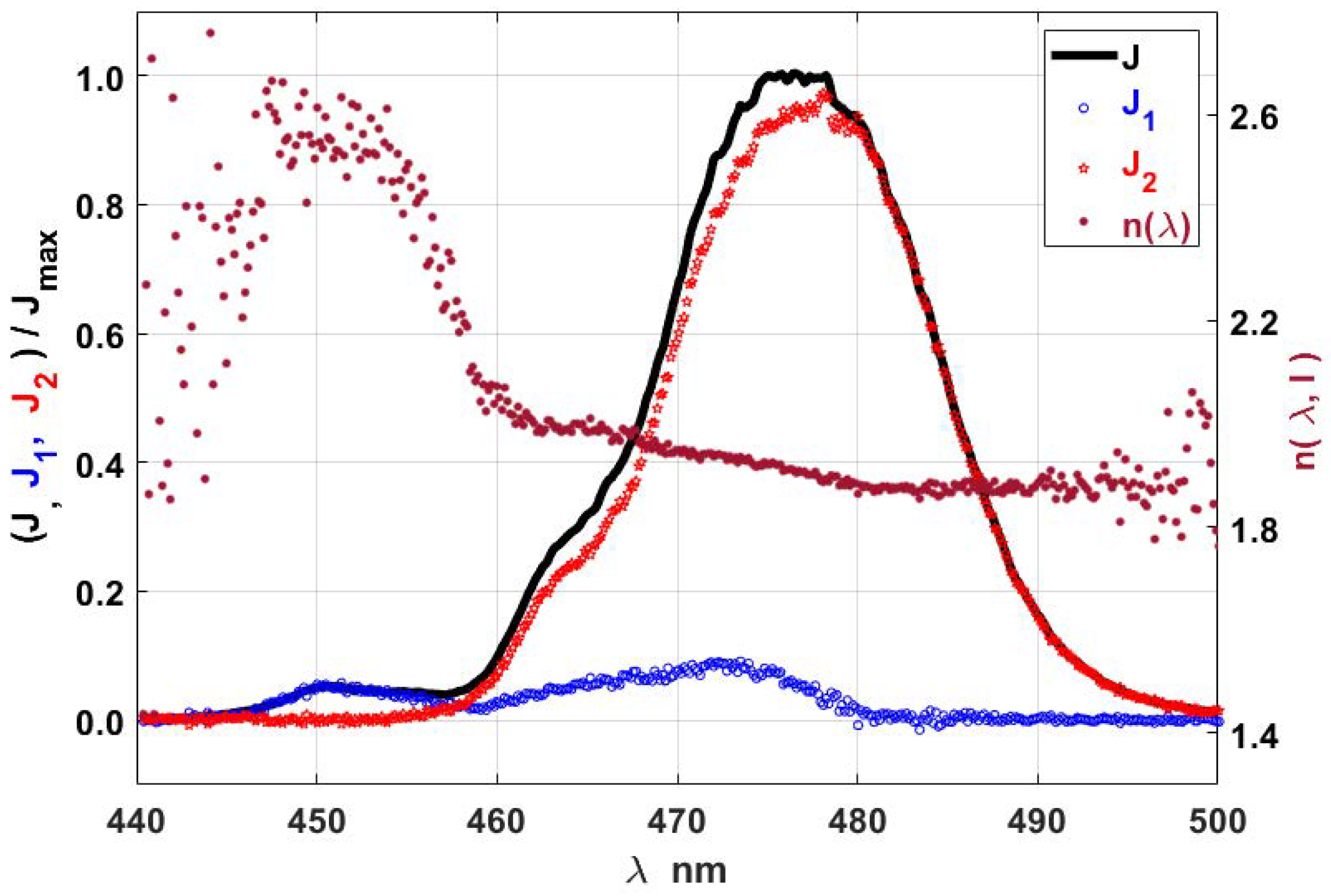
In the region of 440–500 nm, three processes with different ENs are possible as well: very weak UCL at 450 nm ${}^{1}I_6\to {}^{3}H_4$, relatively small UCL at 450 nm ${}^{1}D_2\to {}^{3}F_4$, and almost an order of magnitude more UCL at 475–480 nm ${}^{1}G_4\to {}^{3}H_6$.

3.

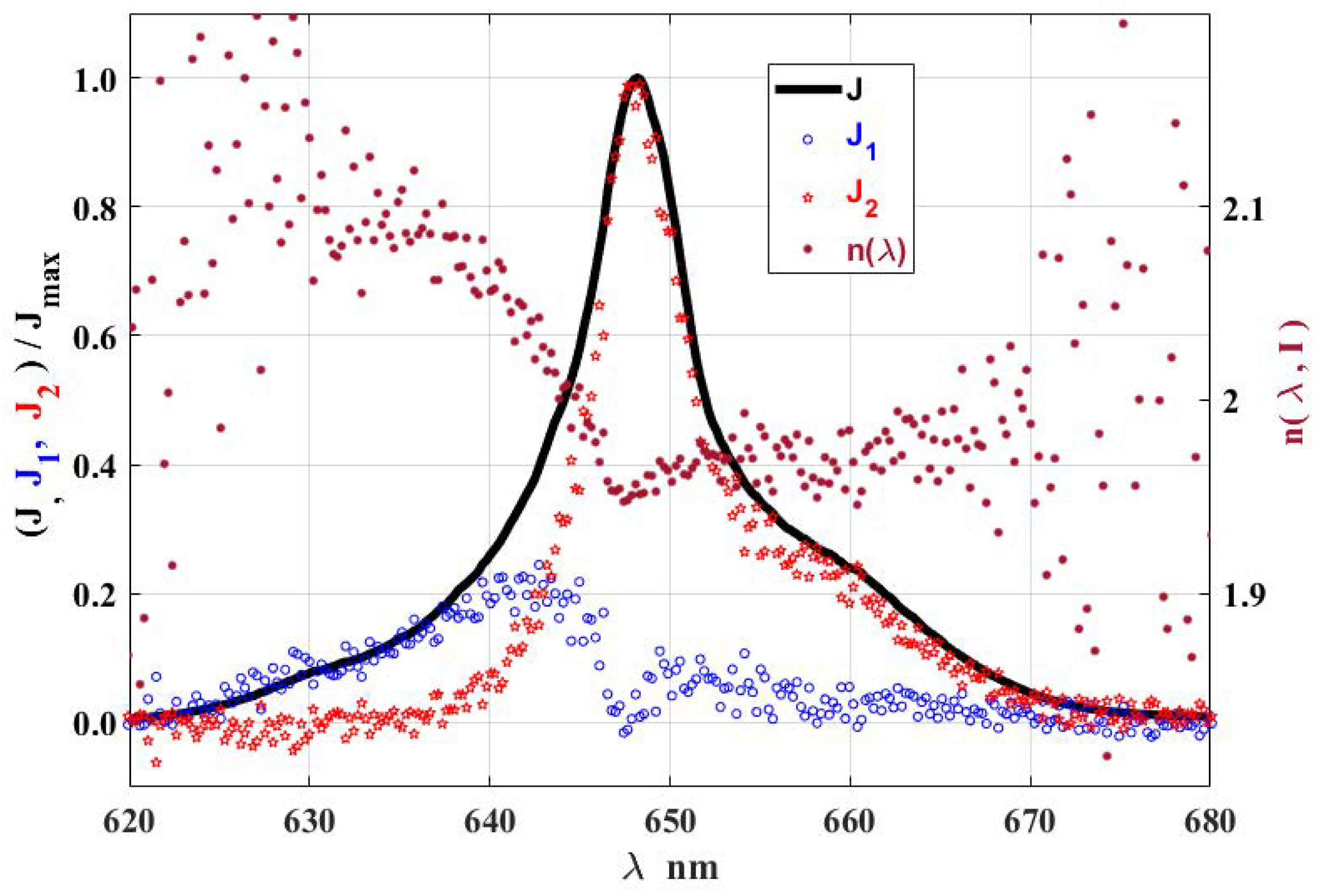
In the third region near 620–680 nm, two significantly overlapping lines are observed ${}^{1}D_2\to {}^{3}H_4$ at 643 nm; and ${}^{1}G_4\to {}^{3}F_4$ at 648 nm.

4.

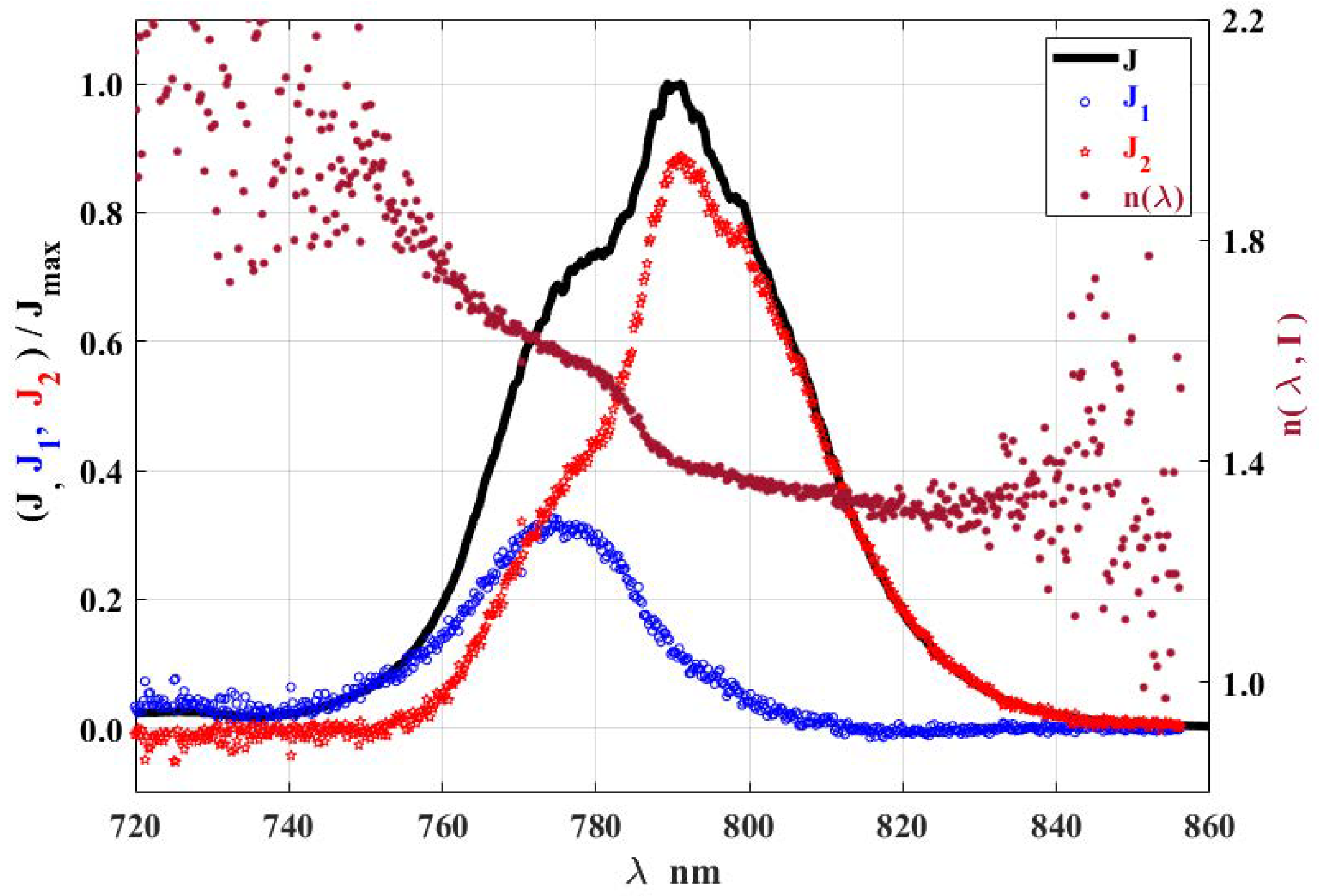
In the IR region at 720–840 nm, two processes of UCL with comparable efficiency are observed ${}^{1}G_4\to {}^{3}H_5$ at 775 nm, and ${}^{3}H_4\to {}^{3}H_6$ at 795 nm. No traces of UCL through processes ${}^{1}D_2\to {}^{3}F_{2,3}$ were observed, apparently because the share in the branching of these processes from level ${}^{1}D_2$ is quite small (4% and 6%) [17], and the excitation process is not sufficiently effective to excite them.

Thus, processes 1–4 correspond to at least two spectrally overlapping UCLs with different ENs in each spectral region. These process we have chosen for demonstrating our inference scheme described by Equations (5)–(7).

4. Results

Here, we demonstrate the spectral components separation for four spectral regions discussed in the previous Section, namely 1–4.

In Figure 3, it is illustrated why the choice of the approach Equations (5)–(7) is reasonable for our case. Figure 3 shows the dependence of UCL $\mathrm{J}(\lambda ,\mathrm{I})$ on pump power $\mathrm{I}$ in log-log scale for several wavelengths corresponding to $\lambda =$ 365 nm, 350 nm, 338 nm, and 370 nm and marked, respectively, with dots, squares, diamonds, and triangles. One can see that even in the region of overlapping spectral lines, it is rather straightforward to estimate the log-log derivatives as in Equation (6). Nevertheless, due to experimental imperfections estimation of log-log derivatives in a close vicinity of particular pump power for different wavelengths might give considerably different results.

To moderate effects of experimental imperfections, for estimating derivatives Equation (5), we used averaging over the sufficiently large regions of variation in pump power near each used pump value: for ${\mathrm{I}}_1=980$ mW, it is from 750 mW to 1250 mW; for ${\mathrm{I}}_2=1435$ mW, it is from 1250 mW to 1550 mW; and for ${\mathrm{I}}_3=1825$ mW, it is from 1250 mW to 1830 mW. That is, as can be seen in Figure 3, to calculate derivatives, in each interval (say, 1–2, 2–3), the dependence of $lnJ(\lambda ,\mathrm{I})$ on $ln\mathrm{I}$ was approximated with a linear dependence; the intervals were chosen in such a way as to provide for a good linear fit in all considered experimental cases.

In Figure 4, the procedure of the spectral components separation is demonstrated for the spectral interval 335–380 nm. The solid line in Figure 4 corresponds to the measured total up-conversion signal power $\mathrm{J}$ normalized to its largest value ${\mathrm{J}}_{max}$ at the pump power 1825 mW. To demonstrate the possibility of self-testing, we use three values the pump power marked by the numbered vertical lines in Figure 3. Large dots, circles, and stars show the estimated $n(\lambda ,{\mathrm{I}}_j)$ with Equation (5) for these pump power values (${\mathrm{I}}_{1,2,3}$). Notice that decrease in the average values of $n(\lambda ,{\mathrm{I}}_j)$ for all $\lambda$ with the growing pump power ${\mathrm{I}}_j$ probably indicates UCL saturation [16]. However, due to relatively low concentration (0.1%) of Tm³⁺ ions, the effects of cross-relaxation exchange between Tm³⁺ ions are not observed. Thus, the factorization condition (2) seems holding and the spectral inference results are close for all the considered intensities. In Figure 4, small dots, circles, and stars for each component spectral shapes (denoted as ${\mathrm{J}}_{1,2}$ in Figure 4) demonstrate the results of the inference described by Equation (7) for the $n(\lambda ,{\mathrm{I}}_j)$ shown by large dots for ${\mathrm{I}}_1$, circles for ${\mathrm{I}}_2$, and stars for ${\mathrm{I}}_3$.

One can see in Figure 4 that the results of the spectral component separation obtained for different pump powers are in good agreement with each other, despite the noise present in the data. The influence of noise is more pronounced for lower levels of the UCL signal at the line edges. Nevertheless, the component spectral shapes inferred for different pump powers are quite close even, at the edges. To add, the $n(\lambda ,{\mathrm{I}}_1)$ evaluated for ${\mathrm{I}}_1$ pump power (large dots in Figure 4) is much noisier and different in values than sets of $n(\lambda ,{\mathrm{I}}_{2,3})$ for two other pump power values ${\mathrm{I}}_{2,3}$. In spite of that, the spectral separation results remain similar.

So, it is possible to conclude that, for the considered UCL processes, our inference procedure (7) is quite robust. It should also be pointed out that such self-testing robustness can also show the region of pump powers when the cross-relaxation influence is significant and leads to factorization breaking in the vicinity of the chosen pump power [15,16]. Notice also that self-testing might uncover more subtle effects of additional nonlinear effects starting to play for some value of pump power, or such experimental imperfection as spectral drift of the pumping laser when increasing power of the output [52].

To give more examples of how our spectral separation works, we performed it for three spectral intervals: 440–500 nm (Figure 5), 620–680 nm (Figure 6), and 720–840 nm (Figure 7). For all of the figures (Figure 5, Figure 6 and Figure 7), the solid line corresponds to the measured compound up-conversion signal $\mathrm{J}$ normalized to its maximal value ${\mathrm{J}}_{max}$; stars and circles correspond to the inferred components spectral profiles; and dots show $n(\lambda ,{\mathrm{I}}_{\mathrm{j}})$ of the compound process estimated at the corresponding wavelength. For Figure 5, the spectral separation was performed for the pump power ${\mathrm{I}}_4$ = 783 mW with the averaging region for finding log-log derivative from 390 mW, to 783 mW. For Figure 6 and Figure 7, the spectral separation was performed for the pump power ${\mathrm{I}}_2$ = 1435 mW with the averaging region for finding log-log derivative from 390 mW, to 1565 mW.

Let us note some interesting features that reveal themselves in separated components of the UCL spectra in Figure 5, Figure 6 and Figure 7. In Figure 5, the processes under study are quite well spectrally separated. Nevertheless, one sees a two-peaked structure (circles) of one component, and a rather deformed side of the other component (stars). One might surmise that this is a consequence of the specific doublet energy levels structure of Tm³⁺ ions manifested, for instance, in the absorption spectra [55,56].This consideration is corroborated by the results of [23,24,55,56,57]. There, it is shown that both UCL processes ${}^{1}D_2\to {}^{3}H_6$ and ${}^{1}G_4\to {}^{3}H_6$ are characterized by a doublet line structure. So, the changes in EN near 470 nm might be indeed connected with additional processes associated with transitions from the upper levels of the ${}^{1}G_4$ band, or perhaps to a transition from ${}^{1}D_2$ band to the upper and lower levels of the ${}^{3}H_6$ band.

Another interesting and insightful feature can be noticed in Figure 6, and especially in Figure 7, where the component spectra are strongly overlapping. Namely, it is hardly possible to estimate effective nonlinearity trying to find it at the position of the component line maximum in the compound spectrum. For example, processing the measured EN at the edges of spectrum in Figure 7 gives for the component processes $n=1.91$ at $\lambda$ = 740 nm and $n=1.33$ at $\lambda =$ 820 nm, whereas just taking the effective nonlinearity at the position of the component lines maxima gives one $n=1.6$ at $\lambda$ = 770 nm and $n=1.39$ at $\lambda$ = 790 nm. Thus, trying to guess component EN at the wavelength of supposed maximal contribution of the component process without a proper spectral separation procedure might lead to quite misleading results.

5. Conclusions

Here, we demonstrated how it is possible to separate components spectra from the compound data corresponding to several nonlinear processes exploiting different pump power dependence (i.e., effective nonlinearity $n(\lambda ,\mathrm{I})$) of the component processes. We demonstrated functionality and robustness of our method with examples of UC doped with rare-earth ions Yb³⁺ and Tm³⁺. Our method is self-testing (i.e., reproducing inference results for different values of the pump power) as long as the factorization of spectral and power dependencies of the component processes holds near the values of the pump power chosen for the spectral separation procedure. It should be stressed out that our spectral separation method relying on self-testing allows one to avoid necessity of knowing characteristics of nonlinear media such as absorption cross-sections and losses rates for particular levels, establishing of system of levels involved into the considered processes, modeling, etc. Just a minimum of verifiable assumptions is used.

Finally, it is worth emphasizing that our method is rather generic and can be used for separation of nonlinear processes of quite general nature, as long as the factorization assumption holds. Also, the method is still can be applicable even when effective nonlinearities of component processes are changing with pump power.