Abstract
Deformable image registration plays a crucial role in medical imaging by aligning anatomical structures across multiple datasets, which is essential for accurate diagnosis and treatment planning. However, existing deep learning-based deformable registration models often face challenges in ensuring anatomical plausibility, leading to unnatural deformations in critical brain structures. This paper proposes a novel framework that uses Bayesian optimization to address these challenges, focusing on registering 3D point clouds that represent brain structures. Our method uses probabilistic modeling to optimize non-rigid transformations, providing smooth and interpretable deformations that align with anatomical constraints. The proposed framework is validated using MRI data from patients diagnosed with hypoxic-ischemic encephalopathy (HIE) due to perinatal asphyxia. These datasets include brain scans taken at multiple time points, enabling the modeling of structural changes over time. By incorporating Bayesian optimization, we enhance the accuracy of the registration process while maintaining anatomical fidelity. Our results demonstrate that the approach provides interpretable, anatomically plausible deformations, outperforming conventional methods in terms of accuracy and reliability. This work offers an improved tool for brain MRI analysis, aiding healthcare professionals in better understanding disease progression and guiding therapeutic interventions.
1. Introduction
Image registration is a fundamental technique in medical imaging that plays a critical role in clinical applications such as image-guided radiation therapy, image-guided surgery, and minimally invasive treatments [1,2]. The primary goal of image registration is to determine an optimal transformation that aligns images from different datasets, which is essential when critical information is distributed across multiple images, such as those captured at different time points or from distinct modalities [3,4]. Accurate registration is crucial for integrating relevant information, enhancing clinical decision-making, and ultimately improving patient outcomes [5,6].
Typically, image registration involves defining one image as the “fixed” image while another, the “moving” image, undergoes transformation with the fixed image as a reference [6,7]. Over the years, registration techniques have evolved significantly, from classical intensity-based methods to advanced machine learning-driven approaches [4,8]. Recently, deep learning-based methods have shown particular promise, achieving efficient and accurate registration through complex transformation models, often using convolutional neural networks (CNNs) to capture intricate patterns in an unsupervised manner [9].
Within this context, deformable registration has emerged as a key approach to aligning anatomical structures that undergo substantial flexibility and variation. Unlike rigid transformations, deformable registration allows for nonlinear adjustments that adapt to local tissue variations, making it especially valuable for imaging complex organs in dynamic scenarios, such as the brain or lungs [8,10]. Techniques such as B-spline free-form deformations (FFDs) [8] and diffeomorphic methods, including large displacement diffeomorphic metric mapping (LDDMM), are extensively used for such tasks, ensuring the preservation of anatomical topology during alignment [11]. However, deformable models must manage flexibility carefully to prevent unnatural deformations in sensitive anatomical regions; this balance is typically achieved through regularization terms that guide the transformations.
A significant recent advancement is the use of 3D point clouds—data representations that capture anatomical structures’ geometric shapes and spatial configurations instead of conventional pixel-based methods in deformable registration. Point clouds, composed of discrete points in 3D space, enable a highly detailed and precise representation of structures, making them particularly suitable for applications requiring anatomical fidelity, such as brain MRI analysis [12]. This shift allows deformable registration approaches to capture complex structural details, yielding a more accurate alignment of 3D anatomical structures and facilitating in-depth analyses of brain regions.
Despite these advancements, several challenges in deformable registration persist. High computational costs, the limited interpretability of deformation fields, and a propensity for anatomically implausible transformations in critical brain regions remain problematic [13,14]. Additionally, the effectiveness of deep learning-based methods is often limited by the availability of large training datasets, which can be scarce in medical imaging contexts [15]. Moreover, local pixel-based loss functions, commonly employed in these models, may overlook the global context of medical images, leading to the potential misalignment or distortion of critical structures.
To address these challenges, we propose a novel probabilistic framework utilizing Conformal Bayesian Optimization (CBO) for the deformable registration of 3D point clouds representing brain structures. CBO builds upon Bayesian optimization (BO), introducing conformal prediction techniques that enable calibrated uncertainty estimates throughout the optimization process [16,17]. This probabilistic approach enhances the registration process by delivering reliable uncertainty quantifications and interpretable deformation models, making it well suited for high-precision tasks in MRI analysis.
Furthermore, CBO’s capacity to incorporate prior anatomical knowledge into its optimization framework allows for enhanced alignment in complex cases where traditional optimization techniques may produce unrealistic deformations or converge on suboptimal local minima. The conformal component in CBO adjusts the confidence intervals around model predictions, facilitating a balance between speed and accuracy, especially in high-dimensional, noisy datasets. This method thus ensures that transformations respect anatomical constraints, yielding clinically relevant outcomes for brain MRI analyses.
In this paper, we present a deformable point cloud registration framework that employs CBO to align the 3D point clouds of brain structures with anatomical plausibility. Our primary contribution is a robust and interpretable model for point cloud alignment that leverages CBO to achieve anatomically accurate deformations in sensitive regions. This framework is evaluated on MRI data from patients diagnosed with hypoxic-ischemic encephalopathy (HIE) due to perinatal asphyxia, underscoring its effectiveness in aligning brain structures across time points. By offering an improved tool for MRI analysis, this method aims to aid healthcare professionals in monitoring disease progression and refining therapeutic interventions.
2. Materials and Methods
2.1. Datasets
This study uses two datasets to evaluate our proposed method for anatomically plausible nonrigid shape-matching via Bayesian optimization.
The first dataset is the TOSCA dataset [18,19], which contains high-resolution three-dimensional nonrigid shapes. The dataset consists of 80 objects with varying poses and shapes, including eleven cats, nine dogs, three wolves, eight horses, six centaurs, four gorillas, twelve female figures, and two male figures, each in 7 and 20 poses.
The second dataset, referred to as the Brain Asphyxia Dataset, comprises Magnetic Resonance Imaging (MRI) scans from patients with perinatal asphyxia acquired during early childhood at a medical center in Colombia. We processed the MRI images using the infant FreeSurfer framework [20] to obtain 3D point cloud representations of the neuroanatomical structures present. Specifically, we segmented 20 different neuroanatomical regions relevant to perinatal asphyxia [21,22]. Each subject’s anatomy is thus represented by a collection of m () point clouds , where each point cloud represents a specific brain structure. Each point cloud consists of points, with each point defined by its coordinates [23].
We tested our approach on 20 different point clouds from the Tosca dataset. We applied random rigid transformations to evaluate the model’s ability to recover rigid transformations from point clouds containing significant variability. For the Brain Asphyxia Dataset, we tested our model using MRI scans acquired at different times from the same patient (e.g., at birth and one year later) to evaluate clinical outcomes. Each patient has 20 different neuroanatomical structures at different ages, including the left and right white matter, caudate nucleus, putamen, and thalamus.
2.2. Deformable Registration of Point Clouds
Let us consider two point clouds: the fixed point cloud and the moving point cloud , where . The goal is to find a transformation that aligns to by minimizing the alignment error.
In the case of nonrigid registration, a global transformation is insufficient to recover point correspondences accurately due to the deformable nature of the shapes. Therefore, we approximate the transformation function locally by grouping points into c clusters, where neighboring points are likely to undergo similar transformations. The deformation of the moving point cloud is modeled as follows:
where represents the affine transformation matrix for cluster j, and is a weight indicating the influence of cluster j on point . The homogeneous coordinate (factor 1) is used to facilitate affine transformations.
The choice of the number of clusters c is crucial; if , where n is the number of points, the problem becomes mathematically and computationally intractable. Conversely, a very low c may not capture the complexity of the deformation. We typically select a c such that is sufficient to model the deformation accurately.
To determine the clusters, we use an initial set of correspondences, possibly obtained through a matching strategy or feature descriptors, to group each point with the key points . We define the surface representation of as and of as . We then partition the surfaces into the patches and based on geodesic distances from the key points.
Each patch and is further divided into r neighboring rings, and , respectively, based on geodesic distances. The entire surface can thus be represented as , and each patch as . The same applies to .
We estimate the deformation hierarchically using different geometric levels: local, intermediate, and global. At the local level, we estimate the transformation for each neighboring ring . At the intermediate level, we estimate the transformation for each patch based on the deformed neighboring rings. Finally, at the global level, we estimate the overall transformation based on the deformed patches.
The estimation of the transformation parameters is performed iteratively, updating one level at a time while keeping the others fixed, as summarized in Algorithm 1.
| Algorithm 1 Estimation of transformation parameters |
| Require: Initial correspondences between and Require: Geodesic surface partitions 1: while Convergence criterion not met do 2: for each patch i do 3: for each neighboring ring j do 4: Compute local transformation by minimizing local energy 5: Update positions of vertices in 6: end for 7: Compute intermediate transformation by minimizing intermediate energy 8: Update positions of vertices in 9: end for 10: Compute global transformation by minimizing global energy 11: Update positions of all vertices in 12: end while |
Energy Model
The total energy function guiding the deformation is composed of three terms:
where , , and are the local, intermediate, and global energy terms, respectively. The core idea is to combine local and global geometric information with an intermediate representation to ensure accurate and smooth deformations.
Local Energy
Local energy operates at the finest level, focusing on small neighboring regions (rings) around each key point. For the i-th patch, we define the j-th neighboring ring as the set of vertices at the geodesic distance j from the key point . The goal is to find the local transformation for each ring that aligns with the corresponding ring in the moving point cloud.
We formulate this as a weighted least squares problem:
where is an influencing factor based on the surface area or other criteria, and is the corresponding point in . The local transformations are assumed to be locally rigid and independent.
Intermediate Energy
We aim to integrate the deformed neighboring rings at the intermediate level to obtain a coherent transformation for each patch . We consider the deformed vertices from the local transformations and model the problem as fitting a Gaussian Mixture Model (GMM), where the deformed vertices are the centroids. The corresponding vertices in are observations.
We minimize the negative log-likelihood
where represents the GMM parameters for patch i.
Global Energy
Global energy corrects any residual misalignments on a global scale. It refines the overall pose of the moving point cloud by finding a global rigid transformation that minimizes
where are the deformed points after the intermediate step and is a weighting factor that may depend on the distance between corresponding points.
2.3. Anatomical Plausibility
While the deformation field provides a mechanism for aligning point clouds, ensuring that the resulting transformations adhere to anatomical constraints is vital for clinical validity. Deformable techniques can yield highly flexible mappings, but without constraints, they risk generating unrealistic or biologically implausible results.
To address this, we incorporate a regularization term into the cost function to enforce anatomical plausibility:
where is the similarity metric between the deformed moving point cloud and the fixed point cloud, is a regularization parameter, and quantifies the smoothness and plausibility of the deformation field.
2.3.1. Regularization Terms
We consider several regularization terms commonly used in deformable registration.
L2 Norm Regularization
This penalizes large gradients in the deformation field:
where is the gradient of the deformation field.
Total Variation (TV) Regularization
This encourages piecewise smoothness while preserving edges:
where .
Bending Energy Regularization
This penalizes curvature in the deformation field to maintain smoothness:
where is the Laplacian operator.
Smoothness Constraints
These enforce smoothness by penalizing differences between neighboring deformation vectors:
2.3.2. Similarity Metric
We use the Hausdorff distance as the similarity metric, which is defined as follows:
This metric is sensitive to outliers and captures the maximum deviation between the point clouds, minimizing the largest errors.
2.4. Conformal Bayesian Optimization with Gaussian Process Priors
To optimize the hyperparameters controlling the deformation model, we employ Bayesian optimization with Gaussian Process (GP) priors. The objective is to minimize the cost function over the bounded domain .
We model as a sample from a GP prior, specified by the mean function (often zero) and the covariance function . The GP provides a probabilistic model of the function, allowing us to predict at unobserved points.
The acquisition function guides the selection of the next hyperparameters to evaluate by balancing exploration and exploitation. We use Conformal Bayesian Optimization [16], which provides robustness against model misspecification and covariate shift, offering coverage guarantees.
Table 1 presents the hyperparameters optimized within the proposed Bayesian framework for deformable point cloud registration. Each hyperparameter plays a crucial role in balancing the accuracy and computational feasibility of the registration process.

Table 1.
Hyperparameters for deformable point cloud registration.
- Number of clusters (c): This parameter determines the granularity of local deformations. A higher number of clusters allows for finer transformations; however, excessively high values may lead to overfitting or increase computational complexity. The range ensures adaptability without compromising efficiency.
- Regularization weight (): This controls the trade-off between alignment precision and deformation smoothness. Higher values promote smoother transformations, which are crucial for maintaining anatomical plausibility, particularly in sensitive brain structures.
- The number of neighboring rings (r): This parameter defines the local neighborhood around each point and influences how adjacent points contribute to the transformation. Smaller values encourage localized deformations, while higher values capture broader contextual relationships.
- Influence factor (): This modulates the importance of local energy contributions from each neighboring ring. This ensures that the algorithm appropriately balances the impact of different regions on the final deformation, which is essential for aligning structures with varying geometric properties.
- Threshold for global energy correction (d): This parameter determines when global transformations, such as translation and rotation, are applied. A lower threshold triggers more frequent global adjustments, ensuring accurate alignment across large-scale transformations.
By integrating anatomical plausibility through regularization and optimizing hyperparameters via Conformal Bayesian Optimization, our method aims to achieve accurate deformable registrations of point clouds.
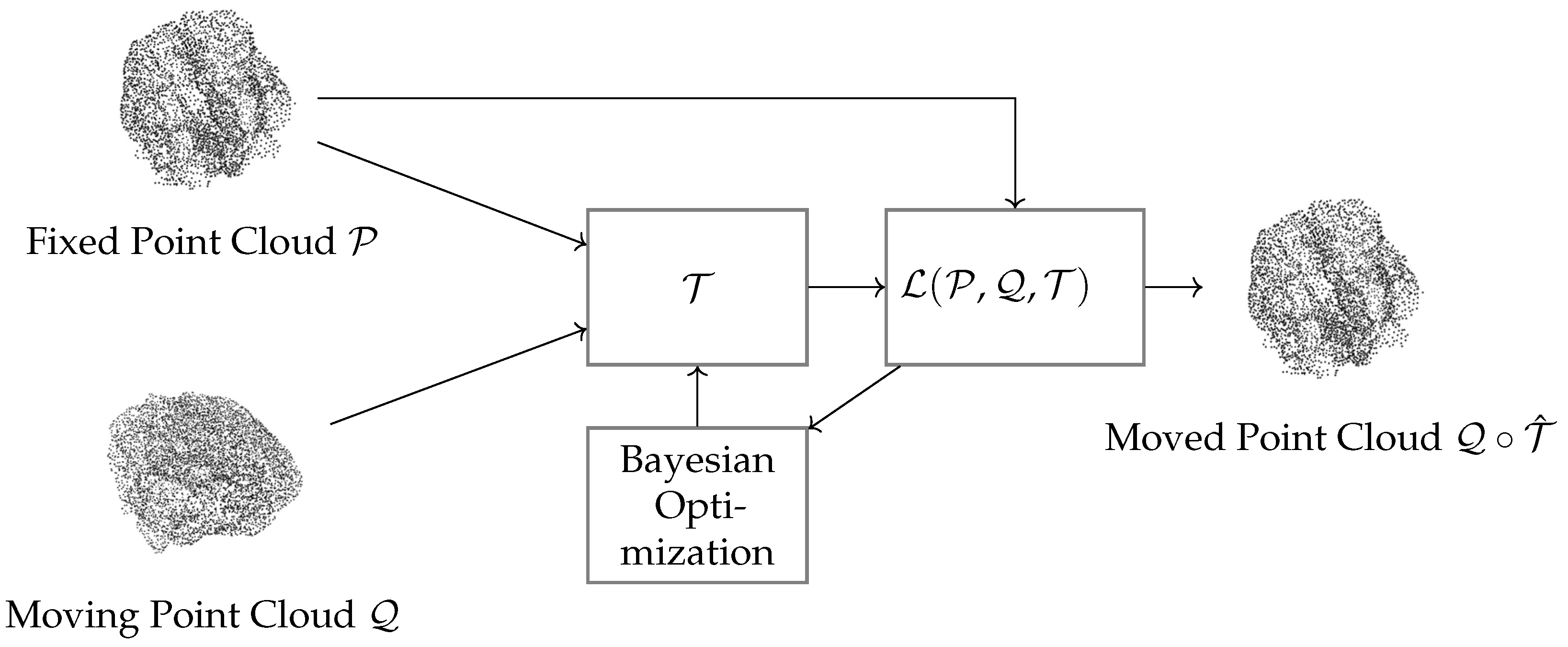
Figure 1 shows the proposed framework for the deformable registration of point clouds, using Bayesian optimization to enhance their alignment. The process starts with two input point clouds: a fixed cloud and a moving cloud . The transformation function estimates the non-rigid transformations needed to align with . In addition, the alignment is driven by a cost function, , combining geometric distance with a regularization term to ensure smooth and anatomically plausible deformations. Bayesian optimization iteratively adjusts the transformation parameters to refine the alignment and optimize the number of initial correspondences. Finally, the output is the deformed point cloud , which is the transformed version of the moving cloud. This approach balances local flexibility and global alignment, ensuring adherence to anatomical constraints. Its modular design and probabilistic strategy make it ideal for medical imaging, where precise and interpretable alignments are essential for clinical decision-making.
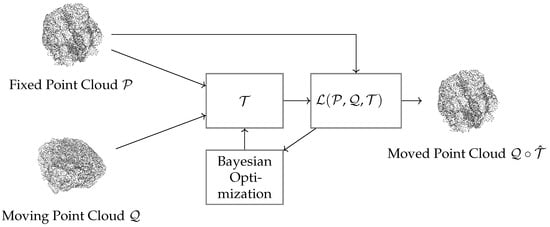
Figure 1.
Proposed approach for the deformable registration of point clouds. In this context, the proposed registration approach based on Bayesian optimization allows for optimizing the number of initial correspondences in the registration process and uses a cost function capable of quantifying the degree of deformation applied.
3. Results
3.1. Tosca Database
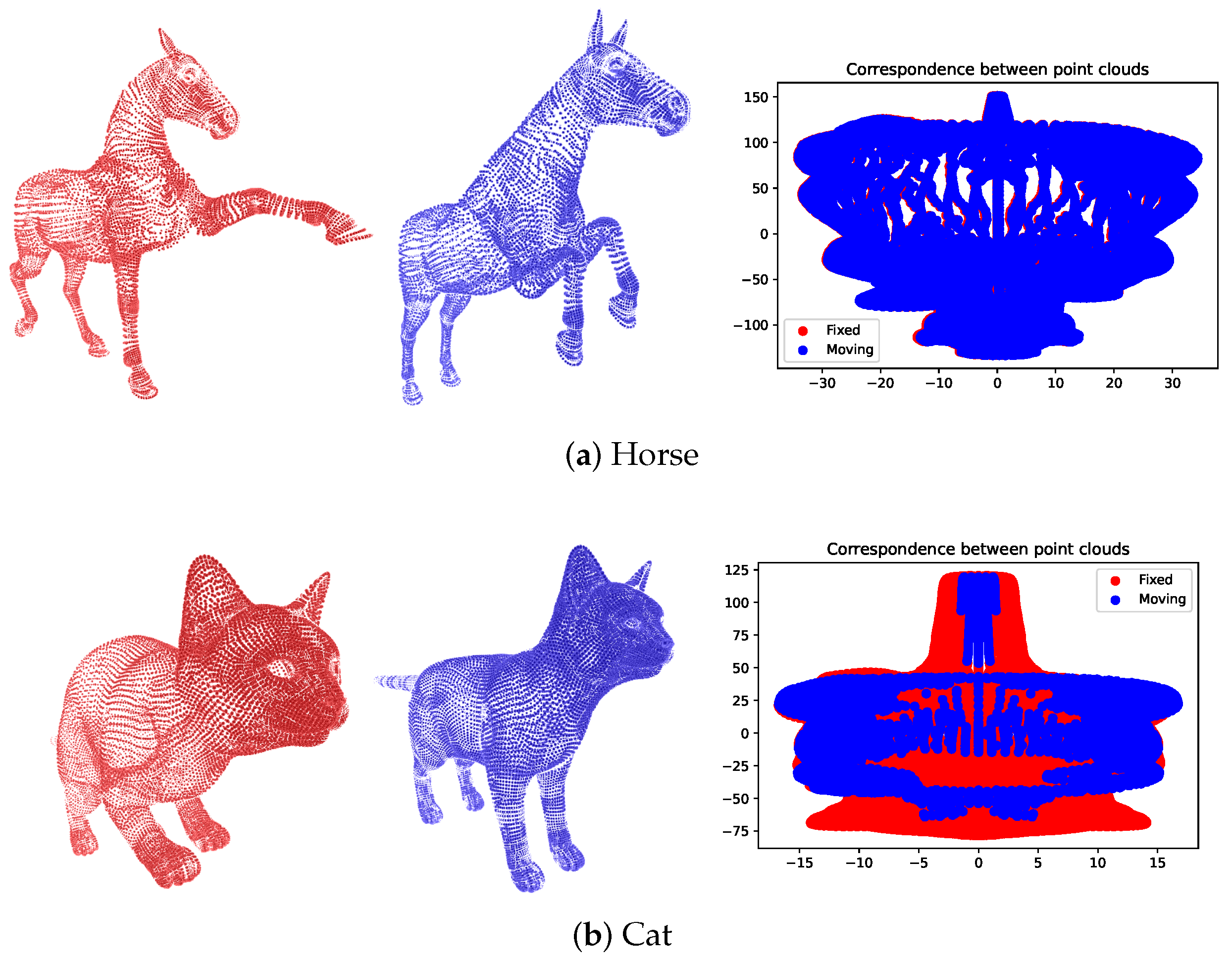
To validate the deformable registration model, the performance of the model was mainly analyzed using synthetic databases, such as the Tosca database. In this context, a series of experiments were initiated that allowed us to identify how the cost function weights the deformations applied to the point clouds. Figure 2 shows an example of the initial correspondence process applied to the point clouds to calculate the deformation . The plots on the right side of each subfigure illustrate the initial correspondences between the fixed (red) and moving (blue) point clouds. Close alignment between the red and blue points indicates successful registration, while more significant gaps suggest areas with alignment discrepancies.
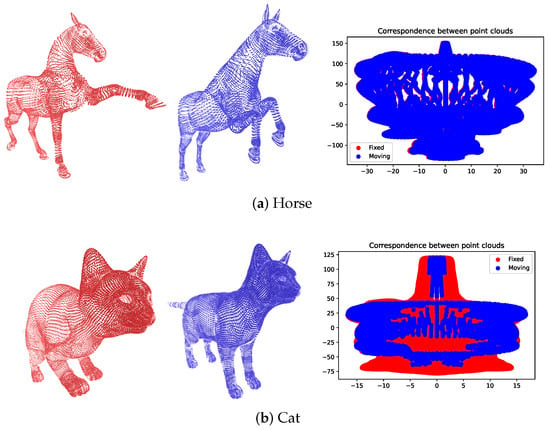
Figure 2.
An example of the deformable registration process in the Tosca database. The figure represents the initial correspondence between the fixed point cloud (red) and the moving point cloud (blue). The plot on the right illustrates the matching points between the two clouds, with red points indicating the fixed positions and blue points indicating the corresponding positions in the moving point cloud.
In our first experiment, we applied the proposed deformable registration method to the Tosca dataset, which consists of non-rigid 3D models of various subjects, such as horses and cats. Figure 2 illustrates the registration process between a fixed point cloud (red) and a moving point cloud (blue). The right side of each subfigure presents the point correspondences established during the initial registration phase. Figure 2a shows the deformable registration of a horse model, where both the fixed and moving point clouds exhibit significant variations in pose. The corresponding points identified between the clouds (shown on the right) highlight the complexity of aligning the limbs and head, which exhibit distinct positional changes. However, the method’s robustness is evident as it can initialize correspondences even when significant structural differences exist between poses. Figure 2b presents a similar process for a cat model, which also underwent non-rigid deformations. The initial correspondences are visualized, indicating a robust alignment of the major body components, such as the torso and limbs. The method’s versatility is demonstrated as it effectively handles variations in pose, with the established correspondences maintaining consistency despite local deformations. The results show that even in highly non-rigid cases, such as those seen in the Tosca dataset, our method successfully aligns the point clouds in an anatomically plausible manner, outperforming conventional rigid alignment techniques.
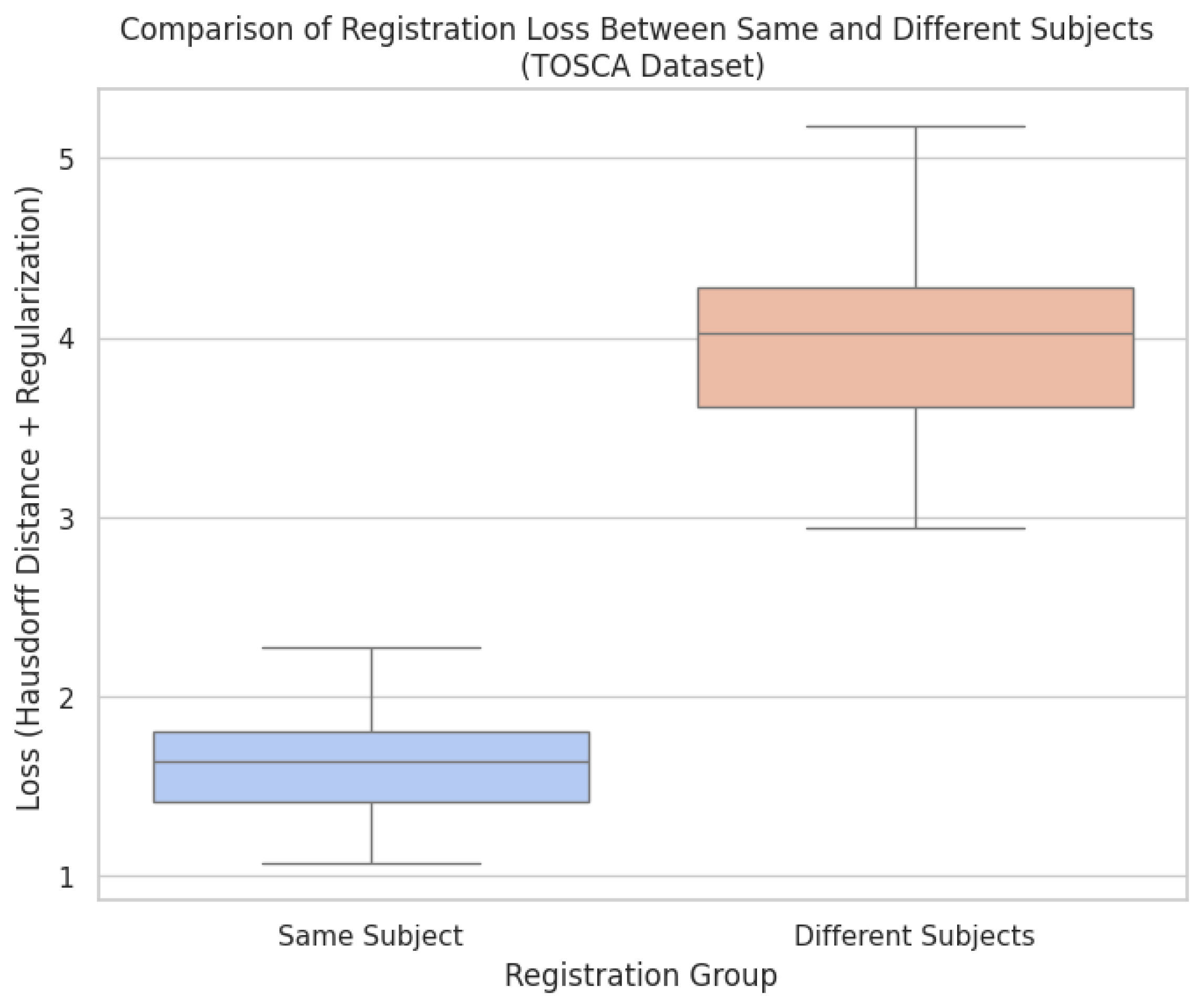
To validate the plausibility of this approach in the Tosca database, we analyzed the behavior of the deformable model for point clouds with variations in pose (Figure 2a) and for point clouds representing different quadrupeds (Figure 2b). Simultaneously, we examined the cost function in Figure 3. Here, “lower cost” refers to the value of the cost function , which combines geometric distance with a regularization term to ensure smooth and anatomically plausible deformations. A lower cost indicates a better alignment with minimal deformation, achieving a more accurate and natural registration. For both experiments, we observed that point clouds from the same subjects generally result in a lower cost, reflecting more effective alignment than those from different subjects.
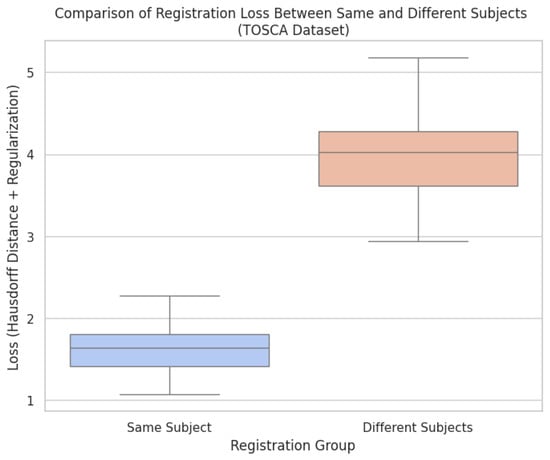
Figure 3.
Comparison of the registration process costs: aligning point clouds from the same subject in different poses versus aligning point clouds from different subjects.
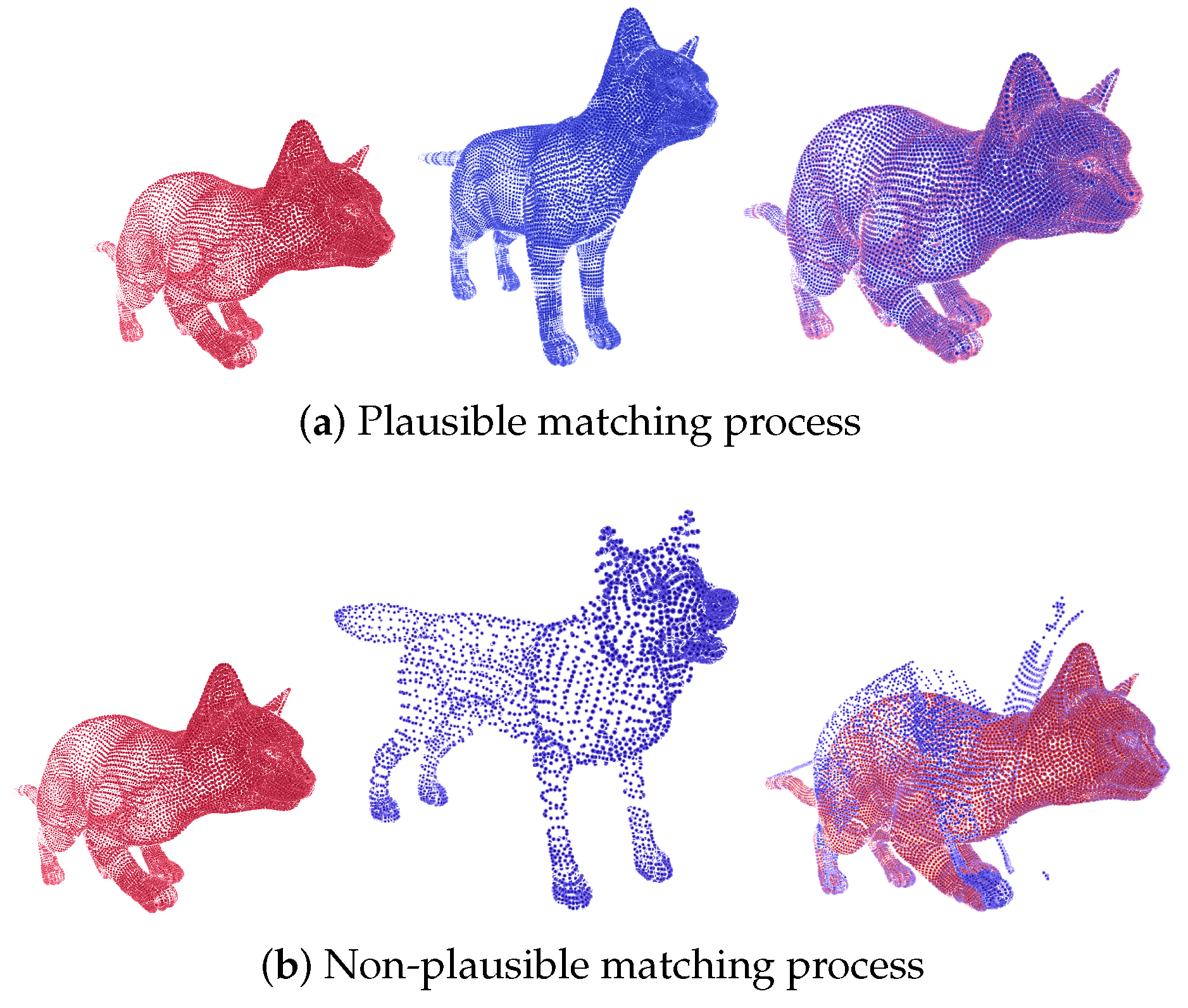
The results shown in Figure 4a,b illustrate the effectiveness and limitations of our deformable registration approach that uses Bayesian optimization. By using a cost function that combines the Hausdorff distance with a regularization term, we achieve a quantifiable measure of alignment quality, where lower values indicate more accurate alignment and anatomically plausible deformations. Figure 4a shows that the method successfully aligns point clouds with significant pose variations, demonstrating its robustness in handling non-rigid deformations. This capability is particularly useful in medical imaging scenarios where anatomical structures exhibit significant but plausible variations over time or due to patient movement. However, as shown in Figure 4b, this method encounters challenges when applied to point clouds with fundamentally different anatomies, resulting in anatomically implausible registrations. This highlights the critical importance of incorporating anatomical constraints into the registration process. This method’s ability to preserve structural consistency in plausible cases underscores its potential for applications in clinical settings, particularly when tracking changes in brain structures over time or within a population.
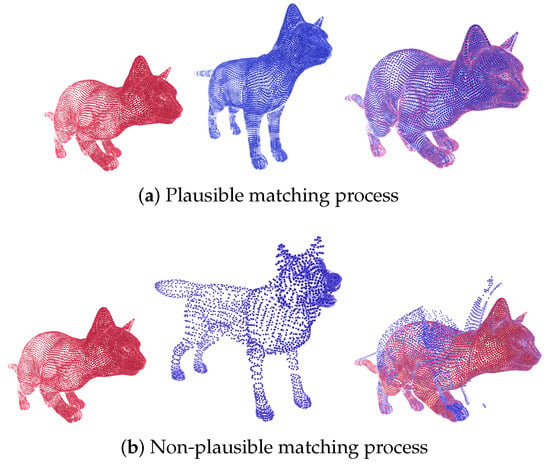
Figure 4.
An example of a deformable registration process in the Tosca database. The figure shows a representation of the registration process in point clouds from figures that have the same anatomy and different poses and from figures with different anatomies. Red and blue correspond to fixed and moving respectively.
The results from Figure 3 provide a quantitative analysis of the registration loss, comparing alignments between point clouds from the same subject in different poses versus point clouds from different subjects. The lower loss values observed in the same group indicate that the deformable registration framework, enhanced by Bayesian optimization, performs well in cases where anatomical consistency is preserved, as demonstrated in Figure 2. The use of the Hausdorff distance combined with regularization effectively captures the quality of the alignment, showing minimal deformation and high anatomical plausibility when the same subject is being registered across varying poses. In contrast, the higher loss values in the different-shapes group, as seen in Figure 4b, reflect the model’s limitations when aligning point clouds with fundamentally different anatomies. These higher loss values indicate that the method struggles to maintain anatomical fidelity when confronted with subjects that deviate significantly in shape and structure, leading to implausible deformations. The results further emphasize the importance of incorporating anatomical constraints and highlight that while the method excels in non-rigid but plausible scenarios, it requires further refinement to handle more complex cases involving diverse anatomies. Compared to well-known approaches in deformable registration, our framework demonstrates distinct advantages in handling anatomical variability. While methods like VoxelMorph [13] leverage convolutional neural networks (CNNs) for efficient and unsupervised image registration, their reliance on pixel-based transformations often leads to limitations in preserving anatomical structure, particularly in cases with high variability or intricate anatomical details. Large Deformation Diffeomorphic Metric Mapping (LDDMM) [11], a widely used technique in medical imaging due to its diffeomorphic properties, excels at handling complex deformations but is computationally intensive, making it less practical for clinical scenarios that require rapid processing. DeepReg [24] integrates deep learning with regularization to improve anatomical accuracy, but its performance can be sensitive to initial conditions, and it may converge to suboptimal solutions when faced with significant shape variations, such as those encountered in neuroanatomical structures affected by perinatal asphyxia.
Our proposed framework, driven by Conformal Bayesian Optimization (CBO), addresses these limitations by introducing probabilistic modeling that dynamically adapts regularization to anatomical structures, ensuring both smooth and plausible deformations.
3.2. Brain Asphyxia Database
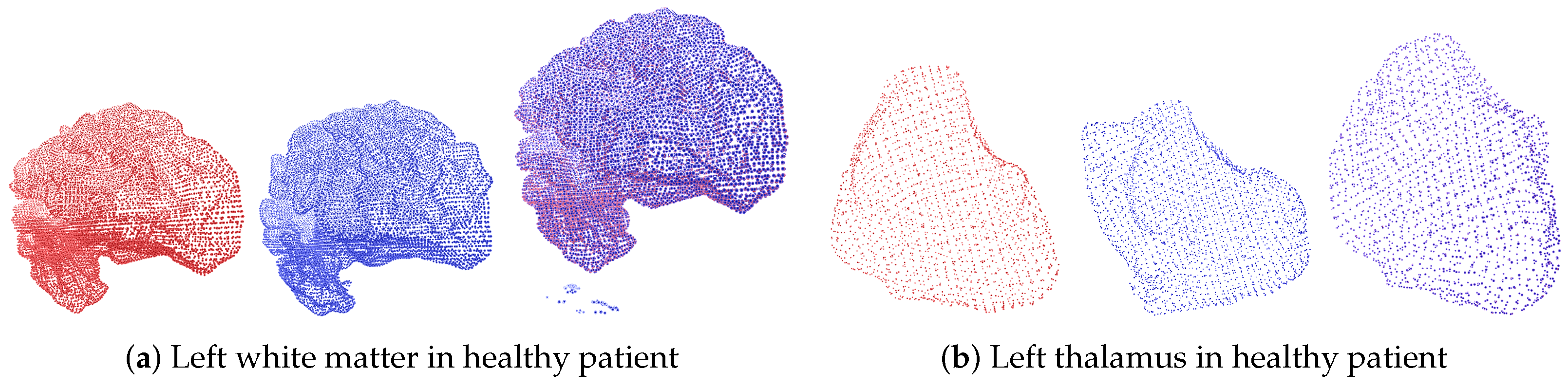
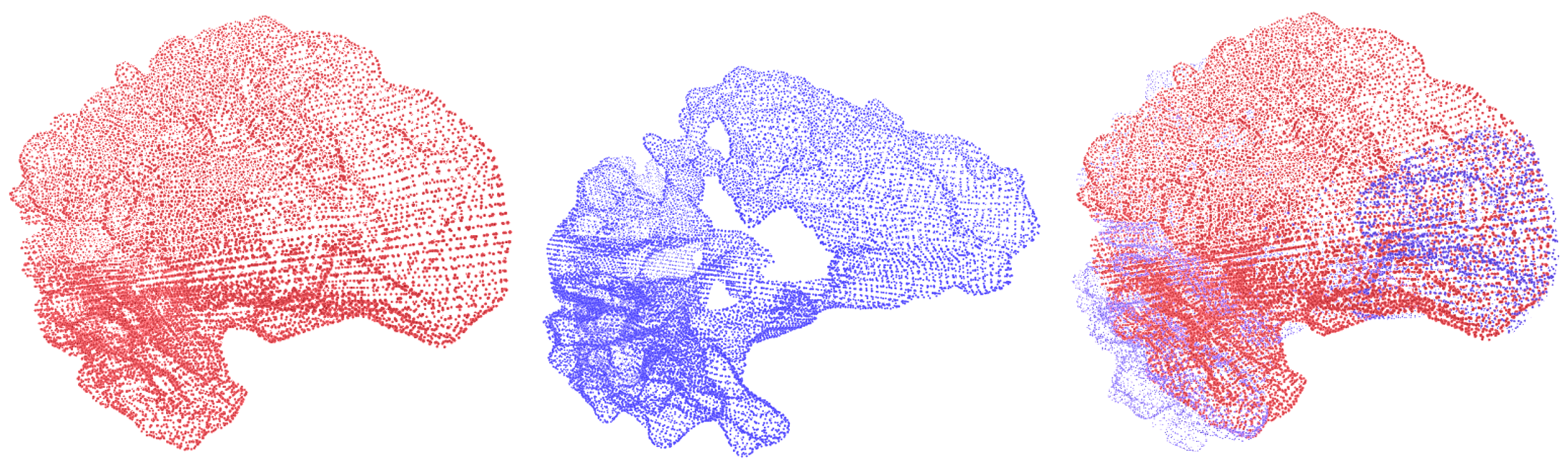
In the case of Brain Asphyxia, two sets of experiments were conducted: one focused on registering the point clouds of brain structures from healthy patients and another on registering point clouds from patients diagnosed with perinatal asphyxia. In the case of healthy patients, the brain structures, while exhibiting non-rigid changes, tend to maintain volumetric consistency across time points. This consistency means that although slight variations in contours may exist, critical features such as size and shape are preserved, as illustrated in Figure 5. These deformations are typically mild, which makes the registration task less challenging. One potential reason for this uniformity is that the point clouds were extracted using probabilistic atlases, which ensure a high level of alignment. On the other hand, brain structures from patients with perinatal asphyxia exhibit a significant degree of variability in both shape and size. This is due to the severe anatomical changes caused by the condition. This increased variability leads to a more complex and challenging registration task, where the model struggles to converge, resulting in a higher cost function, as shown in Figure 6. A comparative analysis of different regularization terms—such as L2 Norm, Total Variation, Bending Energy, and Smoothness Constraints—reveals their distinct impacts on deformable registration performance. For healthy patients, where deformations are relatively small, the L2 Norm effectively maintains the overall smoothness and alignment accuracy of the registration. It imposes a penalty on large deformations, ensuring that the anatomical consistency of brain structures is preserved.
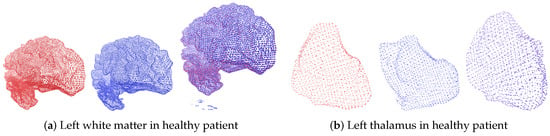
Figure 5.
Example of the deformable registration of point clouds belonging to brain structures from the Brain Asphyxia database. This case shows the registration process in patients with healthy brain structures.
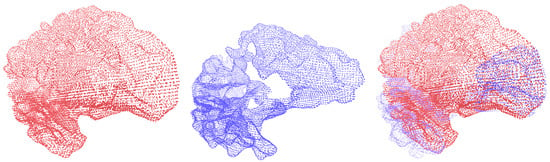
Figure 6.
Example of deformable registration of point clouds belonging to brain structures from the Brain Asphyxia database. This case shows the difference in the registration process between healthy patients’ brain structures (red) and those affected by perinatal asphyxia (blue).
For patients with perinatal asphyxia, where significant deformations are present, the use of more advanced regularization terms like Total Variation and Bending Energy becomes crucial. The Bending Energy regularization helps to maintain the smoothness of large deformations, ensuring anatomically plausible transformations by minimizing sharp or unnatural changes. Total Variation, on the other hand, balances smoothness with the ability to preserve sharp edges or discontinuities in the deformation, which can be critical in pathological cases where certain brain regions undergo more pronounced changes.
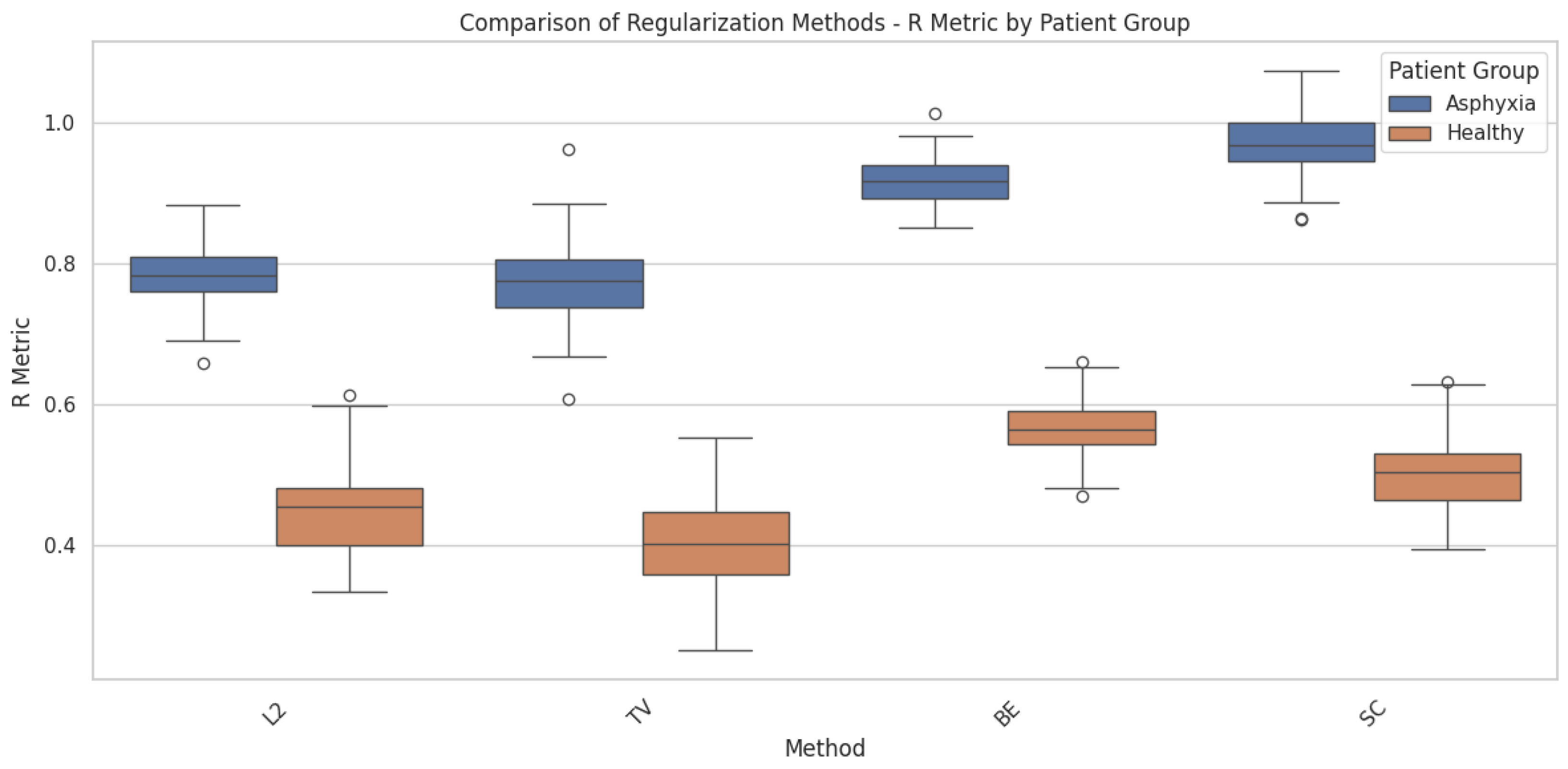
Figure 7 provides a comparative analysis of the loss function across four different regularization methods—L2 norm, Total Variation (TV), Bending Energy (BE), and Smoothness Constraints (SCs). The comparison is presented for two patient groups: healthy individuals and patients diagnosed with perinatal asphyxia. This analysis highlights how each regularization method influences the deformation field in brain structure registration, emphasizing the variability between patient groups. The Smoothness Constraints regularization assists in controlling local deformations, ensuring that small neighborhoods within the brain’s structure undergo consistent transformations without introducing unrealistic distortions. However, its effectiveness diminishes when the variability in the shape and size of the structures is extreme, as seen in perinatal asphyxia cases. This variability explains the more significant performance variance observed for asphyxia patients when using SCs, as illustrated in the figure. These findings further underscore the adaptability of different regularization terms to varying levels of deformation complexity. Standard regularization methods, such as the L2 Norm and Smoothness Constraints, perform well for healthy patients, ensuring smooth transformations and accurate alignment. However, for patients with perinatal asphyxia, more advanced methods like Total Variation and Bending Energy become essential due to their ability to handle complex anatomical alterations. This adaptability highlights the need for case-specific approaches in medical imaging to ensure accurate and anatomically plausible brain structure registrations across diverse clinical scenarios.
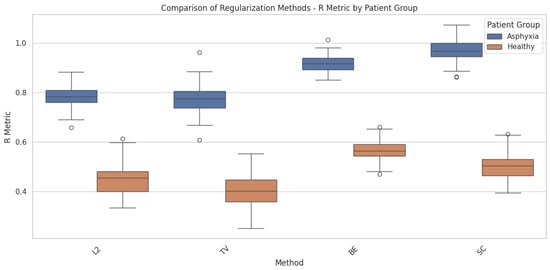
Figure 7.
Comparison of the loss function across different regularization terms—L2 norm, Total Variation, Bending Energy, and Smoothness Constraints—applied to the deformation field in brain structure registration. The analysis includes both healthy patients and patients diagnosed with perinatal asphyxia. The figure highlights how each regularization term influences the deformation model.
Figure 5 and Figure 6 show the deformable registration of point clouds representing brain structures from the Brain Asphyxia database. Figure 5 shows the registration process in healthy patients, focusing on two brain structures: the left white matter and the left thalamus. These examples highlight the algorithm’s ability to align brain structures with minimal deformation, ensuring smooth transformations and accurate alignment. In contrast, Figure 6 presents the difference in registration between the brain structures of healthy patients (red) and those affected by perinatal asphyxia (blue). The comparison reveals a higher degree of structural variability in the asphyxia group, requiring more complex deformation fields to achieve alignment. Despite this complexity, the framework successfully aligns the brain structures, showcasing the robustness of this approach. The benefit of incorporating probabilistic optimization through Conformal Bayesian Optimization (CBO) is evident in these results. CBO enables the framework to iteratively learn plausible shape deformations, balancing local flexibility with global alignment. The probabilistic nature of CBO ensures that transformations adhere to anatomical constraints, reducing the risk of producing unrealistic deformations. This is particularly valuable in cases with significant anatomical variability, such as perinatal asphyxia, where traditional optimization techniques might struggle to maintain anatomical plausibility. The framework’s modular design allows it to adapt to the specific anatomical characteristics of each patient group. In healthy patients, simpler deformations suffice, while in the asphyxia group, the optimization dynamically adjusts the deformation parameters to account for more substantial changes in brain structures. These results demonstrate the effectiveness of the proposed approach in addressing varying levels of complexity, ensuring both accuracy and clinical relevance in brain structure registration.
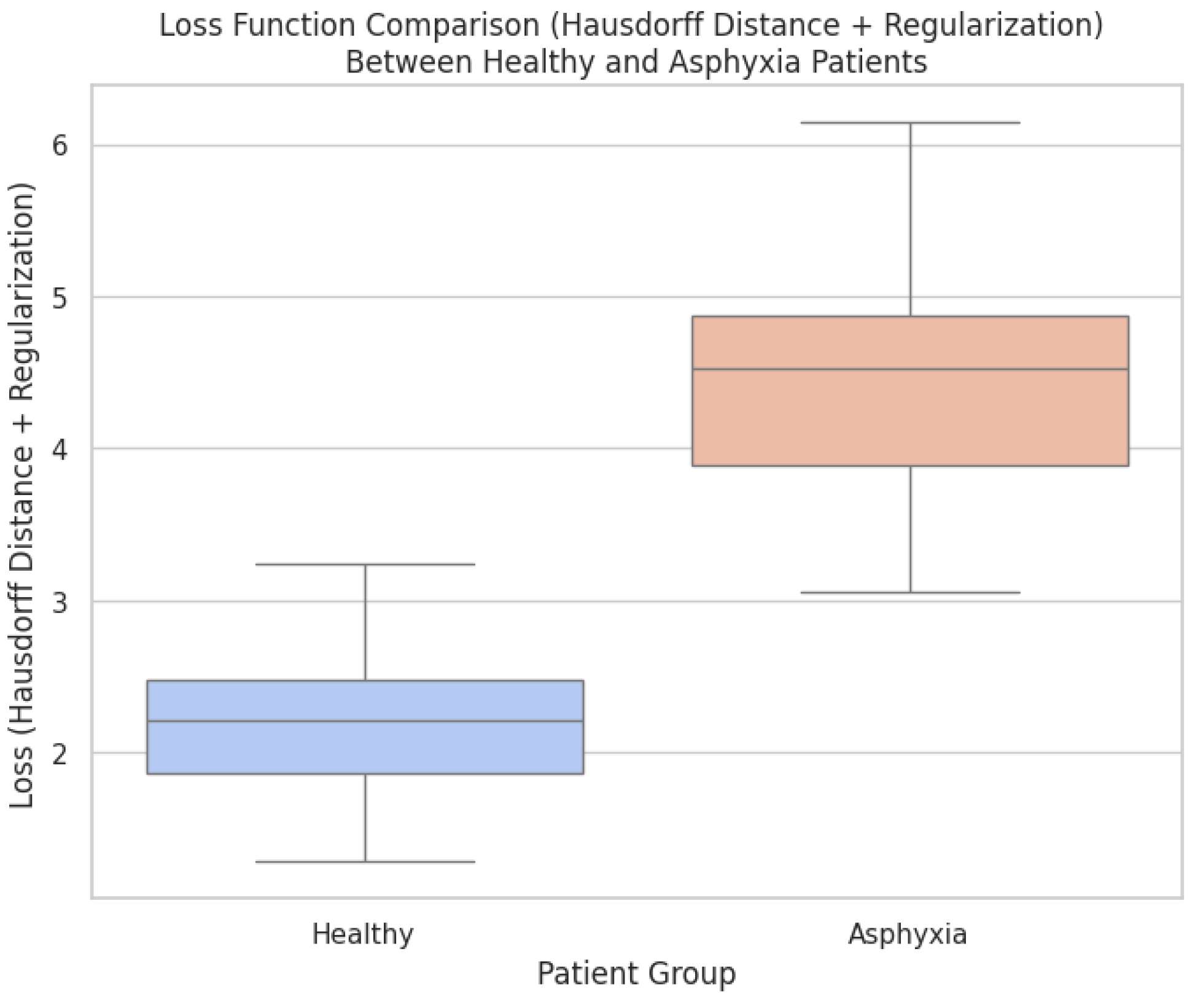
Figure 8 compares the registration costs of aligning brain structures from healthy patients and those affected by perinatal asphyxia. The cost metric combines the Hausdorff distance and regularization terms, reflecting alignment precision and deformation smoothness. As depicted, the registration cost is consistently higher for the asphyxia group, indicating the increased complexity associated with aligning brain structures that exhibit significant anatomical variability. The elevated costs observed in the asphyxia group reflect the more significant structural deformations required to achieve alignment. Brain structures affected by perinatal asphyxia often exhibit altered shapes and sizes, making the registration task more challenging. In contrast, healthy patients display more consistent anatomical features across different scans, lowering registration costs. This contrast highlights the importance of advanced optimization methods, such as Conformal Bayesian Optimization (CBO), in adapting deformation models to varying anatomical conditions. The results further demonstrate the benefit of incorporating regularization into the loss function. While achieving accurate alignment is crucial, the regularization term ensures that the deformations remain anatomically plausible. The balance between alignment precision and regularization promotes meaningful transformations for both patient groups, minimizing the risk of overfitting or producing unrealistic deformations. These findings emphasize the need for adaptive frameworks in medical imaging to address the complexities inherent in pathological conditions like perinatal asphyxia.
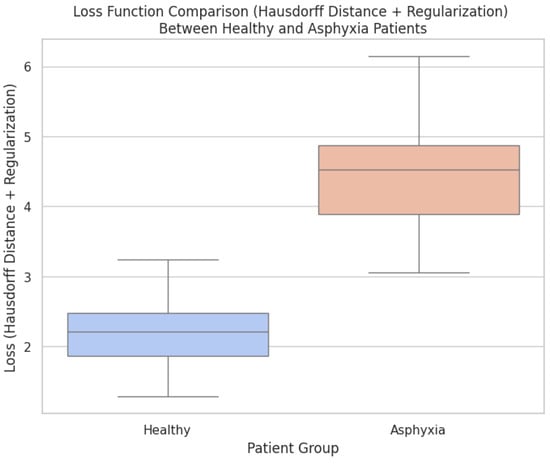
Figure 8.
Cost of registration processes when the model aligns the point clouds of healthy patients and those of patients with abnormalities in their brain structures caused by perinatal asphyxia.
4. Conclusions
This study presents a novel framework for the deformable registration of 3D point clouds representing brain structures, leveraging Conformal Bayesian Optimization (CBO) to enhance alignment precision and maintain anatomical plausibility. The proposed method uses probabilistic modeling to optimize non-rigid transformations, addressing critical challenges in aligning brain structures with significant anatomical variability. Through the combination of the Hausdorff distance and regularization terms, the framework ensures smooth deformations that respect anatomical constraints, reducing the risk of implausible transformations. The experiments conducted on both the Tosca and Brain Asphyxia databases demonstrate the robustness and versatility of this approach. Results from the Tosca database highlight the model’s ability to handle substantial non-rigid deformations, achieving accurate alignments even with significant pose variations. Furthermore, analyzing brain structures from the Brain Asphyxia database underscores the importance of adaptive optimization strategies. The use of CBO enabled the framework to accommodate the anatomical complexities presented by pathological conditions such as perinatal asphyxia, ensuring that transformations remained clinically relevant. Comparative evaluations of different regularization methods revealed the necessity of case-specific configurations to optimize performance. While standard regularization techniques proved sufficient for aligning healthy brain structures, more advanced methods, such as Bending Energy and Total Variation, were critical for managing the more complex deformations observed in asphyxia cases. The modular nature of the proposed framework allows it to adjust to varying anatomical conditions dynamically, enhancing its applicability across diverse clinical scenarios. In addition, integrating CBO into the deformable registration process offers several advantages, including improved alignment accuracy, reduced computational complexity, and better control over deformation smoothness. This framework addresses the key limitations of existing methods by providing an interpretable and adaptable approach that balances alignment precision with anatomical plausibility. The findings of this study demonstrate the potential of CBO-enhanced registration models to support clinical decision-making, particularly in scenarios that require the tracking of anatomical changes over time or across patient populations. Future work will explore the extension of this approach to other imaging modalities and further refine the optimization framework to better address cross-subject anatomical variability.
In future work, we plan to integrate elastic transformations controlled by Bayesian latent variable frameworks into our model to enhance the reliability and robustness of the registration process. Bayesian latent variables will enable probabilistic representations of deformation fields, better capturing global and local anatomical variability. Elastic transformations will offer greater adaptability in handling complex deformations, especially in pathological cases, while maintaining anatomical plausibility. We also aim to optimize the computational cost of these models, ensuring efficient training and uncertainty management. This approach will support more reliable alignments across diverse imaging modalities, promoting better clinical outcomes.
Author Contributions
M.C.-A. and H.F.G. conceptualized the methodology, developed the machine learning methods, and prepared the original draft of the manuscript. M.C.-A. was responsible for data curation, investigation, and validation and contributed to the methodology. G.L.P.-H. and D.C.-P. curated the data and contributed to the original draft’s preparation. D.C.-P., M.C.-A. and H.F.G. contributed to the conceptualization, development of artificial intelligence methods, and took part in writing, reviewing, and editing the original draft. G.L.P.-H. and Á.Á.O.-G. were involved in the conceptualization, reviewing, and editing of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was developed under the project: “SISTEMA DE MONITOREO AUTOMÁTICO PARA LA EVALUACIÓN CLÍNICA DE INFANTES CON ALTERACIONES NEUROLÓGICAS MOTORAS MEDIANTE EL ANÁLISIS DE VOLUMETRÍA CEREBRAL Y PATRÓN DE LA MARCHA” financed by MINCIENCIAS, COLOMBIA with the code COL111089784907.
Institutional Review Board Statement
All procedures performed in this study involving human participants were in accordance with the ethical standards of the Colombian institutional and/or national research committee and with the 8430-1993 Declaration and its later amendments or comparable ethical standards. The Ethics committee Review Board approved the study at COMFAMILIAR RISARALDA CLINIC (Approval No. 00049-2019-05-09). The patients’ legal guardians provided informed consent for their data to be published.
Informed Consent Statement
Written informed consent was obtained from the patient’s parent or guardian for the publication of this case report and any accompanying images.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The authors want to thank the MINISTRY OF SCIENCES COLOMBIA— MINCIENCIAS and the institutions involved in the present project.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HIE | Hypoxic-ischemic encephalopathy |
| MRI | Magnetic Resonance Imaging |
| CBO | Conformal Bayesian Optimization |
| FFD | Free-form deformation |
References
- Darzi, F.; Bocklitz, T. A Review of Medical Image Registration for Different Modalities. Bioengineering 2024, 11, 786. [Google Scholar] [CrossRef] [PubMed]
- Khawaled, S.; Freiman, M. Npbdreg: Uncertainty assessment in diffeomorphic brain mri registration using a non-parametric bayesian deep-learning based approach. Comput. Med. Imaging Graph. 2022, 99, 102087. [Google Scholar] [CrossRef] [PubMed]
- Krebs, J. Robust Medical Image Registration and Motion Modeling Based on Machine Learning. Ph.D. Thesis, Université Côte d’Azur, Côte d’Azur, France, 2020. [Google Scholar]
- Zitová, B.; Flusser, J. Image Registration Methods: A Survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef]
- Maintz, J.; Viergever, M. A Survey of Medical Image Registration. Med. Image Anal. 1998, 2, 1–36. [Google Scholar] [CrossRef]
- Oliveira, F.P.M.; Tavares, J. Medical image registration: A review. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 73–93. [Google Scholar] [CrossRef]
- McKenzie, E.M.; Santhanam, A.; Ruan, D.; O’Connor, D.; Cao, M.; Sheng, K. Multimodality image registration in the head-and-neck using a deep learning-derived synthetic CT as a bridge. Med. Phys. 2020, 47, 1094–1104. [Google Scholar] [CrossRef]
- Rueckert, D.; Sonoda, L.I.; Hayes, C.; Hill, D.L.; Leach, M.O.; Hawkes, D.J. Nonrigid Registration Using Free-Form Deformations: Application to Breast MR Images. IEEE Trans. Med. Imaging 1999, 18, 712–721. [Google Scholar] [CrossRef]
- de Vos, B.D.; Berendsen, F.F.; Viergever, M.A.; Sokooti, H.; Staring, M.; Išgum, I. A Deep Learning Framework for Unsupervised Affine and Deformable Image Registration. Med. Image Anal. 2019, 52, 128–143. [Google Scholar] [CrossRef] [PubMed]
- Ashburner, J. A Fast Diffeomorphic Image Registration Algorithm. NeuroImage 2007, 38, 95–113. [Google Scholar] [CrossRef]
- Beg, M.F.; Miller, M.I.; Trouvé, A.; Younes, L. Computing Large Deformation Metric Mappings via Geodesic Flows of Diffeomorphisms. Int. J. Comput. Vis. 2005, 61, 139–157. [Google Scholar] [CrossRef]
- Xiong, F.; Kong, Y.; Hu, M.; Zhang, Z.; Shen, C.; Kuang, L.; Han, X. A multi-scale covariance matrix descriptor and an accurate transformation estimation for robust point cloud registration. Res. Sq. 2024. preprint. [Google Scholar] [CrossRef]
- Balakrishnan, G.; Zhao, A.; Sabuncu, M.; Guttag, J.; Dalca, A.V. VoxelMorph: A Learning Framework for Deformable Medical Image Registration. IEEE Trans. Med. Imaging 2019, 38, 1788–1800. [Google Scholar] [CrossRef] [PubMed]
- Krebs, J.; Delingette, H.; Mailhé, B.; Ayache, N.; Mansi, T. Learning a Probabilistic Model for Diffeomorphic Registration. IEEE Trans. Med. Imaging 2019, 38, 2165–2176. [Google Scholar] [CrossRef] [PubMed]
- Mansilla, L.; Milone, D.H.; Ferrante, E. Learning Deformable Registration of Medical Images with Anatomical Constraints. Neural Netw. 2020, 124, 269–279. [Google Scholar] [CrossRef] [PubMed]
- Fong, E.; Holmes, C.C. Conformal Bayesian Computation. In Advances in Neural Information Processing Systems; Ranzato, M., Beygelzimer, A., Dauphin, Y., Liang, P., Vaughan, J.W., Eds.; Curran Associates, Inc.: Newry, UK, 2021; Volume 34, pp. 18268–18279. [Google Scholar]
- Stanton, S.; Maddox, W.J.; Wilson, A.G. Bayesian Optimization with Conformal Coverage Guarantees. arXiv 2022, arXiv:2210.12496. [Google Scholar]
- Bronstein, A.M.; Bronstein, M.M.; Kimmel, R. Efficient Computation of Isometry-Invariant Distances Between Surfaces. SIAM J. Sci. Comput. 2006, 28, 1812–1836. [Google Scholar] [CrossRef]
- Bronstein, A.M.; Bronstein, M.M.; Kimmel, R. Calculus of Nonrigid Surfaces for Geometry and Texture Manipulation. IEEE Trans. Vis. Comput. Graph. 2007, 13, 902–913. [Google Scholar] [CrossRef] [PubMed]
- Fischl, B.R. FreeSurfer. NeuroImage 2012, 62, 774–781. [Google Scholar] [CrossRef]
- Satheesan, A.P.; Chinnappa, A.R.; Goudar, G.; Raghoji, C.R. Correlation between early magnetic resonance imaging brain abnormalities in term infants with perinatal asphyxia and neuro developmental outcome at one year. Int. J. Contemp. Pediatr. 2020, 7, 1957–1961. [Google Scholar] [CrossRef]
- Miller, S.P.; Ramaswamy, V.; Michelson, D.J.; Barkovich, A.J.; Holshouser, B.A.; Wycliffe, N.; Glidden, D.V.; Deming, D.D.; Partridge, J.C.; Wu, Y.W.; et al. Patterns of brain injury in term neonatal encephalopathy. J. Pediatr. 2005, 146, 453–460. [Google Scholar] [CrossRef]
- Gutiérrez-Becker, B.; Wachinger, C. Deep Multi-structural Shape Analysis: Application to Neuroanatomy. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2018, Granada, Spain, 16–20 September 2018; Frangi, A.F., Schnabel, J.A., Davatzikos, C., Alberola-López, C., Fichtinger, G., Eds.; Springer: Cham, Switzerland, 2018; pp. 523–531. [Google Scholar]
- Hu, Y.; Modat, M.; Gibson, E.; Li, W.; Ghavami, N.; Bonmati, E.; Wang, G.; Bandula, S.; Moore, C.; Emberton, M.; et al. DeepReg: A deep learning toolkit for medical image registration. J. Open Source Softw. 2020, 5, 2121. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).