Optimization Method for Improving Efficiency of Thermal Field Reconstruction in Concrete Dam

Featured Application

The real-time and accurate acquisition of the thermal field is crucial for the temperature control of concrete dams. The optimization method including interpolation algorithm selection, the monitoring point number, and position analysis can effectively improve the efficiency of thermal field reconstruction. Lightweight application procedures can achieve a good balance of accuracy and efficiency and are used to guide temperature control measures.

Abstract

In an actual concrete dam construction, the efficiency of thermal field reconstruction directly affects the timeliness of temperature control measures. Therefore, using lightweight methods to obtain real-time, accurate thermal fields is crucial for concrete temperature control. To balance both accuracy and efficiency, this study proposes an optimization method for thermal field reconstruction in concrete dams. The method consists of three components: evaluating interpolation algorithms, optimizing the number of monitoring points, and analyzing their positions. Specifically, a distributed temperature sensing system is employed for concrete monitoring, with a “Z-shaped” optical fiber layout. Three interpolation algorithms—Kriging, Natural Neighbor, and Inverse Distance Weighting—are quantitatively evaluated, with Kriging showing the highest accuracy. Sensitivity analysis, combined with the control variable method, is used to assess the impact of the monitoring point number and position. Lightweight application procedures are then proposed, using reconstructed thermal field results to guide strategy formulation and parameter adjustment for the intelligent cooling control system. A case study demonstrates that this method ensures the effectiveness and timeliness of concrete temperature control measures. The proposed approach enables real-time updates of concrete temperature control measures in sync with the progress of the pouring process, providing a valuable reference for similar projects.

1. Introduction

Cement hydration causes thermal deformation and stress in concrete dams, potentially causing cracks if the stress exceeds the tensile strength [1,2]. The temperature of cement hydration significantly affects strength development; while higher temperature can enhance early strength, excessive curing temperature may limit long-term strength development [3,4]. To prevent temperature cracks and balance the strength development, water-cooling technology is commonly employed [5]. This method controls temperature by embedding cooling pipes in concrete and adjusting parameters such as water temperature and flow rate [6]. However, variations in pouring schedules, spatial positions, and constraints lead to significant differences in temperature distribution across concrete blocks [7]. To ensure effective water-cooling, personalized adjustments based on each block’s actual temperature are essential [8]. The efficiency of thermal field reconstruction directly affects temperature control. Thus, an efficient, real-time, and accurate method for thermal field reconstruction is crucial for optimizing temperature control strategies in concrete dams.

Thermal field reconstruction methods for concrete dams can be categorized into three types. The first is the analytical method by solving the heat diffusion equation [9]. Since its inception, the method has been continuously improved and applied in engineering projects [10,11]. The analytical method has clear physical significance [12], but assumptions about the geometry and boundary conditions of concrete blocks may lead to errors. The second method is numerical analysis [13,14]. For example, numerical simulations were conducted to analyze the differences in surface-insulation measures [15]. Numerical analysis methods face challenges such as parameter discrepancies [16], long computation time, and inefficiency [17]. In large-scale simulations with fine meshes, thermal field reconstruction lags, making it difficult to adjust temperature control measures in real time [18]. The third method relies on real monitoring data for interpolation calculations [19]. After collecting substantial monitoring data, interpolation algorithms enable thermal field reconstruction [20,21]. For example, the combination of interpolation algorithms with the distributed temperature sensing (DTS) system has enabled the acquisition of concrete thermal fields [22,23]. Recent improvements such as optimizing monitoring point locations [24] and identifying valid temperature-measuring optical fiber [25] have further enhanced this method’s practicality.

As monitoring data update, interpolation methods can reveal the temporal variation of concrete temperatures in dams [26]. In engineering practice, achieving real-time temperature control for each concrete block requires balancing accuracy and efficiency in thermal field reconstruction. Specifically, the accuracy and efficiency of interpolation methods depend on three main factors: the interpolation algorithm, the number of monitoring points, and their positions. In terms of interpolation algorithms, various algorithms were proposed, and their differences in soil temperature [27], sea surface temperature [28], and air temperature [29] have been analyzed. However, the accuracy of these algorithms in concrete dams still lacks quantitative evaluation.

Regarding the number and position of monitoring points, excessive data can increase computational complexity, while poorly arranged monitoring points can result in unrepresentative data [30]. Several optimization methods have been suggested: a comprehensive data symmetry analysis technique was presented for determining the optimal spatial positioning of valid temperature-measuring optical fibers [25]; the multi-population genetic algorithm was used to optimize the temperature measurement points [21]; and a temperature sensor layout method based on cross-validation principles was presented [24]. However, most of these studies focus on optimizing a single factor. The methods that simultaneously consider interpolation algorithms, the number of monitoring points, and their positions are rare in concrete dams. Additionally, temperature data collected via the DTS system is linear, following the optical fiber layout path [31,32]. Therefore, when optimizing the efficiency of concrete thermal field reconstruction, it is essential to consider site construction conditions and actual fiber layout schemes.

Therefore, this study proposes an optimization method for thermal field reconstruction in concrete dams, achieving a favorable balance between efficiency and accuracy. The method utilizes a DTS system for temperature monitoring in concrete. To ensure its validity and feasibility, the analysis is based on the actual optical fiber layout at the construction site. First, the accuracy of three commonly used interpolation algorithms—Kriging [33], Natural Neighbor [34], and Inverse Distance Weighting [35]—is quantitatively compared in the context of concrete thermal field reconstruction. Next, sensitivity analysis and control variable methods are applied to investigate the effects of the number and positions under a “Z-shaped” optical fiber layout scheme. The reconstruction results are integrated with a water-cooling system, and lightweight engineering application procedures are proposed to meet the requirements for real-time thermal field reconstruction and precise temperature control. Finally, the method was applied to a concrete dam, and the results showed that it can provide real-time and accurate data support for effective temperature control measures.

2. Materials and Methods

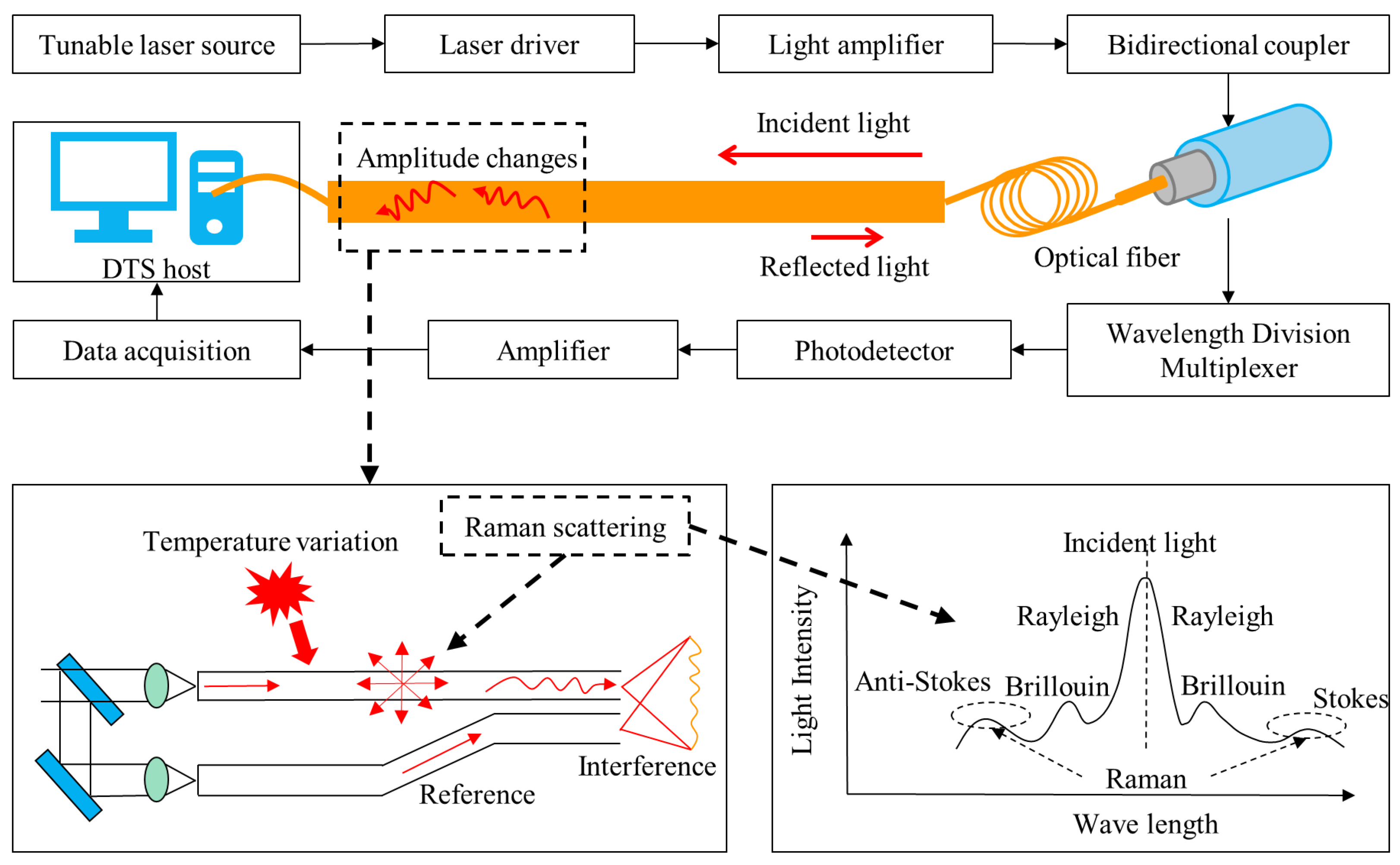
2.1. Distributed Temperature Sensing (DTS)

The DTS system is designed to monitor the temperature inside mass concrete structures by utilizing the principles of Raman scattering and time-domain reflection of light within an optical fiber [36]. This system is characterized by its ability to provide real-time, online, and continuous monitoring of the internal temperature distribution within concrete. DTS technology has been extensively employed in various concrete structures, including dams, roads, and bridges [37]. Compared to the conventional digital thermometer method, DTS temperature measurement technology offers significant advantages, such as continuous monitoring, high spatial resolution, and long-distance coverage [38]. The temperature measurement principle and components of a typical DTS system are shown in Figure 1.

• Principle of Temperature Measurement

The scattering of light in an optical fiber can be categorized into three types: Rayleigh scattering, Brillouin scattering, and Raman scattering [39,40]. When a laser pulse is transmitted through the optical fiber, it undergoes refraction and attenuation as it travels. During this process, some of the light is scattered and reflected toward the source of the pulse, resulting in two distinct types of scattered light: Stokes light and anti-Stokes light [41]. The temperature measurement capability of the DTS system hinges on the unique properties of Raman scattering. Specifically, the system determines the temperature by analyzing the ratio of the intensities of anti-Stokes scattering to Stokes scattering produced by a constant optical pulse. The anti-Stokes scattering is more sensitive to temperature changes than Stokes scattering, making their ratio a reliable indicator of temperature. By carefully measuring this ratio, the DTS system can accurately determine the temperature at various points along the optical fiber. The relationship between the intensity ratio of Stokes light to anti-Stokes light and temperature is as follows:

$${\displaystyle \frac{l_{as}}{l_s}}=a{e}^{{\displaystyle \frac{hcv}{k{T}_K}}}.$$

(1)

where $l_{as}$ and $l_s$ are the optical power of anti-Stokes light and Stokes light (cd), respectively; $h$ is the Planck coefficient (J·s); $a$ is the temperature correlation coefficient; $v$ is the amount of the Raman shift (m⁻¹); $k$ is the Boltzmann constant (J/K); $c$ is the speed of light in vacuum (m/s); $T_K$ is the Kelvin rating.

In addition to the scattering properties, the DTS system also relies on the time of flight of the optical pulse to locate the position of the temperature measurements. The time of flight refers to the time it takes for the light pulse to travel to a specific point in the fiber and back to the pulse-sending end. By measuring this time delay, the system can calculate the exact location along the fiber where the temperature reading is being taken. Specifically, the time difference between the incident pulse signal and the scattered signal at the input terminal is $t$. The distance ($L$) from the incident terminal to the position where the backscattered light occurs can be determined using the velocity–distance formula as follows:

$$L={\displaystyle \frac{c}{n}}\cdot {\displaystyle \frac{t}{2}}.$$

(2)

The combination of the ratio of anti-Stokes to Stokes scattering and the time of flight of the optical pulse allows the DTS system to provide precise temperature measurements at various points along the length of the optical fiber. This makes it an invaluable tool for monitoring the internal temperature of mass concrete structures, ensuring their integrity and safety over time. The temperature of the monitoring point can be obtained as follows:

$$T={\displaystyle \frac{hcv}{k\left[\ln a-\ln \left(\frac{l_{as}}{l_s}\right)\right]}}.$$

(3)

2.

Components of the DTS System

The DTS system comprises several key components, including optical fibers, a laser driver, a light amplifier, an optical splitter and filter, a photoelectric signal converter and amplifier, a data acquisition and processing device, etc. [42]. The laser driver is the main component responsible for generating a pulsed laser, which is then input into the tail fiber. To ensure the pulsed laser can be transmitted over long distances within the optical fiber, the light amplifier is employed to amplify and enhance both the signal and power of the laser. The optical splitter and filter primarily consist of a fiber coupler and an optical wavelength division multiplexer. The fiber coupler functions to divide the input pulsed laser into two or more output signals. Meanwhile, the wavelength division multiplexer, an optical dispersion system, separates the backscattered light signal into Stokes and anti-Stokes light signals. The photoelectric signal converter and amplifier include a photodetector and an amplifier. The photodetector’s role is to convert the optical signal into an electrical signal, which is subsequently amplified by the amplifier. Finally, the data acquisition and processing device comprises a data acquisition card, a personal computer (PC), a mobile client, and a cloud platform, facilitating the collection, analysis, and storage of data. The optical fibers are usually buried in the concrete according to certain rules. This process must consider the ease of construction, cost control, and construction quality. Additionally, it is crucial to ensure that the data collected can support the subsequent reconstruction of the thermal field.

2.2. DTS System Layout and Data Acquisition

To meet the data requirements for reconstructing the temperature field of concrete, the optical fibers are typically laid from the upstream face to the downstream face at the construction site, aiming to cover the entire pour block [19]. Considering the cost of the DTS system and the complex construction environment, specific requirements for the horizontal and vertical layout of the optical fibers are proposed to ensure that the fiber laying aligns with the concrete pouring schedule. These schemes are designed considering the structural characteristics and layout requirements of different dam sections, aiming to optimize the fiber-laying effect and improve the accuracy and reliability of data collection.

In the horizontal direction, there are three common layout schemes: “I” type, “L” type, and “Z” type [19]. The selection of the scheme depends on the type of concrete blocks. For dam foundation areas and gallery blocks with special structural constraints, the simple and easy-to-construct “I”-type scheme is recommended. Large dam blocks without special structural obstructions can achieve continuous fiber embedding using the “L”-type scheme. The “Z”-type scheme is suitable for obtaining temperature data on both sides of the transverse joints and along the axis in the middle of the dam block. To facilitate the construction and reflect the actual thermal field as much as possible, in the vertical direction, the optical fibers are arranged symmetrically between odd and even numbering of dam blocks. The optical fiber is embedded directly in the concrete, making the impact of external factors (e.g., humidity and wind) on temperature measurement accuracy negligible. Additionally, water-blocking material, inner coating plastic steel belt, and PE sheath further shield the fiber from external factors on temperature measurement accuracy.

Figure 2 shows the DTS system layout in a concrete dam using the “Z”-type scheme. The optical fiber is first embedded from the upstream surface to the center of the dam block in the direction parallel to the transverse joint, then follows the direction parallel to the dam axis to the other transverse joint, and finally turns in the direction parallel to the other transverse joint to downstream surface. In this study, three digital thermometers (designated as 7#-1, 7#-2, and 7#-3) were embedded parallel to the transverse joint in the center of the concrete block, and readings were collected synchronously with the DTS system. By comparing the temperatures measured by the three digital thermometers with the temperatures of the reconstructed thermal field at the corresponding positions, the accuracy of the reconstructed thermal field can be evaluated.

The minimum data acquisition interval of the DTS system used in this study is 10 s, allowing for continuous monitoring of the internal temperature of the concrete. The spatial and temperature resolutions of the DTS system were 1.02 m and 0.5 °C, respectively. By setting the temperature of upstream and downstream surfaces to ambient temperature, a two-dimensional (2D) thermal field can be interpolated. Then, a three-dimensional (3D) thermal field can be constructed when combining all adjacent 2D thermal fields. As the temperature of the monitoring points keeps being updated, the real-time thermal field of the whole dam can be obtained. Since optical fiber embedding and concrete pouring occur synchronously, the thermal field digitized via interpolation algorithm analyses can concur with the construction progress.

3. Optimization Method for Thermal Field Reconstruction

The optimization method proposed in this study, as illustrated in Figure 3, comprises three key components: interpolation algorithm evaluation and selection, optimization of the number of monitoring points, and analysis of the impact of monitoring positions. Initially, the optical fiber layout scheme is determined based on actual construction conditions. This step is primarily influenced by the constraints of construction organization, structural characteristics, and temperature-control requirements. Next, for the specific structure of concrete dam blocks, an analysis of the applicability and accuracy of interpolation algorithms is condupcted. Following this, a sensitivity analysis of the number and positions of monitoring points is performed, guided by the selected interpolation algorithm and optical fiber layout scheme, to inform the selection of monitoring data.

3.1. Interpolation Algorithm Evaluation and Selection

3.1.1. Interpolation Algorithm Comparison

Numerous interpolation algorithms have achieved successful applications in the reconstruction of concrete thermal fields. Among these, Kriging [33], Natural Neighbor [34], and Inverse Distance Weighting [35] are three widely used algorithms. Natural Neighbor and Inverse Distance Weighting are convex methods. The estimated value of the convex method is always between the minimum and maximum of the measured values. The estimated value of the non-convex method (e.g., Kriging) can be outside the range of the observed values. The convexity of the estimators may depend on factors such as weights assigned for samples and the difference between the ranges of predictors for the samples and the unobserved locations. The estimated surface of the Natural Neighbor is continuous and smooth except at the data points where the derivative is discontinuous. Inverse Distance Weighting works well with well-spaced data but not spatial clustering samples.

When employing the DTS system for monitoring the temperature in concrete dams, it is essential to evaluate the performance of various algorithms in conjunction with the specific optical fiber layout schemes. The interpolation principle and calculation procedure of each one is shown in Figure 4.

• Kriging

Based on the regionalized variable theory, the Kriging interpolation algorithm takes the variation function as the main tool and obtains the estimated value under the premise of ensuring that the estimated value meets the unbiased condition and the minimum variance condition [43]. If the measured value at the monitoring point position $p_i$ is $f\left(p_i\right)$, then the estimated value at the point $y$ to be interpolated is obtained by the following equation:

$$f(y)={\displaystyle \sum _{i=1}^m{\varphi }_{i}f(p_i)}.$$

(4)

where ${\varphi }_i$ is the weight of position $p_i$, which considers the distances between the points to be interpolated and the monitoring points, as well as their spatial distribution.

2.

Natural Neighbor

Based on the Delaunay triangulation and Voronoi diagram, the Natural Neighbor interpolation algorithm calculates the interpolation result of the point $y$ according to the contribution rate of each Natural Neighbor point [44]. Assuming the Natural Neighbor points of point $y$ count $m$, namely, $p_1,p_2,\cdots ,p_m$, the interpolation algorithm is as follows:

$$f\left(y\right)={\displaystyle \sum _{i=1}^m{w}_i}f\left(p_i\right).$$

(5)

where $f\left(p_i\right)$ is the value at the Natural Neighbor points $p_i$, and $w_i$ is the weight coefficient occupied by the Natural Neighbor point $p_i$ and is determined according to the following principle.

The point $y$ to be interpolated is taken as a new node, added to the generated Voronoi diagram, and a new Voronoi diagram corresponding to the new node is obtained. If the total area enclosed by the Voronoi cell with the point $y$ in is $s$, the Voronoi cell with the new node in it can be divided into $m$ parts by the original Voronoi cell of its Natural Neighbor points. The areas of each part are denoted as $s_1,s_2,\cdots ,s_m$. The weight coefficient for each part is obtained by dividing the area of each part by the total area.

$$w_i={\displaystyle \frac{s_i}{s}}.$$

(6)

The interpolation of each region is not affected by the other regions, and the temperature is interpolated in different regions to complete the reconstruction of the concrete thermal field.

3.

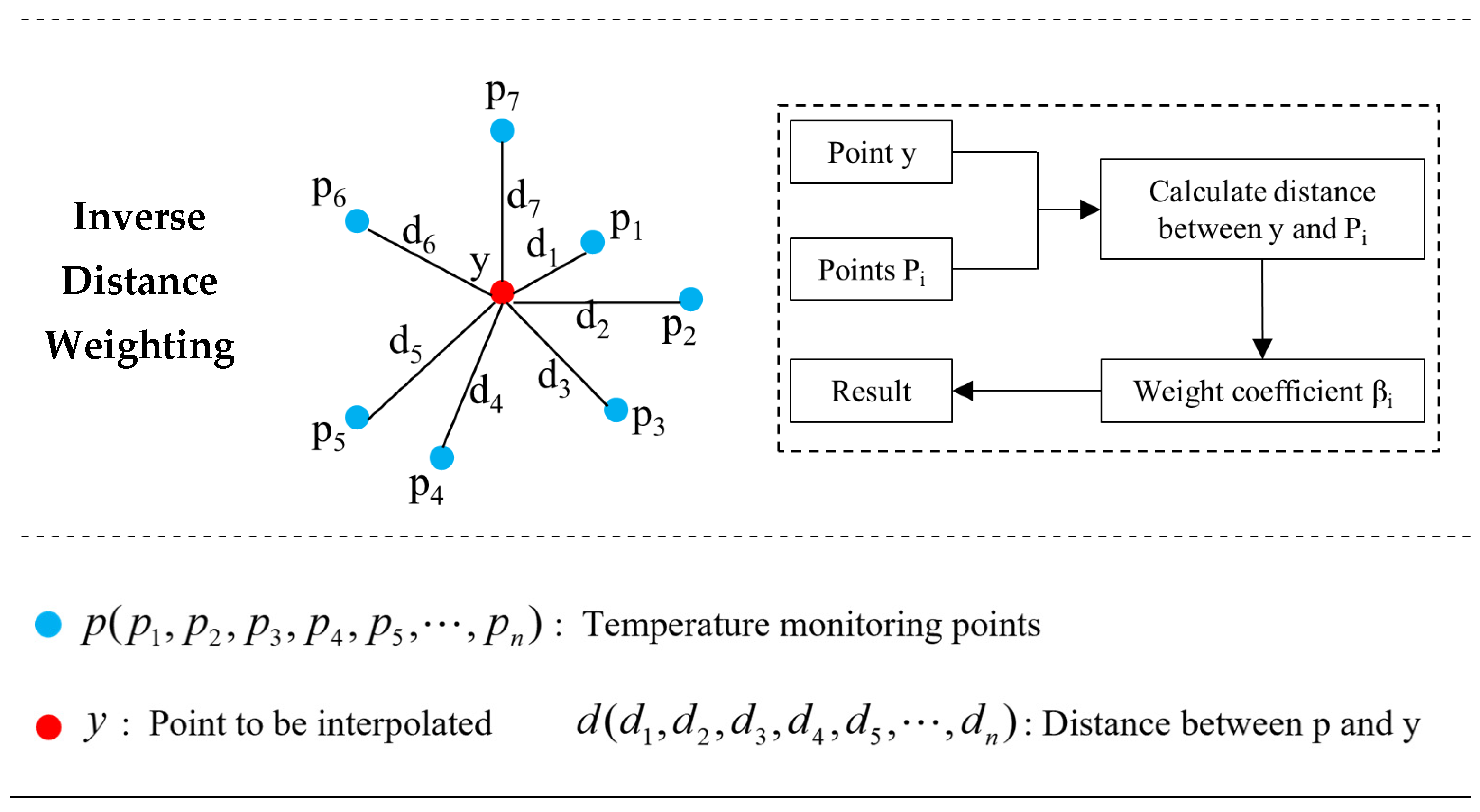
Inverse Distance Weighting

For the Inverse Distance Weighting interpolation algorithm, the distance between the point to be interpolated and the monitoring points is weighted, setting as ${\beta }_i$. The closer a monitoring point is to the point to be interpolated, the greater the weight given to this monitoring point will be [35]. The weight contribution is inversely proportional to the distance between the two points.

$$f\left(y\right)={\displaystyle \sum _{i=1}^m{\beta }_{i}f\left(p_i\right)}.$$

(7)

$${\beta }_i={\displaystyle \frac{d_i^{-1}}{{\displaystyle \sum _{i=1}^m{d}_i^{-1}}}}.$$

(8)

where $f\left(p_i\right)$ is the measured value of the monitoring points; $d_i$ is the distance between the monitoring points and the point to be interpolated; $m$ is the total number of monitoring points.

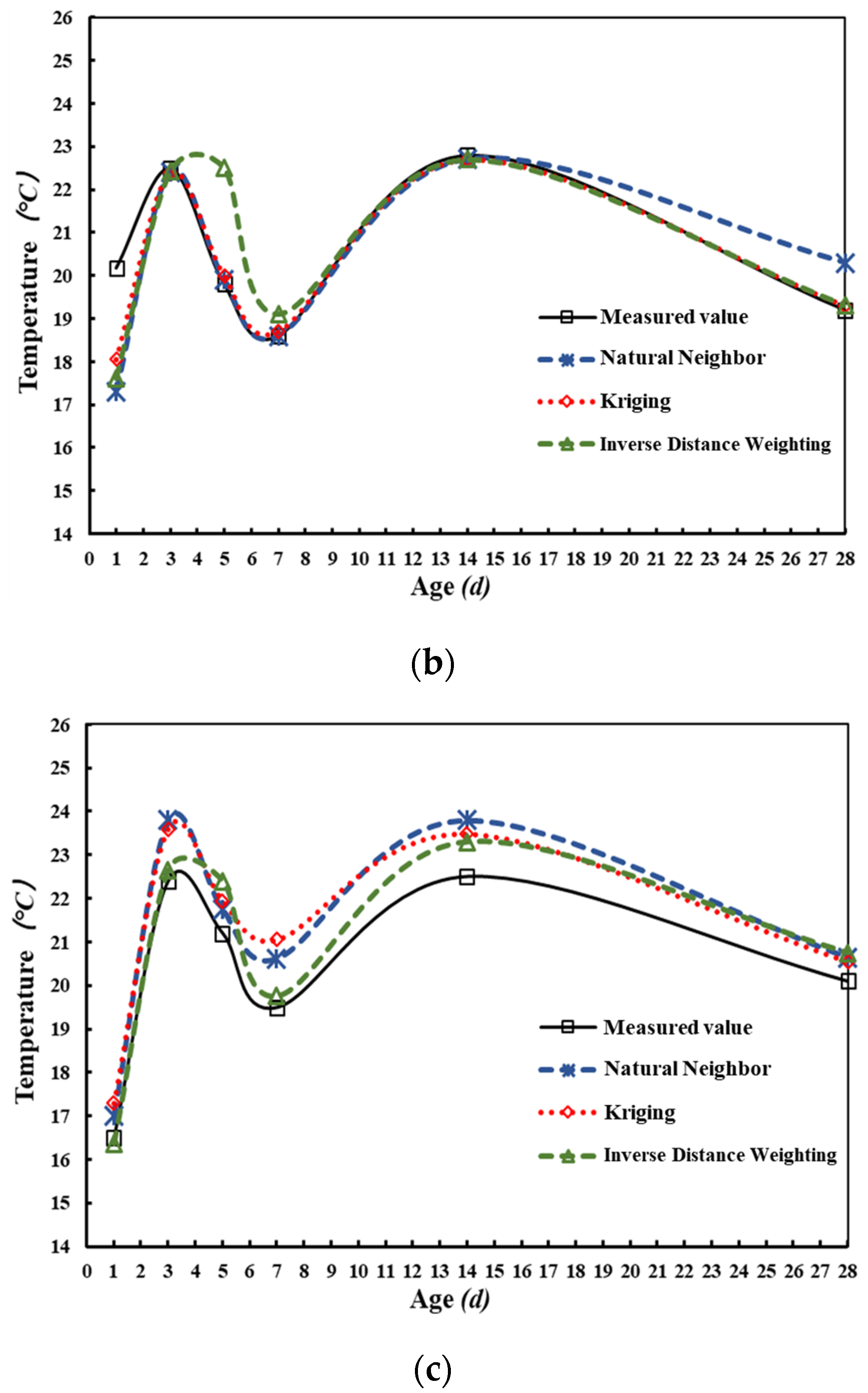
3.1.2. Evaluation of Thermal Field Reconstruction Effectiveness

Surfer (version 14) was employed to perform the three interpolation algorithms, which is professional interpolation software Surfer (version 14) [45]. The data analyzed were collected from the 7#-44 dam block in the WDD dam during its construction, and the optical fiber layout scheme is “Z” type [24], as shown in Figure 5. The low-heat Portland cement was utilized, with a slump of 30–40 mm. The concrete incorporates 35% fly ash and 0.6% water-reducing admixture. Based on the field measurements, the ambient temperature was 19.6 °C on the upstream side and 20.3 °C on the downstream side when 7#-44 was poured. The reconstructed thermal field in this study is based on actual temperature measurements from the optical fibers, meaning that factors such as cooling water, ambient temperature, and pouring temperature are inherently considered. Thermal field reconstruction results are illustrated in Figure 6, Figure 7 and Figure 8, respectively.

• Kriging

When the concrete was initially poured, it was affected by the ambient temperature, with the downstream and upstream sides showing higher temperature than the middle. At the age of 1 d, the middle concrete temperature is lower because of the low pouring temperature (about 16 °C) and less heat of cement hydration. At the age of 3 d, due to the cement hydration, the overall temperature rose sharply, and the maximum temperature rise was 15 °C. Compared with the age of 3 d, the concrete temperature shows a slight decrease at 5 d and 7 d due to water cooling. The selected concrete block 7#-44 is located at the dam corbel, where secondary aggregate grading concrete was poured. This type of concrete contains a higher amount of cement and emits more hydration heat. To control the downstream concrete temperature, the amount and duration of cooling water were increased, and more cooling water pipes were arranged at the downstream side of the concrete block 7#-44. Therefore, the extra heat at the downstream side was dissipated, resulting in a uniform temperature distribution throughout the structure. As shown in Figure 6.

Figure 6. Thermal field based on Kriging interpolation algorithm. (a) Day 1, (b) Day 3, (c) Day 5, (d) Day 7, (e) Day 14, and (f) Day 28.

Figure 6. Thermal field based on Kriging interpolation algorithm. (a) Day 1, (b) Day 3, (c) Day 5, (d) Day 7, (e) Day 14, and (f) Day 28.

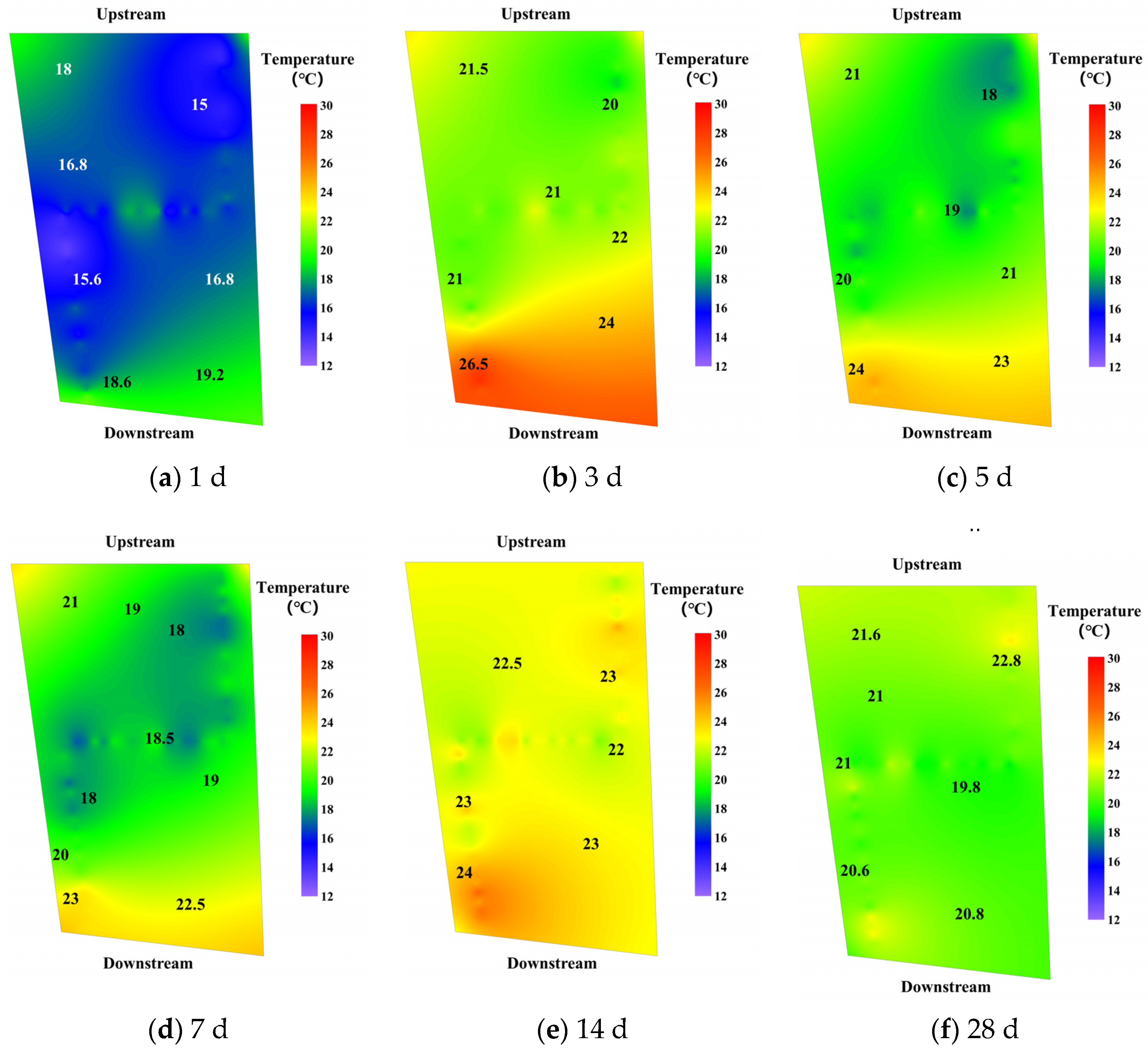
2.

Natural Neighbor

Figure 7 shows that the internal temperature was significantly lower than those near the upstream and downstream surfaces on Day 1. The concrete temperature rose rapidly, and the maximum temperature increase was 16.5 °C at the age of 3 d. At the age of 5 d and 7 d, the temperature distribution tended to be uniform. On Day 28, the highest and lowest temperatures were 19 °C and 22 °C, respectively.

Figure 7. Thermal field based on Natural Neighbor interpolation algorithm. (a) Day 1, (b) Day 3, (c) Day 5, (d) Day 7, (e) Day 14, and (f) Day 28.

Figure 7. Thermal field based on Natural Neighbor interpolation algorithm. (a) Day 1, (b) Day 3, (c) Day 5, (d) Day 7, (e) Day 14, and (f) Day 28.

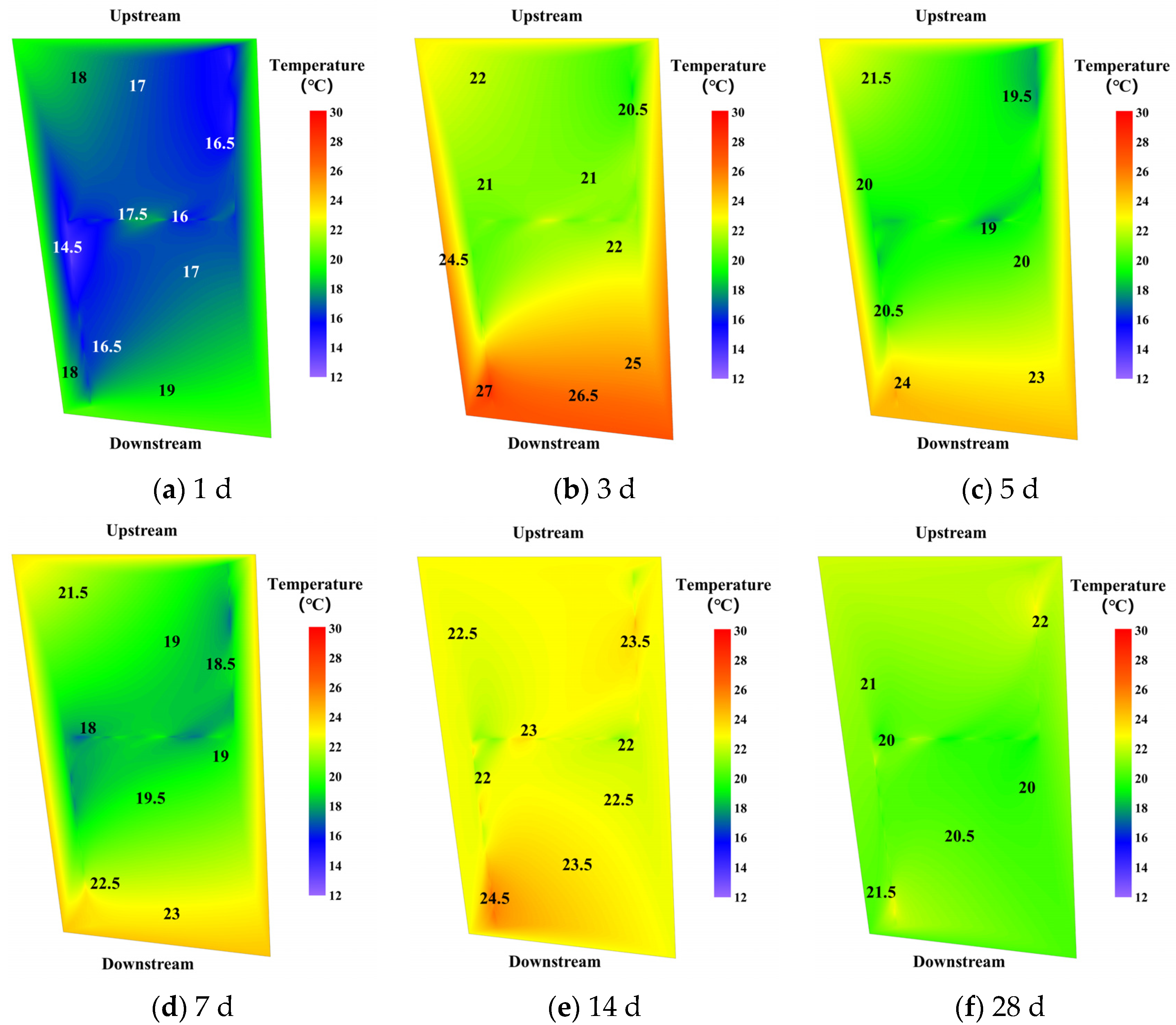
3.

Inverse Distance Weighting

On Day 1, the internal temperature was still low and nonuniform, consistent with the previous two interpolation methods. However, the reconstructed temperature at the same locations is different. On Days 5 and 7, when the temperature distribution was similar and the magnitude of the temperature change was reduced, the temperature distribution tended to be uniform, as illustrated in Figure 8.

Figure 8. Thermal field based on Inverse Distance Weighting interpolation algorithm. (a) Day 1, (b) Day 3, (c) Day 5, (d) Day 7, (e) Day 14, and (f) Day 28.

Figure 8. Thermal field based on Inverse Distance Weighting interpolation algorithm. (a) Day 1, (b) Day 3, (c) Day 5, (d) Day 7, (e) Day 14, and (f) Day 28.

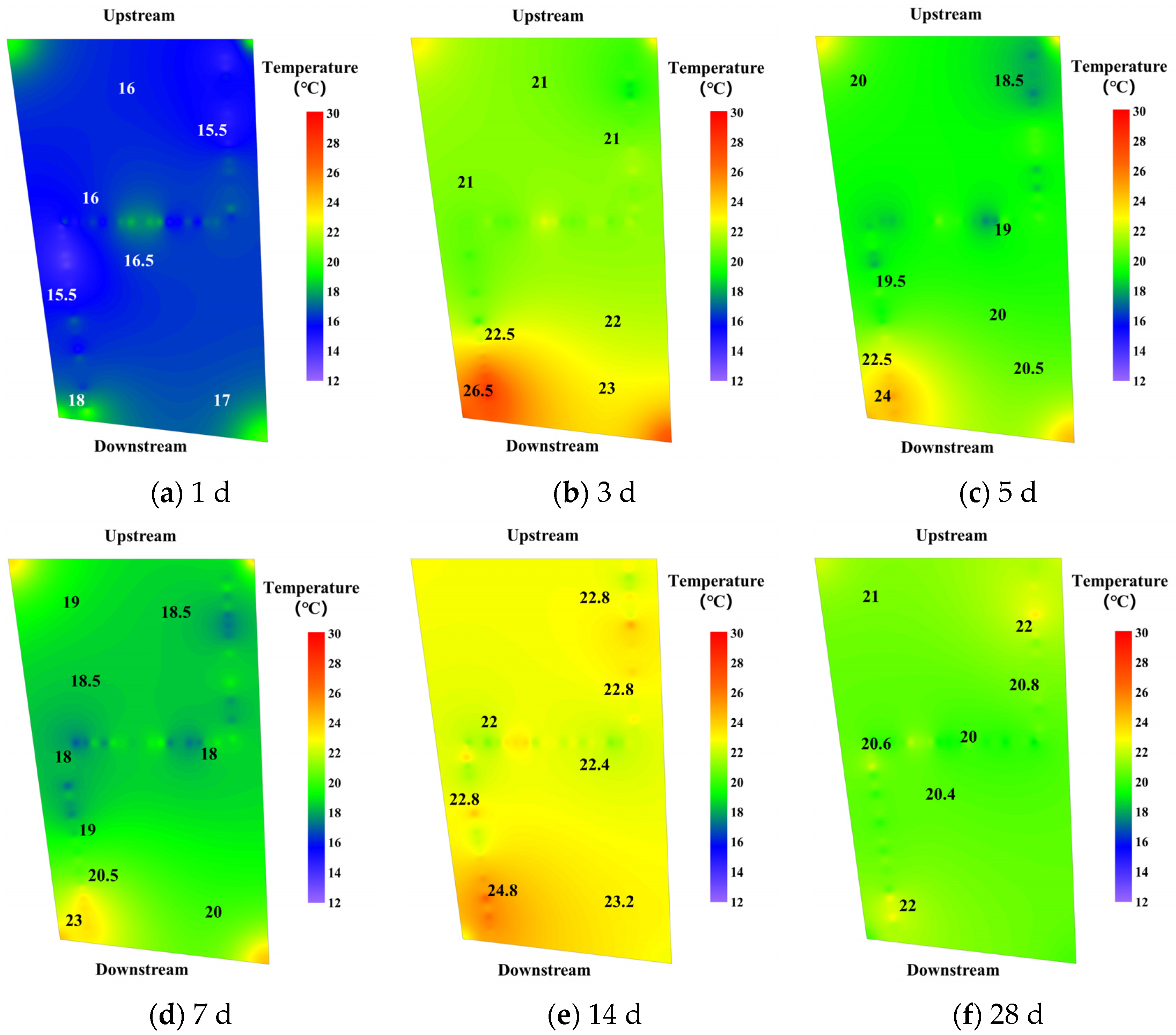
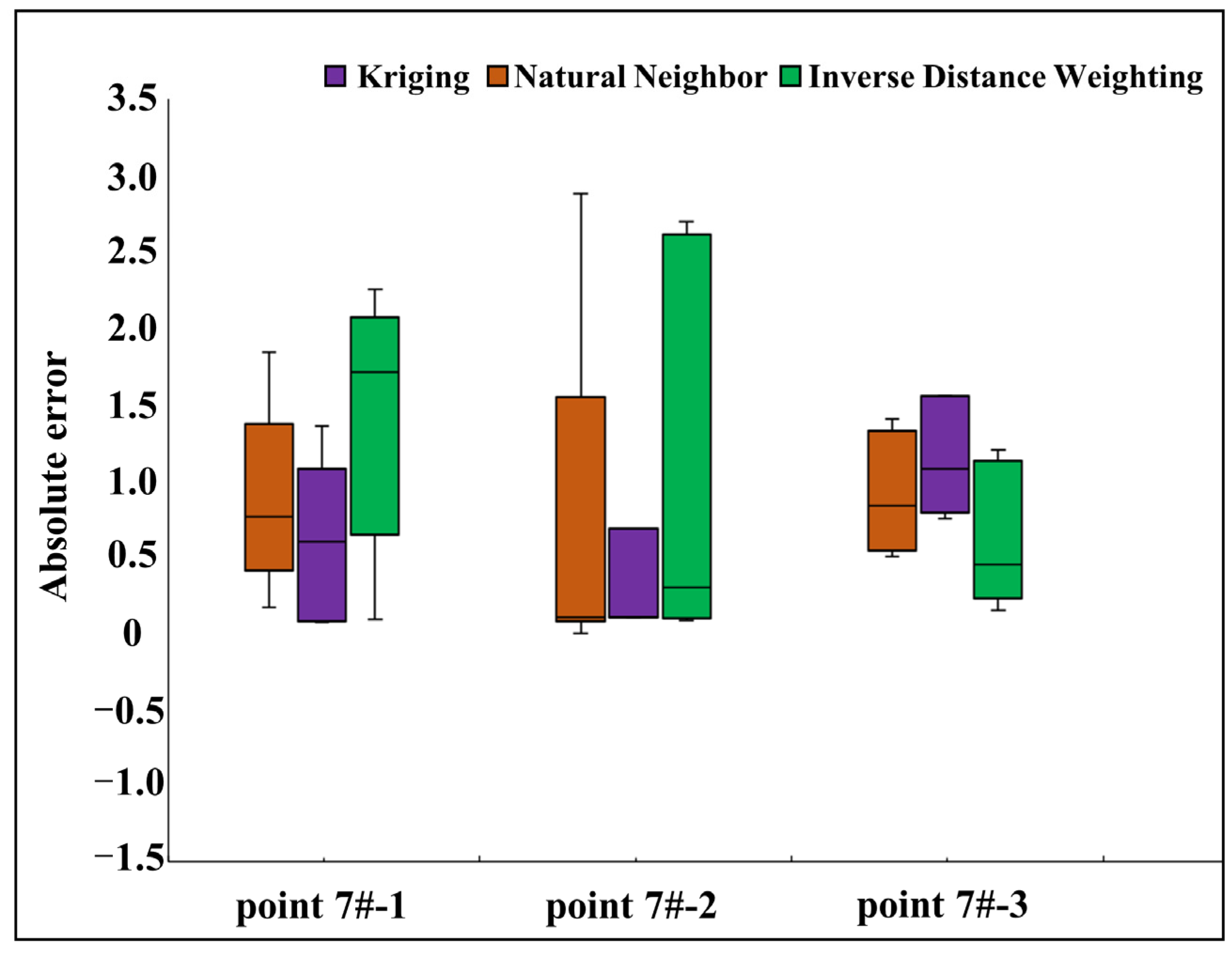
3.1.3. Interpolation Algorithm Selection

To evaluate the interpolation accuracy, the reconstructed temperatures were compared with the measured values collected from the digital thermometers at the same location (Figure 9).

At 7#-1, the maximum error between the reconstructed temperature and the measured temperature was 1.89 °C. After Day 14, the errors decreased and the reconstruction results converged toward the measurement. At 7#-2, the Natural Neighbor and Kriging interpolation worked well before Day 14. From Day 14 to Day 28, the error of Natural Neighbor gradually increased to 1 °C on Day 28. The Inverse Distance Weighting result has a significant error when compared with the measurement. At 7#-3, Natural Neighbor has the maximum error of 1.55 °C.

Table 1. Errors of three interpolation algorithms.

Interpolation Algorithm	Position	Minimum Error (°C)	Maximum Error (°C)	Average Error (°C)
Kriging	7#-1	0.07	1.36	0.76
	7#-2	0.10	2.13
	7#-3	0.75	1.55
Natural Neighbor	7#-1	0.17	1.84	0.81
	7#-2	0.00	2.88
	7#-3	0.50	1.40
Inverse Distance Weighting	7#-1	0.09	2.25	0.96
	7#-2	0.08	2.58
	7#-3	0.15	1.20

presents the errors between the measured temperature values and the reconstructed temperature values for the three interpolation algorithms. The box plots were obtained by calculating the absolute error, as shown in Figure 10. As can be seen, the errors were the greatest by the Inverse Distance Weighting and the smallest by the Kriging, indicating that the Kriging interpolation algorithm works best.

Further, the statistical indicators, mean absolute error (MAE), and root mean squared error (RMSE) were calculated.

$$MAE={\displaystyle \frac{1}{3}}{\displaystyle \sum _{j=1}^3\left|T_{j,t}-T_t\right|},j\in \left[1,2,3\right].$$

(9)

$$RMSE=\sqrt{{\displaystyle \frac{{\displaystyle \sum _{j=1}^3{\left(T_{j,t}-T_t\right)}^2}}{3}}}.$$

(10)

where $T_{j,t}$ is the temperature of the $j-th$ measurement point of the digital thermometer at time $t$, and $T_t$ is the reconstructed temperature at the same point. The MAE and RMSE values are listed in

Table 2. Comparison of MAE and RMSE.

Interpolation Algorithm	Position	MAE	RMSE	Average MAE	Average RMSE
Kriging	7#-1	0.68	0.84	0.75	0.96
	7#-2	0.46	0.88
	7#-3	1.11	1.15
Natural Neighbor	7#-1	0.83	0.97	0.82	1.07
	7#-2	0.71	1.26
	7#-3	0.90	0.98
Inverse Distance Weighting	7#-1	1.26	1.48	0.96	1.25
	7#-2	1.01	1.54
	7#-3	0.60	0.73

. The average MAE and average RMSE values obtained by Kriging were much less than the other two, indicating that Kriging is the most accurate among the three interpolation algorithms.

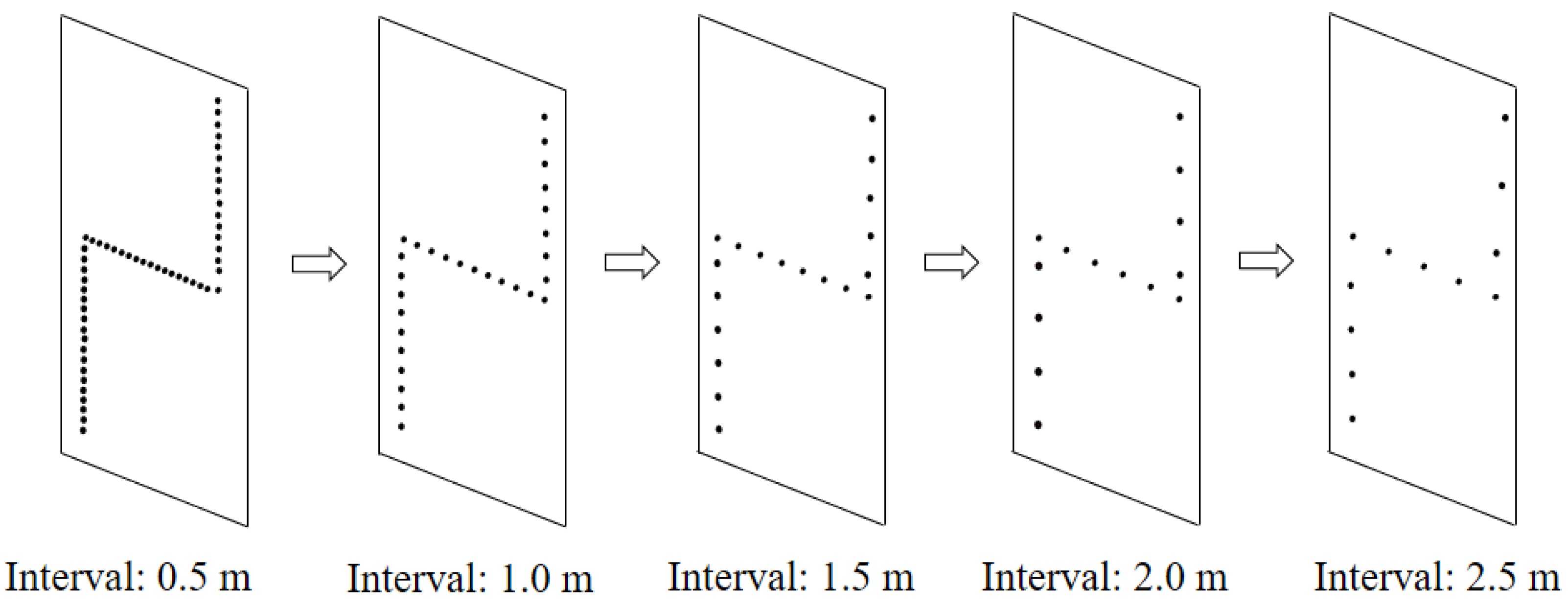
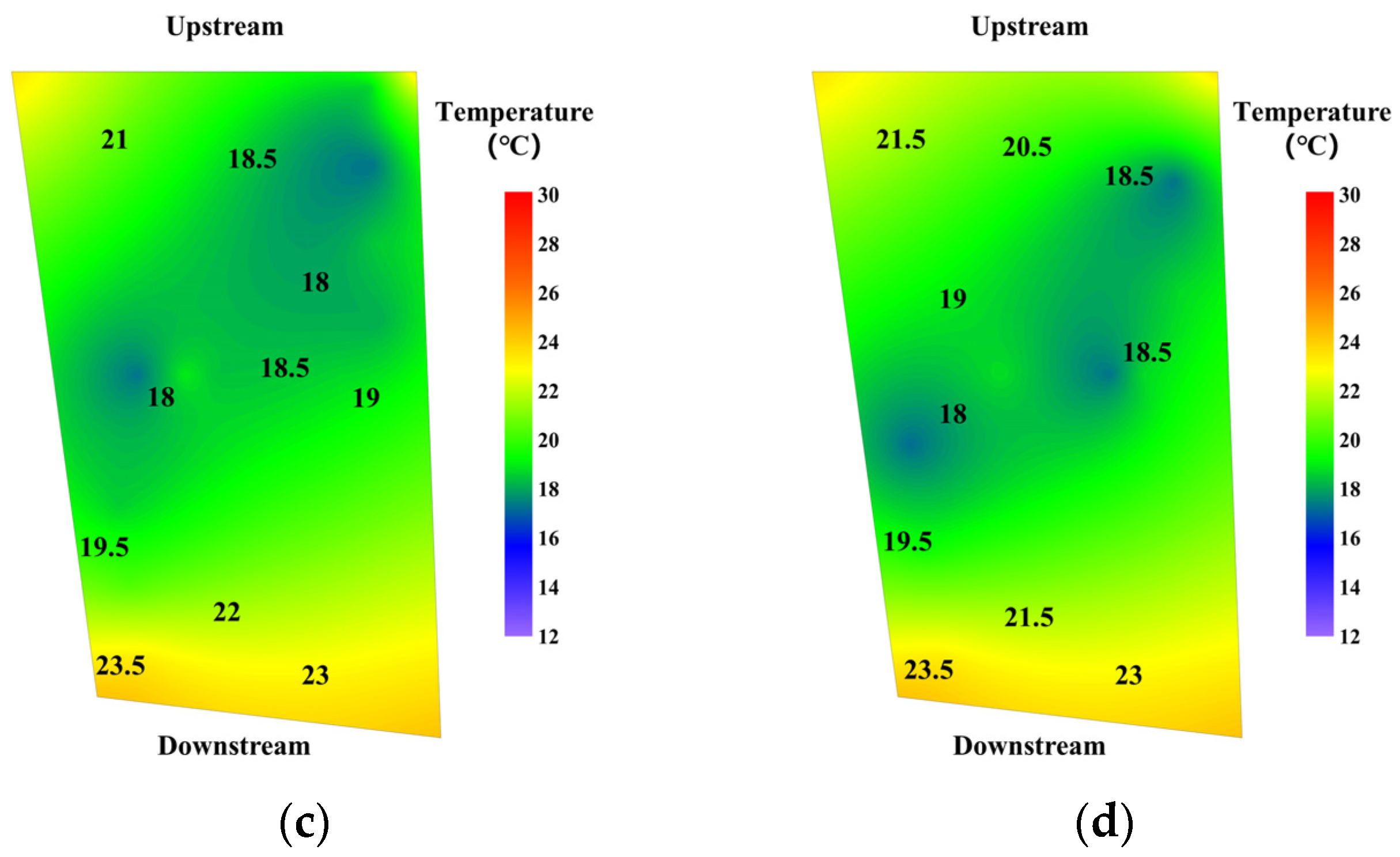
3.2. Monitoring Point Number Optimization

To reduce the calculation load of thermal field reconstruction and improve the response speed, it is crucial to investigate the impact of the number of temperature-monitoring points on the reconstruction results of the thermal field. A total of 58 monitoring points, spaced at 0.5 m intervals, were selected from the 7#-44 concrete block of the WDD dam. Subsequent datasets were generated by setting monitoring point intervals to 1.0 m, 1.5 m, 2.0 m, and 2.5 m, respectively, as illustrated in Figure 11.

By comparing the interpolation results of these datasets with varying intervals (Figure 12), the effect of the number (or density) of temperature measurement points on thermal field reconstruction was analyzed. The analysis revealed that, as the number of temperature-monitoring points decreased, the reconstructed thermal fields remained nearly identical. Minor differences were observed only in the center of the dam block, with the maximum deviation being less than 1 °C. The temperature reconstructions near the upstream surface, downstream surface, and transverse joint surface were virtually identical. Even with a reduced number of monitoring points, the accuracy of the reconstructed thermal field continued to meet the temperature control requirements (e.g., within 1 °C). In summary, the Kriging interpolation algorithm, combined with the “Z” pattern of fiber embedding, allows for a reduction in the number of temperature-monitoring points while still ensuring the accuracy of the reconstructed thermal field.

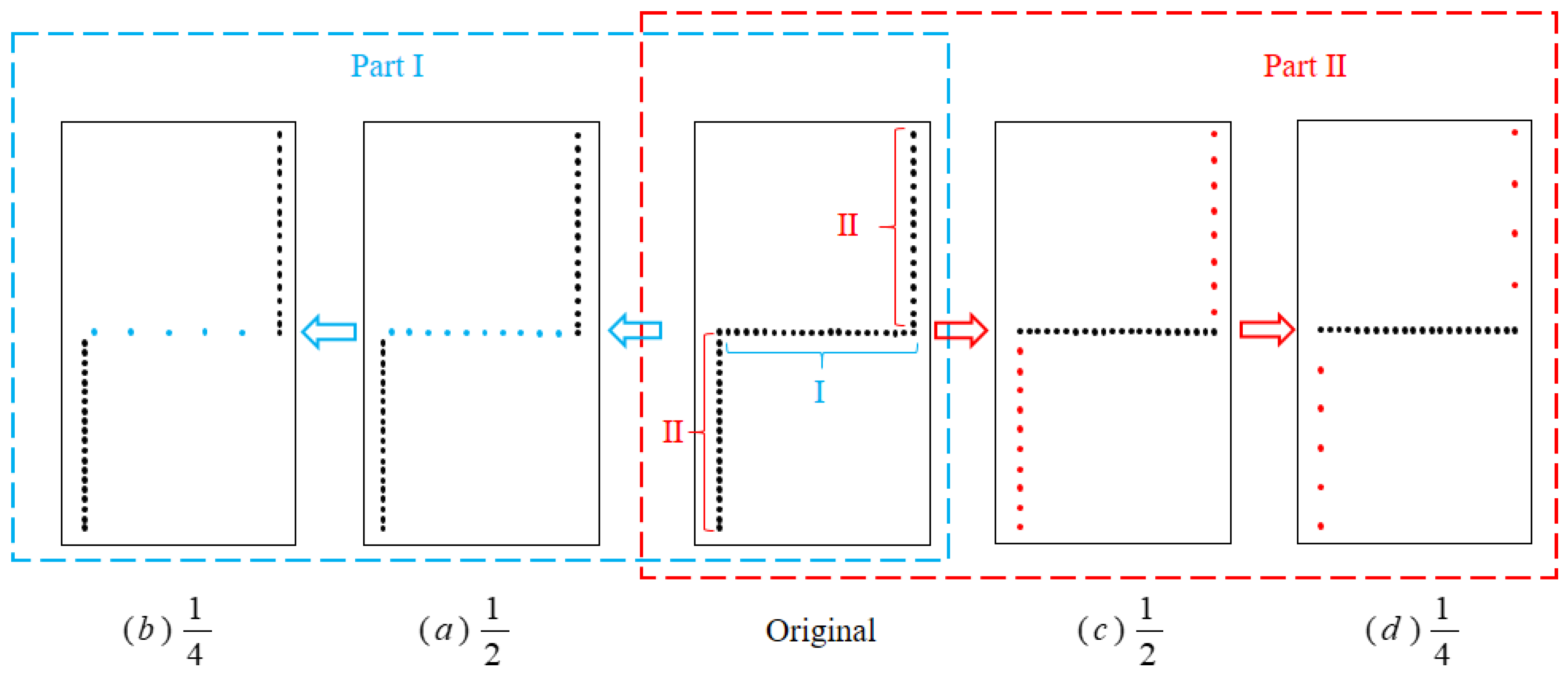
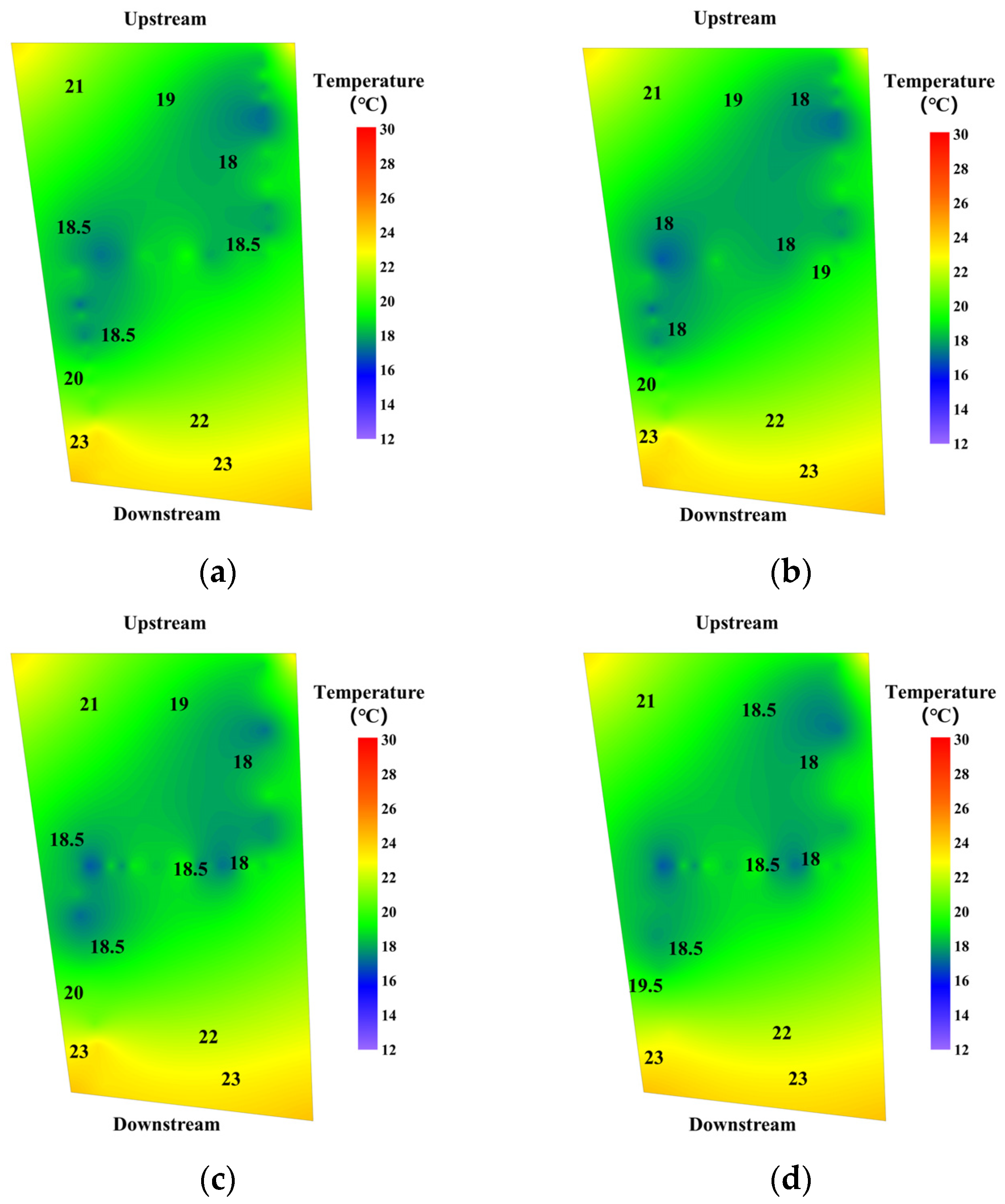
3.3. Analysis of the Impact of Monitoring Positions

In the “Z” pattern, the temperature-monitoring points on the optical fibers can be divided into two segments: (i) Part I, located in the center of the dam block (mid-depth) parallel to the dam axis, and (ii) Part II, situated along the transverse joint, as illustrated in Figure 13. The impact of the placement of temperature-monitoring points in these two segments on thermal field reconstruction was analyzed using the control variable method.

• Part I

The number of Part I temperature-monitoring points was reduced to one-half and one-quarter of the original (Figure 13a,b). The number of Part II temperature-monitoring points remained the same.

2.

Part II

The number of Part I temperature-monitoring points remained unchanged. The number of Part II temperature-monitoring points was reduced to one-half and one-quarter (Figure 13c,d).

The accuracy of reconstruction results was analyzed and compared (Figure 14). By analyzing reconstruction results, it was found that Part I has little effect on the reconstruction accuracy of the thermal field. The maximum temperature error at the same location was less than 0.5 °C. Therefore, the number of temperature-monitoring points at this location can be reduced. For those locations where the temperature control standard is low or the risk of cracking is small, arranging optical fiber in the center of concrete may be sufficient. The number of temperature-monitoring points in Part II has a greater effect on the results than those of Part I. The result substantiates that temperature along the surface has a significant influence on the accuracy of thermal field reconstruction. To improve the accuracy of thermal field reconstruction, the number of monitoring points can be increased accordingly along the transverse joints. For those locations where the temperature may change drastically, or the risk of cracking is high, the number of temperature-monitoring points should be increased.

Considering the complexity of the concrete temperature, engineering structure, and construction conditions, the above statistical validation of the results is insufficient in some cases. For example, areas without optical fibers or changes in the shape of the concrete block can affect the reconstruction results. However, in most cases, the construction conditions of concrete arch dams—including the shape of the concrete blocks, concrete pouring process, and optical fiber embedding—generally follow the approach used in this study. Therefore, the method proposed is expected to be applicable and reliable for similar engineering projects. Due to the complexity of concrete temperature, neither numerical nor analytical methods can accurately reflect its thermal field. The method proposed in this study closely approximates the actual thermal field, effectively reflecting the true properties of concrete. Moreover, it can reduce economic costs and minimize impacts on the construction process.

3.4. Lightweight Application Procedures

The proposed optimization method aims to provide timely and accurate thermal field reconstruction results to guide temperature control measures, such as water cooling. Due to the variations in construction conditions, structural characteristics, and external environments across different projects, the applicability of this method to other projects will be challenged. To solve the practical obstacles, the lightweight application procedures are proposed to enhance the method’s applicability in large-volume concrete temperature control:

• Monitoring system layout and interpolation algorithm selection

Assess on-site concrete pouring conditions, including dimensions, optical fiber layout, and data acquisition frequency. Taking the representative concrete dam block as an example, the accuracy and suitability of different interpolation algorithms are evaluated by employing the method detailed in Section 3.1. In this study, when the concrete dam block employs the “Z” shape optical fiber layout scheme, the Kriging method demonstrates superior accuracy compared to both the Natural Neighbor and Inverse Distance Weighting methods. Additionally, in practical applications, it is feasible to incorporate other interpolation methods, such as spline functions [46], linear interpolation [47], and nearest neighbor interpolation [48], based on specific conditions.

2.

Optimization of thermal field reconstruction Efficiency

This step aims to minimize the volume of monitoring data required, thereby reducing computational complexity and ensuring the real-time acquisition of thermal field distributions within the shortest time frame. However, this must be accomplished while meeting the temperature control requirements specific to different projects, structures, and locations. For instance, in dam temperature control, an interpolation accuracy of no less than 1 °C is essential. Therefore, this step can be executed using the iterative computation methods described in Section 3.2 and Section 3.3 to determine the optimal number and positions of monitoring points. Before large-scale concrete pouring for the dam, calculations can be conducted on a typical dam segment to alleviate the computational load of reconstructing the concrete temperature field, ensuring precise temperature regulation during peak construction periods.

3.

Development and implementation of temperature control measures

Utilize the reconstructed concrete thermal field results to guide the formulation of water-cooling measures and precise parameter control, thereby achieving intelligent temperature control for large-volume concrete. During practical applications, based on construction conditions, concrete dam blocks and their corresponding water control equipment are categorized into temperature control units. The optimized thermal field reconstruction method can be applied independently to each control unit, providing precise guidance for regulating temperature control equipment in accordance with the pouring progress of different dam blocks and the evolution patterns of the concrete temperature field.

4.

Evaluation of temperature control effectiveness

Using the real-time thermal field obtained from the concrete dam blocks, calculate the compliance rate between the actual temperature time curve and temperature control requirements. Throughout the entire concrete pouring process, monitor key indicators such as pouring temperature, maximum temperature, arching temperature, and cooling rate. Guided by the real-time thermal field, achieve precise temperature control for each concrete pouring section. After the pouring is completed, continue with thermal field reconstruction calculations to monitor ongoing changes in the internal temperature of the concrete dam.

4. Case Study

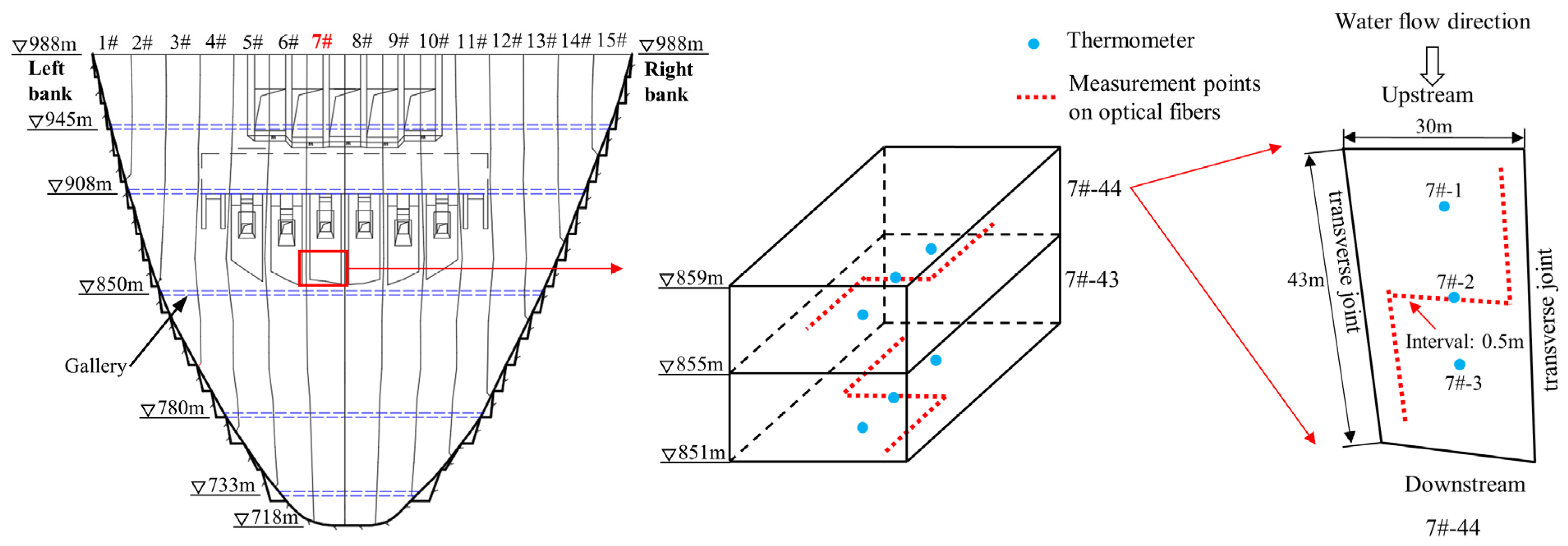
4.1. Project Overview

The WDD hydropower station is on the Jinshajiang River, located in Luquan County, Yunnan Province, China (Figure 15). The WDD concrete dam is a double curvature arch with a maximum height of 270 m and a thickness–height ratio of 0.19. The river valley is dry and hot with large temperature differences of 14 °C during the day and night. The power station is installed with 12 hydroelectric generating units with a total installed capacity of 10,200 MW. The concrete volume of the WDD dam is about 2.8 million m³. The dam consists of fifteen concrete monoliths with no longitudinal joints [22].

Therefore, temperature control during concrete pouring is challenging. To acquire the evolution process of the dam concrete thermal field and avoid temperature cracks, the optical fibers were buried in the 7# river bed dam monolith and the 12# bank slope dam monolith of the WDD dam. The internal temperature of the concrete was monitored using the DTS system, with the “Z”-type fiber layout scheme. Based on the method proposed in this study, real-time thermal fields of the concrete were obtained, and the results were used to guide the formulation of temperature control measures at the construction site.

4.2. Effectiveness Evaluation

The extreme maximum temperature in the WDD reservoir is 42.7 °C, the extreme minimum temperature is −5.8 °C, and the annual average temperature is 20.9 °C. During the period of construction, the concrete pouring volume can reach 100 m³ per hour. Considering multiple factors such as the complex environment and the large volume of concrete pouring, WDD’s temperature control had a high standard. The maximum temperature of concrete must not exceed 27 °C in the area constrained by the dam foundation and 30 °C in other areas. Three stages were stipulated for cooling down. The target temperature after the end of the first stage was between 23 °C and 25 °C. In the second stage, the cooling rate was required to be 0.3 to 0.5 °C/day, and the target temperature after the end of this stage was between 18 °C and 21 °C. The target temperature after the end of the third stage was between 13 °C and 16 °C.

To meet the above temperature control requirements, an intelligent cooling control system (ICCS) for concrete temperature control was implemented in the WDD dam construction, combining water-cooling pipes with thermal field reconstruction. Contractors can log in to the intelligent temperature control system via their mobile phones to query the real-time thermal field of each concrete block, which provides a real-time judgment basis for the evaluation of the concrete temperature control effect. This methodology surpasses traditionally used numerical simulations and analyses that lag far behind construction progress. The maximum temperature of the concrete did not exceed the temperature control requirements, and a great temperature control effect was achieved (Figure 16a,c). The engineering application procedure summarized in Section 3.4 was applied in the ICCS (Figure 16b), and the thermal field was reconstructed.

The 7#-011 concrete block was taken as an example. The real-time thermal field was reconstructed based on the proposed method and used to guide the cooling strategy. The optical fibers were not embedded in the 6#-010, 8#-009, and 9#-012 concrete blocks, serving as the control group. The cooling strategy for these three blocks can only rely on three digital thermometers to obtain the temperature during water cooling, rather than using the proposed method to calculate the thermal field.

By comparing the actual temperature curve of the 6#-010, 7#-011, 8#-009, and 9#-012 blocks, the maximum temperature of the 7#-011 block was significantly lower than the other three, which was 25.4 °C (in line with the temperature control requirement) (Figure 17). The maximum cooling rate of the 7#-011 block was 0.4 °C/d, which also met the temperature control requirement. In addition, the temperature curve of the 7#-011 block was smoother, meaning that the water-cooling strategy for the 7#-011 block was more effective than the other three, and the temperature difference was much lower. Due to the real-time thermal field reconstruction, the cooling strategy was able to be adjusted in time, the temperature stress was well controlled, no temperature cracks appeared, and precise temperature control was achieved. The successful application of the proposed method guaranteed the construction quality of the WDD dam, and, on 16 June 2021, all 12 water turbines were put into operation.

5. Conclusions

This study presented an optimization method for improving the efficiency of thermal field reconstruction in concrete dams, comprising three key components: evaluation and selection of interpolation algorithms, optimization of monitoring point numbers, and analysis of monitoring position impacts. While ensuring accuracy, this method significantly reduced the computational load and enabled real-time, precise thermal field reconstruction based on the construction schedule. The thermal field obtained was used to guide the strategy of the intelligent cooling control system and verified at the WDD dam. The conclusions are as follows:

(1)

An optimization method for improving the efficiency of thermal field reconstruction was proposed. The applicability of Kriging, Natural Neighbor, and Inverse Distance Weighting interpolation algorithms is evaluated quantitatively based on the actual optical fiber layout scheme. The Kriging is the optimal one when the optical fiber is embedded in a “Z shape”. The reconstructed thermal field was in accordance with the point measurements by digital thermometers, and the mean absolute error and root mean squared error were 0.75 and 0.96, respectively.

(2)

The impact of the number and position of monitoring points on thermal field reconstruction was analyzed. Sensitivity analysis indicated that with a “Z-shaped” optical fiber and the Kriging interpolation algorithm, reducing the number of temperature-monitoring points lowers calculation complexity and improves response speed while maintaining accuracy (error < 1 °C). Monitoring points near the transverse joint had a greater effect on reconstruction accuracy than those at the center of the concrete block.

(3)

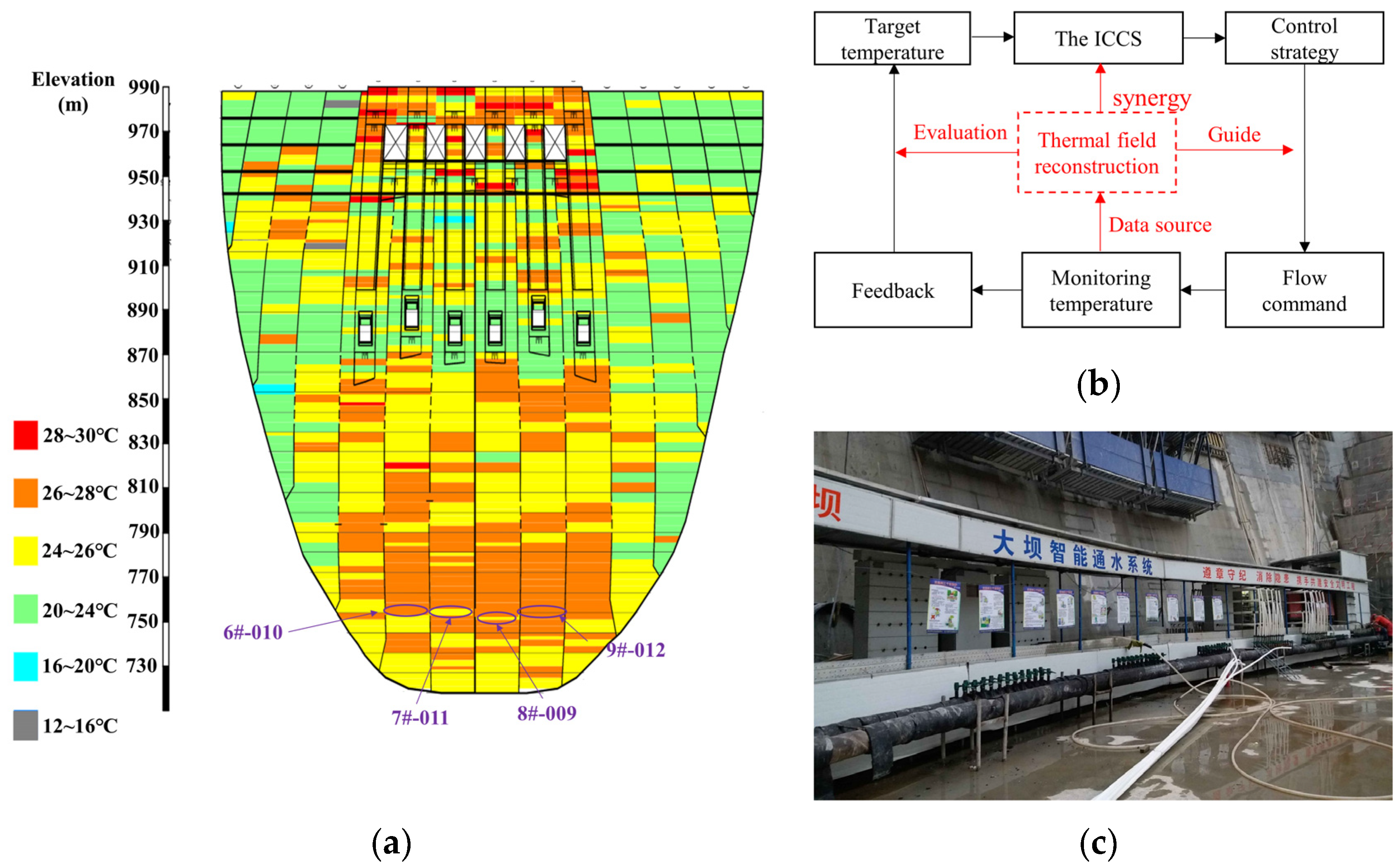
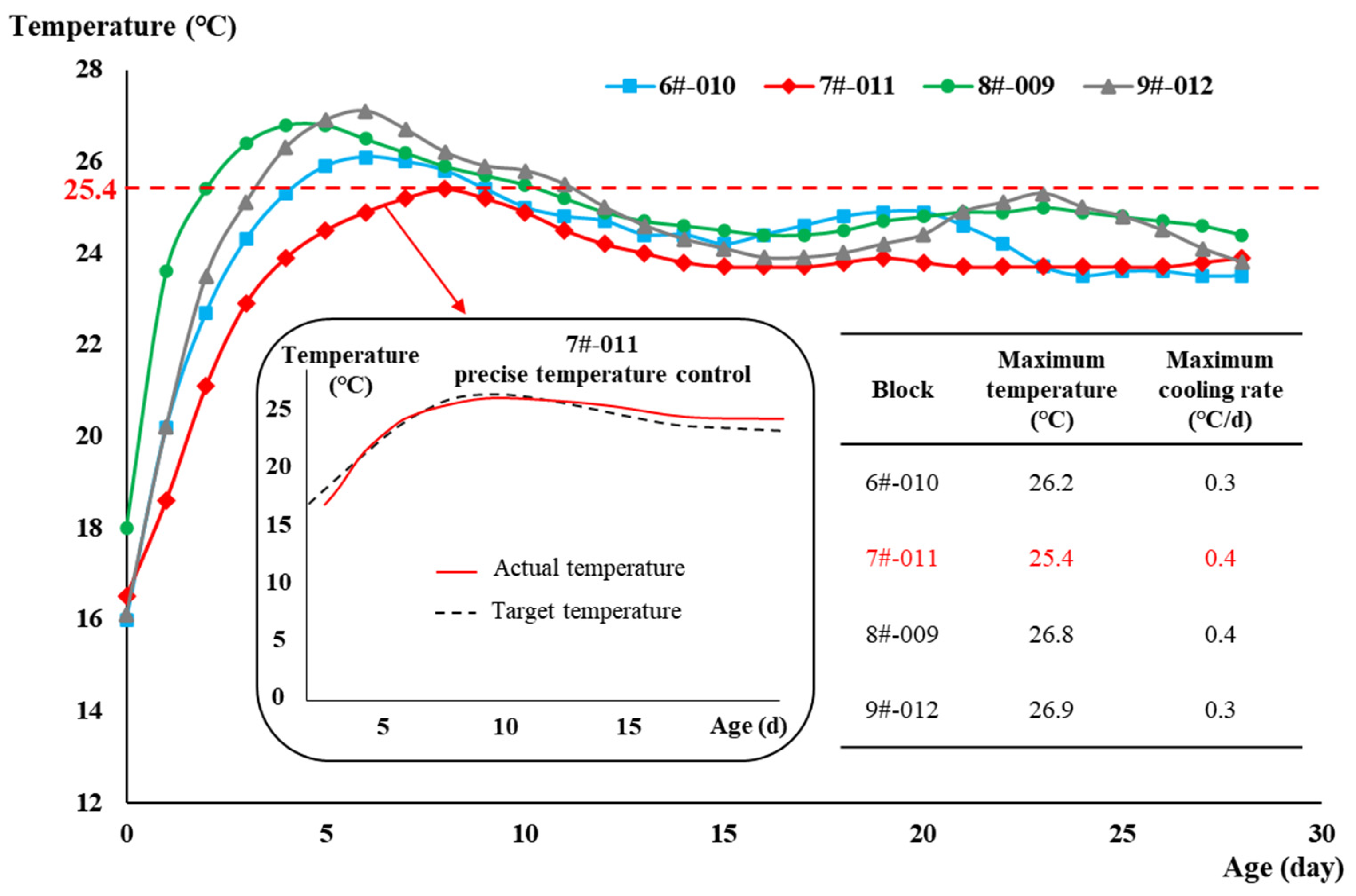
The method was combined with the intelligent cooling control system, and the effectiveness was verified in the 7# dam monolith of the WDD dam. The maximum temperature of the concrete block is 25.4 °C (meeting the requirement of not exceeding 27 °C). Compared with the dam monolith without this method, the 7# dam monolith has a smoother temperature curve and a cooling rate of 0.4 °C/day (meeting the requirement of 0.3–0.5 °C/day).