Computational Fluid Dynamics Analysis of Gas Suction in Coaxial Flow Venturi Injector: Impact of Gas–Liquid Interface Structure in Mixing Section
Abstract
1. Introduction
2. Governing Equation and Calculation Setting
2.1. Multiphase Flow Model
2.2. Turbulence Model
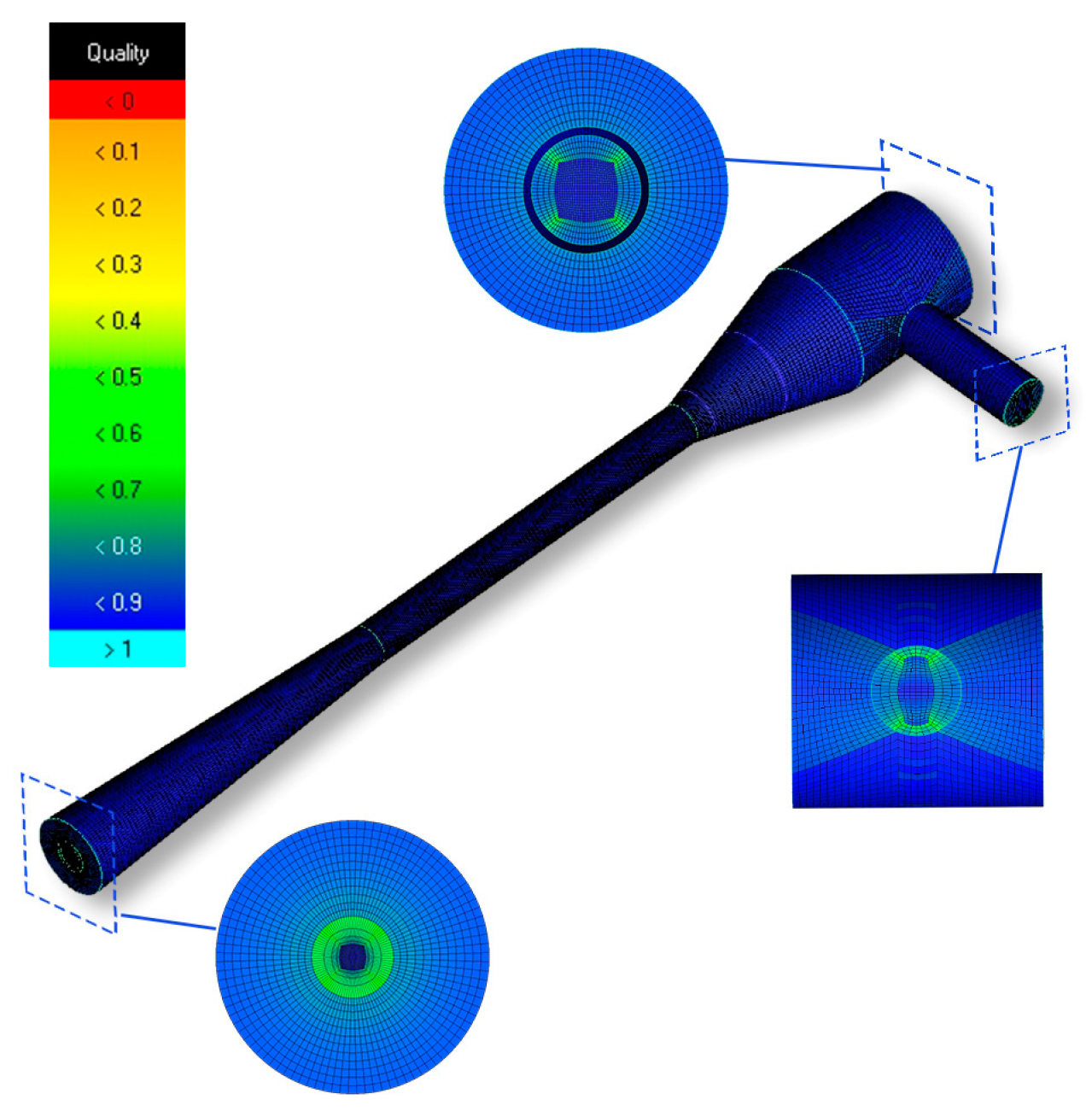
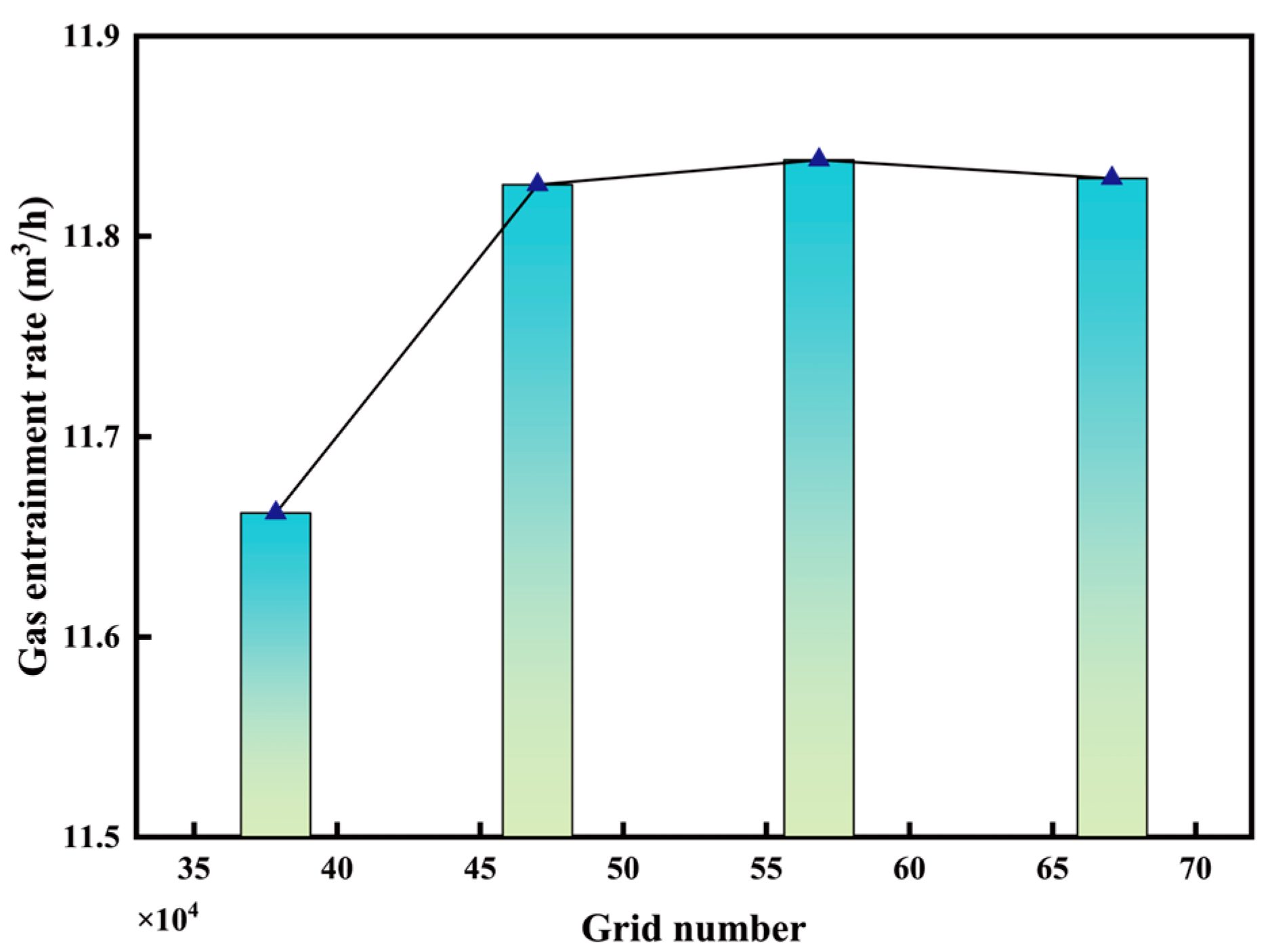
2.3. Mesh Partition and Simulation Setting
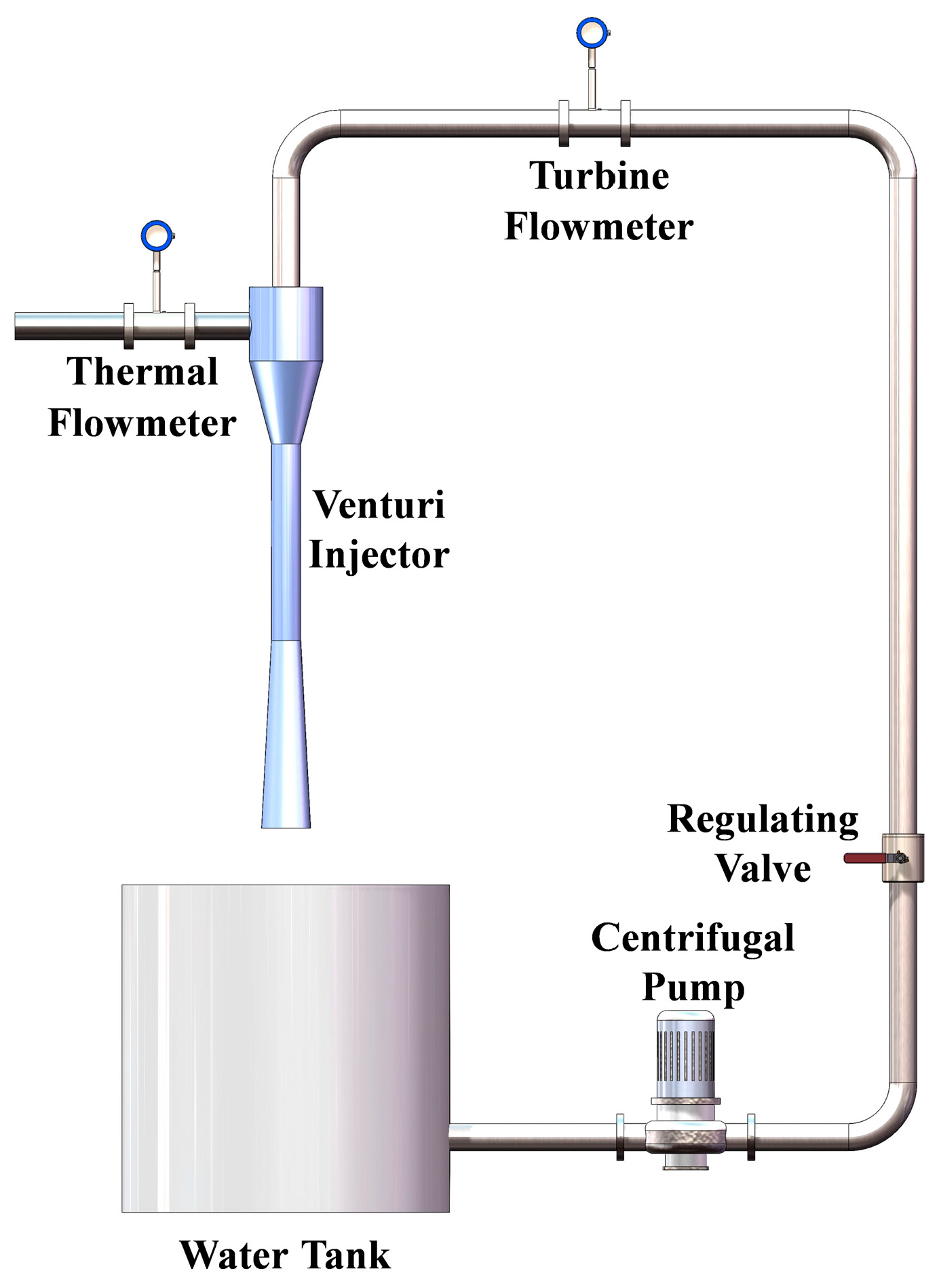
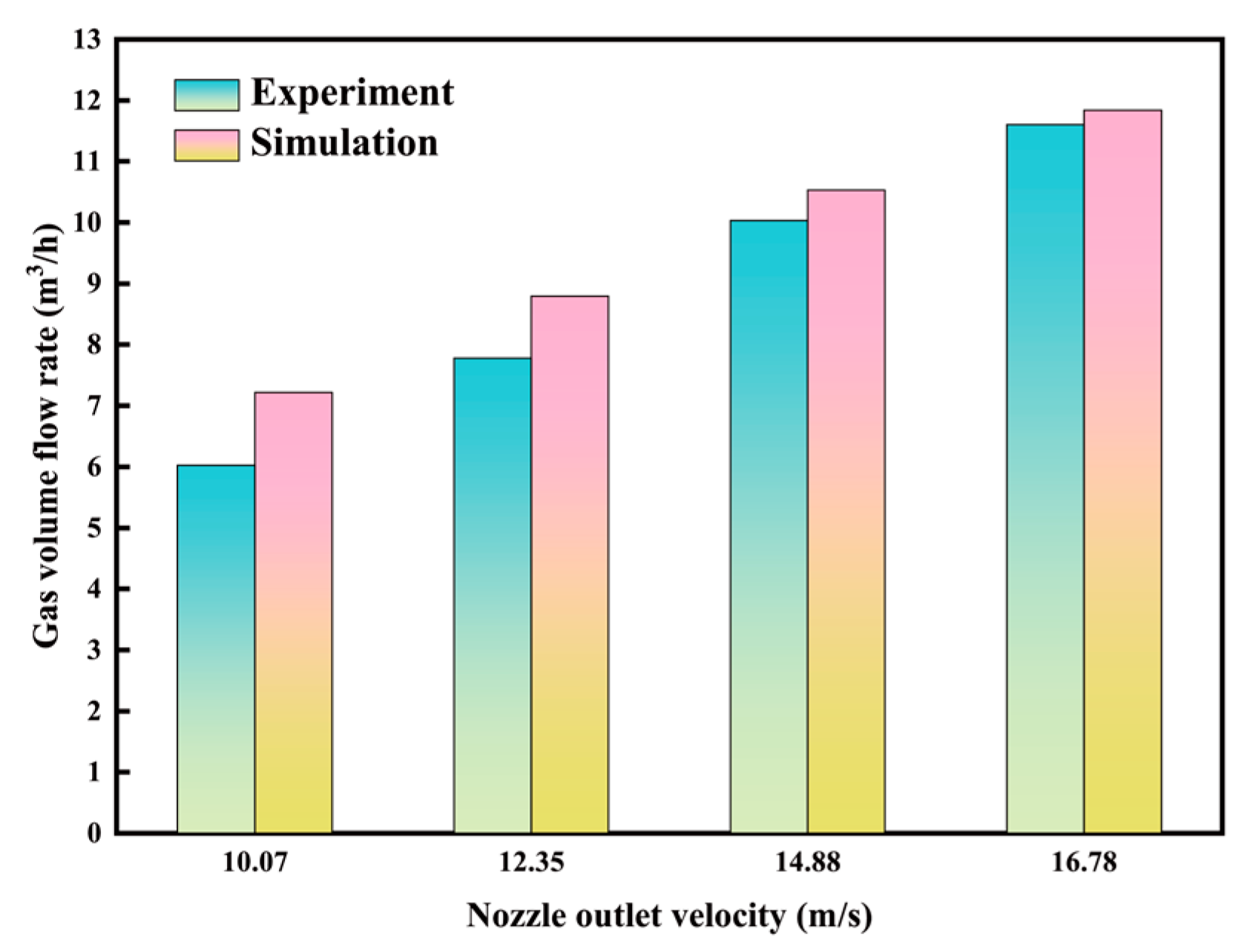
2.4. Model Validation
3. Results and Discussion
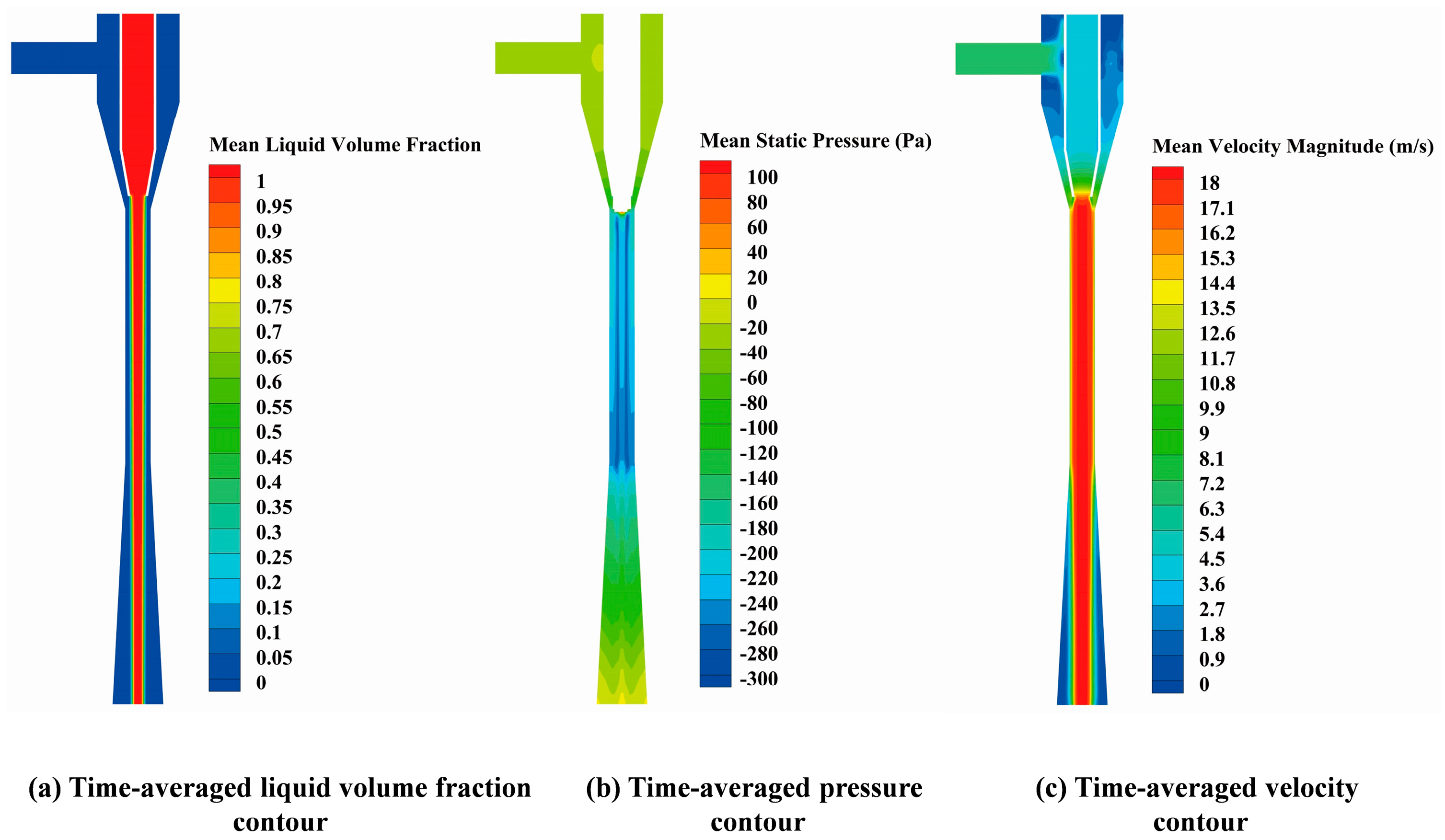
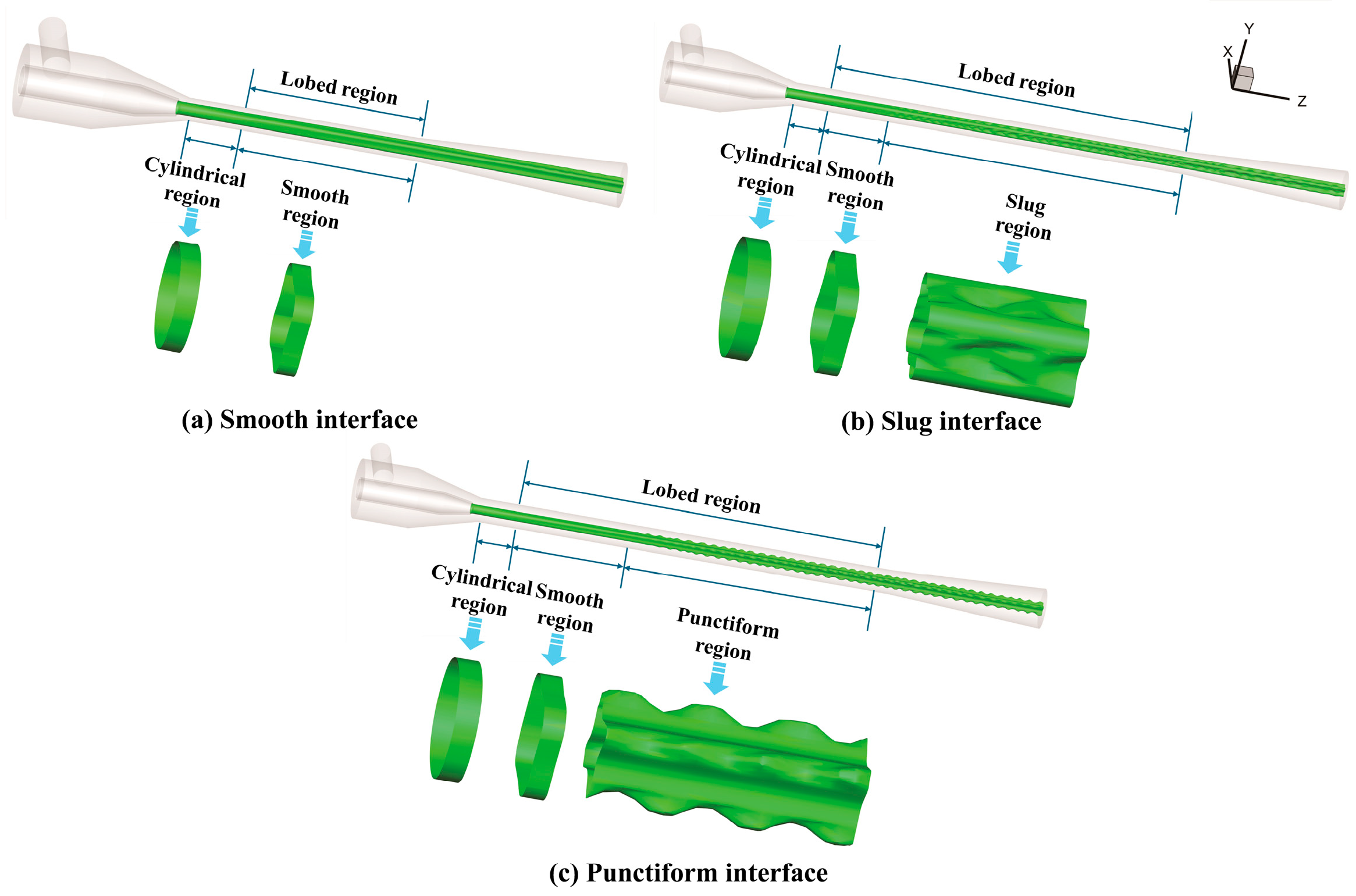
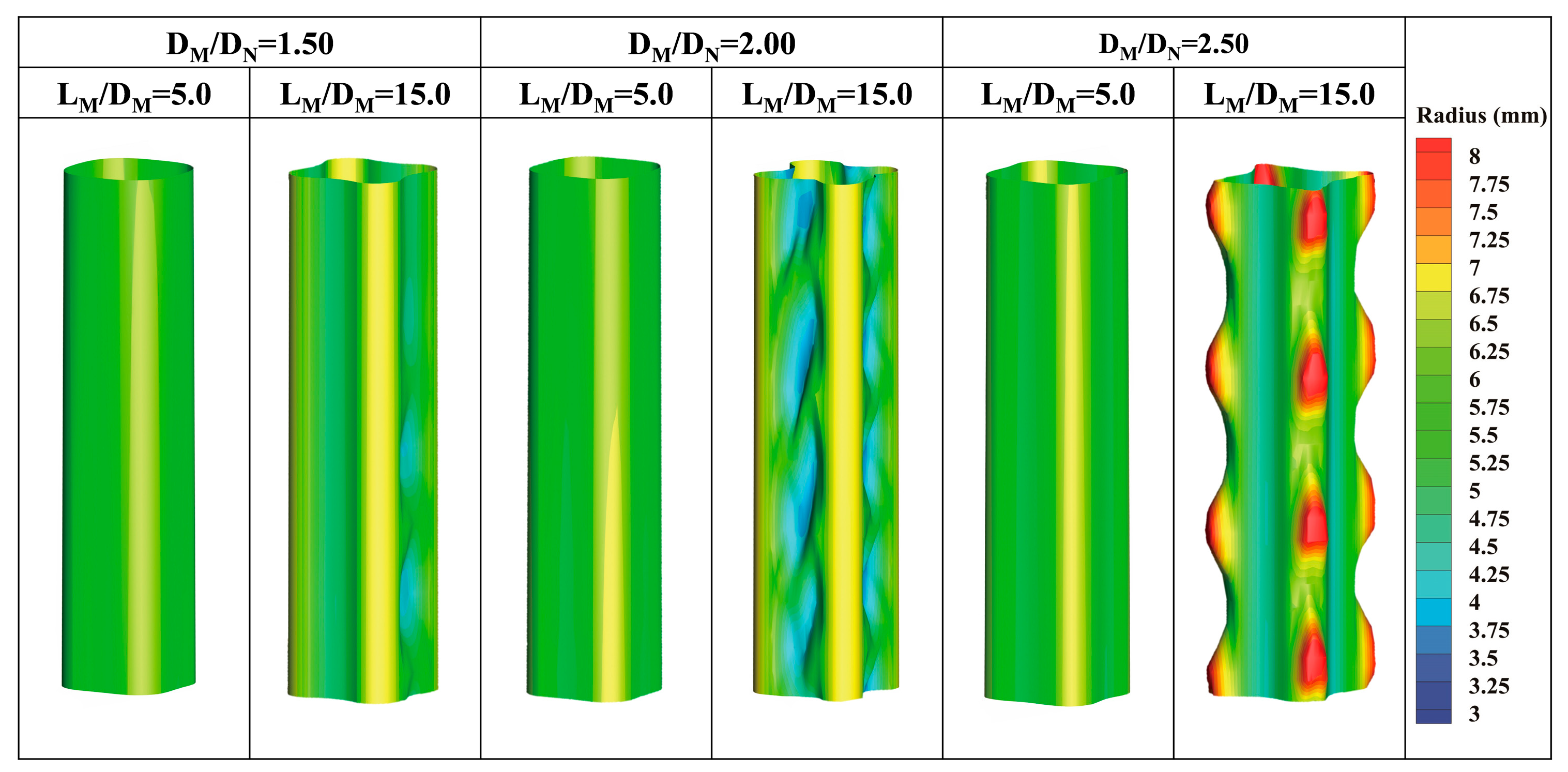
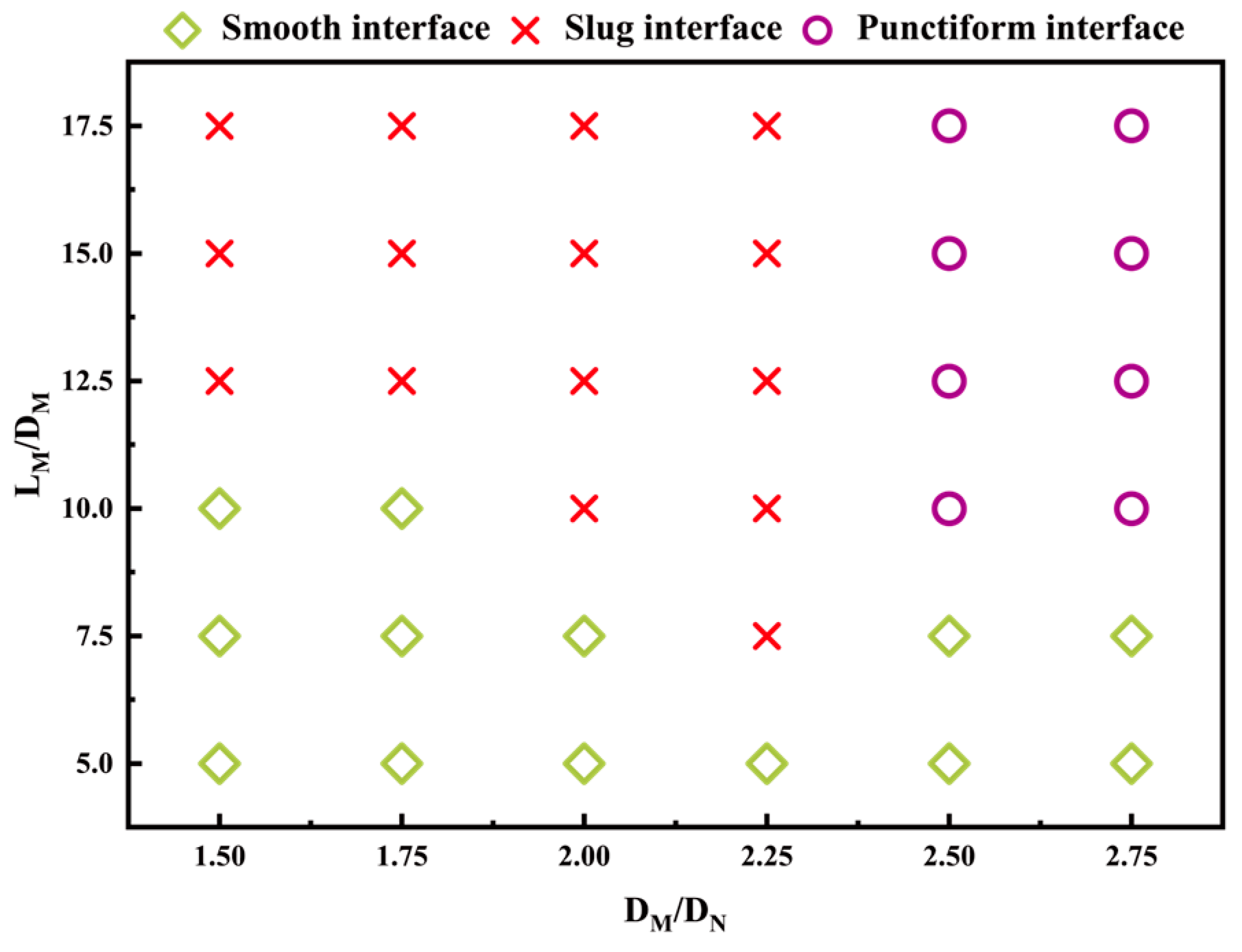
3.1. Gas–Liquid Interface Characteristics in the Mixing Section
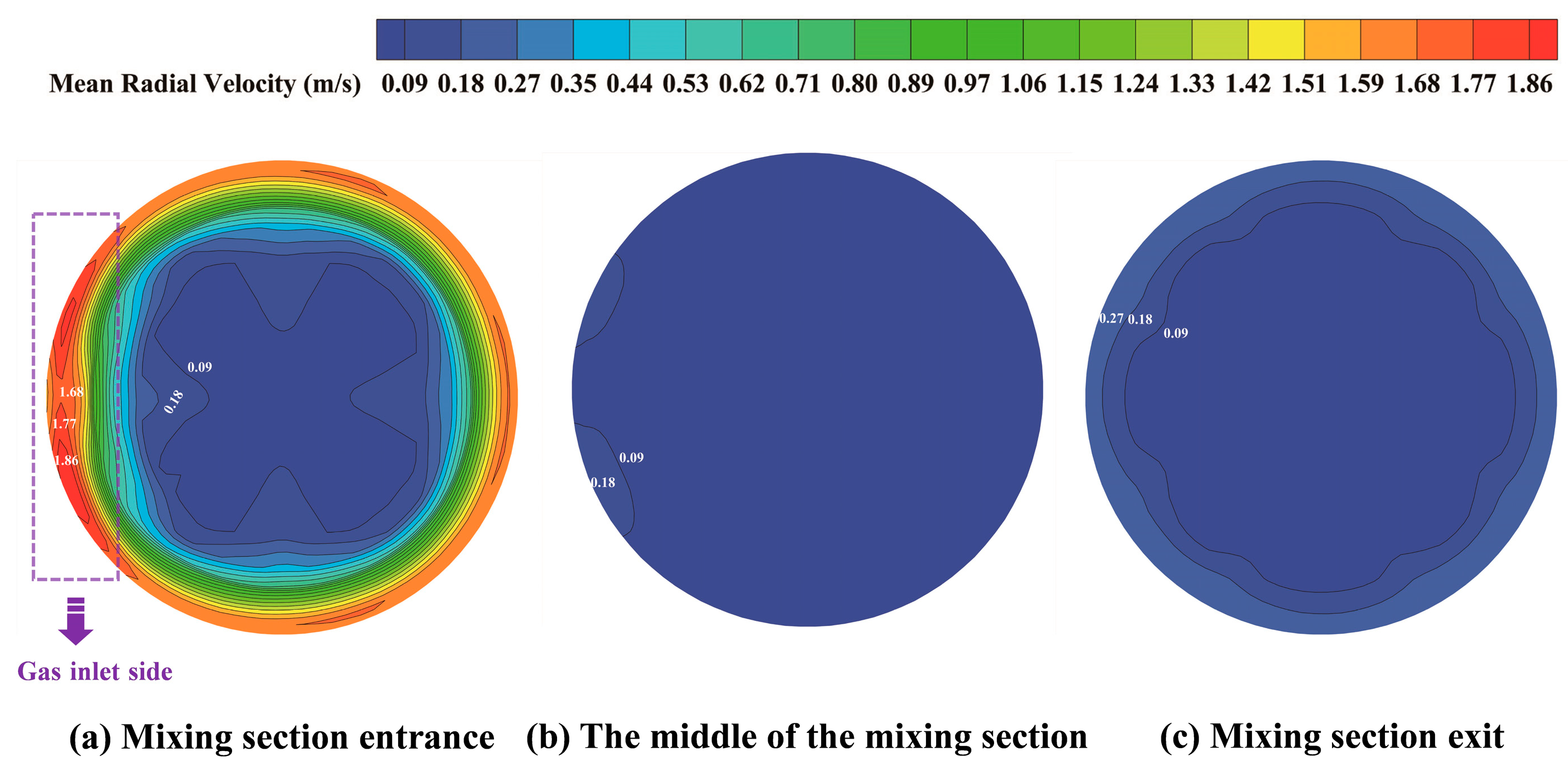
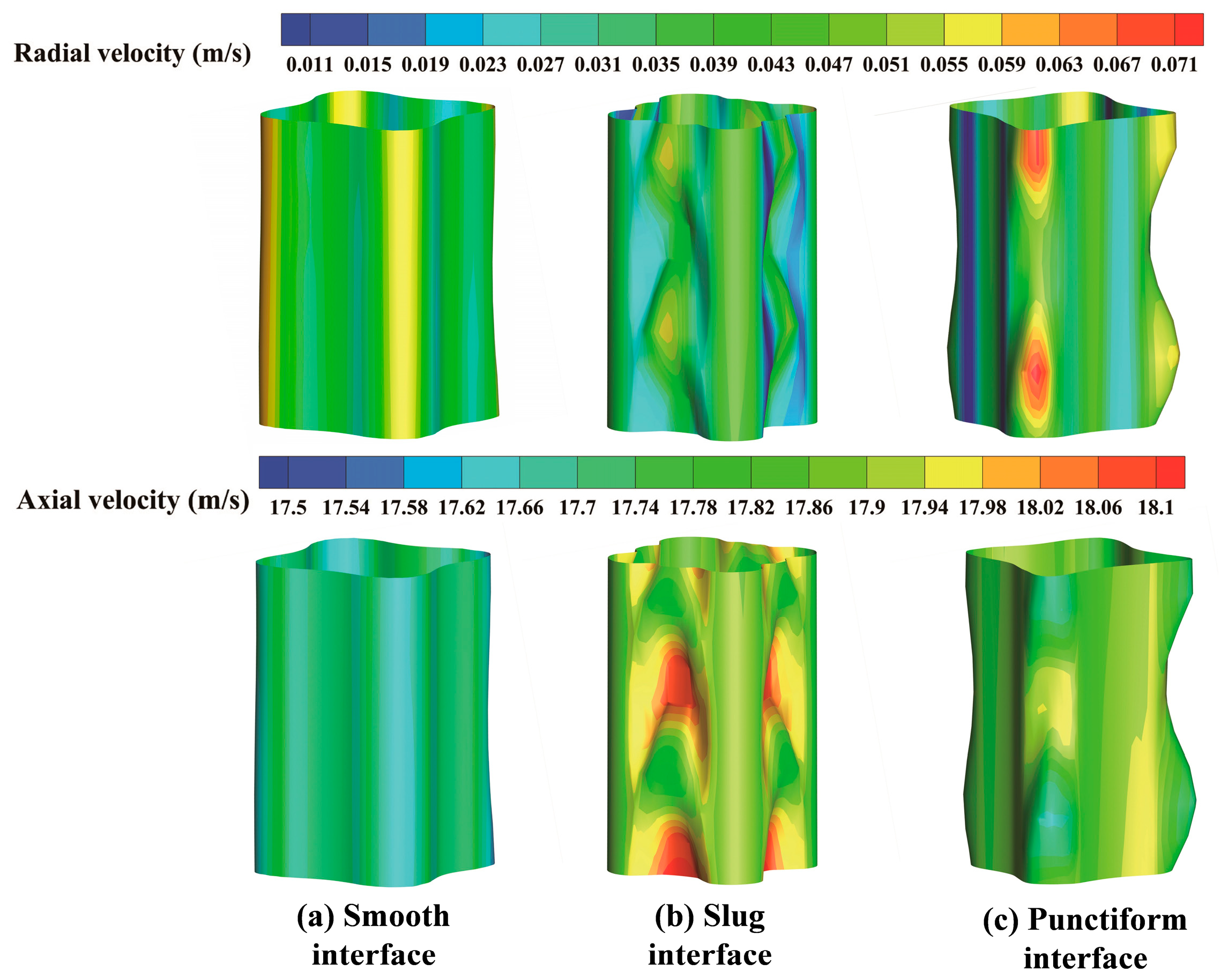
3.2. Effect of Mixing Section Structure on Gas–Liquid Interface
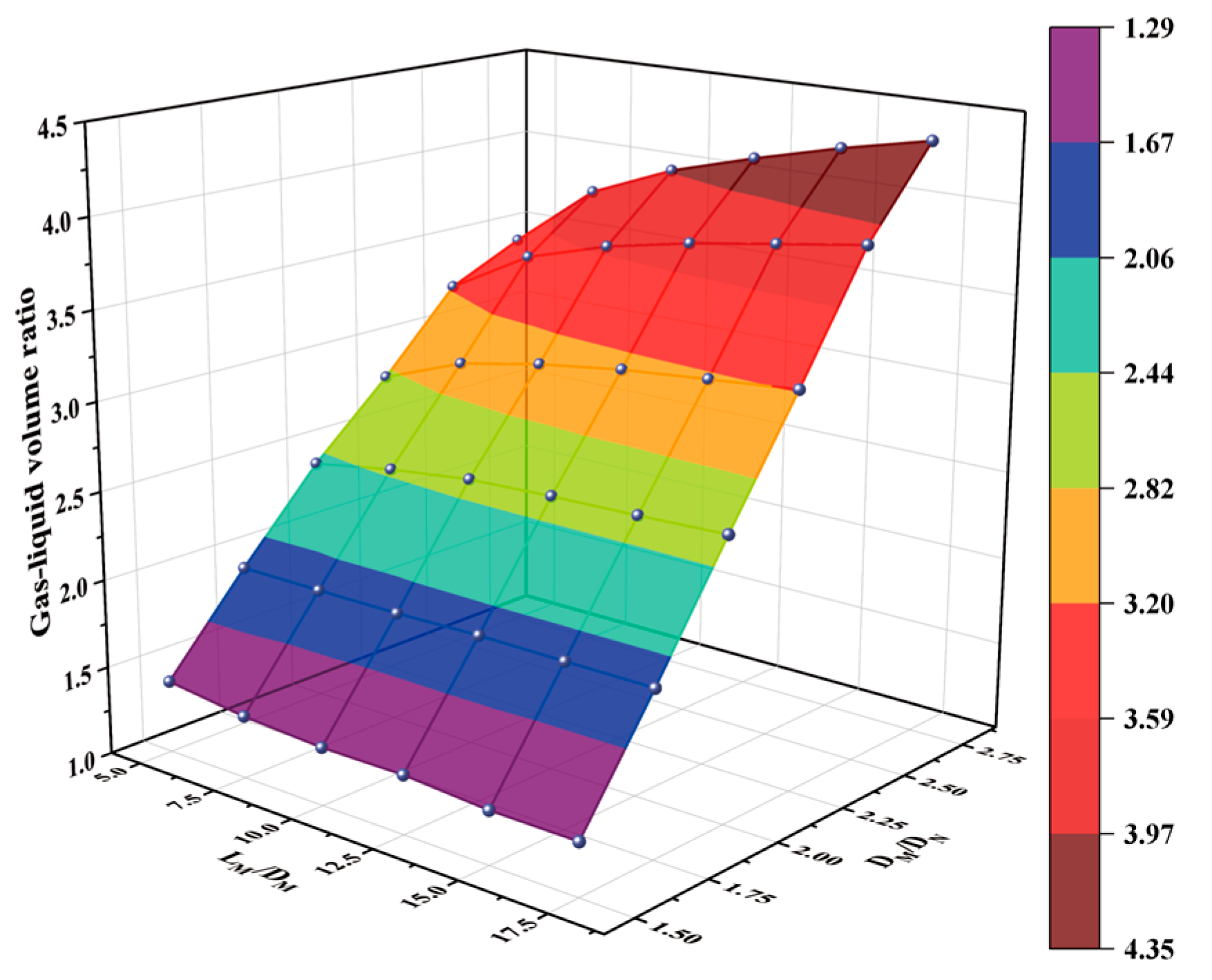
3.3. Effect of Gas–Liquid Interface on Gas–Liquid Volume Ratio
4. Conclusions
- 1.
- Along the jet flow direction, the gas–liquid interface gradually transitions from a smooth cylindrical shape to a lobed pattern. The smooth interface predominantly occurs at low DM/DN or LM/DM. The slug interface primarily appears when DM/DN ≤ 2.25 and LM/DM exceeds a certain critical value, while the punctiform interface only emerges when DM/DN ≥ 2.5 and LM/DM ≥ 10.
- 2.
- The presence of lobed and surface wave structures can reduce the radial flow near the gas–liquid interface, thereby decreasing gas-phase pressure losses. When the gas flow resistance is low (i.e., DM/DN = 2 and LM/DM ≤ 7.5 or DM/DN > 1.75), the lobed interface and surface waves cause the gas-phase axial velocity to increase with LM/DM, subsequently enhancing the gas–liquid volumetric ratio.
- 3.
- The lobed and surface wave structures can increase the axial flow near the gas–liquid interface. However, as DM/DN increases from 2.25 to 2.5, the slug interface transitions to a punctiform interface. This transition significantly reduces the surface area of the interface, thereby decreasing the axial velocity at the interface. This phenomenon reduces the axial flow near the interface, leading to a slower rate of increase in the gas–liquid volumetric ratio as DM/DN increases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hagos, F.Y.; Aziz, A.R.A.; Zainal, E.Z.; Mofijur, M.; Ahmed, S.F. Recovery of gas waste from the petroleum industry: A review. Environ. Chem. Lett. 2022, 20, 263–281. [Google Scholar] [CrossRef]
- Hruška, M.; Variny, M.; Haydary, J.; Janošovský, J. Sulfur recovery from syngas in pulp mills with integrated black liquor gasification. Forests 2020, 11, 1173. [Google Scholar] [CrossRef]
- Kopac, T. Emerging applications of process intensification for enhanced separation and energy efficiency, environmentally friendly sustainable adsorptive separations: A review. Int. J. Energy Res. 2021, 45, 15839–15856. [Google Scholar] [CrossRef]
- Lima, V.N.; Rodrigues, C.S.D.; Borges, R.A.C.; Madeira, L.M. Gaseous and liquid effluents treatment in bubble column reactors by advanced oxidation processes: A review. Crit. Rev. Environ. Sci. Technol. 2018, 48, 949–996. [Google Scholar] [CrossRef]
- Warmeling, H.; Janz, D.; Peters, M.; Vorholt, A.J. Acceleration of lean aqueous hydroformylation in an innovative jet loop reactor concept. Chem. Eng. J. 2017, 330, 585–595. [Google Scholar] [CrossRef]
- Sharma, S.K.; Bhadauria, A.; Kumar, T.N.; Kumar, R. Purification of industrial effluent by gas hydrate-based (HyPurif) process. J. Clean. Prod. 2023, 420, 138424. [Google Scholar] [CrossRef]
- Ughetti, M.; Jussen, D.; Riedlberger, P. The ejector loop reactor: Application for microbial fermentation and comparison with a stirred-tank bioreactor. Eng. Life Sci. 2018, 18, 281–286. [Google Scholar] [CrossRef]
- Wu, Y.; Zu, Y.; Xu, E.; Miao, Z.; Wu, D.; Hu, Y. The effect of swirling shear blade on gas-liquid flow pattern and mass transfer performance in Venturi injector. Chem. Eng. Sci. 2024, 299, 120549. [Google Scholar] [CrossRef]
- Kim, S.-H.; Kim, S.-M.; Ko, T.; Kim, H.; Yoon, J.; Yoon, W.-S.; Lee, J. Effects of back pressure on flow regime and suction performance of gas–liquid swirl ejector. Int. J. Chem. React. Eng. 2019, 17, 20180264. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, Z.; Li, L.; Wang, J.; Liu, J.; Zhou, Y. Influence of driving fluid properties on the performance of liquid-driving ejector. Int. J. Heat Mass Transf. 2016, 101, 20–26. [Google Scholar] [CrossRef]
- Duan, Z.; Li, W.; Lin, L.; Qu, R.; Li, S.; Zhang, J. Investigation on gas induction of liquid–gas ejector in jet loop reactor. Int. J. Chem. React. Eng. 2021, 19, 1271–1285. [Google Scholar] [CrossRef]
- Xu, E.; Jiang, X.; Ding, L. Optimizing conical nozzle of venturi ejector in ejector loop reactor using computational fluid dynamics. Korean J. Chem. Eng. 2020, 37, 1829–1835. [Google Scholar] [CrossRef]
- Yadav, R.L.; Patwardhan, A.W. Design aspects of ejectors: Effects of suction chamber geometry. Chem. Eng. Sci. 2008, 63, 3886–3897. [Google Scholar] [CrossRef]
- Sharma, D.V.; Patwardhan, A.W.; Ranade, V.V. Estimation of gas induction in jet loop reactors: Influence of nozzle designs. Chem. Eng. Res. Des. 2017, 125, 24–34. [Google Scholar] [CrossRef]
- He, H.; Liu, X.; Pan, Q.; Lu, Q.; Ren, Q.; Pan, L. Experimental and theoretical study on formation of interfacial waves on liquid film of annular two-phase flow. Nucl. Eng. Des. 2022, 389, 111683. [Google Scholar] [CrossRef]
- Rivera, Y.; Berna, C.; Muñoz-Cobo, J.L.; Escrivá, A.; Córdova, Y. Experiments in free falling and downward cocurrent annular flows—Characterization of liquid films and interfacial waves. Nucl. Eng. Des. 2022, 392, 111769. [Google Scholar] [CrossRef]
- Cuadros, J.L.; Rivera, Y.; Berna, C.; Escrivá, A.; Muñoz-Cobo, J.L.; Monrós-Andreu, G.; Chiva, S. Characterization of the gas-liquid interfacial waves in vertical upward co-current annular flows. Nucl. Eng. Des. 2019, 346, 112–130. [Google Scholar] [CrossRef]
- Weber, C. Zum Zerfall eines Flüssigkeitsstrahles. Z. Angew. Math. Mech. 1931, 11, 136–154. [Google Scholar] [CrossRef]
- Rayleigh, L. On the instability of jets. Proc. Lond. Math. Soc. 1878, 1, 4–13. [Google Scholar] [CrossRef]
- De, L.; Sterza, R.; de Mendonca, M.T.; de Souza, L.F.; Brandi, A.C. Investigation of the stability of a planar Oldroyd-B jet. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 251. [Google Scholar] [CrossRef]
- Huerre, P.; Monkewitz, P.A. Absolute and convective instabilities in free shear layers. J. Fluid Mech. 1985, 159, 151. [Google Scholar] [CrossRef]
- Arratia, C.; Mowlavi, S.; Gallaire, F. Absolute/convective secondary instabilities and the role of confinement in free shear layers. Phys. Rev. Fluids 2018, 3, 053901. [Google Scholar] [CrossRef]
- Vadivukkarasan, M. Transition from absolute to convective instability in a compound jet. Eur. J. Mech. B/Fluids 2020, 84, 186–192. [Google Scholar] [CrossRef]
- Poole, R.; Turner, M.R. Stability of jets and wakes confined by compliant walls. Phys. Rev. Fluids 2023, 8, 063901. [Google Scholar] [CrossRef]
- Bhutada, S.R.; Pangarkar, V.G. Gas induction and hold-up characteristics of liquid jet loop reactors: Power law fluids. Chem. Eng. Sci. 1988, 43, 2904–2907. [Google Scholar] [CrossRef]
- Cramers, P.H.M.R.; Beenackers, A.A.C.M. Influence of the ejector configuration, scale and the gas density on the mass transfer characteristics of gas–liquid ejectors. Chem. Eng. J. 2001, 82, 131–141. [Google Scholar] [CrossRef]
- Dirix, C.A.M.C.; Van Der Wiele, K. Mass transfer in jet loop reactors. Chem. Eng. Sci. 1990, 45, 2333–2340. [Google Scholar] [CrossRef]
- Farokhipour, A.; Mansoori, Z.; Saffar-Avval, M.; Ahmadi, G. 3D computational modeling of sand erosion in gas-liquid-particle multiphase annular flows in bends. Wear 2020, 450–451, 203241. [Google Scholar] [CrossRef]
- Che, S.; Breitenmoser, D.; Infimovskiy, Y.Y.; Manera, A.; Petrov, V. CFD Simulation of Two-Phase Flows in Helical Coils. Front. Energy Res. 2020, 8, 65. [Google Scholar] [CrossRef]
- Srinivasan, V.; Salazar, A.J.; Saito, K. Modeling the disintegration of modulated liquid jets using volume-of-fluid (VOF) methodology. Appl. Math. Model. 2011, 35, 3710–3730. [Google Scholar] [CrossRef]
- Wu, W.; Hu, C.; Hu, J.; Yuan, S.; Zhang, R. Jet cooling characteristics for ball bearings using the VOF multiphase model. Int. J. Therm. Sci. 2017, 116, 150–158. [Google Scholar] [CrossRef]
- Sekar, M.; Raja, G.G.; Salmen, S.H.; Chinnathambi, A.; Gavurova, B.; Praveenkumar, T.R. Hydrodynamic cavitation phenomena and flow instabilities in wastewater treatment: A multiphase VOF study with a venturi cavitator. J. Taiwan Inst. Chem. Eng. 2024, 105355. [Google Scholar] [CrossRef]
- Turutoglu, C.; Cadirci, S.; Yilmaz, S.; Erdem, D. Calibration of the Reynolds stress model for turbulent round free jets based on jet half-width. Phys. Fluids 2024, 36, 115133. [Google Scholar] [CrossRef]
- Amamou, A.; Habli, S.; Saïd, N.M.; Bournot, P.; Le Palec, G. Numerical study of turbulent round jet in a uniform counterflow using a second order Reynolds Stress Model. J. Hydro-Environ. Res. 2015, 9, 482–495. [Google Scholar] [CrossRef]
- Schalin, A.; Nielsen, P.V. Impact of turbulence anisotropy near walls in room airflow. Indoor Air 2004, 14, 159–168. [Google Scholar] [CrossRef][Green Version]
- Katsis, C.; Akylas, T.R. Wind-generated surface waves on a viscous fluid. J. Appl. Mech. 1985, 52, 208–212. [Google Scholar] [CrossRef]
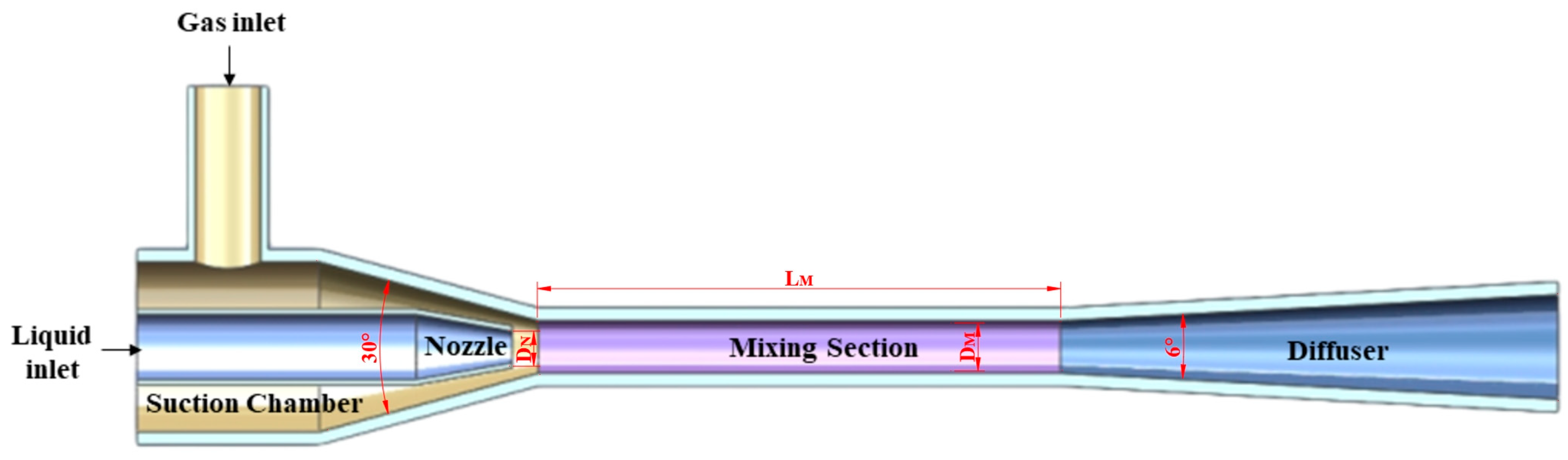

| Structure Parameter | Value |
|---|---|
| Liquid/gas inlet diameter | 25 mm |
| Nozzle outlet diameter (DN) | 12 mm |
| Nozzle contraction angle | 20° |
| Suction chamber inlet diameter | 65 mm |
| Suction chamber contraction angle | 30° |
| Throat nozzle distance | 10 mm |
| Mixing section diameter (DM) | 20 mm |
| Mixing section length (LM) | 200 mm |
| Diffuser contraction angle | 6° |
| Diffuser outlet diameter | 40 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zu, Y.; Zhong, W.; Xu, E.; Miao, Z. Computational Fluid Dynamics Analysis of Gas Suction in Coaxial Flow Venturi Injector: Impact of Gas–Liquid Interface Structure in Mixing Section. Appl. Sci. 2024, 14, 10839. https://doi.org/10.3390/app142310839
Zu Y, Zhong W, Xu E, Miao Z. Computational Fluid Dynamics Analysis of Gas Suction in Coaxial Flow Venturi Injector: Impact of Gas–Liquid Interface Structure in Mixing Section. Applied Sciences. 2024; 14(23):10839. https://doi.org/10.3390/app142310839
Chicago/Turabian StyleZu, Yihan, Wenchen Zhong, Enle Xu, and Zhenyong Miao. 2024. "Computational Fluid Dynamics Analysis of Gas Suction in Coaxial Flow Venturi Injector: Impact of Gas–Liquid Interface Structure in Mixing Section" Applied Sciences 14, no. 23: 10839. https://doi.org/10.3390/app142310839
APA StyleZu, Y., Zhong, W., Xu, E., & Miao, Z. (2024). Computational Fluid Dynamics Analysis of Gas Suction in Coaxial Flow Venturi Injector: Impact of Gas–Liquid Interface Structure in Mixing Section. Applied Sciences, 14(23), 10839. https://doi.org/10.3390/app142310839





