Vehicle Motion Control for Overactuated Vehicles to Enhance Controllability and Path Tracking
Abstract
Featured Application
Abstract
1. Introduction
- predictable (linear) reference vehicle behavior;
- overactuation to generate the predictable (linear) reference vehicle behavior, as well as to enlarge the stable region for maneuvering at the limits;
- linear and therefore fast MPC, instead of a more complex nonlinear variant, by taking advantage of the (linear) reference vehicle behavior;
- a modular approach that allows switching between different actuator configurations with the same control strategy/architecture;
- a modular approach that allows switching between automated and manual driving without changing the control strategy/architecture.
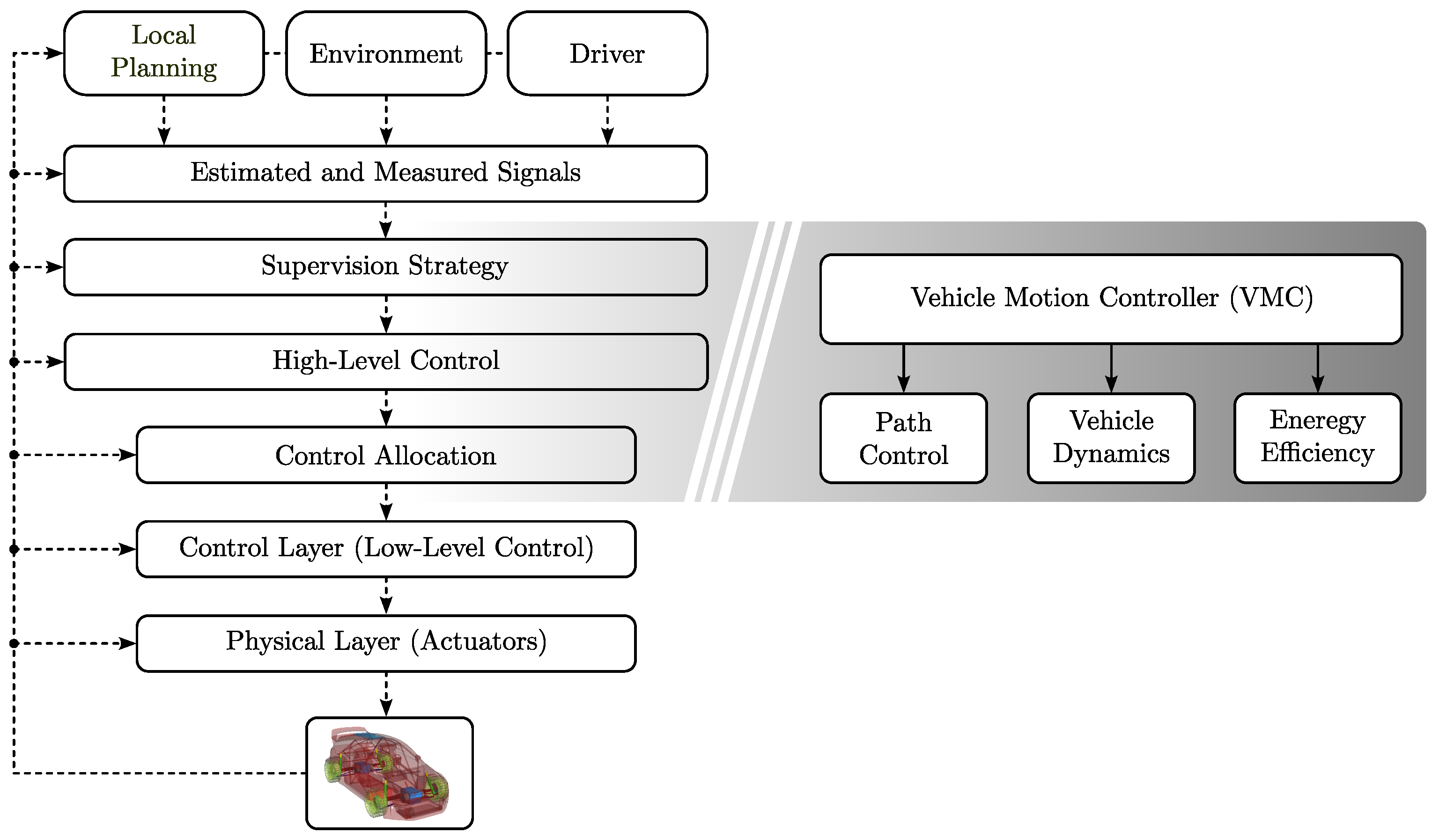
2. Control Architecture
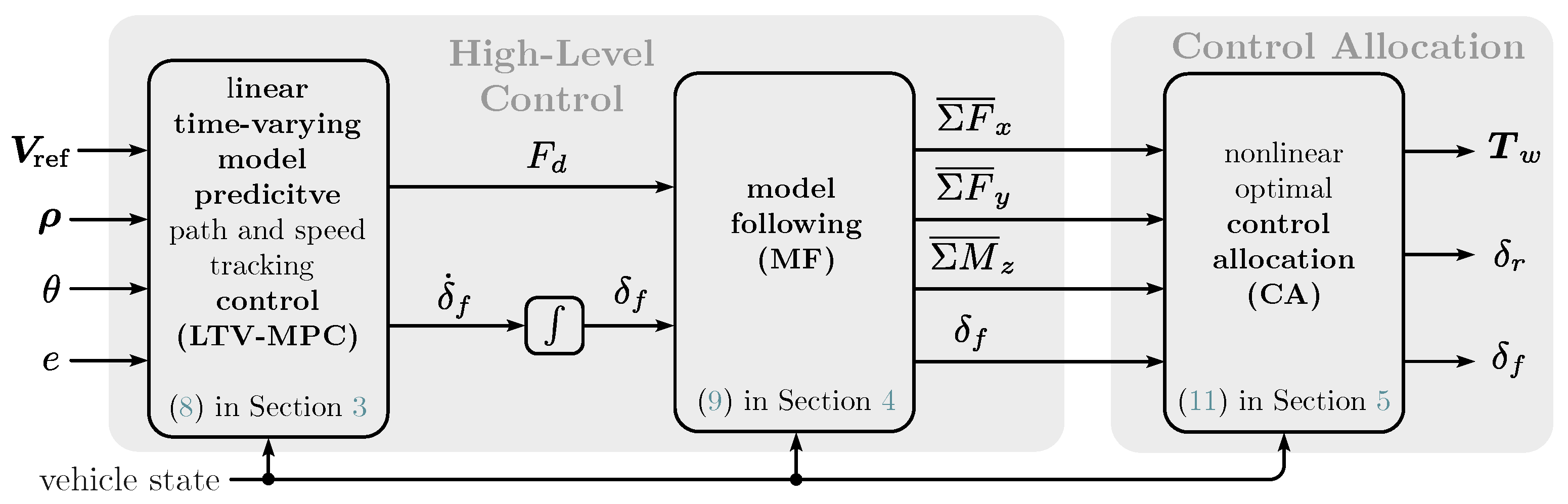
- to optimally allocate TV and rear-wheel steering (RWS) to track the (linear) reference vehicle behavior with respect to handling using MF and CA, and
- to utilize this reference vehicle behavior within the MPC framework to create a fast and robust path tracking controller.
3. Linear Time-Varying Model Predictive Path and Speed Tracking
3.1. Prediction Model
3.2. Linear Time-Varying Model Predictive Control (LTV-MPC)
4. Model Following
5. Nonlinear Optimal Control Allocation
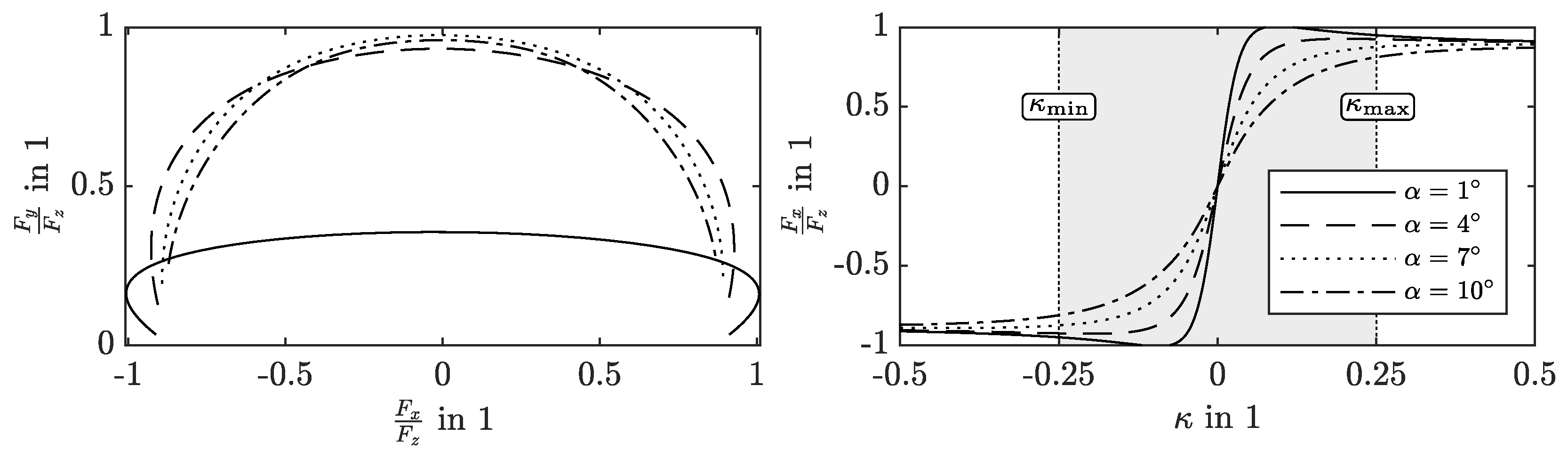
5.1. Tyre and Wheel Load Model
5.2. Nonlinear Optimal Control Allocation
6. Results and Discussion
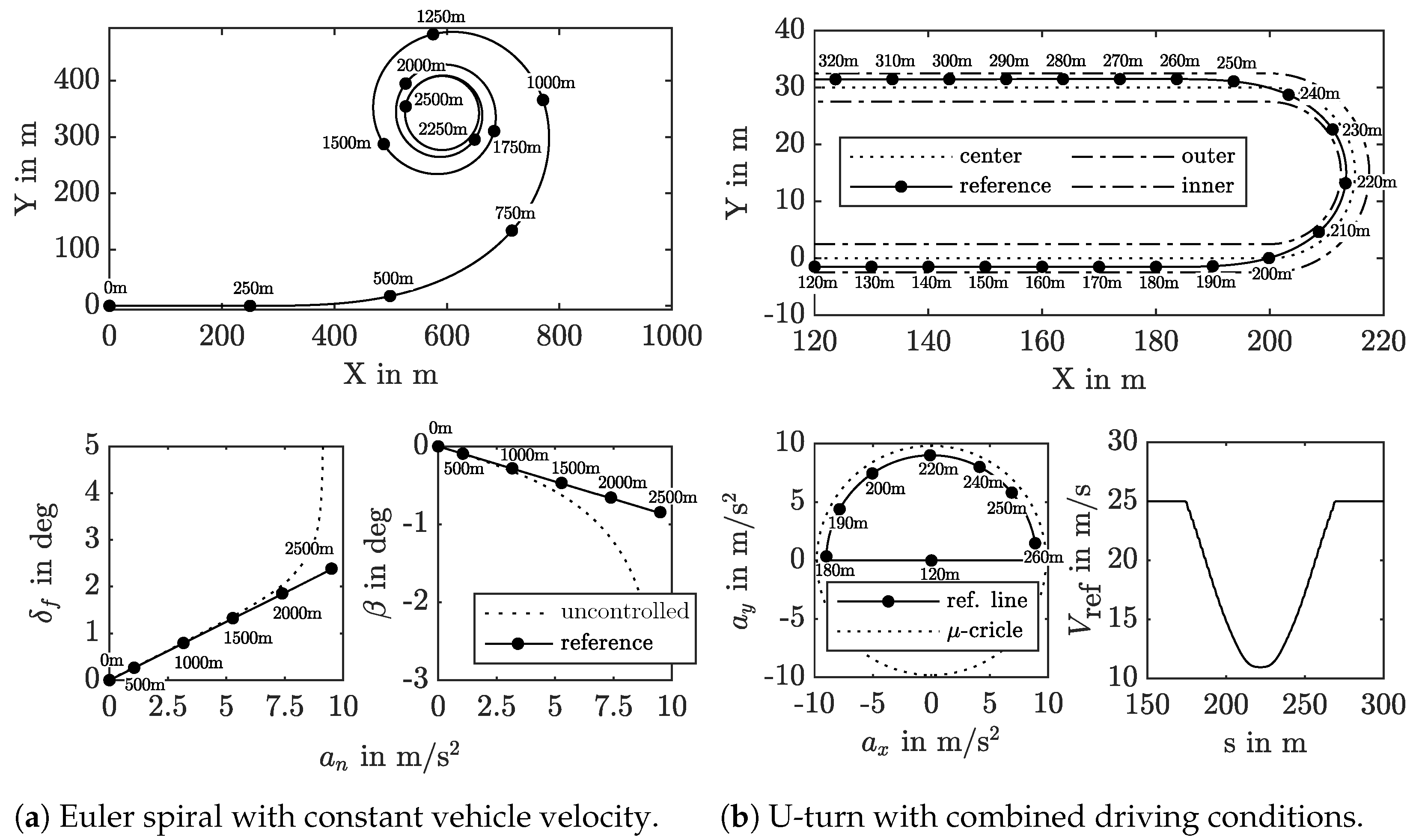
- Euler Spiral (ES). The main aims of this quasi-steady-state maneuver are to examine the effectiveness of MF in following the reference vehicle behavior and to study the respective enhancement of the MPC in path tracking at a constant . Figure 6a (top) illustrates the reference path of the ES. At the bottom, the handling behavior, and over normal acceleration of the uncontrolled vehicle and the respective reference vehicle behavior are displayed.
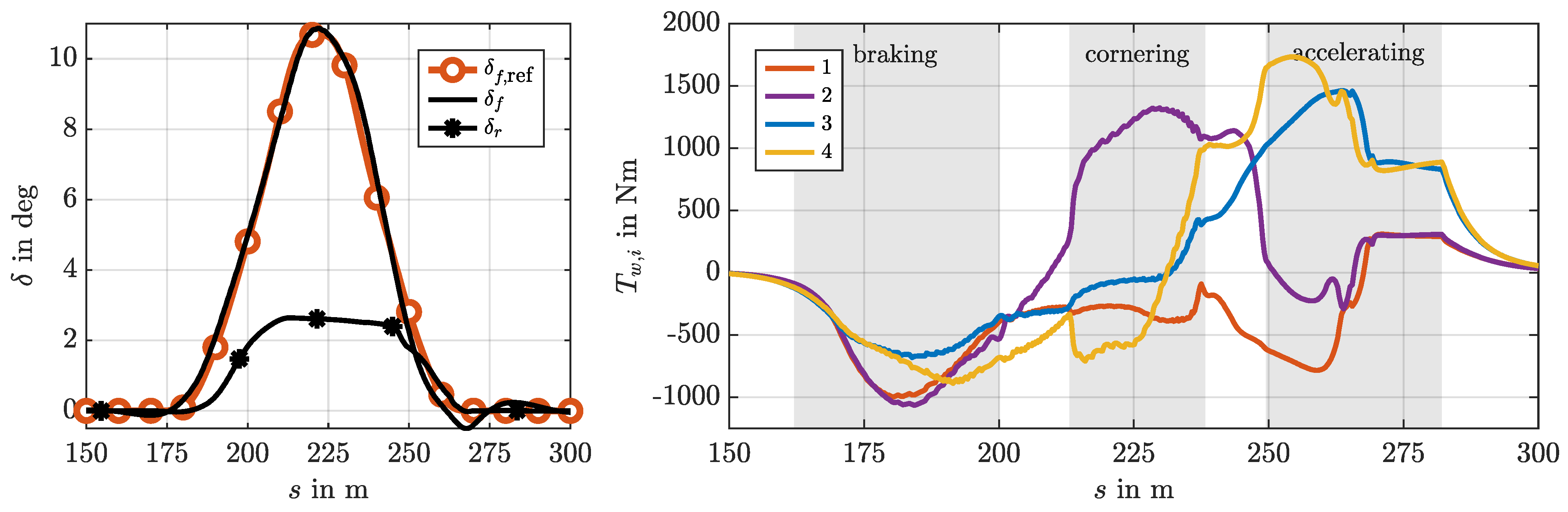
- U-Turn. The main aims of this transient maneuver are to investigate the MF and the MPC performance up to the limits of handling under pure longitudinal, pure lateral, and combined driving conditions. Figure 6b (top) shows the reference path with a left turn; at the bottom, the desired trajectory in the gg diagram and the respective velocity profile are depicted.
6.1. Euler Spiral Maneuver
6.2. U-Turn Maneuver
7. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Doerr, J.; Fröhlich, G.; Stroh, A.; Baur, M. Das elektrische Antriebssystem mit Drei-Motor-Layout im Audi E-tron S. MTZ - Mot. Z. 2020, 81, 18–27. [Google Scholar] [CrossRef]
- Sato, S.; Inoue, H.; Tabata, M.; Inagaki, S. Integrated Chassis Control System for Improved Vehicle Dynamics. In Proceedings of the AVEC’92 (1st International Symposium on Advanced Vehicle Control), Yokohama, Japan, 14–17 September 1992. [Google Scholar]
- Mazzilli, V.; De Pinto, S.; Pascali, L.; Contrino, M.; Bottiglione, F.; Mantriota, G.; Gruber, P.; Sorniotti, A. Integrated chassis control: Classification, analysis and future trends. Annu. Rev. Control 2021, 51, 172–205. [Google Scholar] [CrossRef]
- Vivas-López, C.A.; Hernández-Alcantara, D.; Tudón-Martínez, J.C.; Morales-Menendez, R. Review on Global Chassis Control. IFAC Proc. Vol. 2013, 46, 875–880. [Google Scholar] [CrossRef]
- AUDI AG. Zentraler Fahrdynamik-Rechner—Vision. 2020. Available online: https://www.audi-technology-portal.de/de/fahrwerk/fahrwerksregelsysteme/zentraler-fahrdynamikrechner-de (accessed on 12 November 2024).
- Robert Bosch GmbH. Vehicle Dynamics Control 2.0. 2022. Available online: https://www.bosch-mobility.com/en/solutions/driving-safety/vehicle-dynamics-control/ (accessed on 12 November 2024).
- De Novellis, L.; Sorniotti, A.; Gruber, P.; Shead, L.; Ivanov, V.; Hoepping, K. Torque Vectoring for Electric Vehicles with Individually Controlled Motors: State-of-the-Art and Future Developments. World Electr. Veh. J. 2012, 5, 617–628. [Google Scholar] [CrossRef]
- Meitinger, K.H. New Chassis Systems—Das Fahrwerk des AUDI R8 e-Tron (The Chassis of the AUDI R8 e-Tron). In Proceedings of the 7th International Munich Chassis Symposium, Munich, Germany, 14–15 June 2016; pp. 89–102. [Google Scholar] [CrossRef]
- De Novellis, L.; Sorniotti, A.; Gruber, P. Wheel Torque Distribution Criteria for Electric Vehicles With Torque-Vectoring Differentials. IEEE Trans. Veh. Technol. 2014, 63, 1593–1602. [Google Scholar] [CrossRef]
- Hoffmann, G.M.; Tomlin, C.J.; Montemerlo, M.; Thrun, S. Autonomous Automobile Trajectory Tracking for Off-Road Driving: Controller Design, Experimental Validation and Racing. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 11–13 July 2007; pp. 2296–2301. [Google Scholar] [CrossRef]
- Keviczky, T.; Falcone, P.; Borrelli, F.; Asgari, J.; Hrovat, D. Predictive control approach to autonomous vehicle steering. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; p. 6. [Google Scholar] [CrossRef]
- Beal, C.E.; Gerdes, J.C. Model Predictive Control for Vehicle Stabilization at the Limits of Handling. IEEE Trans. Control Syst. Technol. 2013, 21, 1258–1269. [Google Scholar] [CrossRef]
- Erlien, S.M.; Fujita, S.; Gerdes, J.C. Safe Driving Envelopes for Shared Control of Ground Vehicles. IFAC Proc. Vol. 2013, 46, 831–836. [Google Scholar] [CrossRef]
- Funke, J.; Brown, M.; Erlien, S.M.; Gerdes, J.C. Collision Avoidance and Stabilization for Autonomous Vehicles in Emergency Scenarios. IEEE Trans. Control Syst. Technol. 2017, 25, 1204–1216. [Google Scholar] [CrossRef]
- Bobier-Tiu, C.G.; Beal, C.E.; Kegelman, J.C.; Hindiyeh, R.Y.; Gerdes, J.C. Vehicle control synthesis using phase portraits of planar dynamics. Veh. Syst. Dyn. 2019, 57, 1318–1337. [Google Scholar] [CrossRef]
- Gao, Y.; Gray, A.; Tseng, H.E.; Borrelli, F. A tube-based robust nonlinear predictive control approach to semiautonomous ground vehicles. Veh. Syst. Dyn. 2014, 52, 802–823. [Google Scholar] [CrossRef]
- Mokhiamar, O.; Abe, M. How the four wheels should share forces in an optimum cooperative chassis control. Control Eng. Pract. 2006, 14, 295–304. [Google Scholar] [CrossRef]
- Metzler, M.; Tavernini, D.; Sorniotti, A.; Gruber, P. An explicit nonlinear MPC approach to vehicle stability control. In Proceedings of the AVEC ’18 14th International Symposium on Advanced Vehicle Control, Beijing, China, 16–20 July 2018; p. 6. [Google Scholar]
- Horiuchi, S. Evaluation of chassis control method through optimisation-based controllability region computation. Veh. Syst. Dyn. 2012, 50, 19–31. [Google Scholar] [CrossRef]
- Mokhiamar, O.; Abe, M. Simultaneous Optimal Distribution of Lateral and Longitudinal Tire Forces for the Model Following Control. J. Dyn. Syst. Meas. Control 2005, 126, 753–763. [Google Scholar] [CrossRef]
- Chatzikomis, C.; Sorniotti, A.; Gruber, P.; Bastin, M.; Shah, R.M.; Orlov, Y. Torque-Vectoring Control for an Autonomous and Driverless Electric Racing Vehicle with Multiple Motors. SAE Int. J. Veh. Dyn. Stability NVH 2017, 1, 338–351. [Google Scholar] [CrossRef]
- Falcone, P.; Tufo, M.; Borrelli, F.; Asgari, J.; Tseng, H.E. A linear time varying model predictive control approach to the integrated vehicle dynamics control problem in autonomous systems. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 2980–2985. [Google Scholar] [CrossRef]
- Gordon, T.; Howell, M.; Brandao, F. Integrated Control Methodologies for Road Vehicles. Veh. Syst. Dyn. 2003, 40, 157–190. [Google Scholar] [CrossRef]
- Johansen, T.A.; Fossen, T.I. Control allocation—A survey. Automatica 2013, 49, 1087–1103. [Google Scholar] [CrossRef]
- Pacejka, H.B. Tire and Vehicle Dynamics, 2nd ed.; Number 372 in SAE-R; SAE International: Warrendale, PA, USA, 2006. [Google Scholar]
- Sedlacek, T. Minimum-Time Optimal Control for Automotive Vehicles. Ph.D. Thesis, Technischen Universität München, München, Germany, 2021. [Google Scholar]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi: A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Ferreau, H.; Kirches, C.; Potschka, A.; Bock, H.; Diehl, M. qpOASES: A parametric active-set algorithm for quadratic programming. Math. Program. Comput. 2014, 6, 327–363. [Google Scholar] [CrossRef]
- Lugner, P. (Ed.) Vehicle Dynamics of Modern Passenger Cars; CISM International Centre for Mechanical Sciences; Springer International Publishing: Cham, Switzerland, 2019; Volume 582. [Google Scholar] [CrossRef]
- Van Zanten, A.T.; Erhardt, R.; Pfaff, G.; Kost, F.; Hartmann, U.; Ehret, T. Control aspects of the bosch-VDC. In Proceedings of the AVEC’96 (2nd International Symposium on Advanced Vehicle Control), Aachen University of Technology, Aachen, Germany, 24–28 June 1996. [Google Scholar]


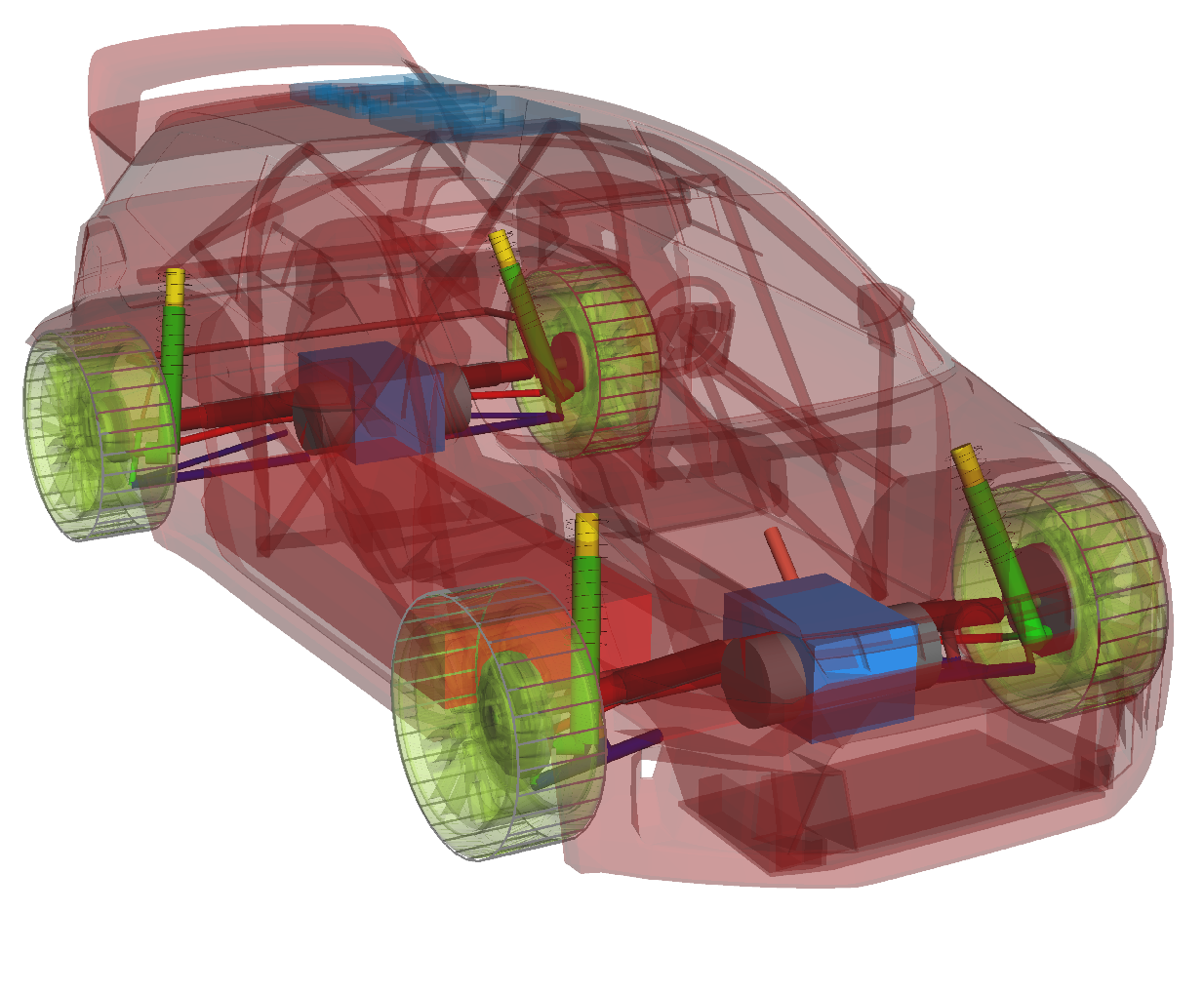
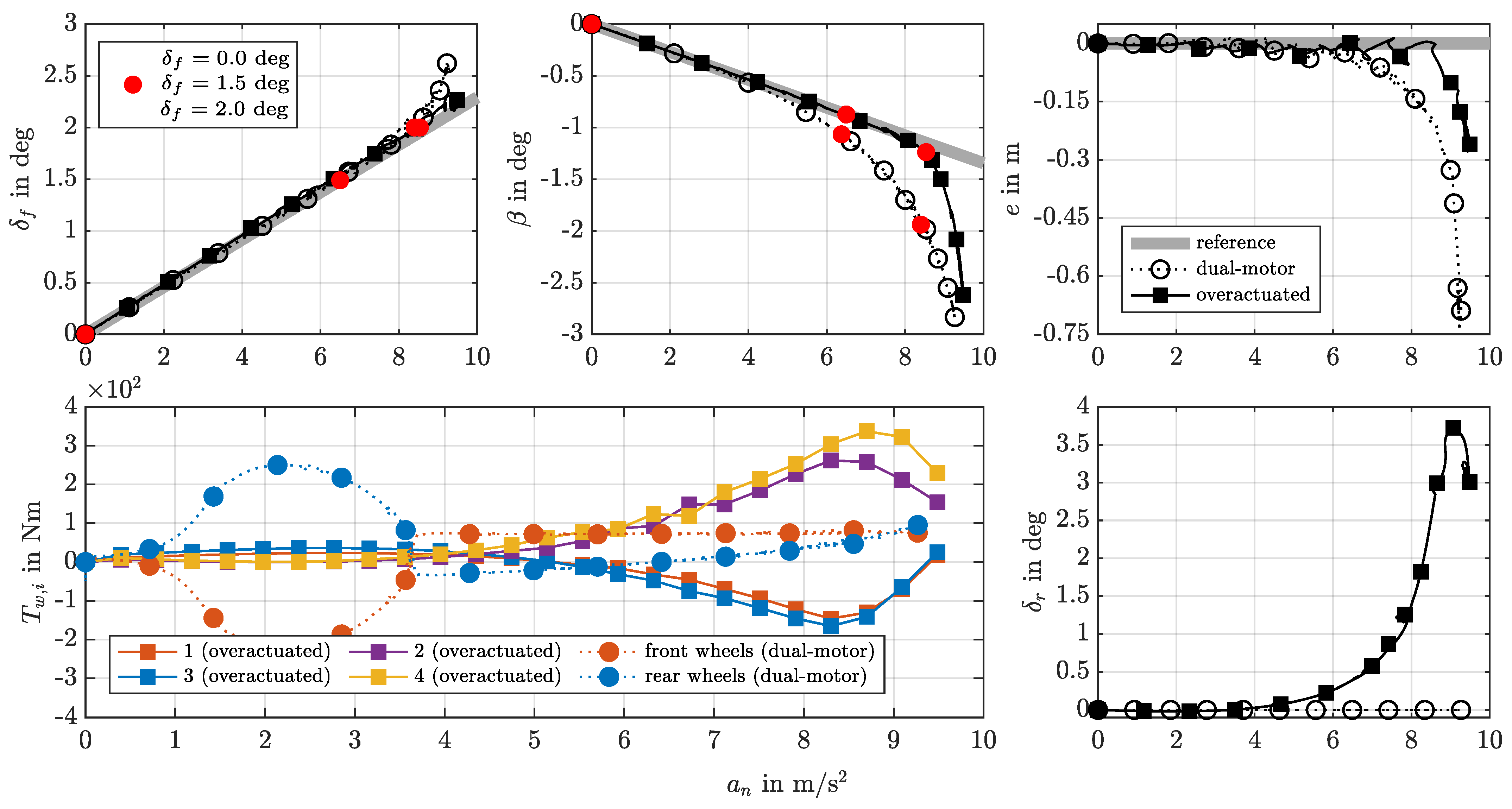
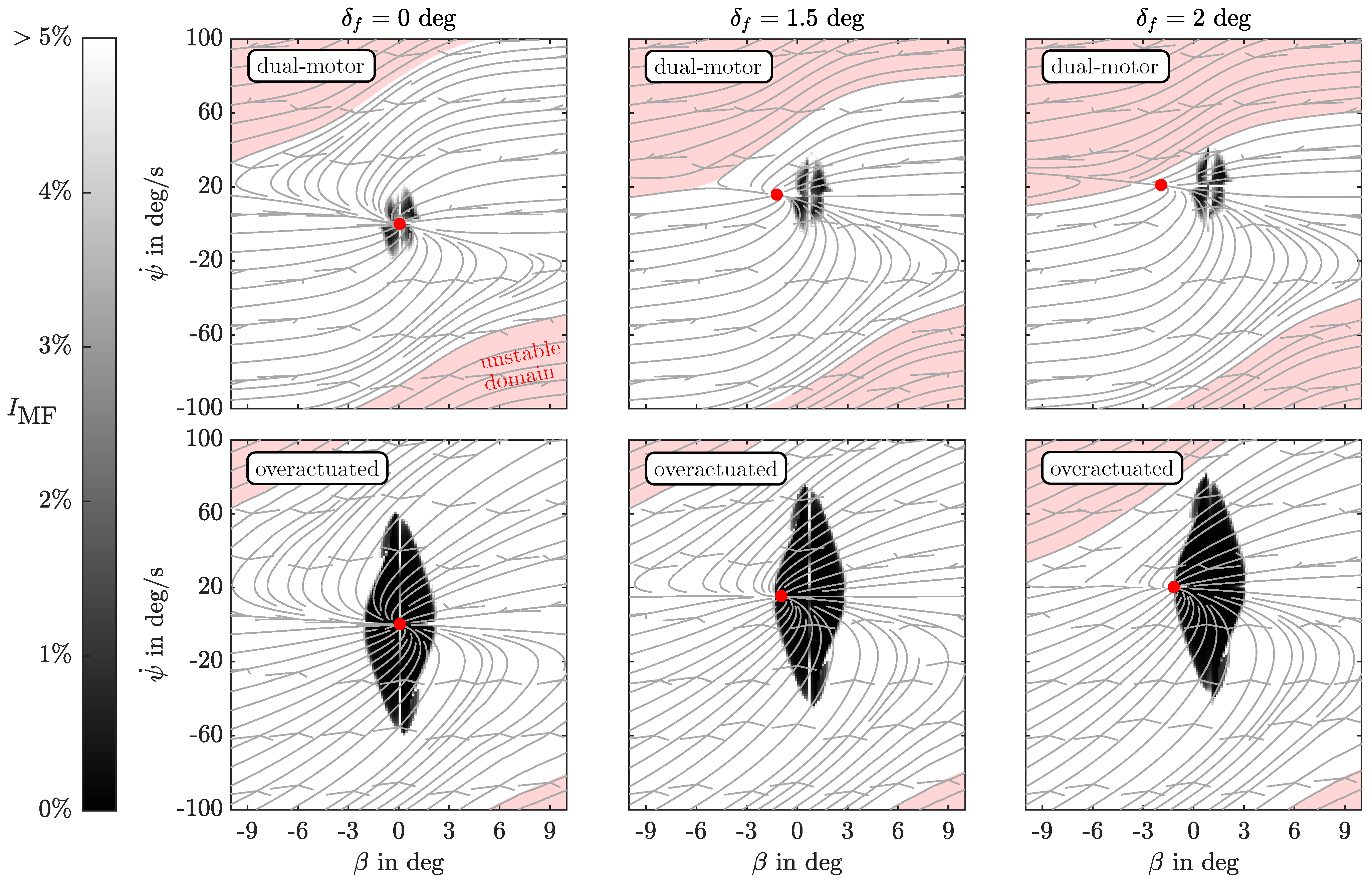
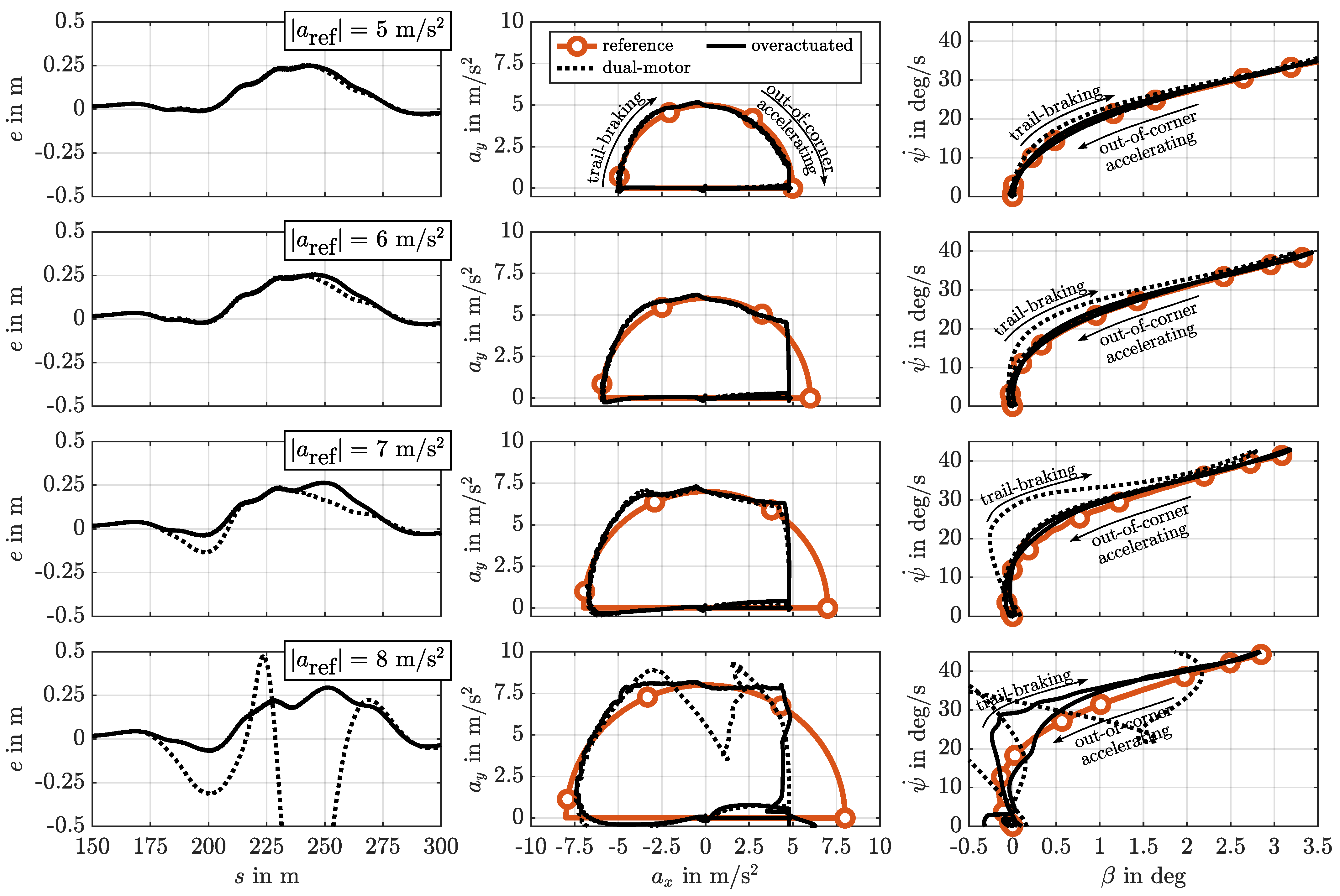
| Name | Value | Unit | |
|---|---|---|---|
| Dual-Motor | Overactuated | ||
| N | 50 | - | |
| 1 | |||
| 0.02 | |||
| [13] | 120 | ||
| [13] | 20 | deg | |
| [13] | 0.175 | ||
| 30 | deg | ||
| 30 | |||
| - | |||
| Name | Value | Unit |
|---|---|---|
| 0.01 | ||
| 0.25 | - | |
| 0.25 | ||
| 10 | deg | |
| 10 | ||
| - | ||
| 0.829 | ||
| 0.826 | ||
| h | 0.507 | |
| h | ||
| 1.08h | ||
| 0.361 |
| Name | Value | Unit |
|---|---|---|
| m | 1310 | |
| 2006 | ||
| 1.387 | ||
| 1.107 | ||
| 140.86 | ||
| 176.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mandl, P.; Edelmann, J.; Plöchl, M. Vehicle Motion Control for Overactuated Vehicles to Enhance Controllability and Path Tracking. Appl. Sci. 2024, 14, 10718. https://doi.org/10.3390/app142210718
Mandl P, Edelmann J, Plöchl M. Vehicle Motion Control for Overactuated Vehicles to Enhance Controllability and Path Tracking. Applied Sciences. 2024; 14(22):10718. https://doi.org/10.3390/app142210718
Chicago/Turabian StyleMandl, Philipp, Johannes Edelmann, and Manfred Plöchl. 2024. "Vehicle Motion Control for Overactuated Vehicles to Enhance Controllability and Path Tracking" Applied Sciences 14, no. 22: 10718. https://doi.org/10.3390/app142210718
APA StyleMandl, P., Edelmann, J., & Plöchl, M. (2024). Vehicle Motion Control for Overactuated Vehicles to Enhance Controllability and Path Tracking. Applied Sciences, 14(22), 10718. https://doi.org/10.3390/app142210718








