Cervical Cancer Prediction Based on Imbalanced Data Using Machine Learning Algorithms with a Variety of Sampling Methods
Abstract
1. Introduction
2. Bibliographic Study
2.1. Classification Algorithms
2.1.1. K-Nearest Neighbors Algorithm
2.1.2. Logistic Regression Algorithm
2.1.3. Random Forest Algorithm
2.2. Sampling Methods
2.2.1. Undersampling Methods
2.2.2. Oversampling Methods
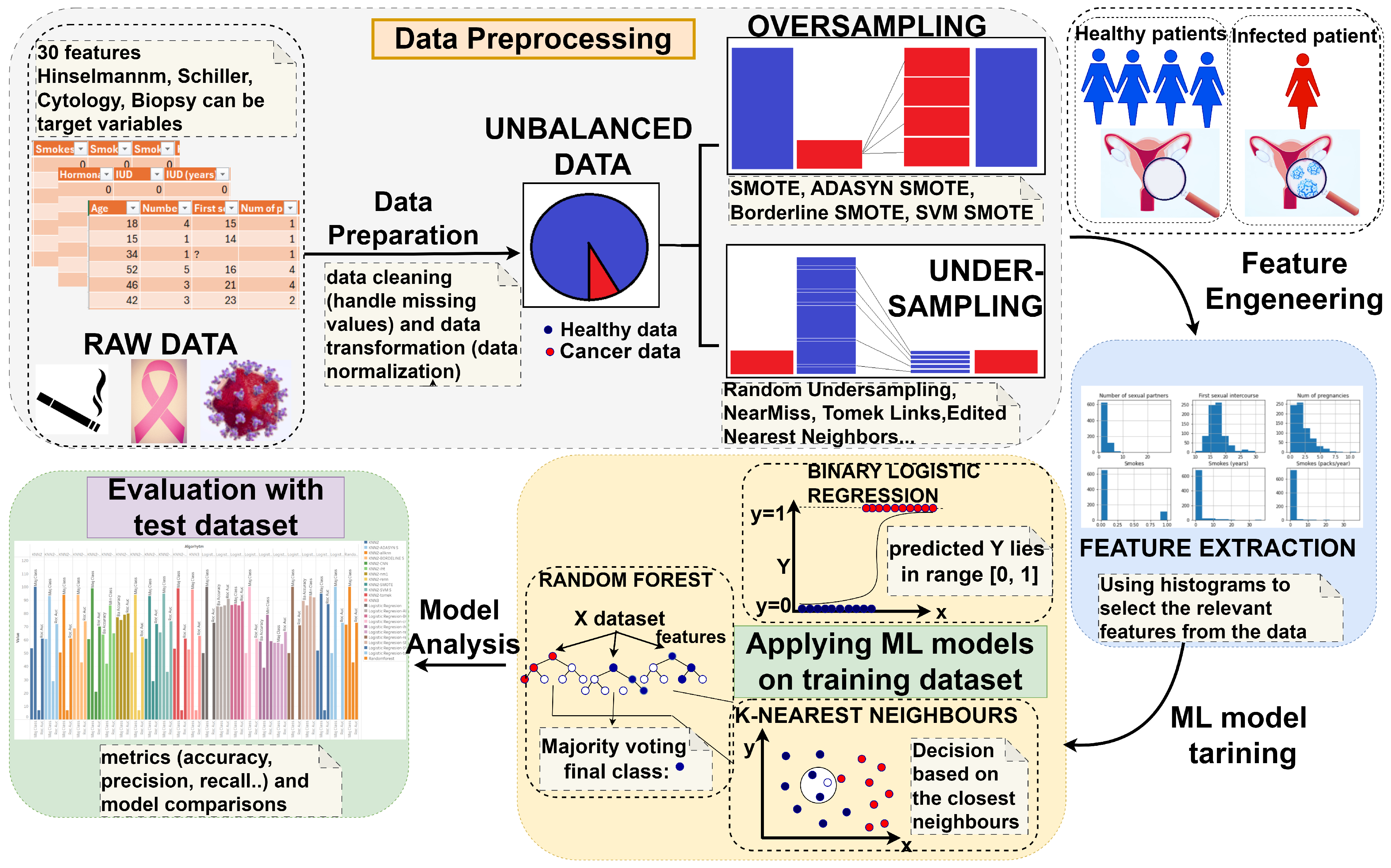
3. Materials and Methods
3.1. Conceptual Description
3.2. Dataset Description
3.3. Data Preprocessing
3.4. Model Training and Evaluation
4. Results
5. Discussions
5.1. Benefits of Prediction in Health Care
5.2. Advances in the Scientific Literature
5.3. Results of This Research
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADASYN | Adaptive Synthetic Sampling Approach for Imbalanced Learning |
| All-KNN | All K-Nearest Neighbors |
| AUC | Area Under the Curve |
| bLR | Binary Logistic Regression |
| CI | Confidence Interval |
| CNN | Condensed Nearest Neighbor |
| EB | Entropy-Based |
| ENN | Edited Nearest Neighbors |
| IB2 | Instance-Based Learning 2 |
| ICA | Independent Component Analysis |
| IHT | Instance Hardness Threshold |
| IR | Imbalance Ratio |
| KNN | K-Nearest Neighbors |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| LDA | Linear Discriminant Analysis |
| LR | Logistic Regression |
| ML | Machine Learning |
| NCR | Neighborhood Cleaning Rule |
| NNs | Neural Networks |
| NM | NearMiss |
| RF | Random Forest |
| RENN | Repeated Edited Nearest Neighbors |
| ROC | Receiver Operating Characteristic |
| SMOTE | Synthetic Minority Oversampling Technique |
| SVM | Support Vector Machine |
| TL | Tomek Links |
| ENN | Edited Nearest Neighbors |
Appendix A
Appendix A.1. Pseudocode of K-Nearest Neighbors Algorithm
| Algorithm A1 K-Nearest Neighbors Algorithm [50] |
|
Appendix A.2. Pseudocode of Logistic Regression Algorithm
| Algorithm A2 Logistic Regression Algorithm [50] |
|
Appendix A.3. Pseudocode of Random Forest Algorithm
| Algorithm A3 Random Forest Algorithm [50] |
|
Appendix B
Model Evaluation Metrics
| Actual | Prediction | |
|---|---|---|
| Positive | Negative | |
| Positive | TP | FN |
| Negative | FP | TN |
Appendix C
Appendix C.1. Dataset Description
| Attribute | Negative | Positive | Missing | Attribute | Negative | Positive | Missing |
|---|---|---|---|---|---|---|---|
| Smokes | 722 | 123 | 13 | STDs: HIV | 735 | 18 | 105 |
| Hormonal contraceptives | 269 | 481 | 108 | STDs: Hepatitis B | 752 | 1 | 105 |
| IUD | 658 | 83 | 117 | STDs: HPV | 751 | 2 | 105 |
| STDs | 674 | 79 | 105 | Dx:Cancer | 840 | 18 | 0 |
| STDs: condylomatosis | 709 | 44 | 105 | Dx:CIN | 849 | 9 | 0 |
| STDs: cervical condylomatosis | 753 | 0 | 105 | Dx:HPV | 840 | 18 | 0 |
| STDs: vaginal condylomatosis | 749 | 4 | 105 | Dx | 834 | 24 | 0 |
| STDs: vulvo-perineal condylomatosis | 710 | 43 | 105 | Hinselmann | 823 | 35 | 0 |
| STDs: syphilis | 735 | 18 | 105 | Schiller | 784 | 74 | 0 |
| STDs: pelvic inflammatory disease | 752 | 1 | 105 | Citology | 814 | 44 | 0 |
| STDs: genital herpes | 752 | 1 | 105 | Biopsy | 803 | 55 | 0 |
| STDs: molluscum contagiosum | 752 | 1 | 105 | STDs: AIDS | 753 | 0 | 105 |
Appendix C.2. Performance Results of KNN3 After Oversampling Techniques
| Metric/Sampling | SMOTE | SVM SMOTE | Borderline SMOTE | ADASYN |
|---|---|---|---|---|
| Accuracy | 86.24 | 89.94 | 88.35 | 87.30 |
| Ba Accuracy | 72.85 | 74.85 | 74.00 | 73.42 |
| Precision (Mac;Wght) | 62.42;91.25 | 67.26;92.10 | 64.48;91.69 | 63.54;91.46 |
| Recall (Mac;Wght) | 72.85;86.24 | 74.85;89.94 | 74.00;88.35 | 73.42;87.30 |
| MajClass | 88.57 | 92.57 | 90.86 | 89.71 |
| MinClass | 57.14 | 57.14 | 57.14 | 51.47 |
| F1 Score (Mac;Wght) | 65.17;88.24 | 70.08;90.84 | 67.81;89.72 | 66.44;88.98 |
| ROC_AUC | 0.71 | 0.73 | 0.73 | 0.72 |
Appendix C.3. Performance Results of bLR After Undersampling Techniques
| Metric/Sampling | CNN | TL | All-KNN | RENN | ENN | NCR | NM1 | IHT |
|---|---|---|---|---|---|---|---|---|
| Accuracy | 92.59 | 92.59 | 92.59 | 92.59 | 92.59 | 92.59 | 58.20 | 41.79 |
| Ba Accuracy | 50.00 | 50.00 | 50.00 | 50.00 | 50.00 | 50.00 | 57.71 | 58.71 |
| Precision (Mac;Wght) | 46.29;85.73 | 46.29;85.73 | 46.29;85.73 | 46.29;85.73 | 46.29;85.73 | 46.29;85.73 | 52.16;88.18 | 52.54;89.37 |
| Recall (Mac;Wght) | 50.00;92.59 | 50.00;92.59 | 50.00;92.59 | 50.00;92.59 | 50.00;92.59 | 50.00;92.59 | 57.71;58.20 | 58.71;41.79 |
| MajClass | 100 | 100 | 100 | 100 | 100 | 100 | 58.29 | 38.86 |
| MinClass | 0 | 0 | 0 | 0 | 0 | 0 | 57.14 | 78.57 |
| F1 Score (Mac;Wght) | 48.07;89.03 | 48.07;89.03 | 48.07;89.03 | 48.07;89.03 | 48.07;89.03 | 48.07;89.03 | 44.46;67.99 | 35.97;67.99 |
| ROC_AUC | 0.61 | 0.73 | 0.71 | 0.71 | 0.72 | 0.72 | 0.66 | 0.59 |
References
- Newaz, A.; Muhtadi, S.; Haq, F.S. An intelligent decision support system for the accurate diagnosis of cervical cancer. Knowl. Based Syst. 2022, 245, 108634. [Google Scholar] [CrossRef]
- Bowden, S.J.; Doulgeraki, T.; Bouras, E.; Markozannes, G.; Athanasiou, A.; Grout-Smith, H.; Kechagias, K.S.; Ellis, L.B.; Zuber, V.; Chadeau-Hyam, M.; et al. Risk factors for human papillomavirus infection, cervical intraepithelial neoplasia and cervical cancer: An umbrella review and follow-up Mendelian randomisation studies. BMC Med. 2023, 21, 274. [Google Scholar] [CrossRef] [PubMed]
- Machado, D.; Santos Costa, V.; Brandão, P. Using Balancing Methods to Improve Glycaemia-Based Data Mining. In Proceedings of the 16th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2023)—Volume 5: HEALTHINF; SciTePress: Setúbal, Portugal, 2023; pp. 188–198. [Google Scholar] [CrossRef]
- Alfakeeh, A.S.; Javed, M.A. Efficient Resource Allocation in Blockchain-Assisted Health Care Systems. Appl. Sci. 2023, 13, 9625. [Google Scholar] [CrossRef]
- Jo, W.; Kim, D. OBGAN: Minority oversampling near borderline with generative adversarial networks. Expert Syst. Appl. 2022, 197, 116694. [Google Scholar] [CrossRef]
- Lopo, J.A.; Hartomo, K.D. Evaluating Sampling Techniques for Healthcare Insurance Fraud Detection in Imbalanced Dataset. J. Ilm. Tek. Elektro Komput. Dan Inform. (JITEKI) 2023, 9, 223–238. [Google Scholar]
- Wang, W.; Chakraborty, G.; Chakraborty, B. Predicting the Risk of Chronic Kidney Disease (CKD) Using Machine Learning Algorithm. Appl. Sci. 2021, 11, 202. [Google Scholar] [CrossRef]
- Papakostas, M.; Das, K.; Abouelenien, M.; Mihalcea, R.; Burzo, M. Distracted and Drowsy Driving Modeling Using Deep Physiological Representations and Multitask Learning. Appl. Sci. 2021, 11, 88. [Google Scholar] [CrossRef]
- Suhas, S.; Manjunatha, N.; Kumar, C.N.; Benegal, V.; Rao, G.N.; Varghese, M.; Gururaj, G. Firth’s penalized logistic regression: A superior approach for analysis of data from India’s National Mental Health Survey, 2016. Indian J. Psychiatry 2023, 65, 1208–1213. [Google Scholar] [CrossRef]
- Yang, C.; Fridgeirsson, E.A.; Kors, J.A.; Reps, J.M.; Rijnbeek, P.R. Impact of random oversampling and random undersampling on the performance of prediction models developed using observational health data. J. Big Data 2024, 11, 7. [Google Scholar] [CrossRef]
- Awe, O.O.; Ojumu, J.B.; Ayanwoye, G.A.; Ojumoola, J.S.; Dias, R. Machine Learning Approaches for Handling Imbalances in Health Data Classification. In Sustainable Statistical and Data Science Methods and Practices; Awe, O.O., Vance, E.A., Eds.; Springer: Cham, Switzerland, 2023; pp. 19–33. [Google Scholar]
- Sajana, T.; Rao, K.V.S.N. Machine Learning Algorithms for Health Care Data Analytics Handling Imbalanced Datasets. In Handbook of Artificial Intelligence; Bentham Science Publishers: Potomac, MD, USA, 2023; p. 75. [Google Scholar]
- Wang, L.; Han, M.; Li, X.; Zhang, N.; Cheng, H. Review of Classification Methods on Unbalanced Data Sets. IEEE Access 2021, 9, 64606–64628. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, R.; Lei, Y.; Liao, W.-H.; Cao, H.; Cao, J. Severity level diagnosis of Parkinson’s disease by ensemble K-nearest neighbor under imbalanced data. Expert Syst. Appl. 2022, 189, 116113. [Google Scholar] [CrossRef]
- Vommi, A.M.; Battula, T.K. A hybrid filter-wrapper feature selection using Fuzzy KNN based on Bonferroni mean for medical datasets classification: A COVID-19 case study. Expert Syst. Appl. 2023, 218, 119612. [Google Scholar] [CrossRef]
- Iantovics, L.B.; Enăchescu, C. Method for Data Quality Assessment of Synthetic Industrial Data. Sensors 2022, 22, 1608. [Google Scholar] [CrossRef] [PubMed]
- Lynam, A.L.; Dennis, J.M.; Owen, K.R.; Oram, R.A.; Jones, A.G.; Shields, B.M.; Ferrat, L.A. Logistic regression has similar performance to optimised machine learning algorithms in a clinical setting: Application to the discrimination between type 1 and type 2 diabetes in young adults. Diagn. Progn. Res. 2020, 4, 6. [Google Scholar] [CrossRef]
- Morgado, J.; Pereira, T.; Silva, F.; Freitas, C.; Negrão, E.; de Lima, B.F.; da Silva, M.C.; Madureira, A.J.; Ramos, I.; Hespanhol, V.; et al. Machine Learning and Feature Selection Methods for EGFR Mutation Status Prediction in Lung Cancer. Appl. Sci. 2021, 11, 3273. [Google Scholar] [CrossRef]
- Saharan, S.S.; Nagar, P.; Creasy, K.T.; Stock, E.O.; James, F.; Malloy, M.J.; Kane, J.P. Logistic Regression and Statistical Regularization Techniques for Risk Classification of Coronary Artery Disease Using Cytokines Transported by High Density Lipoproteins. In Proceedings of the 2023 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 13–15 December 2023; pp. 652–660. [Google Scholar] [CrossRef]
- Ayoub, S.; Mohammed Ali, A.G.; Narhimene, B. Enhanced Intrusion Detection System for Remote Healthcare. In Advances in Computing Systems and Applications; Senouci, M.R., Boulahia, S.Y., Benatia, M.A., Eds.; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2022; Volume 513, pp. 1–11. [Google Scholar] [CrossRef]
- Xin, L.K.; Rashid, N.b.A. Prediction of Depression among Women Using Random Oversampling and Random Forest. In Proceedings of the 2021 International Conference of Women in Data Science at Taif University (WiDSTaif), Taif, Saudi Arabia, 30–31 March 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Loef, B.; Wong, A.; Janssen, N.A.; Strak, M.; Hoekstra, J.; Picavet, H.S.; Boshuizen, H.H.; Verschuren, W.M.; Herber, G.C. Using random forest to identify longitudinal predictors of health in a 30-year cohort study. Sci. Rep. 2022, 12, 10372. [Google Scholar] [CrossRef]
- Filippakis, P.; Ougiaroglou, S.; Evangelidis, G. Prototype Selection for Multilabel Instance-Based Learning. Information 2023, 14, 572. [Google Scholar] [CrossRef]
- Khushi, M.; Shaukat, K.; Alam, T.M.; Hameed, I.A.; Uddin, S.; Luo, S.; Yang, X.; Reyes, M.C. A Comparative Performance Analysis of Data Resampling Methods on Imbalance Medical Data. IEEE Access 2021, 9, 109960–109975. [Google Scholar] [CrossRef]
- AlMahadin, G.; Lotfi, A.; Carthy, M.M.; Breedon, P. Enhanced Parkinson’s Disease Tremor Severity Classification by Combining Signal Processing with Resampling Techniques. SN Comput. Sci. 2022, 3, 63. [Google Scholar] [CrossRef]
- Bounab, R.; Zarour, K.; Guelib, B.; Khlifa, N. Enhancing Medicare Fraud Detection Through Machine Learning: Addressing Class Imbalance With SMOTE-ENN. IEEE Access 2024, 12, 54382–54396. [Google Scholar] [CrossRef]
- Bach, M.; Trofimiak, P.; Kostrzewa, D.; Werner, A. CLEANSE—Cluster-based Undersampling Method. Procedia Comput. Sci. 2023, 225, 4541–4550. [Google Scholar] [CrossRef]
- Tumuluru, P.; Daniel, R.; Mahesh, G.; Lakshmi, K.D.; Mahidhar, P.; Kumar, M.V. Class Imbalance of Bio-Medical Data by Using PCA-Near Miss for Classification. In Proceedings of the 2023 5th International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 3–5 August 2023; pp. 1832–1839. [Google Scholar] [CrossRef]
- Iantovics, L.B.; Rotar, C.; Morar, F. Survey on establishing the optimal number of factors in exploratory factor analysis applied to data mining. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1294. [Google Scholar] [CrossRef]
- Hassanzadeh, R.; Farhadian, M.; Rafieemehr, H. Hospital mortality prediction in traumatic injuries patients: Comparing different SMOTE-based machine learning algorithms. BMC Med. Res. Methodol. 2023, 23, 101. [Google Scholar] [CrossRef] [PubMed]
- Sinha, N.; Kumar, M.A.G.; Joshi, A.M.; Cenkeramaddi, L.R. DASMcC: Data Augmented SMOTE Multi-Class Classifier for Prediction of Cardiovascular Diseases Using Time Series Features. IEEE Access 2023, 11, 117643–117655. [Google Scholar] [CrossRef]
- Bektaş, J. EKSL: An effective novel dynamic ensemble model for unbalanced datasets based on LR and SVM hyperplane-distances. Inf. Sci. 2022, 597, 182–192. [Google Scholar] [CrossRef]
- Ahmed, G.; Er, M.J.; Fareed, M.M.; Zikria, S.; Mahmood, S.; He, J.; Asad, M.; Jilani, S.F.; Aslam, M. DAD-Net: Classification of Alzheimer’s Disease Using ADASYN Oversampling Technique and Optimized Neural Network. Molecules 2022, 27, 7085. [Google Scholar] [CrossRef]
- Cervical Cancer (Risk Factors) Data Set. Available online: https://archive.ics.uci.edu/dataset/383/cervical+cancer+risk+factors (accessed on 1 October 2024).
- Pinheiro, V.C.; do Carmo, J.C.; de O. Nascimento, F.A.; Miosso, C.J. System for the analysis of human balance based on accelerometers and support vector machines. Comput. Methods Programs Biomed. Update 2023, 4, 100123. [Google Scholar] [CrossRef]
- Iantovics, L.B.; Dehmer, M.; Emmert-Streib, F. MetrIntSimil—An Accurate and Robust Metric for Comparison of Similarity in Intelligence of Any Number of Cooperative Multiagent Systems. Symmetry 2018, 10, 48. [Google Scholar] [CrossRef]
- Darville, J.; Yavuz, A.; Runsewe, T.; Celik, N. Effective sampling for drift mitigation in machine learning using scenario selection: A microgrid case study. Appl. Energy 2023, 341, 121048. [Google Scholar] [CrossRef]
- Ibrahim, K.S.M.H.; Huang, Y.F.; Ahmed, A.N.; Koo, C.H.; El-Shafie, A. A review of the hybrid artificial intelligence and optimization modelling of hydrological streamflow forecasting. Alex. Eng. J. 2022, 61, 279–303. [Google Scholar] [CrossRef]
- Naidu, G.; Zuva, T.; Sibanda, E.M. A Review of Evaluation Metrics in Machine Learning Algorithms. In Artificial Intelligence Application in Networks and Systems (CSOC 2023); Silhavy, R., Silhavy, P., Eds.; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2023; Volume 724. [Google Scholar] [CrossRef]
- Chen, R.J.; Wang, J.J.; Williamson, D.F.; Chen, T.Y.; Lipkova, J.; Lu, M.Y.; Sahai, S.; Mahmood, F. Algorithmic fairness in artificial intelligence for medicine and healthcare. Nat. Biomed. Eng. 2023, 7, 719–742. [Google Scholar] [CrossRef] [PubMed]
- Ng, A.P.; Koumchatzky, N. Machine Learning Engineering with Python, 2nd ed.; Packt Publishing: Birmingham, UK, 2023; 462p, ISBN 9781837631964. [Google Scholar]
- Edward, J.; Rosli, M.M.; Seman, A. A New Multi-Class Rebalancing Framework for Imbalance Medical Data. IEEE Access 2023, 11, 92857–92874. [Google Scholar] [CrossRef]
- Manchadi, O.; Ben-Bouazza, F.-E.; Jioudi, B. Predictive Maintenance in Healthcare System: A Survey. IEEE Access 2023, 11, 61313–61330. [Google Scholar] [CrossRef]
- Rubinger, L.; Gazendam, A.; Ekhtiari, S.; Bhandari, M. Machine learning and artificial intelligence in research and healthcare. Injury 2023, 54 (Suppl. 3), S69–S73. [Google Scholar] [CrossRef]
- Badawy, M.; Ramadan, N.; Hefny, H.A. Healthcare predictive analytics using machine learning and deep learning techniques: A survey. J. Electr. Syst. Inf. Technol. 2023, 10, 40. [Google Scholar] [CrossRef]
- Subrahmanya, S.V.; Shetty, D.K.; Patil, V.; Hameed, B.Z.; Paul, R.; Smriti, K.; Naik, N.; Somani, B.K. The role of data science in healthcare advancements: Applications, benefits, and future prospects. Ir. J. Med. Sci. 2022, 191, 1473–1483. [Google Scholar] [CrossRef]
- Alsmariy, R.; Healy, G.; Abdelhafez, H. Predicting Cervical Cancer using Machine Learning Methods. Int. J. Adv. Comput. Sci. Appl. (IJACSA) 2020, 11, 7. [Google Scholar] [CrossRef]
- Toğaçar, M.; Ergen, B.; Cömert, Z.; Özyurt, F. A Deep Feature Learning Model for Pneumonia Detection Applying a Combination of mRMR Feature Selection and Machine Learning Models. Irbm 2020, 41, 212–222. [Google Scholar] [CrossRef]
- Rajendran, R.; Karthi, A. Heart Disease Prediction using Entropy Based Feature Engineering and Ensembling of Machine Learning Classifiers. Expert Syst. Appl. 2022, 207, 117882. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Part of the Springer Series in Statistics (SSS); Springer: New York, NY, USA, 2009. [Google Scholar]
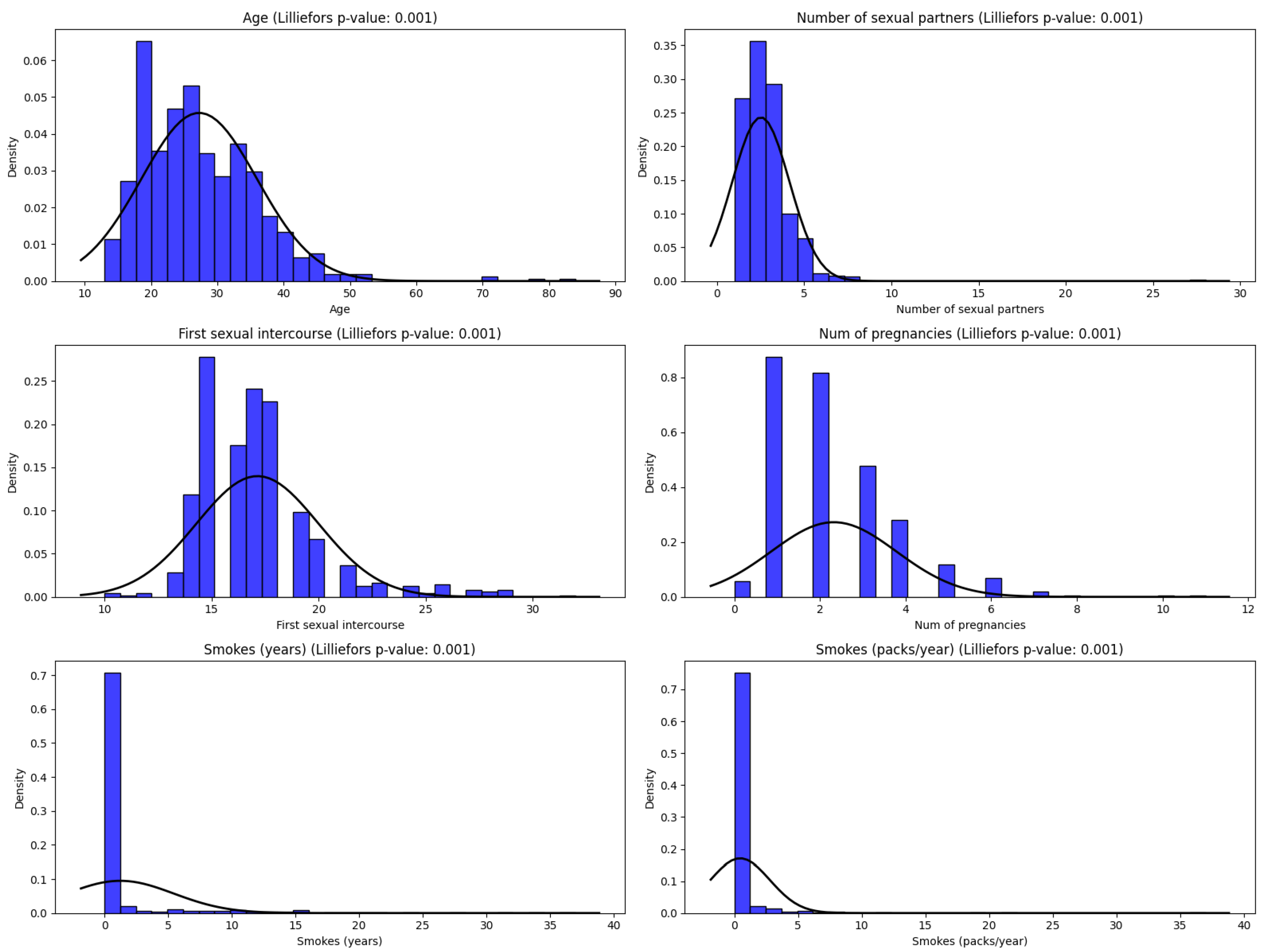
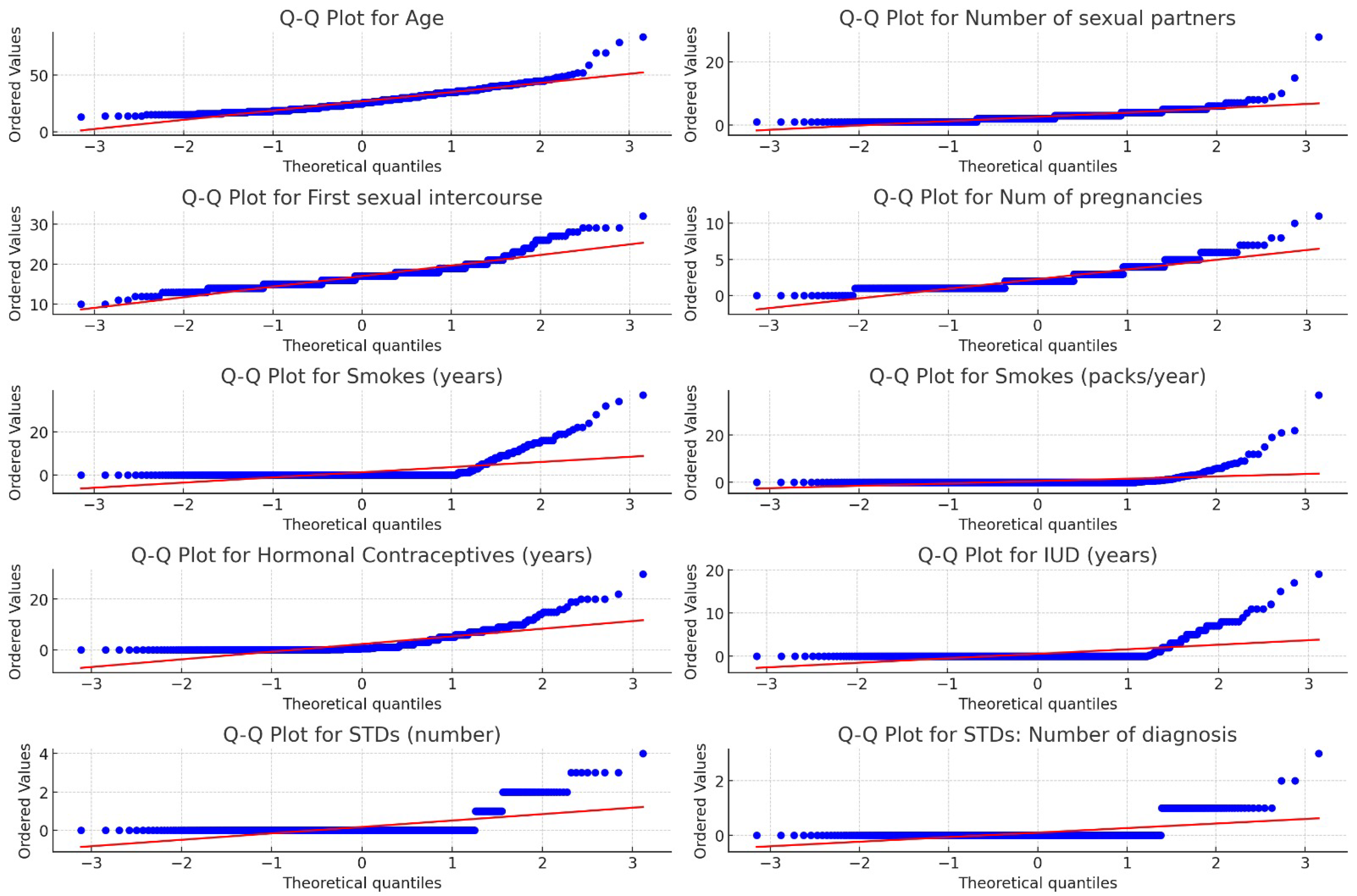

| Attribute | Min | Max | Mean | Std Dev | Median | 95% CI Mean |
|---|---|---|---|---|---|---|
| Age | 13 | 84 | 26.82 | 8.49 | 25 | (26.25, 27.39) |
| Number of sexual partners | 1 | 28 | 2.53 | 1.67 | 2 | (2.41, 2.64) |
| First sexual intercourse | 10 | 32 | 16.99 | 2.80 | 17 | (16.81, 17.18) |
| Number of pregnancies | 0 | 11 | 2.28 | 1.45 | 2 | (2.18, 2.38) |
| Smokes (years) | 0 | 37 | 1.22 | 4.09 | 0 | (0.94, 1.50) |
| Smokes (packs/year) | 0 | 37 | 0.45 | 2.23 | 0 | (0.30, 0.60) |
| Hormonal contraceptives (years) | 0 | 30 | 2.26 | 3.76 | 0.5 | (1.99, 2.53) |
| IUD (years) | 0 | 19 | 0.51 | 1.94 | 0 | (0.37, 0.65) |
| STDs (number) | 0 | 4 | 0.18 | 0.56 | 0 | (0.14, 0.22) |
| STDs: number of diagnoses | 0 | 3 | 0.09 | 0.30 | 0 | (0.07, 0.11) |
| Metric/Sampling | KNN2 | KNN3 | bLR | RF |
|---|---|---|---|---|
| Accuracy | 93.12 | 91.53 | 92.59 | 95.76 |
| Ba Accuracy | 53.57 | 52.71 | 50.00 | 71.42 |
| Precision (Mac;Wght) | 96.54;93.59 | 58.98;87.93 | 46.29;85.73 | 97.81;95.95 |
| Recall (Mac;Wght) | 53.57;93.12 | 52.71;91.53 | 50.00;92.59 | 71.42;95.76 |
| MajClass | 100 | 98.28 | 100 | 100 |
| MinClass | 7.14 | 7.14 | 0 | 42.85 |
| F1-Score (Mac;Wght) | 54.87;90.26 | 53.33;89.30 | 48.07;89.03 | 78.88;94.96 |
| ROC_AUC | 0.61 | 0.63 | 0.71 | 0.99 |
| Metric/Sampling | SMOTE | SVM SMOTE | Borderline SMOTE | ADASYN |
|---|---|---|---|---|
| Accuracy | 88.35 | 91.01 | 90.47 | 87.83 |
| Ba Accuracy | 60.85 | 65.57 | 68.57 | 60.57 |
| Precision (Mac;Wght) | 59.60;89.09 | 66.67;90.70 | 66.43;91.08 | 58.85;87.83 |
| Recall (Mac;Wght) | 60.85;88.35 | 65.57;91.00 | 68.57;90.47 | 60.57;87.83 |
| MajClass | 93.14 | 95.43 | 94.29 | 92.57 |
| MinClass | 28.57 | 35.71 | 42.86 | 28.57 |
| F1 Score (Mac;Wght) | 60.17;88.71 | 66.09;90.85 | 67.41;90.76 | 59.58;88.36 |
| ROC_AUC | 0.72 | 0.74 | 0.74 | 0.72 |
| Metric/Sampling | CNN | TL | All-KNN | RENN | ENN | NCR | NM1 | IHT |
|---|---|---|---|---|---|---|---|---|
| Accuracy | 93.65 | 92.59 | 87.30 | 87.30 | 87.30 | 90.47 | 75.66 | 45.50 |
| Ba Accuracy | 60.42 | 53.28 | 50.42 | 50.42 | 50.42 | 55.42 | 77.00 | 64.00 |
| Precision (Mac;Wght) | 84.52;92.64 | 71.52;89.85 | 50.49;86.40 | 50.49;86.40 | 50.49;86.40 | 59.18;88.30 | 59.07;92.04 | 53.99;90.94 |
| Recall (Mac;Wght) | 60.42;93.65 | 53.28;92.59 | 50.42;87.30 | 50.42;87.30 | 50.42;87.30 | 55.42;90.47 | 77.00;75.66 | 64.00;45.50 |
| MajClass | 99.43 | 99.43 | 93.71 | 93.71 | 93.71 | 96.57 | 75.43 | 42.29 |
| MinClass | 21.43 | 7.14 | 7.14 | 7.14 | 7.14 | 14.29 | 78.57 | 85.71 |
| F1 Score (Mac;Wght) | 65.00;91.97 | 54.31;89.93 | 50.43;86.84 | 50.43;86.84 | 50.43;86.84 | 56.56;89.25 | 58.75;81.24 | 38.93;55.99 |
| ROC_AUC | 0.70 | 0.61 | 0.61 | 0.62 | 0.62 | 0.63 | 0.80 | 0.65 |
| Metric/Sampling | CNN | TL | All-KNN | RENN | ENN | NCR | NM1 | IHT |
|---|---|---|---|---|---|---|---|---|
| Accuracy | 90.47 | 91.53 | 86.24 | 86.24 | 87.30 | 88.35 | 69.84 | 43.91 |
| Ba Accuracy | 68.57 | 52.71 | 49.85 | 49.85 | 50.42 | 54.28 | 77.14 | 63.14 |
| Precision (Mac;Wght) | 66.43;91.08 | 58.98;87.93 | 49.85;86.24 | 49.85;86.24 | 50.49;86.40 | 54.94;87.54 | 58.13;92.40 | 53.80;90.82 |
| Recall (Mac;Wght) | 68.57;90.47 | 52.71;91.53 | 49.85;86.24 | 49.85;86.24 | 50.42;87.30 | 54.28;88.35 | 77.14;69.84 | 63.14;43.91 |
| MajClass | 94.29 | 98.29 | 92.57 | 92.57 | 93.71 | 94.29 | 68.57 | 40.57 |
| MinClass | 42.86 | 7.14 | 7.14 | 7.14 | 7.14 | 14.29 | 85.71 | 85.71 |
| F1 Score (Mac;Wght) | 67.41;90.76 | 53.33;89.30 | 49.85;86.24 | 49.85;86.24 | 50.43;86.84 | 54.56;87.94 | 55.21;77.01 | 37.85;54.38 |
| ROC_AUC | 0.67 | 0.63 | 0.60 | 0.60 | 0.61 | 0.62 | 0.79 | 0.64 |
| Metric/Sampling | SMOTE | SVM SMOTE | Borderline SMOTE | ADASYN |
|---|---|---|---|---|
| Accuracy | 86.77 | 88.35 | 86.77 | 85.18 |
| Ba Accuracy | 89.57 | 51.00 | 86.28 | 85.42 |
| Precision (Mac;Wght) | 67.72;94.66 | 50.89;86.50 | 66.49;93.92 | 65.12;93.70 |
| Recall (Mac;Wght) | 89.57;86.77 | 51.00;88.35 | 86.28;86.77 | 85.42;85.18 |
| MajClass | 86.86 | 94.29 | 86.86 | 85.14 |
| MinClass | 92.86 | 7.14 | 85.71 | 85.71 |
| F1 Score (Mac;Wght) | 72.34;89.66 | 50.74;87.15 | 70.69;89.19 | 68.78;88.05 |
| ROC_AUC | 0.92 | 0.87 | 0.89 | 0.91 |
| Metric/Sampling | SMOTE | SVM SMOTE | Borderline SMOTE | ADASYN |
|---|---|---|---|---|
| Accuracy | 98.41 | 98.41 | 98.41 | 98.41 |
| Ba Accuracy | 92.57 | 92.57 | 92.57 | 98.41 |
| Precision (Mac;Wght) | 95.58;98.37 | 95.58;98.37 | 95.58;98.37 | 95.58;98.37 |
| Recall (Mac;Wght) | 92.57;98.41 | 92.57;98.41 | 92.57;98.41 | 92.57;98.41 |
| MajClass | 99.43 | 99.43 | 99.43 | 99.43 |
| MinClass | 85.71 | 85.71 | 85.71 | 85.71 |
| F1 Score (Mac;Wght) | 94.01;98.38 | 94.01;98.38 | 94.01;98.38 | 94.01;98.38 |
| ROC_AUC | 0.99 | 0.99 | 0.99 | 0.99 |
| Metric/Sampling | CNN | TL | All-KNN | RENN | ENN | NCR | NM1 | IHT |
|---|---|---|---|---|---|---|---|---|
| Accuracy | 98.94 | 95.76 | 95.23 | 97.35 | 96.29 | 96.29 | 95.76 | 76.19 |
| Ba Accuracy | 96.14 | 71.42 | 67.85 | 82.14 | 75.00 | 75.00 | 97.71 | 83.85 |
| Precision (Mac;Wght) | 96.14;98.94 | 97.81;95.95 | 96.14;98.94 | 98.07;96.43 | 98.07;96.43 | 98.07;96.43 | 81.81;97.30 | 61.02;93.58 |
| Recall (Mac;Wght) | 96.14;98.94 | 71.42;95.76 | 67.85;95.23 | 82.14;97.35 | 75.00;96.29 | 75.00;96.29 | 97.71;96.43 | 83.85;76.19 |
| MajClass | 99.43 | 100 | 100 | 100 | 100 | 100 | 95.43 | 74.86 |
| MinClass | 92.86 | 42.86 | 64.29 | 64.29 | 50 | 50 | 100 | 92.86 |
| F1 Score (Mac;Wght) | 96.14;98.94 | 78.88;94.96 | 75.06;94.17 | 82.35;95.71 | 82.35;95.71 | 82.35;95.71 | 87.71;96.18 | 60.98;81.73 |
| ROC_AUC | 0.99 | 0.99 | 1.0 | 1.0 | 0.99 | 0.99 | 0.99 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muraru, M.M.; Simó, Z.; Iantovics, L.B. Cervical Cancer Prediction Based on Imbalanced Data Using Machine Learning Algorithms with a Variety of Sampling Methods. Appl. Sci. 2024, 14, 10085. https://doi.org/10.3390/app142210085
Muraru MM, Simó Z, Iantovics LB. Cervical Cancer Prediction Based on Imbalanced Data Using Machine Learning Algorithms with a Variety of Sampling Methods. Applied Sciences. 2024; 14(22):10085. https://doi.org/10.3390/app142210085
Chicago/Turabian StyleMuraru, Mădălina Maria, Zsuzsa Simó, and László Barna Iantovics. 2024. "Cervical Cancer Prediction Based on Imbalanced Data Using Machine Learning Algorithms with a Variety of Sampling Methods" Applied Sciences 14, no. 22: 10085. https://doi.org/10.3390/app142210085
APA StyleMuraru, M. M., Simó, Z., & Iantovics, L. B. (2024). Cervical Cancer Prediction Based on Imbalanced Data Using Machine Learning Algorithms with a Variety of Sampling Methods. Applied Sciences, 14(22), 10085. https://doi.org/10.3390/app142210085






