A Transferable Meta-Learning Phase Prediction Model for High-Entropy Alloys Based on Adaptive Migration Walrus Optimizer
Abstract
1. Introduction
2. Related Works
2.1. Background Theory of HEAs
2.2. Walrus Optimizer (WO)
2.2.1. Initialization
2.2.2. Danger and Safety Signals
2.2.3. Migration
2.2.4. Reproduction
2.3. Nearest Neighbors-Based Adaptive DPC with an Optimized Allocation Strategy (NADPC)
3. Methodology
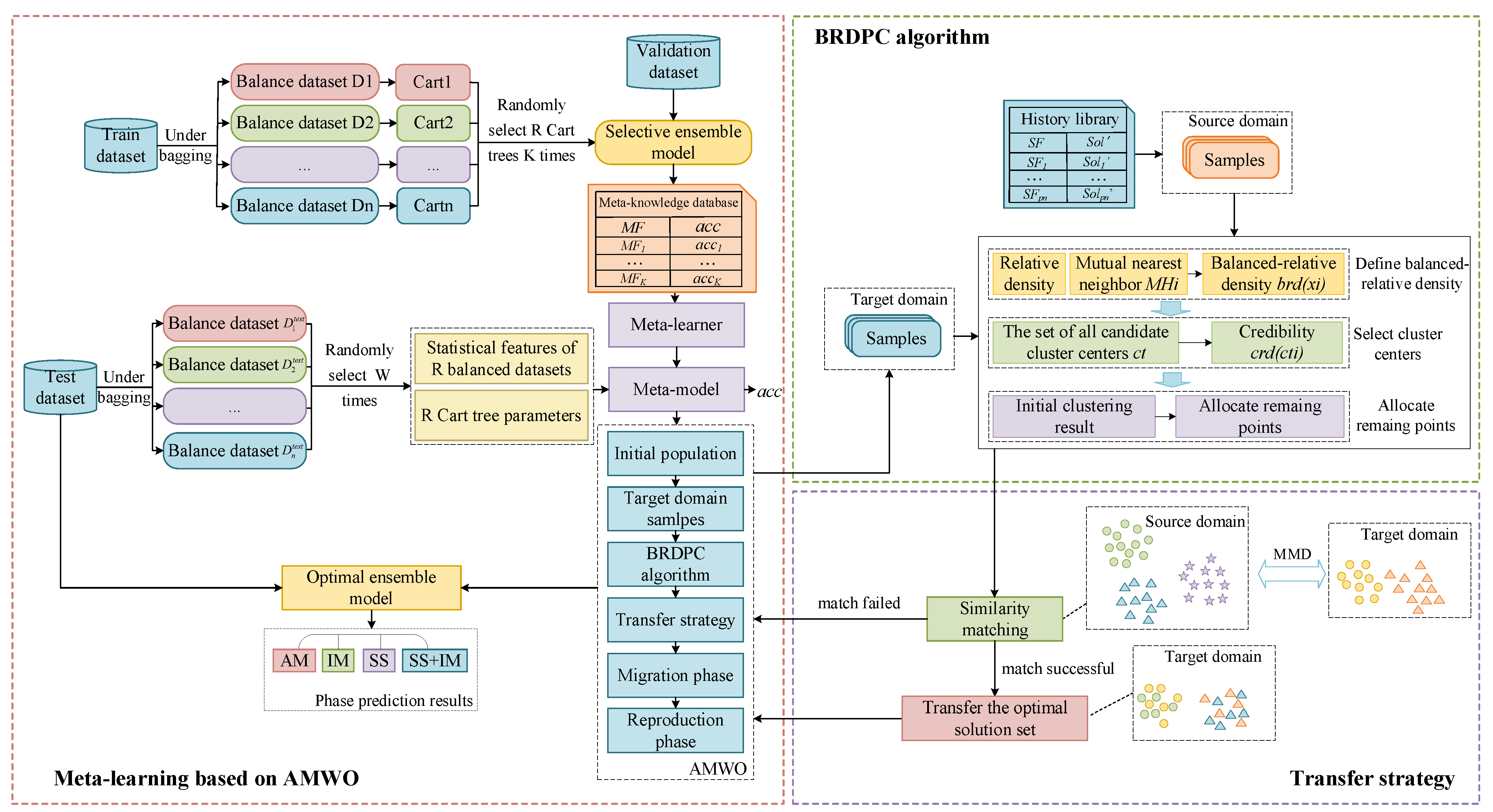
3.1. A Transferable Meta-Learning Algorithm Frame
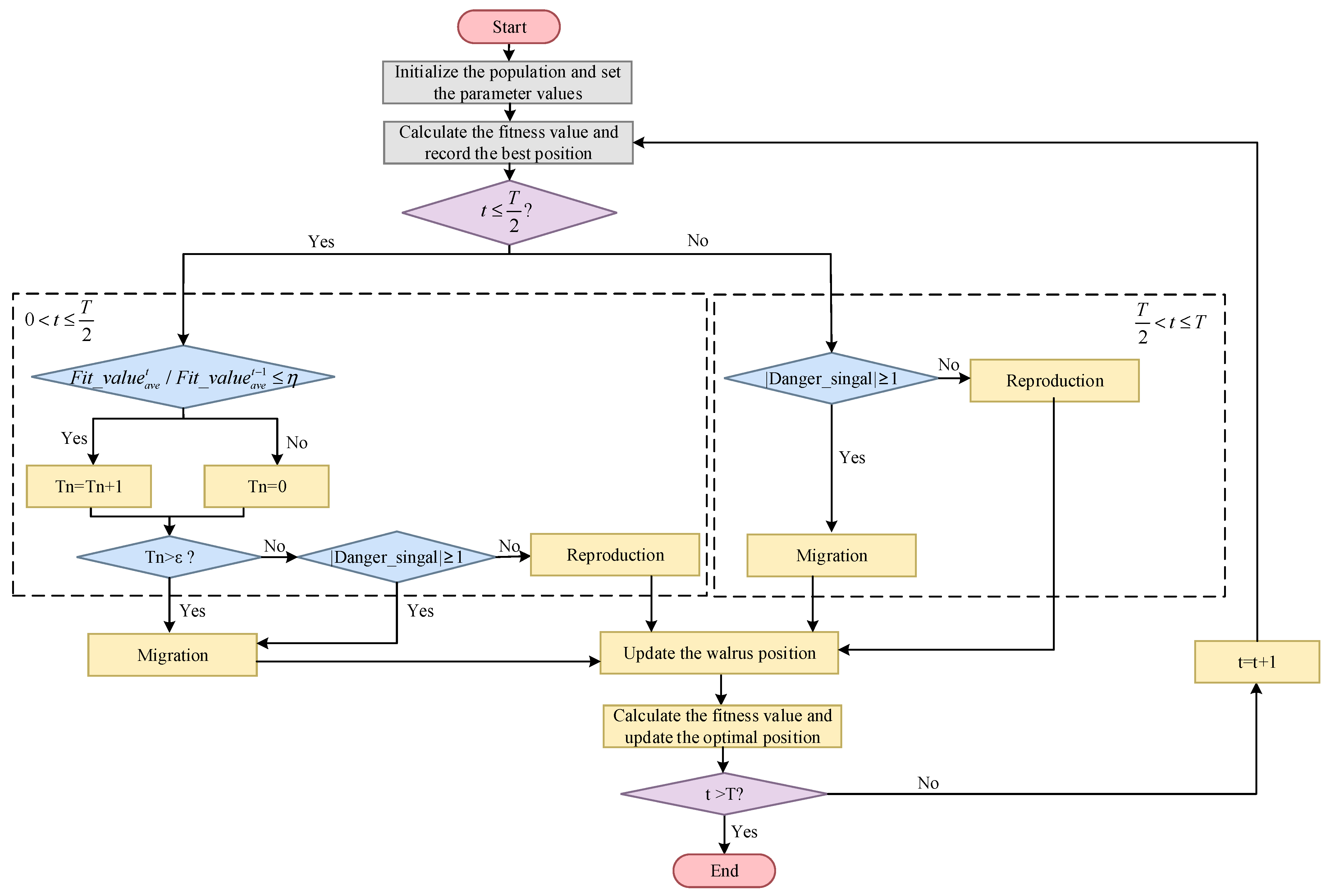
3.2. Adaptive Migration Walrus Optimizer (AMWO)
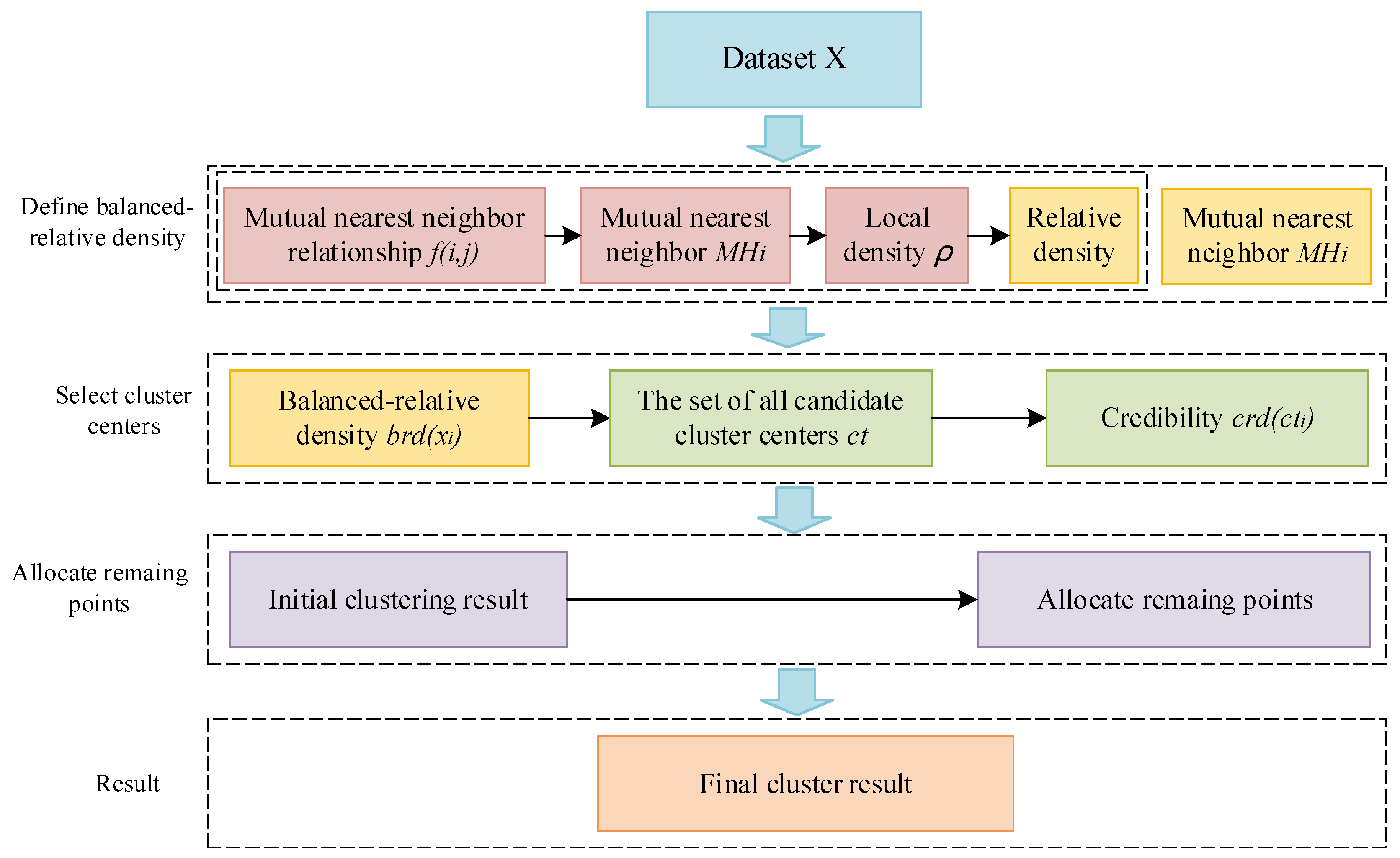
3.3. Balanced-Relative Density Peaks Clustering (BRDPC)
3.3.1. Similarity Matching Algorithm
3.4. Transfer Strategy
3.4.1. Updating the History Library
4. Results and Discussion
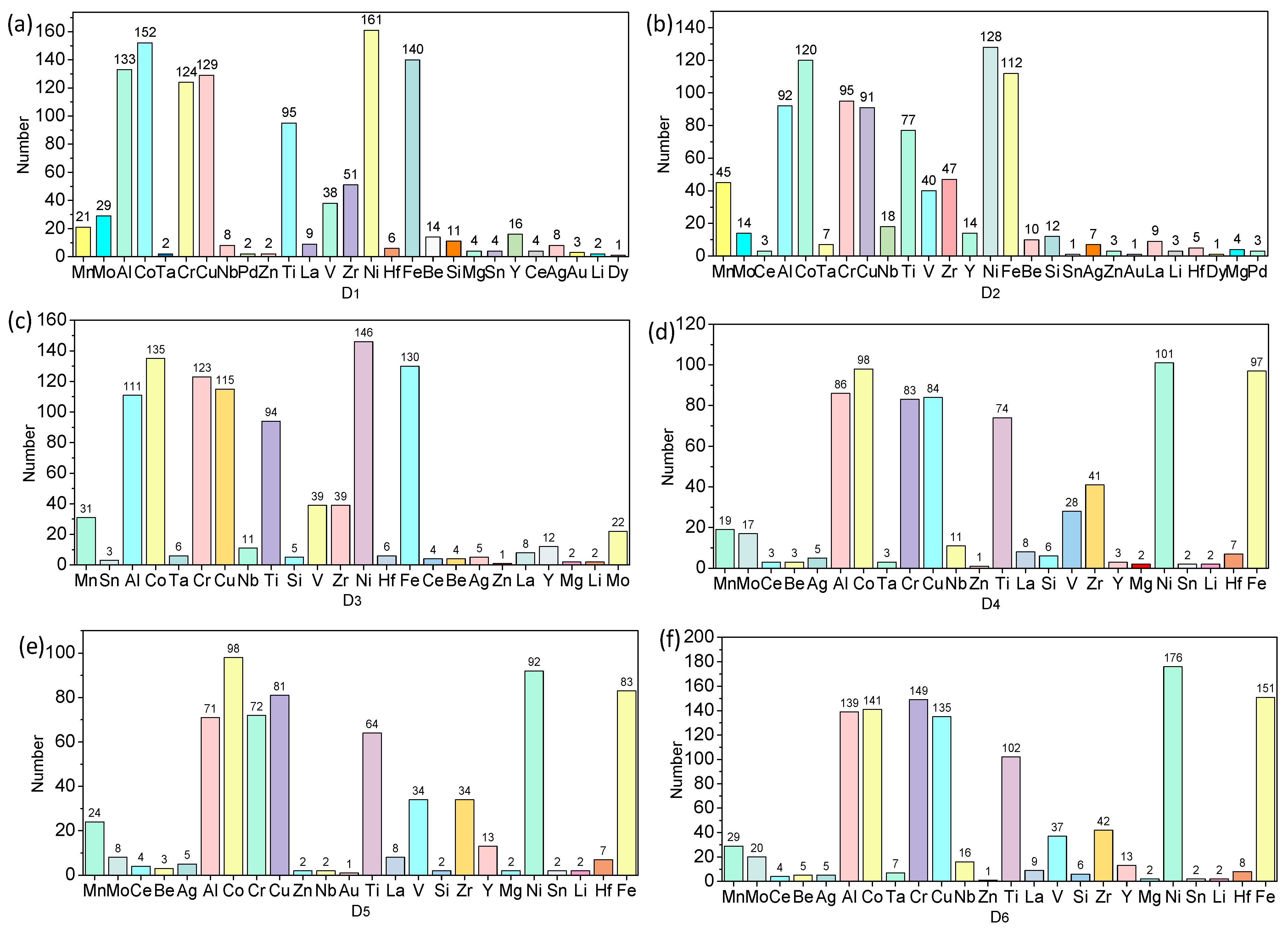
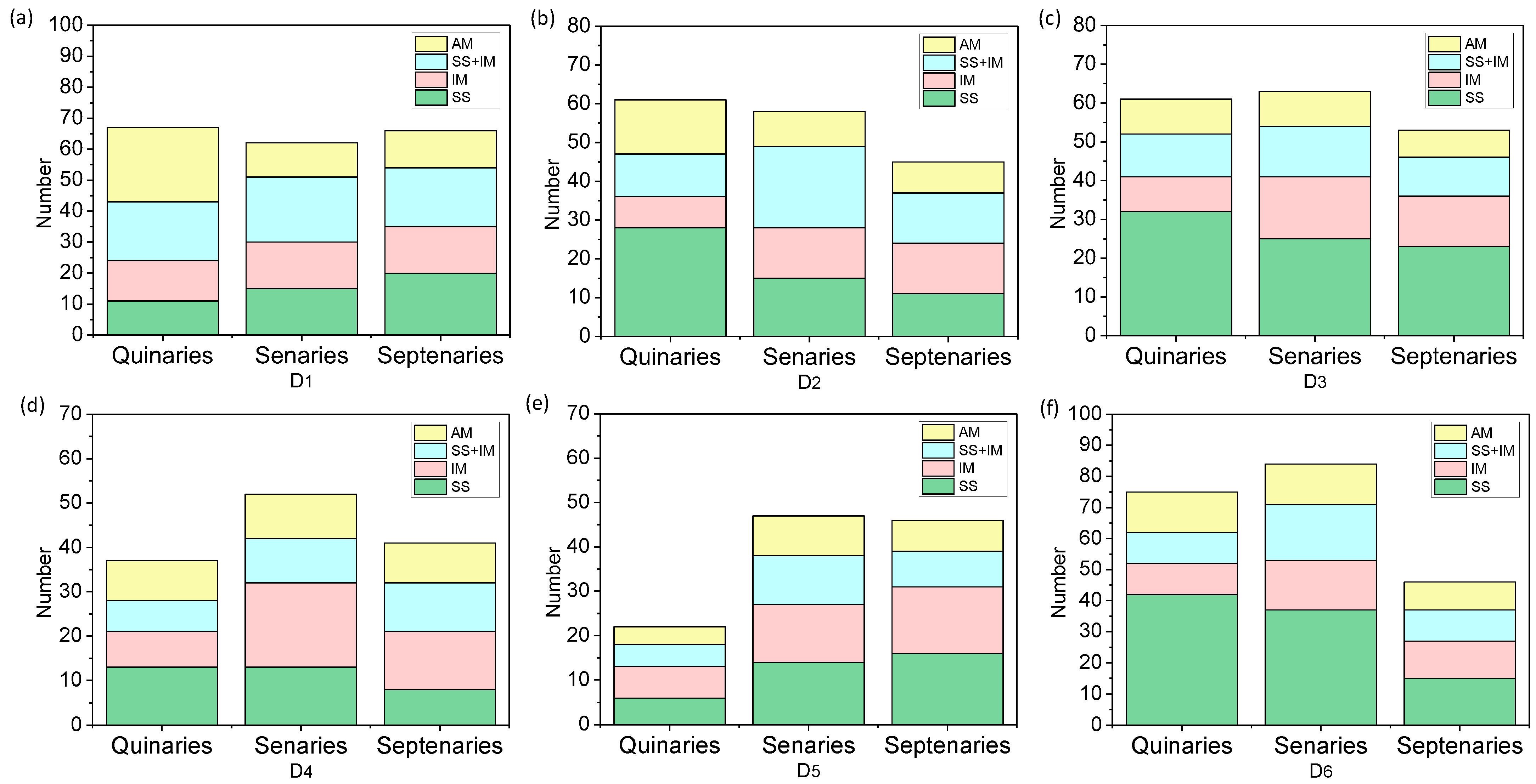
4.1. Experimental Datasets
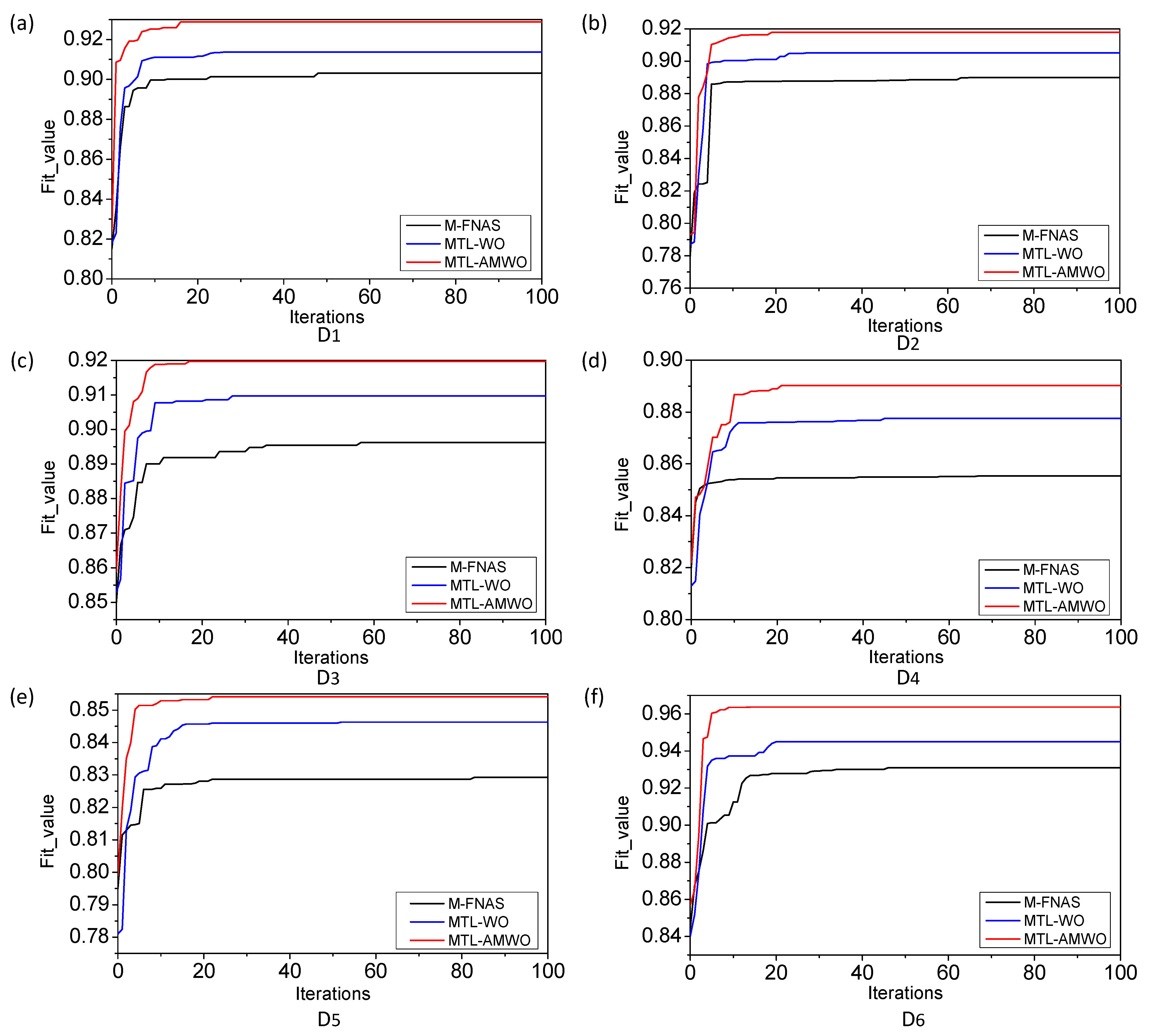
4.2. Comparison of Convergence for MTL-AMWO, MTL-WO, and M-FNAS
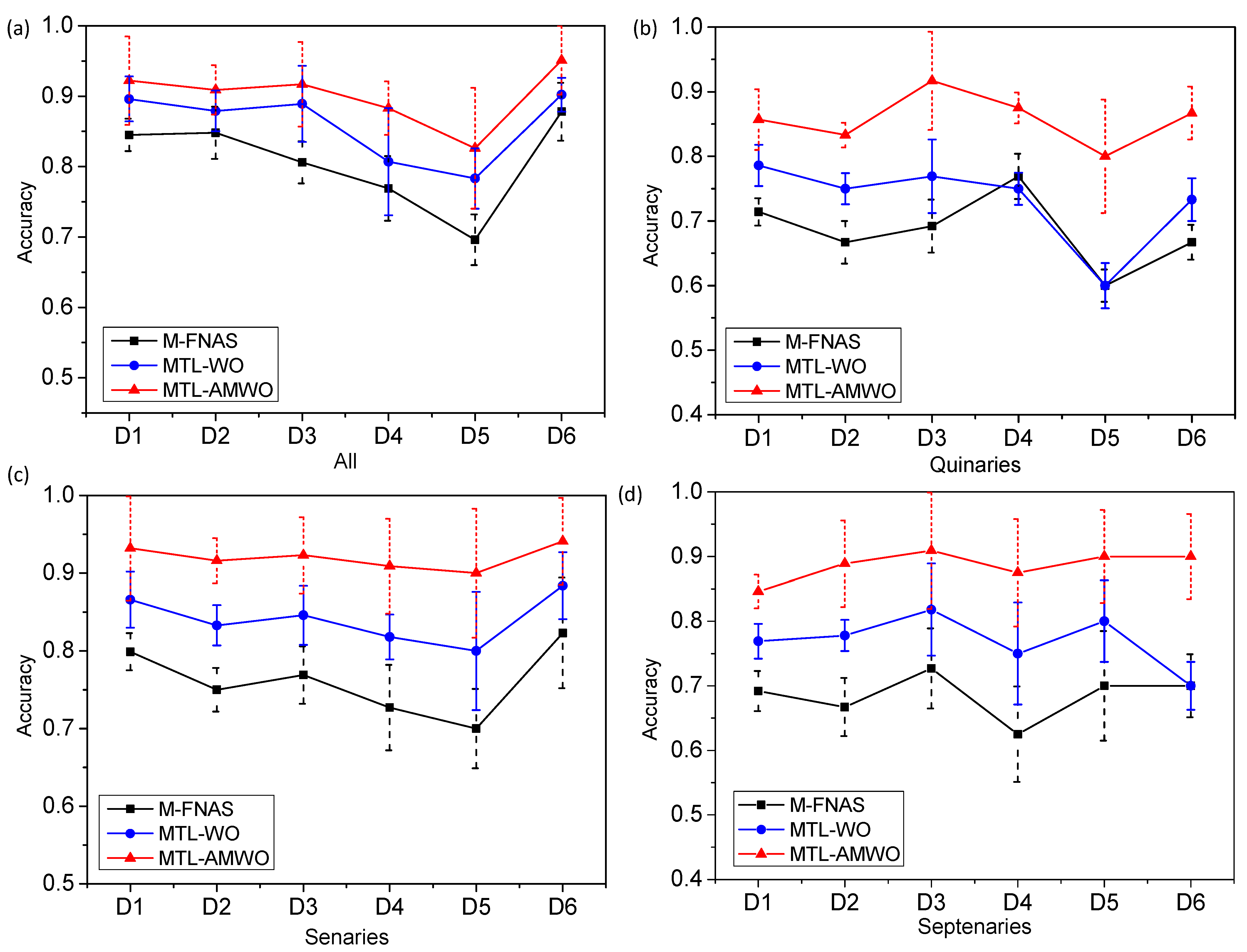
4.3. Accuracy Comparison of MTL-AMWO, MTL-WO and M-FNAS
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, C.; Zhu, J.; Zheng, H.; Li, H.; Liu, S.; Cheng, G.J. A review on microstructures and properties of high entropy alloys manufactured by selective laser melting. Int. J. Extrem. Manuf. 2020, 2, 032003. [Google Scholar] [CrossRef]
- Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Gorniewicz, D.; Przygucki, H.; Kopec, M.; Karczewski, K.; Jóźwiak, S. TiCoCrFeMn (BCC + C14) High-Entropy Alloy Multiphase Structure Analysis Based on the Theory of Molecular Orbitals. Materials 2021, 14, 5285. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Paudel, R.; Liu, Y.; Zhao, X.L.; Zhu, J.C. Theoretical and Experimental Studies of the Structural, Phase Stability and Elastic Properties of AlCrTiFeNi Multi-Principle Element Alloy. Materials 2020, 13, 4353. [Google Scholar] [CrossRef]
- Dai, D.; Xu, T.; Wei, X.; Ding, G.; Xu, Y.; Zhang, J.; Zhang, H. Using machine learning and feature engineering to characterize limited material datasets of high-entropy alloys. Comput. Mater. Sci. 2020, 175, 109618. [Google Scholar] [CrossRef]
- Rickman, J.M.; Chan, H.M.; Harmer, M.P.; Smeltzer, J.A.; Marvel, C.J.; Roy, A.; Balasubramanian, G. Materials informatics for the screening of multi-principal elements and high-entropy alloys. Nat. Commun. 2019, 10, 2618. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y. Prediction of high-entropy stabilized solid-solution in multi-component alloys. Mater. Chem. Phys. 2012, 132, 233–238. [Google Scholar] [CrossRef]
- Senkov, O.N.; Miracle, D.B. A new thermodynamic parameter to predict formation of solid solution or intermetallic phases in high entropy alloys. J. Alloys Compd. 2016, 658, 603–607. [Google Scholar] [CrossRef]
- Gao, M.C.; Zhang, C.; Gao, P.; Zhang, F.; Ouyang, L.Z.; Widom, M.; Hawk, J.A. Thermodynamics of concentrated solid solution alloys. Curr. Opin. Solid State Mater. Sci. 2017, 21, 238–251. [Google Scholar] [CrossRef]
- Ding, Q.; Zhang, Y.; Chen, X.; Fu, X.; Chen, D.; Chen, S.; Yu, Q. Tuning element distribution, structure and properties by composition in high-entropy alloys. Nature 2019, 574, 223–227. [Google Scholar] [CrossRef]
- Zhao, S.; Yuan, R.; Liao, W.; Zhao, Y.; Wang, J.; Li, J.; Lookman, T. Descriptors for phase prediction of high entropy alloys using interpretable machine learning. J. Mater. Chem. A 2024, 12, 2807–2819. [Google Scholar] [CrossRef]
- Li, Z.; Pradeep, K.G.; Deng, Y.; Raabe, D.; Tasan, C.C. Metastable high-entropy dual-phase alloys overcome the strength–ductility trade-off. Nature 2016, 534, 227–230. [Google Scholar] [CrossRef]
- Deshmukh, A.A.; Ranganathan, R. Recent advances in modelling structure-property correlations in high-entropy alloys. J. Mater. Sci. Technol. 2024, 204, 127–151. [Google Scholar] [CrossRef]
- Ye, Y.F.; Wang, Q.; Lu, J.; Liu, C.T.; Yang, Y. High-entropy alloy: Challenges and prospects. Mater. Today 2016, 19, 349–362. [Google Scholar] [CrossRef]
- Singh, P.; Smirnov, A.V.; Alam, A.; Johnson, D.D. First-principles prediction of incipient order in arbitrary high-entropy alloys: Exemplified in Ti0.25CrFeNiAlx. Acta Mater. 2020, 189, 248–254. [Google Scholar] [CrossRef]
- Bobbili, R.; Ramakrishna, B. Prediction of phases in high entropy alloys using machine learning. Mater. Today Commun. 2023, 36, 106674. [Google Scholar] [CrossRef]
- Zhang, X.; Jia, B.; Zeng, Z.; Zeng, X.; Wan, Q.; Pogrebnjak, A.; Zhang, J.; Pelenovich, V.; Yang, B. Machine Learning-Based Design of Superhard High-Entropy Nitride Coatings. ACS Appl. Mater. Interfaces 2024, 16, 36911–36922. [Google Scholar] [CrossRef] [PubMed]
- Yan, Q.; Gong, D.; Shi, Q.; Hengel, A.V.D.; Shen, C.; Reid, I.; Zhang, Y. Attention-guided network for ghost-free high dynamic range imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1751–1760. [Google Scholar]
- Ferrari, D.G.; De Castro, L.N. Clustering algorithm selection by meta-learning systems: A new distance-based problem characterization and ranking combination methods. Inf. Sci. 2015, 301, 181–194. [Google Scholar] [CrossRef]
- Cao, J.; Yuan, W.; Li, W.; E, X. Dynamic ensemble pruning selection using meta-learning for multi-sensor based activity recognition. In Proceedings of the 2019 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computing, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI), Leicester, UK, 19–23 August 2019; pp. 1063–1068. [Google Scholar]
- Li, L.; Wang, Y.; Xu, Y.; Lin, K.Y. Meta-learning based industrial intelligence of feature nearest algorithm selection framework for classification problems. J. Manuf. Syst. 2022, 62, 767–776. [Google Scholar] [CrossRef]
- Hou, S.; Li, Y.; Bai, M.; Sun, M.; Liu, W.; Wang, C.; Lin, D. Phase prediction of high-entropy alloys by integrating criterion and machine learning recommendation method. Materials 2022, 15, 3321. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Dinh, T.T.H.; Chu, T.H.; Nguyen, Q.U. Transfer learning in genetic programming. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 1145–1151. [Google Scholar]
- Feng, L.; Ong, Y.S.; Tan, A.H.; Tsang, I.W. Memes as building blocks: A case study on evolutionary optimization + transfer learning for routing problems. Memetic Comput. 2015, 7, 159–180. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, K.; Hao, G.; Gong, D. Evolutionary optimization framework based on transfer learning of similar historical information. Acta Autom. Sin. 2021, 47, 652–665. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1945–1950. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Han, M.; Du, Z.; Yuen, K.F.; Zhu, H.; Li, Y.; Yuan, Q. Walrus optimizer: A novel nature-inspired metaheuristic algorithm. Expert Syst. Appl. 2024, 239, 122413. [Google Scholar] [CrossRef]
- Ahmed, H.R. An efficient fitness-based stagnation detection method for particle swarm optimization. In Proceedings of the Companion Publication of the 2014 Annual Conference on Genetic and Evolutionary Computation, Vancouver, BC, Canada, 12–16 July 2014; pp. 1029–1032. [Google Scholar]
- Deng, T.; Ye, D.; Ma, R.; Fujita, H.; Xiong, L. Low-rank local tangent space embedding for subspace clustering. Inf. Sci. 2020, 508, 1–21. [Google Scholar] [CrossRef]
- Xu, X.; Ding, S.; Wang, Y.; Wang, L.; Jia, W. A fast density peaks clustering algorithm with sparse search. Inf. Sci. 2021, 554, 61–83. [Google Scholar] [CrossRef]
- Ismkhan, H. Ik-means−+: An iterative clustering algorithm based on an enhanced version of the k-means. Pattern Recognit. 2018, 79, 402–413. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef]
- Hou, J.; Zhang, A.; Qi, N. Density peak clustering based on relative density relationship. Pattern Recognit. 2020, 108, 107554. [Google Scholar] [CrossRef]
- Sun, L.; Qin, X.; Ding, W.; Xu, J. Nearest neighbors-based adaptive density peaks clustering with optimized allocation strategy. Neurocomputing 2022, 473, 159–181. [Google Scholar] [CrossRef]
- Dobrzański, L.A.; Labisz, K.; Jonda, E.; Klimpel, A. Comparison of the surface alloying of the 32CrMoV12-28 tool steel using TiC and WC powder. J. Mater. Process. Technol. 2007, 191, 321–325. [Google Scholar] [CrossRef]
- Zhang, Y.; Zuo, T.T.; Tang, Z.; Gao, M.C.; Dahmen, K.A.; Liaw, P.K.; Lu, Z.P. Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 2014, 61, 1–93. [Google Scholar] [CrossRef]
- Chang, X.; Zeng, M.; Liu, K.; Fu, L. Phase engineering of high-entropy alloys. Adv. Mater. 2020, 32, 1907226. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhou, Y.J.; Lin, J.P.; Chen, G.L.; Liaw, P.K. Solid-solution phase formation rules for multi-component alloys. Adv. Eng. Mater. 2008, 10, 534–538. [Google Scholar] [CrossRef]
- Takeuchi, A.; Amiya, K.; Wada, T.; Yubuta, K.; Zhang, W. High-entropy alloys with a hexagonal close-packed structure designed by equi-atomic alloy strategy and binary phase diagrams. Jom 2014, 66, 1984–1992. [Google Scholar] [CrossRef]
- Chanda, B.; Das, J. Composition dependence on the evolution of nanoeutectic in CoCrFeNiNbx (0.45 ≤ x ≤ 0.65) high entropy alloys. Adv. Eng. Mater. 2018, 20, 1700908. [Google Scholar] [CrossRef]
- Yang, X.; Chen, S.Y.; Cotton, J.D.; Zhang, Y. Phase stability of low-density, multiprincipal component alloys containing aluminum, magnesium, and lithium. Jom 2014, 66, 2009–2020. [Google Scholar] [CrossRef]
- Zhang, Q.; Dai, Y.; Wang, G. Density peaks clustering based on balance density and connectivity. Pattern Recognit. 2023, 134, 109052. [Google Scholar] [CrossRef]
- Borgwardt, K.M.; Gretton, A.; Rasch, M.J.; Kriegel, H.P.; Schölkopf, B.; Smola, A.J. Integrating structured biological data by kernel maximum mean discrepancy. Bioinformatics 2006, 22, e49–e57. [Google Scholar] [CrossRef]
- Toda-Caraballo, I.; Rivera-Díaz-del-Castillo, P.E.J. A criterion for the formation of high entropy alloys based on lattice distortion. Intermetallics 2016, 71, 76–87. [Google Scholar] [CrossRef]
- Leong, Z.; Huang, Y.; Goodall, R.; Todd, I. Electronegativity and enthalpy of mixing biplots for High Entropy Alloy solid solution prediction. Mater. Chem. Phys. 2018, 210, 259–268. [Google Scholar] [CrossRef]
- Poletti, M.G.; Battezzati, L.J.A.M. Electronic and thermodynamic criteria for the occurrence of high entropy alloys in metallic systems. Acta Mater. 2014, 75, 297–306. [Google Scholar] [CrossRef]
- Sheng, G.U.O.; Liu, C.T. Phase stability in high entropy alloys: Formation of solid-solution phase or amorphous phase. Prog. Nat. Sci. Mater. Int. 2011, 21, 433–446. [Google Scholar]
- King, D.J.M.; Middleburgh, S.C.; McGregor, A.G.; Cortie, M.B. Predicting the formation and stability of single phase high-entropy alloys. Acta Mater. 2016, 104, 172–179. [Google Scholar] [CrossRef]
- Andreoli, A.F.; Orava, J.; Liaw, P.K.; Weber, H.; de Oliveira, M.F.; Nielsh, K.; Kaban, I. The elastic-strain energy criterion of phase formation for complex concentrated alloys. Materialia 2019, 5, 100222. [Google Scholar] [CrossRef]
- Peng, Y.T.; Zhou, C.Y.; Lin, P.; Wen, D.Y.; Wang, X.D.; Zhong, X.Z.; Pan, D.H.; Que, Q.; Li, X.; Chen, L.; et al. Preoperative ultrasound radiomics signatures for noninvasive evaluation of biological characteristics of intrahepatic cholangiocarcinoma. Acad. Radiol. 2020, 27, 785–797. [Google Scholar] [CrossRef]

| Index | High Entropy Alloys | ΔHmix | ΔSmix | δ | Δχ | Ω | Phase |
|---|---|---|---|---|---|---|---|
| 0 | Co1.4CrFeMnNi | −4.115226 | 13.295461 | 1.100487 | 0.136445 | 5.792101 | SS |
| 1 | CrCu0.5FeMnNi | 0.098765 | 13.145213 | 1.185478 | 0.142370 | 233.301248 | SS |
| 2 | CoCuFeNiSn0.07 | 5.066134 | 12.050142 | 2.849306 | 0.032278 | 3.909939 | SS + IM |
| 3 | AlCoCrFeNiSi0.2 | −16.390533 | 14.221597 | 5.634042 | 0.120530 | 1.456954 | SS |
| 4 | CoFeMoNiTiVZr | −21.800000 | 16.178297 | 8.800000 | 0.254045 | 1.529411 | AM |
| 5 | CoCrFeMnNbNi | −12.000000 | 14.896688 | 5.900000 | 0.140643 | 2.424436 | IM |
| ID | M-FNAS | MTL-WO | MTL-AMWO |
|---|---|---|---|
| D1 | 0.845 ± 0.023 | 0.896 ± 0.032 | 0.922 ± 0.063 |
| D2 | 0.848 ± 0.037 | 0.879 ± 0.029 | 0.909 ± 0.035 |
| D3 | 0.806 ± 0.030 | 0.889 ± 0.054 | 0.917 ± 0.060 |
| D4 | 0.769 ± 0.046 | 0.807 ± 0.076 | 0.883 ± 0.038 |
| D5 | 0.696 ± 0.036 | 0.783 ± 0.043 | 0.826 ± 0.086 |
| D6 | 0.878 ± 0.041 | 0.902 ± 0.024 | 0.951 ± 0.049 |
| ID | M-FNAS | MTL-WO | MTL-AMWO |
|---|---|---|---|
| D1 | 0.714 ± 0.021 | 0.786 ± 0.032 | 0.857 ± 0.047 |
| D2 | 0.667 ± 0.033 | 0.750 ± 0.024 | 0.833 ± 0.019 |
| D3 | 0.692 ± 0.041 | 0.769 ± 0.057 | 0.917 ± 0.076 |
| D4 | 0.769 ± 0.035 | 0.750 ± 0.025 | 0.875 ± 0.024 |
| D5 | 0.600 ± 0.025 | 0.600 ± 0.035 | 0.800 ± 0.088 |
| D6 | 0.667 ± 0.027 | 0.733 ± 0.033 | 0.867 ± 0.041 |
| ID | M-FNAS | MTL-WO | MTL-AMWO |
|---|---|---|---|
| D1 | 0.799 ± 0.024 | 0.866 ± 0.036 | 0.932 ± 0.067 |
| D2 | 0.750 ± 0.028 | 0.833 ± 0.026 | 0.916 ± 0.029 |
| D3 | 0.769 ± 0.037 | 0.846 ± 0.038 | 0.923 ± 0.049 |
| D4 | 0.727 ± 0.055 | 0.818 ± 0.029 | 0.909 ± 0.061 |
| D5 | 0.700 ± 0.051 | 0.800 ± 0.076 | 0.900 ± 0.083 |
| D6 | 0.823 ± 0.071 | 0.884 ± 0.043 | 0.941 ± 0.056 |
| ID | M-FNAS | MTL-WO | MTL-AMWO |
|---|---|---|---|
| D1 | 0.692 ± 0.031 | 0.769 ± 0.027 | 0.846 ± 0.026 |
| D2 | 0.667 ± 0.045 | 0.778 ± 0.024 | 0.889 ± 0.067 |
| D3 | 0.727 ± 0.062 | 0.818 ± 0.071 | 0.909 ± 0.090 |
| D4 | 0.625 ± 0.074 | 0.750 ± 0.079 | 0.875 ± 0.083 |
| D5 | 0.700 ± 0.085 | 0.800 ± 0.063 | 0.900 ± 0.072 |
| D6 | 0.700 ± 0.049 | 0.700 ± 0.037 | 0.900 ± 0.066 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, S.; Zhou, M.; Bai, M.; Liu, W.; Geng, H.; Yin, B.; Li, H. A Transferable Meta-Learning Phase Prediction Model for High-Entropy Alloys Based on Adaptive Migration Walrus Optimizer. Appl. Sci. 2024, 14, 9977. https://doi.org/10.3390/app14219977
Hou S, Zhou M, Bai M, Liu W, Geng H, Yin B, Li H. A Transferable Meta-Learning Phase Prediction Model for High-Entropy Alloys Based on Adaptive Migration Walrus Optimizer. Applied Sciences. 2024; 14(21):9977. https://doi.org/10.3390/app14219977
Chicago/Turabian StyleHou, Shuai, Minmin Zhou, Meijuan Bai, Weiwei Liu, Hua Geng, Bingkuan Yin, and Haotong Li. 2024. "A Transferable Meta-Learning Phase Prediction Model for High-Entropy Alloys Based on Adaptive Migration Walrus Optimizer" Applied Sciences 14, no. 21: 9977. https://doi.org/10.3390/app14219977
APA StyleHou, S., Zhou, M., Bai, M., Liu, W., Geng, H., Yin, B., & Li, H. (2024). A Transferable Meta-Learning Phase Prediction Model for High-Entropy Alloys Based on Adaptive Migration Walrus Optimizer. Applied Sciences, 14(21), 9977. https://doi.org/10.3390/app14219977







