Key Frame Selection for Temporal Graph Optimization of Skeleton-Based Action Recognition
Abstract
1. Introduction
- We propose a new multi-stage method that conducts key frame selection to align action sequences within the same category as well as preserves the most representative frames including both salient and subtle dynamic information for skeleton-based action recognition.
- We propose a plug-and-play module based on variational inference to simultaneously refine temporal relationships for constructing the spatial–temporal graph and optimize the parameters of the GNNs.
- The proposed method achieves state-of-the-art performances on two large-scale datasets.
2. Related Work
2.1. Skeleton-Based Action Recognition
2.2. Key Frame Selection for Action Recognition
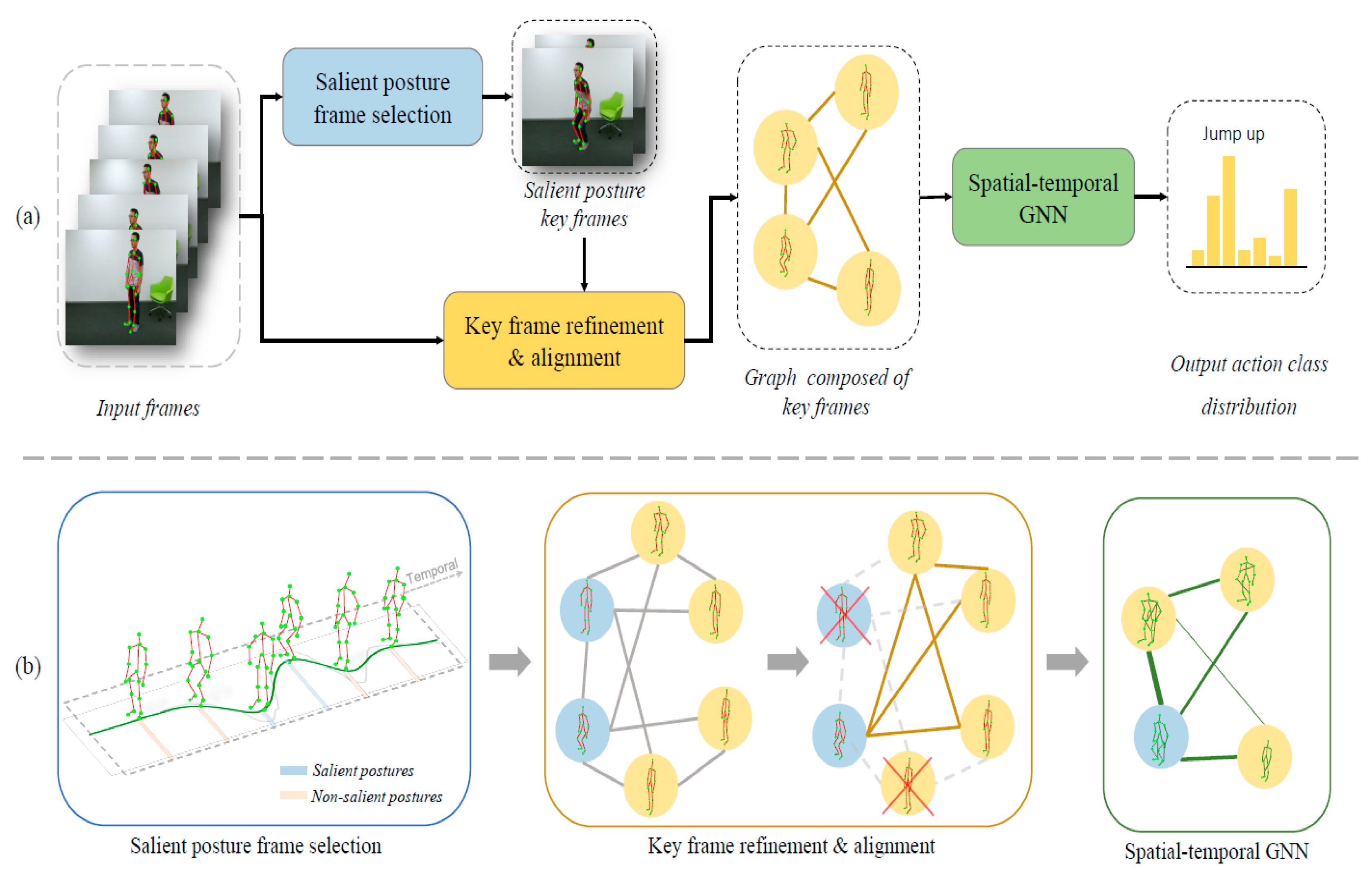
3. Multi-Stage Key Frame Selection
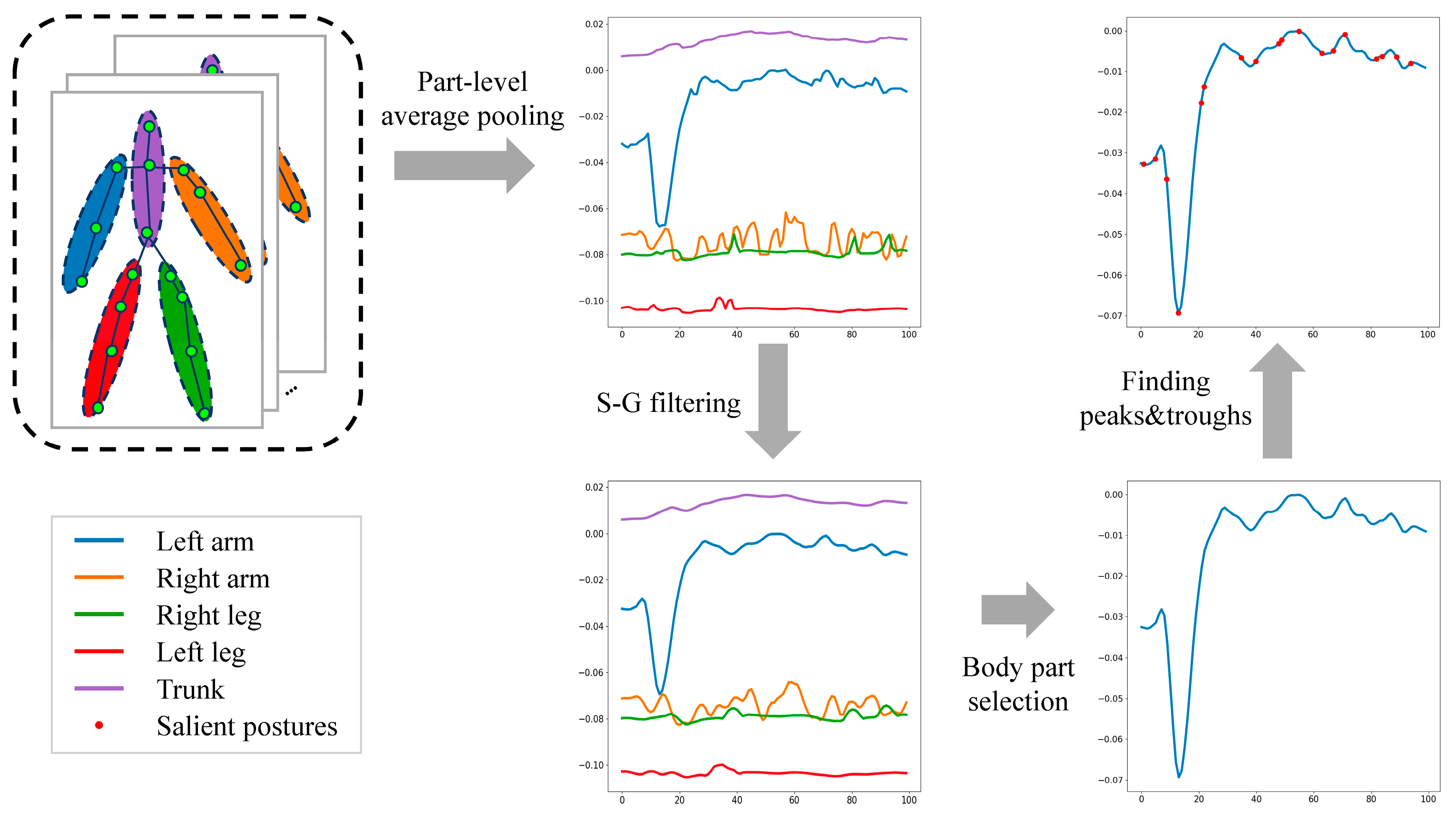
3.1. Salient Posture Frame Selection
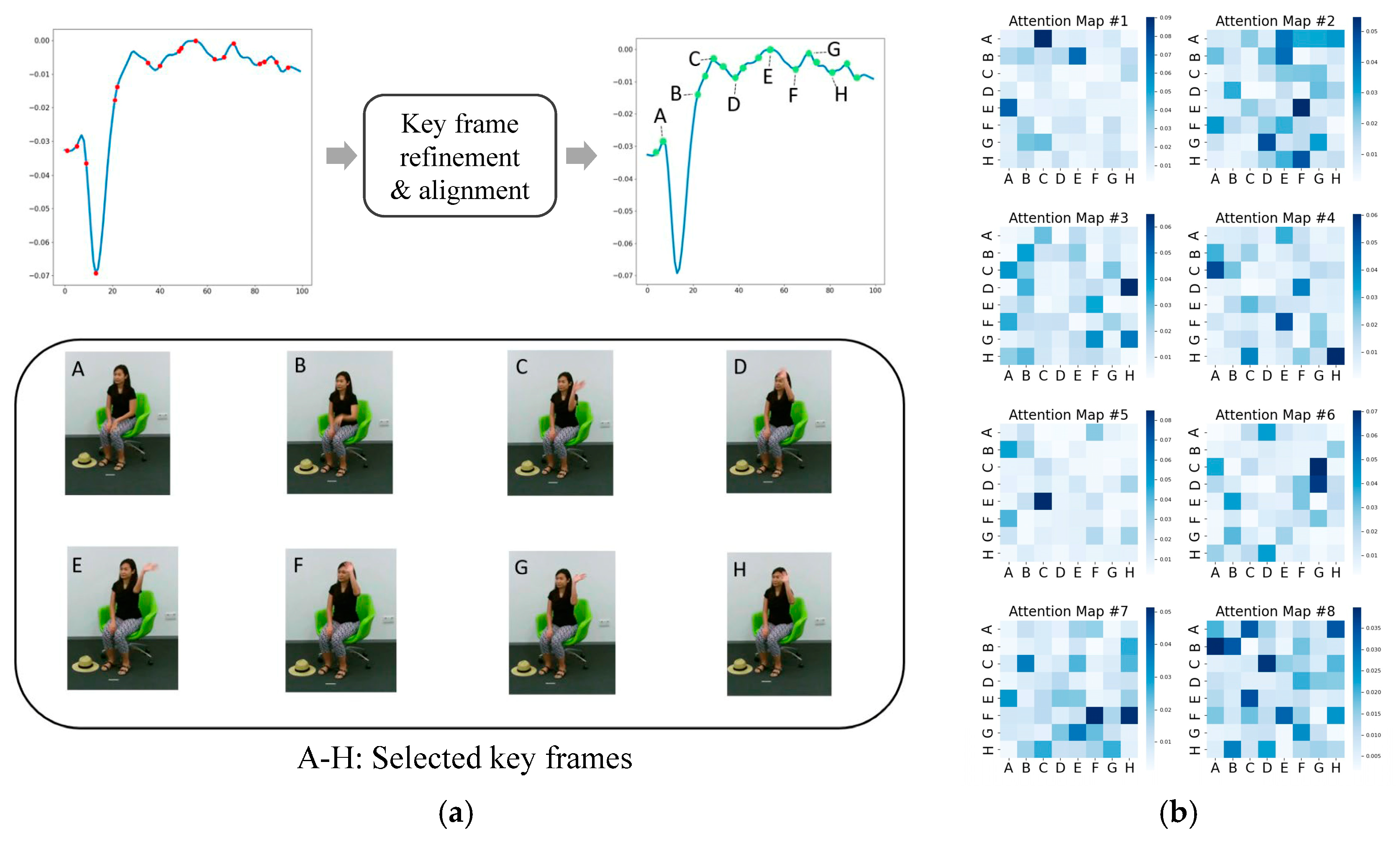
3.2. Key Frame Refinement and Alignment
3.3. Skeleton-Based Action Recognition
4. Experiments
4.1. Datasets
4.2. Implementation Details
4.3. Comparison with the State-of-the-Art Methods
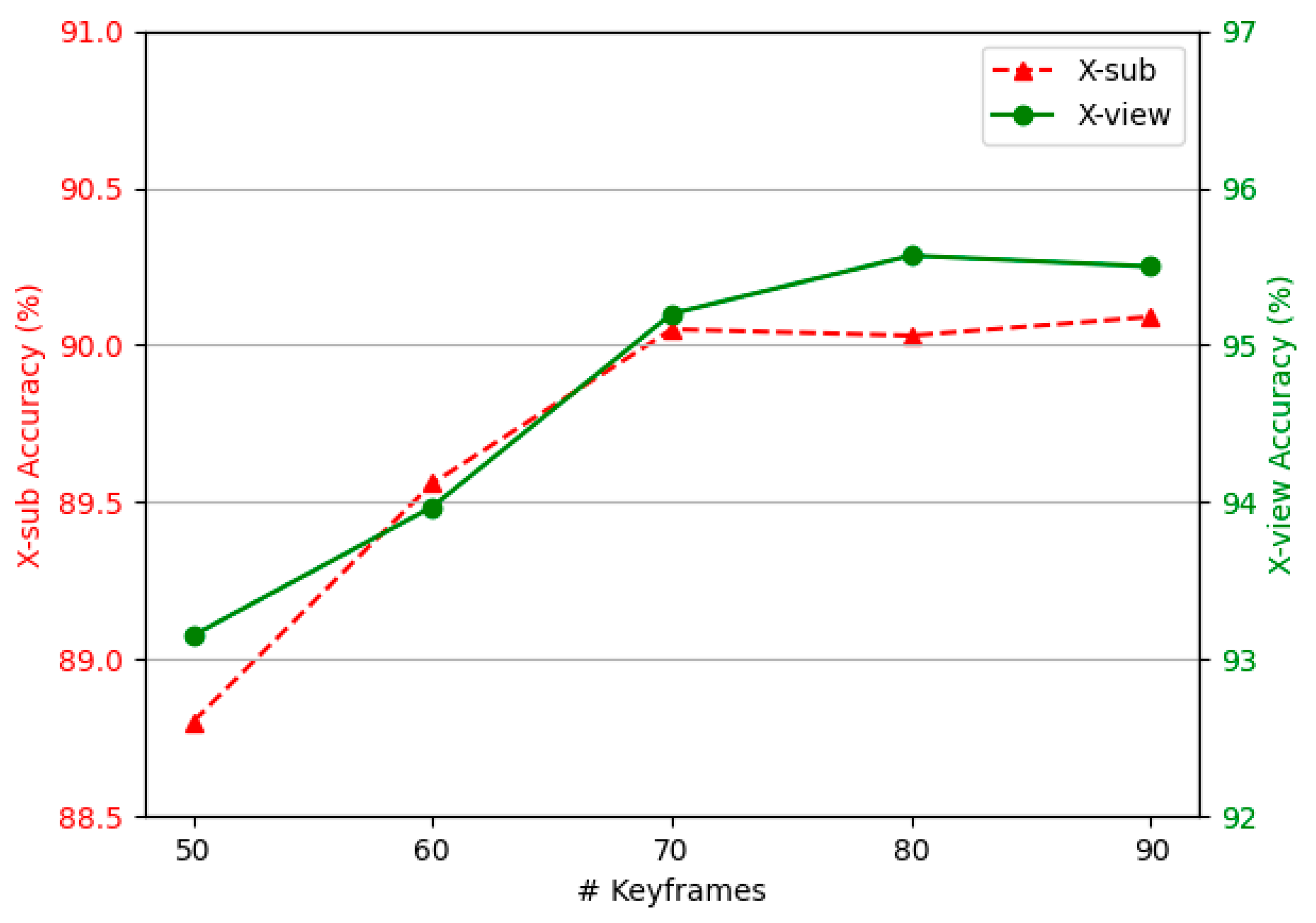
4.4. Analysis on the Length of Key Frame Sequence
4.5. Ablation Study
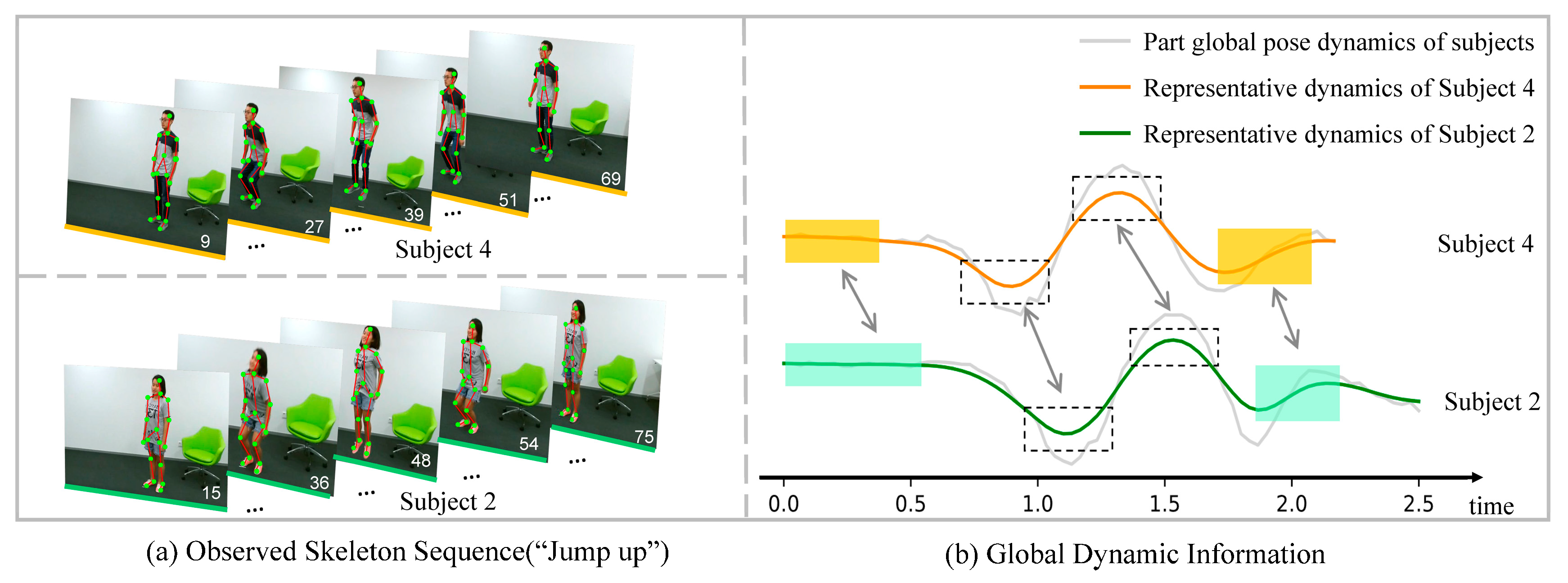
4.6. Visualization Result
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, S.; Xiong, Y.; Lin, D. Spatial temporal graph convolutional networks for skeleton-based action recognition. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 7444–7452. [Google Scholar]
- Li, M.; Chen, S.; Chen, X.; Zhang, Y.; Wang, Y.; Tian, Q. Actional-structural graph convolutional networks for skeleton-based action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; IEEE: New York, NY, USA, 2019; pp. 3595–3603. [Google Scholar]
- Shi, L.; Zhang, Y.; Cheng, J.; Lu, H. Two-stream adaptive graph convolutional networks for skeleton-based action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 12026–12035. [Google Scholar]
- Peng, W.; Hong, X.; Chen, H.; Zhao, G. Learning graph convolutional network for skeleton-based human action recognition by neural searching. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 2669–2676. [Google Scholar]
- Ye, F.; Pu, S.; Zhong, Q.; Li, C.; Xie, D.; Tang, H. Dynamic GCN: Context-enriched topology learning for skeleton-based action recognition. In Proceedings of the ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; pp. 55–63. [Google Scholar]
- Shi, L.; Zhang, Y.; Cheng, J.; Lu, H. Skeleton-based action recognition with multi-stream adaptive graph convolutional networks. IEEE Trans. Image Process. 2020, 29, 9532–9545. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; He, T.; Zhou, X.; Ge, S. Focusing and diffusion: Bidirectional attentive graph convolutional networks for skeleton-based action recognition. arXiv 2019, arXiv:1912.11521. [Google Scholar]
- Zeng, A.; Sun, X.; Yang, L.; Zhao, N.; Liu, M.; Xu, Q. Learning skeletal graph neural networks for hard 3d pose estimation. In Proceedings of the IEEE International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 11416–11425. [Google Scholar]
- Chen, Y.; Zhang, Z.; Yuan, C.; Li, B.; Deng, Y.; Hu, W. Channel-wise topology refinement graph convolution for skeleton-based action recognition. In Proceedings of the IEEE International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 13339–13348. [Google Scholar]
- Zhou, Y.; Yan, X.; Cheng, Z.-Q.; Yan, Y.; Dai, Q.; Hua, X.-S. Blockgcn: Redefine topology awareness for skeleton-based action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 2049–2058. [Google Scholar]
- Song, Y.; Zhang, Z.; Wang, L. Richly activated graph convolutional network for action recognition with incomplete skeletons. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1–5. [Google Scholar]
- Song, Y.; Zhang, Z.; Shan, C.; Wang, L. Richly activated graph convolutional network for robust skeleton-based action recognition. IEEE Trans. Circuit Syst. Video Technol. 2021, 31, 1915–1925. [Google Scholar] [CrossRef]
- Li, S.; Yi, J.; Farha, Y.A.; Gall, J. Pose refinement graph convolutional network for skeleton-based action recognition. IEEE Robot. Autom. Lett. 2021, 6, 1028–1035. [Google Scholar] [CrossRef]
- Cheng, K.; Zhang, Y.; He, X.; Chen, W.; Cheng, J.; Lu, H. Skeleton-based action recognition with shift graph convolutional network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 180–189. [Google Scholar]
- Song, Y.; Zhang, Z.; Shan, C.; Wang, L. Constructing stronger and faster baselines for skeleton-based action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 1474–1488. [Google Scholar] [CrossRef] [PubMed]
- Shahroudy, A.; Liu, J.; Ng, T.; Wang, G. NTU RGB+D: A large scale dataset for 3d human activity analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1010–1019. [Google Scholar] [CrossRef]
- Duan, H.; Zhao, Y.; Chen, K.; Shao, D.; Lin, D.; Dai, B. Revisiting skeleton-based action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 2969–2978. [Google Scholar]
- Sun, Z.; Ke, Q.; Rahmani, H.; Bennamoun, M.; Wang, G.; Liu, J. Human action recognition from various data modalities: A review. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 3200–3225. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Hu, W.; Tang, J.; Liu, J.; Guo, Z. Optimized skeleton-based action recognition via sparsified graph regression. In Proceedings of the ACM International Conference on Multimedia, New York, NY, USA, 21–25 October 2019; pp. 601–610. [Google Scholar]
- Yang, D.; Li, M.M.; Fu, H.; Fan, J.; Leung, H. Centrality graph convolutional networks for skeleton-based action recognition. arXiv 2020, arXiv:2003.03007. [Google Scholar]
- Chen, T.; Zhou, D.; Wang, J.; Wang, S.; Guan, Y.; He, X.; Ding, E. Learning multi-granular spatio-temporal graph network for skeleton-based action recognition. In Proceedings of the ACM International Conference on Multimedia, Virtual, 20–24 October 2021; pp. 4334–4342. [Google Scholar]
- Liu, H.; Liu, Y.; Chen, Y.; Yuan, C.; Li, B.; Hu, W. Transkeleton: Hierarchical spatial-temporal transformer for skeleton-based action recognition. IEEE Trans. Circuit Syst. Video Technol. 2023, 33, 4137–4148. [Google Scholar] [CrossRef]
- Pang, C.; Lu, X.; Lyu, L. Skeleton-based action recognition through contrasting two-stream spatial-temporal networks. IEEE Trans. Multimed. 2023, 25, 8699–8711. [Google Scholar] [CrossRef]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked autoencoders are scalable vision learners. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16000–16009. [Google Scholar]
- Tong, Z.; Song, Y.; Wang, J.; Wang, L. Videomae: Masked autoencoders are data-efficient learners for self-supervised video pre-training. arXiv 2022, arXiv:2203.12602. [Google Scholar]
- Tang, Y.; Tian, Y.; Lu, J.; Li, P.; Zhou, J. Deep progressive reinforcement learning for skeleton-based action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5323–5332. [Google Scholar]
- Zhao, Z.; Elgammal, A.M. Information theoretic key frame selection for action recognition. In Proceedings of the British Machine Vision Conference (BMVC), Leeds, UK, 1–4 September 2008; Everingham, M., Needham, C.J., Fraile, R., Eds.; British Machine Vision Association: Durham, UK, 2008; pp. 1–10. [Google Scholar]
- Ding, C.; Wen, S.; Ding, W.; Liu, K.; Belyaev, E. Temporal segment graph convolutional networks for skeleton-based action recognition. Eng. Appl. Artif. Intell. 2022, 110, 104675. [Google Scholar] [CrossRef]
- Dong, W.; Zhang, Z.; Song, C.; Tan, T. Identifying the key frames: An attention-aware sampling method for action recognition. Pattern Recognit. 2022, 130, 108797. [Google Scholar] [CrossRef]
- Du, Y.; Wang, W.; Wang, L. Hierarchical recurrent neural network for skeleton based action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1110–1118. [Google Scholar]
- Maddison, C.J.; Mnih, A.; Teh, Y.W. The concrete distribution: A continuous relaxation of discrete random variables. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Liu, J.; Shahroudy, A.; Perez, M.; Wang, G.; Duan, L.; Kot, A.C. NTU RGB+D 120: A large-scale benchmark for 3d human activity understanding. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2684–2701. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Lan, C.; Zeng, W.; Xing, J.; Xue, J.; Zheng, N. Semantics-guided neural networks for efficient skeleton-based human action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1112–1121. [Google Scholar]
- Lan, G.; Wu, Y.; Hu, F.; Hao, Q. Vision-based human pose estimation via deep learning: A survey. IEEE Trans. Hum.-Mach. Syst. 2023, 53, 253–268. [Google Scholar] [CrossRef]
- Si, C.; Jing, Y.; Wang, W.; Wang, L.; Tan, T. Skeleton-based action recognition with spatial reasoning and temporal stack learning. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8 September 2018; pp. 106–121. [Google Scholar]
- Liu, Z.; Zhang, H.; Chen, Z.; Wang, Z.; Ouyang, W. Disentangling and unifying graph convolutions for skeleton-based action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 140–149. [Google Scholar]
- Huang, L.; Huang, Y.; Ouyang, W.; Wang, L. Part-level graph convolutional network for skeleton-based action recognition. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 11045–11052. [Google Scholar]
- Chen, Z.; Li, S.; Yang, B.; Li, Q.; Liu, H. Multi-scale spatial temporal graph convolutional network for skeleton-based action recognition. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; pp. 1113–1122. [Google Scholar]
- Zhou, H.; Liu, Q.; Wang, Y. Learning discriminative representations for skeleton based action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 10608–10617. [Google Scholar]
- Shi, L.; Zhang, Y.; Cheng, J.; Lu, H. Skeleton-based action recognition with directed graph neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7912–7921. [Google Scholar]
- Xu, K.; Ye, F.; Zhong, Q.; Xie, D. Topology-aware convolutional neural network for efficient skeleton-based action recognition. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; pp. 2866–2874. [Google Scholar]
- Wu, C.; Wu, X.-J.; Xu, T.; Shen, Z.; Kittler, J. Motion complement and temporal multifocusing for skeleton-based action recognition. IEEE Trans. Circuit Syst. Video Technol. 2023, 34, 34–45. [Google Scholar] [CrossRef]
- Lee, J.; Lee, M.; Lee, D.; Lee, S. Hierarchically decomposed graph convolutional networks for skeleton-based action recognition. In Proceedings of the IEEE International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 10410–10419. [Google Scholar]
| Methods | Features | X-Sub | X-View |
|---|---|---|---|
| ST-GCN [1] | Joint | 81.5 | 88.3 |
| SR-TSL [35] | Joint | 78.8 | 88.2 |
| AS-GCN [2] | Joint | 86.8 | 94.2 |
| AGCN [3] | Joint | - | 93.7 |
| MS-G3D [36] | Joint | 89.4 | 95.0 |
| PL-GCN [37] | Joint | 84.0 | 90.5 |
| MST-GCN [38] | Joint | 89.0 | 95.1 |
| Skeletal [8] | Joint | 89.0 | 95.3 |
| DualHead-Net [21] | Joint | 90.3 | 96.1 |
| TranSkeleton [22] | Joint | 90.1 | 95.4 |
| FR Head [39] | Joint | 90.3 | 95.3 |
| BlockGCN [10] | Joint | 90.9 | 95.4 |
| Ours (CTR-GC [9]) | Joint | 90.2 | 95.6 |
| Ours (Block-GC [10]) | Joint | 91.5 | 96.1 |
| DGNN [40] | Fusion-4s | 89.9 | 96.1 |
| Shift-GCN [14] | Fusion-4s | 90.7 | 96.5 |
| Dynamic GCN [5] | Fusion-4s | 91.5 | 96.0 |
| MST-GCN [38] | Fusion-4s | 91.5 | 96.6 |
| Skeletal [8] | Fusion-4s | 91.6 | 96.7 |
| CTR-GCN [9] | Fusion-4s | 92.4 | 96.8 |
| DualHead-Net [21] | Fusion-4s | 92.0 | 96.6 |
| Ta-CNN+ [41] | Fusion-4s | 90.7 | 95.1 |
| MCTM-Net [42] | Fusion-4s | 92.8 | 96.8 |
| FR Head [39] | Fusion-4s | 92.8 | 96.8 |
| BlockGCN [10] | Fusion-4s | 93.1 | 97.0 |
| Ours (CTR-GC [9]) | Fusion-4s | 92.7 | 96.9 |
| Ours (Block-GC [10]) | Fusion-4s | 93.1 | 97.1 |
| Methods | Features | X-Sub | X-Setup |
|---|---|---|---|
| MST-GCN [38] | Joint | 82.8 | 84.5 |
| Skeletal [8] | Joint | 83.5 | 85.7 |
| DualHead-Net [21] | Joint | 84.6 | 85.9 |
| TranSkeleton [22] | Joint | 84.9 | 86.3 |
| HDGCN [43] | Joint | 85.7 | 87.3 |
| FR Head [39] | Joint | 85.5 | 87.3 |
| BlockGCN [10] | Joint | 86.9 | 88.2 |
| Ours (CTR-GC [9]) | Joint | 86.2 | 88.7 |
| Ours (Block-GC [10]) | Joint | 86.7 | 88.6 |
| Shift-GCN [14] | Fusion-4s | 85.9 | 87.6 |
| Dynamic GCN [5] | Fusion-4s | 87.3 | 88.6 |
| MST-GCN [38] | Fusion-4s | 87.5 | 88.8 |
| Skeletal [8] | Fusion-4s | 87.5 | 89.2 |
| CTR-GCN [9] | Fusion-4s | 88.9 | 90.6 |
| DualHead-Net [21] | Fusion-4s | 88.2 | 89.3 |
| Ta-CNN+ [41] | Fusion-4s | 85.7 | 87.3 |
| MCTM-Net [42] | Fusion-4s | 89.3 | 91.0 |
| FR Head [39] | Fusion-4s | 89.5 | 87.3 |
| BlockGCN [10] | Fusion-4s | 90.3 | 91.5 |
| Shift-GCN [14] | Fusion-4s | 85.9 | 87.6 |
| Ours (CTR-GC [9]) | Fusion-4s | 89.1 | 90.9 |
| Ours (Block-GC [10]) | Fusion-4s | 90.4 | 91.7 |
| Methods | w/o KFRA (%) | w/KFRA (%) | |||
|---|---|---|---|---|---|
| Top 1 | Top 5 | Top 1 | Top 5 | ||
| All | X-sub | 92.3 | 98.2 | - | - |
| X-view | 96.3 | 99.4 | - | - | |
| Uniform sampling | X-sub | 92.1 | 98.3 | 92.1 | 97.9 |
| X-view | 95.6 | 98.6 | 95.8 | 98.7 | |
| Salient posture (ours) | X-sub | 92.2 | 98.1 | 92.5 | 98.9 |
| X-view | 96.1 | 98.8 | 96.9 | 99.7 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, J.; Su, L.; Zhao, Y. Key Frame Selection for Temporal Graph Optimization of Skeleton-Based Action Recognition. Appl. Sci. 2024, 14, 9947. https://doi.org/10.3390/app14219947
Hou J, Su L, Zhao Y. Key Frame Selection for Temporal Graph Optimization of Skeleton-Based Action Recognition. Applied Sciences. 2024; 14(21):9947. https://doi.org/10.3390/app14219947
Chicago/Turabian StyleHou, Jingyi, Lei Su, and Yan Zhao. 2024. "Key Frame Selection for Temporal Graph Optimization of Skeleton-Based Action Recognition" Applied Sciences 14, no. 21: 9947. https://doi.org/10.3390/app14219947
APA StyleHou, J., Su, L., & Zhao, Y. (2024). Key Frame Selection for Temporal Graph Optimization of Skeleton-Based Action Recognition. Applied Sciences, 14(21), 9947. https://doi.org/10.3390/app14219947





