Spectrogram-Based Arrhythmia Classification Using Three-Channel Deep Learning Model with Feature Fusion
Abstract
1. Introduction
2. Datasets and Algorithms
2.1. Dataset Preparation
2.2. Generated Images
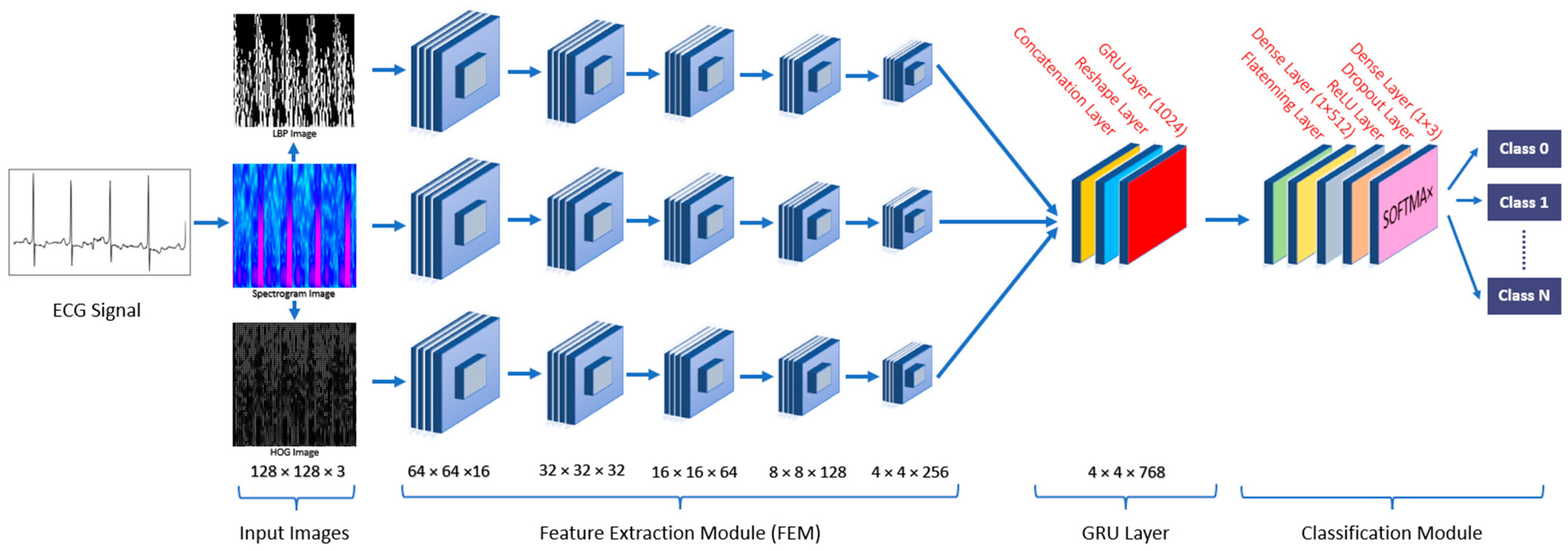
2.2.1. Spectrogram Image
2.2.2. Local Binary Pattern (LBP) Image
2.2.3. Histogram of Oriented Gradients (HOG) Image
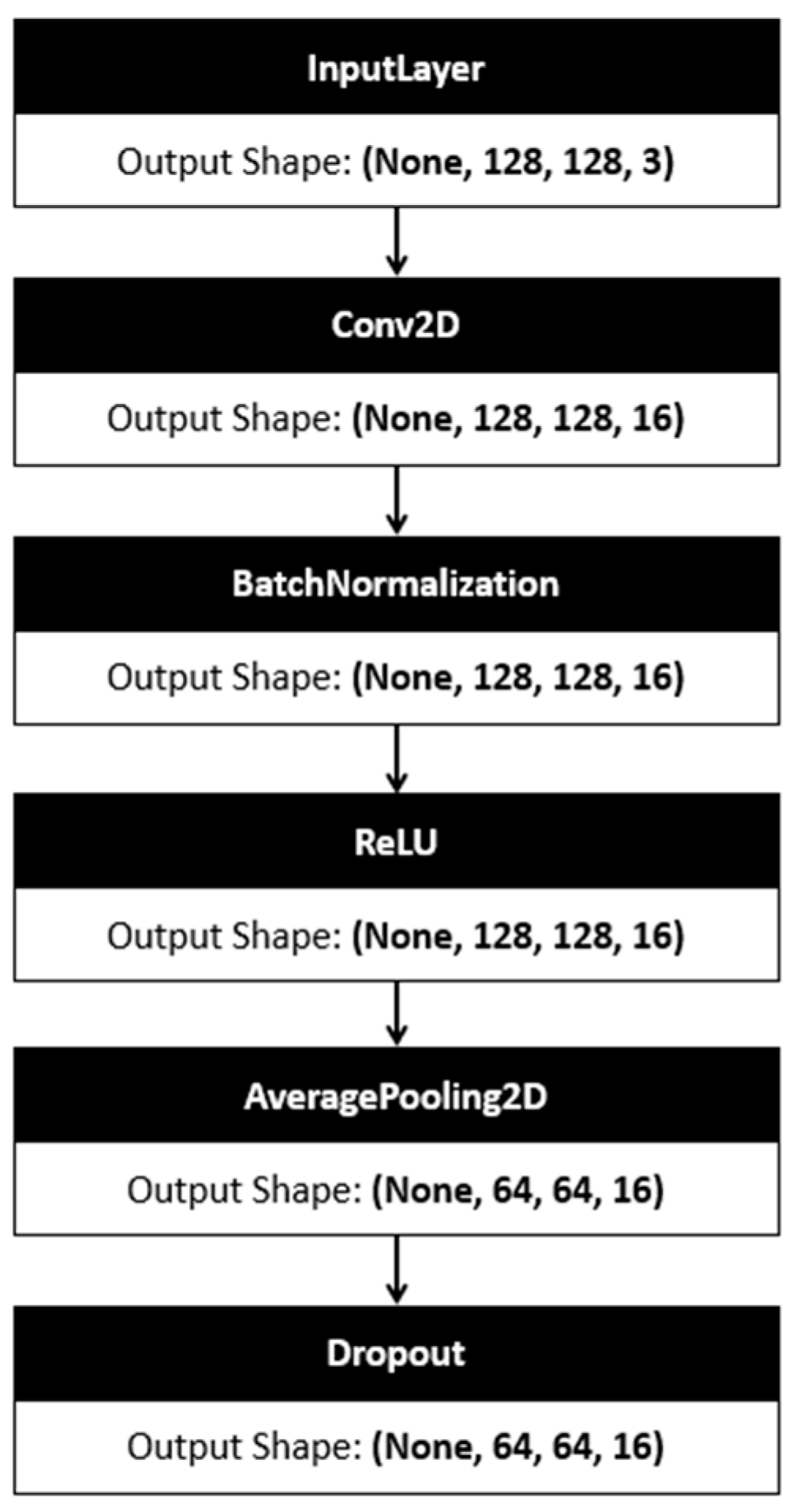
2.3. Deep Learning Algorithms
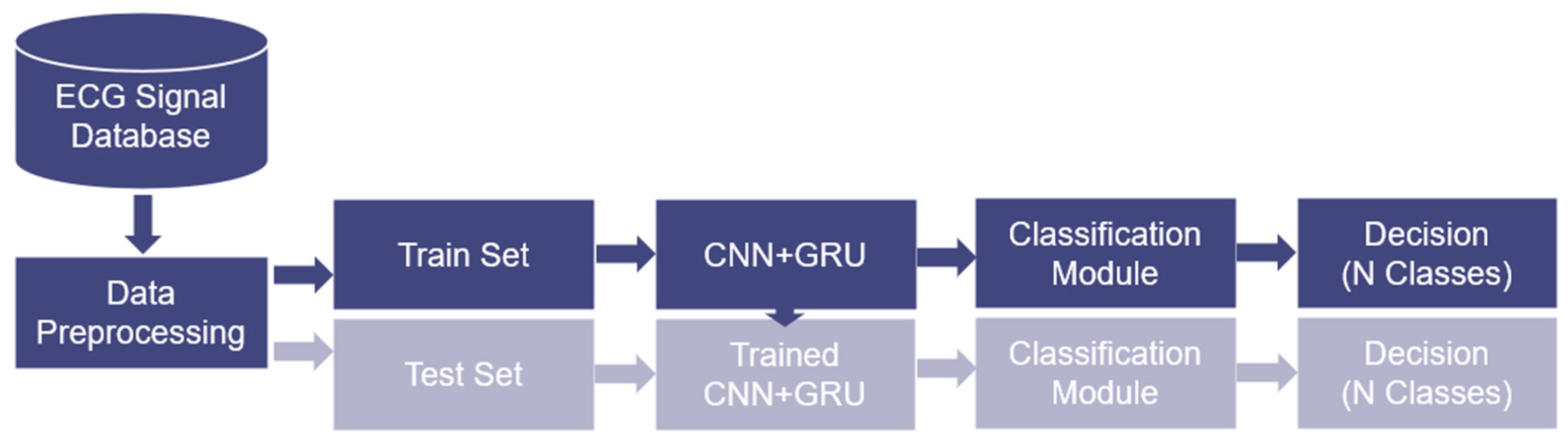
3. Methodology
4. Results and Discussion
4.1. Ablation Study
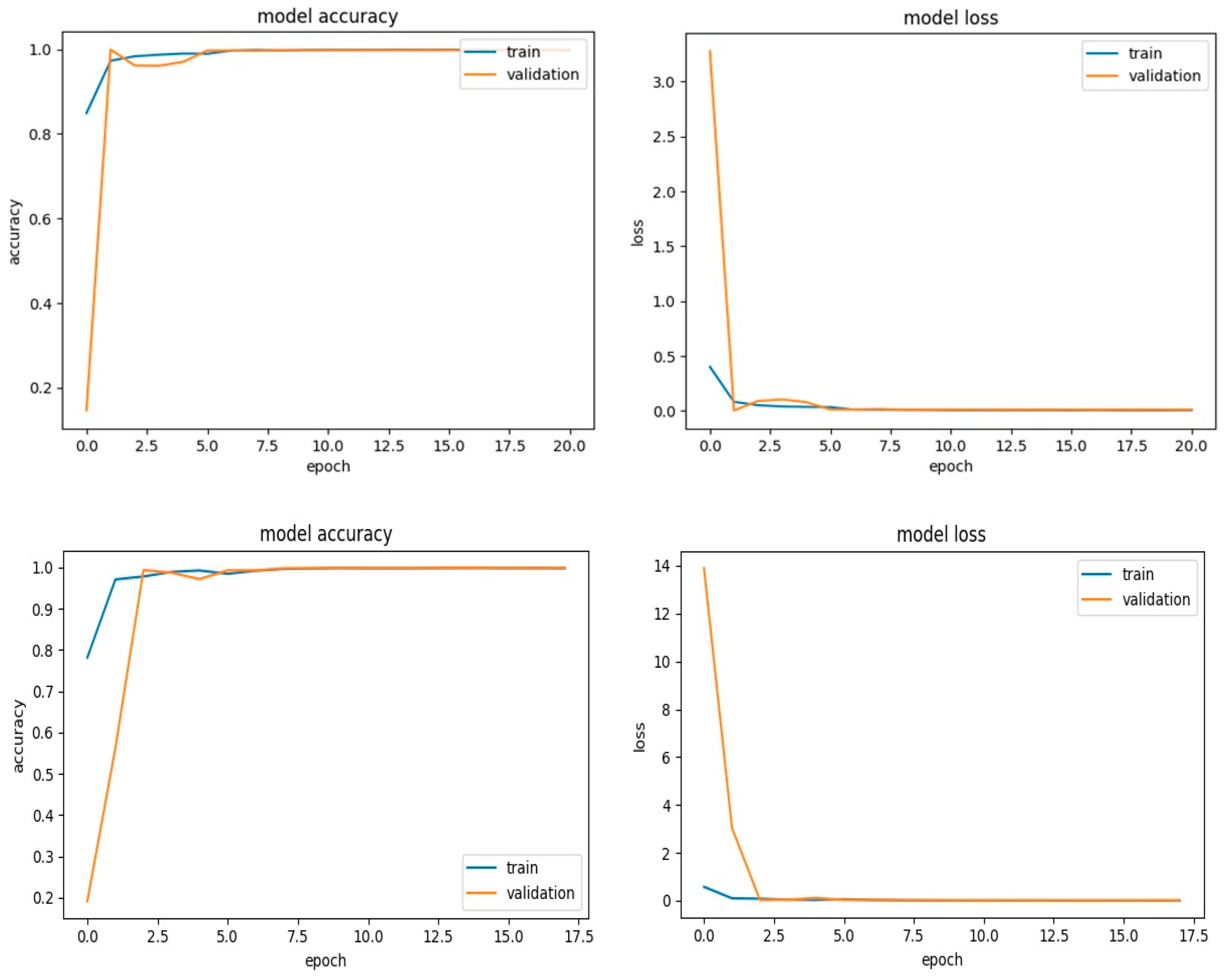
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dubatovka, A. Interpretable and robust Machine Learning Models for Time-Series Analysis in Cardiology. Doctoral Dissertation, ETH Zurich, Zurich, Switzerland, 2024. [Google Scholar] [CrossRef]
- Haseena, H.H.; Joseph, P.K.; Mathew, A.T. Classification of arrhythmia using hybrid networks. J. Med. Syst. 2011, 35, 1617–1630. [Google Scholar] [CrossRef] [PubMed]
- Sannino, G.; De Pietro, G. A deep learning approach for ECG-based heartbeat classification for arrhythmia detection. Future Gener. Comput. Syst. 2018, 86, 446–455. [Google Scholar] [CrossRef]
- Çınar, A.; Tuncer, S.A. Classification of normal sinus rhythm, abnormal arrhythmia and congestive heart failure ECG signals using LSTM and hybrid CNN-SVM deep neural networks. Comput. Methods Biomech. Biomed. Eng. 2021, 24, 203–214. [Google Scholar] [CrossRef] [PubMed]
- Eleyan, A.; AlBoghbaish, E.; AlShatti, A.; AlSultan, A.; AlDarbi, D. RHYTHMI: A deep learning-based mobile ECG device for heart disease prediction. Appl. Syst. Innov. 2024, 7, 77. [Google Scholar] [CrossRef]
- Qammar, N.W.; Vainoras, A.; Navickas, Z.; Jaruševičius, G.; Ragulskis, M. Early Diagnosis of Atrial Fibrillation Episodes: Comparative Analysis of Different Matrix Architectures. Appl. Sci. 2024, 14, 6191. [Google Scholar] [CrossRef]
- Deng, J.; Ma, J.; Yang, J.; Liu, S.; Chen, H.; Wang, X.; Zhang, X. An Energy-Efficient ECG Processor Based on HDWT and a Hybrid Classifier for Arrhythmia Detection. Appl. Sci. 2024, 14, 342. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Gabbouj, M. Real-time patient-specific ECG classification by 1-D convolutional neural networks. IEEE Trans. Biomed. Eng. 2016, 63, 664–675. [Google Scholar] [CrossRef]
- Jeong, Y.; Lee, J.; Shin, M. Enhancing Inter-Patient Performance for Arrhythmia Classification with Adversarial Learning Using Beat-Score Maps. Appl. Sci. 2024, 14, 7227. [Google Scholar] [CrossRef]
- Acharya, U.R.; Oh, S.L.; Hagiwara, Y.; Tan, J.H.; Adam, M.; Gertych, A.; San Tan, R. A deep convolutional neural network model to classify heartbeats. Comput. Biol. Med. 2017, 89, 389–396. [Google Scholar] [CrossRef]
- Hannun, A.Y.; Rajpurkar, P.; Haghpanahi, M.; Tison, G.H.; Bourn, C.; Turakhia, M.P.; Ng, A.Y. Cardiologist-level arrhythmia detection and classification in ambulatory electrocardiograms using a deep neural network. Nat. Med. 2019, 25, 65–69. [Google Scholar] [CrossRef]
- Hammad, M.; Iliyasu, A.M.; Subasi, A.; Ho, E.S.L.; El-Latif, A.A.A. A multitier deep learning model for arrhythmia detection. IEEE Trans. Instrum. Meas. 2021, 70, 2502809. [Google Scholar] [CrossRef]
- Petmezas, G.; Haris, K.; Stefanopoulos, L.; Kilintzis, V.; Tzavelis, A.; Rogers, J.A.; Katsaggelos, A.K.; Maglaveras, N. Automated atrial fibrillation detection using a hybrid CNN-LSTM network on imbalanced ECG datasets. Biomed. Signal Process. Control 2021, 63, 102194. [Google Scholar] [CrossRef]
- Tuncer, T.; Dogan, S.; Plawiak, P.; Subasi, A. A novel discrete wavelet-concatenated mesh tree and ternary chess pattern-based ECG signal recognition method. Biomed. Signal Process. Control 2022, 72, 103331. [Google Scholar] [CrossRef]
- Ma, K.; Zhan, C.A.; Yang, F. Multi-classification of arrhythmias using ResNet with CBAM on CWGAN-GP augmented ECG Gramian Angular Summation Field. Biomed. Signal Process. Control 2022, 77, 103684. [Google Scholar] [CrossRef]
- Merbouti, M.A.; Cherifi, D. Machine learning based electrocardiogram peaks analyzer for Wolff-Parkinson-White syndrome. Biomed. Signal Process. Control 2023, 86, 105302. [Google Scholar] [CrossRef]
- Park, J.; Lee, K.; Park, N.; You, S.C.; Ko, J. Self-attention LSTM-FCN model for arrhythmia classification and uncertainty assessment. Artif. Intell. Med. 2023, 142, 102570. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, A.; Zhao, C.; Yang, H.; Dou, M. Categorization of ECG signals based on the dense recurrent network. Signal Image Video Process. 2024, 18, 3373–3381. [Google Scholar] [CrossRef]
- Eleyan, A.; Alboghbaish, E. Electrocardiogram signals classification using deep-learning-based incorporated convolutional neural network and long short-term memory framework. Computers 2024, 13, 55. [Google Scholar] [CrossRef]
- Prusty, M.R.; Pandey, T.N.; Lekha, P.S.; Lellapalli, G.; Gupta, A. Scalar invariant transform-based deep learning framework for detecting heart failures using ECG signals. Sci. Rep. 2024, 14, 2633. [Google Scholar] [CrossRef]
- Eleyan, A.; Alboghbaish, E.; Eleyan, G. Performance comparison between transform-based deep learning approaches for ECG signal classification. In Proceedings of the 11th International Conference on Electrical & Electronics Engineering (ICEEE24), Marmaris, Turkey, 22–24 April 2024. [Google Scholar]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH arrhythmia database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef]
- Baim, D.S.; Colucci, W.S.; Monrad, E.S.; Smith, H.S.; Wright, R.F.; Lanoue, A.; Gauthier, D.F.; Ransil, B.J.; Grossman, W.; Braunwald, E. Survival of patients with severe congestive heart failure treated with oral milrinone. J. Am. Coll. Cardiol. 1986, 7, 661–670. [Google Scholar] [CrossRef] [PubMed]
- Portnoff, M. Time-frequency representation of digital signals and systems based on short-time Fourier analysis. IEEE Trans. Acoust. Speech Signal Process 1980, 28, 55–69. [Google Scholar] [CrossRef]
- Zhao, G.; Pietikainen, M. Dynamic texture recognition using local binary patterns with an application to facial expressions. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 915–928. [Google Scholar] [CrossRef]
- Eleyan, A. Face recognition using ensemble statistical local descriptors. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 9. [Google Scholar] [CrossRef]
- Basar, S.; Ali, M.; Ochoa-Ruiz, G.; Waheed, A.; Rodriguez-Hernandez, G.; Zareei, M. A novel defocused image segmentation method based on PCNN and LBP. IEEE Access 2021, 9, 87219–87240. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikäinen, M.; Harwood, D. A comparative study of texture measures with classification based on featured distributions. Pattern Recognit. 1996, 29, 51–59. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution grayscale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Eleyan, A. Statistical local descriptors for face recognition: A comprehensive study. Multimed. Tools Appl. 2023, 82, 32485–32504. [Google Scholar] [CrossRef]
- Ji, P.; Feng, J.; Ma, F.; Wang, X.; Li, C. Fingertip detection algorithm based on maximum discrimination hog feature in complex background. IEEE Access 2023, 11, 3160–3173. [Google Scholar] [CrossRef]
- Karakaya, F.; Altun, H.; Cavuslu, M.A. Implementation of HOG algorithm for real-time object recognition applications on FPGA based embedded system. In Proceedings of the 2009 IEEE 17th Signal Processing and Communications Applications Conference, Antalya, Turkey, 9–11 April 2009; pp. 508–511. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 886–893. [Google Scholar]
- Liu, S.; Wang, L.; Yue, W. An efficient medical image classification network based on multi-branch CNN, token grouping Transformer and mixer MLP. Appl. Soft Comput. 2024, 153, 111323. [Google Scholar] [CrossRef]
- Bayram, F.; Eleyan, A. COVID-19 detection on chest radiographs using feature fusion-based deep learning. Signal Image Video Process. 2022, 16, 1455–1462. [Google Scholar] [CrossRef] [PubMed]
- Zou, C.; Muller, A.; Wolfgang, U.; Ruckert, D.; Muller, P.; Becker, M.; Steger, A.; Martens, E. Heartbeat classification by random forest with a novel context feature: A segment label. IEEE J. Transl. Eng. Health Med. 2022, 10, 1900508. [Google Scholar] [CrossRef] [PubMed]
- Khan, F.; Yu, X.; Yuan, Z.; Rehman, A.U. ECG classification using 1-D convolutional deep residual neural network. PLoS ONE 2023, 18, 4. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Lu, C.; Sun, Y.; Yang, M.; Liu, C.; Ou, C. Automatic ECG classification using continuous wavelet transform and convolutional neural network. Entropy 2021, 23, 119. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2024, arXiv:1412.3555. [Google Scholar]
- Bolboacă, S.D.; Jäntschi, L. Predictivity Approach for Quantitative Structure-Property Models. Application for Blood-Brain Barrier Permeation of Diverse Drug-Like Compounds. Int. J. Mol. Sci. 2011, 12, 4348–4364. [Google Scholar] [CrossRef]
- Hu, R.; Chen, J.; Zhou, L. A transformer-based deep neural network for arrhythmia detection using continuous ECG signals. Comput. Biol. Med. 2022, 144, 105325. [Google Scholar] [CrossRef]
- Xia, Y.; Wulan, N.; Wang, K.; Zhang, H. Detecting atrial fibrillation by deep convolutional neural networks. Comput. Biol. Med. 2018, 93, 84–92. [Google Scholar] [CrossRef]
- Kim, Y.K.; Lee, M.; Song, H.S.; Lee, S.-W. Automatic cardiac arrhythmia classification using residual network combined with long short-term memory. IEEE Trans. Instrum. Meas. 2022, 71, 4005817. [Google Scholar] [CrossRef]
- Zubair, M.; Yoon, C. Cost-sensitive learning for anomaly detection in imbalanced ECG data using convolutional neural networks. Sensors 2022, 22, 4075. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhang, F.; Sun, Z.; Li, D.; Kong, X.; Zhang, Y. Automatic heartbeat classification using S-shaped reconstruction and a squeeze-and-excitation residual network. Comput. Biol. Med. 2022, 140, 105108. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Jin, H.; Zheng, B.; Luo, W. Deep Learning Modeling of Cardiac Arrhythmia Classification on Information Feature Fusion Image with Attention Mechanism. Entropy 2023, 25, 1264. [Google Scholar] [CrossRef]
- Kumar, V.; Kumar, S.; Raj, K.K.; Assaf, M.H.; Groza, V.; Kumar, R.R. ECG multi-class classification using machine learning techniques. In Proceedings of the 2023 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Jeju, Republic of Korea, 14–16 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Rahuja, N.; Valluru, S.K. A comparative analysis of deep neural network models using transfer learning for electrocardiogram signal classification. In Proceedings of the 2021 International Conference on Recent Trends on Electronics, Information, Communication & Technology (RTEICT), Bengaluru, Karnataka, India, 27–28 August 2021; pp. 285–290. [Google Scholar] [CrossRef]
- Madan, P.; Singh, V.; Singh, D.P.; Diwakar, M.; Pant, B.; Kishor, A.A. Hybrid deep learning approach for ECG-based arrhythmia classification. Bioengineering 2022, 9, 152. [Google Scholar] [CrossRef] [PubMed]
- Daydulo, Y.D.; Thamineni, B.L.; Dawud, A.A. Cardiac arrhythmia detection using deep learning approach and time-frequency representation of ECG signals. BMC Med. Inform. Decis. Mak. 2023, 23, 232. [Google Scholar] [CrossRef]
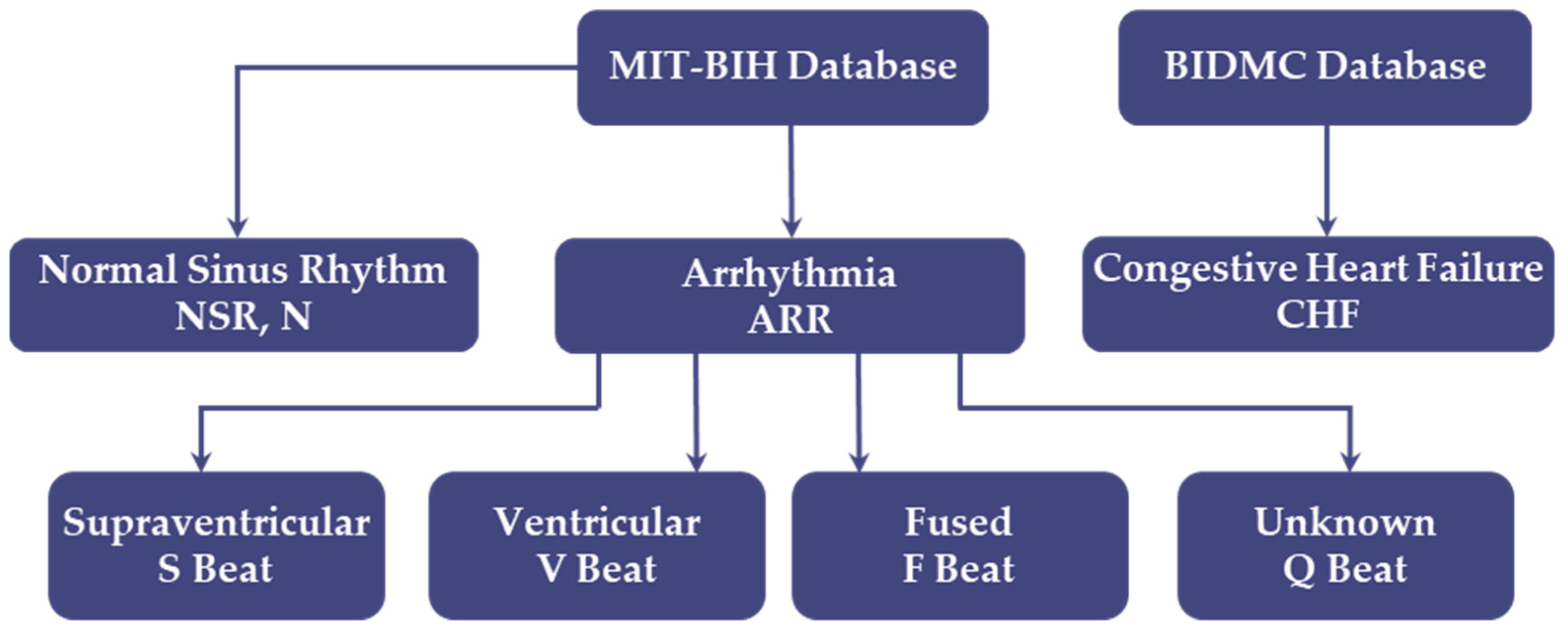
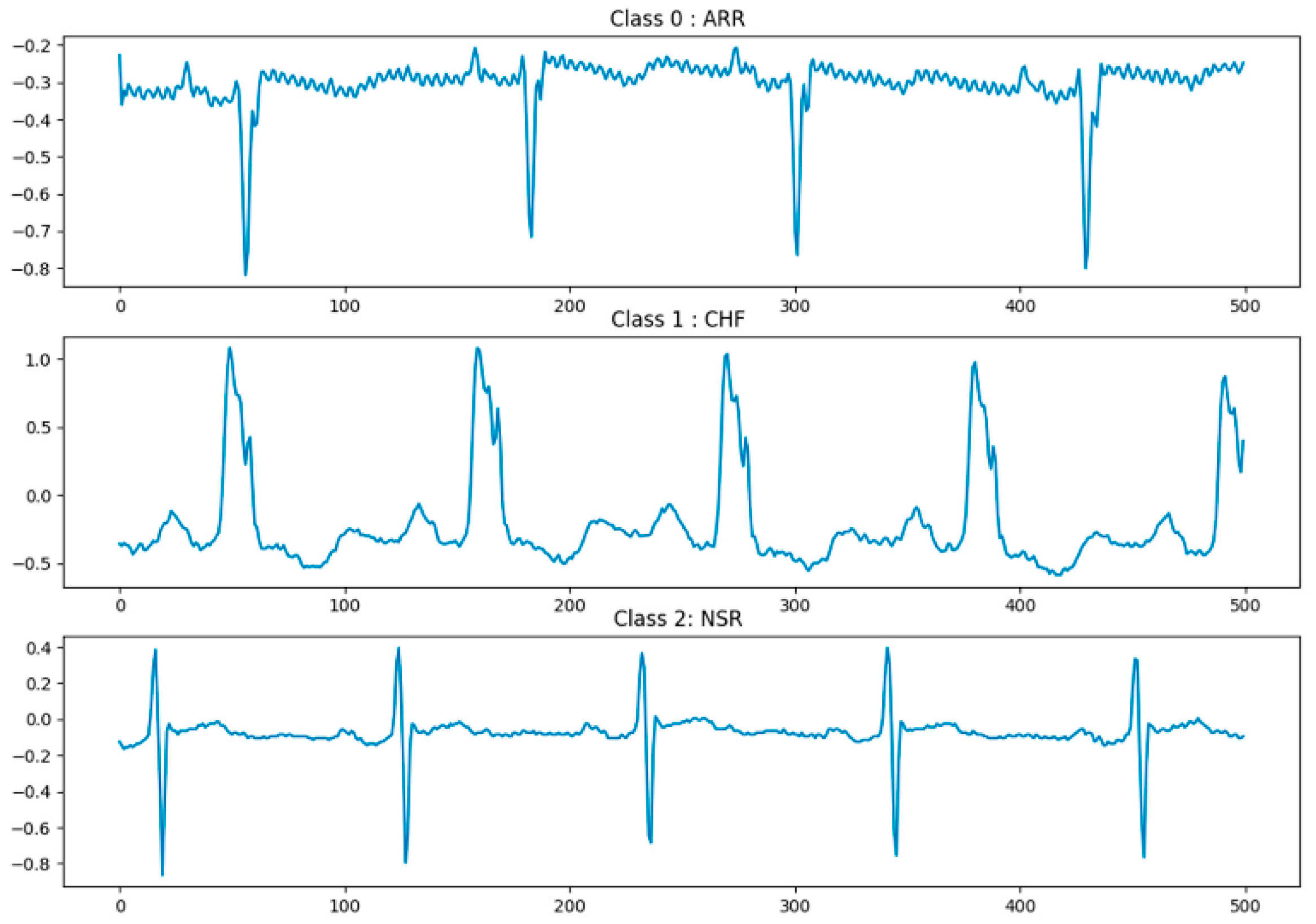
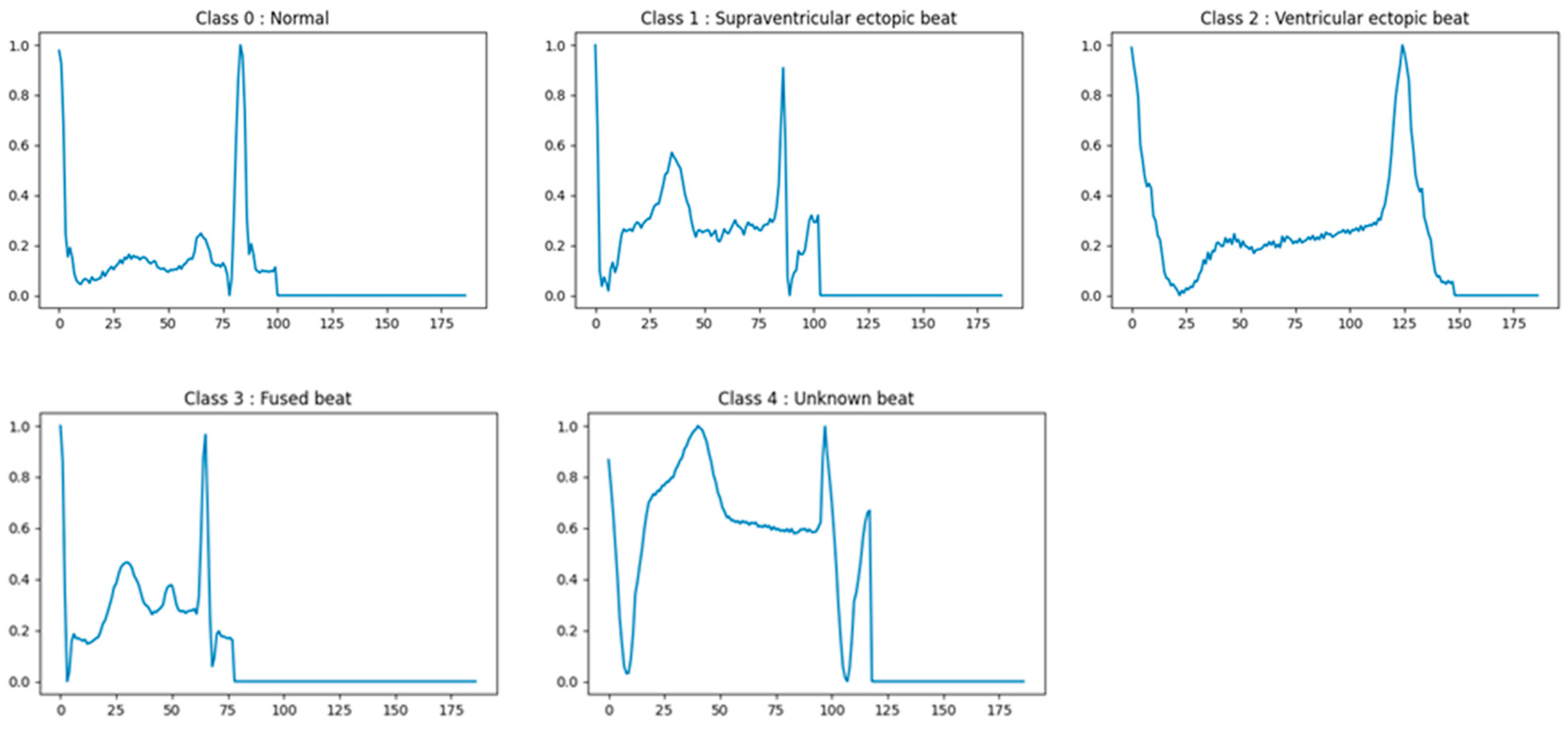

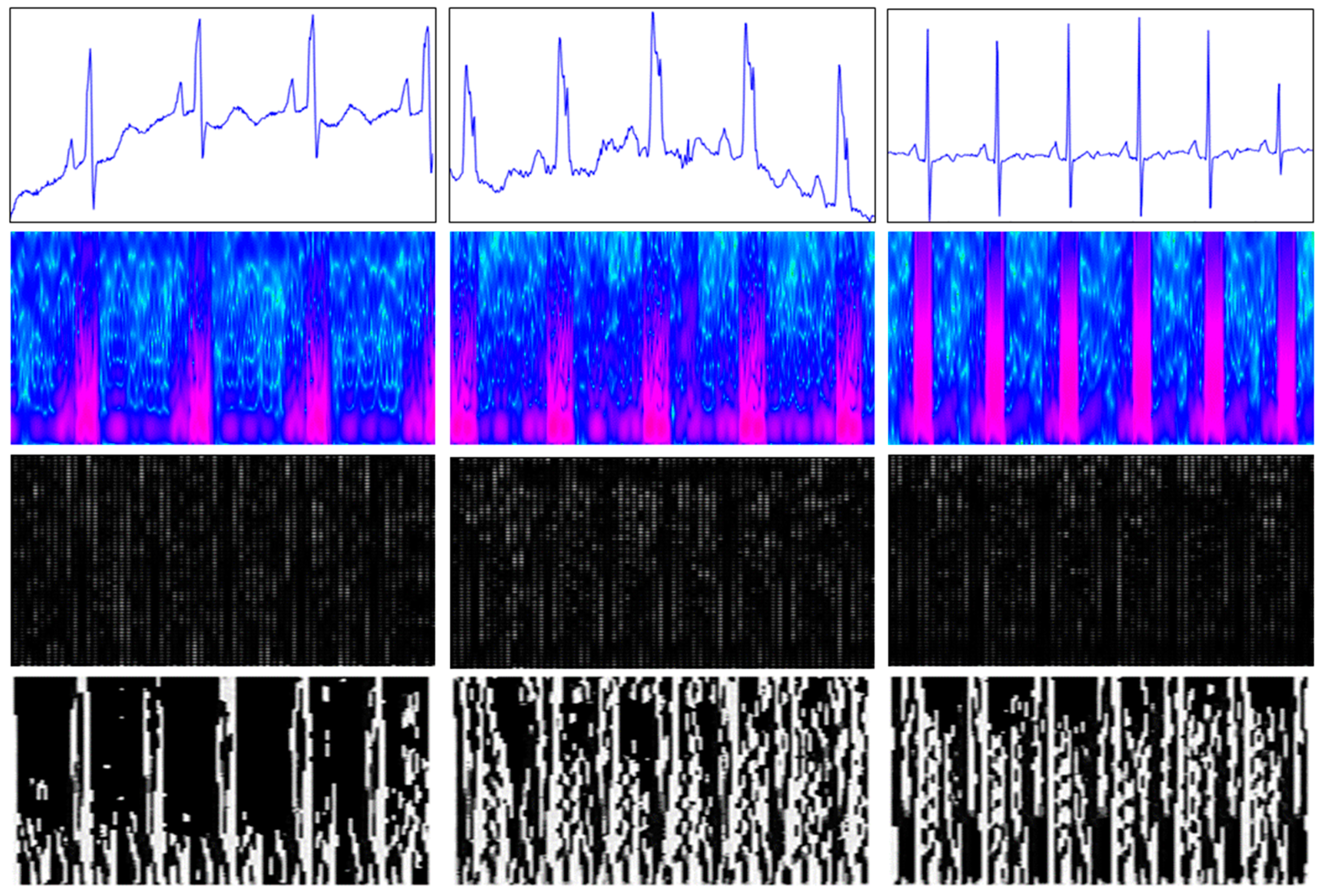
| Datasets | No. of Classes | No. of Samples | Train | Test | Sample Length | Sample in Sec | Classes |
|---|---|---|---|---|---|---|---|
| MIT-BIH | 5 classes | 10,000 | 8000 | 2000 | 187 | 1.46 | N, S, V, F, Q |
| MIT-BIH + BIDMC | 3 classes | 11,790 | 9432 | 2358 | 500 | 3.90 | ARR, SNR, CHF |
| 3-Class Dataset (MIT-BIH + BIDMC) | 5-Class Dataset (MIT-BIH) | |||
|---|---|---|---|---|
| Parameters | Accuracy | Loss | Accuracy | Loss |
| ReLU + Average Pooling | 99.796 | 0.0106 | 99.780 | 0.0246 |
| ReLU + Max Pooling | 98.922 | 0.0359 | 96.969 | 0.1098 |
| Leaky ReLU + Average Pooling | 99.270 | 0.0214 | 99.760 | 0.0285 |
| Leaky ReLU + Max Pooling | 98.905 | 0.0364 | 90.589 | 0.3724 |
| 3-Channel Model | 1-Channel Model | |||
|---|---|---|---|---|
| Spectrogram | LBP | HOG | ||
| Training time (min) | 3.48 | 1.47 | 1.46 | 1.74 |
| Prediction time (sec/image) | 0.0027 | 0.0010 | 0.0010 | 0.0010 |
| Loss rate | 0.0189 | 0.29 | 0.029 | 0.031 |
| Accuracy rate | 99.75 | 98.69 | 98.53 | 98.51 |
| 3-Class Dataset (MIT-BIH + BIDMC) | 5-Class Dataset (MIT-BIH) | |||||||
|---|---|---|---|---|---|---|---|---|
| Precision | Recall | F1-Score | Accuracy | Precision | Recall | F1-Score | Accuracy | |
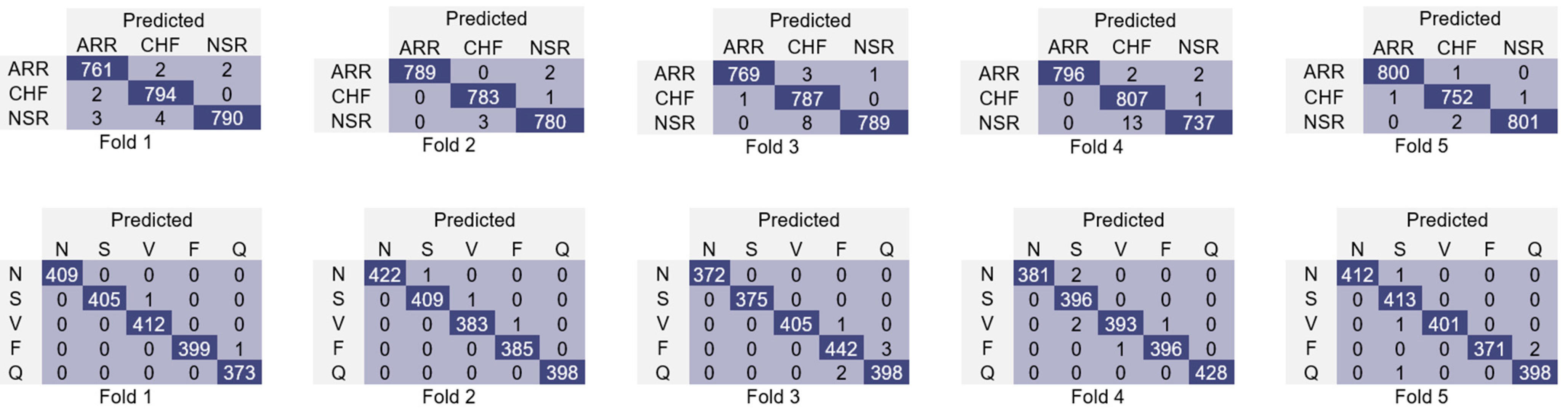
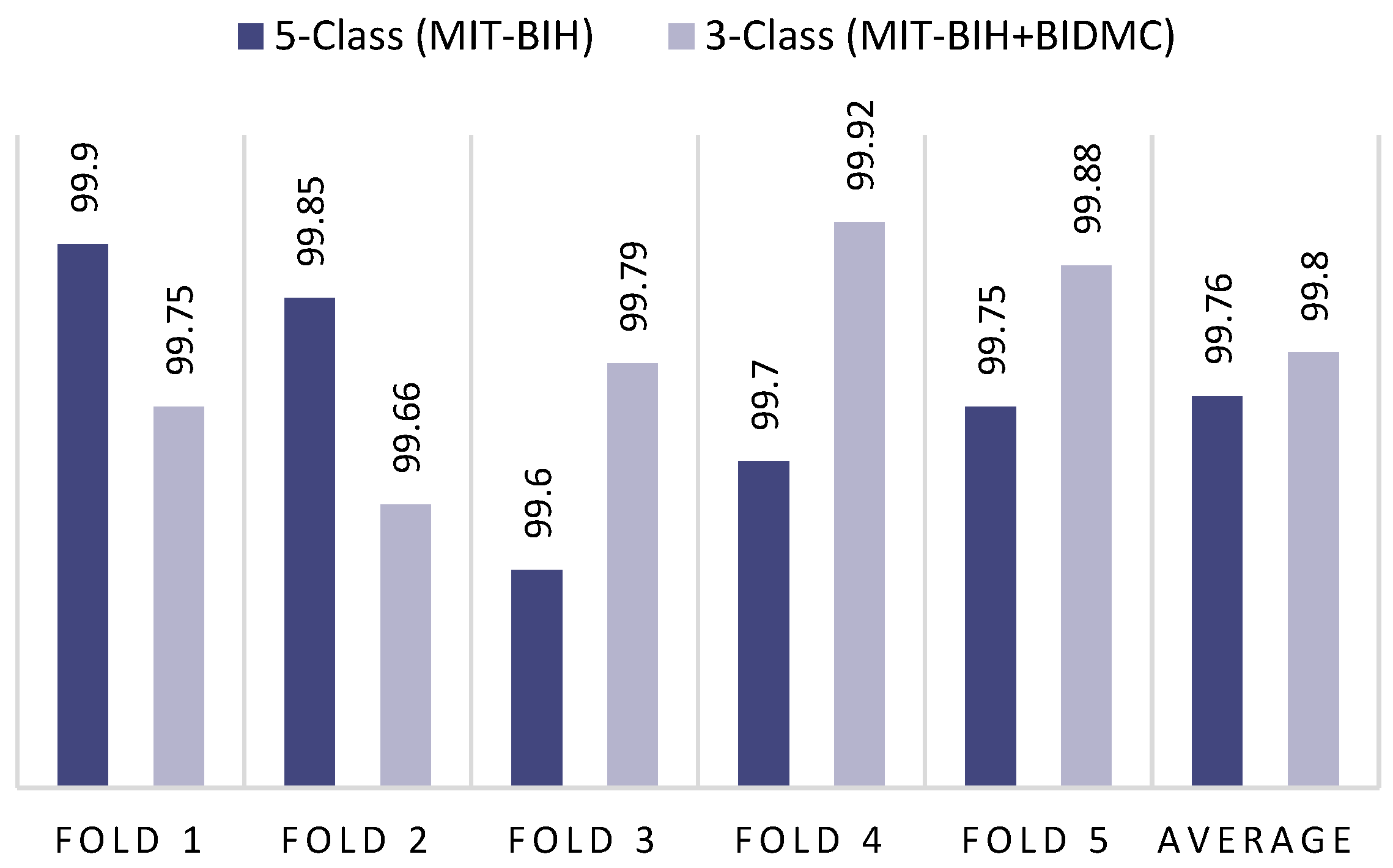
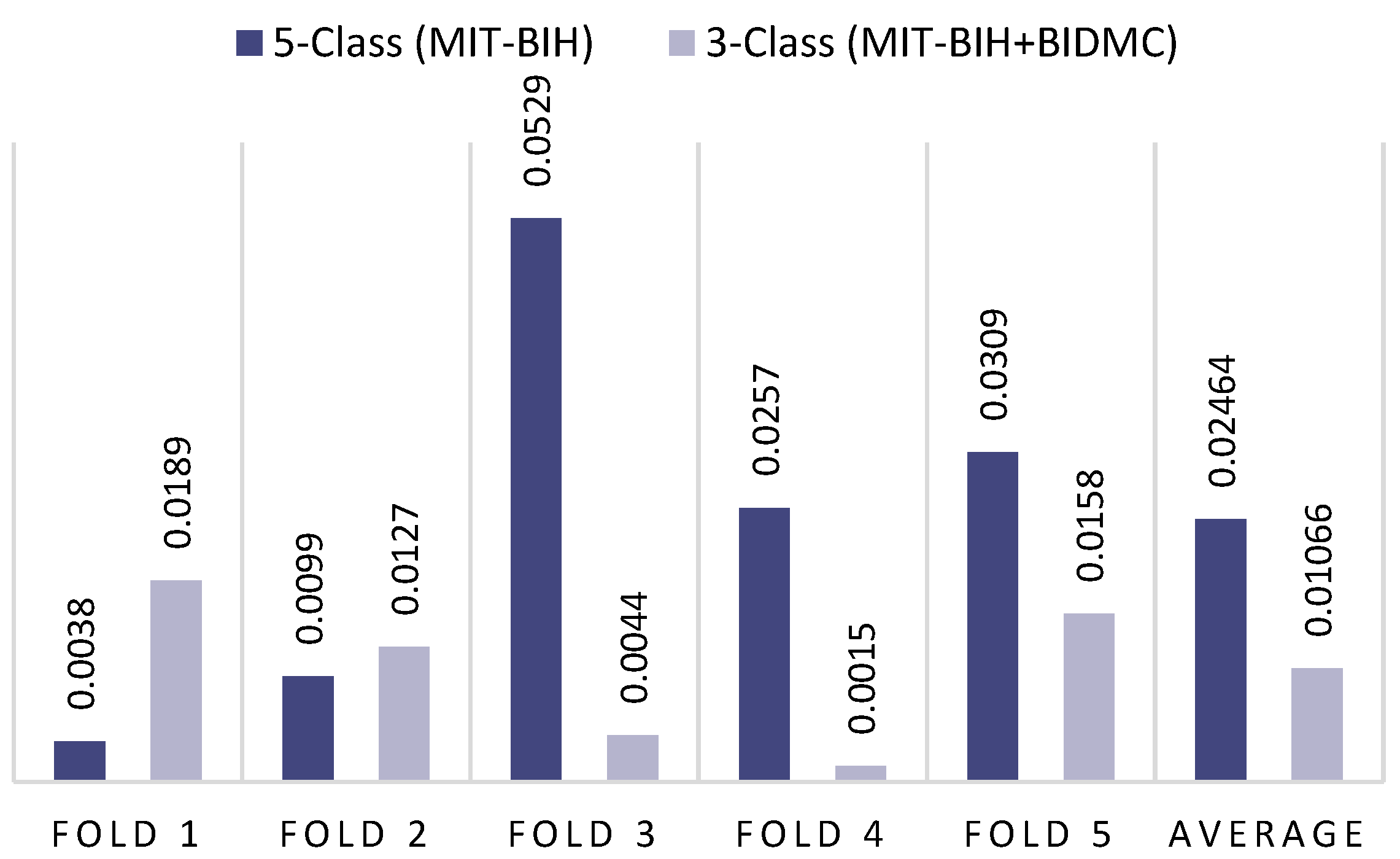
| 1st Fold | 99.75 | 99.75 | 99.75 | 99.75 | 99.90 | 99.90 | 99.90 | 99.90 |
| 2nd Fold | 99.66 | 99.66 | 99.66 | 99.66 | 99.85 | 99.85 | 99.85 | 99.85 |
| 3rd Fold | 99.79 | 99.79 | 99.79 | 99.79 | 99.60 | 99.60 | 99.60 | 99.60 |
| 4th Fold | 99.92 | 99.92 | 99.92 | 99.92 | 99.70 | 99.70 | 99.70 | 99.70 |
| 5th Fold | 99.87 | 99.87 | 99.87 | 99.88 | 99.75 | 99.75 | 99.75 | 99.75 |
| Average | 99.80 | 99.80 | 99.80 | 99.80 | 99.76 | 99.76 | 99.76 | 99.76 |
| Ref. | Year | Datasets | Algorithm | Train/TestRatio | No. of Classes | Precision | Recall | F1-Score | Accuracy |
|---|---|---|---|---|---|---|---|---|---|
| [13] | 2021 | MIT-BIH AF | CNN + LSTM | 90/10 | 4 | - | 97.87 | - | - |
| [14] | 2022 | St. Petersburg | DW-CMT + TCP+SVM | 90/10 | 4 | 97.80 | 97.80 | 97.80 | 97.80 |
| [42] | 2022 | MIT-BIH AF | CNN + Transformers | 90/10 | 4 | 95.38 | 92.51 | 93.88 | 99.49 |
| [10] | 2017 | MIT-BIH | 9 layers CNN | 90/10 | 5 | 97.86 | 96.71 | 97.28 | 94.03 |
| [12] | 2021 | MIT-BIH | CNN + GA | 80/20 | 5 | 95.80 | 99.70 | 89.70 | 98.00 |
| [14] | 2022 | MIT-BIH | DW-CMT + TCP + kNN | 90/10 | 5 | 95.18 | 98.51 | 96.69 | 96.60 |
| [15] | 2022 | MIT-BIH | CBAM-ResNet | 80/20 | 5 | 99.13 | 97.50 | 98.29 | 99.23 |
| [19] | 2024 | MIT-BIH | FT + CNN-LSTM | 80/20 | 5 | 97.30 | 97.40 | 97.30 | 97.40 |
| [36] | 2022 | MIT-BIH | CNN + RF | 80/20 | 5 | 76.00 | 78.00 | 74.00 | 96.00 |
| [37] | 2023 | MIT-BIH | CNN | 90/10 | 5 | 92.86 | 92.41 | 92.63 | 98.63 |
| [38] | 2021 | MIT-BIH | CWT + CNN | 50/50 | 5 | 70.75 | 67.47 | 68.76 | 98.74 |
| [43] | 2018 | MIT-BIH AF | SWT + DCNN | 90/10 | 5 | - | 98.79 | - | 98.63 |
| [44] | 2022 | MIT-BIH | ResNet + BiLSTM | 80/20 | 5 | 92.23 | 91.23 | 91.69 | 99.20 |
| [45] | 2022 | MIT-BIH | CNN + TTM | 90/10 | 5 | 48.10 | 70.60 | 57.12 | 96.36 |
| [46] | 2022 | MIT-BIH | SE-ResNet | 90/10 | 5 | 93.87 | 93.78 | 93.82 | 99.61 |
| [47] | 2023 | MIT-BIH | RPM + Gam-Resnet18 | 80/20 | 5 | 98.76 | 98.90 | - | 99.30 |
| Ours | 2024 | MIT-BIH | 3-Channel CNN + GRU | 80/20 | 5 | 99.76 | 99.76 | 99.76 | 99.76 |
| [48] | 2022 | MIT-BIH + BIDMC | LSTM | 80/20 | 3 | - | - | - | 96.00 |
| [49] | 2021 | MIT-BIH + BIDMC | CWT + AlexNet | - | 3 | 97.70 | 97.80 | 97.70 | 97.8 |
| [50] | 2022 | MIT-BIH + BIDMC | CWT + CNN + LSTM | 90/10 | 3 | 98.00 | 98.00 | 97.30 | 98.90 |
| [51] | 2023 | MIT-BIH + BIDMC | ResNet50 | 80/20 | 3 | 99.20 | 99.20 | 99.20 | 99.20 |
| Ours | 2024 | MIT-BIH + BIDMC | 3-Channel CNN + GRU | 80/20 | 3 | 99.80 | 99.80 | 99.80 | 99.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eleyan, A.; Bayram, F.; Eleyan, G. Spectrogram-Based Arrhythmia Classification Using Three-Channel Deep Learning Model with Feature Fusion. Appl. Sci. 2024, 14, 9936. https://doi.org/10.3390/app14219936
Eleyan A, Bayram F, Eleyan G. Spectrogram-Based Arrhythmia Classification Using Three-Channel Deep Learning Model with Feature Fusion. Applied Sciences. 2024; 14(21):9936. https://doi.org/10.3390/app14219936
Chicago/Turabian StyleEleyan, Alaa, Fatih Bayram, and Gülden Eleyan. 2024. "Spectrogram-Based Arrhythmia Classification Using Three-Channel Deep Learning Model with Feature Fusion" Applied Sciences 14, no. 21: 9936. https://doi.org/10.3390/app14219936
APA StyleEleyan, A., Bayram, F., & Eleyan, G. (2024). Spectrogram-Based Arrhythmia Classification Using Three-Channel Deep Learning Model with Feature Fusion. Applied Sciences, 14(21), 9936. https://doi.org/10.3390/app14219936






