Abstract
This paper aims to investigate the effect of glass fiber-reinforced polymer (GFRP) and carbon fiber-reinforced polymer (CFRP) strengthening materials on the static and dynamic behavior of reinforced concrete (R/C) beams subjected to progressive damage. Four identical beams, each strengthened with either GFRP or CFRP, are tested under a cyclic quasi-static loading pattern. Impact hammer tests are performed for undamaged states and various damage levels of the beams. The dynamic test data are analyzed using the Enhanced Frequency Domain Decomposition (EFDD) method to estimate the dynamic characteristics of the beams. In this context, the first three vibration modes in both vertical and horizontal directions are considered. Strengthening is applied to both pre-damaged and undamaged beams, enabling a comparison of their performance before and after the strengthening procedure. Beams strengthened with CFRP exhibit a higher load-bearing capacity and stiffness but also fail at lower displacement levels compared to those strengthened with GFRP, which demonstrate more ductile behavior. Furthermore, the modal frequency ratios indicate that the first vibration mode is more sensitive to damage than the second and third modes. This study highlights the effectiveness of both strengthening materials in enhancing the structural performance of both undamaged and damaged beams.
1. Introduction
Reinforced concrete (R/C) structures are widely used in civil engineering due to their high strength and ductility. However, despite these advantages, R/C structures are prone to long-term degradation caused by factors such as environmental exposure, aging, and seismic activity. These factors can compromise the structural integrity of R/C structures, making strengthening essential to prolong their service life and ensure safety, particularly in the aftermath of seismic events. Among the various strengthening methods, fiber-reinforced polymer (FRP) composites have gained significant attention due to their high strength-to-weight ratio, excellent corrosion resistance, and ease of installation. Interest in using FRP for structural strengthening began to grow in the early 1990s. In particular, analytical studies in these years have paved the way for their use in strengthening R/C members by contributing to the improvement of these methods [1,2,3,4]. FRP strengthening methods significantly improve the mechanical performance of R/C structures, increasing their load-carrying capacity and resistance to cracking under both flexural and shear stresses. Today, FRP composites are widely regarded as an ideal solution for strengthening R/C members, especially in seismic regions, thanks to their flexibility, durability, and ability to significantly enhance structural performance [5,6,7,8,9]. FRP is typically used to strengthen or rehabilitate R/C beams through two main techniques. The first involves externally bonding FRP sheets or strips to the surface of the concrete, while the second involves embedding FRP rods into grooves cut into the concrete surface, a method referred to as the Near-Surface Mounted (NSM) technique [10,11,12,13,14,15,16]. Although NSM is proposed as a way to improve bond strength and mitigate issues such as premature debonding, it presents significant challenges in terms of installation complexity and cost. Furthermore, the difficulty of ensuring accurate placement in NSM applications makes it less practical for many real-world strengthening projects [17]. In contrast, externally bonded FRP strips offer a far simpler and more cost-effective solution, with easier application and proven effectiveness in enhancing the structural performance of R/C elements.
Despite the advantages of FRP, experimental and numerical studies have shown that this strengthening technique can also introduce brittle failure mechanisms, such as debonding of the FRP, which diminish its effectiveness and reduce the overall stiffness of the structure. Jankowiak [18] examined the deformation behavior and stiffness characteristics of R/C beams strengthened with carbon fiber-reinforced polymer (CFRP) strips under various load levels. The research focuses on how CFRP strengthening affects the beams’ load-bearing capacity, stiffness, and displacement patterns. Experimental results demonstrated that the application of CFRP significantly enhances the load-bearing capacity of R/C beams while reducing the displacement and hence the ductility. Jian-He et al. [19] investigated the flexural behavior of pre-damaged R/C beams strengthened with CFRP. A total of 25 R/C beams were tested, considering different pre-damage levels, shear span-depth ratios, and CFRP thicknesses. The primary objective was to understand how CFRP strengthening affects the load-carrying capacity, stiffness, and failure modes of R/C beams subjected to progressive damage. The results demonstrated that CFRP significantly improves the flexural load capacity of pre-damaged beams, with minimal influence from the initial damage levels. However, the shear span-to-depth ratio plays a crucial role in determining failure modes, transitioning from intermediate crack debonding to cover separation near the CFRP end as the ratio decreases. Furthermore, adding more CFRP layers enhances the load-bearing capacity in some cases but may reduce ductility depending on the failure mode. In addition to traditional failure modes such as concrete crushing, rebar yielding, and shear cracking, FRP-strengthened R/C structures are also vulnerable to premature failures like plate-end and intermediate crack-induced interfacial debonding.
To address the risks mentioned above and to mitigate the lack of information on damage progression, Structural Health Monitoring (SHM) methods are widely employed. These methods involve placing sensors on structural components to record regular measurements and using mathematical models to assess changes in dynamic properties as damage progresses. By analyzing changes in natural vibration frequencies, mode shapes, and modal damping factors, SHM enables the non-destructive detection of damage, identification of its location, and assessment of the associated failure risk over the structure’s lifespan [20,21,22,23]. Thereby, alterations in dynamic properties, such as modal frequencies, mode shapes, and modal damping ratios, can be effectively used. Previous studies have utilized experimental dynamic testing and modal analysis to identify the progression of damage in strengthened R/C structures [24,25,26,27]. Prado et al. [28] focused on evaluating shear-damaged R/C beams that were strengthened using CFRP strengthening with the NSM method. Modal analysis was used to assess the effectiveness of the strengthening by examining changes in the beams’ dynamic properties, such as the modal frequencies and mode shapes. The study highlights how these changes can provide insights into the extent of shear damage and the improvements in structural performance after CFRP strengthening with the NSM method. Capozucca [7] investigated the effects of glass fiber-reinforced polymer (GFRP) strengthening on damaged R/C beams through vibration analysis. The findings show that GFRP application improves the dynamic behavior of the beams, particularly by increasing their modal frequencies and reducing the extent of damage-induced frequency drops. The vibration analysis effectively captures the improvements in structural performance, indicating that GFRP strengthening enhances both stiffness and overall damage resistance in the R/C beams. Bonfiglioli et al. [29] showed that after a significant reduction in the first modal frequency value of an R/C beam induced by cracking under loading, the application of a composite plate along the flexural face of the beam provides an increase in the modal frequencies and small variations in the damping ratios. Zanardo et al. [30] presented notable findings from the dynamic-based analysis, highlighting both the effectiveness of the strengthening technique and the reliability of using a numerical finite element model to assess the increase in the load-bearing capacity of the strengthened bridge. Baghiee et al. [31] investigated the use of vibration monitoring methods to assess damage and evaluate the effectiveness of FRP strengthening in R/C beams. They explored how vibration-based methods can detect structural damage and monitor improvements after FRP application. The study focuses on comparing modal parameters, such as frequency changes, to identify damage and assess the impact of FRP strengthening. The findings suggest that vibration monitoring is an effective technique for both detecting damage and evaluating the performance of FRP strengthening in enhancing the structural integrity of R/C beams. In the literature, wavelet transform techniques are also effectively applied to detect and localize damage in beam-type structures, using both static and dynamic tests. Jahangir et al. [32] performed wavelet analysis to R/C beams subjected to gradually applied static bending tests, while Cao and Qiao [33] integrated wavelet transform with mode shapes to detect damage. Together, these works underscore the effectiveness of wavelet-based approaches in identifying structural damage in various loading conditions.
Recent studies in the literature have proposed innovative materials and/or application methods to overcome issues such as debonding associated with traditional FRP strengthening techniques. Heydari et al. [34] emphasized that early debonding is prevented in R/C beams strengthened with CFRP using the proposed method in the study. Similarly, Rostamiyan et al. [35] suggested a plan for the installation sequence of FRP sheets that prevents and delays the debonding of FRP sheets from R/C members. Wang et al. [36] examined the lateral impact behavior of a hybrid FRP-concrete–steel double-skin tubular column (DSTC) using a numerical approach. The results show that hybrid DSTC demonstrates ductile behavior under lateral impact. While the FRP tube does not directly contribute to the impact resistance, it significantly enhances the concrete’s ability to withstand impact. Ashteyat et al. [37] conducted experiments to determine the structural performance of beams exposed to high temperatures that were repaired and reinforced with basalt-FRP and carbon-FRP ropes and strips. It was concluded that the beams reinforced with basalt-FRP exhibited a significant increase in load-carrying capacity and were cost-effective. Zapris et al. [38] performed experiments to strengthened T-shaped R/C beams using closed-form CFRP ropes. The study indicated that this method, which is straightforward, fast, and requires minimal intervention, enhances the shear capacity of R/C beams. Although numerous studies in the literature have focused on the static behavior of R/C members strengthened with GFRP and CFRP, comprehensive experimental studies examining the static and dynamic behavior of these members strengthened under different damage conditions are quite limited, and there is a need for further research in this area.
In this study, the effects of different strengthening materials, namely glass fiber-reinforced polymer (GFRP) and carbon fiber-reinforced polymer (CFRP), on the static and dynamic behavior of reinforced concrete (R/C) beams subjected to cyclic quasi-static loading pattern are investigated. Four identical R/C beams were tested for this purpose in the Structural Mechanics Laboratory at Dokuz Eylul University. Two of the beams were strengthened before any damage was applied, while the other two beams were strengthened after the pre-determined damage was induced. Notably, only one strengthening material was used per beam. This experimental design allows for a comparative evaluation of the influence of GFRP and CFRP applications on both undamaged and pre-damaged beams, contributing to a deeper understanding of optimal strengthening strategies for enhancing or restoring the static and dynamic performance of R/C beams. To observe the effect of these two strengthening materials on the dynamic performance of the beams, vibration datasets from impact hammer tests were recorded using accelerometers placed at five stations on each beam. Subsequently, the beams were subjected to pre-determined damage levels through a four-point bending test. At each damage level, the quasi-static loading was paused, and the loads on the beams were removed to perform the dynamic tests. The recorded dynamic datasets at each damage level were processed using the Enhanced Frequency Domain Decomposition (EFDD) method [39,40,41,42,43,44], and the first three vibration modes in both the vertical and horizontal directions were estimated. The changes in the modal frequencies of these modes are presented, demonstrating the effects of the two strengthening materials on the dynamic characteristics of the beams. The study compares multiple vibration modes, identifying notable differences between the performance of GFRP- and CFRP-strengthened beams, thereby clarifying each material’s role in restoring or improving static and dynamic properties. In addition to dynamic data, the load–displacement data recorded during the static tests are visualized and interpreted. While numerous studies in the literature evaluate strengthening using GFRP and CFRP within a static framework, dynamic assessments remain very limited. Unlike the existing research in the literature, this study offers a comprehensive evaluation by incorporating both static and dynamic test results at various damage levels, for beams strengthened either initially or after sustaining damage, thereby providing a more holistic assessment of the strengthening methods employed.
2. Test Setup
2.1. R/C Beams and Strengthening Methods
Four R/C beams, each with distinct strengthening conditions, were tested under cyclic quasi-static loading along vertical direction. The length of the tested beams was 3200 mm, while the cross-sectional dimensions were 150 mm by 250 mm. Since the primary focus of this study was to investigate the contribution of the FRP materials to the flexural behavior of the beams, the reinforcement arrangement was intentionally designed to have insufficient flexural capacity. The reinforcement details of the beams are presented in Figure 1.

Figure 1.
Reinforcement details of the beams.
The beams were strengthened by the externally bonding FRP technique using two different materials, namely GFRP and CFRP. Prior to the strengthening process, the beam surface intended for contact with the strengthening material (i.e., bottom surface of the beam) was thoroughly roughened and cleaned to improve adhesion. Pre-cut woven glass or carbon fibers, having dimensions of 150 mm by 2800 mm, were bonded to the beam with an adhesive. Two layers of glass or carbon fibers were applied in all strengthening procedures. During the bonding process, each layer was meticulously flattened and pressed with a roller to remove air bubbles and ensure full saturation. A thin layer of adhesive was applied between each fiber layer. After completing the strengthening process, the beam was maintained at room temperature for a week to cure the strengthening material and ensure a good bond between the beam and the strengthening material. The FRP thickness in the beams strengthened with GFRP was 2.6 mm, with a fiber volume fraction of 11%, while the FRP thickness in the beams strengthened with CFRP was 2.1 mm, with a fiber volume fraction of 19%. Examples of GFRP and CFRP applications on beams are provided in Figure 2.

Figure 2.
(a) GFRP and (b) CFRP applications on beams.
The materials used for strengthening each beam, as well as the timing of the strengthening process, are summarized in Table 1. In this context, the term ‘pre-strengthened’ refers to a beam that was strengthened before any damage was induced (i.e., in the undamaged state). In contrast, the term ‘post-strengthened’ indicates that the strengthening process was applied after a beam had sustained a pre-defined level of damage.

Table 1.
Strengthening materials and timing for each beam.
2.2. Materials
The average 28th day cylinder compressive strength of the concrete was ~20 MPa. The concrete mixture consisted of 275 kg/m3 cement, 190 kg/m3 water, 450 kg/m3 11–22 mm aggregate, 450 kg/m3 4–11 mm aggregate, 900 kg/m3 0–4 mm aggregate, and 2.8 kg/m3 plasticizer. The reinforcing bars had a yield strength of 420 MPa, a tensile strength of 500 MPa, an elastic modulus of 200 GPa, and a Poisson’s ratio of 0.3. The mechanical properties [45,46] and physical properties of the glass fiber and carbon fiber materials used for strengthening the beams are presented in Table 2. The adhesive was prepared by combining thixotropic epoxy resin and hardener in a 4:1 ratio. It exhibited a tensile strength, modulus of elasticity, and elongation at break of 30 MPa, 4.5 GPa, and 0.9%, respectively [47].

Table 2.
Mechanical and physical properties of the strengthening materials.
2.3. Instrumentation Details
A total of 2 tri-axial and 6 uni-axial piezoelectric type accelerometers, resulting in 12 measurement points, were used to capture the dynamic responses of the beams. The amplitude range, frequency bandwidth, and sensitivity of the accelerometers were ±5 g, 0.25–3000 Hz, and 1000 mV/g, respectively. The data acquisition system employed was an NI-PXI system, which included a PXI-4472 A/D card having simultaneous sampling capability and anti-aliasing filters. The layout of the accelerometers, with their positive polarities, is presented in Figure 3a. At this stage, the mode shapes of a preliminary numerical model were analyzed, with the primary motivation of capturing as many dynamic responses as possible. In Figure 3a, Sta-1 and Sta-5 (where ‘Sta’ denotes accelerometer stations) each contains one tri-axial accelerometer, whereas Sta-2, Sta-3, and Sta-4 each has two uni-axial accelerometers placed in the vertical and horizontal (i.e., perpendicular to the beam axis) directions. Additionally, 3 Linear Variable Displacement Transducers (LVDTs), with a capacity of 100 mm, were used to measure the static responses during the quasi-static tests. Two of the transducers (i.e., one at each support) were positioned to monitor vertical movements at the supports, while the third transducer was employed to measure and cross-check the midspan displacement of the beam, which was imposed by a load cell with a pressure capacity of 300 kN. A four-point bending test setup was adopted in order to create a region in the center of the beam free from shear forces, allowing the experimental variables to be studied under the influence of bending moments alone. Since for an a/d (i.e., shear span/effective depth) ratio greater than approximately 6, the beam will fail in flexure before the formation of inclined shear cracks, and given that the main objective was to investigate the flexural response, the a/d ratio was set at 6.3, with a and d being 1350 mm and 215 mm, respectively. A schematic presentation of the static test system and the general view of the test setup are shown in Figure 3b,c.

Figure 3.
(a) Layout of the accelerometers, (b) schematic presentation of the static test system, and (c) general view of the test setup.
2.4. Static and Dynamic Test Procedure
The beams were tested under cyclic quasi-static loading conditions with incrementally increasing midspan drift ratios applied in the vertical direction. The loading was performed using a speed-controlled electric hydraulic system, set at a loading speed of 20 kg/s. A total of 5 drift ratios, corresponding to specific damage levels, were defined: 0.00% (undamaged state), 1.00%, 1.50%, 2.00%, and 2.50%. The midspan displacements during the drift ratios were calculated by multiplying the drift ratios by the span length of the beam (i.e., 3000 mm). Accordingly, the beams experience cyclic midspan displacements in the vertical direction, ranging from 30 mm (i.e., 1.00% drift ratio) to 75 mm (i.e., 2.50% drift ratio). It should be noted that a test was terminated if failure was observed in a beam. Consequently, drift ratios exceeding 2.50% may occur. The drift ratios, corresponding midspan displacements, and damage levels are presented in Table 3.

Table 3.
Drift ratios, corresponding midspan displacements, and damage levels.
In the undamaged state and at the end of each pre-determined damage level (i.e., D1, D2, D3, and D4), impact hammer tests were performed by hitting the beams at midspan in both the vertical and horizontal directions to excite the beams with an input of broad-band characteristics. If a test was terminated beyond the D4 damage level due to failure, no dynamic testing was conducted at the end of the test. Dynamic response data were recorded at a sampling rate of 1000 Hz. Pre-processing of the data was carried out in MATLAB [48]. Operational modal analysis (OMA) was conducted in the ARTeMIS Modal Pro [49] environment, employing a non-parametric frequency-domain method known as EFDD. The load cell was detached from the beams before the dynamic tests to prevent any restraining effects that could alter the stiffness characteristics of the beams. It should be noted that once the beams entered the severe non-linear range, they retained varying levels of residual deformations. When the load cell was detached before the dynamic tests, a certain amount of residual deformation remained on the beams. In other words, the dynamic tests were performed at zero vertical force but not at zero residual displacement. After completing the dynamic test for a specific damage level, the load cell was reattached, and the quasi-static test proceeded to the next targeted damage level. Note that for Beam_GFRP_PostStr and Beam_CFRP_PostStr only, the quasi-static test was paused after the dynamic test at the D1 damage level (i.e., corresponding to 30 mm midspan displacement). At this stage, the beam was removed from the test setup and strengthened as described in Table 1. A week later, once a sufficient bond between the beam and the strengthening material was achieved, the beam was reattached to the test setup, and the dynamic test at the D1 damage level was repeated. This was performed to investigate the effect of the strengthening process on the dynamic properties of the beam. Afterward, the quasi-static test continued from where it left off. In summary, Beam_GFRP_PreStr and Beam_CFRP_PreStr were strengthened in the undamaged state, while Beam_GFRP_PostStr and Beam_CFRP_PostStr were strengthened at the D1 damage level. Consequently, Beam_GFRP_PostStr and Beam_CFRP_PostStr can be regarded as bare beams prior to the strengthening process.
3. Test Results
3.1. Static Test Results and Damage Observations
During the quasi-static loading test of Beam_GFRP_PreStr, the first flexural crack appears in the midspan region when the load reached 23.89 kN (i.e., at 7.47 mm displacement), corresponding to approximately 46% of the ultimate load of 51.94 kN. As the load increased, additional flexural cracks formed, and at a load of 49.18 kN (i.e., at 18.44 mm displacement), the longitudinal steel reinforcement yielded. Note that the yielding displacements of all beams were determined based on the reduced stiffness equivalent elasto-plastic yield [50]. When the deflection reached 55.87 mm, the cracks in the concrete cover became more pronounced and propagated horizontally toward the right. A reduction in load values was observed during the third and fourth loading cycles (i.e., the D3 and D4 damage levels). At a displacement of 78.89 mm (i.e., at 44.45 kN load), the GFRP layer debonded from the concrete interface, leading to failure. At this stage, the concrete in the compression zone was fully crushed. As illustrated by the load–displacement curve in Figure 4, Beam_GFRP_PreStr exhibits a ductile flexural failure mechanism. The failure mode of Beam_GFRP_PreStr is shown in Figure 5.
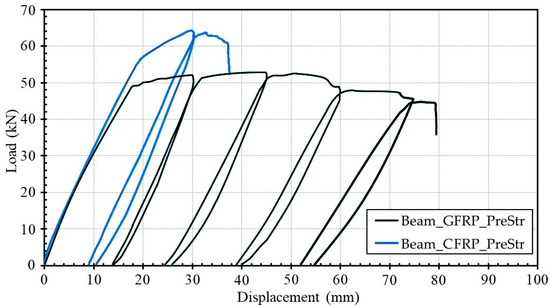
Figure 4.
Load–displacement curves for Beam_GFRP_PreStr and Beam_CFRP_PreStr.

Figure 5.
The failure mode of Beam_GFRP_PreStr.
During the static loading test of Beam_CFRP_PreStr, the first flexural crack appeared in the tensile zone of the concrete when the applied load approached 24.51 kN (i.e., at 7.21 mm displacement), corresponding to approximately 37% of the ultimate load of 66.24 kN. As the load increased, numerous flexural cracks formed. These cracks were not concentrated in the midspan region but were distributed along the length of the beam. At a load of 58.12 kN (i.e., 21.34 mm displacement), the longitudinal steel reinforcement yielded. After the load reached a maximum of 66.24 kN, the cracks in the concrete cover became more pronounced and started to propagate toward the left. At a displacement of 37.65 mm (i.e., at 60.56 kN load), failure occurred due to the debonding of the CFRP strengthening material along with the concrete cover, resulting in a sudden drop in load and the termination of the test (see Figure 4). Although slight crushing was observed in the concrete compression zone, debonding happened before the beam reached its full flexural capacity. Compared to Beam_GFRP_PreStr, which was strengthened with GFRP, Beam_CFRP_PreStr failed at a lower displacement level while bearing a higher load value (see Figure 4). The failure mode of Beam_CFRP_PreStr is illustrated in Figure 6.

Figure 6.
The failure mode of Beam_CFRP_PreStr.
As mentioned earlier, Beam_GFRP_PostStr and Beam_CFRP_PostStr, which were initially bare beams, were pre-damaged up to 30 mm displacement (i.e., D1 damage level) and strengthened with GFRP and CFRP, respectively. The load–displacement curves of Beam_GFRP_PostStr and Beam_CFRP_PostStr are presented in Figure 7. The pre-damaging procedure serves as a reference for the pre-strengthened beams, namely Beam_GFRP_PreStr and Beam_CFRP_PreStr. The first crack in the midspan region occurred at 18.83 kN (i.e., at 5.98 mm displacement) and 19.23 kN (i.e., at 6.18 mm displacement) for Beam_GFRP_PostStr and Beam_CFRP_PostStr, respectively. As the load increased, additional flexural cracks formed. The longitudinal steel reinforcement yielded at 42.61 kN (i.e., at 15.11 mm displacement) for Beam_GFRP_PostStr and 41.86 kN (i.e., at 15.23 mm displacement) for Beam_CFRP_PostStr. Representations of Beam_GFRP_PostStr and Beam_CFRP_PostStr at the D1 damage level are given in Figure 8.
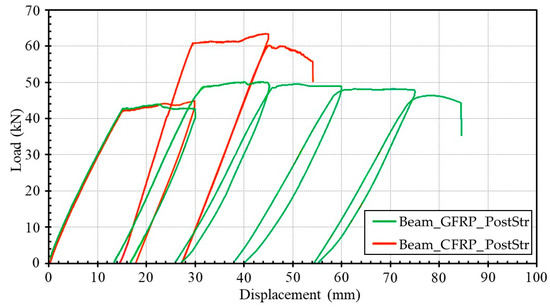
Figure 7.
Load–displacement curves of Beam_GFRP_PostStr and Beam_CFRP_PostStr.

Figure 8.
Bare beams (Beam_GFRP_PostStr and Beam_CFRP_PostStr) at the D1 damage level.
During the static test conducted after the strengthening of Beam_GFRP_PostStr with GFRP, the first new crack formed at a load value of 43.05 kN (i.e., at 28.71 mm displacement). As the load increased, additional flexural cracks developed. After the strengthening procedure, the maximum load value increased by 14.15% compared to the pre-strengthening state. At a midspan displacement of 62.52 mm, cracks in the concrete cover became more pronounced and extended horizontally to the right. A decrease in load values was observed during the fourth and fifth loading cycles. When the displacement reached 84.32 mm (i.e., at 44.13 kN load), the GFRP layer debonded from the concrete interface, leading to failure. Complete crushing occurred in the concrete of the compression zone, and Beam_GFRP_PostStr exhibited ductile flexural behavior similar to that of Beam_GFRP_PreStr, as shown in the load–displacement curve (see Figure 7). The failure mode of Beam_GFRP_PostStr is presented in Figure 9.

Figure 9.
The failure mode of Beam_GFRP_PostStr.
During the static test performed after the strengthening process of Beam_CFRP_PostStr strengthened with CFRP, the first new crack formed at a load value of 47.74 kN (i.e., at 26.12 mm displacement). As the load increased, additional flexural cracks developed. After the strengthening procedure, the maximum load value for Beam_CFRP_PostStr increased by 41.65% compared to the pre-strengthening state. After reaching a maximum load of 63.22 kN, cracks in the concrete cover became more pronounced and began to propagate to the right. After this point, the load decreased to 55.94 kN (i.e., at 54.32 mm displacement), and debonding of the CFRP with the concrete cover was observed as the failure mode, resulting in a sudden drop in load and the termination of the test (see Figure 7). Beam_CFRP_PostStr exhibited a similar behavior trend to Beam_CFRP_PreStr. The failure mode of Beam_CFRP_PostStr is presented in Figure 10. The static test results for all beams are collectively presented in Table 4.

Figure 10.
The failure mode of Beam_CFRP_PostStr.

Table 4.
Static test results for all beams.
In the table above, Fcr, Fy, Fu, and Ff denote the first crack, steel yield, ultimate, and failure loads, respectively, while δcr, δy, δu, and δf represent their corresponding displacements. In addition, the ductility ratio is calculated and presented in Table 4.
Beam_CFRP_PreStr shows a slightly higher load but a slightly lower displacement at first crack compared to Beam_GFRP_PreStr. This suggests that CFRP provides greater initial stiffness than GFRP, leading to a higher load capacity with less deformation before cracking occurs. Beam_GFRP_PostStr and Beam_CFRP_PostStr, which are bare frames in the undamaged state, exhibit lower loads and displacements at first crack compared to the beams that are strengthened before loading. After the strengthening of pre-damaged beams, Beam_GFRP_PostStr shows a lower first crack load compared to Beam_CFRP_PostStr, indicating the superior effect of CFRP in improving stiffness. Beam_CFRP_PreStr exhibits the highest yield load, followed by Beam_GFRP_PreStr, showing that CFRP provides a greater improvement in load-carrying capacity before yielding in pre-strengthened beams. The static test results reveal that Beam_GFRP_PreStr, which is strengthened with GFRP in the undamaged state, exhibits a good balance between strength and ductility, effectively enhancing load-bearing capacity while maintaining ductility. In contrast, Beam_CFRP_PreStr, strengthened with CFRP in the undamaged state, has the highest ultimate load capacity but demonstrates the lowest ductility ratio which is consistent with the findings of similar studies by Jankowiak [18] and Jian-He et al. [19]. Beams strengthened with GFRP exhibit significantly more ductile behavior compared to those strengthened with CFRP. This difference can be attributed to the increased internal forces within the CFRP-strengthened beams, corresponding to a substantial rise in the maximum load carried. Consequently, the debonding of the strengthening material from the concrete cover occurs at lower displacements. Beam_GFRP_PostStr, which is pre-damaged and then strengthened with GFRP, presents a slightly reduced load-carrying capacity compared to Beam_GFRP_PreStr; however, it shows improved ductility, suggesting that GFRP can still enhance the deformation capacity of damaged beams. Beam_CFRP_PostStr, strengthened with CFRP after pre-damage, exhibits a slightly lower load capacity than Beam_CFRP_PreStr but demonstrates greater ductility, indicating that CFRP effectively restores some structural performance even when applied to a damaged beam. Overall, CFRP consistently provided superior strength enhancement, while GFRP contributed more to ductility, demonstrating the varied benefits of each material.
3.2. Dynamic Test Results at Different Damage Levels
Using the collected dynamic data from various beams (i.e., Beam_GFRP_PreStr, Beam_CFRP_PreStr, Beam_GFRP_PostStr, and Beam_CFRP_PostStr) at different damage levels (i.e., the undamaged state, D1, D2, D3, and D4), modal parameters were estimated. In this context, the first three vibration modes of the beams in both vertical and horizontal directions were considered. Table 5 provides the modal frequency estimates for all beams in their undamaged states.

Table 5.
Undamaged state modal frequency estimates for all beams.
In the table above, f1, f2, and f3 indicate modal frequency estimates for the first, second, and third vibration modes, respectively, in both vertical and horizontal directions. As previously mentioned, Beam_GFRP_PostStr and Beam_CFRP_PostStr are bare in the undamaged state. Since the modal frequencies of these two identical beams are found to be very close to each other, they are presented in a single row in Table 5. The results denote that strengthening with both GFRP and CFRP leads to noticeable increases in the frequency estimates of the beams, reflecting an improvement in their stiffness values. Among the two strengthening materials, CFRP provides a more significant increase in the frequency estimates in both directions, suggesting that it is more effective in enhancing structural rigidity compared to GFRP. The bare beams exhibit lower frequencies, confirming the baseline stiffness characteristics in the absence of any strengthening. The near-identical values between the two bare beams validate the consistency and reliability of the testing setup.
Figure 11 shows the mode shapes of Beam_GFRP_PostStr and Beam_CFRP_PostStr in the undamaged state, along with the corresponding modal frequencies. Additionally, Table 6 presents the Modal Assurance Criterion (MAC) values of the mode shapes of strengthened beams compared to those of the bare beams (i.e., the reference mode shapes). The MAC value quantifies the similarity between two mode shapes, with values closer to 100% indicating greater similarity [51].
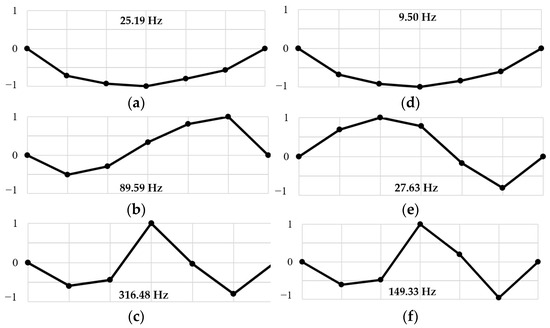
Figure 11.
Mode shapes of the bare beams in the undamaged state: (a) first, (b) second, and (c) third mode in the vertical direction; (d) first, (e) second, and (f) third mode in the horizontal direction.

Table 6.
MAC values of the mode shapes of the strengthened beams.
The high MAC values, particularly in the first modes exceeding 90%, indicate that the mode shapes of the strengthened beams closely resemble those of the bare beams. This suggests that the strengthening process does not significantly alter the first mode shapes in both the vertical and horizontal directions, but rather enhances the stiffness values. The reduction in MAC values in the second and third modes reflects certain deviations in the mode shapes, likely due to the effects of the strengthening process.
Modal frequency ratios were calculated by dividing the modal frequency estimates at different damage levels by those in the undamaged state, enabling the proportional change in modal frequencies to be monitored. The focus was on the relative changes in frequency ratios rather than the absolute frequency values, highlighting the influence of damage and strengthening on the dynamic behavior of the beams. Table 7 provides the modal frequency ratios for Beam_GFRP_PreStr at various damage levels, encompassing both the vertical and horizontal directions. These ratios offer insight into the effect of progressive damage on the modal frequencies of the beam. Figure 12 illustrates the variation in these ratios for the vertical and horizontal directions.

Table 7.
Modal frequency ratios at different damage levels for Beam_GFRP_PreStr.
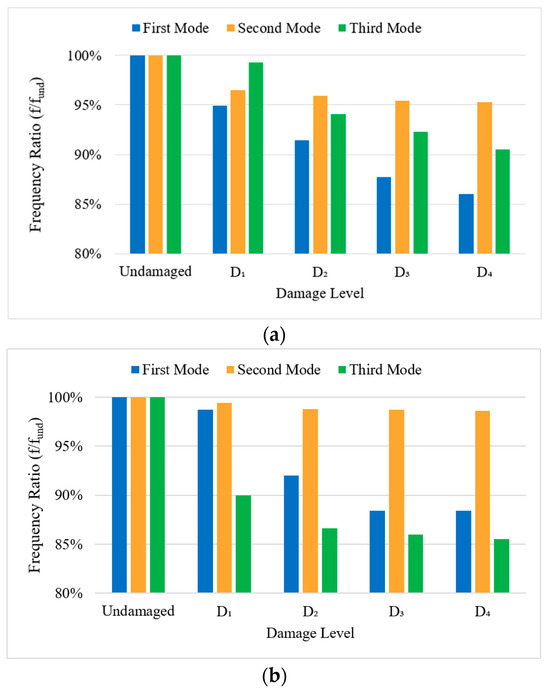
Figure 12.
Variation in modal frequency ratios at different damage levels for Beam_GFRP_PreStr in (a) the vertical direction and (b) the horizontal direction.
In the table above, f1und, f2und, and f3und are the undamaged state modal frequencies of the first, second, and third modes, respectively.
As the level of damage increases, the modal frequencies of Beam_GFRP_PreStr decrease progressively. This indicates a reduction in stiffness caused by the damage and resulting in lower frequency values. The most significant reduction in the vertical direction is observed in the first mode, while the second mode is less affected. The second and third modes exhibit a slower rate of decline, indicating that higher modes are less sensitive to damage in the vertical direction. In the horizontal direction, the third mode shows the largest decrease in modal frequencies, whereas the second mode remains more stable across various damage levels. These findings highlight the influence of structural damage on dynamic properties, with the first mode being the most sensitive to changes in structural integrity.
Table 8 presents the modal frequency ratios for Beam_CFRP_PreStr at the D1 damage level, comparing the modal frequency estimates in both vertical and horizontal directions to those in the undamaged state. As previously mentioned, Beam_CFRP_PreStr failed before reaching the D2 damage level. Therefore, only the frequency ratios at the D1 damage level are given. Figure 13 illustrates the variation in these modal frequency ratios for Beam_CFRP_PreStr in both directions, highlighting the effects of structural damage on the dynamic behavior of the beam.

Table 8.
Modal frequency ratios at different damage levels for Beam_CFRP_PreStr.
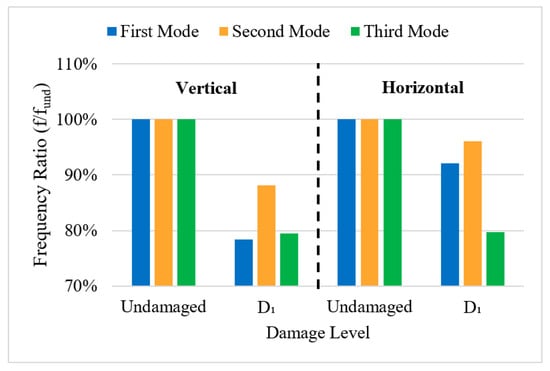
Figure 13.
Variation in modal frequency ratios at different damage levels for Beam_CFRP_PreStr in both directions.
Table 8 and Figure 13 show a significant reduction in modal frequencies as the beam was damaged at the D1 damage level, particularly in the vertical direction. The first and third modes exhibit the most pronounced decreases, indicating that these modes are more sensitive to damage. The second mode, however, shows a relatively moderate reduction, suggesting greater stability under damage. In the horizontal direction, the first and second modes exhibit smaller reductions compared to the vertical direction, indicating that horizontal dynamic behavior is less sensitive to damage at lower modes. These results suggest that while damage affects both directions, the vertical dynamic response is more significantly impacted, particularly in the first mode for the beam strengthened with CFRP.
Table 9 presents the modal frequency ratios for Beam_GFRP_PostStr at various damage levels. Initially, Beam_GFRP_PostStr is a bare beam, and the modal frequencies are estimated for both the undamaged state and the D1 damage level. Subsequently, the beam is strengthened with GFRP, and the modal frequencies are extracted again at the D1 damage level. The beam is then subjected to further damage, and the modal frequencies are estimated at the D2, D3, and D4 damage levels. Figure 14 illustrates the variation in modal frequency ratios in both directions, tracking the effects of both damage progression and strengthening.

Table 9.
Modal frequency ratios at different damage levels for Beam_GFRP_PostStr.
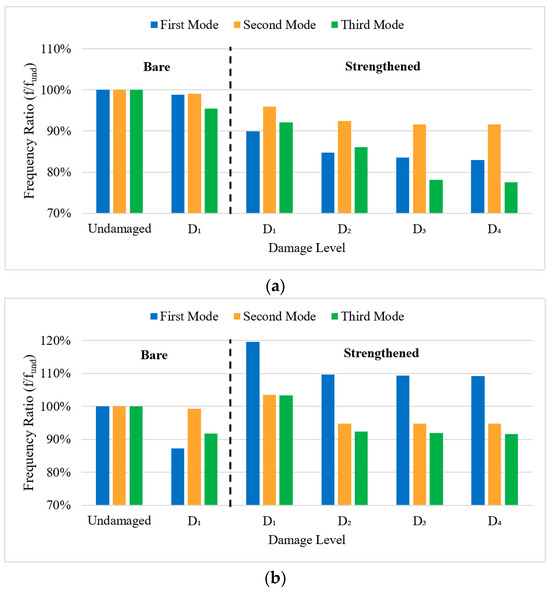
Figure 14.
Variation in modal frequency ratios at different damage levels for Beam_GFRP_PostStr in (a) the vertical direction and (b) the horizontal direction.
Table 9 and Figure 14 present the dynamic response of Beam_GFRP_PostStr throughout its testing process. Initially, the bare beam exhibits a consistent decrease in modal frequencies as damage increases from the undamaged state to the D1 damage level. After GFRP strengthening, the modal frequencies in the vertical direction show a decrease, which can be attributed to the effects of the beam’s transport during the strengthening process and the week-long waiting period for the strengthening material to cure under its own weight (i.e., in the vertical direction), potentially leading to additional damage. In the vertical direction, the third mode exhibits a more gradual decline, while the second mode remains relatively stable until higher damage levels. In the horizontal direction, after strengthening with GFRP at the D1 damage level, the modal frequencies show a significant recovery, with all modes increasing beyond their undamaged state. This suggests that GFRP strengthening is effective in restoring and even enhancing the beam’s stiffness, particularly in the horizontal direction. However, as the beam is subjected to further damage at the D2, D3, and D4 damage levels, the modal frequencies progressively decrease again, indicating that the strengthening cannot fully mitigate the impact of higher damage levels. In overall, the results suggest that the GFRP strengthening improves the dynamic response of Beam_GFRP_PostStr at lower damage levels, but its effectiveness diminishes as more severe damage is introduced.
Table 10 shows the modal frequency ratios for Beam_CFRP_PostStr at different damage levels, both in the vertical and horizontal directions. Initially, Beam_CFRP_PostStr is tested as a bare beam, with modal frequencies estimated in the undamaged state and at the D1 damage level. Subsequently, the beam is strengthened using CFRP, and the modal frequencies are estimated again at the D1 damage level. The beam is then subjected to further damage, with modal frequencies estimated at the D2 damage level. Figure 15 illustrates the variation in modal frequency ratios in both directions.

Table 10.
Modal frequency ratios at different damage levels for Beam_CFRP_PostStr.
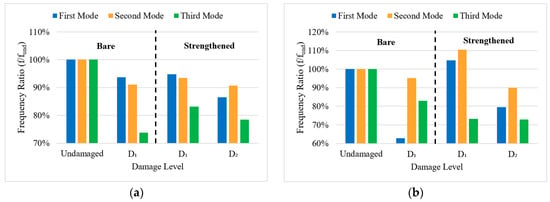
Figure 15.
Variation in modal frequency ratios at different damage levels for Beam_CFRP_PostStr in (a) the vertical direction and (b) the horizontal direction.
Initially, as a bare beam, Beam_CFRP_PostStr experiences a reduction in modal frequencies at the D1 damage level. After strengthening with CFRP, there is a recovery in modal frequencies, especially in the horizontal direction, reflecting the effectiveness of CFRP in restoring stiffness. However, as damage progresses to the D2 damage level, a general decrease in modal frequency ratios is observed across all modes in both directions, signaling a reduction in stiffness as the beam’s structural integrity continues to degrade. In the vertical direction, the third mode shows a noticeable reduction in frequency at the D1 damage level, prior to strengthening. After strengthening with CFRP, there is a slight improvement at the D1 damage level, but the modal frequencies do not fully recover to the undamaged state. At the D2 damage level, all modes show further reductions, with the third mode being the most affected. In the horizontal direction, CFRP strengthening leads to a more pronounced recovery in modal frequencies at the D1 damage level. The first and second mode exceed their undamaged state values after strengthening, indicating a significant enhancement in stiffness due to CFRP strengthening. However, as the beam reaches the D2 damage level, all modes experience reductions in modal frequency estimates, with the third mode showing the most substantial decrease. Despite the decrease, the vertical direction remains more resilient to damage compared to the horizontal direction, indicating the effectiveness of CFRP in enhancing the beam’s dynamic behavior in the vertical direction.
Figure 16 presents the modal frequency ratios for all beams in the vertical direction across different damage levels. Note that these ratios represent the proportional changes in frequencies relative to each beam’s undamaged state, enabling a comparative analysis of how each beam responds to damage in relative terms.
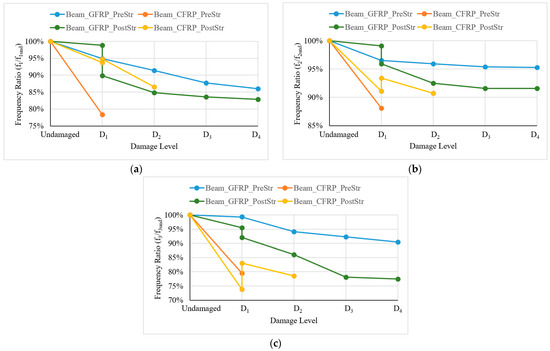
Figure 16.
Modal frequency ratios in the vertical direction for the (a) first, (b) second, and (c) third modes of all beams.
In the vertical direction, Beam_GFRP_PreStr displays a relatively stable frequency ratio for all modes. This indicates that GFRP contributes to maintaining the frequency ratios more consistently, with smaller proportional decreases as the damage level increases. Beam_CFRP_PreStr exhibits a larger decrease in the first and second modes compared to the other beams, reflecting a greater sensitivity to damage in these modes. After strengthening, Beam_CFRP_PostStr shows an increase in modal frequency values, while Beam_GFRP_PostStr exhibits a decrease. This difference in behavior can be attributed to the effects of transporting during the strengthening process and the week-long curing period for the strengthening material under the beam’s own weight, potentially leading to additional damage, especially in the vertical direction. When Beam_GFRP_PostStr and Beam_CFRP_PostStr are subjected to the D2 damage level, the second and third modal frequencies for both beams exhibit a similar decrease. However, the first modal frequency of Beam_CFRP_PostStr shows a more significant drop compared to Beam_GFRP_PostStr. This suggests that while both GFRP and CFRP help to maintain stability in the second and third modes, CFRP is less effective in preventing reductions in the first mode under higher damage levels.
Figure 17 illustrates the modal frequency ratios for all beams in the horizontal direction across different damage levels. This figure highlights the effect of damage and strengthening on the dynamic behavior of each beam in the horizontal direction.
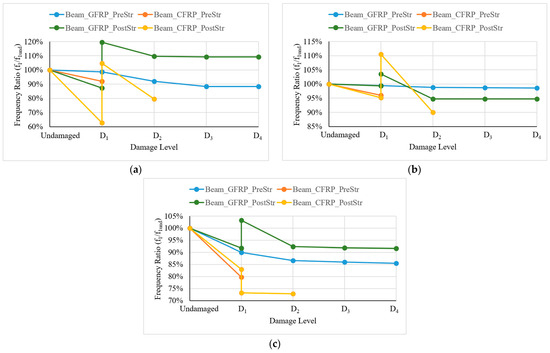
Figure 17.
Modal frequency ratios in the horizontal direction for the (a) first, (b) second, and (c) third modes of all beams.
Beam_GFRP_PreStr and Beam_GFRP_PostStr show stable frequency ratios across all modes, with the ratios remaining close to 100% after damage, indicating that GFRP is effective in maintaining the beams’ horizontal stiffness values. Beam_CFRP_PreStr displays a more significant reduction in all modes compared to Beam_GFRP_PreStr, suggesting that CFRP is less effective than GFRP in the horizontal direction. Significant recovery in modal frequencies is observed in the first two modes of Beam_GFRP_PostStr and Beam_CFRP_PostStr after strengthening. The greater proportional recovery in Beam_CFRP_PostStr compared to Beam_GFRP_PostStr indicates that CFRP contributes more to the increase in stiffness than GFRP. The second mode remains the least affected across all beams, indicating that it is generally more resilient to damage.
4. Conclusions
The primary objective of this study was to evaluate the influence of GFRP and CFRP strengthening materials on the static and dynamic behavior of R/C beams subjected to progressive damage. Four beams were strengthened in both the undamaged and pre-damaged states. Dynamic impact tests were performed on the beams in their undamaged states, as well as at different damage levels. Modal frequencies corresponding to the first three vibration modes in both vertical and horizontal directions were estimated using the EFDD method, facilitating an evaluation of the beams’ dynamic behavior before and after strengthening.
The results show that CFRP significantly enhances the stiffness of R/C beams compared to GFRP. CFRP-strengthened beams exhibit a notable increase in load-bearing capacity but fail at lower displacement levels, suggesting less ductility compared to beams strengthened with GFRP, which display more ductile behavior under similar conditions. The improvement in stiffness provided by CFRP is particularly evident in dynamic tests, where modal frequencies revealed a more substantial increase in CFRP-strengthened beams, especially at lower damage levels. The first vibration mode, in both the vertical and horizontal directions, proves to be the most sensitive to progressive damage, while the second and third modes show more stability across damage levels. This finding is a natural consequence of the fact that the first modes in both directions have the highest participation in the dynamic responses of the beams. The results also indicate that while both materials are effective in improving the structural performance of undamaged and damaged beams, the specific choice of strengthening material depends on the required balance between load capacity and ductility. Beams strengthened with GFRP may be more suitable for applications where greater ductility is desired, while CFRP may be preferable when maximizing stiffness and load capacity is a priority.
The absence of end anchorage in the study may have contributed to some degree of debonding, particularly in the CFRP-strengthened beams, where higher stiffness and load-bearing capacity were achieved but at the cost of reduced ductility. This highlights the potential for incorporating end anchorage in future experiments to further enhance the performance of FRP-strengthened beams, particularly for preventing early debonding and achieving greater structural efficiency. In addition, a more detailed investigation into the long-term performance of GFRP and CFRP under environmental factors such as temperature changes, moisture, and sustained loading would be valuable. Numerical simulations and analytical models may be developed to predict the behavior of R/C beams with different types and configurations of fiber-reinforced polymers under different loading conditions. The effects of GFRP and CFRP on the damage formation mechanisms of beams will be better understood by updating the pre-calibrated analytical model based on the modal parameters extracted from different damage levels of the strengthened beams. Exploring hybrid strengthening techniques that combine the benefits of both GFRP and CFRP may also lead to improved performance in terms of both stiffness and ductility.
Author Contributions
Conceptualization, O.O., U.Y., C.K. and E.D.; methodology, O.O., U.Y., C.K. and E.D.; experimental test, O.O., U.Y., C.K. and E.D.; analysis, O.O.; investigation E.D.; writing—original draft preparation, O.O., U.Y., C.K. and E.D; writing—review and editing, O.O. and U.Y.; visualization, O.O.; supervision, O.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets presented in this article are not readily available because the data are part of ongoing studies. Requests to access the datasets should be directed to the corresponding author.
Acknowledgments
The authors would like to extend their gratitude to Batı Prefabrik Manufacturing and Trading Inc. for providing test specimens. The authors also greatly acknowledge Ozgur Ozcelik and Hasan Murat Tanarslan for their support and encouragement.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Triantafillou, T.C.; Plevris, N. Strengthening of RC beams with epoxy-bonded fibre-composite materials. Mater. Struc. 1992, 25, 201–211. [Google Scholar] [CrossRef]
- Saadatmanesh, H.; Ehsani, M.R. RC beams strengthened with GFRP plates. I: Experimental study. J. Struc. Eng. 1991, 117, 3417–3433. [Google Scholar] [CrossRef]
- An, W.; Saadatmanesh, H.; Ehsani, M.R. RC beams strengthened with FRP plates. II: Analysis and parametric study. J. Struc. Eng. 1991, 117, 3434–3455. [Google Scholar] [CrossRef]
- Meier, U. Strengthening of structures using carbon fibre/epoxy composites. Constr. Build. Mater. 1995, 9, 341–351. [Google Scholar] [CrossRef]
- Capozucca, R.; Magagnini, E. RC beam models damaged and strengthened with GFRP strips under bending loading and free vibration. Compos. Struct. 2020, 253, 112730. [Google Scholar] [CrossRef]
- Zhu, W.; Li, M.; Qin, H.; Fu, F.; Liu, F. Behavior of RC Beams Strengthened Using Steel-Wire–Carbon-Fiber-Reinforced Plates. Mater. 2020, 13, 3996. [Google Scholar] [CrossRef]
- Capozucca, R. Vibration analysis of damaged RC beams strengthened with GFRP. Compos. Struct. 2018, 200, 624–634. [Google Scholar] [CrossRef]
- Shen, J.; Dai, H.; Zhou, G.; Shi, J. Flexural behavior of pre-damaged RC beams strengthened with UHPFRC-CFRP grid layer. Eng. Struct. 2024, 317, 118669. [Google Scholar] [CrossRef]
- Siddika, A.; Al Mamun, M.A.; Alyousef, R.; Amran, Y.M. Strengthening of reinforced concrete beams by using fiber-reinforced polymer composites: A review. J. Build. Eng. 2019, 25, 100798. [Google Scholar] [CrossRef]
- Zhang, S.S.; Yu, T.; Chen, G.M. Reinforced concrete beams strengthened in flexure with near-surface mounted (NSM) CFRP strips: Current status and research needs. Compos. Part B Eng. 2017, 131, 30–42. [Google Scholar] [CrossRef]
- El-Hacha, R.; Rizkalla, S.H. Near-surface-mounted fiber-reinforced polymer reinforcements for flexural strengthening of concrete structures. Struct. J. 2004, 101, 717–726. [Google Scholar] [CrossRef]
- De Lorenzis, L.; Teng, J.G. Near-surface mounted FRP reinforcement: An emerging technique for strengthening structures. Compos. Part B Eng. 2007, 38, 119–143. [Google Scholar] [CrossRef]
- Szabó, Z.K.; Balázs, G.L. Near surface mounted FRP reinforcement for strengthening of concrete structures. Period. Polytech. Civ. Eng. 2007, 51, 33–38. [Google Scholar] [CrossRef]
- Capozucca, R.; Magagnini, E.; Vecchietti, M.V. Experimental static and dynamic response of RC beams damaged and strengthened with NSM GFRP rod. Compos. Struct. 2020, 241, 112100. [Google Scholar] [CrossRef]
- Capozucca, R. Static and dynamic response of damaged RC beams strengthened with NSM CFRP rods. Compos. Struct. 2009, 91, 237–248. [Google Scholar] [CrossRef]
- Bettucci, E.; Capozucca, R.; Magagnini, E.; Vecchietti, M.V. Detection in RC Beams Damaged and Strengthened with NSM CFRP/GFRP Rods by Free Vibration Monitoring. Buildings 2023, 13, 979. [Google Scholar] [CrossRef]
- Capozucca, R. Analysis of bond-slip effects in RC beams strengthened with NSM CFRP rods. Compos. Struct. 2013, 102, 110–123. [Google Scholar] [CrossRef]
- Jankowiak, I. The State of Deformation and Stiffness Analysis of RC Beams Strengthened by Means of CFRP Strips at Different Load Levels. Appl. Sci. 2022, 12, 9929. [Google Scholar] [CrossRef]
- Jian-He, X.; Yong-Chang, G.; Yi-Feng, L.; Gong-Fa, C. Experimental study on flexural behaviour of pre-damaged reinforced concrete beams strengthened with CFRP. Mater. Plast. 2014, 51, 370–375. [Google Scholar] [CrossRef]
- Musiał, M. Laboratory tests of reinforced concrete beams with the use of operational modal analysis. Mater. Sci. Forum 2016, 866, 124–128. [Google Scholar] [CrossRef]
- Benedetti, A.; Pignagnoli, G.; Tarozzi, M. Damage identification of cracked reinforced concrete beams through frequency shift. Mater. Struct. 2018, 51, 147. [Google Scholar] [CrossRef]
- Altunişik, A.C.; Karahasan, O.S.; Genc, A.F.; Okur, F.Y.; Gunaydin, M.; Kalkan, E.; Adanur, S. Modal parameter identification of RC frame under undamaged, damaged, repaired and strengthened conditions. Measurement 2018, 124, 260–276. [Google Scholar] [CrossRef]
- Capozucca, R. Assessment of CFRP strengthened RC beams through dynamic tests. Compos. Part B Eng. 2013, 46, 69–80. [Google Scholar] [CrossRef]
- De Maio, U.; Gaetano, D.; Greco, F.; Lonetti, P.; Pranno, A. The damage effect on the dynamic characteristics of FRP-strengthened reinforced concrete structures. Compos. Struct. 2023, 309, 116731. [Google Scholar] [CrossRef]
- Massenzio, M.; Jacquelin, E.; Ovigne, P.A. Natural frequency evaluation of a cracked RC beam with or without composite strengthening for a damage assessment. Mater. Struct. 2005, 38, 865–873. [Google Scholar] [CrossRef]
- Capozucca, R.; Cerri, M.N. Static and dynamic behaviour of RC beam model strengthened by CFRP-sheets. Construction and Build. Mater. 2002, 16, 91–99. [Google Scholar] [CrossRef]
- Musiał, M.; Trapko, T.; Grosel, J. Static and Dynamic Stiffness of Reinforced Concrete Beams Strengthened with Externally Bonded CFRP Strips. Materials 2021, 14, 910. [Google Scholar] [CrossRef]
- Prado, D.M.; Araujo, I.D.G.; Haach, V.G.; Carrazedo, R. Assessment of shear damaged and NSM CFRP retrofitted reinforced concrete beams based on modal analysis. Eng. Struct. 2016, 129, 54–66. [Google Scholar] [CrossRef]
- Bonfiglioli, B.; Pascale, G.; Martinez de Mingo, S. Dynamic testing of reinforced concrete beams damaged and repaired with fiber reinforced polymer sheets. J. Mater. Civ. Eng. 2004, 16, 400–406. [Google Scholar] [CrossRef]
- Zanardo, G.; Hao, H.; Xia, Y.; Deeks, A.J. Evaluation of the effectiveness of strengthening intervention by CFRP on MRWA bridge no. 3014. J. Compos. Constr. 2007, 11, 363–374. [Google Scholar] [CrossRef]
- Baghiee, N.; Esfahani, M.R.; Moslem, K. Studies on damage and FRP strengthening of reinforced concrete beams by vibration monitoring. Eng. Struct. 2009, 31, 875–893. [Google Scholar] [CrossRef]
- Jahangir, H.; Hasani, H.; Esfahani, M.R. Wavelet-based damage localization and severity estimation of experimental RC beams subjected to gradual static bending tests. Structures 2021, 4, 3055–3069. [Google Scholar] [CrossRef]
- Cao, M.; Qiao, P. Integrated wavelet transform and its application to vibration mode shapes for the damage detection of beam-type structures. Smart Mater. Struct. 2008, 17, 055014. [Google Scholar] [CrossRef]
- Heydari, P.; Mostofinejad, D.; Eftekhar, M.R.; Saljoughian, A. Seismic flexural rehabilitation of RC coupling beams with FRP sheets: Evaluation of EBROG technique. Structures 2024, 68, 107076. [Google Scholar] [CrossRef]
- Rostamiyan, E.; Golafshar, A.; Saghafi, M.H. Presenting a strategy to prevent FRP debonding for strengthening RC connections. Eng. Struct. 2023, 283, 115823. [Google Scholar] [CrossRef]
- Wang, W.; Wu, C.; Yu, Y.; Zeng, J.J. Dynamic responses of hybrid FRP-concrete-steel double-skin tubular column (DSTC) under lateral impact. Structures 2021, 32, 1115–1144. [Google Scholar] [CrossRef]
- Ashteyat, A.; Almahadin, W.; Almuaythir, S. Shear Repairing of Reinforced Concrete Beams Exposed to High Temperature Using Basalt Fiber Reinforcing Bars and CFRP Ropes and Strips. Compos. Part C Open Access. 2024, 100517. [Google Scholar] [CrossRef]
- Zapris, A.G.; Kytinou, V.K.; Gribniak, V.; Chalioris, C.E. Novel approach for strengthening T-beams deficient in shear with near-surface mounted CFRP ropes in form of closed stirrups. Dev. Built Environ. 2024, 18, 100394. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441–445. [Google Scholar] [CrossRef]
- Brincker, R.; Ventura, C.; Andersen, P. Damping Estimation by Frequency Domain Decomposition. In Proceedings of the 19th International Modal Analysis Conference (IMAC), Orlando, FL, USA, 5–8 February 2001; pp. 698–703. [Google Scholar]
- Gentile, C.; Gallino, N. Ambient vibration testing and structural evaluation of an historic suspension footbridge. Adv. Eng. Softw. 2008, 39, 356–366. [Google Scholar] [CrossRef]
- Magalhães, F.; Cunha, Á.; Caetano, E.; Brincker, R. Damping estimation using free decays and ambient vibration tests. Mech. Syst. Signal Process. 2010, 24, 1274–1290. [Google Scholar] [CrossRef]
- Brincker, R.; Ventura, C. Introduction to Operational Modal Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Astroza, R.; Ebrahimian, H.; Conte, J.P.; Restrepo, J.I.; Hutchinson, T.C. System identification of a full-scale five-story reinforced concrete building tested on the NEES-UCSD shake table. Struct. Control Health Monit. 2016, 23, 535–559. [Google Scholar] [CrossRef]
- SikaWrap® 300 BI-C/30. Heat-Set Bidirectional Carbon Fibre Fabric for Structural Strengthening Applications. Available online: https://gbr.sika.com/dms/getdocument.get/bc9a03c4-86dc-3890-89fb-189fbb43488a/SikaWrap%20300%20BI%20C_30%20PDS.pdf (accessed on 23 October 2024).
- Dostkimya. Composite Products Product Sheets. Available online: https://www.dostkimya.com/en/documents (accessed on 23 October 2024).
- Buliding Trust Sika. Product Data Sheet, Sikadur®-330. Available online: https://gbr.sika.com/dam/dms/gb01/l/sikadur_-330.pdf (accessed on 23 October 2024).
- MATLAB; The MathWorks Inc.: Natick, MA, USA, 2021. Available online: https://www.mathworks.com/products/matlab.html (accessed on 27 October 2024).
- ARTeMIS Modal Pro; Structural Vibration Solutions: Aalborg, Denmark, 2016. Available online: https://www.svibs.com/artemis-modal/ (accessed on 27 October 2024).
- Park, R. Ductility Evaluation from Laboratory and Analytical Testing. In Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo, Japan, 2–9 August 1988; pp. 605–616. [Google Scholar]
- Allemang, R.J. The modal assurance criterion—Twenty years of use and abuse. J. Sound Vib. 2003, 37, 14–23. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).