Development and Experimental Study of an Experimental Setup for an Online Vibrating Tube Liquid Densitometer
Abstract
Featured Application
Abstract
1. Introduction
2. Study on the Working Principle of an Online Vibrating Tube Liquid Densitometer
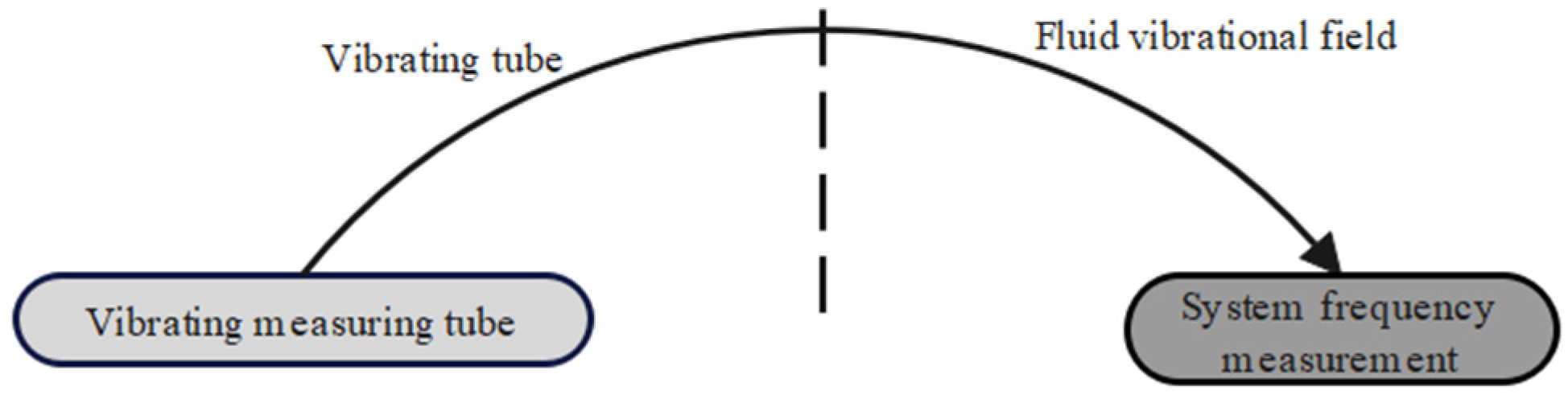
2.1. Working Principle of the Online Vibrating Tube Liquid Densitometer
2.2. Effect of Temperature Variation on Measurement Results
2.3. Pressure Effects on Measurement Results
3. Research and Development of the Experimental Setup
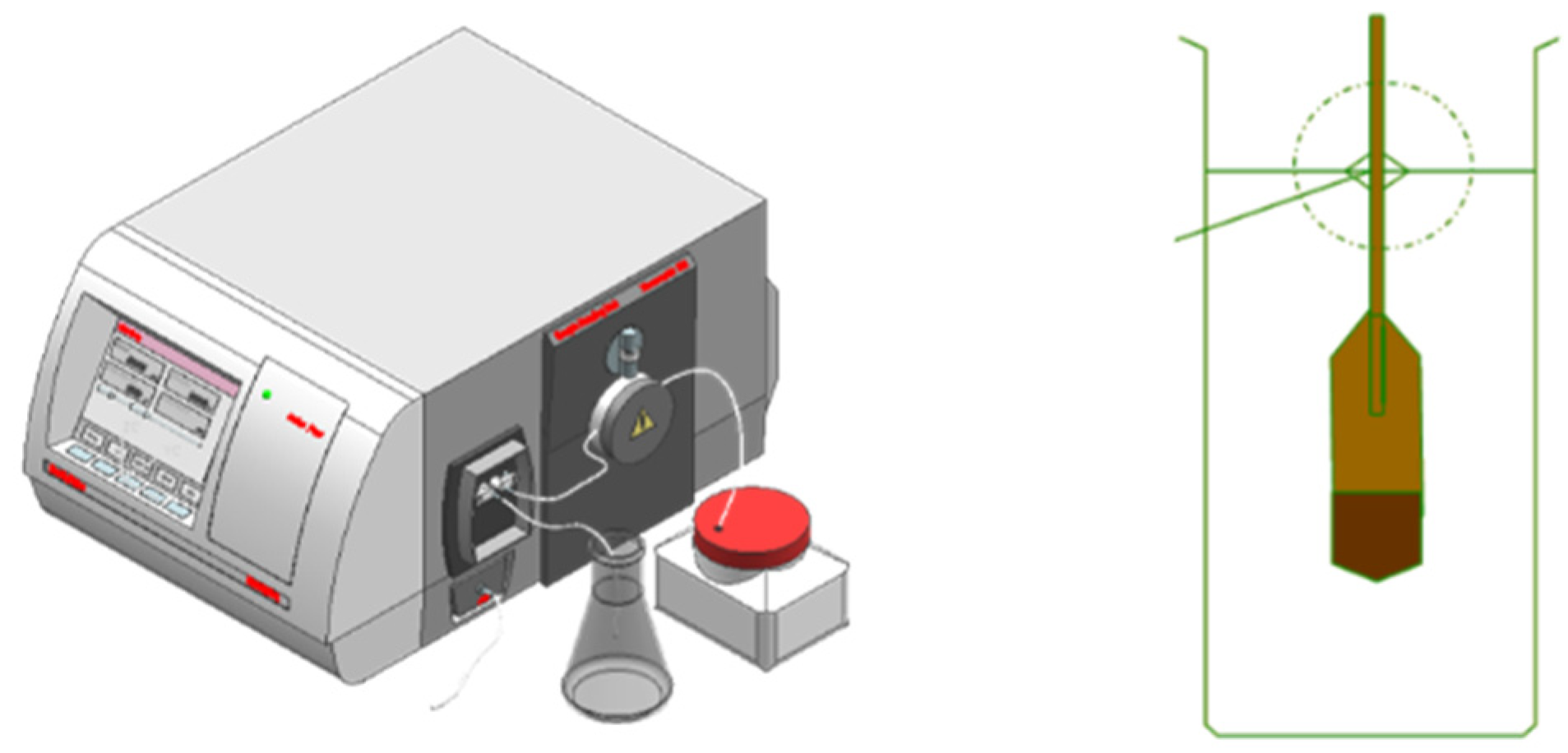
3.1. Establishing the Traceability Chain
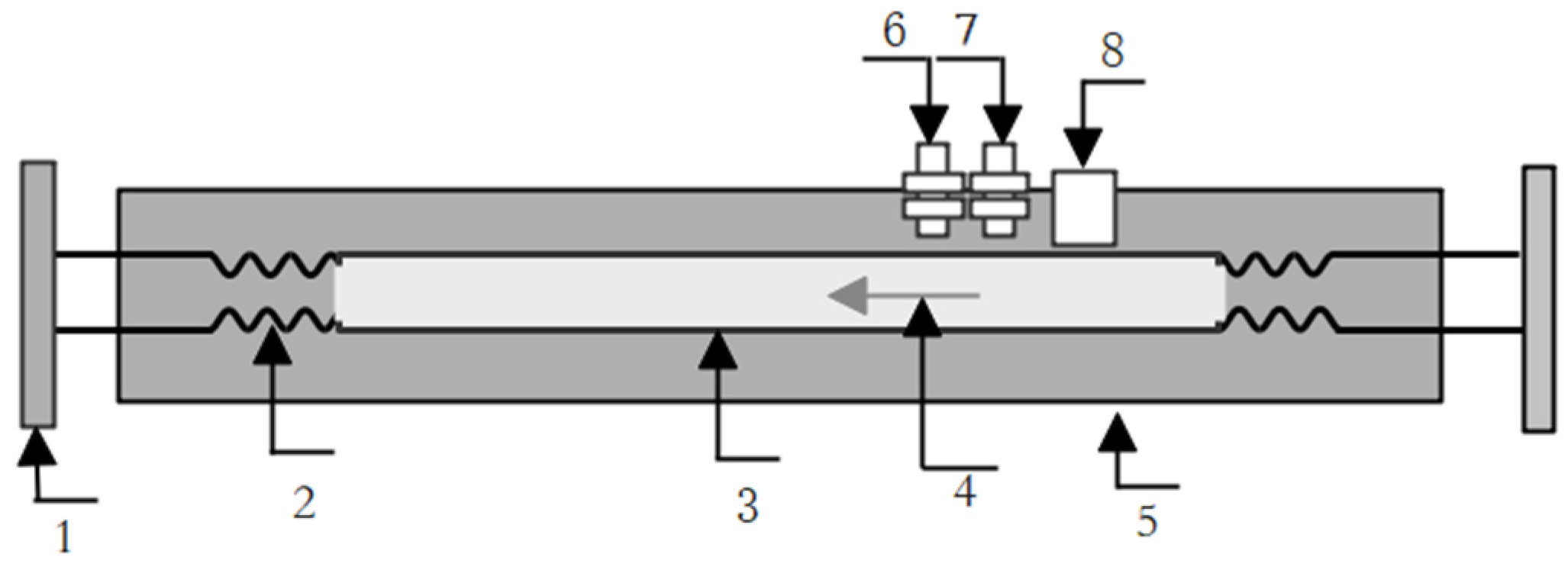
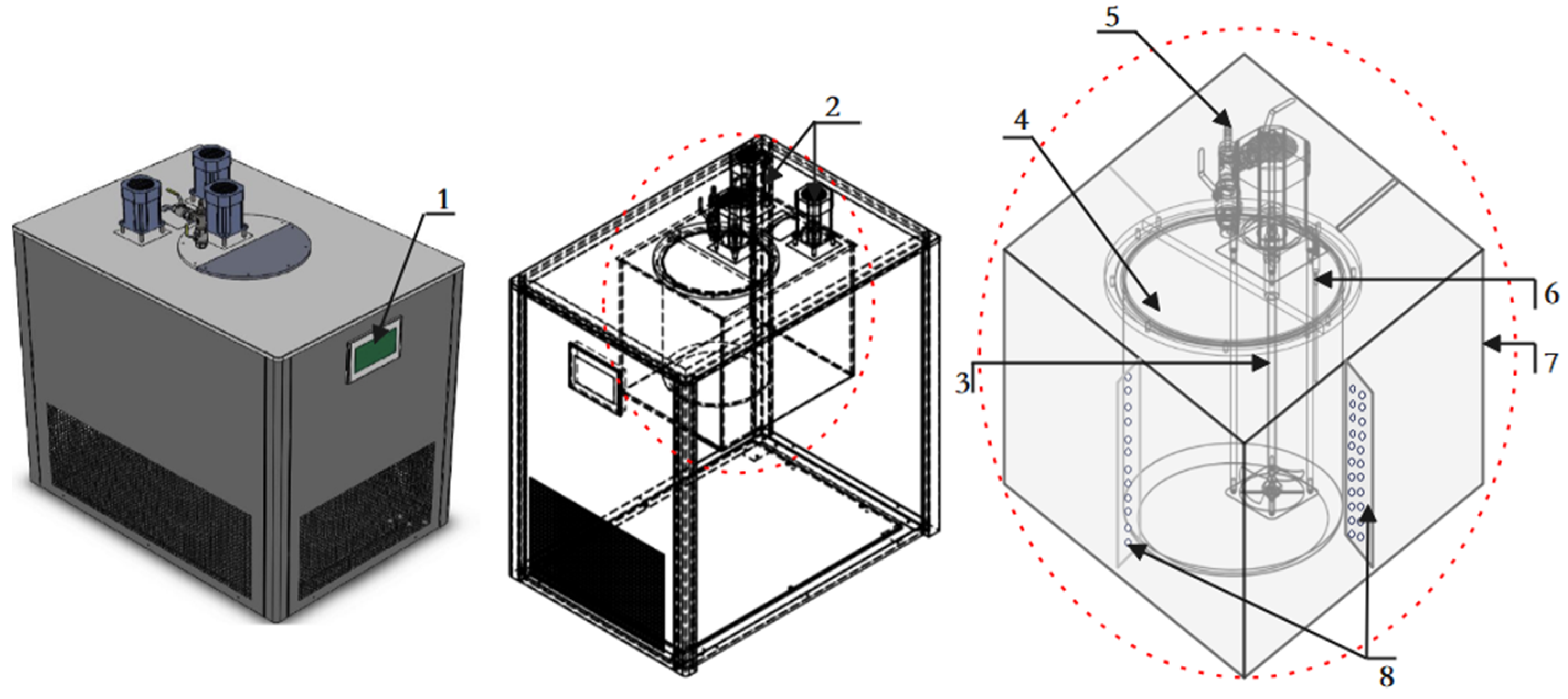
3.2. Device Composition and Structure
3.3. Device Uncertainty Assessment
3.4. Workflow of the Experimental Setup
4. Online Vibrating Tube Densitometer Measurement Performance Experiment
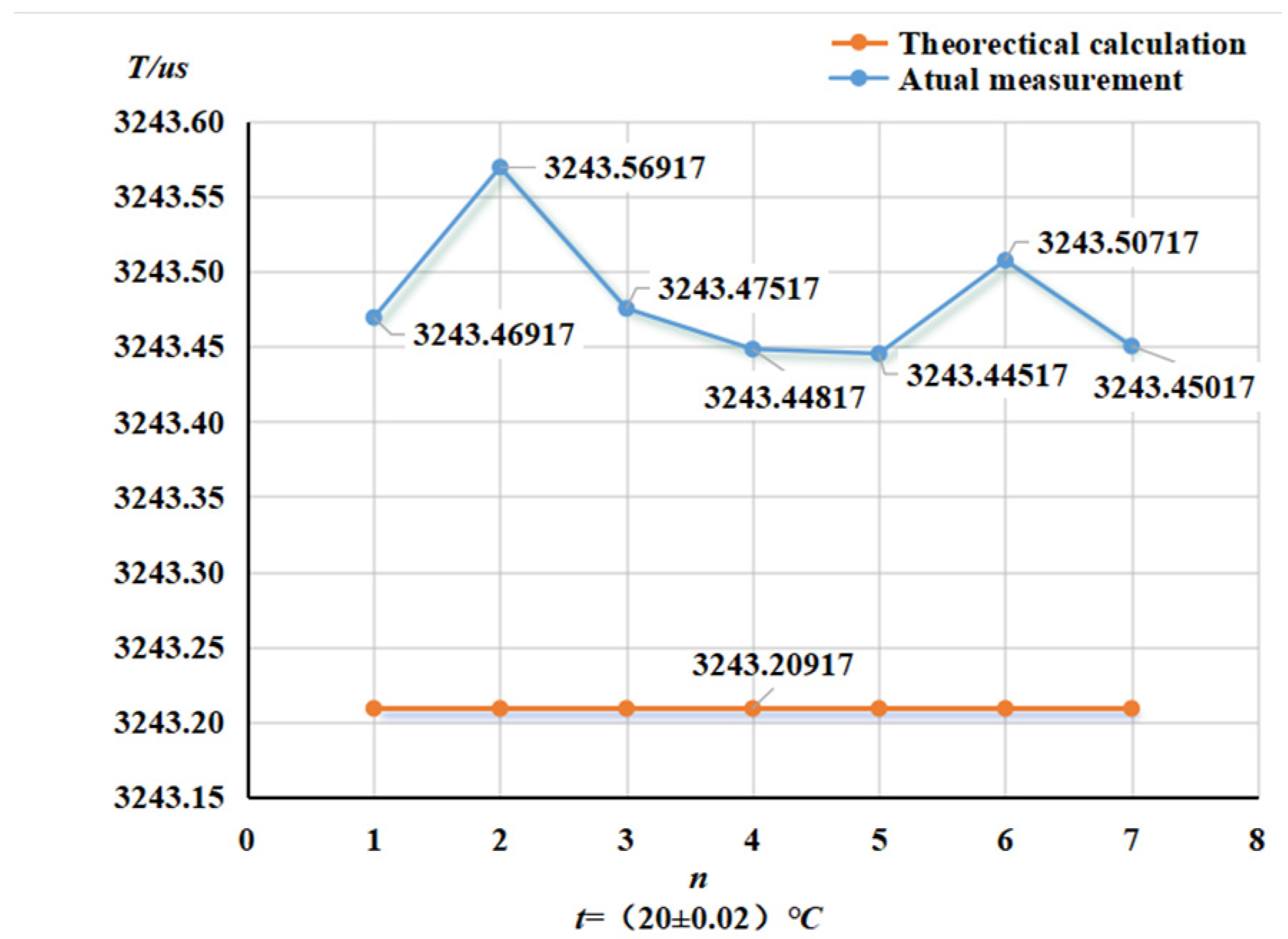
4.1. Temperature Vibration Frequency Test
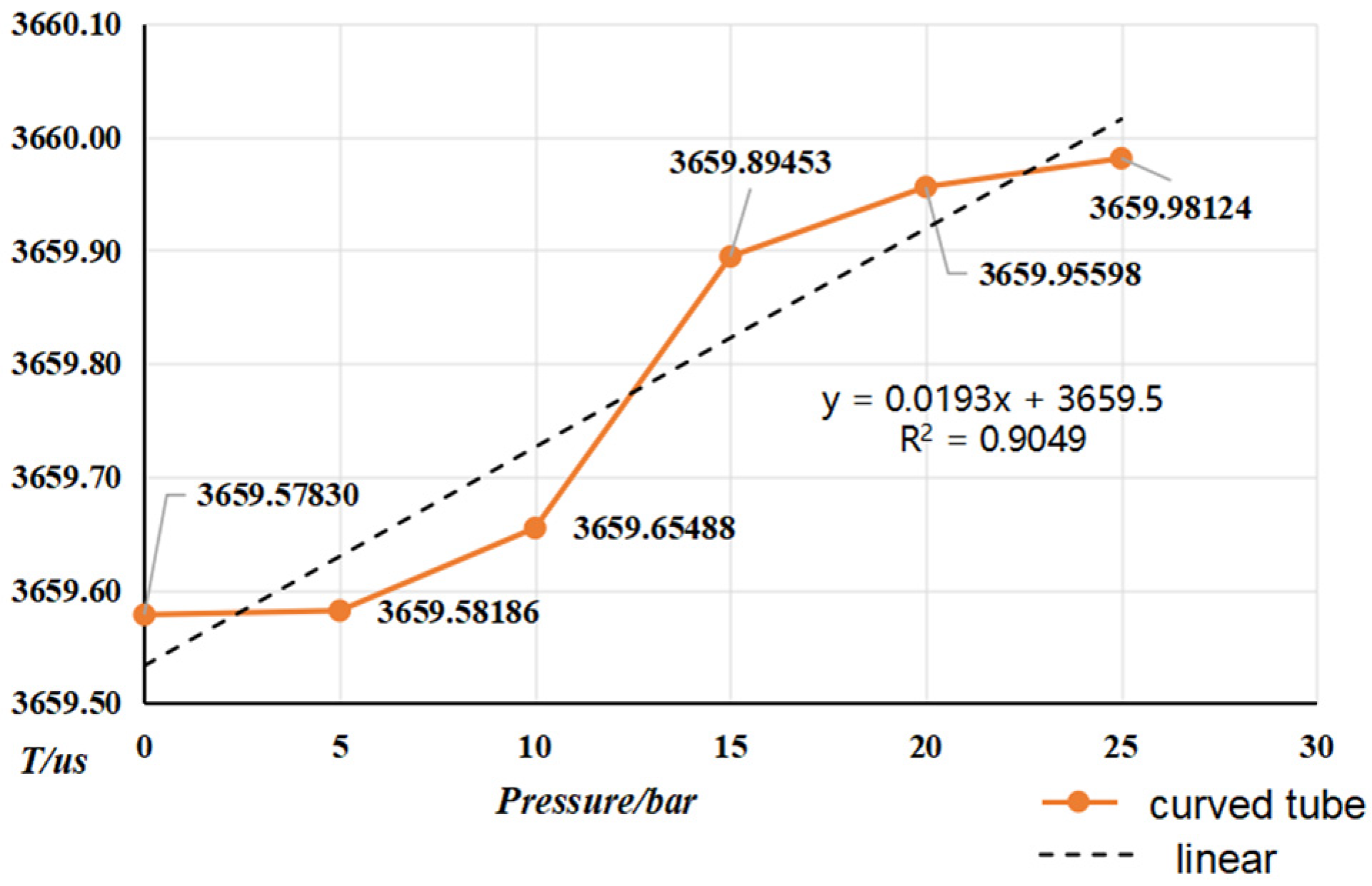
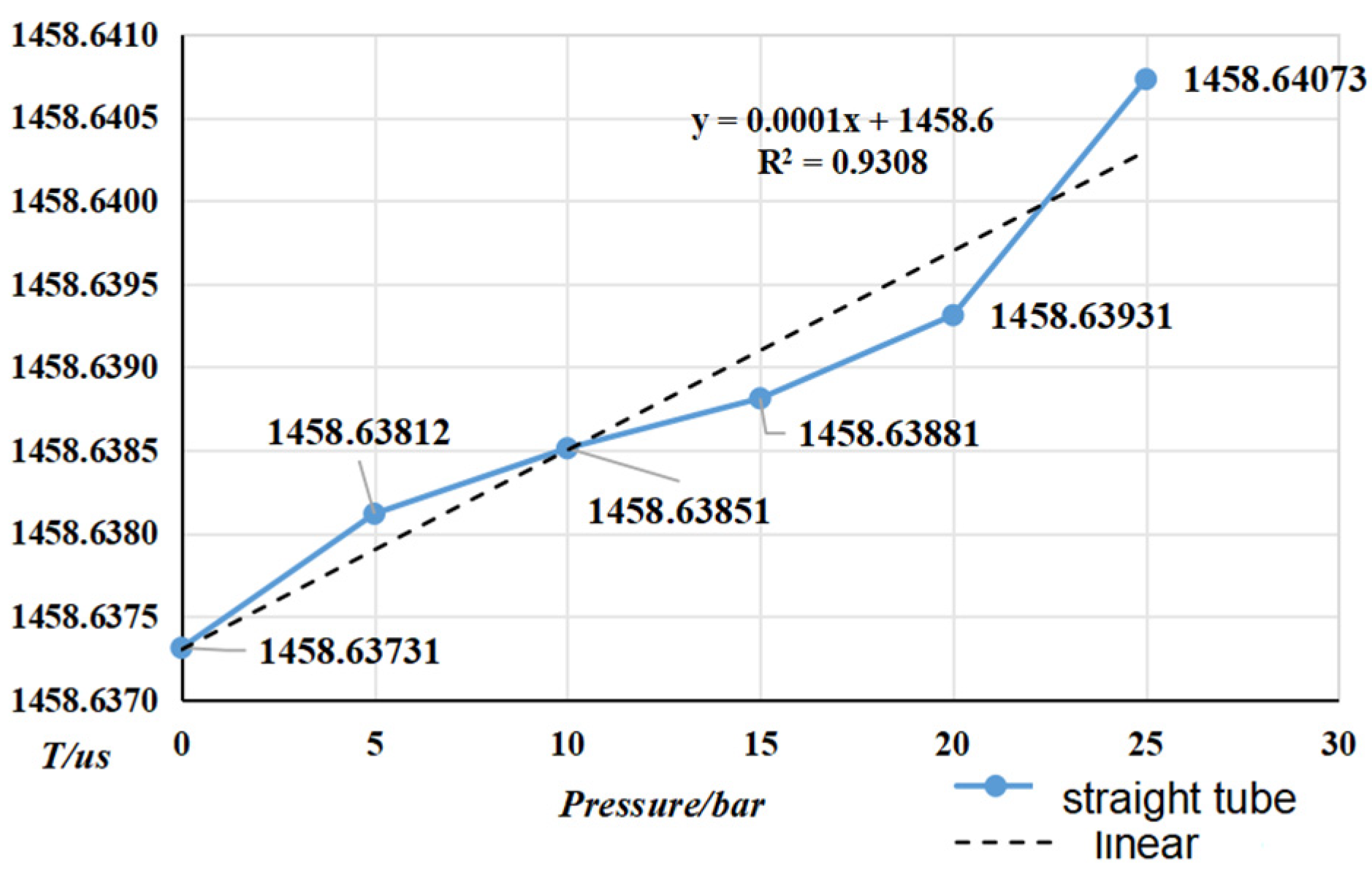
4.2. Pressure Frequency Experiment
5. Conclusions
- A set of online vibrating tube liquid densitometer experimental devices were built based on a quantity and value transfer system. The whole device consists of a desktop densitometer, multi-temperature thermostatic stirring system, walk-in thermostat, blowing system, and frequency acquisition system. The experimental research on five densitometers can be carried out at the same time under different temperatures and densities, and the device evaluates an accuracy of U = 0.08 kg/m3, k = 2;
- This device solves the problem of the traceability of online vibrating tube liquid densitometers, and can carry out the assessments of quantity and value transfer at (750~1400) kg/m3, (15~45) °C, and (0~25) bar and the accuracy grade ≥±0.1 kg/m3 of online vibrating tube liquid densitometer, and it is proved that this device has the ability to assess quantity and value transfer, as in the previous experiments;
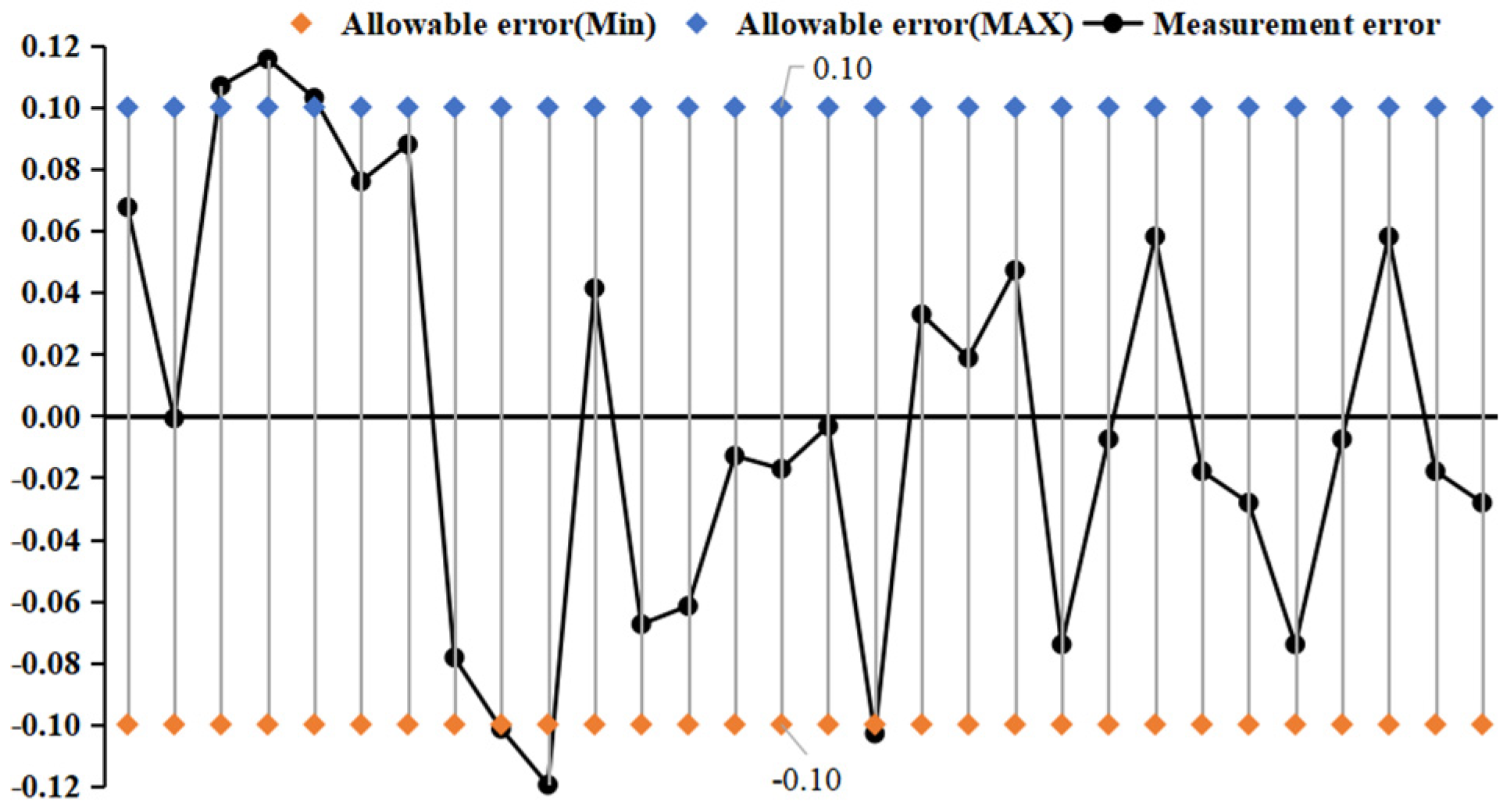
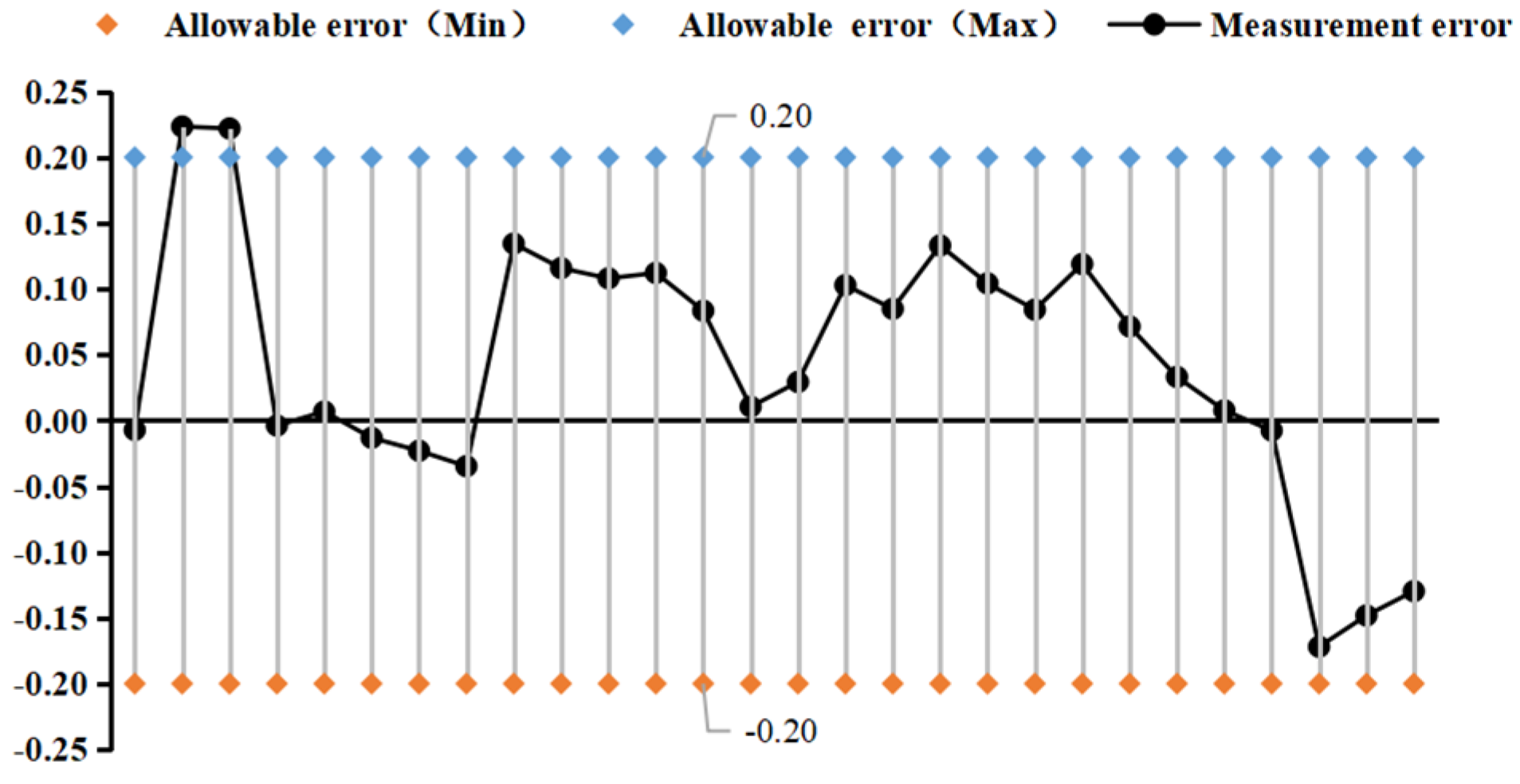
- We selected straight-tube-type and elbow-type densitometers, at (15~45) °C, and selected five kinds of liquids to carry out online vibrating tube densitometer metrological experiments. We concluded that different density vibration tube frequencies increased with density and decreased with the increase in temperature. Using the frequency and density values obtained from the experiments, we calculated the K coefficient of the theoretical equations and determined the fitted density difference. The fitting errors of the two densitometers are basically within the nominal error, which indicates that the device has a good degree of differentiation and reasonableness. The fitting errors of the two densitometers at (15~45) °C are not a linear result in a uniform direction (positive or negative), and the factors contributing to this result still need to be determined by further research;
- From the (0~25) bar carried out the online vibrating tube densitometer pressure–frequency experiments, it is concluded that the vibration frequency increases with the increase in pressure in the vibrating tube. The pressure in the pipe and the interaction of the coefficients of the vibrating tube at both ends of the equivalent elasticity coefficient of the corrugated pipe, K, deviate from the pressure and the elasticity coefficient of the K change rule. This still needs to be studied further. The trend of change in the curved-type density meter by the pressure is more obvious;
- The experimental device will be used to carry out more experiments and tests in the later stage. It will assess the pressure and viscosity concerning the vibration frequency, combined with the fluid Reynolds number, inlet effect, and other factors to explore the influence of the velocity profile on fitting coefficients. At the same time, a set of standard density values of liquids under a wide range of temperatures and pressures will be assessed with the test device, because the standard density of the current test values at different pressures is only a theoretical calculation of the value;
- Through the experiment, the rationality and scientific value of the device were verified, and the change rule of vibration frequency with the temperature and pressure of online vibrating tube densitometers was studied, which has certain significance for the use of an online vibrating tube densitometer and its subsequent applications.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lagourette, B.; Boned, C.; Saint-Guirons, H.; Xans, P.; Zhou, H. Densimeter Calibration Method versus Temperature and Pressure. Meas. Sci. Technol. 1992, 3, 699–703. [Google Scholar] [CrossRef]
- Wang, D.l.; Yang, T.T.; Mao, S.; Yuan, J. Analysis of liquid density measurement methods. Meas. Test. Technol. 2019, 46, 55–60. [Google Scholar] [CrossRef]
- Xu, C. Research on Online Monitoring System of Pipeline liquid Density; Harbin Institute of Technology: Harbin, China, 2021. [Google Scholar] [CrossRef]
- Puttmer, A.; Hauptmann, P.; Henning, B. Ultrasonic Density Sensor for Liquids. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2000, 47, 85–92. [Google Scholar] [CrossRef] [PubMed]
- Lv, F.; Zhang, X.Z. Experimental study on the performance of single straight tube vibrating fluid densitometer. Nucl. Power Eng. 2012, 33, 19–22. Available online: https://kns.cnki.net/kcms2/article/abstractv (accessed on 10 December 2023).
- Higuti, R.T.; Buiochi, F.; Adamowski, J.C.; de Espinosa, F.M. Ultrasonic Density Measurement Cell Design and Simulation of Non-Ideal Effects. Ultrasonics 2006, 44, 302–309. [Google Scholar] [CrossRef] [PubMed]
- Zheng, D.Z.; Ji, Y.S.; Shang, S.F. Design and Theoretical Analysis of a Resonant Sensor for Liquid Density Measurement. Sensors 2012, 12, 7905–7916. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Wu, J.; Meng, X.; Abdulagatov, I. Compressed Liquid Density Measurements of Dimethyl Ether with a Vibrating Tube Densimeter. J. Chem. Thermodyn. 2011, 43, 1371–1374. [Google Scholar] [CrossRef]
- Majer, V.; Hui, L.; Crovetto, R.; Wood, R.H. Volumetric Properties of Aqueous 1-1 Electrolyte Solutions near and above the Critical Temperature of Water I. Densities and Apparent Molar Volumes of NaCl (Aq) from 0.0025 Mol·kg−1 to 3.1 Mol·kg−1, 604.4 K to 725.5 K, and 18.5 MPa to 38.0 MPa. J. Chem. Thermodyn. 1991, 23, 213–229. [Google Scholar] [CrossRef]
- Aida, T.; Yamazaki, A.; Akutsu, M.; Ono, T.; Kanno, A.; Hoshina, T.A.; Ota, M.; Watanabe, M.; Sato, Y.; Smith, R.L.; et al. Laser-Doppler Vibrating Tube Densimeter for Measurements at High Temperatures and Pressures. Rev. Sci. Instrum. 2007, 78, 115111. [Google Scholar] [CrossRef] [PubMed]
- JJF 1059-1999; Measurement Uncertainty Assessment and Representation. China National Metrological Specifications, Issued by the China Quality and Technical Supervision Bureau: Lanzhou, China, 1999.


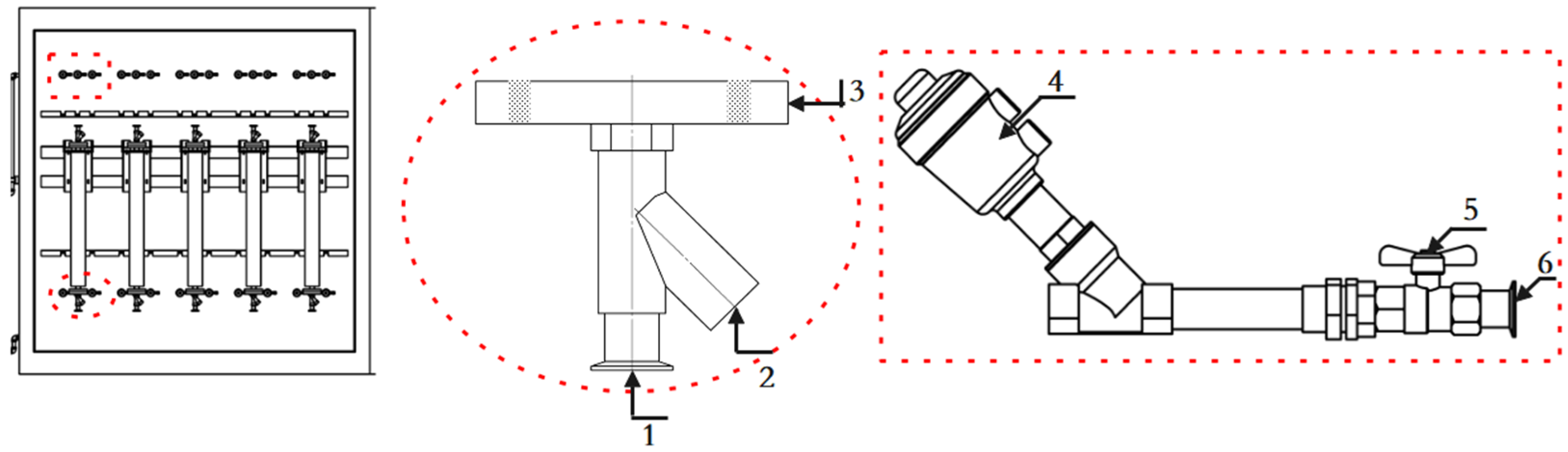




| NO. | Source | Type | u(xi) (kg/m³) | Combined Expanded Uncertainty | Combined Expanded Uncertainty |
|---|---|---|---|---|---|
| 1 | Desktop density meter | B | 0.0225 | 0.039 kg/m3 | U = 0.08 kg/m3 k = 2 |
| 2 | Densitometer measurement | A | 5.592 × 10−5 | ||
| 3 | Frequency meter measurement | B | 0.00092 | ||
| 4 | Temperature measurement | B | 0.007 | ||
| 5 | Fit process | A | 0.031 |
| Liquid Name | Measuring Temperature (°C) | Vibration Period (us) | Standard Density (kg/m3) | Fit Density (kg/m3) | Fit Error (kg/m3) |
|---|---|---|---|---|---|
| N-Tridecane | 20.00 | 1378.541607 | 756.226 | 756.226 | 0.00 |
| Anhydrous ethanol | 20.00 | 1401.152815 | 823.136 | 823.136 | 0.00 |
| Aqueous alcohol 1 | 19.99 | 1415.154277 | 865.123 | 865.123 | 0.00 |
| Industrial white oil | 20.00 | 1403.815470 | 831.088 | 831.088 | 0.00 |
| Aqueous alcohol 2 | 19.99 | 1423.031064 | 888.930 | 888.930 | 0.00 |
| Pure water | 20.00 | 1458.638571 | 998.226 | 998.226 | 0.00 |
| Tungstate solution | 20.01 | 1584.048720 | 1405.012 | 1405.013 | 0.01 |
| Liquid Name | Measuring Temperature (°C) | Vibration Period (us) | Standard Density (kg/m3) | Fit Density (kg/m3) | Fit Error (kg/m3) |
|---|---|---|---|---|---|
| Tridecane | 15.50 | 1379.68479 | 759.442 | 759.526 | −0.08 |
| 20.00 | 1378.53900 | 756.226 | 756.218 | 0.01 | |
| 29.41 | 1376.25237 | 749.509 | 749.630 | −0.12 | |
| 40.23 | 1374.62239 | 745.123 | 744.991 | 0.13 | |
| 45.21 | 1372.95320 | 740.369 | 740.170 | 0.20 | |
| Anhydrous ethanol l | 14.25 | 1404.62236 | 833.236 | 833.425 | −0.19 |
| 20.00 | 1403.81547 | 831.088 | 831.088 | 0.00 | |
| 30.12 | 1402.83650 | 828.369 | 828.295 | 0.07 | |
| 40.22 | 1402.19565 | 826.326 | 826.512 | −0.19 | |
| 45.24 | 1400.63691 | 822.136 | 821.925 | 0.21 | |
| Anhydrous ethanol 2 | 14.95 | 1424.40283 | 892.909 | 893.021 | −0.11 |
| 20.00 | 1423.03450 | 888.930 | 888.940 | −0.01 | |
| 29.10 | 1420.48395 | 881.237 | 881.340 | −0.10 | |
| 36.42 | 1419.56231 | 878.639 | 878.651 | −0.01 | |
| 44.22 | 1418.32352 | 875.236 | 875.011 | 0.22 | |
| Water | 14.36 | 1459.03692 | 999.191 | 999.382 | −0.19 |
| 15.56 | 1458.90888 | 999.009 | 999.002 | 0.01 | |
| 20.00 | 1458.63911 | 998.221 | 998.228 | −0.01 | |
| 29.26 | 1457.84188 | 995.898 | 995.885 | 0.01 | |
| 43.89 | 1456.12524 | 990.651 | 990.767 | −0.12 | |
| Tungstate solution | 14.65 | 1585.58569 | 1410.236 | 1410.112 | 0.12 |
| 20.00 | 1584.04872 | 1405.012 | 1405.012 | 0.00 | |
| 29.25 | 1582.86922 | 1401.236 | 1401.194 | 0.04 | |
| 40.12 | 1582.01231 | 1398.369 | 1398.496 | −0.13 | |
| 45.37 | 1580.97900 | 1395.237 | 1395.104 | 0.13 |
| Liquid Name | Measuring Temperature (°C) | Vibration Period (us) | Standard Density (kg/m3) | Fit Density (kg/m3) | Fit Error (kg/m3) |
|---|---|---|---|---|---|
| Tridecane | 20.00 | 3659.93511 | 998.226 | 998.208 | −0.02 |
| Anhydrous ethanol | 20.00 | 3607.10110 | 865.123 | 865.198 | 0.08 |
| Mixture 1 | 20.00 | 3590.20928 | 823.136 | 823.080 | −0.06 |
| Industrial white oil | 20.00 | 3563.23146 | 756.226 | 756.225 | −0.00 |
| Mixing solution 2 | 19.99 | 3593.46230 | 831.088 | 831.176 | 0.09 |
| Pure water | 20.00 | 3616.59763 | 888.930 | 888.963 | 0.03 |
| Tungstate solution | 20.01 | 3816.98624 | 1405.012 | 1405.004 | −0.01 |
| Liquid Name | Measuring Temperature (°C) | Vibration Period (us) | Standard Density (kg/m3) | Fit Density (kg/m3) | Fit Error (kg/m3) |
|---|---|---|---|---|---|
| Tridecane | 15.55 | 3564.05124 | 759.442 | 759.510 | 0.07 |
| 20.00 | 3563.23146 | 756.226 | 756.225 | 0.00 | |
| 29.31 | 3561.62569 | 749.509 | 749.616 | 0.11 | |
| 40.19 | 3561.10569 | 745.123 | 745.239 | 0.12 | |
| 45.11 | 3559.74569 | 740.369 | 740.472 | 0.10 | |
| Anhydrous ethanol l | 14.33 | 3593.69892 | 833.236 | 833.312 | 0.08 |
| 20.00 | 3593.46230 | 831.088 | 831.176 | 0.09 | |
| 30.00 | 3593.40000 | 828.369 | 828.291 | −0.08 | |
| 40.22 | 3593.69000 | 826.326 | 826.225 | −0.10 | |
| 45.25 | 3592.55426 | 822.136 | 822.016 | −0.12 | |
| Anhydrous ethanol 2 | 14.54 | 3617.61236 | 892.909 | 892.950 | 0.04 |
| 20.00 | 3616.55763 | 888.93 | 888.862 | −0.07 | |
| 29.03 | 3614.44563 | 881.237 | 881.175 | −0.06 | |
| 36.44 | 3614.21369 | 878.639 | 878.626 | −0.01 | |
| 44.22 | 3613.68000 | 875.236 | 875.219 | −0.02 | |
| Water | 14.21 | 3659.75236 | 999.191 | 999.188 | 0.00 |
| 15.11 | 3659.73000 | 999.009 | 998.906 | −0.10 | |
| 20.00 | 3659.95351 | 998.221 | 998.254 | 0.03 | |
| 29.15 | 3659.93123 | 995.898 | 995.917 | 0.02 | |
| 43.54 | 3659.29000 | 990.651 | 990.698 | 0.05 | |
| Tungstate solution | 14.65 | 3818.55000 | 1410.236 | 1410.162 | −0.07 |
| 20.00 | 3816.98624 | 1405.012 | 1405.004 | −0.01 | |
| 29.33 | 3816.26000 | 1401.236 | 1401.294 | 0.06 | |
| 40.02 | 3815.92360 | 1398.369 | 1398.496 | −0.13 | |
| 45.44 | 3815.13123 | 1395.237 | 1395.104 | 0.13 |
| Fit Factor | k20a | k20b | k21a | k21b |
|---|---|---|---|---|
| Straight tube | −1.4209 × 10−4 | −2.74958× 10−7 | 1.88777 × 10−1 | 2.47360 × 10−4 |
| Curved tube | 1.49944 × 10−2 | 0.00 | 0.00 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, D.; Sun, Y.; Chen, W.; Mu, J.; Peng, W. Development and Experimental Study of an Experimental Setup for an Online Vibrating Tube Liquid Densitometer. Appl. Sci. 2024, 14, 9905. https://doi.org/10.3390/app14219905
Xu D, Sun Y, Chen W, Mu J, Peng W. Development and Experimental Study of an Experimental Setup for an Online Vibrating Tube Liquid Densitometer. Applied Sciences. 2024; 14(21):9905. https://doi.org/10.3390/app14219905
Chicago/Turabian StyleXu, Defu, Yaoning Sun, Welin Chen, Jun Mu, and Wang Peng. 2024. "Development and Experimental Study of an Experimental Setup for an Online Vibrating Tube Liquid Densitometer" Applied Sciences 14, no. 21: 9905. https://doi.org/10.3390/app14219905
APA StyleXu, D., Sun, Y., Chen, W., Mu, J., & Peng, W. (2024). Development and Experimental Study of an Experimental Setup for an Online Vibrating Tube Liquid Densitometer. Applied Sciences, 14(21), 9905. https://doi.org/10.3390/app14219905





