Ship Type Selection and Cost Optimization of Marine Container Ships Based on Genetic Algorithm
Abstract
1. Introduction
2. Establishment of the Bi-Level Programming Model
2.1. Assumptions and Variable Descriptions
- The international cargo transport service covers only transportation and simple value-added services (e.g., sorting, packing, etc.), and costs are calculated per container.
- Logistics service costs consist only of fixed costs, transportation costs, and value-added service costs, with fixed unit prices for transportation and value-added services.
- Different types of ships used by the shipping company correspond to fixed routes.
- The transportation cost of logistics business is related only to the unit transportation cost of the ship and the shipment volume, while the value-added service cost is related only to the handling volume.
2.2. Constraints
- (1)
- Transport Cost in for Single Shipping Task for the Shipping Company
- (2)
- Value-Added Service Cost for a Single Shipping Task for the Shipping Company
- (3)
- Fixed Cost in a Single Shipping Task for the Shipping Company
- (4)
- Emissions Generated by Completing a Single Order
- (5)
- Total Operating Cost of the Shipping Company
2.3. Objective Function
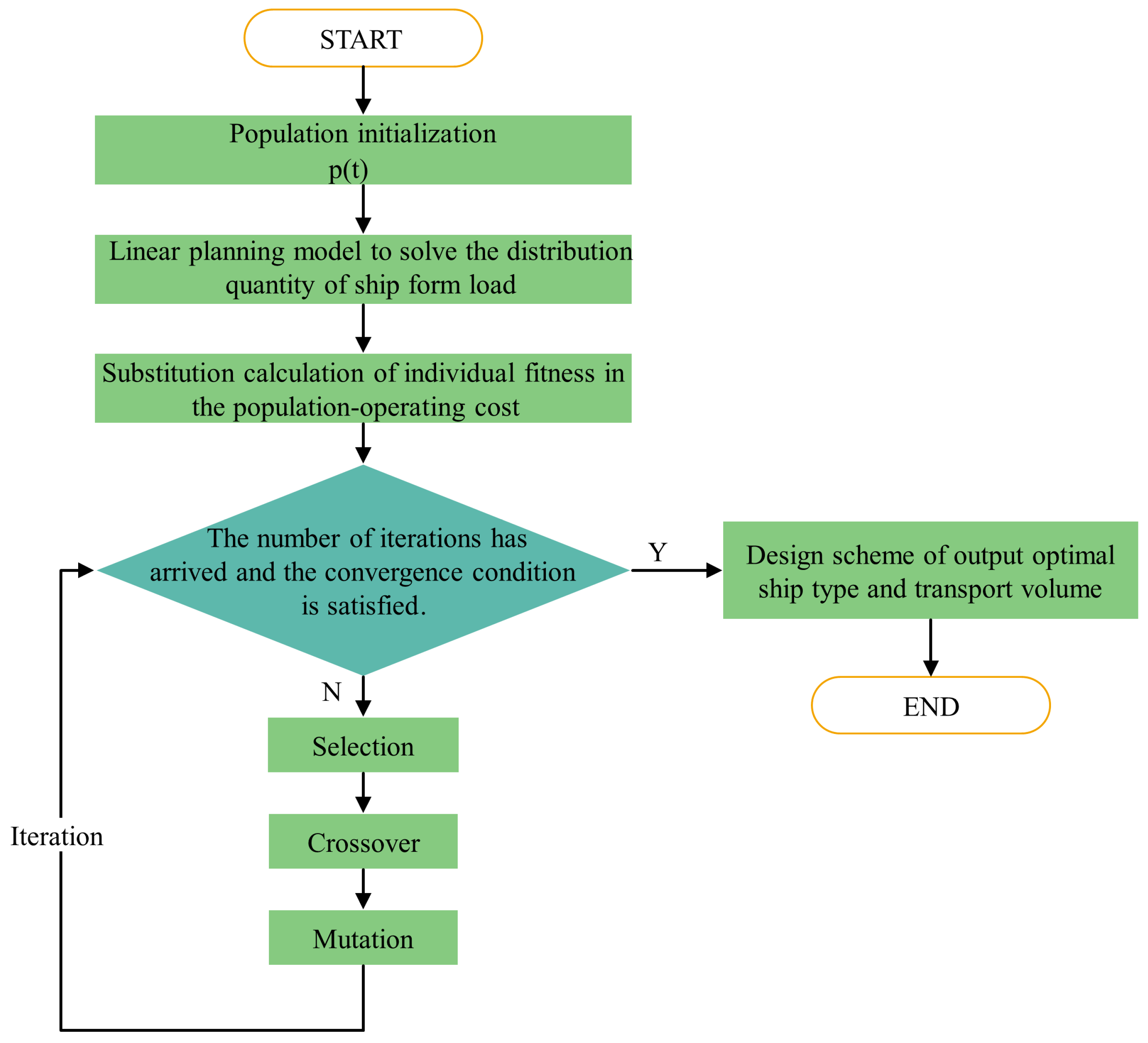
2.4. Model Solution
- (1)
- Encoding Strategy
- (2)
- Random Initialization of Population
- (3)
- Fitness Calculation
- (4)
- Selection of crossover operation
- (5)
- Mutation Operation
- (6)
- First termination condition judgment
- (7)
- Second termination condition judgment
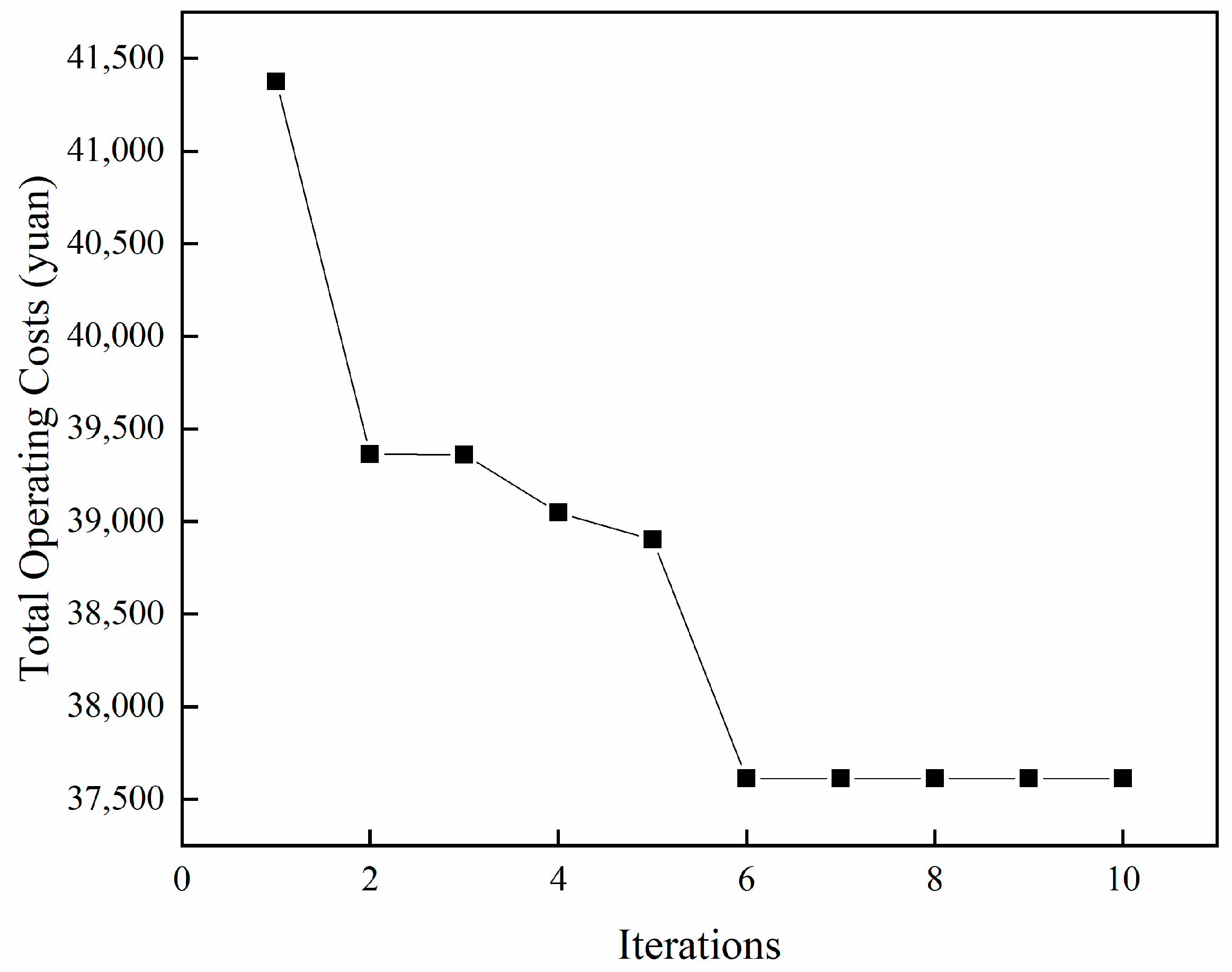
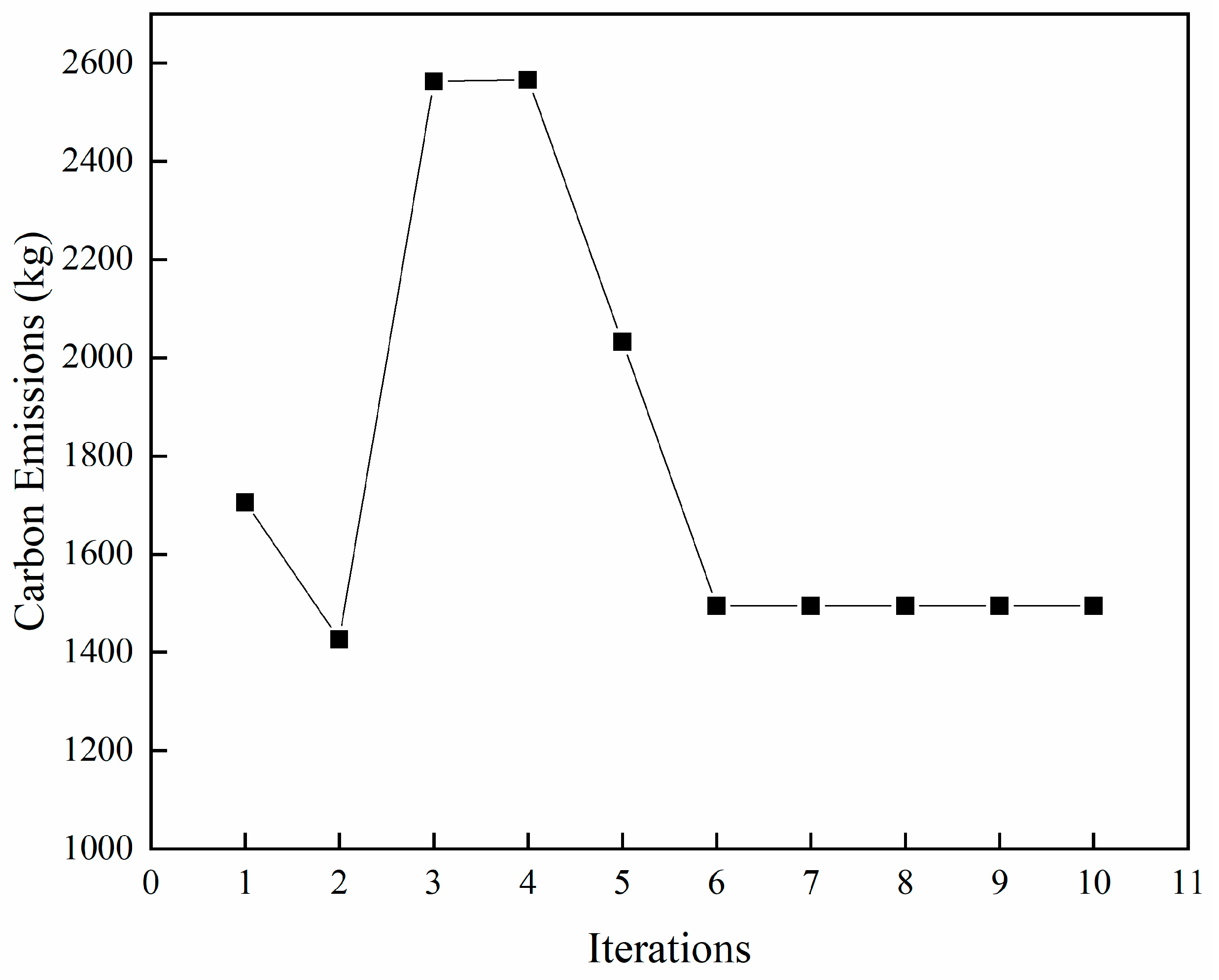
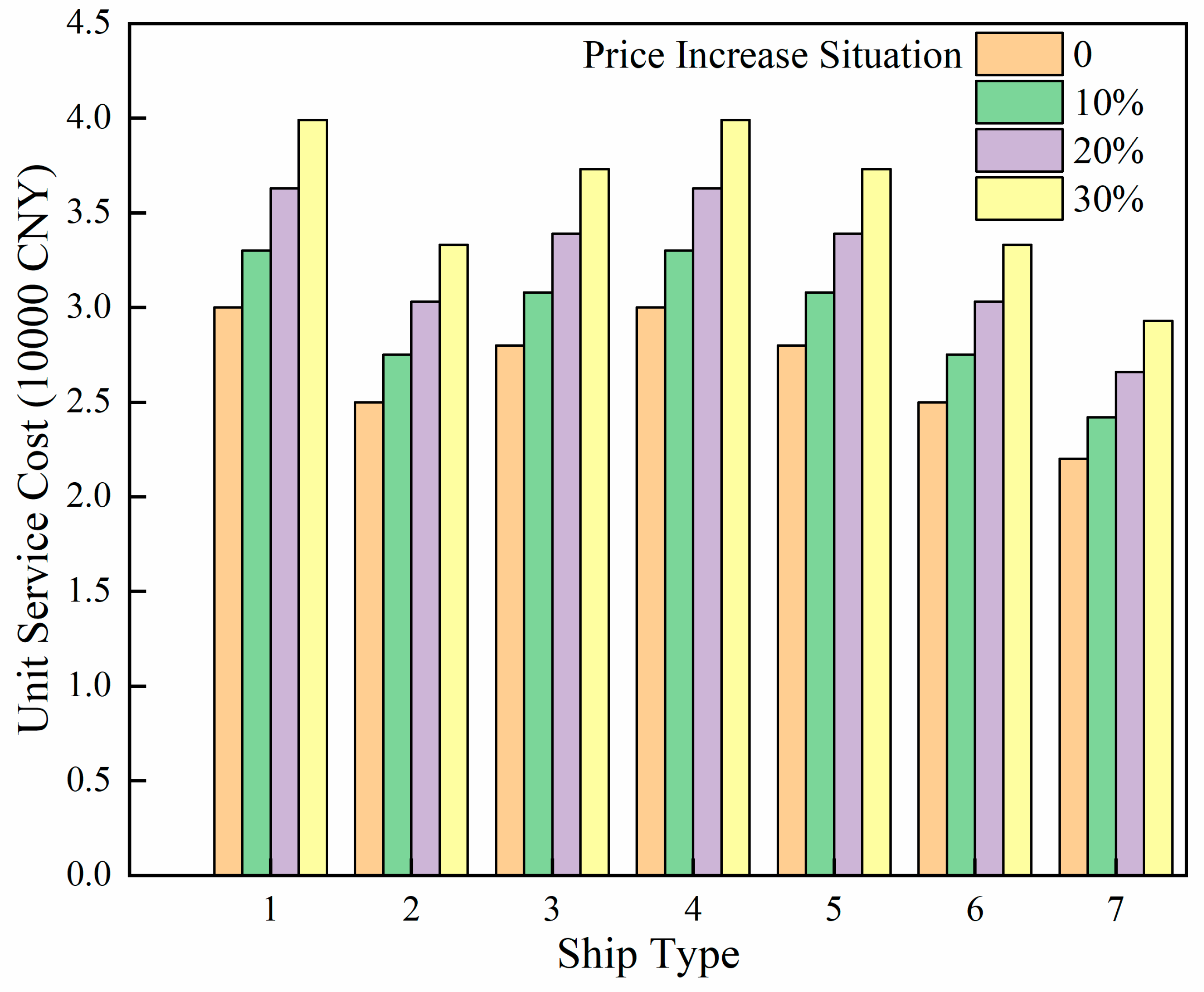
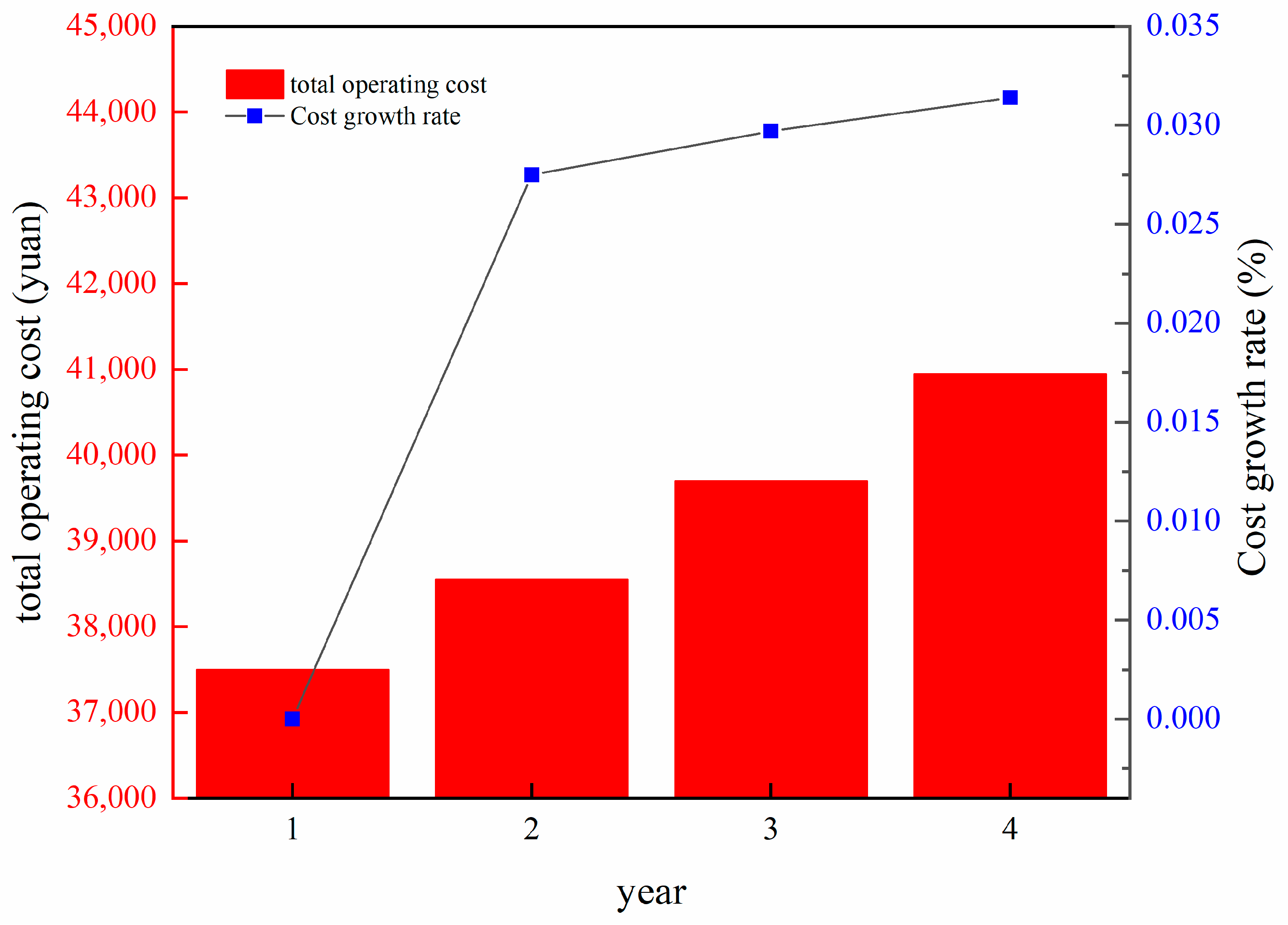
3. Case Study Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Meng, Q.; Wang, S. Liner ship fleet deployment with week-dependent container shipment demand. Eur. J. Oper. Res. 2012, 222, 241–252. [Google Scholar] [CrossRef]
- Meng, Q.; Wang, T.; Wang, S. Short-term liner ship fleet planning with container transshipment and uncertain container shipment demand. Eur. J. Oper. Res. 2012, 223, 96–105. [Google Scholar] [CrossRef]
- Wang, S.; Meng, Q. Liner ship fleet deployment with container transshipment operations. Transp. Res. Part E Transp. Res. Part 2012, 48, 470–484. [Google Scholar] [CrossRef]
- Wang, S.; Meng, Q. Container liner fleet deployment: A systematic overview. Transp. Res. Part C Emerg. Technol. 2017, 77, 389–404. [Google Scholar] [CrossRef]
- Ng, M.W. Distribution-free vessel deployment for liner shipping. Eur. J. Oper. Res. 2014, 238, 858–862. [Google Scholar] [CrossRef]
- Ng, M.W. Container vessel fleet deployment for liner shipping with stochastic dependencies in shipping demand. Transp. Res. Part B Methodol. 2015, 74, 79–87. [Google Scholar] [CrossRef]
- Ng, M.W. Revisiting a class of liner fleet deployment models. Eur. J. Oper. Res. 2017, 257, 773–776. [Google Scholar] [CrossRef]
- Bukljaš, M.; Rogić, K.; Jerebić, V. Distributionally Robust Model and Metaheuristic Frame for Liner Ships Fleet Deployment. Sustainability 2022, 14, 5551. [Google Scholar] [CrossRef]
- Gelareh, S.; Meng, Q. A novel modeling approach for the fleet deployment problem within a short-term planning horizon. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 76–89. [Google Scholar] [CrossRef]
- Sheng, D.; Meng, Q.; Li, Z.C. Optimal vessel speed and fleet size for industrial shipping services under the emission control area regulation. Transp. Res. Part C Emerg. Technol. 2019, 105, 37–53. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, Y.; Wang, H. Nonlinear programming for fleet deployment, voyage planning and speed optimization in sustainable liner shipping. Electron. Res. Arch. 2023, 31, 147–168. [Google Scholar] [CrossRef]
- Ronen, D. The effect of oil price on containership speed and fleet size. J. Oper. Res. Soc. 2011, 62, 211–216. [Google Scholar] [CrossRef]
- Wang, S.; Meng, Q.; Liu, Z. Bunker consumption optimization methods in shipping: A critical review and extensions. Transp. Res. Part E Logist. Transp. Rev. 2013, 53, 49–62. [Google Scholar] [CrossRef]
- Cariou, P. Is slow steaming a sustainable means of reducing CO2 emissions from container shipping? Transp. Res. Part D Transp. Environ. 2011, 16, 260–264. [Google Scholar] [CrossRef]
- Norstad, I.; Fagerholt, K.; Laporte, G. Tramp ship routing and scheduling with speed optimization. Transp. Res. Part C Emerg. Technol. 2011, 19, 853–865. [Google Scholar] [CrossRef]
- Song, D.P.; Li, D.; Drake, P. Multi-objective optimization for planning liner shipping service with uncertain port times. Transp. Res. Part E Logist. Transp. Rev. 2015, 84, 1–22. [Google Scholar] [CrossRef]
- Lindstad, H.E.; Rehn, C.F.; Eskeland, G.S. Sulphur abatement globally in maritime shipping. Transp. Res. Part D. Transp. Environ. 2017, 57D, 303–313. [Google Scholar] [CrossRef]
- Xiao, P.; Wang, H. Operation Optimization of the Sea Container Fleet Based on the Double-Level Planning Model. Appl. Sci. 2024, 14, 1624. [Google Scholar] [CrossRef]
- Wang, C.; Xu, C. Sailing speed optimization in voyage chartering ship considering different carbon emissions taxation. Comput. Ind. Eng. 2015, 89, 108–115. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X. Effects of carbon emission reduction policies on transportation mode selections with stochastic demand. Transp. Res. Part E. Logist. Transp. Rev. 2016, 90E, 196–205. [Google Scholar] [CrossRef]
- Chang, Y.-T.; Danao, D. Green Shipping Practices of Shipping Firms. Sustainability 2017, 9, 829. [Google Scholar] [CrossRef]
- Zhu, M.; Yuen, K.F.; Ge, J.W.; Li, K.X. Impact of maritime emissions trading system on fleet deployment and mitigation of CO2 emission. Transp. Res. Part D Transp. Environ. 2018, 62, 474–488. [Google Scholar] [CrossRef]
- Xing, Y.; Yang, H.; Ma, X.; Zhang, Y. Optimization of ship speed and fleet deployment under carbon emissions policies for container shipping. Transport 2019, 34, 260–274. [Google Scholar] [CrossRef]
- Tian, X.; Yan, R.; Qi, J.; Zhuge, D.; Wang, H.J.S. A Bi-Level Programming Model for China’s Marine Domestic Emission Control Area Design. Sustainability 2022, 14, 3562. [Google Scholar] [CrossRef]
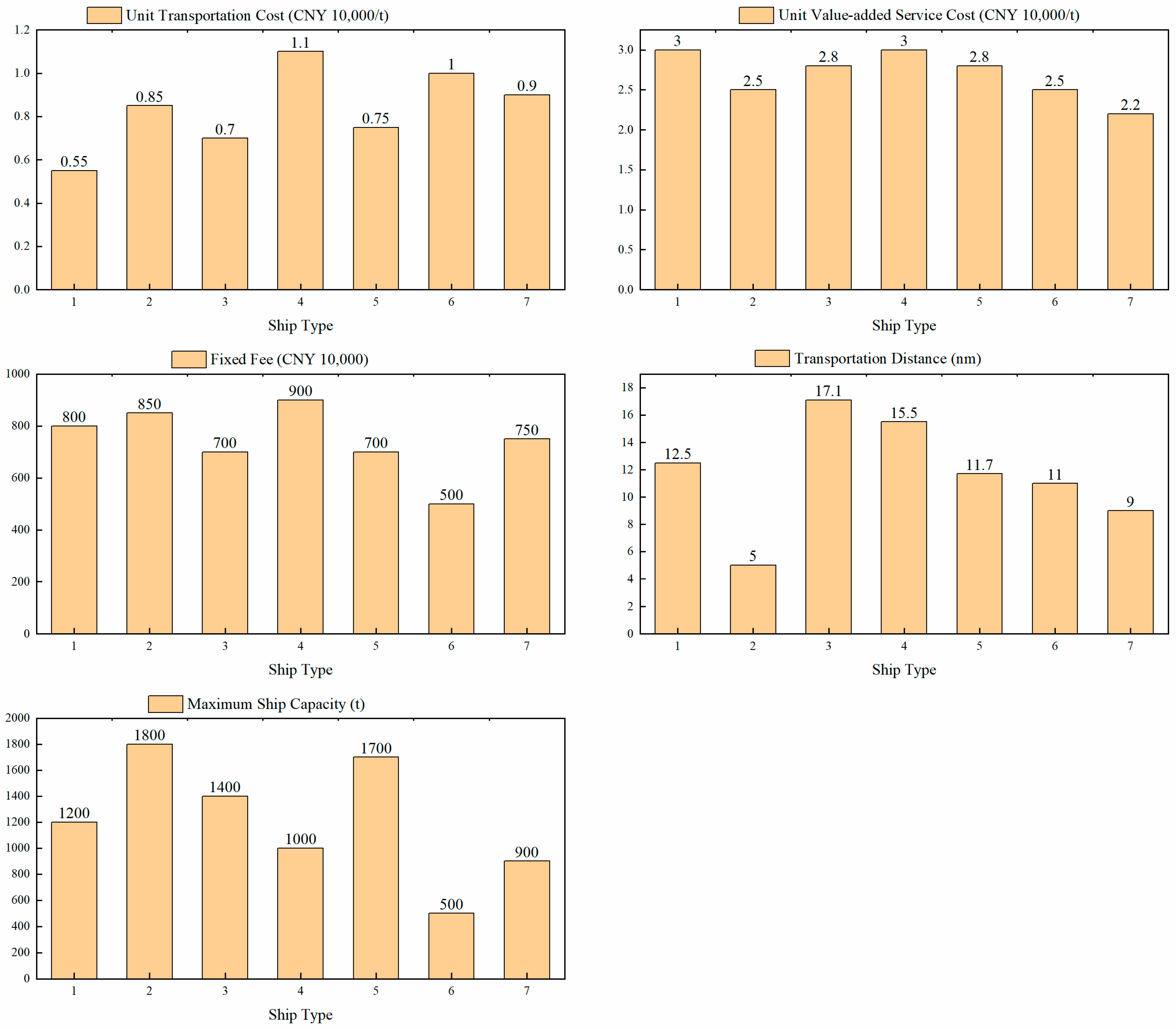
| Variable | Meaning |
|---|---|
| Total operating cost of a single transport mission for the shipping company | |
| Transport cost for a single transport mission of the shipping company | |
| Value-added service cost of the transportation of a single unit of cargo by ship | |
| Fixed cost of transportation of a single unit of cargo by ship | |
| 0–1 variable: 1 when type ship is configured on the route, otherwise 0 | |
| Transportation cost per nautical mile (nm) | |
| Indicates the value-added service cost per unit ton of cargo incurred when the type ship provides simple value-added services (such as handling, sorting, etc.) | |
| Indicates the fixed cost incurred when selecting type ship | |
| Indicates the logistics business volume that type ship receives from the shipping company’s business, that is, the cargo volume (TEU) | |
| The number of different types of ships owned by the shipping company | |
| The distance from the destination for which type ship provides logistics services; varies with the different routes arranged by different ships. | |
| The total carbon emissions of a single transport mission of the shipping company | |
| Ship energy efficiency design index of type ship | |
| The maximum cargo carrying capacity of ship in a single transport |
| Ship Type | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| EEDI/(g(CO2)t·nm) | 22.8 | 103.4 | 5.38 | 6.26 | 80.77 | 49.27 | 19.56 |
| Ship Type | Allocated Cargo Volume (t) | Transport Cost/CNY | Service Cost/CNY | Fixed Cost/CNY | Total Operating Cost/CNY | Carbon Emissions (kg) | Operating Cost per Unit of Cargo/CNY | Carbon Emissions per Unit of Cargo/CNY |
|---|---|---|---|---|---|---|---|---|
| 1 | 1200 | 8250 | 3600 | 800 | 12,650 | 342 | 10.54 | 0.285 |
| 2 | 1800 | 150.1 | 493.9 | 850 | 13,000 | 930.6 | 7.22 | 0.517 |
| 6 | 100 | 1100 | 250 | 500 | 1850 | 54.2 | 18.5 | 0.542 |
| 7 | 900 | 7290 | 1980 | 750 | 10,020 | 158.4 | 11.13 | 0.176 |
| Total | 4000 | 8682.5 | 4982.7 | 2900 | 37,520 | 1485.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, P.; Wang, H. Ship Type Selection and Cost Optimization of Marine Container Ships Based on Genetic Algorithm. Appl. Sci. 2024, 14, 9816. https://doi.org/10.3390/app14219816
Xiao P, Wang H. Ship Type Selection and Cost Optimization of Marine Container Ships Based on Genetic Algorithm. Applied Sciences. 2024; 14(21):9816. https://doi.org/10.3390/app14219816
Chicago/Turabian StyleXiao, Ping, and Haiyan Wang. 2024. "Ship Type Selection and Cost Optimization of Marine Container Ships Based on Genetic Algorithm" Applied Sciences 14, no. 21: 9816. https://doi.org/10.3390/app14219816
APA StyleXiao, P., & Wang, H. (2024). Ship Type Selection and Cost Optimization of Marine Container Ships Based on Genetic Algorithm. Applied Sciences, 14(21), 9816. https://doi.org/10.3390/app14219816






