Abstract
Robust localization and mapping are crucial for autonomous systems, but traditional handcrafted feature-based visual SLAM often struggles in challenging, textureless environments. Additionally, monocular SLAM lacks scale-aware depth perception, making accurate scene scale estimation difficult. To address these issues, we propose D3L-SLAM, a novel monocular SLAM system that integrates deep keypoints, deep depth estimates, deep pose priors, and a line detector. By leveraging deep keypoints, which are more resilient to lighting variations, our system improves the robustness of visual SLAM. We further enhance perception in low-texture areas by incorporating line features in the front-end and mitigate scale degradation with learned depth estimates. Additionally, point-line feature constraints optimize pose estimation and mapping through a tightly coupled point-line bundle adjustment (BA). The learned pose estimates refine the feature matching process during tracking, leading to more accurate localization and mapping. Experimental results on public and self-collected datasets show that D3L-SLAM significantly outperforms both traditional and learning-based visual SLAM methods in localization accuracy.
1. Introduction
Simultaneous localization and mapping (SLAM) is a foundational technology that plays a crucial role in the autonomous navigation of robots, underwater platforms [1], and self-driving vehicles [2]. It enables unmanned systems to accurately determine their position within an unknown environment while simultaneously constructing a detailed map of the surroundings in real-time. By integrating data from various sensors such as LiDAR, cameras, and inertial measurement units (IMUs), SLAM provides a comprehensive understanding of the environment, which is essential for safe and efficient operation. In robotics, visual SLAM is widely utilized due to its cost-effectiveness and versatility, aiding in tasks like industrial automation, exploration, and service delivery. Drones rely on SLAM for obstacle avoidance and mapping in GPS-denied environments, while autonomous vehicles depend on it to navigate and make decisions in complex traffic scenarios. Overall, visual SLAM is indispensable for the development of intelligent systems capable of operating autonomously in the physical world.
Visual SLAM can be broadly categorized into two approaches based on the type of visual features: handcrafted feature-based and direct methods. The feature-based approach is widely adopted due to its efficiency and precision. In this method, the SLAM front-end tracks keypoints in adjacent frames and optimizes positioning and mapping using multi-view geometry optimization techniques. However, handcrafted local features rely on low-level image information, such as pixel gradients, for keypoint detection and descriptor generation. These features are sensitive to changes in lighting conditions, leading to unstable tracking and potential SLAM failures. Furthermore, monocular SLAM lacks the ability to perceive the depth of keypoints, resulting in ambiguous scale estimation for mapping.
To address the limitations of handcrafted feature-based methods, some studies have incorporated deep learning techniques into visual SLAM [3,4,5,6,7,8,9,10,11,12,13,14,15]. These approaches, known as learning-based visual SLAM, can be divided into end-to-end learning methods and learning-feature-based SLAM methods. End-to-end learning approaches directly convert images into pose or depth estimates, achieving globally consistent scale estimation by training on large-scale datasets. However, these methods lack additional optimization modules and cannot correct accumulated localization errors. In contrast, learning-feature-based SLAM combines deep neural networks for visual feature extraction with traditional multi-view geometry models in the back-end, offering a hybrid approach of “geometric model + learning.” These methods leverage self-supervised local features for scene perception, exhibiting robustness in complex environments with significant lighting variations. However, they may struggle in texture-sparse scenes, where the front-end lacks global feature perception, and monocular keypoints do not provide depth information, leading to scale degradation. Additionally, feature matching in these methods often relies on a constant velocity model, which may not align with real-world motion, further limiting their robustness and performance.
In light of these challenges, we propose a novel hybrid visual SLAM system that combines end-to-end visual methods with learning-feature-based approaches. Our system, D3L-SLAM, integrates Deep keypoints, Deep depth estimation, Deep pose priors, and a Line detector to enhance the SLAM front-end’s performance in complex lighting conditions. By incorporating learned local features, trained in a self-supervised manner, into the tracking module, D3L-SLAM improves feature tracking in challenging environments. To ensure stable performance in texture-sparse scenarios, we introduce line features into the front-end. Additionally, we integrate self-supervised pose estimation as a motion model for adjacent frames, refining the matching of point–line features. To address the inherent scale inconsistency in monocular SLAM, we employ globally consistent depth estimation to transform monocular SLAM into a virtual stereo SLAM system, ensuring that pose estimation and mapping are scale-consistent. In the back end, we construct a bundle adjustment for learned point and line features to optimize pose estimation, and we develop an online binary bag-of-words (BoW) model to correct accumulated errors.
We validate our proposed D3L-SLAM on both the public benchmark, i.e., the KITTI dataset, and our self-collected dataset, comparing its performance against model-based benchmarks like ORB-SLAM3, LDSO, and VISO-M, as well as the learning-based benchmark LIFT-SLAM. The experimental results demonstrate that D3L-SLAM achieves a 39.42% improvement in translation accuracy compared to the traditional handcrafted feature-based ORB-SLAM3 and a 75.95% improvement compared to the learning-based LIFT-SLAM. On our self-collected dataset, D3L-SLAM outperforms ORB-SLAM3 by 43.36% in terms of localization accuracy.
In summary, our contributions are as follows:
- We propose D3L-SLAM, a hybrid monocular visual SLAM system that integrates deep keypoints, deep pose priors, deep depth estimation, and a line detector, enabling robust operation in complex, low-texture environments.
- To enhance SLAM performance in low-texture scenarios, we incorporate point–line feature constraints to optimize pose estimation and mapping through the construction of a tightly coupled point–line bundle adjustment (BA).
- To ensure scale-consistent pose and map estimates in monocular visual SLAM, we employ self-supervised depth estimation with RGB images to form a pseudo-RGBD sensor and integrate a virtual baseline to create a pseudo-stereo SLAM system.
- We conducted extensive experiments on both public and self-collected datasets, demonstrating that D3L-SLAM significantly outperforms representative traditional SLAM (e.g., ORB-SLAM3) and learning-based SLAM (e.g., LIFT-SLAM).
2. Related Works
2.1. Deep-Learning-Based Visual SLAM
The integration of deep learning neural networks into visual SLAM has emerged as a promising research direction for end-to-end pose estimation and depth perception. Learning-based SLAM methods can be categorized into supervised and self-supervised approaches based on their supervision types. For instance, DeepVO [5] represents a typical supervised odometry approach that uses convolutional neural networks (CNNs) for visual feature extraction and fully connected layers for pose regression. It follows the local mapping approach of traditional SLAM, optimizing visual features of image sequences using LSTM. DROID-SLAM [16] merges pose and depth estimation tasks, constructing a complete learned SLAM system by integrating a hidden state optimization model based on GRU [17] with traditional bundle adjustment models. NeuralBundler [18] employs both stereo DepthNet and PoseNet, along with monocular and stereo photometric loss functions, to build a scalable framework. It also utilizes a bag-of-words (BoW) model for loop closure detection and constructs a pose graph optimization model to correct positioning errors. DeepSLAM [9] features three modules—mapping net, tracking net, and pretrained loop net—dedicated to depth estimation, pose estimation, and loop closure, respectively.
In other approaches, [19,20] leverage the optical flow estimation network PWC-Net [21] to track keypoints between adjacent frames and construct an epipolar geometry model for relative pose estimation. [19] integrates DepthNet’s depth estimates to form a photometric loss, using triangulation to maintain depth scale consistency by constructing 3D spatial points corresponding to matching keypoints. The framework adopts a self-supervised training approach, initially constructing photometric loss with PWC-Net and then jointly optimizing DepthNet and PWC-Net parameters.
2.2. Hybrid Visual SLAM
Combining model-based and learning-based SLAM approaches to form a hybrid system leverages the strengths of both methods. GCN-SLAM [11] utilizes a deep learning feature extraction algorithm [22] to generate binary descriptors similar to ORB descriptors, which are directly applicable to SLAM. By deploying GCN on the front-end of the ORB-SLAM2 system and using a single-layer image pyramid for feature extraction, the algorithm improves efficiency. GCN-SLAM also trains a BoW model offline for loop node detection and closure, showing improved performance over ORB-SLAM2 in indoor scenes. DXSLAM [10] incorporates learning-based floating local features from [23] and constructs a loop node recognition module using the fast bag-of-words model FBow [24], which is faster than DBow2 and DBow3. DXSLAM further integrates NetVLAD [25] for global feature extraction and relocalization. It uses NetVLAD to identify candidate loop keyframes similar to the current frame’s global feature, then performs local feature extraction and loop node detection using a BoW model built with FBow. LIFT-SLAM [12] uses a learned LEFT extractor for feature extraction and constructs a loop closure module with an offline-trained BoW model. Despite this, experimental results indicate only modest improvements compared to traditional VSLAM methods. SC-Depth [14] proposes a pseudo RGBD VSLAM system, enhancing monocular SLAM by incorporating depth and pose estimation for improved perception and feature tracking. Ref. [26] combines self-supervised depth labels as a pseudo depth sensor and constructs a pseudo stereo SLAM with a virtual baseline to improve localization performance. AirVO [3] uses SuperPoint [27] for feature extraction and stereo images as input, enhancing perception in low-texture environments by also extracting line features. The framework employs Nvidia TensorRT for real-time inference, showing superior performance in low-light conditions compared to model-based visual VO or SLAM. However, AirVO lacks a loop closure module, which limits its ability to correct accumulated errors. SP-Loop [15] converts SuperPoint descriptors into 32-bit integer descriptors through binarization and trains an offline BoW model for loop closure. SL-SLAM [13] combines stereo and IMU data to form a robust feature extraction front-end for scenes with poor lighting. It uses SuperPoint with LightGlue [28] for feature extraction and matching, trains a BoW model based on SuperPoint features using DBow3, and performs loop correction with this BoW model. SL-SLAM demonstrates superior performance across various datasets compared to model-based ORB-SLAM3. Ref. [29] introduces depth estimates generated by the LiDAR depth completion network to form an RGB-L visual SLAM system, benefiting from the precise global absolute scale of LiDAR for accurate pose and depth estimation. D3VO [4] integrates learned pose and depth priors into the direct method DSO [30], enhancing the front end’s feature matching rate and serving as an initial value for depth filtering. However, D3VO lacks a loop closure module and is unable to perform error correction. These two works [31,32] also introduce line features in SLAM. Among them, PLDS-SLAM [31] uses semantic segmentation to identify dynamic objects in the scene, and when estimating pose and mapping, it removes the negative impact of dynamic objects.
A comparison of these methods with the proposed D3L-SLAM is summarized in Table 1. The table highlights how D3L-SLAM integrates deep learning techniques more comprehensively.

Table 1.
A comparison of key visual SLAM modules of our proposed D3L-SLAM with other representative works.
3. Hybrid Visual SLAM with Deep Keypoints, Depths, Poses, and Line Features
3.1. Framework
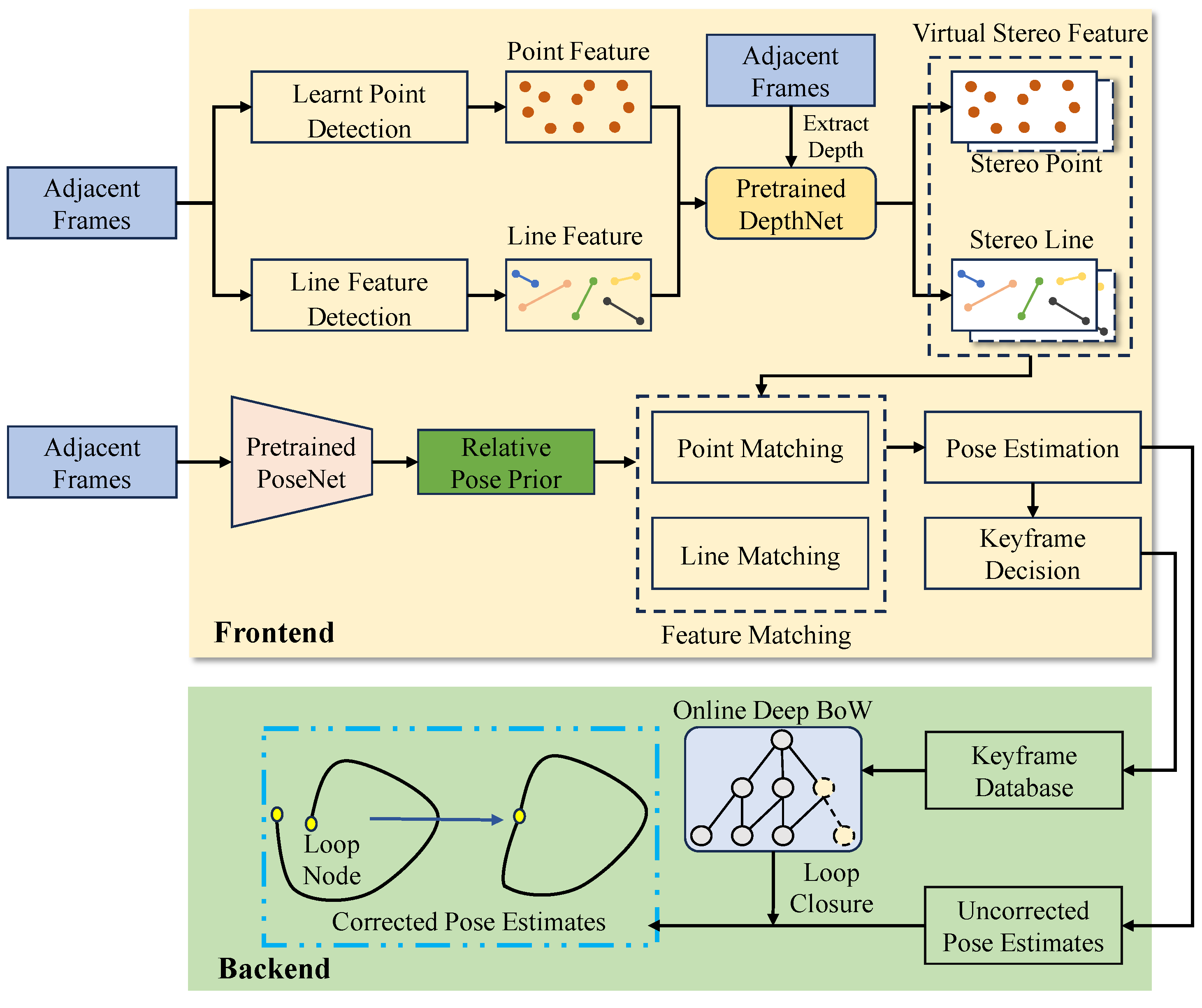
Figure 1 illustrates our proposed D3L-SLAM, a novel hybrid SLAM framework that integrates learning-based keypoints, poses, depths, and line detectors. In the front end, we utilize a learning-based local feature extractor to identify keypoints from images. To enhance feature detection in low-texture regions, we incorporate a handcrafted line extractor. Additionally, to ensure that the detected features are scaled, we introduce depth estimates from a self-supervised depth estimation network. Although these depth estimates lack absolute scale, they maintain global consistency. We further transform monocular SLAM into virtual stereo SLAM by designing a virtual baseline. Leveraging these learned depths, D3L-SLAM can recognize relative object distances in the scene, mitigating scale drift caused by insufficient tracking features. In traditional model-based SLAM, the initial selection range for adjacent frame feature matching is determined by a uniform motion model. However, this model is often too idealized and does not reflect real-world scenarios, thereby limiting feature matching accuracy. To address this limitation, we introduce relative pose estimates derived from a self-supervised pose estimation network as a prior. These estimates, obtained through extensive data training with self-supervised methods based on photometric loss, are more accurate and robust compared to uniform motion models. Finally, in the back end, we design an online learning bag-of-words (BoW) module that uses binary descriptors for online training. This module converts float descriptors from selected keyframes into binary descriptors. The online learning-based BoW addresses the issue of low generalization in learning-based descriptors. The detected loop closures are then utilized to correct accumulated errors in pose estimation.
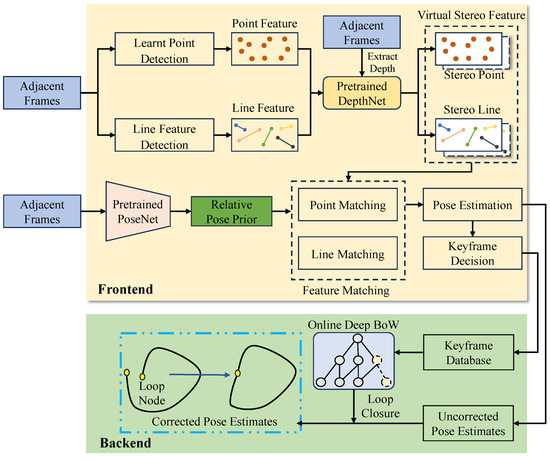
Figure 1.
An overview of our proposed D3L-SLAM system that integrates deep keypoints, deep pose priors, deep depth estimates, and a line detector. Deep keypoints indicate the self-supervised keypoint extraction method. Deep pose and depth mean the self-supervised pose and depth estimates.
3.2. Integrating Line Features and Deep Keypoints in the Front End
3.2.1. Line Feature Detection
To enhance the stability and robustness of feature extraction, we detect line features alongside point features. Point features typically capture keypoints with significant gradient changes, while line features represent regions composed of sets of points with such changes. As a result, line features depict object edges in the image, providing stable and recognizable information from various perspectives. Introducing line features into the SLAM front-end tracking module significantly improves feature tracking stability, especially in scenes with drastic lighting variations.
In our feature tracking module, we employ the line segment detector (LSD) [33], a method for extracting line segment features from images. We then compute binary descriptors for the line features using the line band descriptor (LBD) [34] and track the line segments accordingly. As shown in Equation (1), our LSD feature extraction method first utilizes a two-dimensional kernel function to calculate the image gradient, which includes the horizontal and vertical components of the image coordinates . Here, represents the pixel value at the coordinate point in the image.
We compute the gradient magnitude, , at point in the image, as well as the angle relative to the horizontal axis.
and then, LSD uses non-maximum suppression to enhance real edges and reduce noise. Next, it connects adjacent edge points to form line segments, possibly involving clustering and sorting. Finally, it refines these segments by removing points that do not fit a line segment and merging close segments to create more accurate and complete line representations.
Before conducting line feature tracking and matching, a brute force matching method is employed to identify corresponding line features based on the Hamming distance. Next, the 3D line features’ start and end points in world coordinates are projected onto the current frame using the initial pose estimation.
3.2.2. Self-Supervised Learning of Deep Keypoints
Traditional handcrafted keypoint methods, such as ORB [35] and SURF [36], detect corners with significant brightness changes in the image using image gradient operators and then use the local low-level features around the corner as descriptors. However, low-level image features are quite sensitive to lighting changes in environment. If the same scene is captured at different times, the same keypoint may have different descriptors due to varying lighting conditions. This low robustness introduces considerable uncertainty in SLAM feature matching, especially in scenarios with loop closures. In contrast, learning-based keypoint extraction methods transform images into descriptor and keypoint tensors end-to-end. These tensors are derived from the high-level features of the neural network. These high-level features are essentially global features of the image. Compared to the local features obtained by traditional methods, global features are more robust. Learning-based keypoint extraction methods employ supervised training, and the supervised signals come from the self-labeled method [27].
The backbone of our local feature extractor is a convolutional neural network (CNN). Similar to other learned local feature methods, it is divided into an encoder and a decoder. The encoder leverages the convolutional layers of VGG16, while the decoder consists of two parts: a keypoint position decoder and a descriptor decoder. The keypoint position decoder converts high-dimensional visual features from the encoder into a heatmap of the same size as the input image, where each pixel value represents the probability of a keypoint’s presence. A threshold is preset, and pixels in the heatmap that exceed this threshold are considered candidate keypoints. The descriptor decoder, on the other hand, transforms the high-dimensional visual features from the encoder into 256-dimensional descriptors. These descriptors are extracted at the candidate keypoint positions to serve as the output descriptors.
Our local feature extractor employs a self-supervised approach, using self-labeled training data to supervise the extraction process. Initially, we pretrain corner extractors on a synthetic geometric dataset. Then, we use the pretrained corner extractor to detect keypoints on the COCO dataset [37], treating these detected keypoints as annotations for the corresponding RGB images. We combine the RGB images with the self-annotated keypoints to form the training set for our learned local feature method.
The training loss is composed of two components: keypoint localization loss and descriptor loss. The keypoint localization loss measures the discrepancy between the predicted keypoint locations and the self-annotated positions. As shown in Equation (3), we train the keypoint localization loss using both the original image and its homography-warped version. We employ CrossEntropy loss as the metric for keypoint localization. This loss consists of the raw keypoint localization loss and the homography-warped keypoint localization loss . Here, and denote the height and width of the heatmap, with and , while i represents the keypoint position index, and H and W denote the height and width of the input image. The variables and represent the keypoint positions and keypoint label positions, respectively.
Unlike SuperPoint, we implement a sparse descriptor loss. This sparse descriptor loss is computed between the original image and its homography-warped version. It consists of two main components: the loss for descriptors matched through homography and the loss for those that are unmatched . The matched descriptor loss, , is defined in Equation (4), involving N pairs of aligned keypoint locations with indices i ranging from 0 to N. The unmatched descriptor loss, , is outlined in Equation (5) and considers Z pairs of descriptors near the matched ones, with indices j ranging from 0 to Z, representing unmatched keypoint pairs .
The overall descriptor loss, , described in Equation (6), incorporates a margin boundary b and is designed to minimize the feature discrepancy among corresponding descriptors while maximizing it among non-corresponding ones. The total training loss, , integrates the detector and descriptor losses, with a balancing factor that controls the influence of each component.
3.3. Virtual Stereo Visual SLAM
Integrating self-supervised depth estimation as a pseudo depth sensor provides keypoints with depth perception, addressing the issue of scale degradation. We first introduce methods for self-supervised depth and pose estimation, then discuss the integration of the learned depth into SLAM, and finally, explain how to incorporate the learned pose into the SLAM framework.
3.3.1. Self-Supervised Learning of Pose and Depth
The self-supervised visual method uses a dual-network framework consisting of PoseNet for pose estimation and DepthNet for depth estimation. The depth estimates are obtained end-to-end by DepthNet. DepthNet is composed of an encoder and a decoder. Both are convolutional neural networks. The encoder transforms the image into high-level features, while the decoder converts these high-level features into depth estimates. The depth estimate is dense, with each pixel corresponding to the depth value of an object in the scene. The pose estimates are derived end-to-end from PoseNet. The input to PoseNet is a tensor that combines adjacent frame images along the RGB channel. A photometric model is employed to construct a self-supervised loss function, which integrates adjacent images, depth estimates, and pose estimates. Through multiple training epochs, PoseNet and DepthNet learn to accurately estimate both pose and depth. As shown in Equation (8), the relative pose estimate between adjacent frames preserves the luminance consistency of the target image with respect to the source image . By combining the depth estimate of the target frame with the camera’s intrinsic matrix , the source image is projected onto the target frame’s perspective. This projection process generates a synthesized image from the viewpoint of the target frame, maintaining photometric consistency with the source image. Here, and represent the pixel points of the source and target frames, respectively.
The synthesized image and the target image not only maintain photometric consistency but also exhibit structural similarity. As shown in Equation (9), we incorporate this quantified similarity as a structural loss into the photometric loss to preserve the structural details of the synthesized image. Here, represents the structural similarity loss [38], with and set to 0.15 and 0.85, respectively.
In addition, to maintain depth scale consistency throughout the sequence, we introduce the 3D geometry consistency loss . The equation for this loss is shown in 10. refers to the reconstructed depth in the source frame, which should be consistent with the transformed depth obtained through , and the operation represents the transformation of the target frame’s depth estimate into the source frame’s perspective using the relative pose estimate .
As shown in Equation (11), we combine the photometric loss and the 3D geometric consistency loss to form the self supervised training loss , where is 0.5.
3.3.2. Virtual Features Derived from Learned Depth
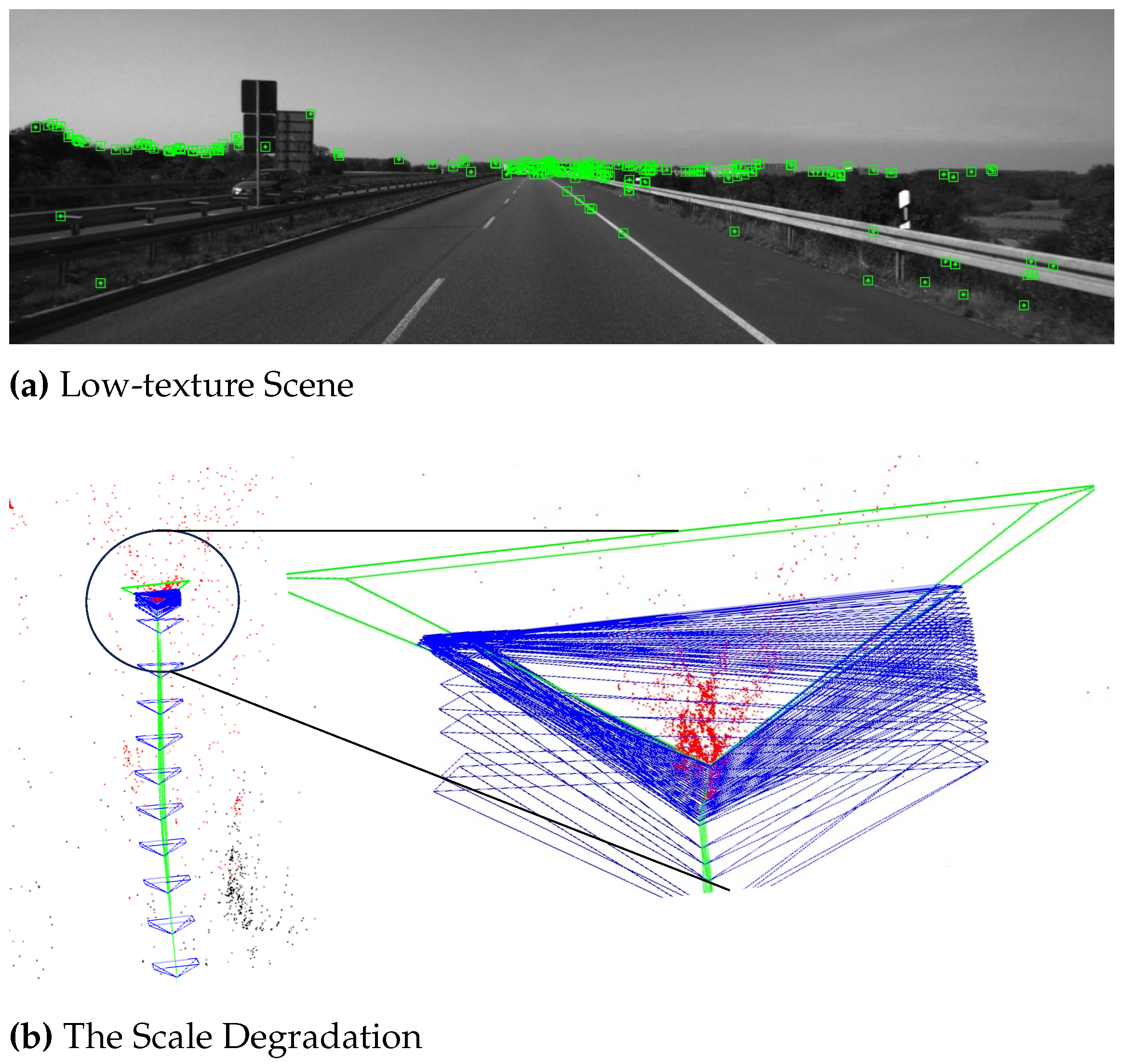
In low-texture areas, ensuring an even distribution of detected keypoints across the entire image is challenging. Consequently, monocular SLAM struggles to achieve consistent scale in pose estimates through local feature matching alone. As shown in Figure 2a, this is a typical area with sparse texture. There is a lack of outdoor scenes such as vegetation and buildings. In close proximity to the camera, there are fewer feature points on the road. Therefore, it is difficult for the SLAM front-end to track sufficient feature points in close proximity areas. However, there are objects with obvious pixel gradients on the horizon. This enables the front end to stably track these distant features. It is worth noting that monocular SLAM exhibits scale ambiguity. It cannot distinguish between nearby and distant objects from a single image. Specifically, the positions of keypoints near the horizon remain largely unchanged as the camera moves. This leads SLAM to mistakenly assume that the camera has not moved significantly, resulting in degradation of scale estimation. As shown in Figure 2b, monocular SLAM exhibits scale degradation in the low-texture area. SLAM cannot correctly predict the depth of spatial points. Incorrect depth estimation of spatial points can also lead to incorrect keyframe pose estimation. At the same time, it is impossible to correct scale errors in the scene without loop nodes.
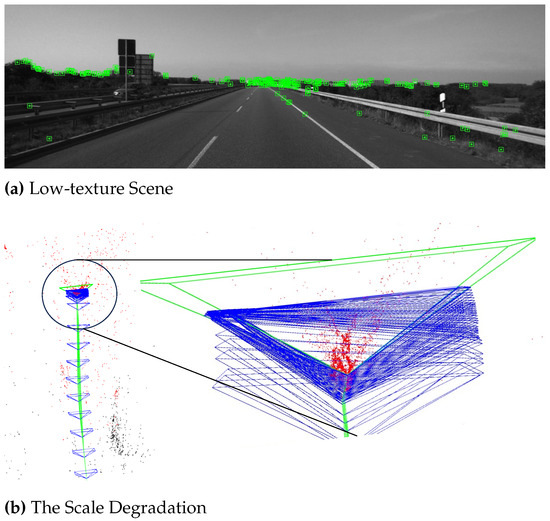
Figure 2.
The Scale Degradation of Monocular VSLAM In Low-texture Scene.
To enable monocular SLAM to achieve scale awareness of the scene, we integrate a self-supervised visual ego motion estimator into the proposed monocular SLAM framework. Depth estimates from DepthNet in the estimator serve as a pseudo-depth sensor. These depth estimates provide a relative depth value for each detected keypoint . While this depth value lacks an absolute scale, it accurately represents the relative distance of each object in the image. The use of relative depth values enhances the performance of positioning and mapping.
As shown in Equation (12), we incorporate self-supervised depth labels into monocular SLAM to create a pseudo RGBD SLAM system. For each keypoint , we use the virtual baseline and depth value to compute a virtual matching point in the right view, where represents the focal length.
The stereo keypoints and line features obtained through the pseudo depth sensor are referred to as virtual local features. The post-processing of these virtual local features follows the same procedures as in stereo SLAM. In the back-end optimization, we construct a re-projection error function based on both point and line features.
We combine the observed local features with the projected virtual features to formulate the optimization function.
3.3.3. The Motion Model from PoseNet
In traditional handcrafted feature-based SLAM (i.e., ORB-SLAM3), the tracking module first uses a constant velocity motion model to estimate the relative pose between adjacent frames and then combines the pose of the last frame to calculate an initial pose for the current frame. Subsequently, the initial pose of the current frame is used to project the 3D points in the mapping onto the image coordinates of the current frame. The 3D points in the mapping correspond to the keypoints of the last frame. Then we match the keypoints within a certain radius centered on the projected points in the current frame. Keypoints with similarity exceeding a certain threshold are considered to be matching keypoints with the keypoints of the last frame. Finally, as Equation (14) shows, we construct the pose-only optimization error from the matching keypoints of adjacent frames. Then we use this optimization equation to find the optimal pose estimate of the current frame. However, the constant velocity motion model is too ideal and does not conform to real motion, which leads to a large difference between the initial pose and the ground truth, thereby affecting the pose optimization result. In view of this, we replace the constant velocity motion model with the pose estimate of the self-supervised PoseNet. The photometric loss and 3D geometry consistency loss theoretically originate from the multi-view geometry model. In summary, compared with the constant velocity motion model, the estimation of PoseNet is more consistent with the real motion model. In our implementation, we combine the rotation estimates from PoseNet with the translation from the constant velocity motion model to form the motion model.
3.4. Line–Point Bundle Adjustment and Online BoW in the Back End
3.4.1. Line–Point Pose-Only Bundle Adjustment Optimization
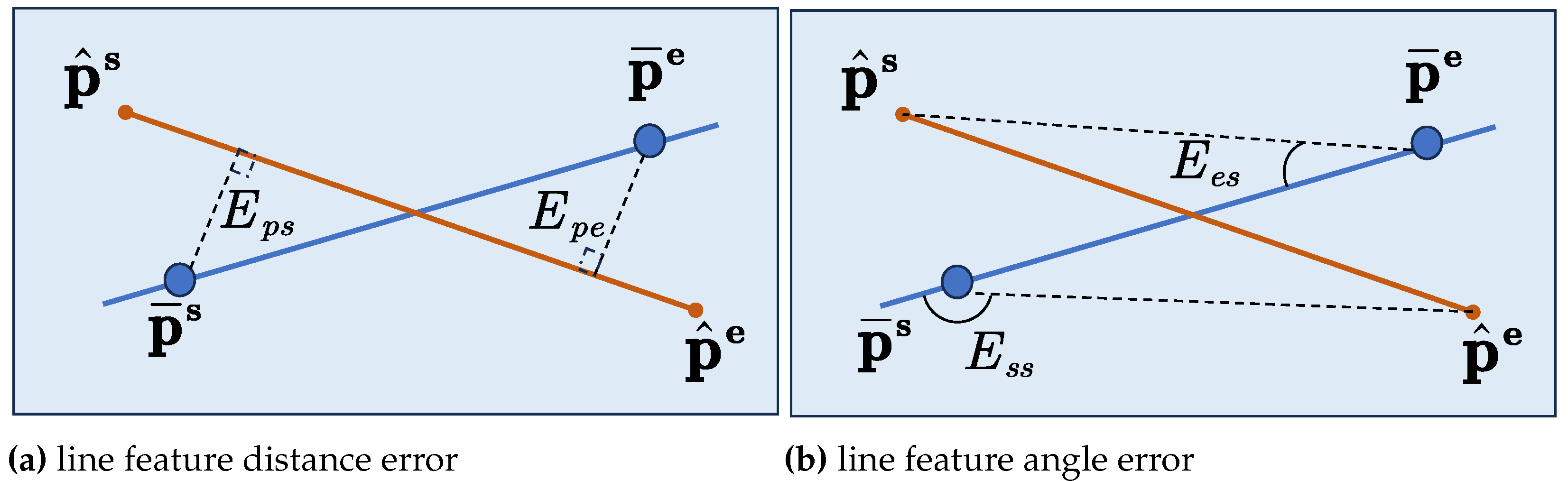
Similar to point features, line features use the difference between projected and observed features to compute the optimization error. SLAM localization is optimized by adjusting the pose estimate to minimize this difference. As illustrated in Figure 3, the blue line represents the observed line segment, while the red line denotes the projected line segment.
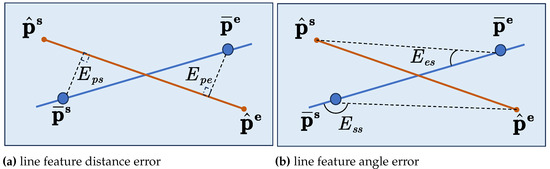
Figure 3.
Diagram Of Projection Line Feature Error.
As shown in Equation (15), we construct a line feature error function to refine the relative pose estimates between adjacent frames. Two types of line feature error functions are designed: the line feature distance error and the line feature angle error .
As shown in Formula 16, we first compute the line coefficient , which represents the infinite line passing through the starting point and the ending point . In this coefficient, and denote the homogeneous coordinates of the endpoints of the observed line.
Next, we calculate the vertical distance between the observed starting point and the projected line, as well as the vertical distance between the observed ending point and the projected line. The sum of these two vertical distances constitutes the projection line distance error .
Additionally, as shown in Equations (18) and (19), the endpoints of the projected lines in the image adhere to the pinhole camera model. We project the 3D points in world coordinates into the image coordinates using the camera pose and intrinsic matrix. Here, represents the starting point of the 3D line in world coordinates, while and denote the rotation and translation matrices that transform coordinates from the world frame w to the camera frame . The index i indicates the i-th camera frame. are the components of the 3D line’s starting point in the i-th camera coordinate system. We then use the intrinsic matrix to project onto the image coordinates . This projection process is similarly applied to the ending point of the 3D line.
As illustrated in Figure 3, the line feature angle error measures the angular discrepancy between the endpoints of the projected line and the observed line. As shown in Equation (20), we calculate the inner product between the directed line segments and . This inner product represents the angle error. When the relative pose between the projected and observed lines is closer to the ground truth, the line feature angle errors and approach zero.
The current frame acquires matched keypoints and line features through the feature tracking module and projects the 3D points and line segment endpoints into the current frame’s image coordinates using the pinhole camera model. The error equation is formed by the coordinate differences between the observed point–line features and the projected point–line features. This error is minimized by adjusting the pose of the current frame. When the error converges, the pose of the current frame reaches an optimal solution. The error equation based on point–line features includes the projection keypoint error and the projection line endpoint error .
We use Equations (18) and (19) to transform the 3D coordinates of keypoint features to the current image frame as . The corresponding keypoint in the current frame is . The index j denotes the j-th keypoint in the current image frame . We calculate the difference between and as the projection point error, as shown in Equation (21).
As shown in Equation (22), we combine the line feature error from Equation (15) and the point error from Equation (21) to form the total optimization error. The optimal pose of the current frame, , is determined using the Newton descent method. In this context, and represent the covariances of the observed keypoints and line features, respectively. denotes the Huber kernel function, N is the total number of tracked keypoints, and M is the total number of tracked line features. The index k indicates the k-th line feature in the current image frame .
3.4.2. Binary Descriptors and Online-Learning-Based BoW
Loop closure in SLAM systems is a critical function that identifies when a robot or autonomous vehicle revisits a previously explored area, allowing the system to correct accumulated localization errors. This module also enhances map consistency and improves overall system robustness. The loop closure module optimizes localization by leveraging the information of already mapped environments. This process is essential for maintaining the integrity and accuracy of the map, especially in dynamic or large-scale environments. The main component of loop closure is the bag-of-words (BoW) models. The BoW models can abstract scene information and obtain the global features of each scene. By comparing the euclidean distance of global features, we can find out the loop nodes in the sequence.
We have developed a learned local feature extractor at the front end that produces floating-point descriptors with values ranging between . The existing visual SLAM loop closure modules, however, rely on offline BoW models designed for binary descriptors. Additionally, deep learning methods often face challenges with generalization; a BoW model trained offline may not perform well in novel environments. To address these issues, we employ an online-trained BoW model (iBoW) [39] for the loop closure module.
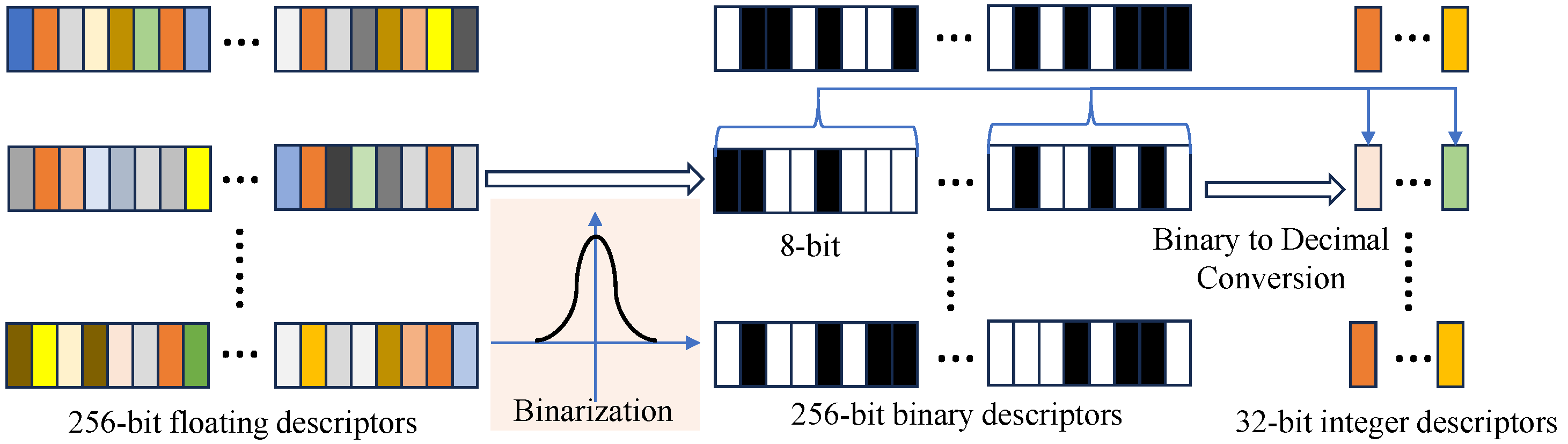
As shown in [15], floating-point descriptors are difficult to organize into a tree-structured dictionary and thus are challenging to use in loop closure. Ref. [15] also indicates that the distribution of learned descriptor values is normally distributed. Therefore, a binary hashing transformation is applied to the learned descriptors. We binarize the descriptors by mapping vector values above zero to 1 and values equal to or below zero to 0. The transformed descriptors are 256-bit binary descriptors, with values being either 0 or 1. Subsequently, following the descriptor generation process of ORB, the binary descriptors are converted into integer descriptors. The conversion method involves transforming each 8-bit binary descriptor into a decimal integer, allowing 256 binary elements to be converted into 32 integer elements. Finally, the descriptors input into iBoW is 32-bit integer descriptors. The process is illustrated in Figure 4.
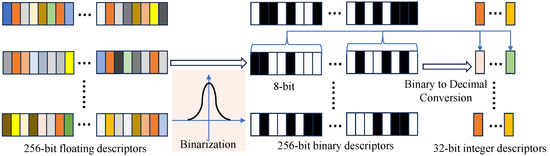
Figure 4.
The process of converting floating learned descriptors into integer descriptors.
4. Experiments
4.1. Implementation Details
In our D3L-SLAM system, the learned local feature extraction module was implemented and trained using PyTorch, with a total of 200,000 training iterations. The RGB training dataset was sampled from the COCO dataset, and the batch size was set to 8. For improved inference efficiency, the trained local features were deployed using TensorRT. Additionally, the self-supervised visual odometry system was developed and trained using PyTorch (https://pytorch.org/), with a batch size of 4. Both learning methods were trained and evaluated on an NVIDIA RTX 3090 GPU (NVIDIA, Santa Clara, CA, USA).
4.2. Evaluation on the KITTI Odometry Dataset
We first conducted experiments using the publicly available KITTI dataset, which is a standard benchmark to evaluate visual SLAM for autonomous vehicles scenarios. For the proposed hybrid visual SLAM, we trained the self-supervised odometry system on KITTI odometry 11–20 sequences. We also evaluated the localization performance of the proposed SLAM and baselines on sequences 0–10. The traditional visual baselines (VISO-M, LDSO and ORB-SLAM3) do not include the training process. Moreover, LIFT-SLAM uses the COCO dataset [37] to supervise the training of LIFT extractor. We also use the COCO dataset to supervise the training of the proposed deep keypoint. We set the maximum number of keypoints to 3000 and the number of layers in the image pyramid to 3. Due to the scarcity of local features, many monocular SLAM systems struggle with sequence 01. Consequently, we did not assess the performance of our SLAM method on this sequence to ensure fairness. We calculated the mean square error of translation and rotation estimates on different length sequences and took their mean as the mean square error of translation and rotation estimates. These two mean square errors are used as accuracy indicators for SLAM localization metric and rotation metric . The specific calculation of these two metrics is shown in Equation (23), where i and j represent the index of two frames separated by a fixed distance. represents the fixed distance, which is . and represent the rotation and translation difference. ⊖ means calculating the relative pose estimate between two frames. Additionally, represents the relative pose from the frame to the frame. and represent the estimated and ground truth pose, respectively. N indicates the sum of fixed distances.
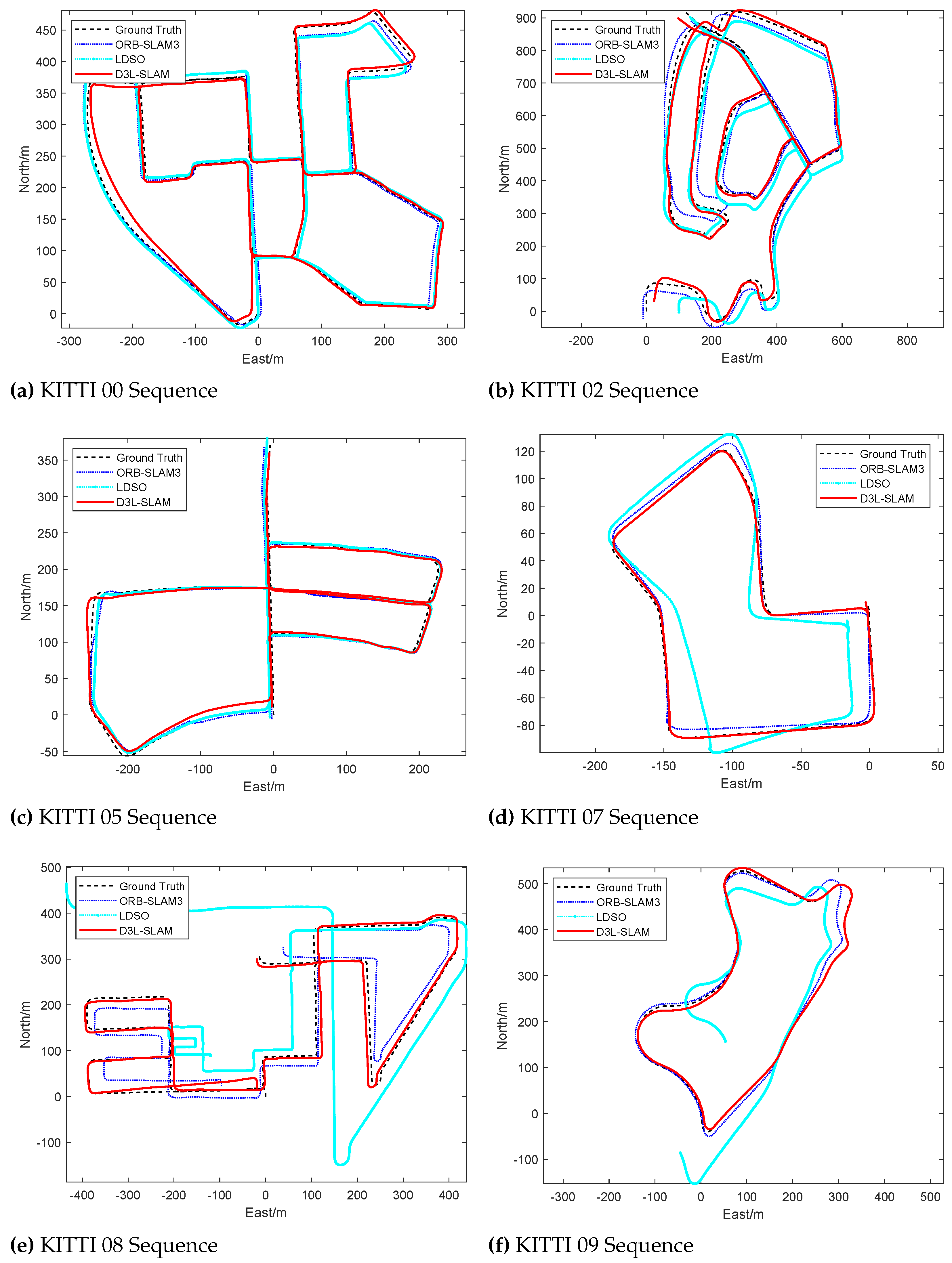
To thoroughly evaluate the performance of the proposed SLAM, we compared it against several benchmark methods, including traditional feature-based visual SLAM approaches such as VISO-M [40,41], ORB-SLAM3 [42], and the direct method LDSO [43], as well as the learning-based method LIFT-SLAM [12]. VISO-M RMSE is not shown in Table 2, because its absolute error in KITTI was not indicated in the original paper [40,41]. The results demonstrate that incorporating learned depth estimates significantly improves SLAM localization performance. As shown in Figure 5 and Table 2, sequence 08, which lacks loop nodes and is demanding in terms of feature tracking and scale degradation suppression, highlights the effectiveness of our approach. Our method achieved superior localization accuracy and closely matched the ground truth trajectory.

Table 2.
Comparison of Pose Estimation Between the Proposed D3L-SLAM and Representative Traditional and Learning-Based Visual SLAM Methods. Sequence 01 is excluded from the evaluation due to inherent challenges that affect all monocular SLAM baselines, preventing the generation of reasonable comparative results. Root mean square error(RMSE) is the absolute localization error between predicted trajectory and ground truth.
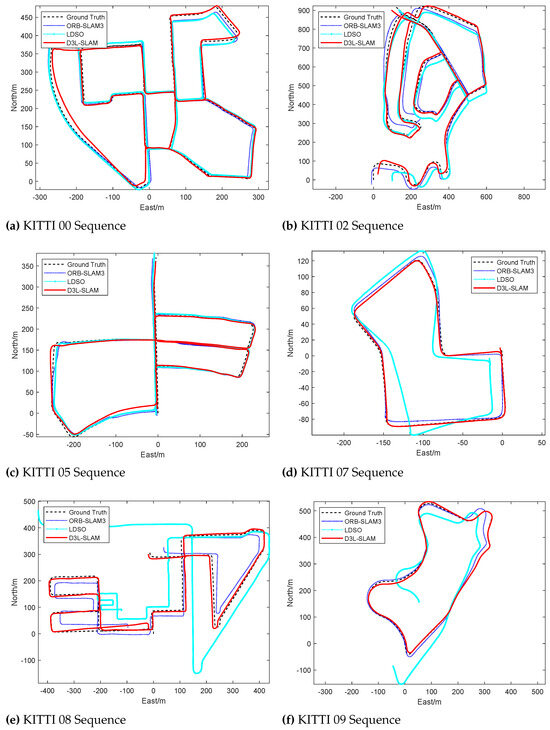
Figure 5.
Comparison of Trajectories Generated by the Proposed D3L-SLAM and Representative Visual SLAM Baselines: ORB-SLAM3 and LDSO.
Monocular SLAM systems often struggle to accurately estimate the scale in long-distance open-loop sequences. In low-texture areas, the front-end of monocular SLAM may only detect keypoints at the distant skyline, leading to the incorrect assumption that the camera is stationary, which results in scale degradation. Our proposed SLAM method mitigates this issue by incorporating DepthNet’s depth estimates. Each valid keypoint is assigned a depth estimate, and we use the pseudo-baseline and keypoint depth to compute the corresponding virtual right-view keypoint, effectively converting the monocular SLAM into a stereo SLAM. This approach enhances scale awareness and prevents scale degradation caused by low-texture areas. Additionally, our line–point front end leverages line features for matching and pose optimization, further improving localization and mapping performance.
However, it is important to note that the introduction of depth estimation has led to a decrease in pose determination accuracy. This may be attributed to the inability of depth estimation to provide accurate global absolute metrics and its limited generalization performance in unfamiliar scenes, which affects rotation estimation accuracy. Despite this, the learned pose estimates enhance feature matching rates between adjacent frames, thereby improving front-end pose estimation performance.
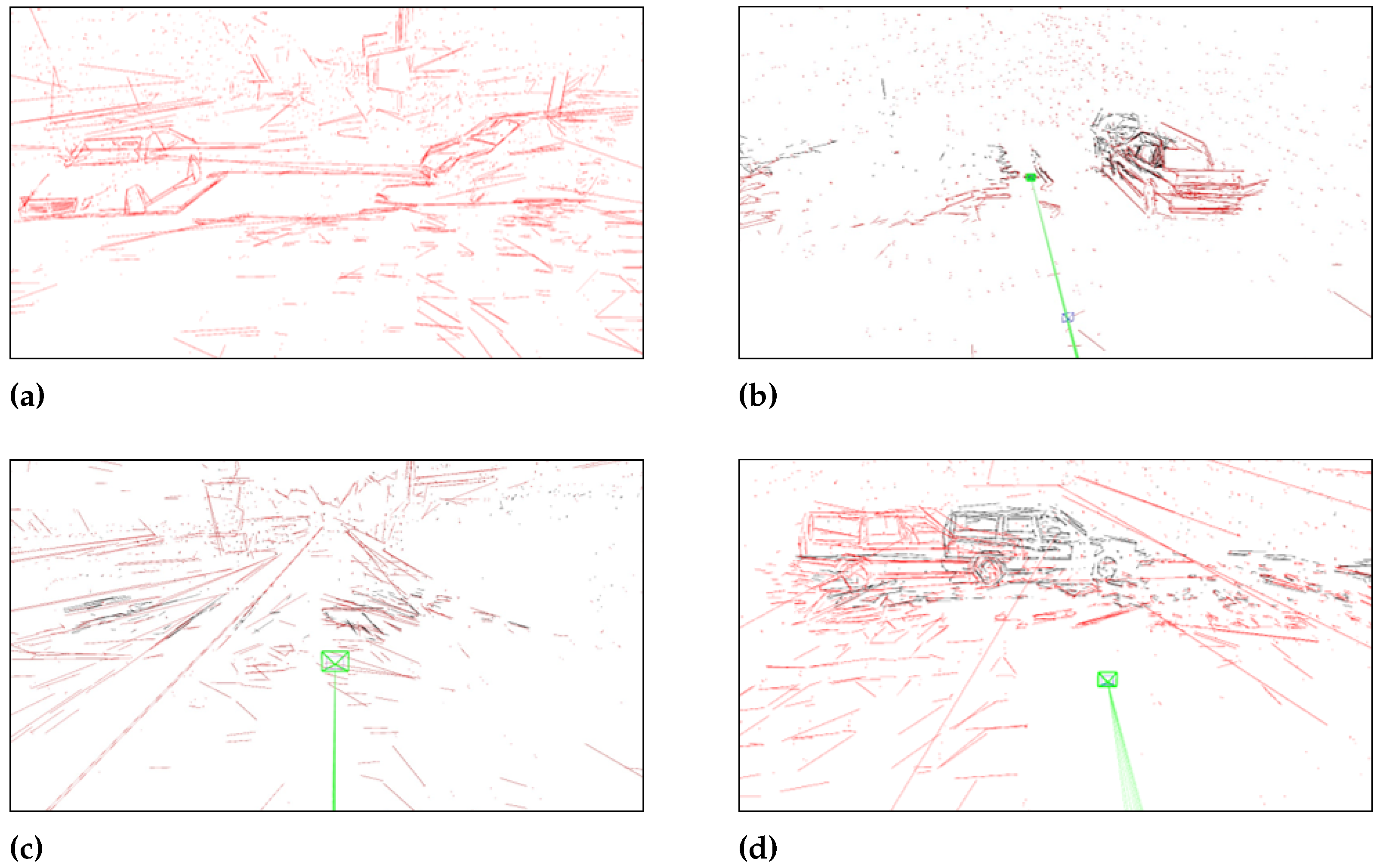
We also present the mapping results with point and line details of our proposed D3L-SLAM in Figure 6a–d. The line–point front end provides comprehensive feature perception, while the learned depth estimates enhance scale perception. This combination allows the mapping structures to maintain relatively accurate spatial relationships.
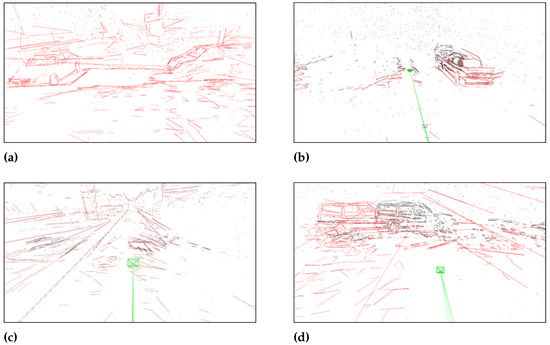
Figure 6.
Mapping Results with Point and Line Details of the Proposed D3L-SLAM.
4.3. Evaluation with Self-Collected Dataset
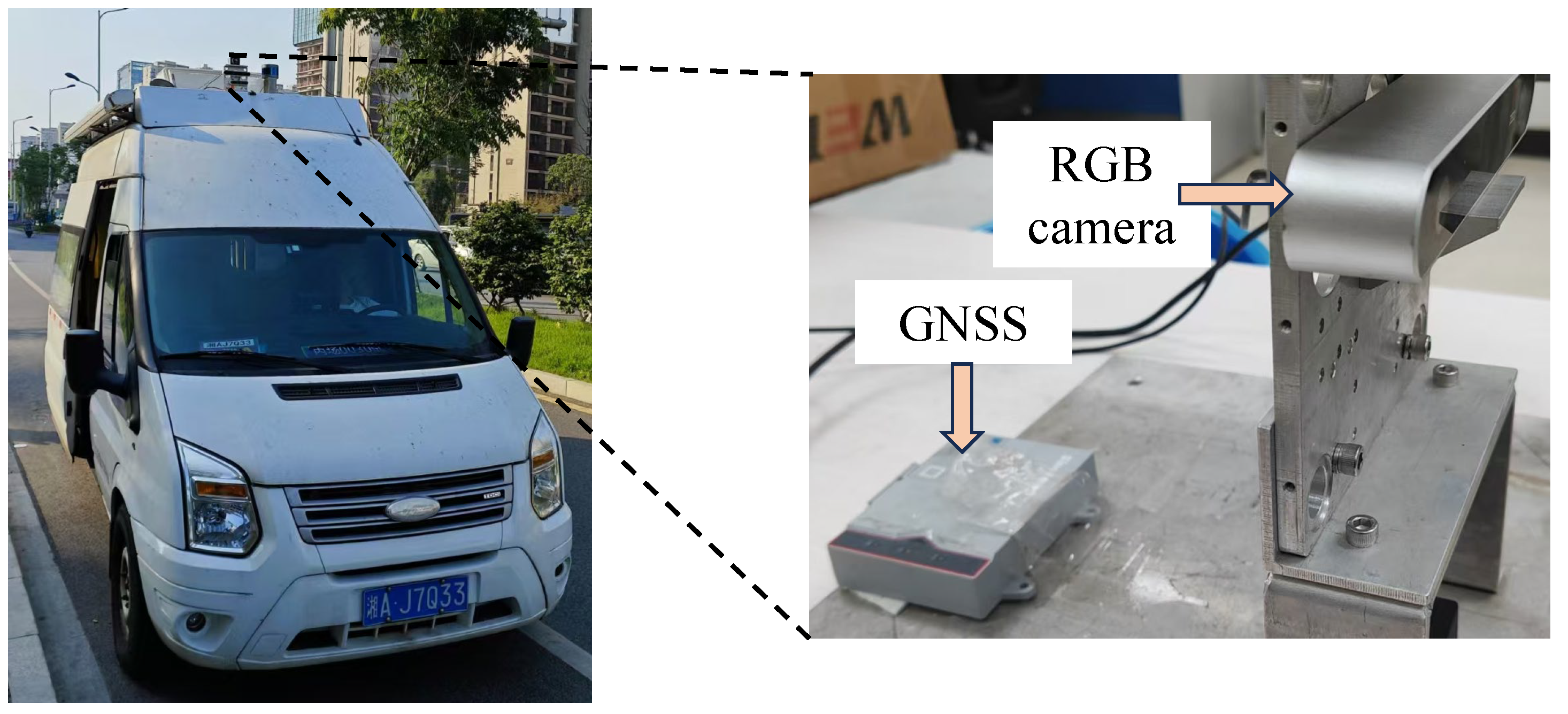
As illustrated in Figure 7, we constructed a car-driving experiment platform equipped with an RGB camera and a high-precision GNSS system to provide ground truth location data for evaluation.

Figure 7.
Our Platform Used for Collecting a Large-Scale Car-Driving Dataset for Evaluating Visual SLAM.
Our car-driving dataset was collected using RGB images from Zed cameras and positioning data from Sinognss Navigation’s GNSS system. The data collection occurred in Changsha, China, covering three distinct scenarios: campus, urban street, and residential areas. The training dataset comprises 57,948 images, encompassing various scene types, while the testing dataset includes 14,972 images, focusing on campus and urban street scenes. Example images from these scenarios are shown in Figure 8. Four sequences were selected for testing: sequences 01, 03, and 04 represent urban data, and sequence 02 represents campus data.

Figure 8.
Examples of Images from Three Different Scenes in Our Self-Collected Car-Driving Dataset.
Given the centimeter-level positioning accuracy of the GNSS system, we assessed the positioning accuracy of the proposed SLAM using root mean square error (RMSE). Since the proposed SLAM does not provide absolute scaled poses, trajectory scaling is necessary before evaluating pose estimates. The RMSE formula is given by
where denotes the three-dimensional location estimate at the frame, N is the total number of frames, and represents the ground truth location.
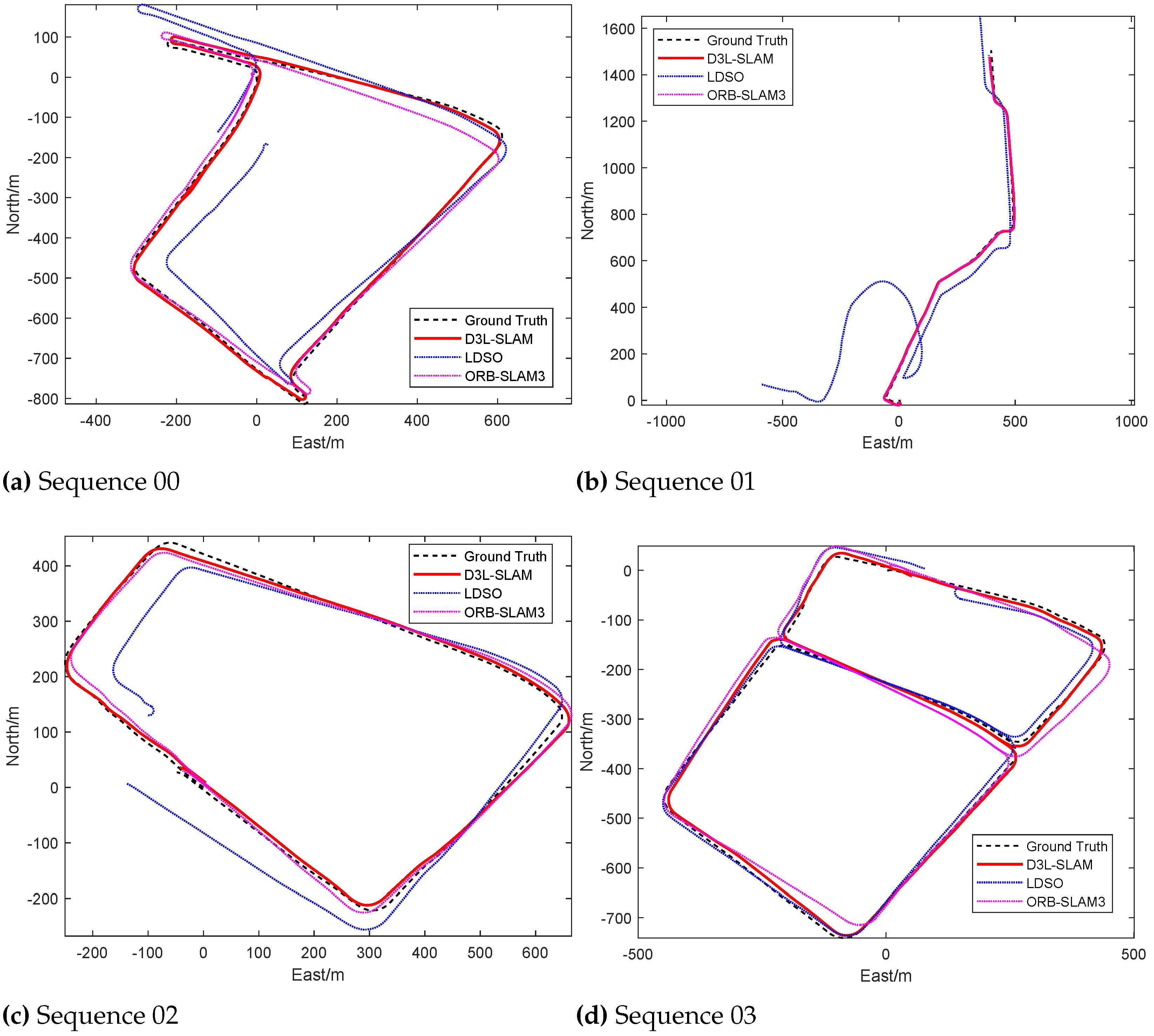
As shown in Figure 9 and Table 3, the trajectory of the proposed D3L-SLAM closely aligns with the ground truth. In terms of average positioning error, D3L-SLAM demonstrates the best performance. Traditional handcrafted visual SLAM methods often suffer from scale degradation in expansive urban scenes due to the vast distances and sparse textures in such environments. These methods may struggle to accurately reflect camera motion in low-texture areas, leading to scale ambiguity.
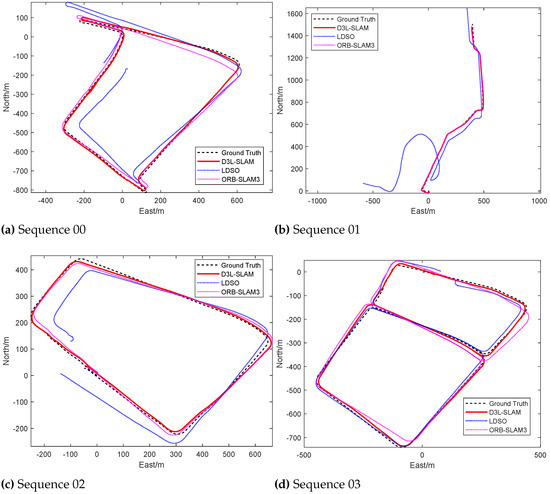
Figure 9.
Comparison of Trajectories Generated by the Proposed D3L-SLAM and Representative Visual SLAM Baselines (i.e., ORB-SLAM3 and LDSO).

Table 3.
Comparison Of Pose Estimation Results Between The Proposed D3L-SLAM and Representative Visual SLAM Baselines (i.e., ORB-SLAM3 and LDSO).
In contrast, the self-supervised monocular depth estimation framework in D3L-SLAM achieves a globally consistent scale for the scene through training, offering relatively accurate relative depth information. This enables the SLAM system to maintain a consistent scale in mapping. The integration of learned pose priors ensures that feature matching between adjacent frames adheres to the true motion model, enhancing localization accuracy. Additionally, incorporating line features improves perception in low-texture areas, mitigating localization degradation.
However, it is important to note that the positioning accuracy of sequence 02 is not as high as that of traditional ORB-SLAM3. This discrepancy may be attributed to the presence of numerous small-sized dynamic objects, such as people and bicycles, in the campus environment. The instability of line features on these small objects can negatively impact feature tracking performance.
4.4. Ablation Study
To validate the contribution of each component in D3L-SLAM, we perform an ablation study. The results are summarized in Table 4. In the table, “DK” refers to deep keypoints, which utilize learned local features as the SLAM front-end. “Depth” denotes the use of learned depth estimates as a pseudo depth sensor. “Pose” signifies the incorporation of pose priors into the front end. “Line” indicates the addition of line features at the front end and line segment errors at the back end.

Table 4.
The ablation study into the key modules in our D3L-SLAM system.
From the results labeled as Ours1, it is evident that deep keypoints substantially enhance both localization and rotation accuracy compared to the handcrafted feature-based ORB-SLAM. This improvement suggests that learned local features are more effective in handling scenes with limited texture. Comparing Ours1 and Ours2, it is clear that learned depth estimates significantly boost SLAM’s localization accuracy. These globally consistent depth estimates prevent scale degradation in mapping, even in low-texture areas, by providing relative depth information for each keypoint. However, the rotation accuracy shows a decrease, which may be attributed to inaccuracies in depth estimation for fine details such as edges, affecting rotation estimates. From Ours2 and Ours3, it can be observed that incorporating pose priors enhances the feature matching rate between adjacent frames. This improvement in matching accuracy results from the learned pose priors better aligning with the real motion model, as opposed to the uniform models used in traditional visual SLAM. Finally, comparing Ours3 and Ours4 demonstrates that integrating line features enhances SLAM performance, likely due to the robustness of line features in low-texture environments.
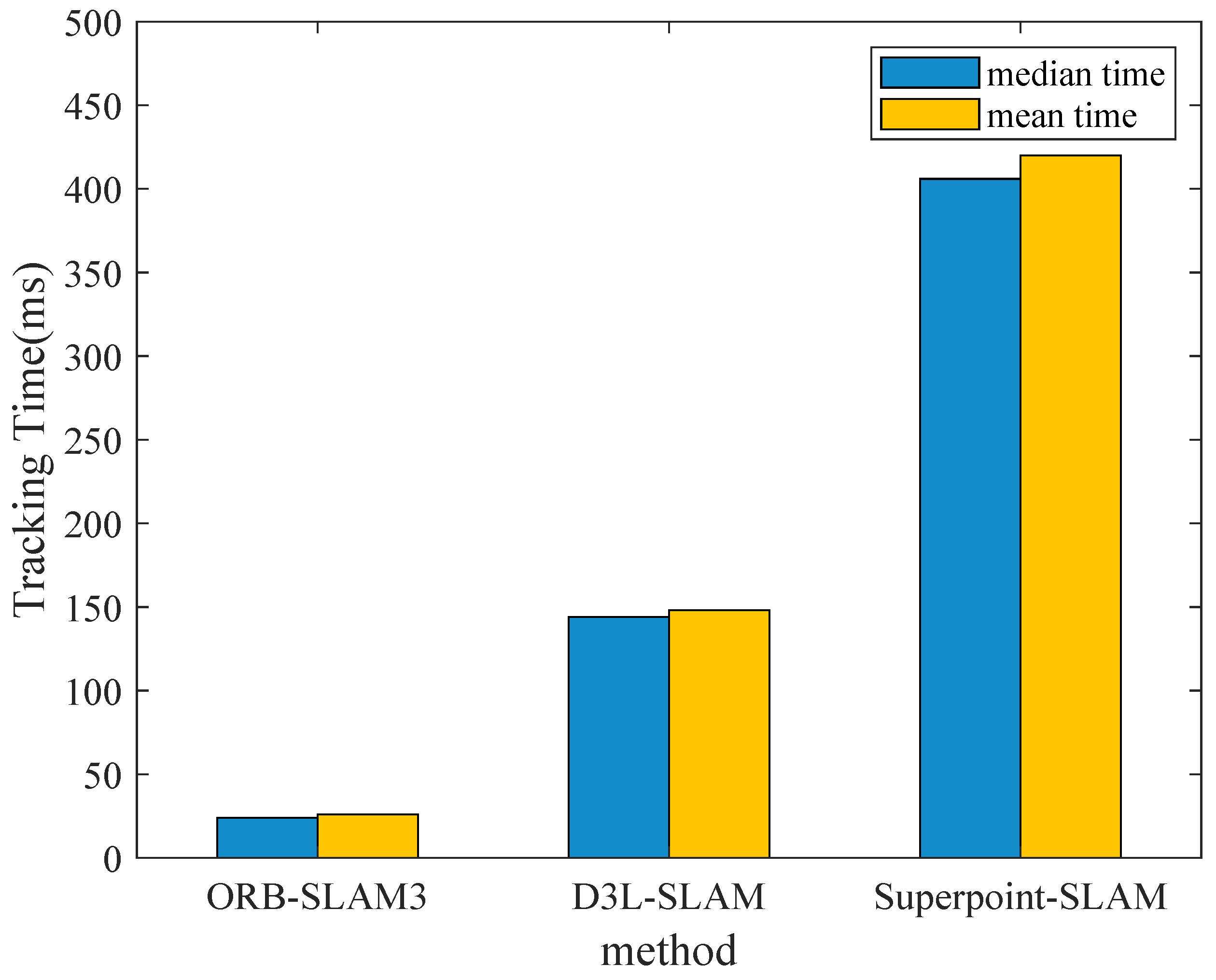
In addition to performance comparisons, we also test the efficiency of our proposed SLAM. The experiment baselines are the handcrafted traditional SLAM: ORB-SLAM3 and SuperPoint-SLAM [44], which is similar to our proposed SLAM. To ensure fairness, all these methods are set with a pyramid of 3 levels and a total number of keypoints set to 3000. SuperPoint-SLAM uses libtorch [45] to combine superpoint with ORB-SLAM2, while our framework is based on the C++ version TensorRT. The test data used are KITTI, and we measure the median and mean feature tracking time of the three methods. From the bar chart Figure 10, it can be seen that the efficiency of the traditional handcrafted method ORB-SLAM3 is the highest, which is because traditional SLAM only needs to run on CPU and RAM, and ORB is a low-level image feature. Therefore the ORB-SLAM3 is more efficient. Our proposed method uses various deep learning models running on the GPU: DepthNet, PoseNet, and Deep Keypoint, thus it is less efficient than traditional methods. However, we use the C++ version TensorRT to deploy the learning models. In contrast, SuperPoint-SLAM runs on libtorch. It converts each single image to a tensor on the GPU, and then it inferences an image through the learned model. Libtorch transfers the output keypoints and descriptors from the GPU to the CPU for subsequent processing. TensorRT, on the other hand, caches multiple images on the GPU before inference. This caching mechanism can greatly reduce the data transfer time from GPU to CPU, enhancing the efficiency of learning-based SLAM.
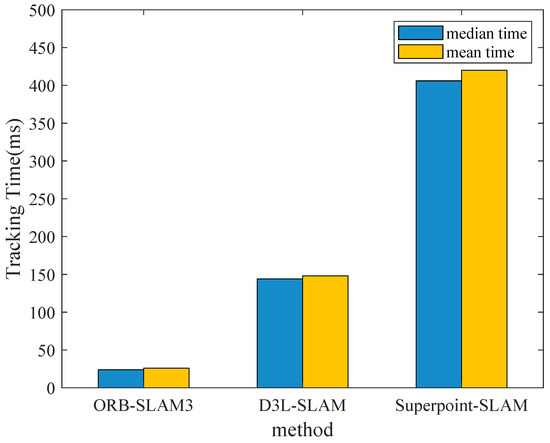
Figure 10.
Comparison of tracking time of ORB-SLAM3, D3L-SLAM, and Superpoint-SLAM.
5. Conclusions
The core technology of navigation for unmanned platforms and autonomous driving systems is SLAM, and visual SLAM is widely used due to its low cost advantage. However, monocular visual SLAM often struggles with accurate positioning and mapping in large-scale scenes with low texture due to a lack of local features. Although loop closure methods can correct mapping scale, accurate localization remains challenging in large-scale environments without sufficient loop nodes. This paper proposes a hybrid monocular SLAM system that integrates a self-supervised ego motion estimator with a multi-view geometry model. Our approach combines self-supervised depth and pose estimates. The depth estimates assign depth values to each keypoint, enabling the front end to perceive the relative distances between objects. We achieve this by designing a virtual baseline that transforms the pseudo-RGBD front end into a virtual stereo front end. Additionally, we replace the uniform motion model in the tracking thread with pose priors to better reflect the real motion model, enhancing feature matching accuracy and, consequently, localization precision. To further improve SLAM performance in low-texture environments, we developed a hybrid line–point front end and added more constraints in the optimization back end. The experiments conducted on both publicly available and self-collected datasets, compared to typical benchmarks, demonstrate that our proposed D3L-SLAM significantly improves localization accuracy. However, we observed a decrease in rotation accuracy, likely due to the fact that the learned depth estimates are not actual depth measurements, which can introduce ambiguity and increase rotation estimation errors. Despite this, the rotation accuracy of D3L-SLAM remains comparable to that of traditional SLAM systems.
The future work will focus on enhancing rotation estimation accuracy by incorporating IMU data to create a virtual “stereo+IMU” SLAM. We also plan to introduce stereo data during the training of the self-supervised ego motion estimator to optimize scale estimation, enabling the SLAM framework to obtain absolute scale poses. In addition, we also plan to apply the proposed SLAM to the unmanned aerial vehicles and autonomous vehicles, to achieve accurate positioning in complex lighting environments.
Author Contributions
Conceptualization, H.Q. and C.C.; methodology, H.Q. and C.C.; software, H.Q.; validation, H.Q., Y.X. and C.W.; formal analysis, H.Q.; investigation, L.Z.; resources, X.H.; writing—original draft preparation, H.Q. and C.C.; writing—review and editing, H.Q. and C.C.; visualization, C.W.; supervision, X.H.; project administration, X.H. and C.C.; funding acquisition, C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Natural Science Foundation of China (NFSC) under the Grant Number of 62103427, 62073331, 62103430, and Major Project of Natural Science Foundation of Hunan Province (No. 2021JC0004). Changhao Chen is funded by Young Elite Scientist Sponsorship Program by CAST (No. YESS20220181).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, X.; Fan, X.; Shi, P.; Ni, J.; Zhou, Z. An Overview of Key SLAM Technologies for Underwater Scenes. Remote Sens. 2023, 15, 2496. [Google Scholar] [CrossRef]
- Chen, W.; Zhou, C.; Shang, G.; Wang, X.; Li, Z.; Xu, C.; Hu, K. SLAM Overview: From Single Sensor to Heterogeneous Fusion. Remote Sens. 2022, 14, 6033. [Google Scholar] [CrossRef]
- Xu, K.; Hao, Y.; Yuan, S.; Wang, C.; Xie, L. AirVO: An Illumination-Robust Point-Line Visual Odometry. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; pp. 3429–3436. [Google Scholar] [CrossRef]
- Yang, N.; von Stumberg, L.; Wang, R.; Cremers, D. D3VO: Deep Depth, Deep Pose and Deep Uncertainty for Monocular Visual Odometry. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1278–1289. [Google Scholar] [CrossRef]
- Wang, S.; Clark, R.; Wen, H.; Trigoni, N. Deepvo: Towards end-to-end visual odometry with deep recurrent convolutional neural networks. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2043–2050. [Google Scholar]
- Jin, J.; Bai, J.; Xu, Y.; Huang, J. Unifying Deep ConvNet and Semantic Edge Features for Loop Closure Detection. Remote Sens. 2022, 14, 4885. [Google Scholar] [CrossRef]
- Liu, T.; Wang, Y.; Niu, X.; Chang, L.; Zhang, T.; Liu, J. LiDAR Odometry by Deep Learning-Based Feature Points with Two-Step Pose Estimation. Remote Sens. 2022, 14, 2764. [Google Scholar] [CrossRef]
- Wang, S.; Gou, G.; Sui, H.; Zhou, Y.; Zhang, H.; Li, J. CDSFusion: Dense Semantic SLAM for Indoor Environment Using CPU Computing. Remote Sens. 2022, 14, 979. [Google Scholar] [CrossRef]
- Li, R.; Wang, S.; Gu, D. DeepSLAM: A robust monocular SLAM system with unsupervised deep learning. IEEE Trans. Ind. Electron. 2020, 68, 3577–3587. [Google Scholar] [CrossRef]
- Li, D.; Shi, X.; Long, Q.; Liu, S.; Yang, W.; Wang, F.; Wei, Q.; Qiao, F. DXSLAM: A Robust and Efficient Visual SLAM System with Deep Features. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 4958–4965. [Google Scholar]
- Tang, J.; Ericson, L.; Folkesson, J.; Jensfelt, P. GCNv2: Efficient Correspondence Prediction for Real-Time SLAM. IEEE Robot. Autom. Lett. 2019, 4, 3505–3512. [Google Scholar] [CrossRef]
- Bruno, H.M.S.; Colombini, E. LIFT-SLAM: A deep-learning feature-based monocular visual SLAM method. Neurocomputing 2020, 455, 97–110. [Google Scholar] [CrossRef]
- Xiao, Z.; Li, S. SL-SLAM: A robust visual-inertial SLAM based deep feature extraction and matching. arXiv 2024, arXiv:2405.03413. [arXiv:cs.RO/2405.03413]. [Google Scholar]
- Bian, J.; Li, Z.; Wang, N.; Zhan, H.; Shen, C.; Cheng, M.M.; Reid, I. Unsupervised scale-consistent depth and ego-motion learning from monocular video. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Wang, Y.; Xu, B.; Fan, W.; Xiang, C. A robust and efficient loop closure detection approach for hybrid ground/aerial vehicles. Drones 2023, 7, 135. [Google Scholar] [CrossRef]
- Teed, Z.; Deng, J. Droid-slam: Deep visual slam for monocular, stereo, and rgb-d cameras. Adv. Neural Inf. Process. Syst. 2021, 34, 16558–16569. [Google Scholar]
- Dey, R.; Salem, F.M. Gate-variants of gated recurrent unit (GRU) neural networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; pp. 1597–1600. [Google Scholar]
- Li, Y.; Ushiku, Y.; Harada, T. Pose graph optimization for unsupervised monocular visual odometry. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 5439–5445. [Google Scholar]
- Zhao, W.; Liu, S.; Shu, Y.; Liu, Y.J. Towards Better Generalization: Joint Depth-Pose Learning Without PoseNet. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 9148–9158. [Google Scholar] [CrossRef]
- Zhan, H.; Weerasekera, C.S.; Bian, J.; Garg, R.; Reid, I.D. DF-VO: What Should Be Learnt for Visual Odometry? arXiv 2021, arXiv:2103.00933. [Google Scholar]
- Sun, D.; Yang, X.; Liu, M.Y.; Kautz, J. PWC-Net: CNNs for Optical Flow Using Pyramid, Warping, and Cost Volume. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8934–8943. [Google Scholar]
- Tang, J.; Folkesson, J.; Jensfelt, P. Geometric Correspondence Network for Camera Motion Estimation. IEEE Robot. Autom. Lett. 2018, 3, 1010–1017. [Google Scholar] [CrossRef]
- Sarlin, P.E.; Cadena, C.; Siegwart, R.Y.; Dymczyk, M. From Coarse to Fine: Robust Hierarchical Localization at Large Scale. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 12708–12717. [Google Scholar]
- Galvez-López, D.; Tardos, J.D. Bags of Binary Words for Fast Place Recognition in Image Sequences. IEEE Trans. Robot. 2012, 28, 1188–1197. [Google Scholar] [CrossRef]
- Arandjelović, R.; Gronat, P.; Torii, A.; Pajdla, T.; Sivic, J. NetVLAD: CNN Architecture for Weakly Supervised Place Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 218, 5297–5307. [Google Scholar] [CrossRef]
- Tiwari, L.; Ji, P.; Tran, Q.H.; Zhuang, B.; Anand, S.; Chandraker, M. Pseudo rgb-d for self-improving monocular slam and depth prediction. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 437–455. [Google Scholar]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. SuperPoint: Self-Supervised Interest Point Detection and Description. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 337–33712. [Google Scholar]
- Lindenberger, P.; Sarlin, P.E.; Pollefeys, M. LightGlue: Local Feature Matching at Light Speed. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 17581–17592. [Google Scholar] [CrossRef]
- Sauerbeck, F.; Obermeier, B.; Rudolph, M.; Betz, J. RGB-L: Enhancing Indirect Visual SLAM Using LiDAR-Based Dense Depth Maps. In Proceedings of the 2023 3rd International Conference on Computer, Control and Robotics (ICCCR), Shanghai, China, 24–26 March 2023; pp. 95–100. [Google Scholar]
- Engel, J.; Koltun, V.; Cremers, D. Direct Sparse Odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 611–625. [Google Scholar] [CrossRef]
- Yuan, C.; Xu, Y.; Zhou, Q. PLDS-SLAM: Point and Line Features SLAM in Dynamic Environment. Remote Sens. 2023, 15, 1893. [Google Scholar] [CrossRef]
- Rong, H.; Gao, Y.; Guan, L.; Ramirez-Serrano, A.; Xu, X.; Zhu, Y. Point-Line Visual Stereo SLAM Using EDlines and PL-BoW. Remote Sens. 2021, 13, 3591. [Google Scholar] [CrossRef]
- Grompone von Gioi, R.; Jakubowicz, J.; Morel, J.M.; Randall, G. LSD: A Fast Line Segment Detector with a False Detection Control. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 722–732. [Google Scholar] [CrossRef]
- Zhang, L.; Koch, R. An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency. J. Vis. Commun. Image Represent. 2013, 24, 794–805. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-Up Robust Features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Lin, T.Y.; Maire, M.; Belongie, S.J.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Fidalgo, E.; Ortiz, A. iBoW-LCD: An Appearance-Based Loop-Closure Detection Approach Using Incremental Bags of Binary Words. IEEE Robot. Autom. Lett. 2018, 3, 3051–3057. [Google Scholar] [CrossRef]
- Geiger, A.; Ziegler, J.; Stiller, C. StereoScan: Dense 3d reconstruction in real-time. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 963–968. [Google Scholar] [CrossRef]
- Wei, P.; Hua, G.; Huang, W.; Meng, F.; Liu, H. Unsupervised Monocular Visual-inertial Odometry Network. In Proceedings of the International Joint Conference on Artificial Intelligence, Rhodes, Greece, 12–18 September 2020. [Google Scholar]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.; Tardós, J. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual–Inertial, and Multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Gao, X.; Wang, R.; Demmel, N.; Cremers, D. LDSO: Direct Sparse Odometry with Loop Closure. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2198–2204. [Google Scholar] [CrossRef]
- Deng, C.; Qiu, K.; Xiong, R.; Zhou, C. Comparative Study of Deep Learning Based Features in SLAM. In Proceedings of the 2019 4th Asia-Pacific Conference on Intelligent Robot Systems (ACIRS), Nagoya, Japan, 13–15 July 2019; pp. 250–254. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Chintala, S. PyTorch: An Imperative Style, High-Performance Deep Learning Library; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).