CFD Analysis of the Thermal-Hydraulic Performance of Traditional and Alternative Oils for Transformer Cooling
Abstract
1. Introduction
2. Materials and Methods
2.1. Case Study
2.2. Governing Equations and Discretization Schemes
2.3. Thermophysical Model
2.4. Meshing and BCs
3. Results and Discussion
3.1. Asymptotic Behavior of the Numerical Solution
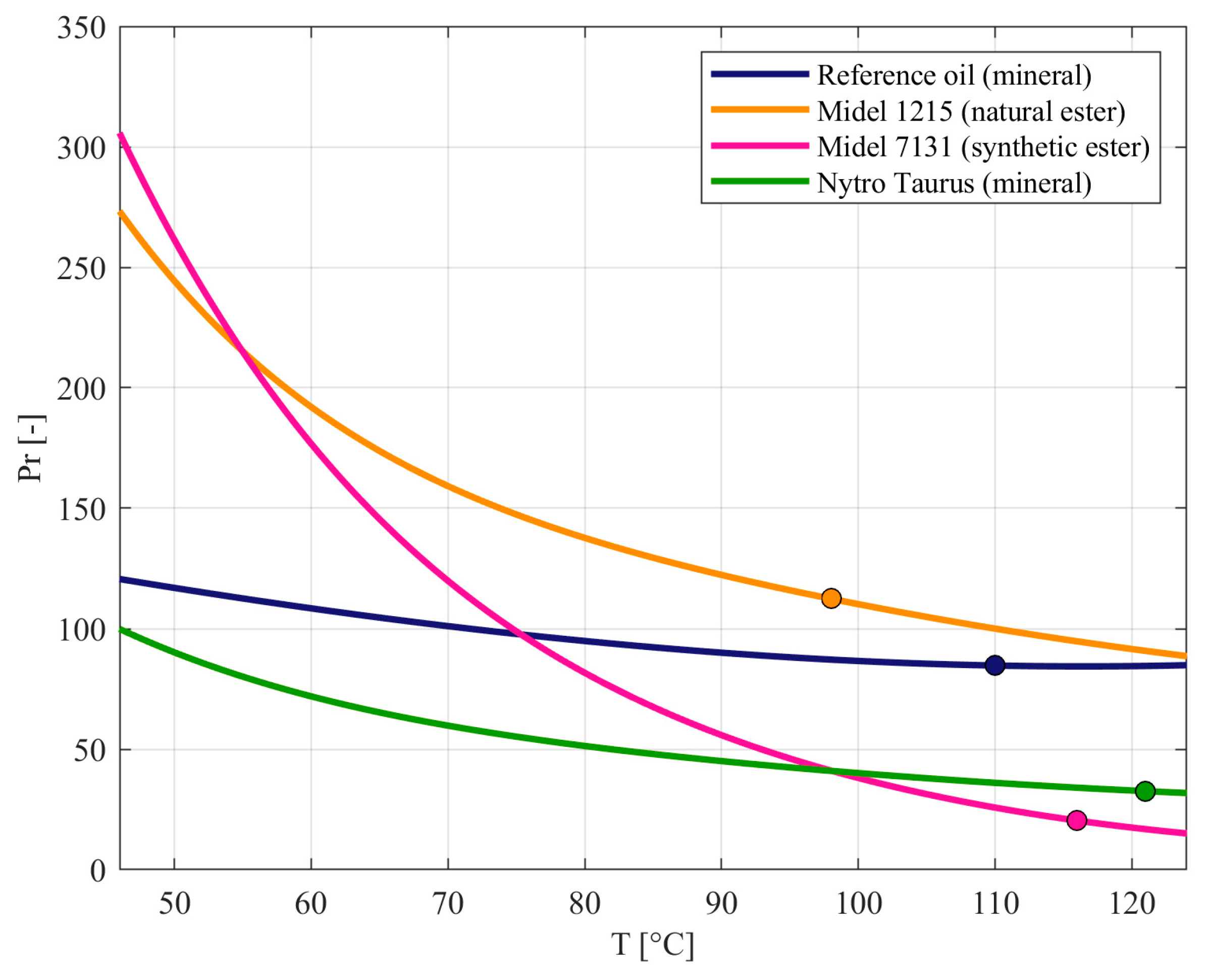
3.2. Thermal-Hydraulic Performance
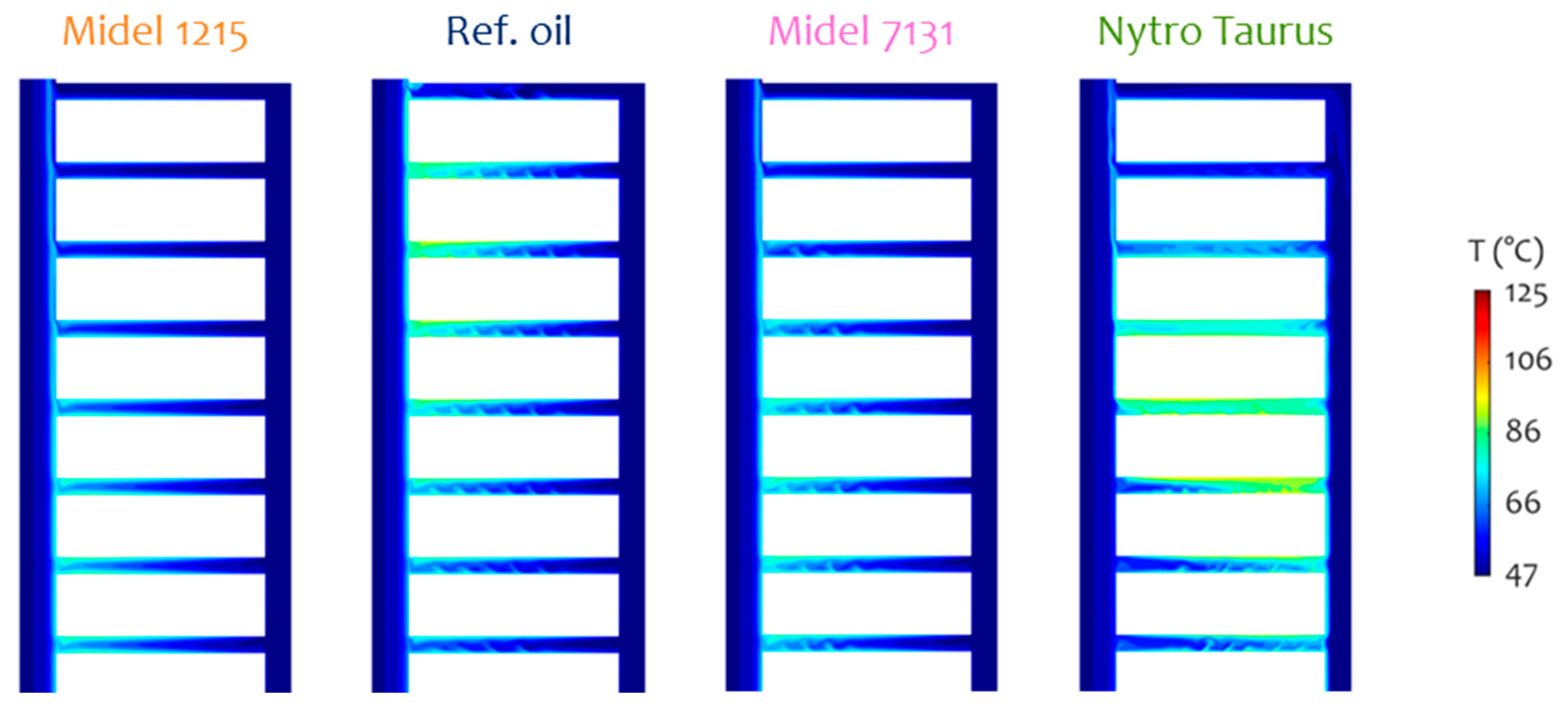
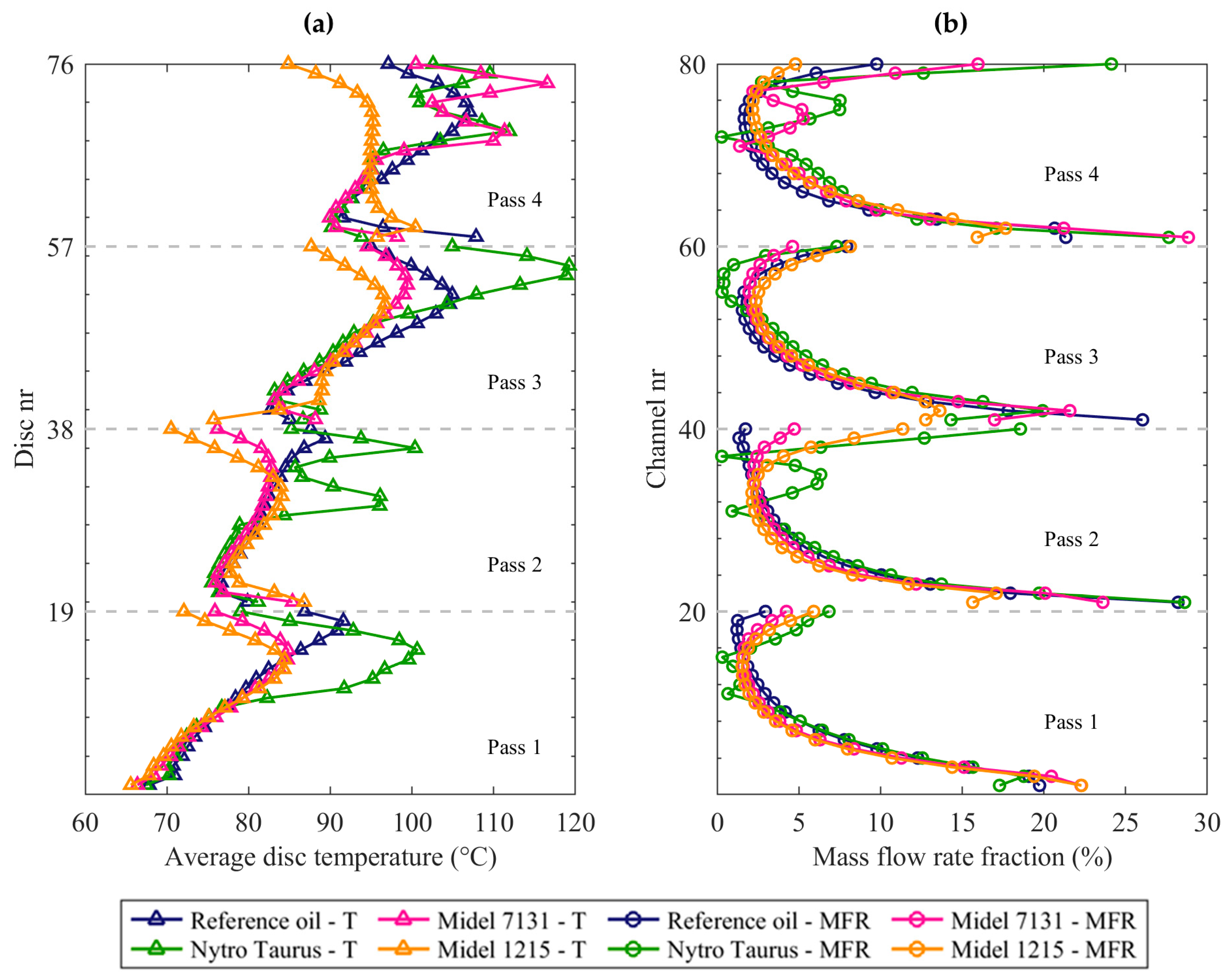
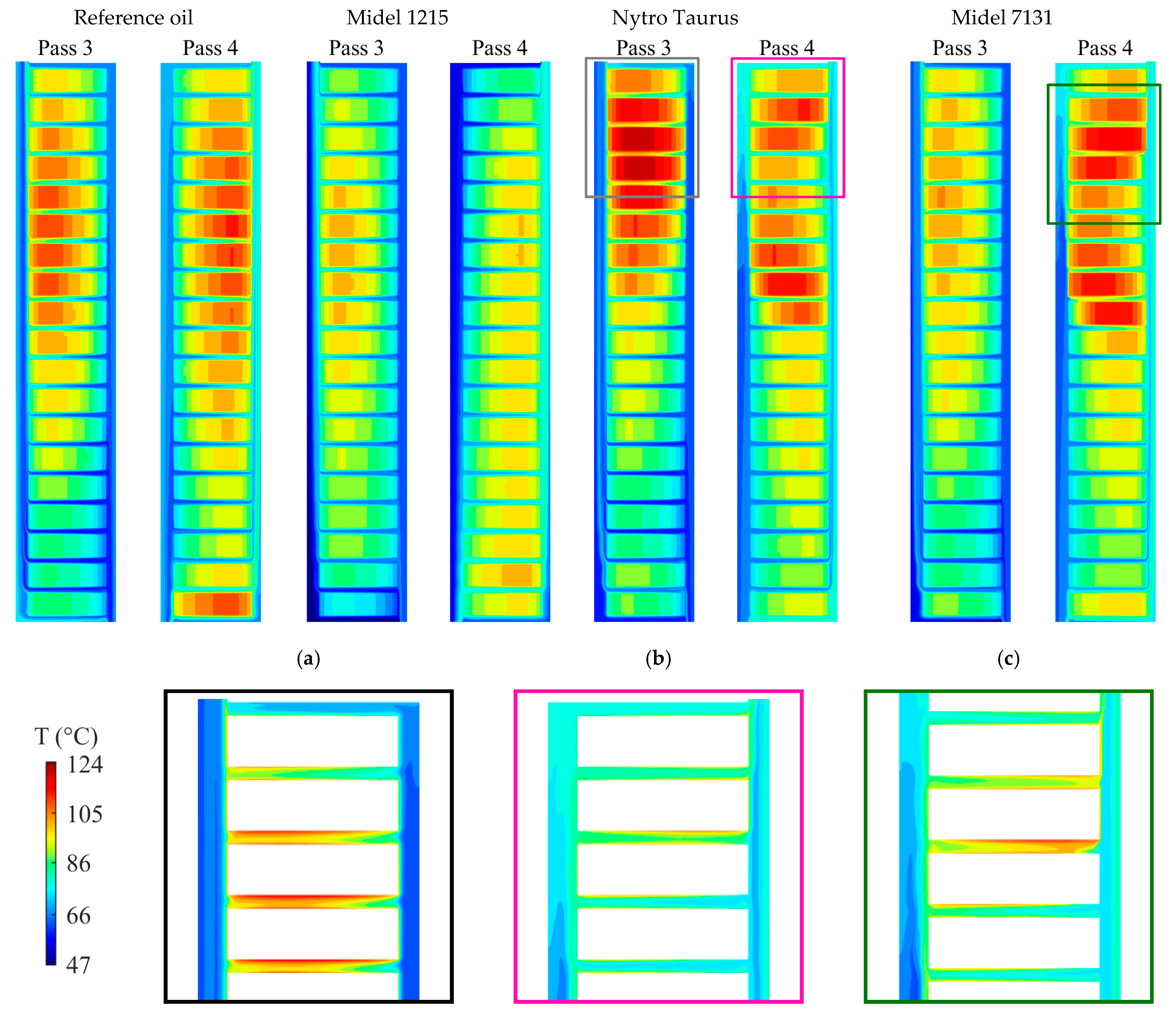
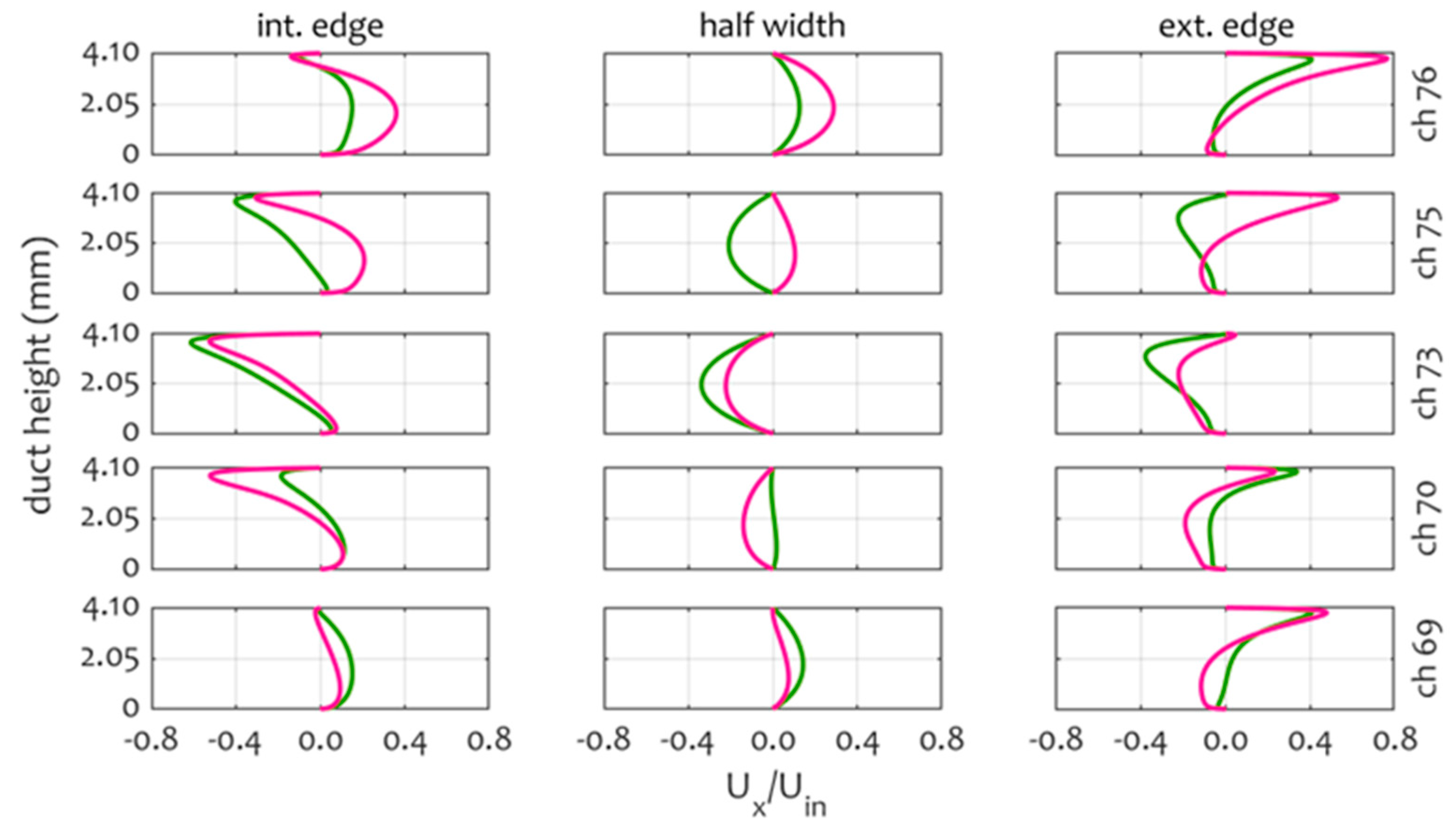
3.3. Temperature and Velocity Distributions
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Heathcote, M.J. The J & P Transformer Book; Newnes: Oxford, UK, 1998. [Google Scholar]
- Shen, Z.; Wang, F.; Wang, Z.; Li, J. A critical review of plant-based insulating fluids for transformer: 30-year development. Renew. Sustain. Energy Rev. 2021, 141, 110783. [Google Scholar] [CrossRef]
- Rouse, T.O. Mineral oil in transformers. IEEE Electr. Insul. Mag. 1998, 14, 6–16. [Google Scholar] [CrossRef]
- Fofana, I. 50 years in the development of insulating liquids. IEEE Electr. Insul. Mag. 2013, 29, 13–25. [Google Scholar] [CrossRef]
- Rafiq, M.; Lv, Y.Z.; Zhou, Y.; Ma, K.B.; Wang, W.; Li, C.R.; Wang, Q. Use of vegetable oils as transformer oils—A review. Renew. Sustain. Energy Rev. 2015, 52, 308–324. [Google Scholar] [CrossRef]
- IEC 60076-7:2018; Power Transformers—Part 7. International Electrotechnical Commission: Geneva, Switzerland, 2018.
- Nadolny, Z.; Dombek, G. Thermal properties of mixtures of mineral oil and natural ester in terms of their application in the transformer. E3S Web Conf. 2017, 19, 01040. [Google Scholar] [CrossRef]
- Achille, K.; Ghislain, M.M.; Louis, M.; Adolphe, M.I. Determination at Variable Temperatures and Analysis of the Physico-Thermal Properties of Palm Kernel and Castor Oil Methyl Esters as Dielectrics for Power Transformers. Int. J. Heat Technol. 2023, 41, 63–71. [Google Scholar] [CrossRef]
- Salama, M.M.M.; Mansour, D.-E.A.; Dagrah, M.; Abdelkasoud, S.M.; Abbas, A.A. Thermal performance of transformers filled with environmentally friendly oils under various loading conditions. Electr. Power Energy Syst. 2020, 118, 105743. [Google Scholar] [CrossRef]
- Raeisian, L.; Niazman, L.; Ebrahimnia-Bajestan, E.; Werle, P. Feasibility study of waste vegetable oil as an alternative cooling medium in transformers. Appl. Therm. Eng. 2019, 151, 308–317. [Google Scholar] [CrossRef]
- Garelli, L.; Rodriguez, G.A.R.; Kubiczek, K.; Lasek, P.; Stepien, M.; Smolka, J.; Storti, M.; Pessolani, F.; Amadei, M. Thermo-magnetic-fluid dynamics analysis of an ONAN distribution transformer cooled with mineral oil and biodegradable esters. Therm. Sci. Eng. Prog. 2021, 23, 100861. [Google Scholar] [CrossRef]
- Daghrah, M.; Yang, Z.; Hilker, A.; Gyore, A. Experimental Study of the Influence of Different Liquids on the Transformer Cooling Performance. IEEE Trans. Power Deliv. 2019, 34, 588–595. [Google Scholar] [CrossRef]
- Couto, S.; Ferreira, E.M.; Sá, D.; Corte-Real, C.; Lima, P.; Lopes, R.C.; Costa, A.; Sá, C.A.; Monteiro, P.; Soares, M. Comparison of the Thermal Performance of Mineral Oil and Natural Ester for Safer Eco-Friendly Power Transformers. RE&PQJ 2021, 19, 149–154. [Google Scholar]
- Santisteban, A.; Fernandez, F.O.; Delgado, I.F.F.; Ortiz, A.; Renedo, C.J. Thermal analysis of natural esters in a low-voltage disc-type winding of a power transformer. In Proceedings of the 19th IEEE International Conference on Dielectric Liquids (ICDL), Manchester, UK, 25–29 June 2017; pp. 1–4. [Google Scholar]
- Torriano, F.; Chaaban, M.; Picher, P. Numerical study of parameters affecting the temperature distribution in a disc-type transformer winding. Appl. Therm. Eng. 2010, 30, 2034–2044. [Google Scholar] [CrossRef]
- Torriano, F.; Picher, P.; Chaaban, M. Numerical investigation of 3D flow and thermal effects in a disc-type transformer winding. Appl. Therm. Eng. 2012, 40, 121–131. [Google Scholar] [CrossRef]
- Salerno, E.; Leonforte, A.; Angeli, D. Influence of the Thermophysical Model on the CFD Analysis of Oil-Cooled Transformer Windings. J. Phys. Conf. Ser. 2021, 1868, 012031. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comp. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Gray, D.D.; Giorgini, A. The validity of the Boussinesq approximation for liquids and gases. Int. J. Heat Mass Transf. 1976, 19, 545–551. [Google Scholar] [CrossRef]

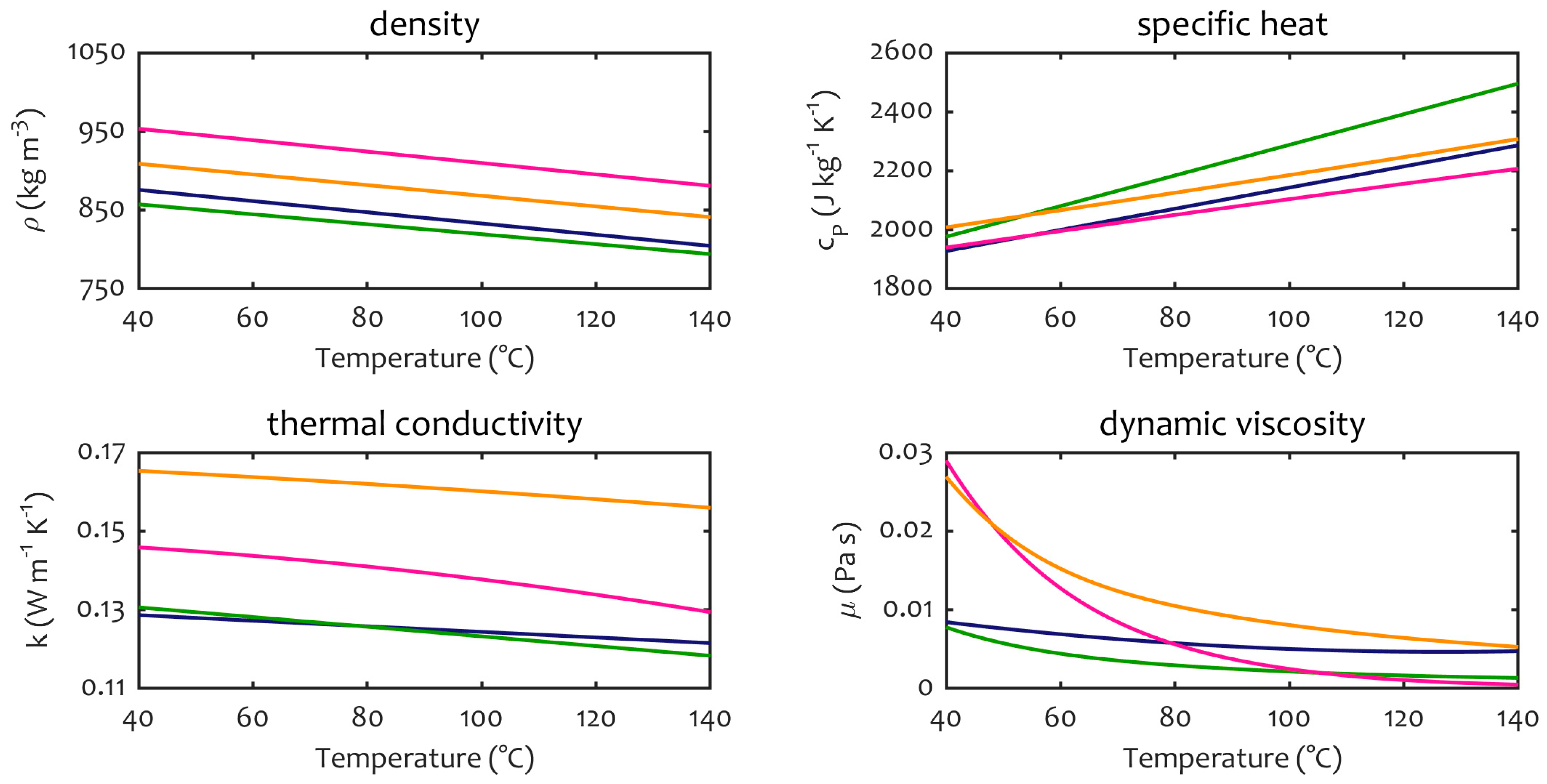


| Density, ρ [kg m−3] | Dynamic Viscosity, μ [Pa s] | ||||||||
| a0 | a1 | a0 | a1 | a2 | a3 | a4 | a5 | ||
| Reference oil | 1098.72 | −0.712 | 0.08467 | −4 × 10−4 | 5 × 10−7 | - | - | - | |
| Midel 1215 | 1121.09 | −0.678 | 44.41 | −0.575 | 2.99 × 10−3 | −7.76 × 10−6 | 1.01 × 10−8 | −5.24 × 10−12 | |
| Midel 7131 | 1180.20 | −0.724 | 36.81 | −0.465 | 2.36 × 10−3 | −6.00 × 10−6 | 7.66 × 10−9 | −3.92 × 10−12 | |
| Nytro Taurus | 1055.27 | −0.632 | 11.68 | −0.152 | 7.88 × 10−4 | −2.05 × 10−6 | 2.68 × 10−9 | −1.40 × 10−12 | |
| Specific Heat, cp [J kg−1 K−1] | Thermal Conductivity, k [W m−1 K−1] | ||||||||
| a0 | a1 | a2 | a0 | a1 | a2 | ||||
| Reference oil | 807.2 | 3.580 | - | 0.1509 | 7.10 × 10−5 | - | |||
| Midel 1215 | 1200 | 2.267 | 1 × 10−3 | 0.1715 | 3.65 × 10−5 | 1.80 × 10−7 | |||
| Midel 7131 | 898.1 | 3.824 | −1.59 × 10−3 | 0.1044 | 3.58 × 10−4 | −7.19 × 10−7 | |||
| Nytro Taurus | 352.4 | 5.187 | - | 0.1691 | −1.23 × 10−4 | - | |||
| Symbol/Formula | Unit | Ref. Oil | Midel 1215 | Nytro Taurus | Midel 7131 | |
|---|---|---|---|---|---|---|
| Hot-spot temperature | Ths | °C | 113.7 | 103.5 (−15.2%) | 124.8 (+16.6%) | 120.0 (+9.4%) |
| Hot-spot location | - | - | disc 71 (Pass 4) | disc 51 (Pass 3) | disc 54 (Pass 3) | disc 74 (Pass 4) |
| Average disc temperature | Tave,Cu | °C | 89.0 | 85.3 (−8.7%) | 90.9 (+4.5%) | 87.5 (−3.5%) |
| Bulk outlet oil temperature | Tout,oil | °C | 80.3 | 82.0 | 79.0 | 80.4 |
| Average bulk oil temperature | Tave,oil | °C | 63.5 | 64.3 | 62.8 | 63.6 |
| Mean Cu-oil gradient | ΔTCu-oil = Tave,Cu − Tave,oil | °C | 25.5 | 20.9 (−17.9%) | 28.1 (+10.1%) | 24.0 (−6.1%) |
| Hot-spot factor | HSF = (Ths − Tave,oil)/ΔTCu-oil | - | 1.96 | 1.87 (−5.0%) | 2.21 (+12.1%) | 2.36 (+19.7%) |
| Overall heat transfer coefficient | U = q”/ΔTCu-oil | W m−2 °C−1 | 100.4 | 122.2 (+21.7%) | 91.1 (−9.2%) | 106.9 (+6%) |
| Overall pressure drop | Δp = pin − pout | kPa | 12.87 | 13.47 (+4.7%) | 12.60 (−2.1%) | 14.06 (+9.3%) |
| Pumping power | W | 11.5 | 11.6 | 11.5 | 11.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salerno, E.; Leonforte, A.; Grespan, M.; Angeli, D.; Corticelli, M.A. CFD Analysis of the Thermal-Hydraulic Performance of Traditional and Alternative Oils for Transformer Cooling. Appl. Sci. 2024, 14, 9736. https://doi.org/10.3390/app14219736
Salerno E, Leonforte A, Grespan M, Angeli D, Corticelli MA. CFD Analysis of the Thermal-Hydraulic Performance of Traditional and Alternative Oils for Transformer Cooling. Applied Sciences. 2024; 14(21):9736. https://doi.org/10.3390/app14219736
Chicago/Turabian StyleSalerno, Elisabetta, Adriano Leonforte, Mattia Grespan, Diego Angeli, and Mauro A. Corticelli. 2024. "CFD Analysis of the Thermal-Hydraulic Performance of Traditional and Alternative Oils for Transformer Cooling" Applied Sciences 14, no. 21: 9736. https://doi.org/10.3390/app14219736
APA StyleSalerno, E., Leonforte, A., Grespan, M., Angeli, D., & Corticelli, M. A. (2024). CFD Analysis of the Thermal-Hydraulic Performance of Traditional and Alternative Oils for Transformer Cooling. Applied Sciences, 14(21), 9736. https://doi.org/10.3390/app14219736








