Experimental and Numerical Evaluation of Calcium-Silicate-Based Mineral Foam for Blast Mitigation
Abstract
1. Introduction
2. Air-Blast Experiments
2.1. Main Structure and Front Skin Materials
2.2. Calcium-Silicate-Based Mineral Foam as Crushable Core
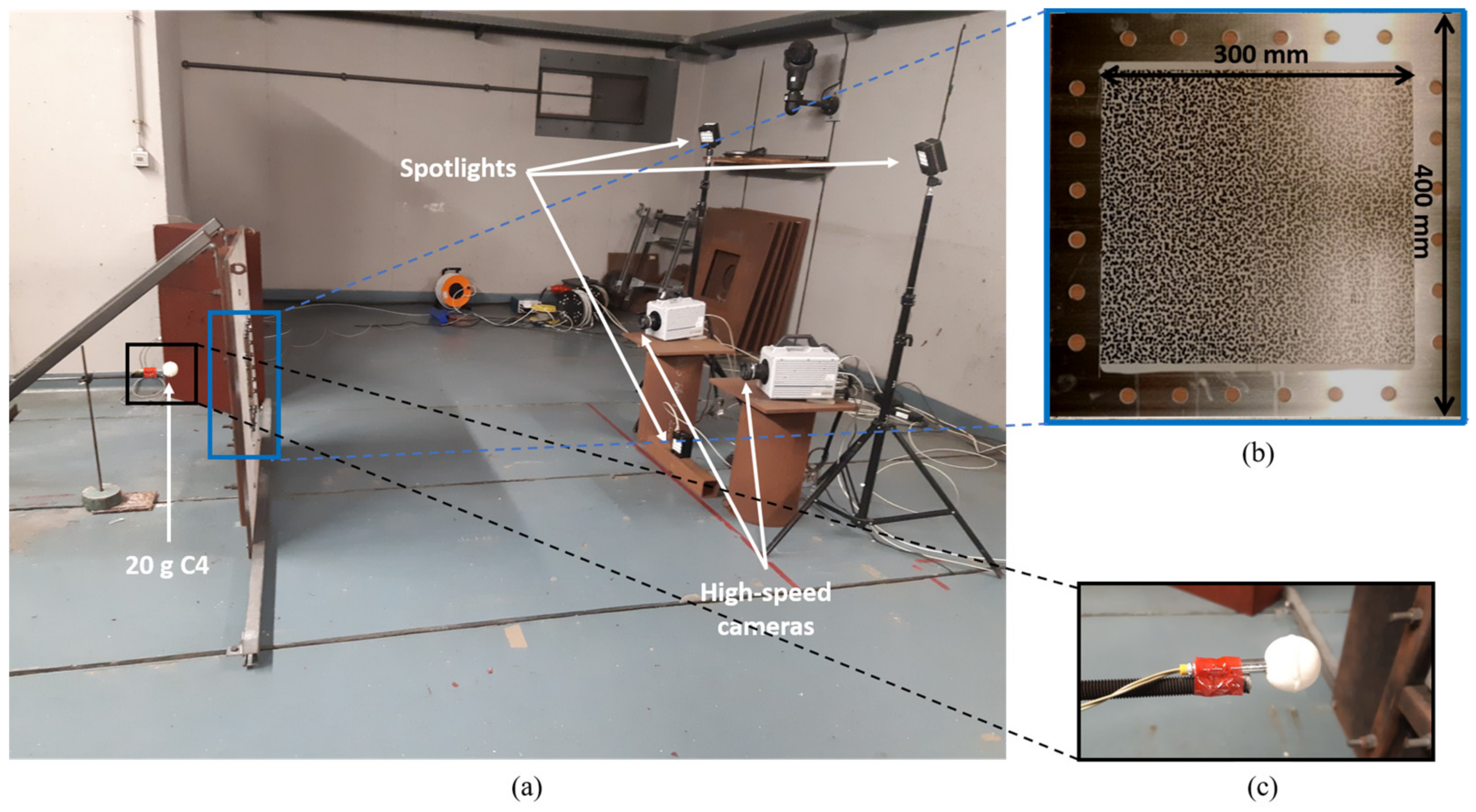
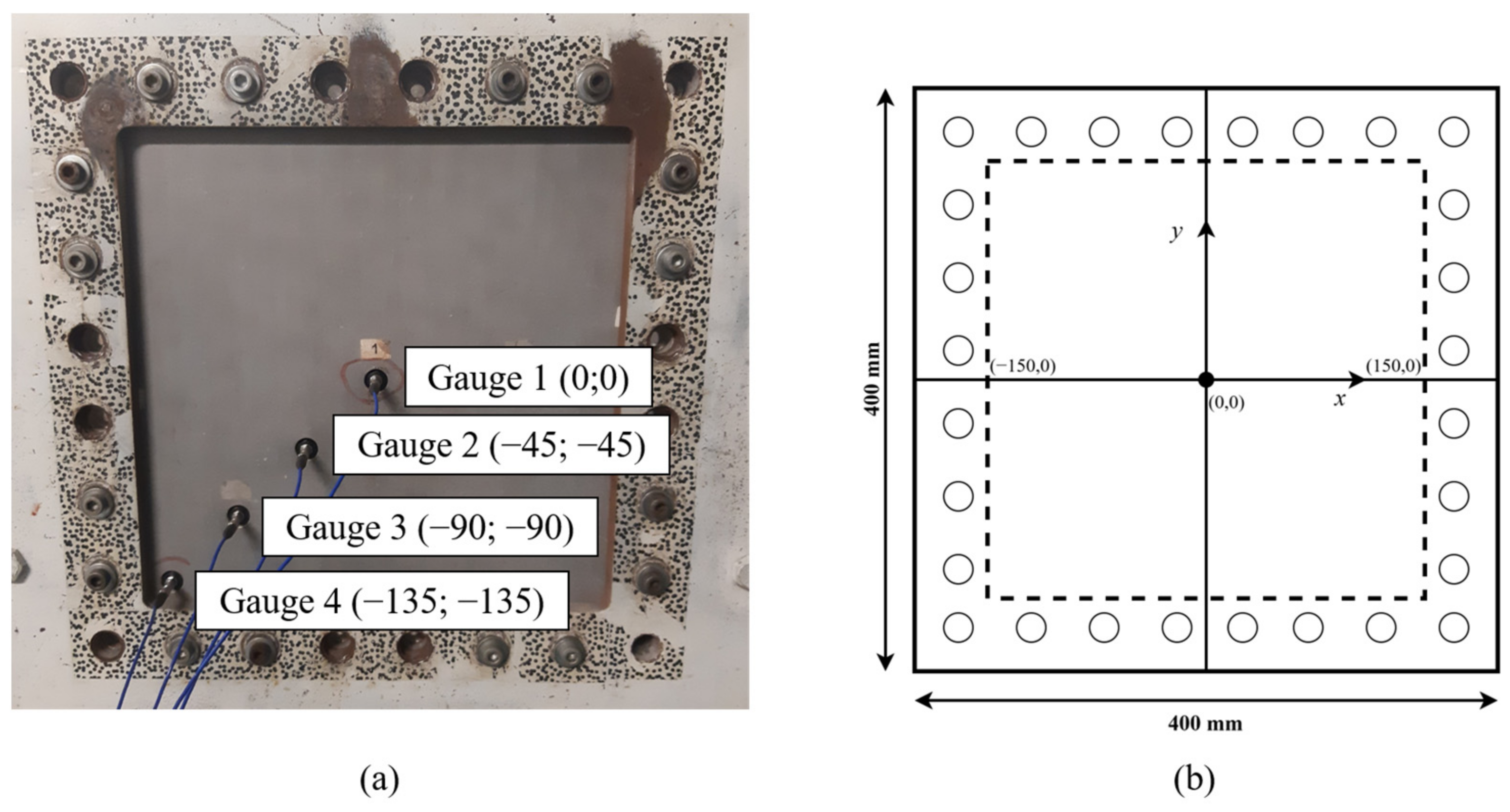
2.3. Experimental Set-Up
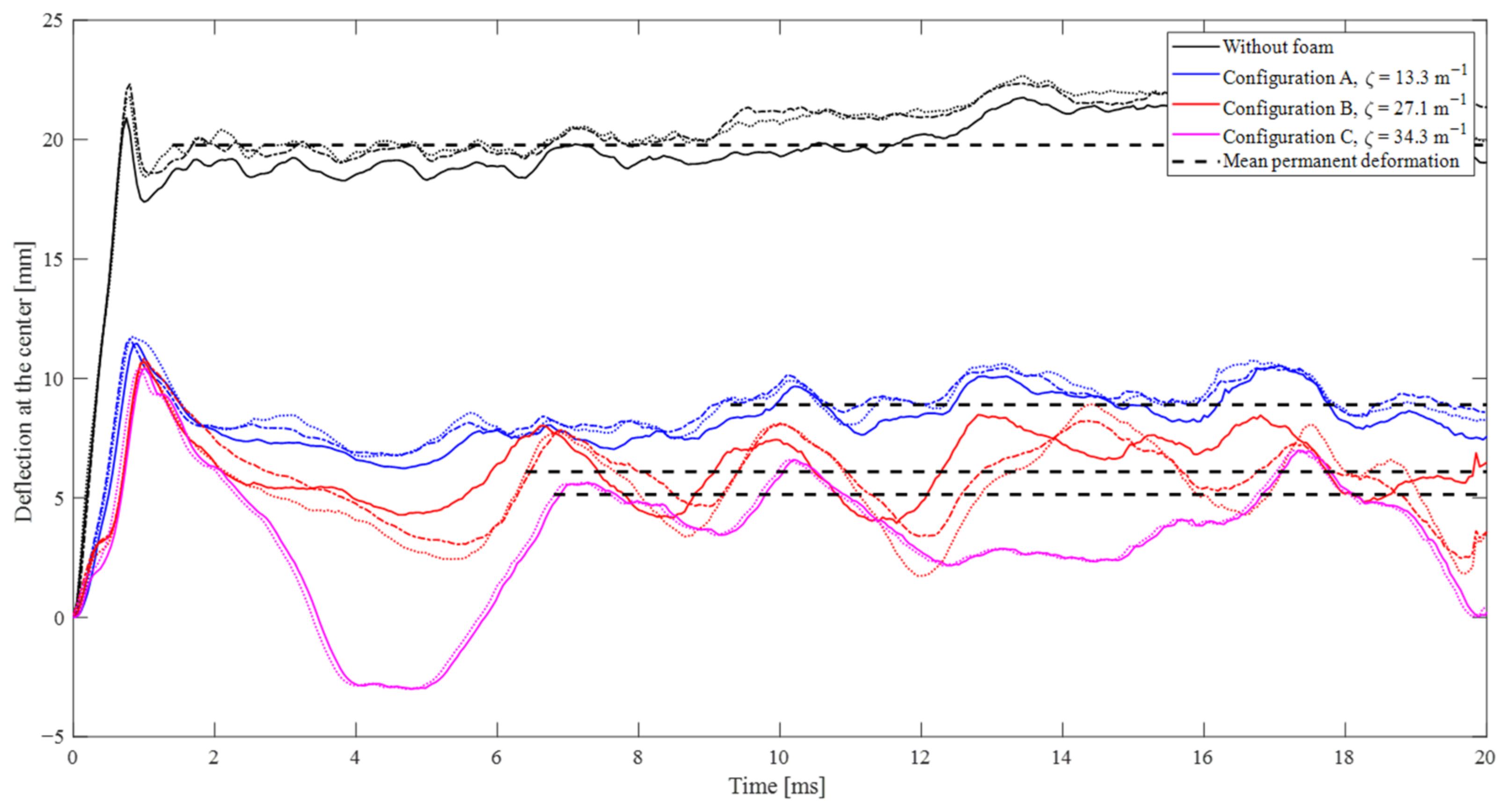
2.4. Results from Experiments
2.4.1. Blast Loading
2.4.2. Response of the Bare Aluminum Plate
2.4.3. Response of the Aluminum Backplate with the Protective Foam
3. Numerical Modeling
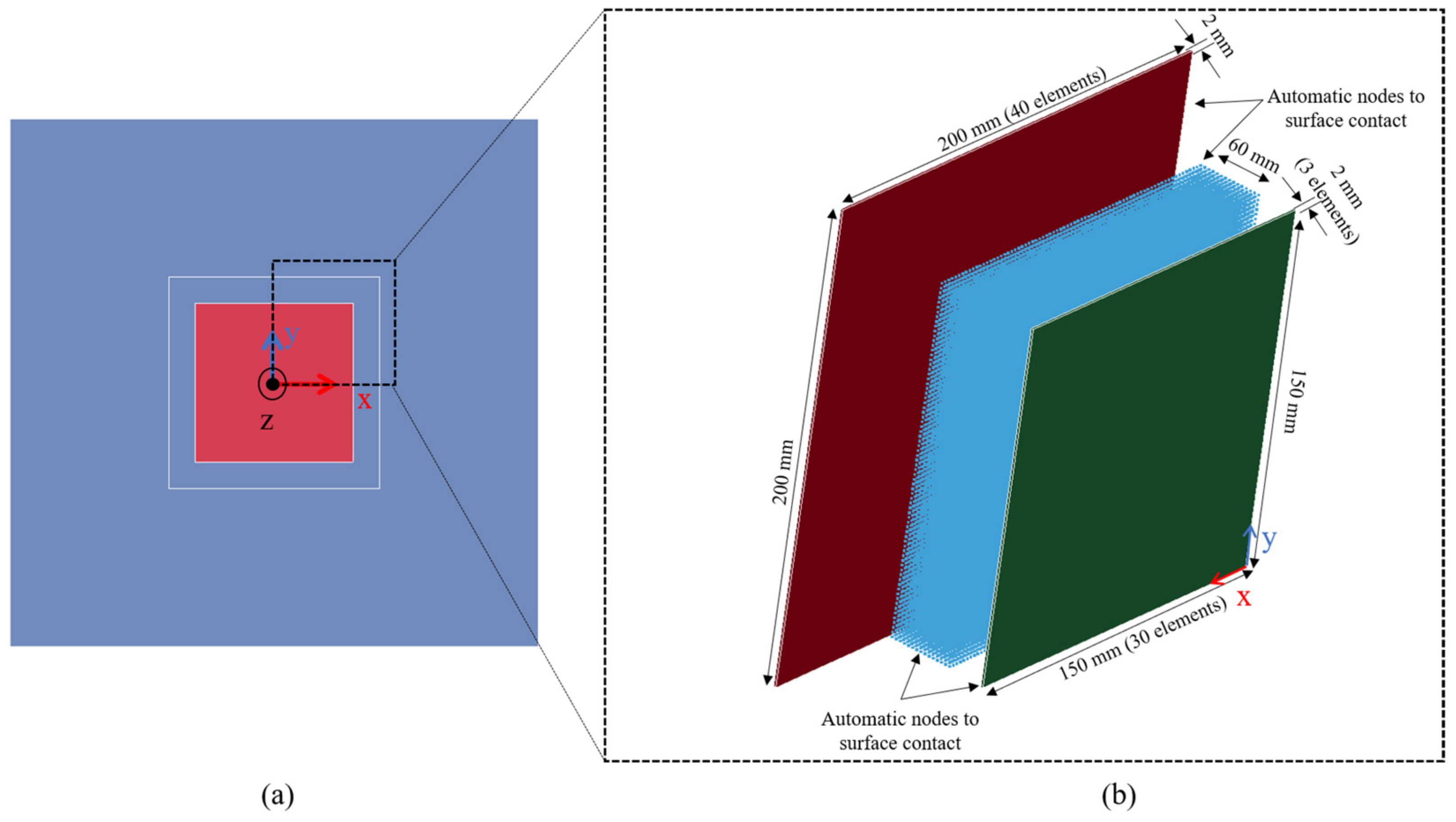
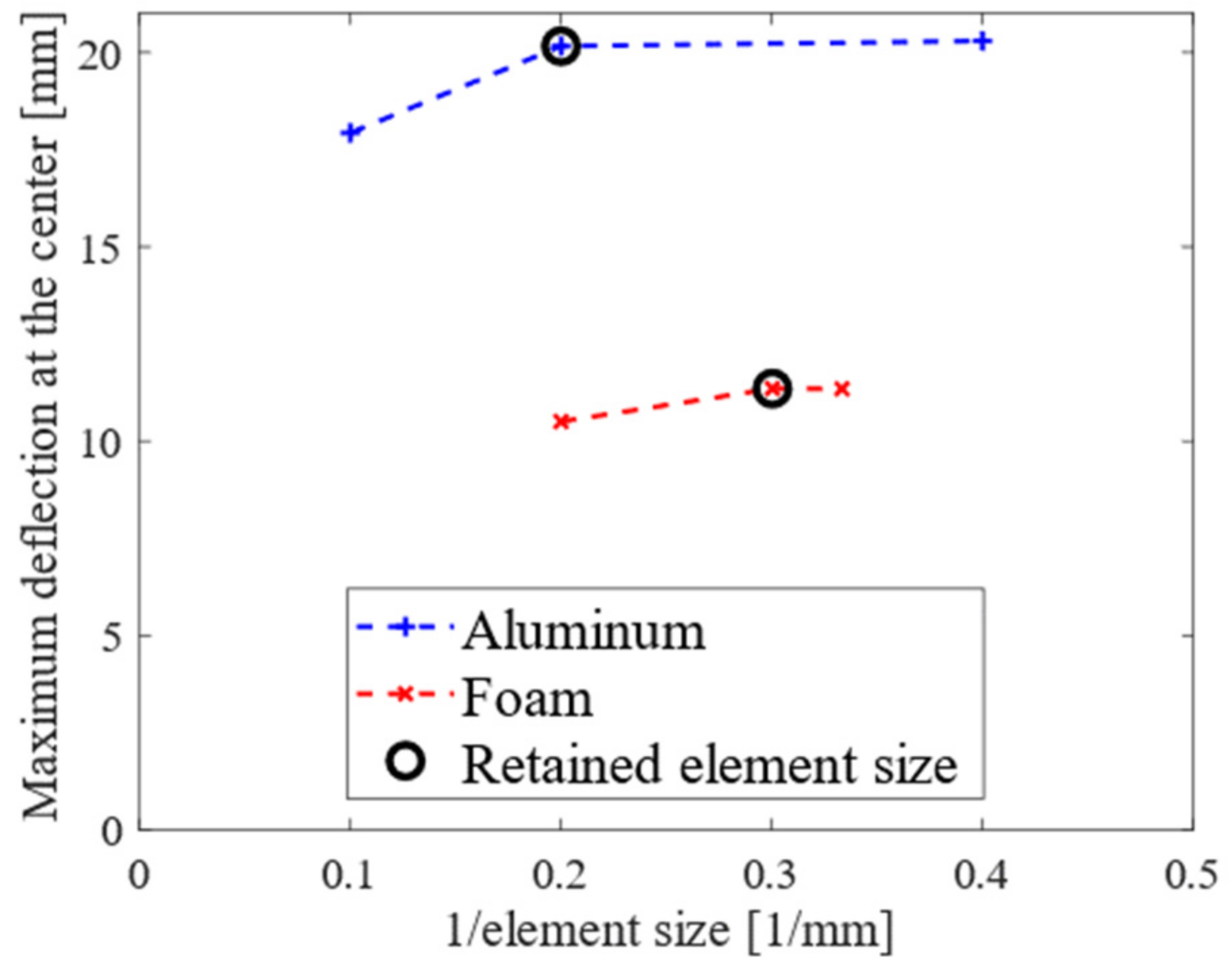
3.1. Modeling Method
3.2. Material Modeling
| (kg/m−3) | (GPa) | Strain Rate Effects |
|---|---|---|
| 110 | 30 | Tabulated stress-strain curves for various ranges (See Figure 15) |
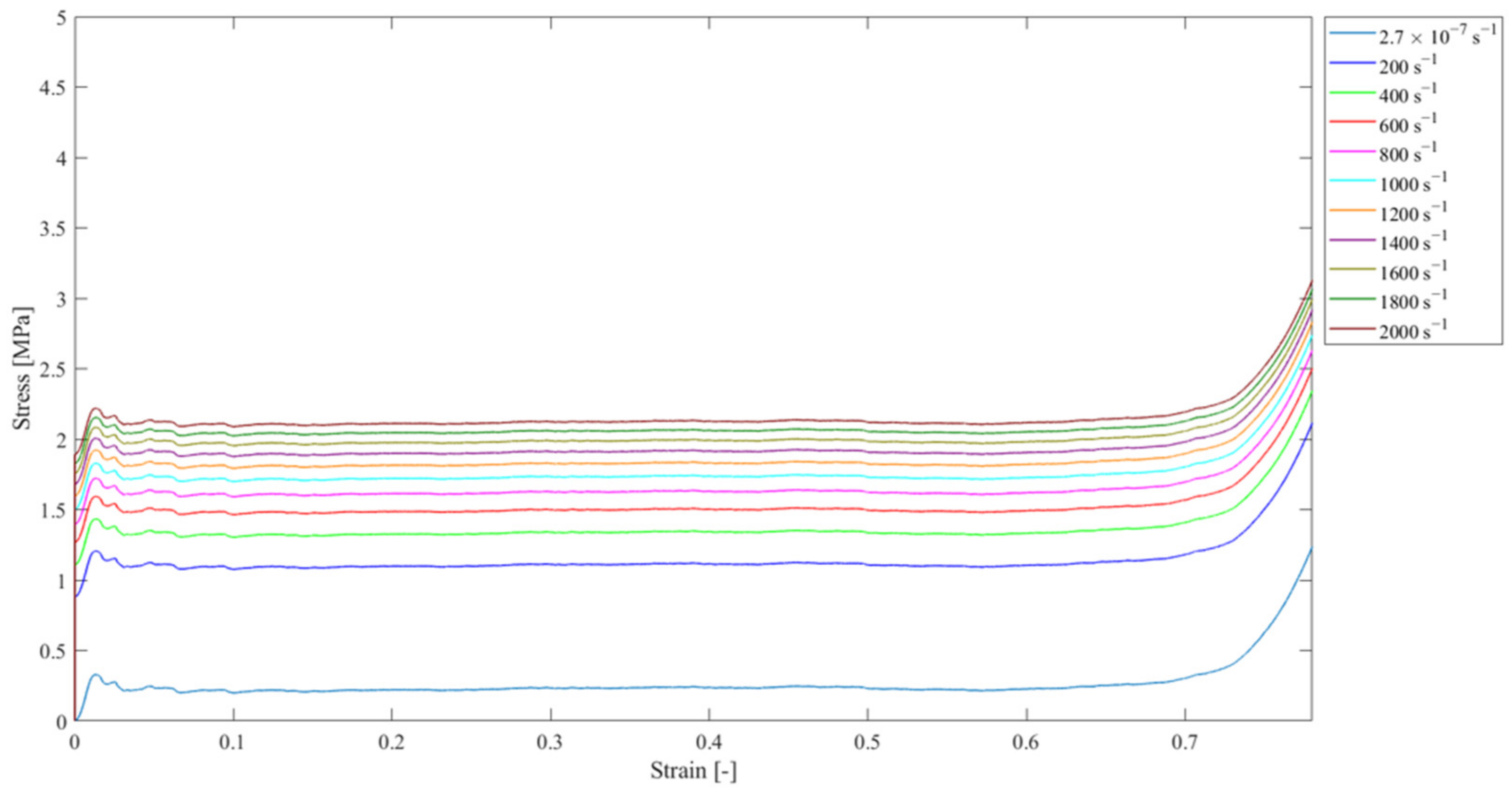
4. Results from Simulations
4.1. Validation of the Blast Loading
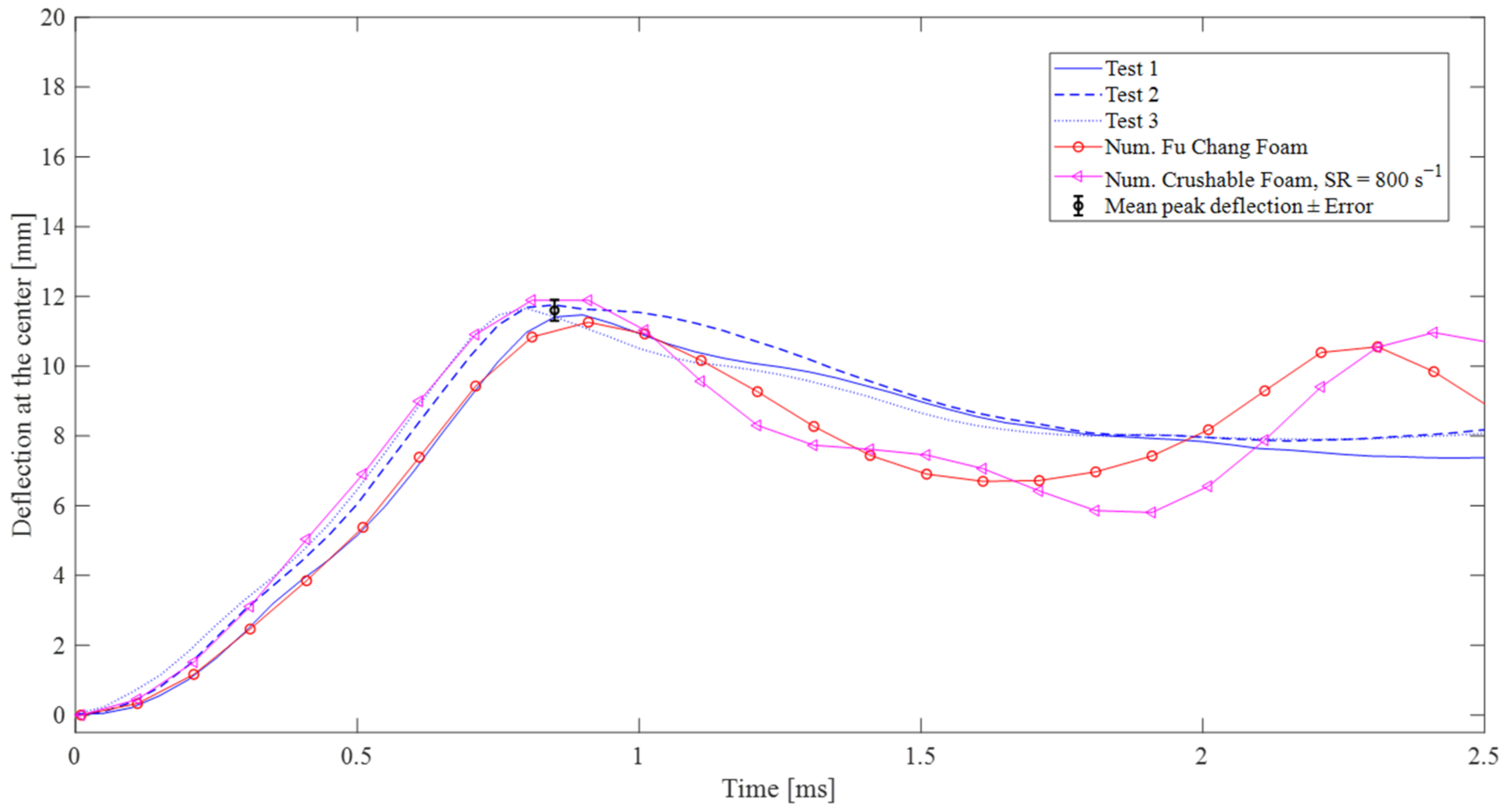
4.2. Comparison Between Experimental and Numerical Results
4.3. Parametric Study
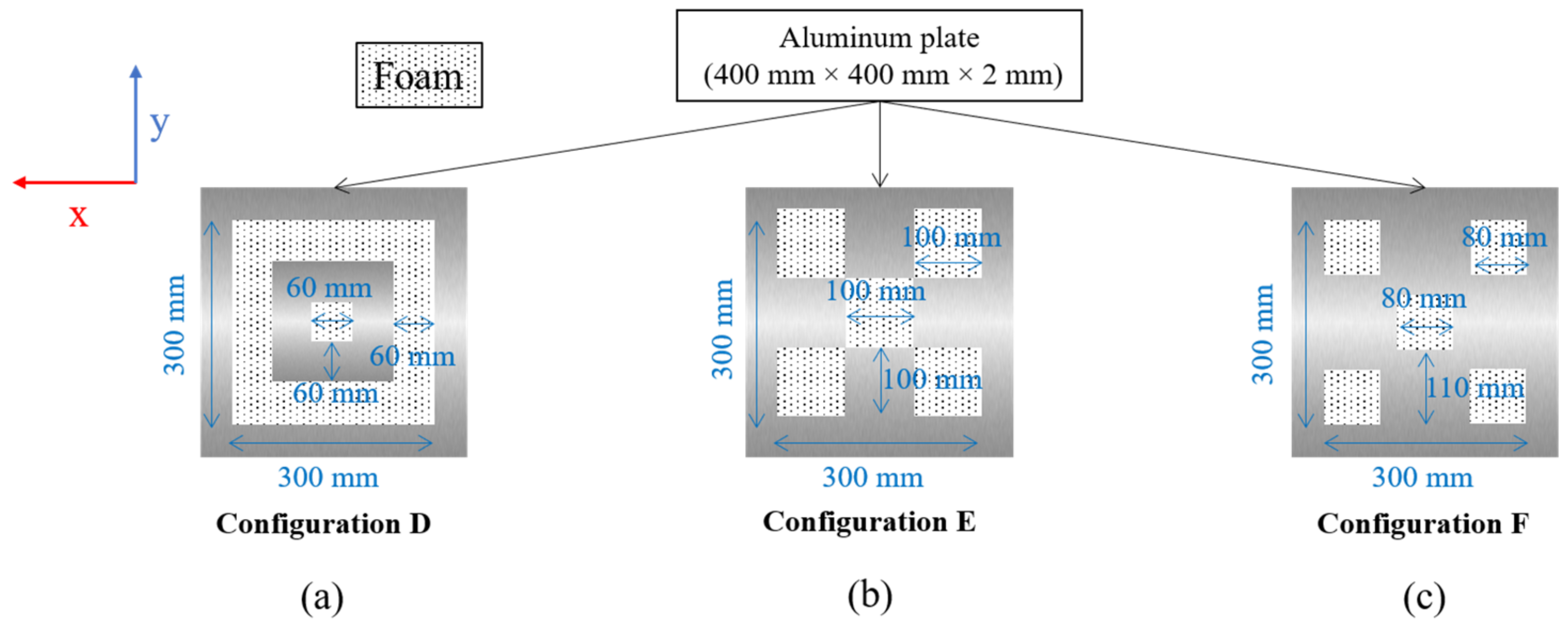
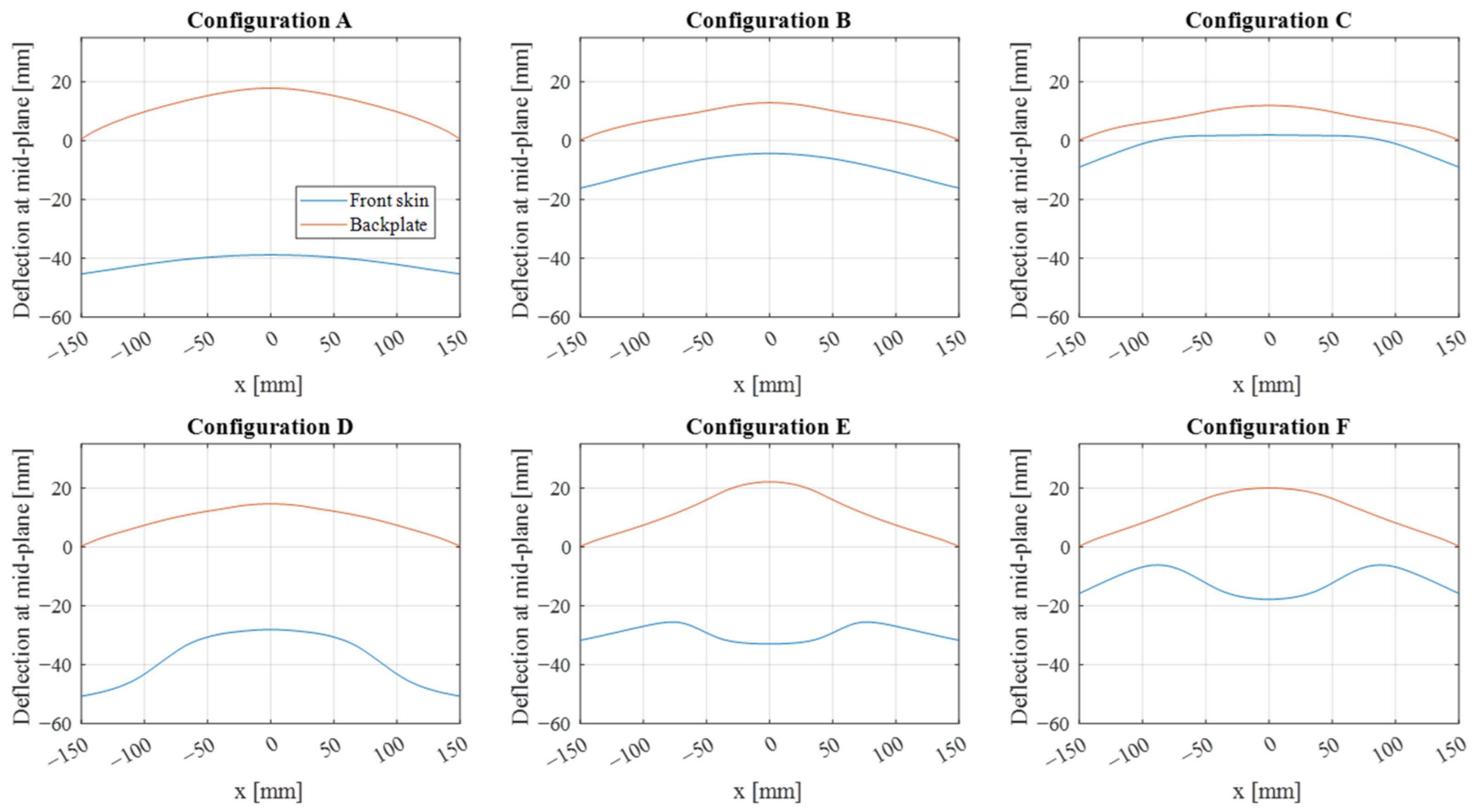
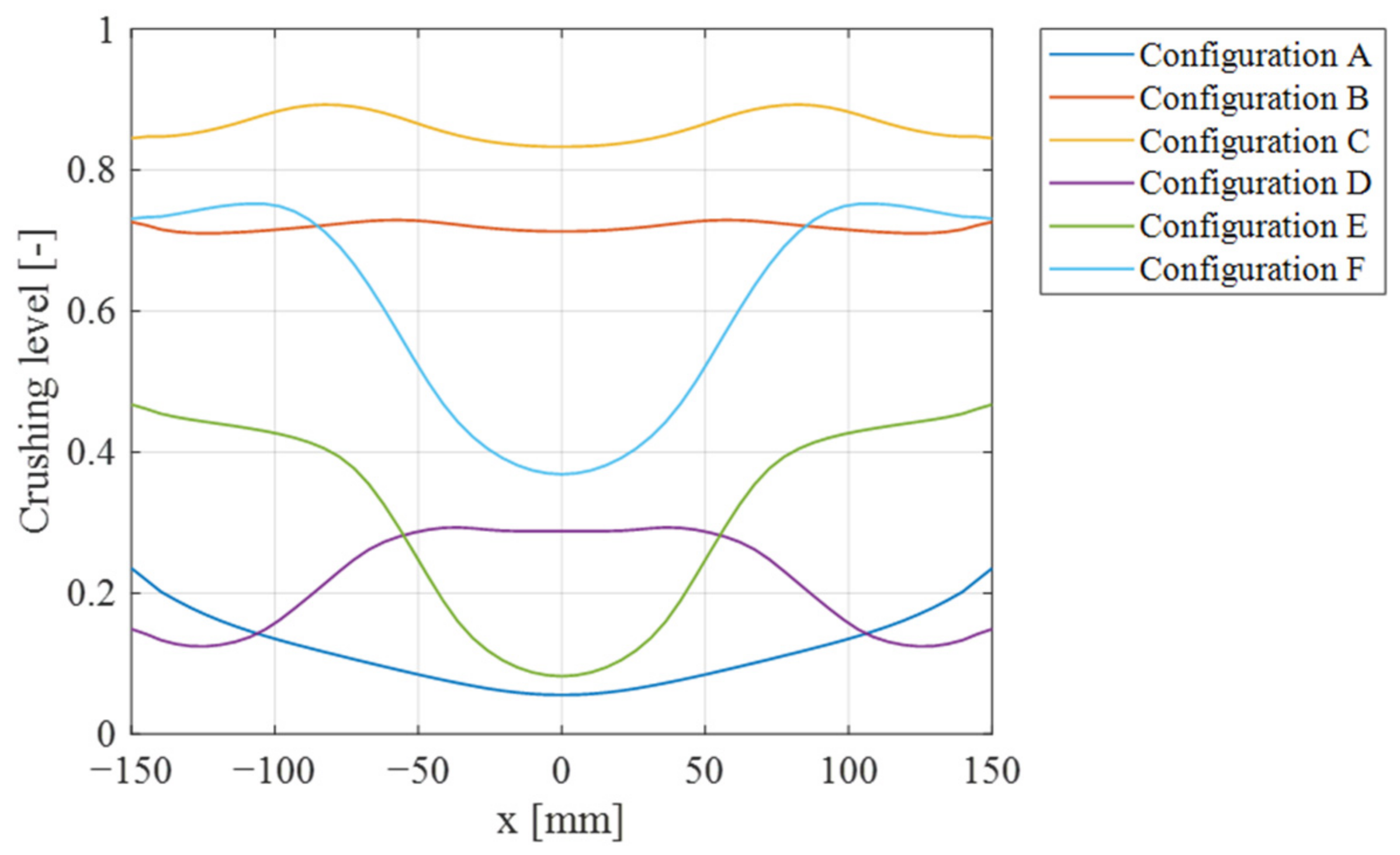
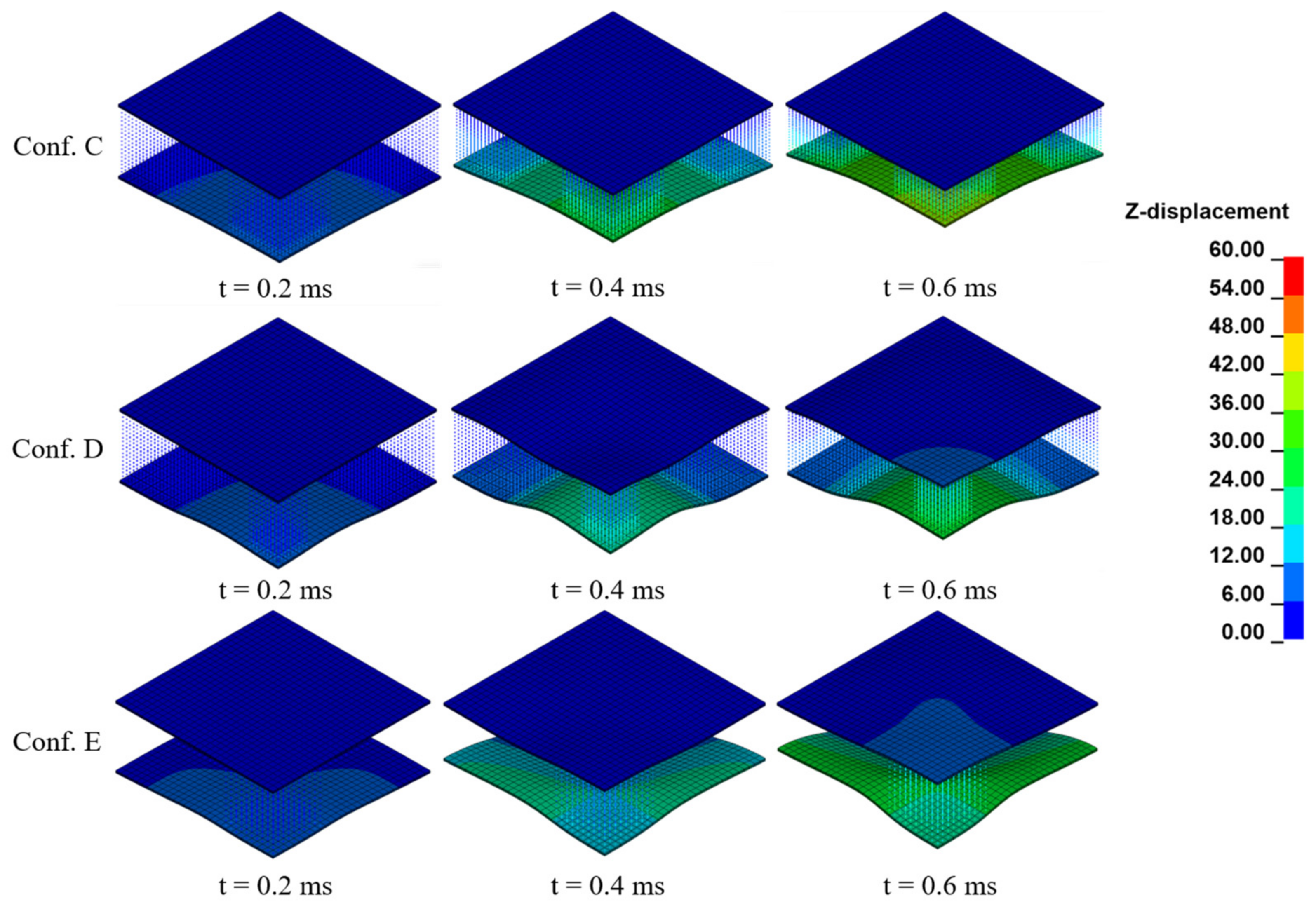
4.3.1. Influence of the Core Configuration
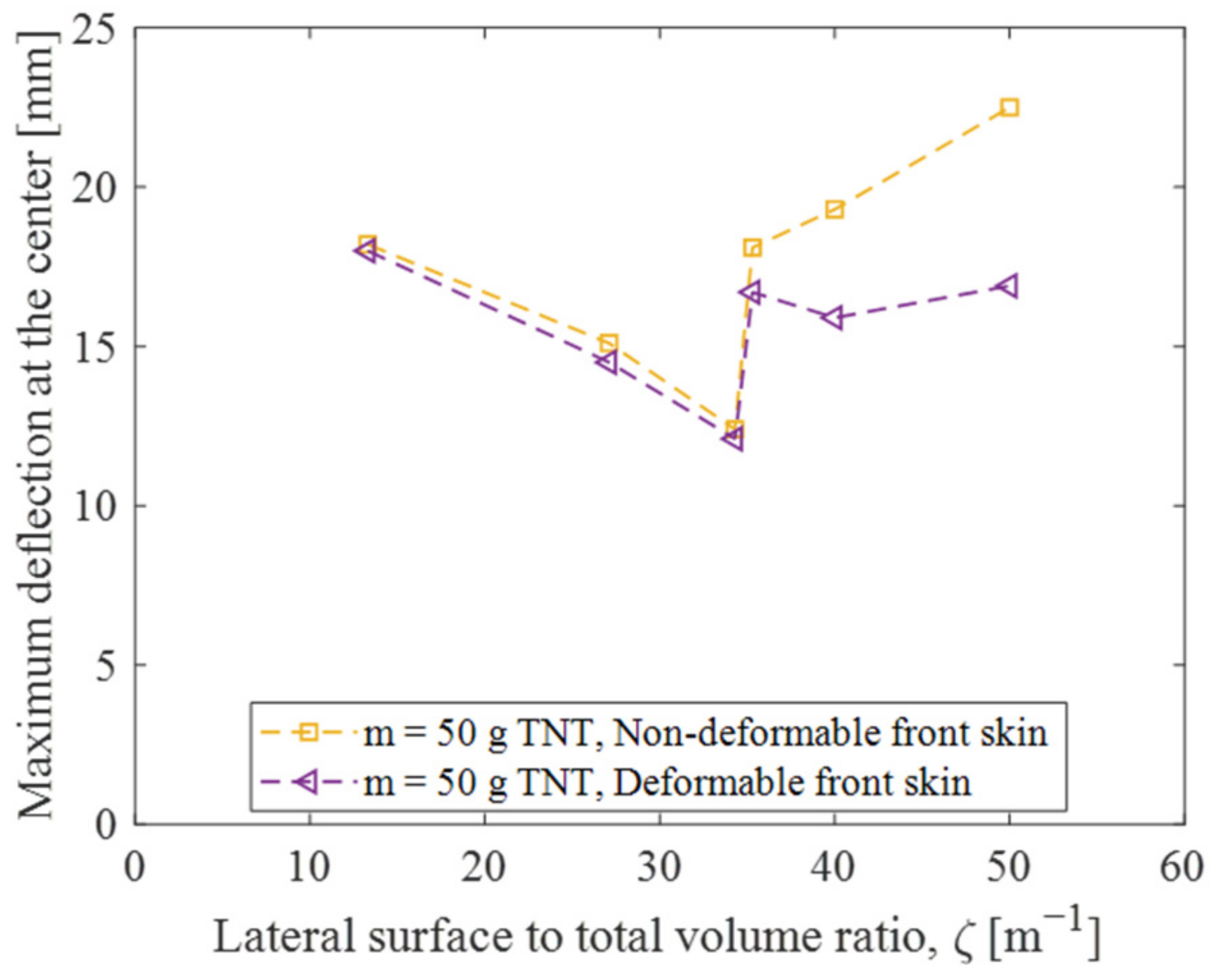
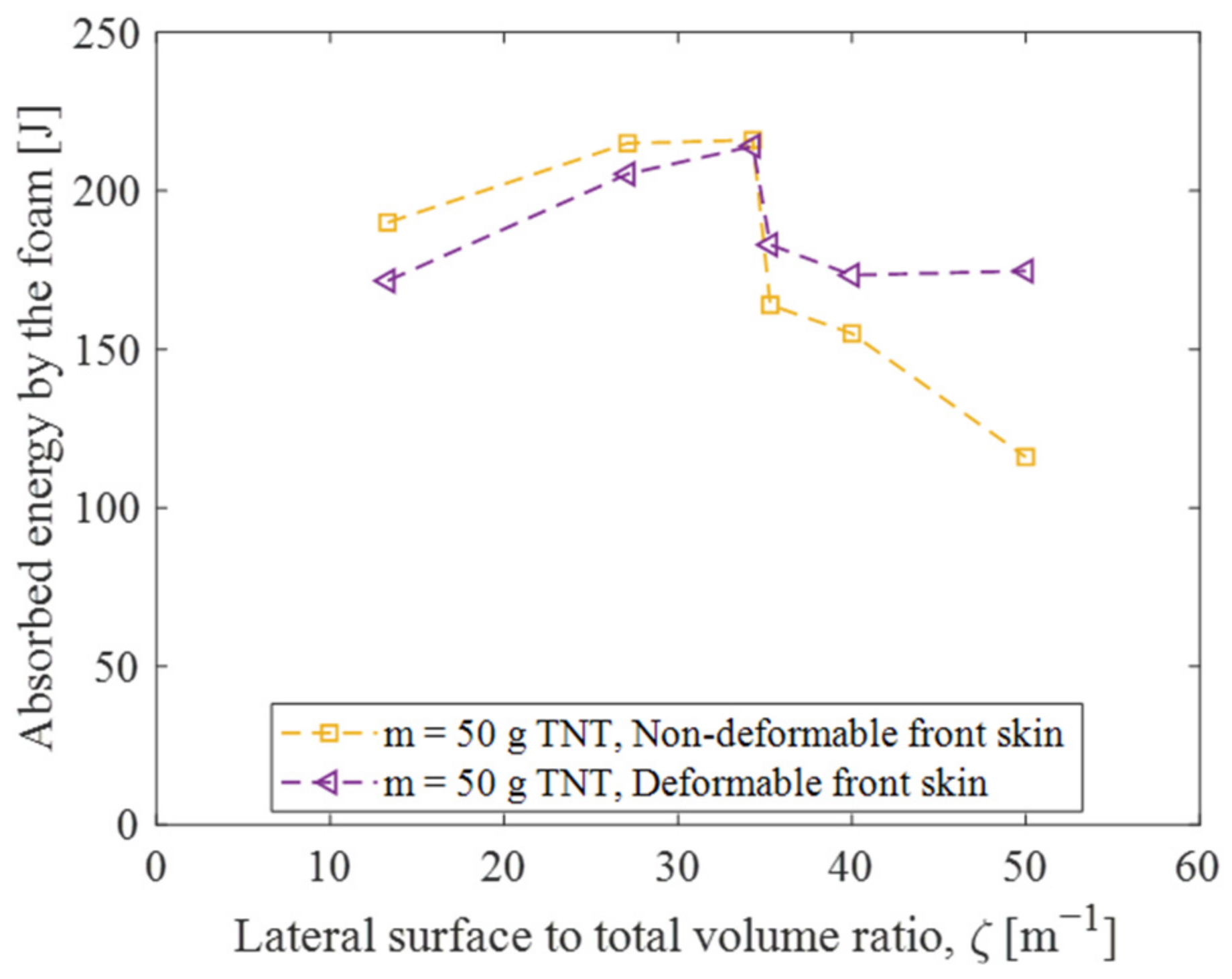
4.3.2. Influence of the Deformability of the Front Skin
5. Conclusions
- (1)
- The numerical model accurately reproduces the deflection profile at mid-span with a relative error of about 5%. Notably, the SPH approach proves to be robust in predicting the experimental results.
- (2)
- The sacrificial cladding exhibits a favorable protective effect on the aluminum plate, reducing the maximum deflection and mean permanent deformation at the center of the plate by at least 30% in configuration F and up to 70% in configuration C.
- (3)
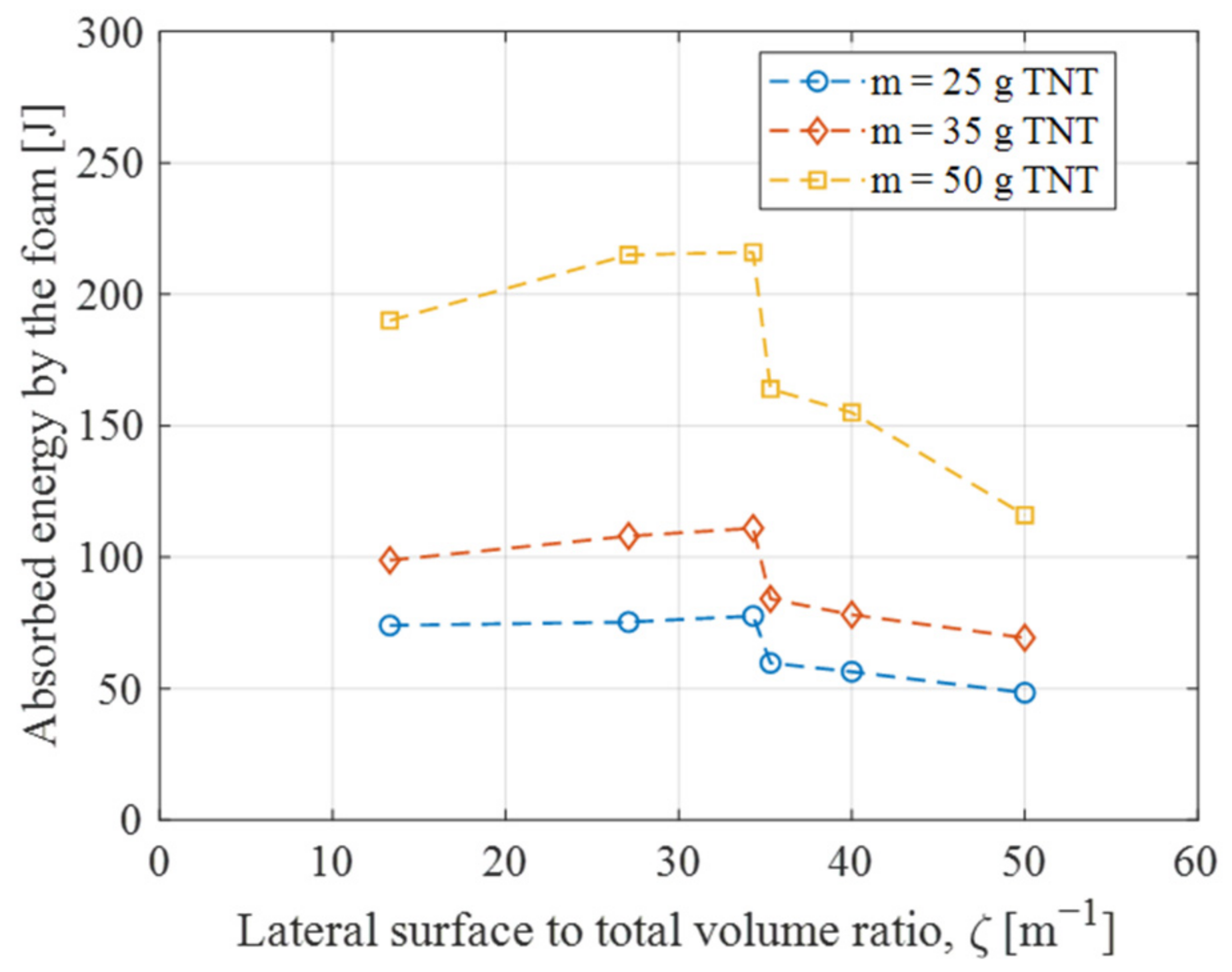
- The foam configuration significantly influences the energy dissipation of the sacrificial cladding. Specifically, increasing the ζ value, denoting the ratio of the foam’s lateral surface to its total volume, results in an enhanced protective effect of the cladding. However, when ζ exceeds an optimal value, the performance of the SC is decreased. This optimal ζ value minimizes the maximum deflection and permanent deformation while maximizing the absorbed energy by the foam. The SC’s decrease in effectiveness is primarily due to excessive front skin deformation leading to non-uniform foam crushing.
- (4)
- Non-deformable front skin has been adopted to address the influence of front skin deformability. This latter demonstrates an increased effectiveness of the SC, particularly for ζ values above the optimal value obtained when using a deformable front skin. Notably, non-deformable front skin increases maximum deflection reduction and foam energy absorption by up to approximately 30%.
- (5)
- Positive protection effects are observed for all loading conditions examined.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schunck, T.; Eckenfels, D.; Sinniger, L. Blast disruption using 3D grids/perforated plates for vehicle protection. Def. Technol. 2023, 25, 60–68. [Google Scholar] [CrossRef]
- Xu, H.B.; Chen, L.K. Mitigation effects on the reflected overpressure of blast shock with water surrounding an explosive in a confined space. Def. Technol. 2021, 17, 1071–1080. [Google Scholar] [CrossRef]
- Schunck, T.; Bastide, M.; Eckenfels, D.; Legendre, J.F. Blast mitigation by water mist: The effect of the detonation configuration. Shock Waves 2020, 30, 629–644. [Google Scholar] [CrossRef]
- Breda, C.; Kerampran, S.; Sturtzer, M.O.; Arrigoni, M.; Legendre, J.F. Analysis of planar and spherical shock-wave mitigation by wet aqueous foams. In Shock Wave Interactions; RaiNew 2017; Kontis, K., Ed.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Luo, X.; Aref, A.J.; Dargush, G.F. Optimal Design of Bundled Layered Elastic Stress Wave Attenuators. J. Comput. Civ. Eng. 2012, 26, 387–395. [Google Scholar] [CrossRef]
- Li, Y.; Lv, Z.; Wang, Y. Blast response of aluminum foam sandwich panel with double V-shaped face plate. Int. J. Impact Eng. 2020, 144, 103666. [Google Scholar] [CrossRef]
- Berger, S.; Sadot, O.; Ben-Dor, G. Experimental investigation on the shock-wave load attenuation by geometrical means. Shock Waves 2010, 20, 29–40. [Google Scholar] [CrossRef]
- Igra, O.; Falcovitz, J.; Houas, L.; Jourdan, G. Review of methods to attenuate shock/blast waves. Prog. Aerosp. Sci. 2012, 58, 1–35. [Google Scholar] [CrossRef]
- Ye, Z.Q.; Ma, G.W. Effects of Foam Claddings for Structure Protection against Blast Loads. J. Eng. Mech. 2007, 133, 41–47. [Google Scholar] [CrossRef]
- Aleyaasin, M.; Harrigan, J.J.; Reid, S.R. Air-blast response of cellular material with a face plate: An analytical-numerical approach. Int. J. Mech. Sci. 2015, 91, 64–70. [Google Scholar] [CrossRef]
- Ma, G.W.; Ye, Z.Q. Analysis of foam claddings for blast alleviation. Int. J. Impact Eng. 2007, 34, 60–70. [Google Scholar] [CrossRef]
- Lan, X.K.; Feng, S.S.; Huang, Q.; Zhou, T. Blast response of continuous-density graded cellular material based on the 3D Voronoi model. Def. Technol. 2018, 14, 433–440. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, S.; Zhao, K.; Zheng, Z.; Yang, L.; Yu, J. Blast Alleviation of Cellular Sacrificial Cladding: A Nonlinear Plastic Shock Model. Int. J. Appl. Mech. 2016, 8, 1650057. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Hao, H. Blast mitigation performance of cladding using square dome-shape kirigami folded structure as core. Int. J. Mech. Sci. 2018, 145, 83–95. [Google Scholar] [CrossRef]
- Van Paepegem, W.; Palanivelu, S.; Degrieck, J.; Vantomme, J.; Reymen, B.; Kakogiannis, D.; Van Hemelrijck, D.; Wastiels, J. Blast performance of a sacrificial cladding with composite tubes for protection of civil engineering structures. Compos. B Eng. 2014, 65, 131–146. [Google Scholar] [CrossRef]
- Vavilala, S.; Shirbhate, P.; Mandal, J.; Goel, M.D. Blast mitigation of RC column using polymeric foam. Mater. Today Proc. 2019, 26, 1347–1351. [Google Scholar] [CrossRef]
- Ousji, H.; Belkassem, B.; Louar, M.A.; Reymen, B.; Pyl, L.; Vantomme, J. Experimental Study of the Effectiveness of Sacrificial Cladding Using Polymeric Foams as Crushable Core with a Simply Supported Steel Beam. Adv. Civ. Eng. 2016, 2016, 8301517. [Google Scholar] [CrossRef]
- Langdon, G.S.; Karagiozova, D.; Theobald, M.D.; Nurick, G.N.; Lu, G.; Merrett, R.P. Fracture of aluminium foam core sacrificial cladding subjected to air-blast loading. Int. J. Impact Eng. 2010, 37, 638–651. [Google Scholar] [CrossRef]
- Kostopoulos, V.; Kalimeris, G.D.; Giannaros, E. Blast protection of steel reinforced concrete structures using composite foam-core sacrificial cladding. Compos. Sci. Technol. 2022, 230, 109330. [Google Scholar] [CrossRef]
- Rebelo, H.B.; Lecompte, D.; Cismasiu, C.; Jonet, A.; Belkassem, B.; Maazoun, A. Experimental and numerical investigation on 3D printed PLA sacrificial honeycomb cladding. Int. J. Impact. Eng. 2019, 131, 162–173. [Google Scholar] [CrossRef]
- Abada, M.; Ibrahim, A.; Jung, S.J. Improving Blast Performance of Reinforced Concrete Panels Using Sacrificial Cladding with Hybrid-Multi Cell Tubes. Modelling 2021, 2, 149–165. [Google Scholar] [CrossRef]
- Bonsmann, J.; Fourney, W.L. Mitigation of Accelerations Caused by Blast Loading Utilizing Polymeric-Coated Metallic Thin-Walled Cylinders. J. Dyn. Behav. Mater. 2015, 1, 259–274. [Google Scholar] [CrossRef]
- Palanivelu, S.; Van Paepegem, W.; Degrieck, J.; Reymen, B.; Ndambi, J.-M.; Vantomme, J.; Kakogiannis, D.; Wastiels, J.; Van Hemelrijck, D. Close-range blast loading on empty recyclable metal beverage cans for use in sacrificial cladding structure. Eng. Struct. 2011, 33, 1966–1987. [Google Scholar] [CrossRef]
- Imbalzano, G.; Linforth, S.; Ngo, T.D.; Lee, P.V.S.; Tran, P. Blast resistance of auxetic and honeycomb sandwich panels: Comparisons and parametric designs. Compos. Struct. 2018, 183, 242–261. [Google Scholar] [CrossRef]
- Patel, M.; Patel, S.; Ahmad, S. Blast analysis of efficient honeycomb sandwich structures with CFRP/Steel FML skins. Int. J. Impact Eng. 2023, 178, 104609. [Google Scholar] [CrossRef]
- Tiwari, G.; Khaire, N. Ballistic performance and energy dissipation characteristics of cylindrical honeycomb sandwich structure. Int. J. Impact Eng. 2022, 160, 104065. [Google Scholar] [CrossRef]
- Usta, F.; Türkmen, H.S.; Scarpa, F. Low-velocity impact resistance of composite sandwich panels with various types of auxetic and non-auxetic core structures. Thin-Walled Struct. 2021, 163, 107738. [Google Scholar] [CrossRef]
- Bohara, R.P.; Linforth, S.; Nguyen, T.; Ghazlan, A.; Ngo, T. Anti-blast and -impact performances of auxetic structures: A review of structures, materials, methods, and fabrications. Eng. Struct. 2023, 276, 115377. [Google Scholar] [CrossRef]
- Bohara, R.P.; Linforth, S.; Nguyen, T.; Ghazlan, A.; Ngo, T. Dual-mechanism auxetic-core protective sandwich structure under blast loading. Compos. Struct. 2022, 299, 116088. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, Y. Simplified Analysis of Foam Cladding Protected Reinforced Concrete Slabs against Blast Loadings. Int. J. Prot. Struct. 2011, 2, 351–365. [Google Scholar] [CrossRef]
- Sun, G.; Wang, E.; Zhang, J.; Li, S.; Zhang, Y.; Li, Q. Experimental study on the dynamic responses of foam sandwich panels with different facesheets and core gradients subjected to blast impulse. Int. J. Impact Eng. 2020, 135, 103327. [Google Scholar] [CrossRef]
- Shen, J.; Lu, G.; Wang, Z.; Zhao, L. Experiments on curved sandwich panels under blast loading. Int. J. Impact Eng. 2010, 37, 960–970. [Google Scholar] [CrossRef]
- Xia, X.; Zhao, W.; Wei, Z.; Wang, Z. Effects of specimen aspect ratio on the compressive properties of Mg alloy foam. Mater. Des. 2012, 42, 32–36. [Google Scholar] [CrossRef]
- Gabriel, S.; von Klemperer, C.J.; Yuen, S.C.K.; Langdon, G.S. Towards an understanding of the effect of adding a foam core on the blast performance of glass fibre reinforced epoxy laminate panels. Materials 2021, 14, 7118. [Google Scholar] [CrossRef] [PubMed]
- Sandhu, I.S.; Thangadurai, M.; Alegaonkar, P.S.; Saroha, D.R. Mitigation of Blast Induced Acceleration using open cell natural rubber and Synthetic Foam. Def. Sci. J. 2019, 69, 53–57. [Google Scholar] [CrossRef]
- Aminou, A.; Rhouma, M.B.; Belkassem, B.; Ousji, H. Blast Absorption Capacity of Brittle Mineral Foam: An Experimental Evaluation. Hormigón Y Acero Sep. 2023. [Google Scholar] [CrossRef]
- Aminou, A.; Belkassem, B.; Atoui, O.; Pyl, L.; Lecompte, D. Numerical modeling of brittle mineral foam in a sacrificial cladding under blast loading. Mech. Ind. 2023, 24, 27. [Google Scholar] [CrossRef]
- Liu, C.; Hou, J.; Hao, Y.; Hao, H.; Meng, X. Effect of high strain rate and confinement on the compressive properties of autoclaved aerated concrete. Int. J. Impact Eng. 2021, 156, 103943. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Hao, H. Mechanical properties of carbon foams under quasi-static and dynamic loading. Int. J. Mech. Sci. 2019, 161–162, 105039. [Google Scholar] [CrossRef]
- Matsagar, V.A. Comparative performance of composite sandwich panels and non-composite panels under blast loading. Mater. Struct. Mater. Et Constr. 2016, 49, 611–629. [Google Scholar] [CrossRef]
- Brekken, K.A.; Reyes, A.; Børvik, T.; Berstad, T.; Langseth, M. Sandwich panels with polymeric foam cores exposed to blast loading: An experimental and numerical investigation. Appl. Sci. 2020, 10, 9061. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, X.; Wang, X.; Du, X.; Yu, S.; Wang, Y.; Jiang, J. Protection effectiveness of sacrificial cladding for near-field blast mitigation. Int. J. Impact Eng. 2022, 170, 104361. [Google Scholar] [CrossRef]
- Louar, M.A.; Belkassem, B.; Ousji, H.; Spranghers, K.; Pyl, L.; Vantomme, J. Estimation of the Strain Rate Hardening of Aluminium Using an Inverse Method and Blast Loading. J. Dyn. Behav. Mater. 2017, 3, 347–361. [Google Scholar] [CrossRef]
- Eccles, W. Design Guidelines for Torque Controlled Tightening of Bolted Joints. SAE Int. 1993. [Google Scholar] [CrossRef]
- Aune, V.; Fagerholt, E.; Hauge, K.O.; Langseth, M.; Børvik, T. Experimental study on the response of thin aluminium and steel plates subjected to airblast loading. Int. J. Impact Eng. 2016, 90, 106–121. [Google Scholar] [CrossRef]
- Bojanowski, C. Numerical modeling of large deformations in soil structure interaction problems using FE, EFG, SPH, and MM-ALE formulations. Arch. Appl. Mech. 2014, 84, 743–755. [Google Scholar] [CrossRef]
- LSTC. Ls-Dyna® Keyword User’s Manual Volume I. July 2017. Available online: www.lstc.com (accessed on 24 February 2021).

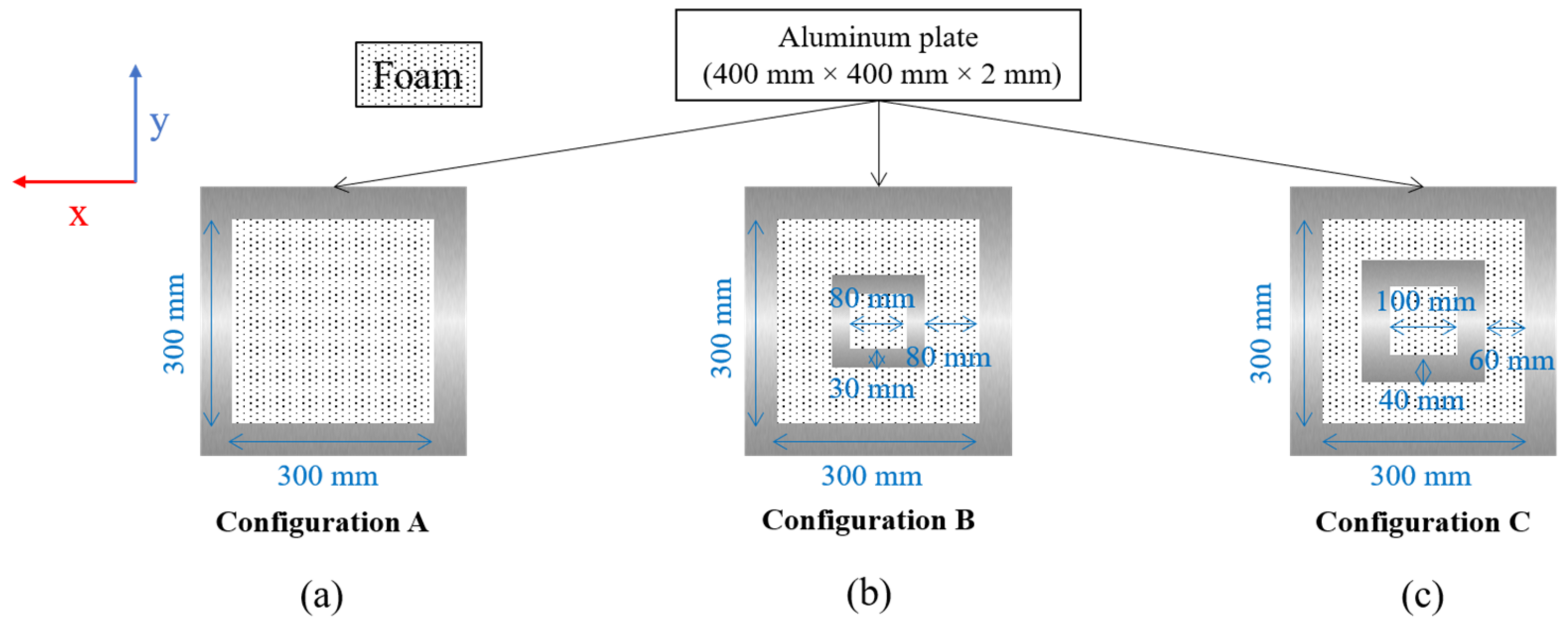
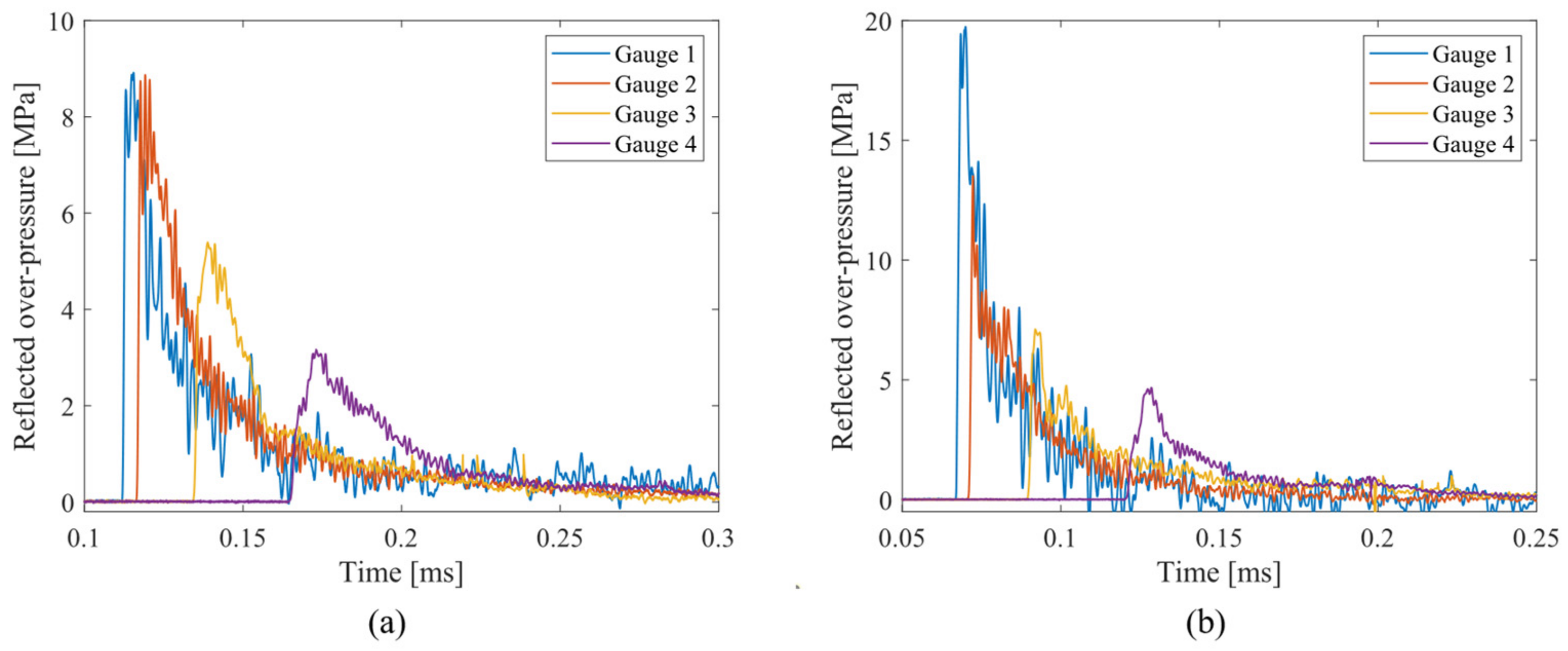
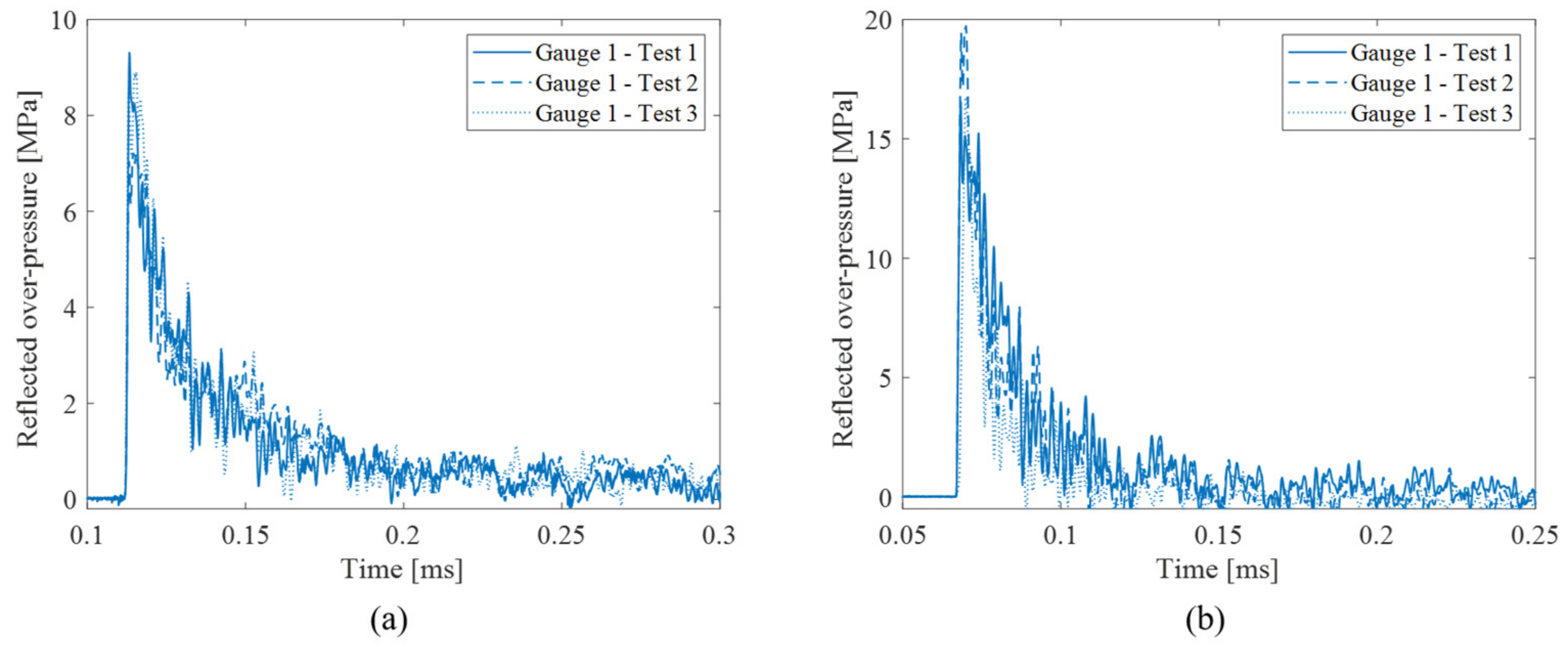
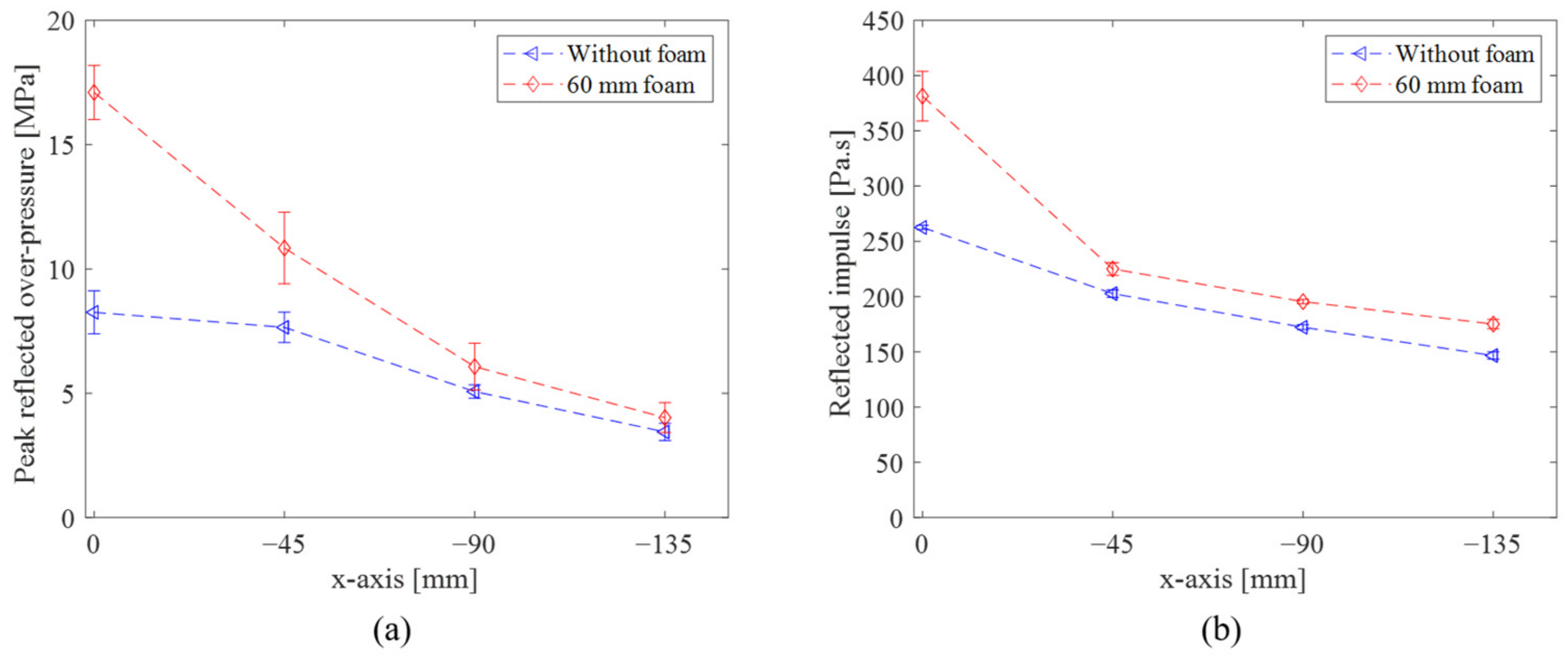

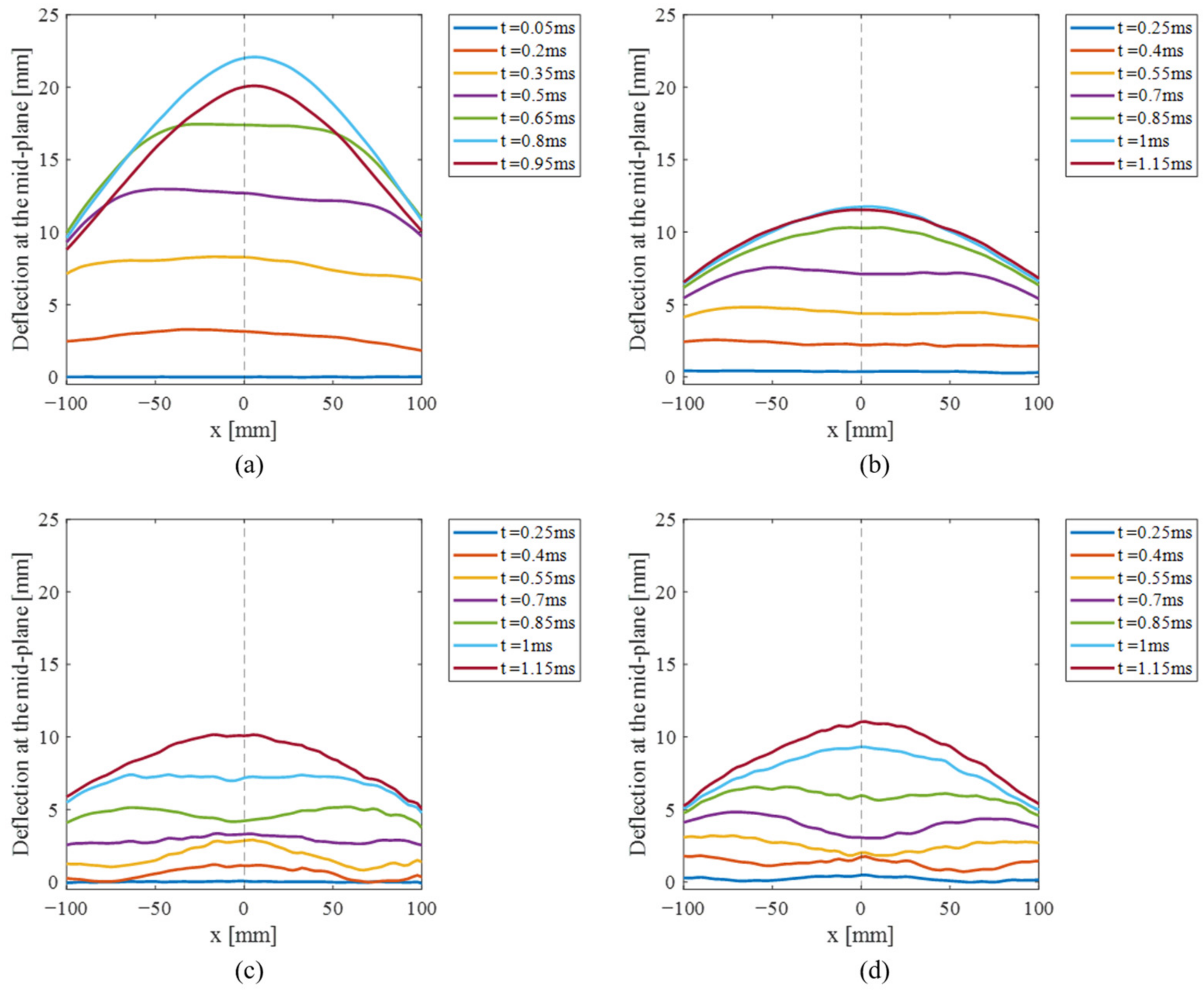







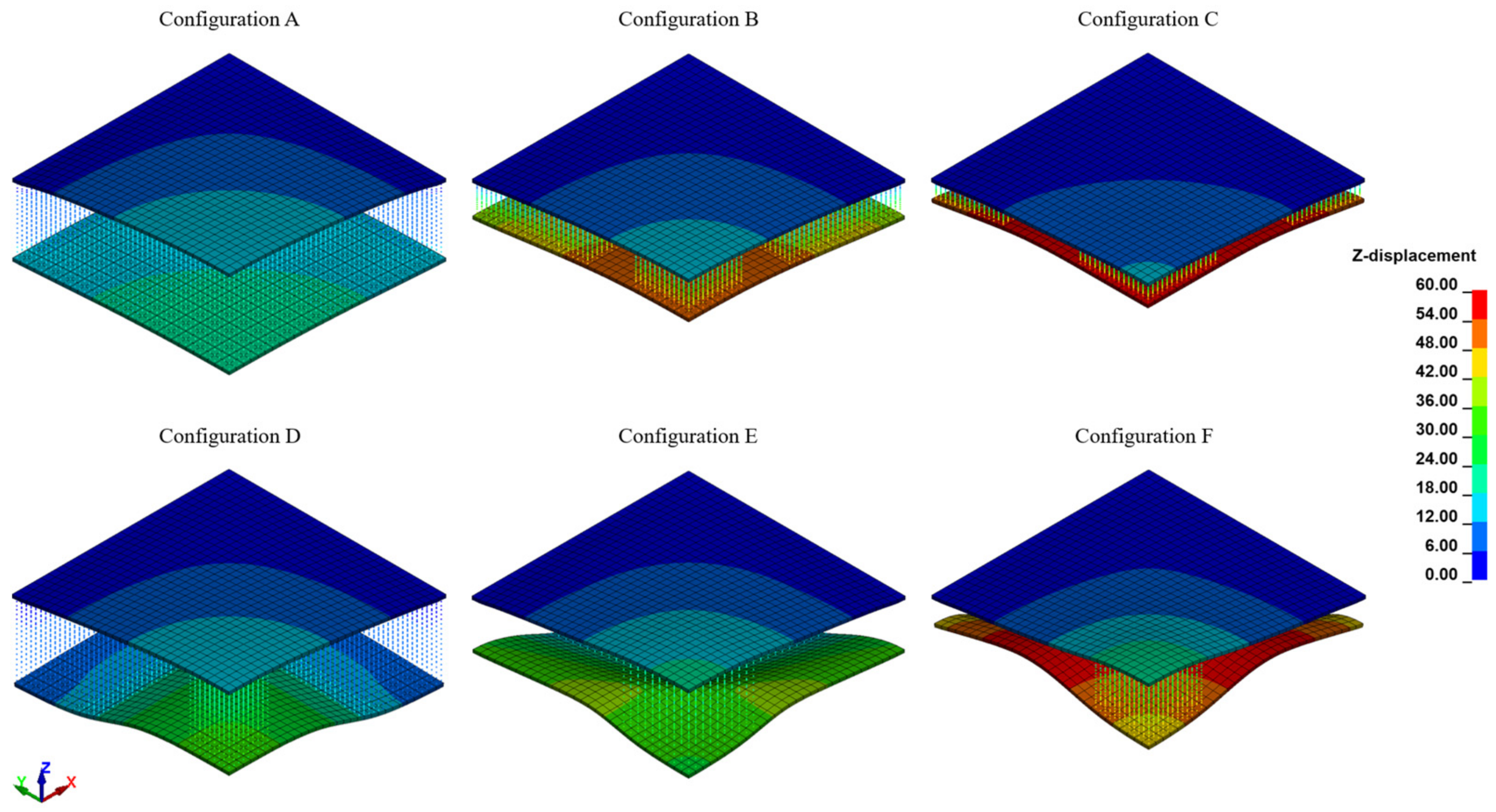
| Configuration | Foam Mass (g) | pr (MPa) | ir (Pa.s) | Maximum OPD (mm) | δ 1 (mm) |
|---|---|---|---|---|---|
| Without foam (WF) | 0 | 7.3 | 235 | 21 ± 0.7 | 19.8 ± 0.6 |
| A | 595 ± 8 | 16.3 | 389 | 11.6 ± 0.1 | 8.9 ± 0.3 |
| B | 508 ± 8 | 16.3 | 389 | 10.9 ± 0.4 | 6.1 ± 0.4 |
| C | 446 ± 5 | 16.3 | 389 | 10.6 ± 0.2 | 5.1 ± 1.1 |
| (kg/m−3) | (GPa) | (−) | (J/(kg∙K)−1) | (K−1) | (ms−1) | (K) | (−) |
| 2710 | 69 | 0.33 | 899 | 1.2 × 10−5 | 1 | 293 | 1 |
| (GPa) | (GPa) | (−) | (GPa) | (−) | (−) | (−) | (−) |
| 0.065 | 0.014 | 0.014 | 0.025 | 3324 | 0.019 | 533 | 0.36 |
| Configuration | Foam Mass (g) | (g) | (mm) | OPDNum (mm) | OPDExp (mm) | δNum (mm) | δExp (mm) | Internal Energy (J) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| FS | Foam | BP | ||||||||
| WF | 0 | 25 | 250 | 20.1 | 21 ± 0.7 | 17.6 | 19.8 ± 0.6 | 0 | 0 | 48.8 |
| A | 594 | 188 | 11.3 | 11.6 ± 0.1 | 8.2 | 8.9 ± 0.3 | 0.9 | 74 | 15.8 | |
| B | 507 | 10.7 | 10.9 ± 0.4 | 7.1 | 6.1 ± 0.4 | 2.5 | 75.3 | 12.4 | ||
| C | 446 | 9.2 | 10.6 ± 0.2 | 5.5 | 5.1 ± 1.1 | 4 | 77.6 | 9.2 | ||
| D | 404 | 12.8 | - | 10 | - | 9.2 | 59.7 | 16.5 | ||
| E | 330 | 13 | - | 10.4 | - | 10.6 | 56.4 | 17.1 | ||
| F | 211 | 14.4 | - | 12.3 | - | 18.7 | 48.4 | 17.9 | ||
| WF | 0 | 35 | 250 | 25.7 | - | 24.3 | - | 0 | 0 | 82.7 |
| A | 594 | 188 | 14.4 | - | 11.1 | - | 1.4 | 98.8 | 26.4 | |
| B | 507 | 12.4 | - | 10.2 | - | 4.2 | 108 | 15.1 | ||
| C | 446 | 10.5 | - | 8.2 | - | 7.3 | 111 | 10.1 | ||
| D | 404 | 15.6 | - | 13.4 | - | 17.4 | 84.1 | 26.3 | ||
| E | 330 | 16 | - | 14.1 | - | 18.4 | 78.1 | 30.2 | ||
| F | 211 | 18 | - | 16.5 | - | 29.8 | 69.3 | 29.7 | ||
| WF | 0 | 50 | 250 | 30.9 | - | 29.9 | - | 0 | 0 | 123 |
| A | 594 | 188 | 18.2 | - | 16.3 | - | 3.7 | 190 | 46.2 | |
| B | 507 | 15.1 | - | 13.1 | - | 13.2 | 215 | 27.1 | ||
| C | 446 | 12.4 | - | 10.5 | - | 20 | 216 | 19.2 | ||
| D | 404 | 18.1 | - | 17.4 | - | 36.4 | 164 | 42.9 | ||
| E | 330 | 19.3 | - | 19.1 | - | 36.9 | 155 | 51.4 | ||
| F | 211 | 22.5 | - | 21.8 | - | 75.4 | 116 | 53.9 | ||
| WF | 0 | 50 | 250 | 30.9 | - | 29.9 | - | 0 | 0 | 123 |
| A (Non-Def) | 594 | 188 | 18 | - | 16.2 | - | 0 | 171.6 | 43.1 | |
| B (Non-Def) | 507 | 14.5 | - | 12.6 | - | 0 | 205.3 | 21.5 | ||
| C (Non-Def) | 446 | 12.1 | - | 10.1 | - | 0 | 214.1 | 14.1 | ||
| D (Non-Def) | 404 | 16.7 | - | 15.1 | - | 0 | 183 | 38.9 | ||
| E (Non-Def) | 330 | 15.9 | - | 14.3 | - | 0 | 173.4 | 45.5 | ||
| F (Non-Def) | 211 | 16.9 | - | 15.3 | - | 0 | 174.7 | 48.1 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aminou, A.; Ben Rhouma, M.; Belkassem, B.; Ousji, H.; Pyl, L.; Lecompte, D. Experimental and Numerical Evaluation of Calcium-Silicate-Based Mineral Foam for Blast Mitigation. Appl. Sci. 2024, 14, 9656. https://doi.org/10.3390/app14219656
Aminou A, Ben Rhouma M, Belkassem B, Ousji H, Pyl L, Lecompte D. Experimental and Numerical Evaluation of Calcium-Silicate-Based Mineral Foam for Blast Mitigation. Applied Sciences. 2024; 14(21):9656. https://doi.org/10.3390/app14219656
Chicago/Turabian StyleAminou, Aldjabar, Mohamed Ben Rhouma, Bachir Belkassem, Hamza Ousji, Lincy Pyl, and David Lecompte. 2024. "Experimental and Numerical Evaluation of Calcium-Silicate-Based Mineral Foam for Blast Mitigation" Applied Sciences 14, no. 21: 9656. https://doi.org/10.3390/app14219656
APA StyleAminou, A., Ben Rhouma, M., Belkassem, B., Ousji, H., Pyl, L., & Lecompte, D. (2024). Experimental and Numerical Evaluation of Calcium-Silicate-Based Mineral Foam for Blast Mitigation. Applied Sciences, 14(21), 9656. https://doi.org/10.3390/app14219656







