Systematic Analysis of Low-Precision Training in Deep Neural Networks: Factors Influencing Matrix Computations
Abstract
:1. Introduction
2. Related Work
2.1. Quantization
2.2. QAT
2.3. FQT
3. Low Precision in Matrix Calculations
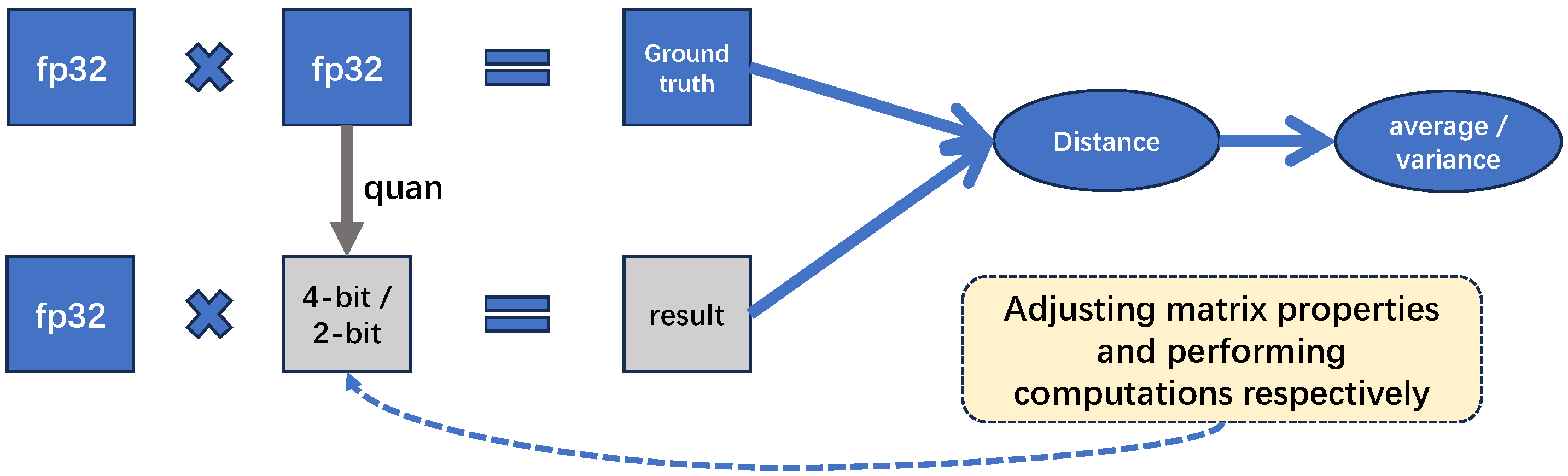
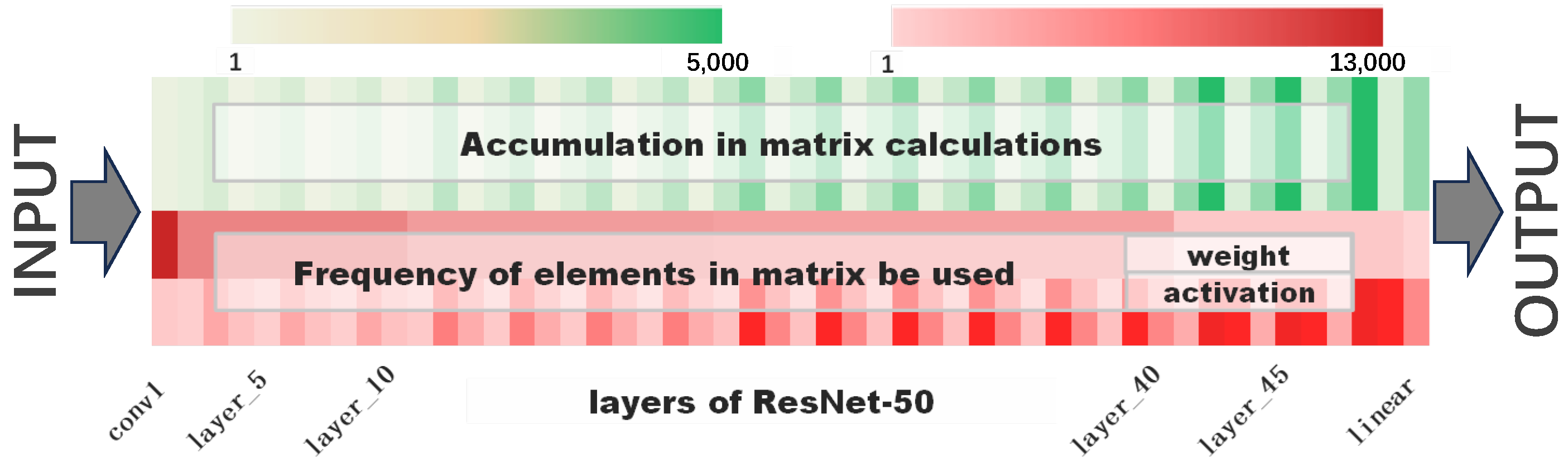
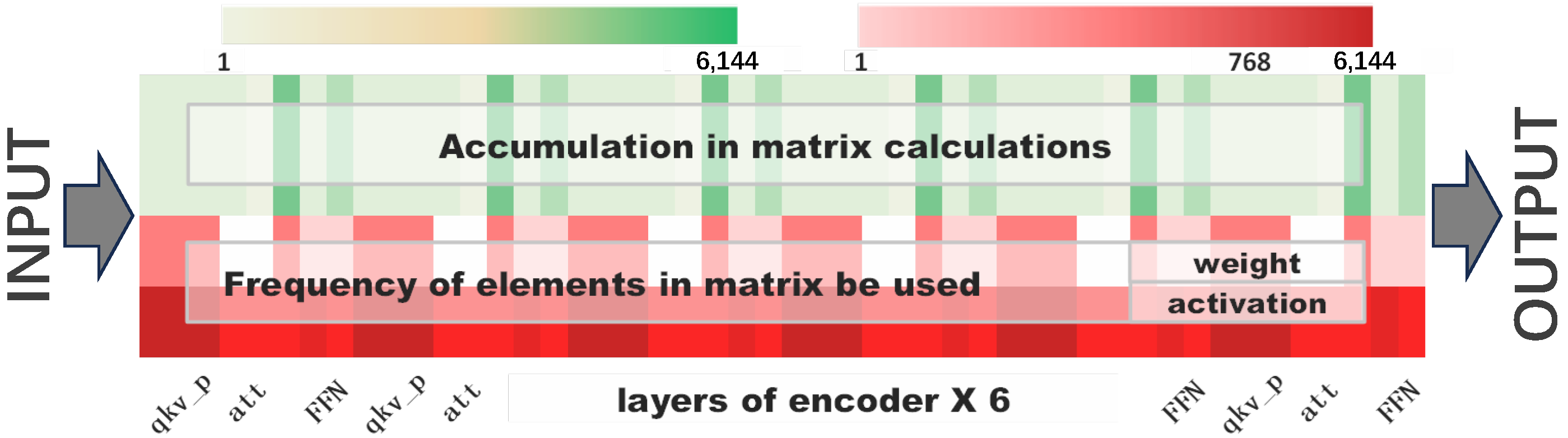
3.1. Accumulation in Matrix Calculations
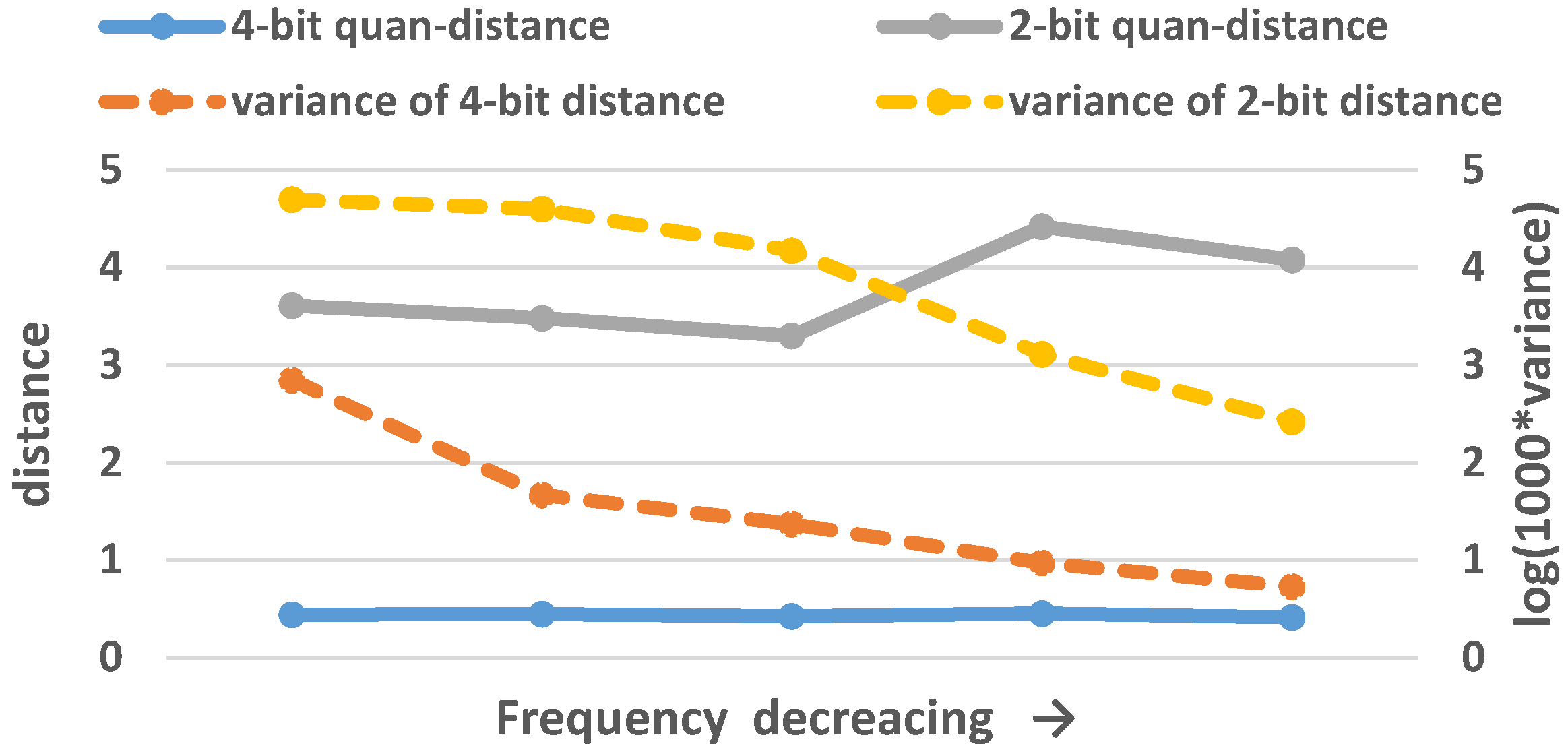
3.2. Frequency of Elements in the Matrix Used
3.3. Depth of Matrix in DNN
4. Experimental Results on DNNs
4.1. Experimental Setup
- A: The training bit-width is set based on the number of Accumulations in matrix multiplication during computation.
- F: The training bit-width is set based on the Frequency with which elements in the matrix are used during computation.
- D: The training bit-width is set based on the Depth of the matrix within the model.
- U: Regardless of the variations in the comparative factors, assign the same training bit-width to all layers (the method proposed in [34]).
- C+: Set the training bit-width according to the comparative factors, with a positive correlation to the comparative factors.
- C−: Set the training bit-width according to the comparative factors, with a negative correlation to the comparative factors.
- R: Randomly assign training bit-widths to each layer.
4.2. Performance on Commonly Used Models
4.3. In-Depth Evaluation on Customized Models
5. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DNN | Deep Neural Network |
| QAT | Quantization-Aware Training |
| FQT | Full Quantization Training |
References
- Gholami, A.; Yao, Z.; Kim, S.; Hooper, C.; Mahoney, M.W.; Keutzer, K. Ai and memory wall. arXiv 2024, arXiv:2403.14123. [Google Scholar] [CrossRef]
- Lewis, M.; Bhosale, S.; Dettmers, T.; Goyal, N.; Zettlemoyer, L. Base layers: Simplifying training of large, sparse models. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 6265–6274. [Google Scholar]
- Courbariaux, M.; Bengio, Y.; David, J.P. Binaryconnect: Training deep neural networks with binary weights during propagations. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2015; Volume 28. [Google Scholar]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and training of neural networks for efficient integer-arithmetic-only inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2704–2713. [Google Scholar]
- Lin, X.; Zhao, C.; Pan, W. Towards accurate binary convolutional neural network. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Yang, H.; Duan, L.; Chen, Y.; Li, H. BSQ: Exploring bit-level sparsity for mixed-precision neural network quantization. arXiv 2021, arXiv:2102.10462. [Google Scholar]
- Van Baalen, M.; Louizos, C.; Nagel, M.; Amjad, R.A.; Wang, Y.; Blankevoort, T.; Welling, M. Bayesian bits: Unifying quantization and pruning. Adv. Neural Inf. Process. Syst. 2020, 33, 5741–5752. [Google Scholar]
- Chen, J.; Gai, Y.; Yao, Z.; Mahoney, M.W.; Gonzalez, J.E. A statistical framework for low-bitwidth training of deep neural networks. Adv. Neural Inf. Process. Syst. 2020, 33, 883–894. [Google Scholar]
- Yang, C.; Wu, Z.; Chee, J.; De Sa, C.; Udell, M. How Low Can We Go: Trading Memory for Error in Low-Precision Training. arXiv 2021, arXiv:2106.09686. [Google Scholar]
- Chen, J.; Zheng, L.; Yao, Z.; Wang, D.; Stoica, I.; Mahoney, M.; Gonzalez, J. Actnn: Reducing training memory footprint via 2-bit activation compressed training. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 1803–1813. [Google Scholar]
- Köster, U.; Webb, T.; Wang, X.; Nassar, M.; Bansal, A.K.; Constable, W.; Elibol, O.; Gray, S.; Hall, S.; Hornof, L.; et al. Flexpoint: An adaptive numerical format for efficient training of deep neural networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Fox, S.; Rasoulinezhad, S.; Faraone, J.; Boland, D.; Leong, P. A block minifloat representation for training deep neural networks. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020; pp. 1–16. [Google Scholar]
- Zhou, S.; Wu, Y.; Ni, Z.; Zhou, X.; Wen, H.; Zou, Y. Dorefa-net: Training low bitwidth convolutional neural networks with low bitwidth gradients. arXiv 2016, arXiv:1606.06160. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv 2015, arXiv:1510.00149. [Google Scholar]
- Cai, H.; Gan, C.; Wang, T.; Zhang, Z.; Han, S. Once for All: Train One Network and Specialize it for Efficient Deployment. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020; pp. 1–15. [Google Scholar]
- Yao, Z.; Dong, Z.; Zheng, Z.; Gholami, A.; Yu, J.; Tan, E.; Wang, L.; Huang, Q.; Wang, Y.; Mahoney, M.; et al. Hawq-v3: Dyadic neural network quantization. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 11875–11886. [Google Scholar]
- Banner, R.; Nahshan, Y.; Soudry, D. Post training 4-bit quantization of convolutional networks for rapid-deployment. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Kim, M.; Smaragdis, P. Bitwise neural networks. arXiv 2016, arXiv:1601.06071. [Google Scholar]
- Li, F.; Liu, B.; Wang, X.; Zhang, B.; Yan, J. Ternary weight networks. arXiv 2016, arXiv:1605.04711. [Google Scholar]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. Xnor-net: Imagenet classification using binary convolutional neural networks. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016; pp. 525–542. [Google Scholar]
- Baskin, C.; Liss, N.; Schwartz, E.; Zheltonozhskii, E.; Giryes, R.; Bronstein, A.M.; Mendelson, A. Uniq: Uniform noise injection for non-uniform quantization of neural networks. ACM Trans. Comput. Syst. (TOCS) 2021, 37, 1–15. [Google Scholar] [CrossRef]
- Widrow, B.; Kollar, I.; Liu, M.C. Statistical theory of quantization. IEEE Trans. Instrum. Meas. 1996, 45, 353–361. [Google Scholar] [CrossRef]
- Qin, H.; Gong, R.; Liu, X.; Bai, X.; Song, J.; Sebe, N. Binary neural networks: A survey. Pattern Recognit. 2020, 105, 107281. [Google Scholar] [CrossRef]
- Wu, S.; Li, G.; Chen, F.; Shi, L. Training and inference with integers in deep neural networks. arXiv 2018, arXiv:1802.04680. [Google Scholar]
- Zhuang, B.; Shen, C.; Tan, M.; Liu, L.; Reid, I. Towards effective low-bitwidth convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7920–7928. [Google Scholar]
- Martinez, B.; Yang, J.; Bulat, A.; Tzimiropoulos, G. Training binary neural networks with real-to-binary convolutions. arXiv 2020, arXiv:2003.11535. [Google Scholar]
- Chakrabarti, A.; Moseley, B. Backprop with approximate activations for memory-efficient network training. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Yang, G.; Zhang, T.; Kirichenko, P.; Bai, J.; Wilson, A.G.; De Sa, C. SWALP: Stochastic weight averaging in low precision training. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 7015–7024. [Google Scholar]
- Choi, J.; Wang, Z.; Venkataramani, S.; Chuang, P.I.J.; Srinivasan, V.; Gopalakrishnan, K. Pact: Parameterized clipping activation for quantized neural networks. arXiv 2018, arXiv:1805.06085. [Google Scholar]
- Das, D.; Mellempudi, N.; Mudigere, D.; Kalamkar, D.; Avancha, S.; Banerjee, K.; Sridharan, S.; Vaidyanathan, K.; Kaul, B.; Georganas, E.; et al. Mixed precision training of convolutional neural networks using integer operations. arXiv 2018, arXiv:1802.00930. [Google Scholar]
- Zhang, D.; Yang, J.; Ye, D.; Hua, G. Lq-nets: Learned quantization for highly accurate and compact deep neural networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 365–382. [Google Scholar]
- Esser, S.K.; McKinstry, J.L.; Bablani, D.; Appuswamy, R.; Modha, D.S. Learned step size quantization. arXiv 2019, arXiv:1902.08153. [Google Scholar]
- Gholami, A.; Kwon, K.; Wu, B.; Tai, Z.; Yue, X.; Jin, P.; Zhao, S.; Keutzer, K. Squeezenext: Hardware-aware neural network design. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1638–1647. [Google Scholar]
- Banner, R.; Hubara, I.; Hoffer, E.; Soudry, D. Scalable methods for 8-bit training of neural networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Zhu, F.; Gong, R.; Yu, F.; Liu, X.; Wang, Y.; Li, Z.; Yang, X.; Yan, J. Towards unified int8 training for convolutional neural network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 1969–1979. [Google Scholar]
- Lee, S.; Park, J.; Jeon, D. Toward Efficient Low-Precision Training: Data Format Optimization and Hysteresis Quantization. In Proceedings of the International Conference on Learning Representations, Virtual, 3–7 May 2021. [Google Scholar]
- Yang, Y.; Deng, L.; Wu, S.; Yan, T.; Xie, Y.; Li, G. Training high-performance and large-scale deep neural networks with full 8-bit integers. Neural Netw. 2020, 125, 70–82. [Google Scholar] [CrossRef]
- Wang, N.; Choi, J.; Brand, D.; Chen, C.Y.; Gopalakrishnan, K. Training deep neural networks with 8-bit floating point numbers. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Xi, H.; Li, C.; Chen, J.; Zhu, J. Training Transformers with 4-bit Integers. arXiv 2023, arXiv:2306.11987. [Google Scholar]
- Han, R.; Si, M.; Demmel, J.; You, Y. Dynamic scaling for low-precision learning. In Proceedings of the 26th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, Virtual, 27 February 2021; pp. 480–482. [Google Scholar]
- Micikevicius, P.; Narang, S.; Alben, J.; Diamos, G.; Elsen, E.; Garcia, D.; Ginsburg, B.; Houston, M.; Kuchaiev, O.; Venkatesh, G.; et al. Mixed precision training. arXiv 2017, arXiv:1710.03740. [Google Scholar]
- Sun, X.; Choi, J.; Chen, C.Y.; Wang, N.; Venkataramani, S.; Srinivasan, V.V.; Cui, X.; Zhang, W.; Gopalakrishnan, K. Hybrid 8-bit floating point (HFP8) training and inference for deep neural networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Sun, X.; Wang, N.; Chen, C.Y.; Ni, J.; Agrawal, A.; Cui, X.; Venkataramani, S.; El Maghraoui, K.; Srinivasan, V.V.; Gopalakrishnan, K. Ultra-low precision 4-bit training of deep neural networks. Adv. Neural Inf. Process. Syst. 2020, 33, 1796–1807. [Google Scholar]
- Ma, Z.; He, J.; Qiu, J.; Cao, H.; Wang, Y.; Sun, Z.; Zheng, L.; Wang, H.; Tang, S.; Zheng, T.; et al. BaGuaLu: Targeting brain scale pretrained models with over 37 million cores. In Proceedings of the 27th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, Seoul, Republic of Korea, 2–6 April 2022; pp. 192–204. [Google Scholar]
- Drumond, M.; Lin, T.; Jaggi, M.; Falsafi, B. Training dnns with hybrid block floating point. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Fu, Y.; Guo, H.; Li, M.; Yang, X.; Ding, Y.; Chandra, V.; Lin, Y.L. CPT: Efficient Deep Neural Network Training via Cyclic Precision. In Proceedings of the 9th International Conference on Learning Representations 2021 (ICLR 2021), Virtual, 3–7 May 2021; pp. 1–14. [Google Scholar]
- Wikipedia Contributors. Propagation of Uncertainty—Wikipedia, The Free Encyclopedia. 2024. Available online: https://en.wikipedia.org/wiki/Propagation_of_uncertainty (accessed on 22 October 2024).
- Raghu, M.; Poole, B.; Kleinberg, J.; Ganguli, S.; Sohl-Dickstein, J. On the expressive power of deep neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 2847–2854. [Google Scholar]
- He, C.; Li, S.; Soltanolkotabi, M.; Avestimehr, S. Pipetransformer: Automated elastic pipelining for distributed training of transformers. arXiv 2021, arXiv:2102.03161. [Google Scholar]
- Raghu, M.; Gilmer, J.; Yosinski, J.; Sohl-Dickstein, J. Svcca: Singular vector canonical correlation analysis for deep learning dynamics and interpretability. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Rahaman, N.; Baratin, A.; Arpit, D.; Draxler, F.; Lin, M.; Hamprecht, F.; Bengio, Y.; Courville, A. On the spectral bias of neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 5301–5310. [Google Scholar]
- Xu, Z.Q.J.; Zhang, Y.; Luo, T.; Xiao, Y.; Ma, Z. Frequency principle: Fourier analysis sheds light on deep neural networks. arXiv 2019, arXiv:1901.06523. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images. Master’s Thesis, University of Tront, Toronto, ON, Canada, 2009. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Merity, S.; Xiong, C.; Bradbury, J.; Socher, R. Pointer Sentinel Mixture Models. In Proceedings of the International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016; pp. 1–13. [Google Scholar]
- Graves, A.; Graves, A. Long short-term memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- Marcus, M.P.; Marcinkiewicz, M.A. Building a Large Annotated Corpus of English: The Penn Treebank. Comput. Linguist. 1993, 19, 313–330. [Google Scholar]
- Wang, X.; Yu, F.; Dou, Z.Y.; Darrell, T.; Gonzalez, J.E. Skipnet: Learning dynamic routing in convolutional networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 409–424. [Google Scholar]
- Baevski, A.; Auli, M. Adaptive Input Representations for Neural Language Modeling. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018; pp. 1–13. [Google Scholar]
- Merity, S.; Keskar, N.S.; Socher, R. Regularizing and optimizing LSTM language models. arXiv 2017, arXiv:1708.02182. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Wei, X.; Zhang, Y.; Li, Y.; Zhang, X.; Gong, R.; Guo, J.; Liu, X. Outlier Suppression+: Accurate quantization of large language models by equivalent and effective shifting and scaling. In Proceedings of the 2023 Conference on Empirical Methods in Natural Language Processing, Singapore, 6–10 December 2023; pp. 1648–1665. [Google Scholar]
- Guo, C.; Tang, J.; Hu, W.; Leng, J.; Zhang, C.; Yang, F.; Liu, Y.; Guo, M.; Zhu, Y. OliVe: Accelerating Large Language Models via Hardware-friendly Outlier-Victim Pair Quantization. In Proceedings of the 50th Annual International Symposium on Computer Architecture, Orlando, FL, USA, 17–21 June 2023; pp. 1–15. [Google Scholar]
- Guo, C.; Zhang, C.; Leng, J.; Liu, Z.; Yang, F.; Liu, Y.; Guo, M.; Zhu, Y. Ant: Exploiting adaptive numerical data type for low-bit deep neural network quantization. In Proceedings of the 2022 55th IEEE/ACM International Symposium on Microarchitecture (MICRO), Chicago, IL, USA, 1–5 October 2022; pp. 1414–1433. [Google Scholar]
- Frantar, E.; Ashkboos, S.; Hoefler, T.; Alistarh, D. GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023; pp. 1–16. [Google Scholar]
- Ali, R.; Tang, O.Y.; Connolly, I.D.; Fridley, J.S.; Shin, J.H.; Sullivan, P.L.Z.; Cielo, D.; Oyelese, A.A.; Doberstein, C.E.; Telfeian, A.E.; et al. Performance of ChatGPT, GPT-4, and Google Bard on a neurosurgery oral boards preparation question bank. Neurosurgery 2023, 93, 1090–1098. [Google Scholar] [CrossRef]
- Erhan, D.; Courville, A.; Bengio, Y.; Vincent, P. Why does unsupervised pre-training help deep learning? In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Chia Laguna Resort, Sardinia, Italy, 13–15 May 2010; pp. 201–208. [Google Scholar]
- Nichol, A.Q.; Dhariwal, P. Improved denoising diffusion probabilistic models. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 8162–8171. [Google Scholar]
- Fedus, W.; Zoph, B.; Shazeer, N. Switch transformers: Scaling to trillion parameter models with simple and efficient sparsity. J. Mach. Learn. Res. 2022, 23, 1–39. [Google Scholar]
- Liu, S.y.; Liu, Z.; Huang, X.; Dong, P.; Cheng, K.T. LLM-FP4: 4-Bit Floating-Point Quantized Transformers. In Proceedings of the 2023 Conference on Empirical Methods in Natural Language Processing, Singapore, 6–10 December 2023; pp. 592–605. [Google Scholar]
- Fu, F.; Hu, Y.; He, Y.; Jiang, J.; Shao, Y.; Zhang, C.; Cui, B. Don’t waste your bits! Squeeze activations and gradients for deep neural networks via tinyscript. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 3304–3314. [Google Scholar]
- Ma, S.; Wang, H.; Ma, L.; Wang, L.; Wang, W.; Huang, S.; Dong, L.; Wang, R.; Xue, J.; Wei, F. The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits. arXiv 2024, arXiv:2402.17764. [Google Scholar]



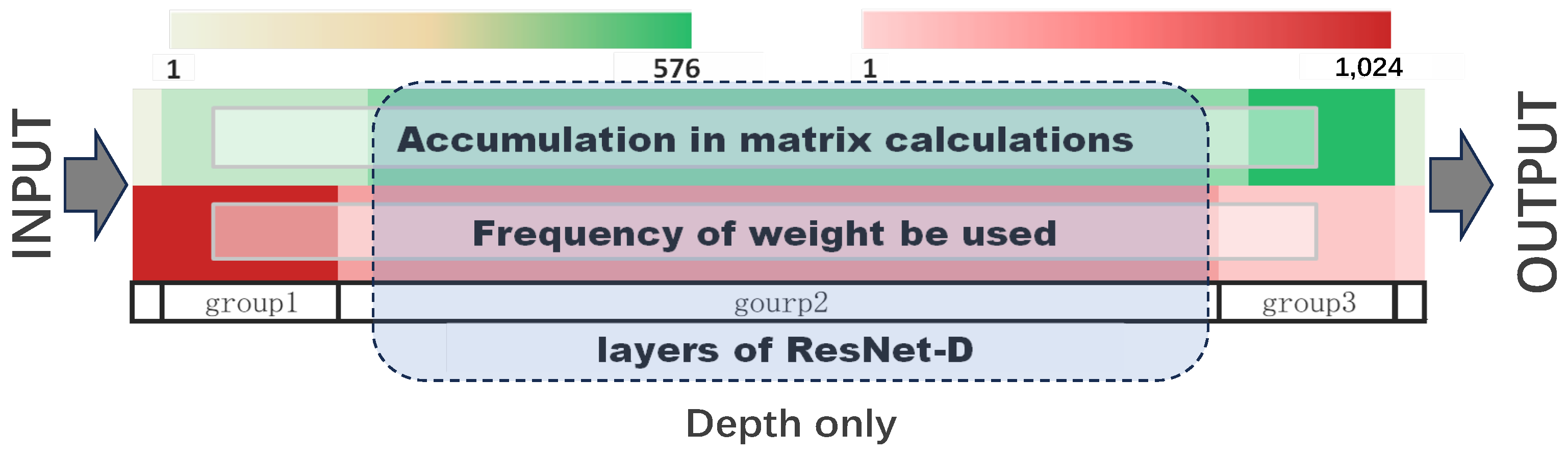
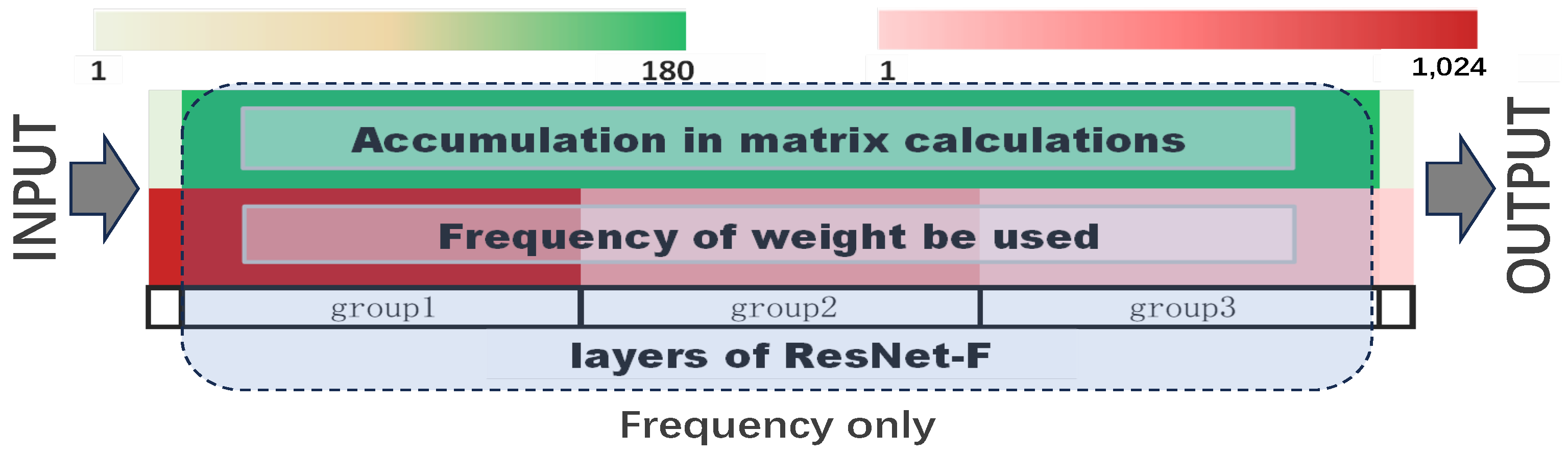
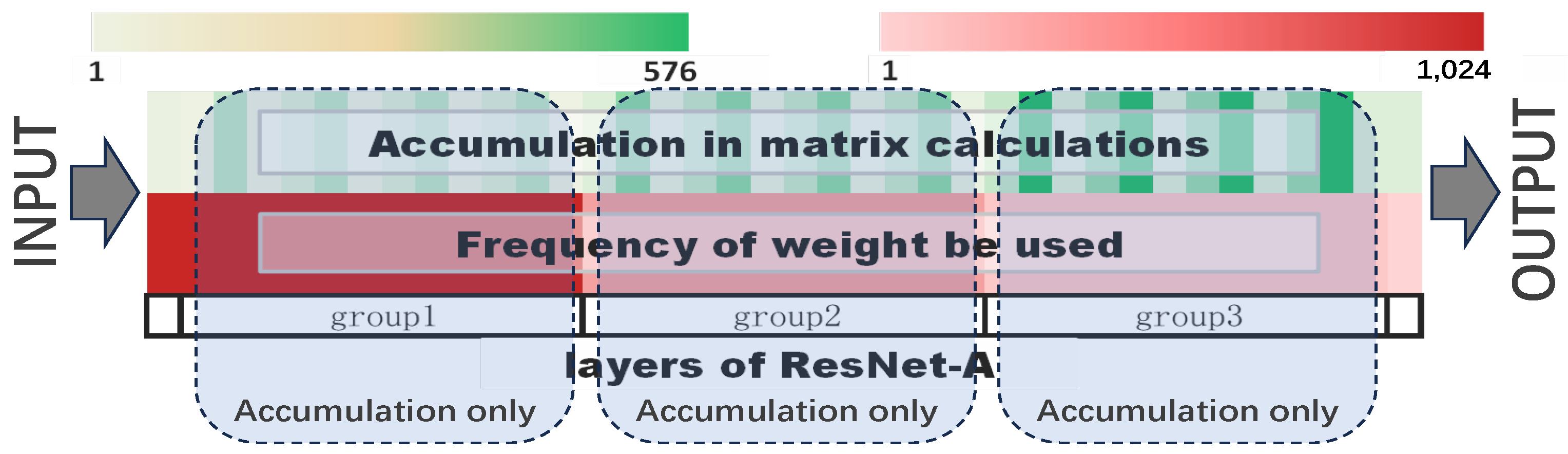
| Model | Dataset | #Bit | Strategy | Acc-A | Acc-F | Acc-D |
|---|---|---|---|---|---|---|
| AlexNet | CIFAR-10 | 6 | U | 85.46 | 85.46 | 85.46 |
| AlexNet | CIFAR-10 | 4 to 8 | C+ | 85.51 | 85.88 | 85.27 |
| AlexNet | CIFAR-10 | 4 to 8 | C− | 86.00 | 85.27 | 85.88 |
| ResNet-20 | CIFAR-10 | 6 | U | 91.51 | 91.51 | 91.51 |
| ResNet-20 | CIFAR-10 | 4 to 8 | C+ | 91.09 | 91.57 | 91.02 |
| ResNet-20 | CIFAR-10 | 4 to 8 | C− | 91.64 | 91.02 | 91.57 |
| ResNet-20 | CIFAR-100 | 6 | U | 68.40 | 68.40 | 68.40 |
| ResNet-20 | CIFAR-100 | 4 to 8 | C+ | 68.37 | 68.60 | 68.33 |
| ResNet-20 | CIFAR-100 | 4 to 8 | C− | 68.71 | 68.33 | 68.60 |
| ResNet-50 | ImageNet | 6 | U | 76.30 | 76.30 | 76.30 |
| ResNet-50 | ImageNet | 4 to 8 | C+ | 75.92 | 76.45 | 76.11 |
| ResNet-50 | ImageNet | 4 to 8 | C− | 76.56 | 76.11 | 76.45 |
| MobileNet-V2 | ImageNet | 6 | U | 66.45 | 66.45 | 66.45 |
| MobileNet-V2 | ImageNet | 4 to 8 | C+ | 65.19 | 66.67 | 64.31 |
| MobileNet-V2 | ImageNet | 4 to 8 | C− | 66.79 | 64.31 | 66.67 |
| MobileNet-V2 () | ImageNet | 6 | U | 55.61 | 55.61 | 55.61 |
| MobileNet-V2 () | ImageNet | 4 to 8 | C+ | 53.47 | 55.67 | 53.06 |
| MobileNet-V2 () | ImageNet | 4 to 8 | C− | 55.85 | 52.13 | 55.67 |
| Transformer | WikiText-103 | 7 | U | 32.30 | 32.30 | 33.09 |
| Transformer | WikiText-103 | 6 to 8 | C+ | 33.89 | 31.57 | 32.53 |
| Transformer | WikiText-103 | 6 to 8 | C− | 31.60 | 33.55 | 31.30 |
| 2-LSTM | PTB | 7 | U | 97.98 | 97.98 | 97.98 |
| 2-LSTM | PTB | 6 to 8 | C+ | 98.46 | 97.84 | 97.91 |
| 2-LSTM | PTB | 6 to 8 | C− | 97.21 | 97.88 | 98.00 |
| Model | Dataset | #Bit | Strategy | Size-A | Size-F | Size-D |
|---|---|---|---|---|---|---|
| ResNet-20 | CIFAR-10/100 | 6 | U | 1.12 | 1.12 | 1.12 |
| ResNet-20 | CIFAR-10/100 | 4 to 8 | C+ | 1.08 | 1.05 | 1.20 |
| ResNet-20 | CIFAR-10/100 | 4 to 8 | C− | 1.01 | 1.20 | 1.05 |
| ResNet-50 | ImageNet | 6 | U | 176 | 176 | 176 |
| ResNet-50 | ImageNet | 4 to 8 | C+ | 216 | 129 | 222 |
| ResNet-50 | ImageNet | 4 to 8 | C− | 140 | 222 | 129 |
| Transformer | WikiText-103 | 7 | U | 991 | 991 | 991 |
| Transformer | WikiText-103 | 6 to 8 | C+ | 977 | 1076 | 963 |
| Transformer | WikiText-103 | 6 to 8 | C− | 1005 | 906 | 1019 |
| #Bit | Strategy | Acc-D | Variance |
|---|---|---|---|
| 4 to 8 | R | 92.63 | 0.20 |
| 6 | U | 92.62 | 0.34 |
| 4 to 8 | C+ | 92.83 | 0.31 |
| 4 to 8 | C− | 92.73 | 0.17 |
| 8 to 16 | R | 92.82 | 0.22 |
| 12 | U | 92.94 | 0.22 |
| 8 to 16 | C+ | 92.92 | 0.23 |
| 8 to 16 | C− | 92.87 | 0.19 |
| #Bit | Strategy | Acc-F | Variance |
|---|---|---|---|
| 4 to 8 | R | 90.56 | 0.41 |
| 6 | U | 90.88 | 0.32 |
| 4 to 8 | C+ | 90.71 | 0.41 |
| 4 to 8 | C− | 90.54 | 0.60 |
| 8 to 16 | R | 91.77 | 0.36 |
| 12 | U | 92.02 | 0.33 |
| 8 to 16 | C+ | 91.99 | 0.31 |
| 8 to 16 | C− | 91.79 | 0.60 |
| #Bit | Strategy | Acc-A | Variance |
|---|---|---|---|
| 6 | U | 86.61 | 2.37 |
| 4 to 8 | C+ | 83.47 | 5.30 |
| 4 to 8 | C− | 86.67 | 1.49 |
| 7 | U | 92.32 | 0.39 |
| 6 to 8 | C+ | 90.30 | 4.37 |
| 6 to 8 | C− | 92.41 | 0.29 |
| 12 | U | 92.81 | 0.23 |
| 8 to 16 | C+ | 92.44 | 0.34 |
| 8 to 16 | C− | 92.85 | 0.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, A.; Lai, Z.; Zhang, L. Systematic Analysis of Low-Precision Training in Deep Neural Networks: Factors Influencing Matrix Computations. Appl. Sci. 2024, 14, 10025. https://doi.org/10.3390/app142110025
Shen A, Lai Z, Zhang L. Systematic Analysis of Low-Precision Training in Deep Neural Networks: Factors Influencing Matrix Computations. Applied Sciences. 2024; 14(21):10025. https://doi.org/10.3390/app142110025
Chicago/Turabian StyleShen, Ao, Zhiquan Lai, and Lizhi Zhang. 2024. "Systematic Analysis of Low-Precision Training in Deep Neural Networks: Factors Influencing Matrix Computations" Applied Sciences 14, no. 21: 10025. https://doi.org/10.3390/app142110025
APA StyleShen, A., Lai, Z., & Zhang, L. (2024). Systematic Analysis of Low-Precision Training in Deep Neural Networks: Factors Influencing Matrix Computations. Applied Sciences, 14(21), 10025. https://doi.org/10.3390/app142110025






