Design and Research of a Virtual Laboratory for Coding Theory
Abstract
1. Introduction
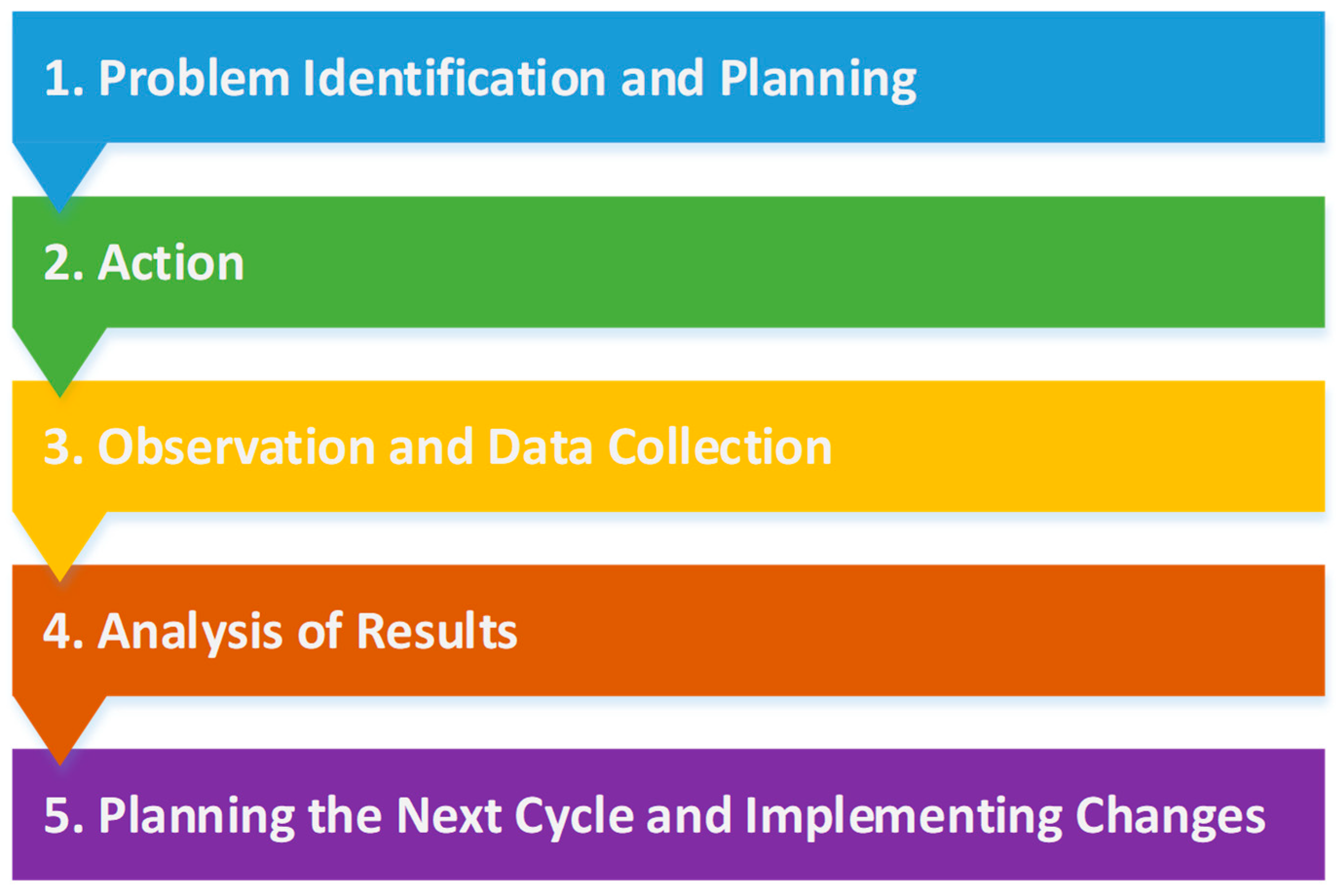
2. Materials and Methods
- Stage 1. Problem Identification and Planning.
- o
- Problem Identification. The research problem originates from the need to improve students’ practical skills and understanding, as well as to overcome the lack of motivation in using the traditional written teaching method by implementing intuitive interactive software models for solving coding theory tasks. Another good reason for the creation of such a system is the need to provide a tool for working in the conditions of distance learning, as was the situation with COVID-19 [22].
- o
- Formulating the Goal. The purpose of the research is to create and examine the impact of using a coding theory virtual lab on student achievement and engagement.
- o
- Action Planning. For the purpose of the research, two groups of students will be formed: the control group (the students in this group solve the tasks according to the traditional written method) and the experimental group (the students in this group solve the tasks using the tools of a virtual laboratory). During the study, data will be collected from control works (tests) [23].
- Stage 2. Action.
- o
- Design and Creation of a Coding Theory Virtual Laboratory. This action will be discussed in detail in point 2.1. Methodology for designing and implementing a virtual laboratory on coding theory.
- o
- Implementation of the Virtual Laboratory. Students in the experimental group will use the virtual lab to study different coding theory codes over several semesters. The lab will include a variety of interactive tasks, simulations, and tests.
- o
- Training and Preparation. Short training sessions will be held with both students and teachers to familiarize them with the functionalities of the virtual laboratory.
- Stage 3. Monitoring and Data Collection.
- o
- Observation. This includes monitoring students’ participation in the virtual lab, the degree of completion of the tasks, and students’ engagement with the material, as well as conducting regular tests to measure student progress.
- o
- Data Collection. This includes assessments from tests, a survey, and data from the statistical modules of the virtual lab on student engagement.
- Stage 4. Analysis of Results (Data Analysis).
- o
- Data Analysis. A comparison of scores (grades) between the two groups will be conducted to determine if there is a statistically significant difference in student achievement. This will be presented in detail in Section 3.2. An analysis of the results of the student opinion survey will also be carried out to determine their perceptions and satisfaction with the use of the virtual laboratory. Data from the virtual lab statics modules will also be analyzed to determine the impact on student engagement and learning of the material.
- Stage 5. Planning the Next Cycle and Implementing Changes.
- o
- Corrections and Improvements. Based on the obtained results, observations, and feedback, it is considered whether to make any adjustments (e.g., improvements in the interface, adding new functionalities and tasks).
- o
- Sharing the Results. Documenting and sharing results with other faculty teachers and institutions, as well as the publication of scientific papers or articles, through which the results of the use of a virtual laboratory in a learning process are provided.
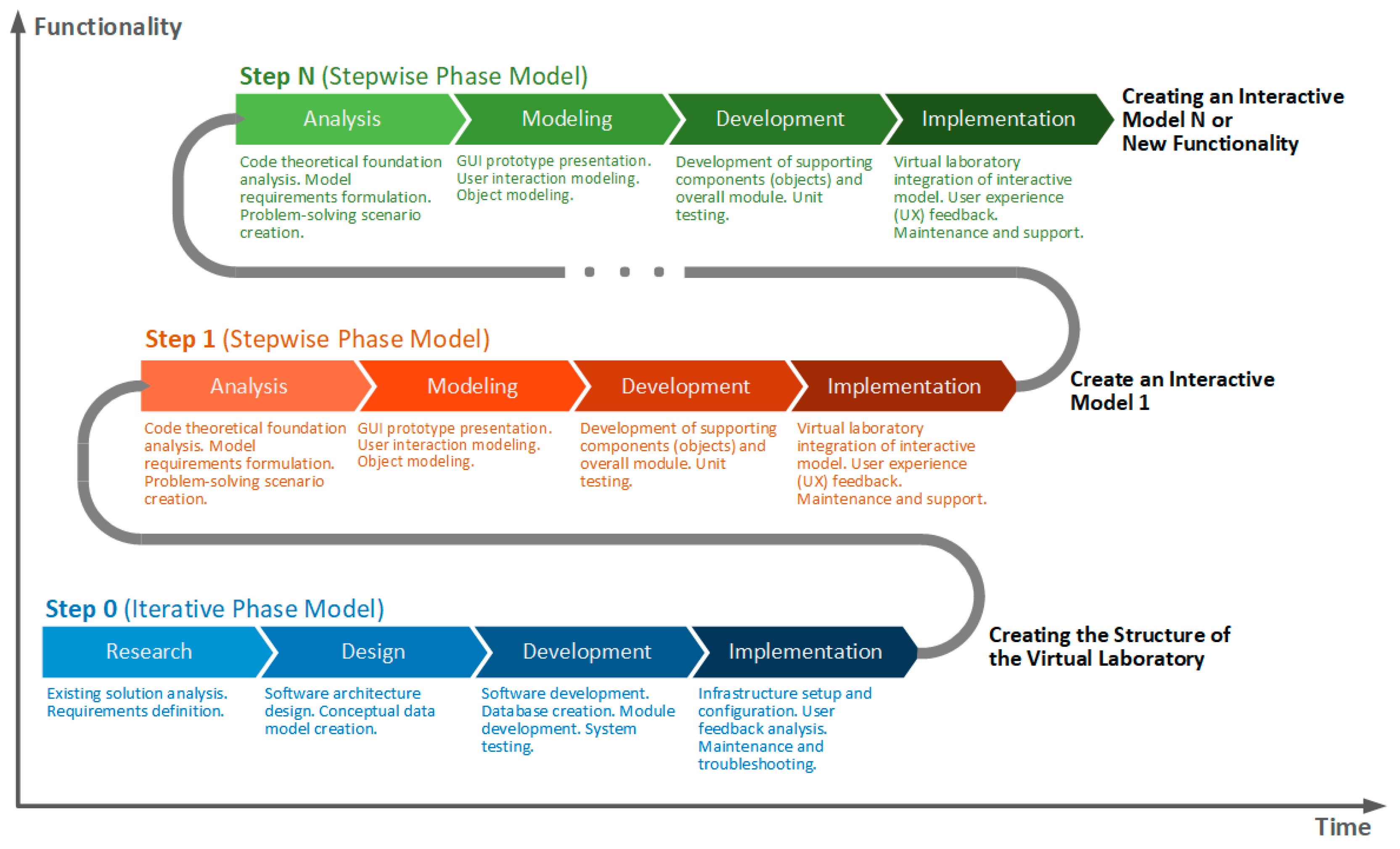
2.1. Methodology for Designing and Implementing a Virtual Laboratory on Coding Theory
- Delivery of part or full functionality of the system after each step enables operation and testing by the customer before the entire product is ready;
- The result of the initial steps can serve as a prototype to facilitate the formulation of the requirements for developments in the following steps;
- Due to the incremental nature of development, errors and malfunctions can be fixed at early stages, which reduces the risk of failure of the entire project;
- The most important functionalities implemented in the initial steps are tested the most, as multiple system testing is performed after each step.
- As disadvantages that can be observed with the phase models, we can point out [25]:
- The need for active participation of the client during the implementation of the individual steps of the process may lead to a delay in the implementation of the project;
- The ability to achieve a good level of communication and coordination is of great importance; otherwise, a problem may occur during development;
- Additional informal requirements for system improvement after a completed step can lead to confusion;
- Carrying out too many steps (iterations) can increase the scope of the application without the process being convergent.
2.2. Designing the Virtual Laboratory
- Formulation of requirements for the virtual laboratoryWell-thought-out and documented requirements for a software product are essential for its successful implementation. Requirements can be categorized into two groups: functional and non-functional. Functional requirements aim to define the desired behavior of the system through its functions, services, or what the system must perform. Through the non-functional requirements, the aim is to determine the quality of the software system through a set of standards used to assess the specific work, for example, speed, security, flexibility, etc. [26]
- o
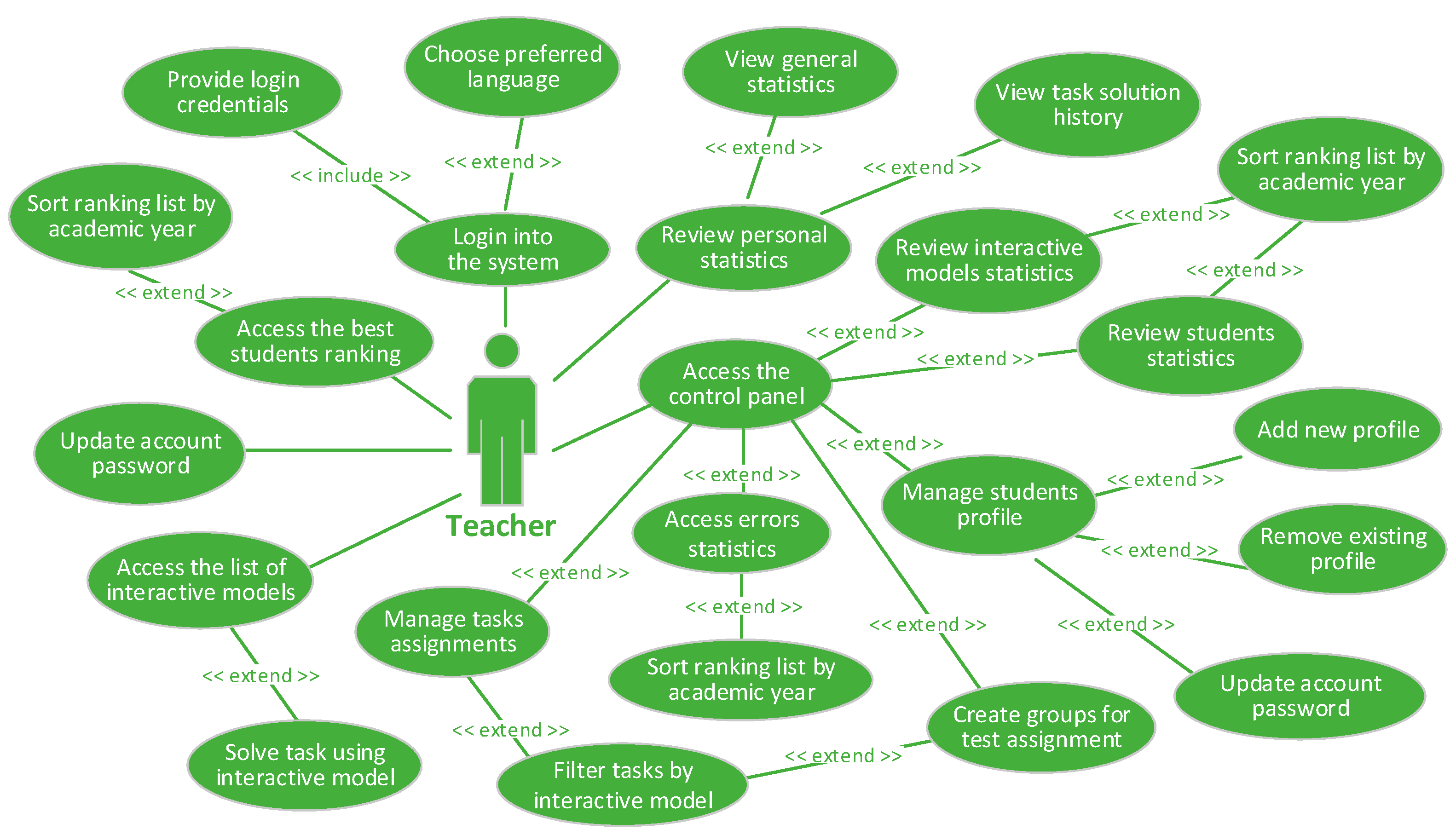
- Functional requirements
The following functional requirements are formulated for the virtual laboratory:- -
- The system interface should be in Bulgarian and English;
- -
- Logging into the system should be performed using a username and password;
- -
- The system should support two types of users—students and teachers;
- -
- Ability to control users—add, remove, change passwords, and manage groups for control work (tests);
- -
- Ability to control the conditions of the tasks;
- -
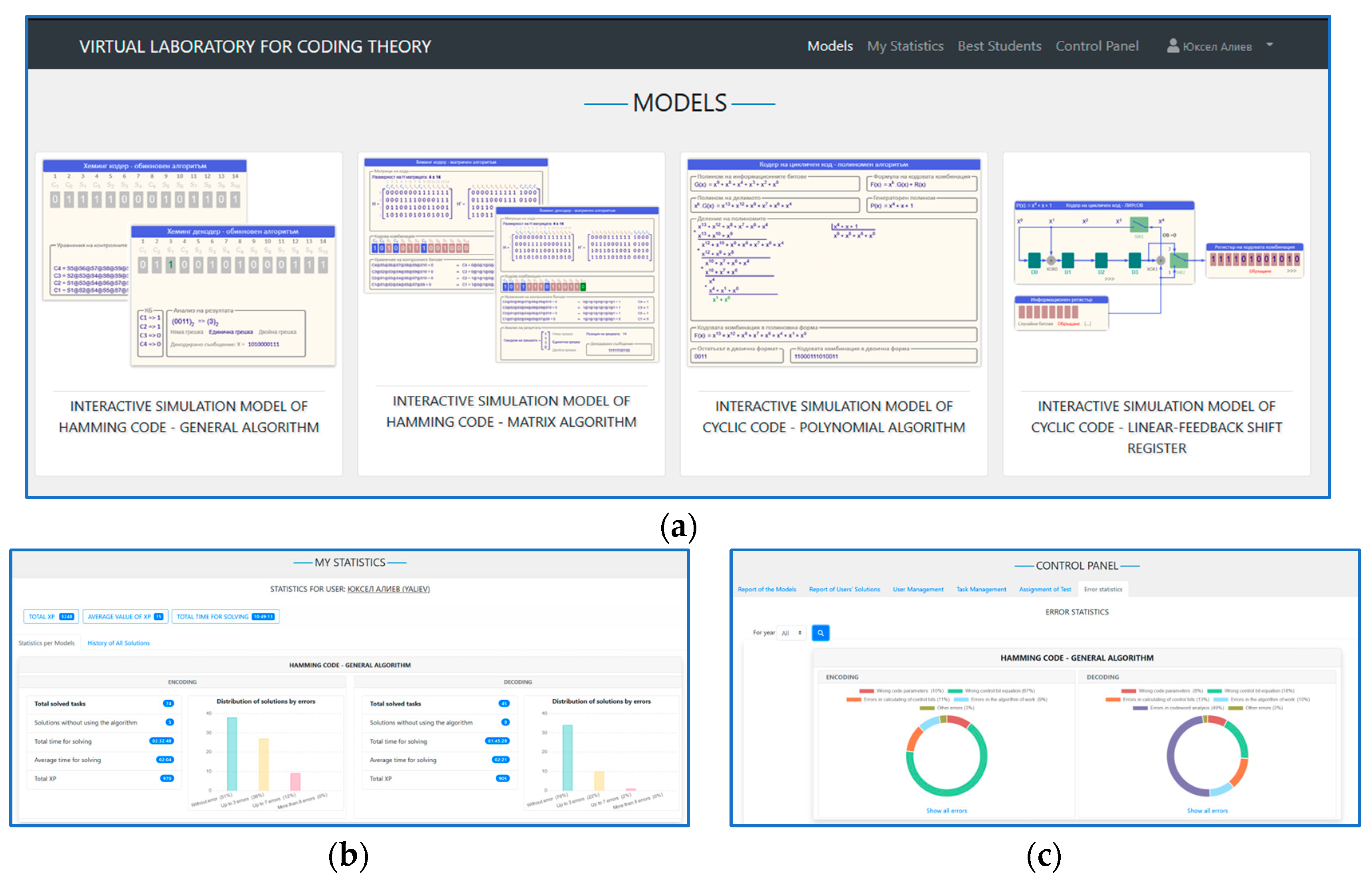
- Ability to include in its composition a set of interactive models for solving tasks for the following types of error control codes: Hamming code by general method—encoding mode and decoding mode; Hamming code by matrix method—encoding mode and decoding mode; Cyclic code by polynomial method—encoding mode; Cyclic code using linear feedback shift register—encoding mode.
- -
- For each solved task, the user receives incentive points according to previously specified criteria;
- -
- The system should support three modes for solving tasks:
- -
- “Training” mode (no set condition);
- -
- “Task” mode (solving a specific condition);
- -
- “Control work” mode (limited number of models launched).
- -
- The system should store information about the solved tasks, including data about the name of the software model used, including the mode of operation (encoding or decoding); time to solve the task; the number of mistakes made; the mistakes made; the number of points received from the task; and the condition of the task (only in “Control work” mode).
- -
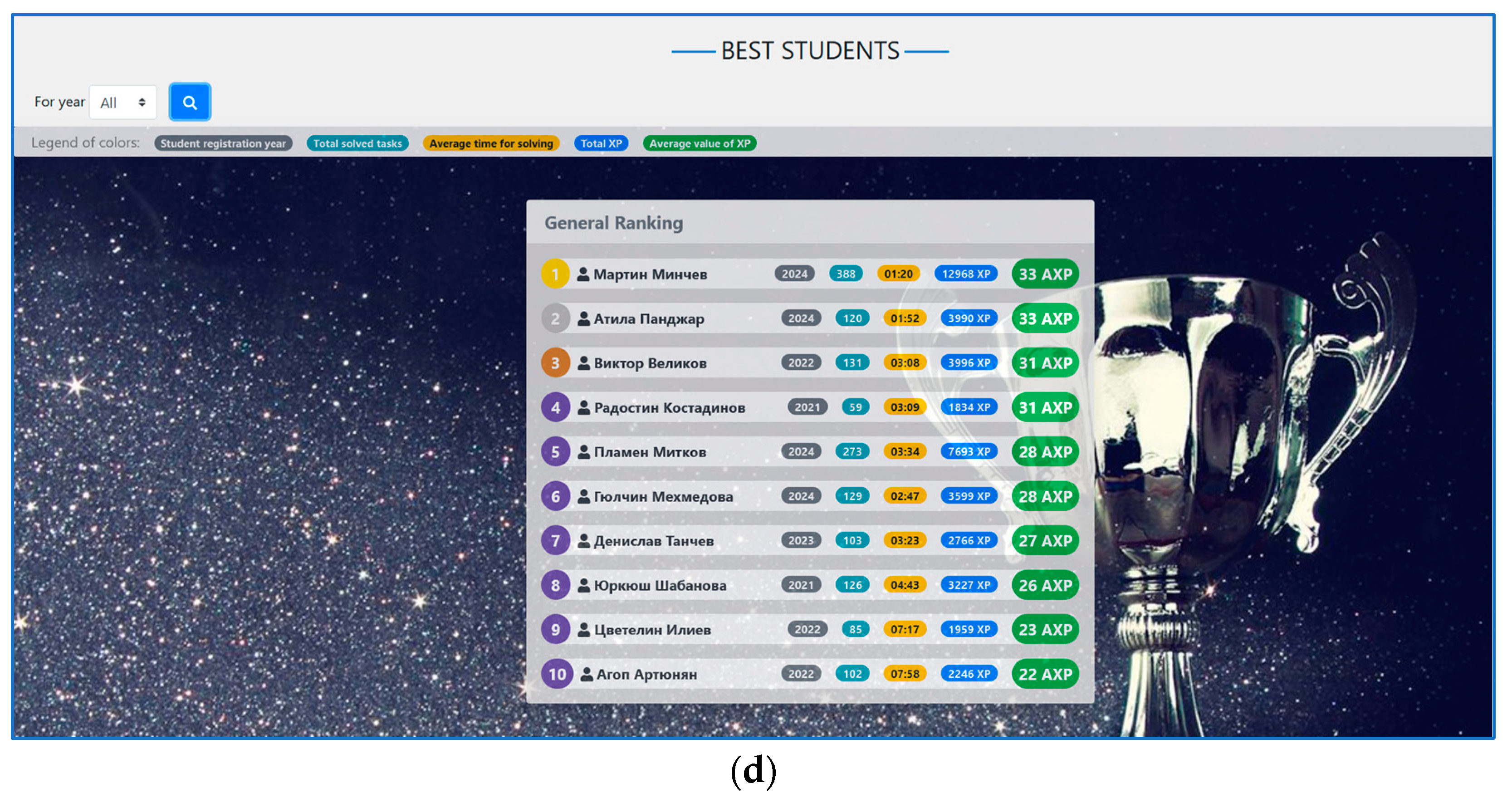
- Obtaining reports from accumulated statistical data as follows: reference for the solved tasks of a specific user; reference for program models based on all tasks solved by users; report on the mistakes made when solving the tasks; ranking for the most active students.
- o
- Non-functional requirements
The non-functional requirements for the virtual lab are as follows:- -
- The system should be platform-independent;
- -
- The system should be web-based and work with the most popular web browsers, such as Mozilla Firefox, Google Chrome, Microsoft Edge, Safari, etc.;
- -
- Data processing and system response should take minimal time;
- -
- Access to the system should be allowed only for registered users;
- -
- Access to the virtual laboratory should be possible at any time and from any place;
- -
- Not requiring the installation of additional software to work with the virtual laboratory;
- -
- The graphic interface of the administrative part and the interactive models should be intuitive and unified;
- -
- Data should be protected from illegal attacks.
- Architecture of the virtual laboratoryThe general architecture of the designed virtual laboratory is given in Figure 3. It consists of four layers:
- o
- Presentation Layer. This layer represents the user interface through which users interact with the system. Its main purpose is to deliver information to and collect information from users. As can be seen from the architecture, the system is intended to support two types of users—students and teachers.
- o
- Business Logic Layer. It is the most important layer of the architecture and deals with the extraction, processing, transformation, and management of application data; enforcement of business rules and policies; and ensuring data consistency and validity. This layer consists of three main groups of modules:
- -
- Interactive models for solving tasks—this module includes the four planned software models: Hamming code by general and matrix method, cyclic code by polynomial method, and cyclic code by linear feedback shift register;
- -
- Modules for statistical reference—these modules summarize the accumulated data and provide information about the usability of the models for solving tasks, student activity, and the most active students and the mistakes made when solving the tasks;
- -
- Administrative modules—these modules serve to manage user profiles; manage assignment conditions and group students for control works.
- o
- Data Access Layer. Through this layer, a connection between the application and the data store (the database) is provided.
- o
- Data Layer. This layer takes care of storing the user profiles and the collected data from the work in the virtual laboratory.
3. Results
3.1. Implementation of a Coding Theory Virtual Laboratory
- The interface design of individual interactive models was improved;
- Errors (bugs) related to the operation of the interactive models were fixed;
- Additional modules and functionalities were developed both for the entire virtual laboratory and for individual software models for studying the various codes.
3.2. Analysis of the Results of the Student Success Rate
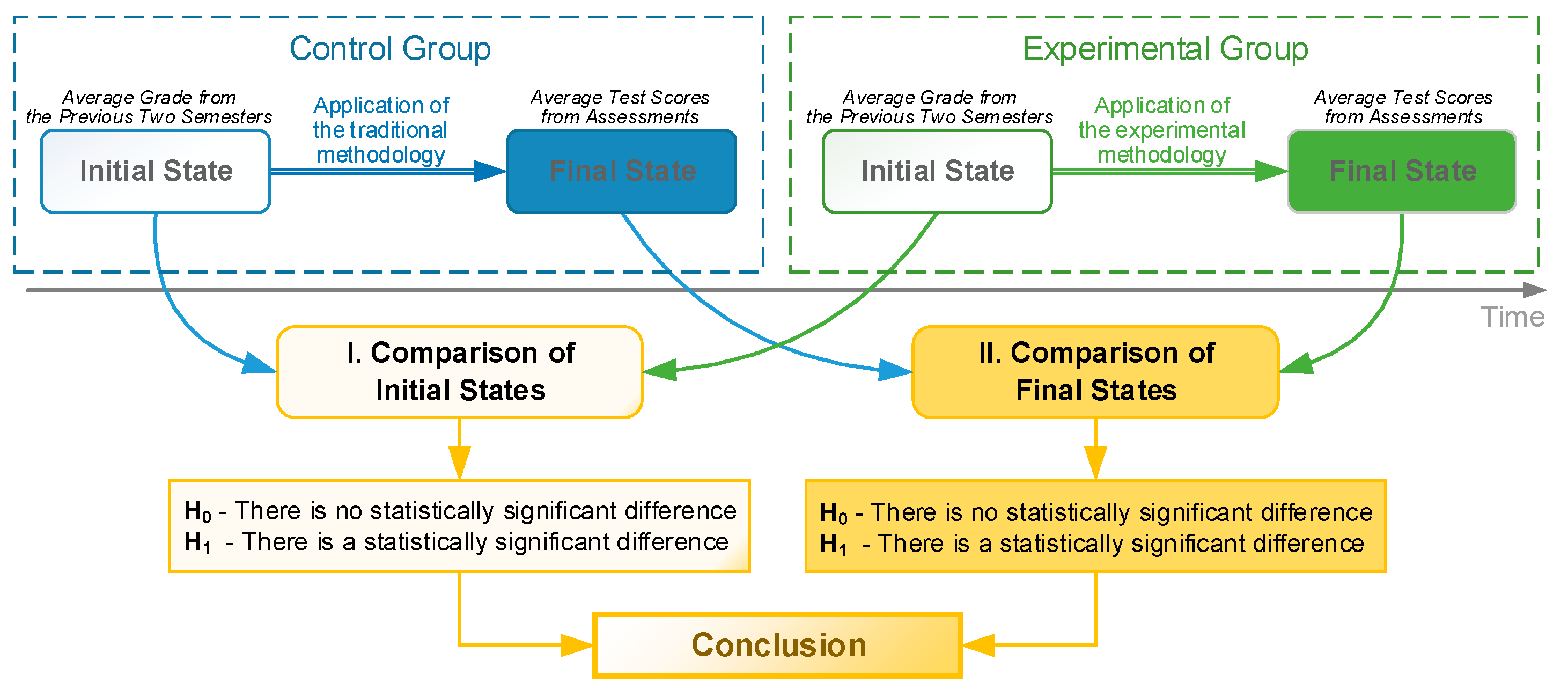
3.2.1. Statistical Hypothesis Checking of the Initial State of the Two Groups
- Formulation of the hypotheses H0 and H1The following two hypotheses for the average grades are formulated:
- o
- Null hypothesis —There is no statistically significant difference;
- o
- Alternative hypothesis —There is a statistically significant difference.
- Determination of the risk of error α
- Selection of criteria for checking the hypothesis
- o
- Determining whether the samples are dependent or independent
- o
- Determining whether the criterion is parametric or non-parametric
- o
- Checking for normal distribution by hypothesis testing
- (1)
- Formulation of the hypotheses for a normal distribution:
- -
- Null hypothesis H0—the variable has a normal distribution;
- -
- Alternative hypothesis H1—the variable does not follow a normal distribution.
- (2)
- Testing for normal distribution of the parameter for both groups.
- o
- Parametric test for two independent samples
- -
- Application in null hypothesis testing;
- -
- The comparison parameter (average grade) is quantitative;
- -
- The comparison parameter has a normal distribution;
- -
- The two samples must be independent.
- -
- If ≤ , the hypothesis H0 is accepted (there is no statistically significant difference );
- -
- If > , the hypothesis H1 is accepted (there is a statistically significant difference ).
- Analysis of results
- -
- Checking for equality of variances
- -
- Test for statistically significant difference
- -
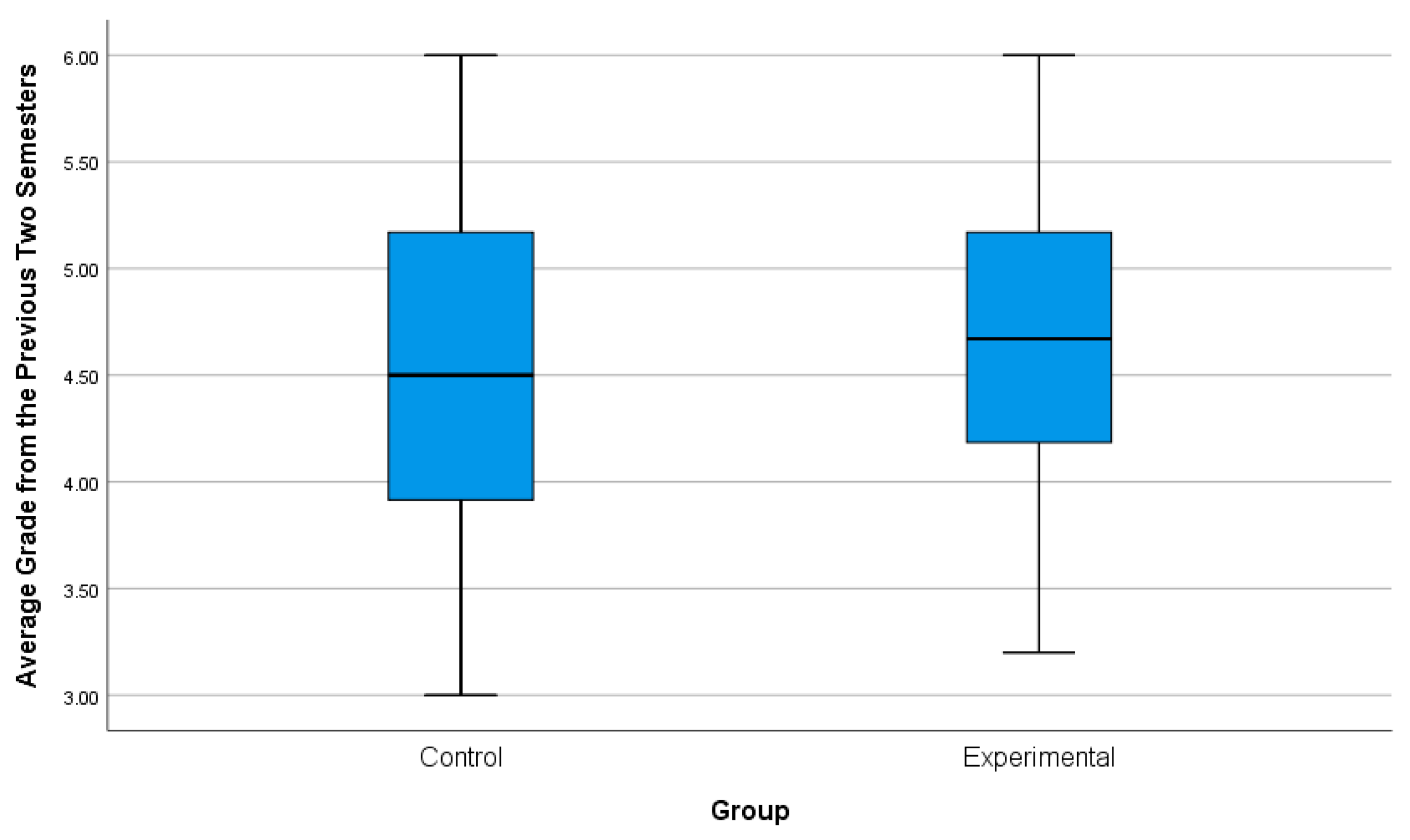
- and are the mean values of average grades for the control and experimental groups, respectively, where and (Table 1).
- -
- is the average standard deviation of the two groups, which is calculated as follows:where
3.2.2. Statistical Testing of Hypotheses About the Final State of the Two Groups
- -
- Hamming code by general method;
- -
- Hamming code by matrix method;
- -
- Cyclic code by polynomial method.
- Formulation of the hypotheses H0 and H1
- o
- Null hypothesis —There is no statistically significant difference;
- o
- Alternative hypothesis —There is a statistically significant difference.
- Determination of the risk of error α
- Selection of criteria for testing the hypothesis
- o
- Determining whether the samples are dependent or independent
- o
- Checking for normal distribution by hypothesis testing
- Checking for normal distribution by hypothesis testing
- (1)
- Formulation of the hypotheses for a normal distribution:
- -
- Null hypothesis H0—the variable has a normal distribution;
- -
- Alternative hypothesis H1—the variable does not follow a normal distribution.
- (2)
- Testing for normal distribution of the parameter for both groups.
- o
- Non-parametric test for two independent samples
- -
- If ≤ , the hypothesis H0 is accepted (there is no statistically significant difference );
- -
- If > , the hypothesis H1 is accepted (there is a statistically significant difference ).
- Analysis of the results
3.2.3. Conclusion of the Analysis
- Effectiveness of the training method: the difference in average grades after the experiment shows that the web-based virtual laboratory had a positive impact on student achievements. Since the control of the initial conditions was equalized (no statistically significant difference before the beginning), it can be concluded that the training method itself was a key factor in improving the results of the experimental group.
- Potential of technology in education: the success of the experimental group suggests that using virtual labs may be a more effective way to learn than the traditional written method. Virtual labs likely provide greater opportunities for interactivity, visualization, and hands-on experiences that enhance understanding and absorption of material.
- Recommendation for implementation of new technologies: the results of the experiment support the idea that integrating web-based platforms into the learning process can be beneficial. Based on these data, expanded use of such technologies can be recommended to improve learning outcomes and student engagement.
- Need for additional research: despite the positive result, it is useful to conduct further research to evaluate the long-term effect of the use of virtual laboratories, as well as to examine different areas of learning to find out whether this method works equally effectively in different subjects.
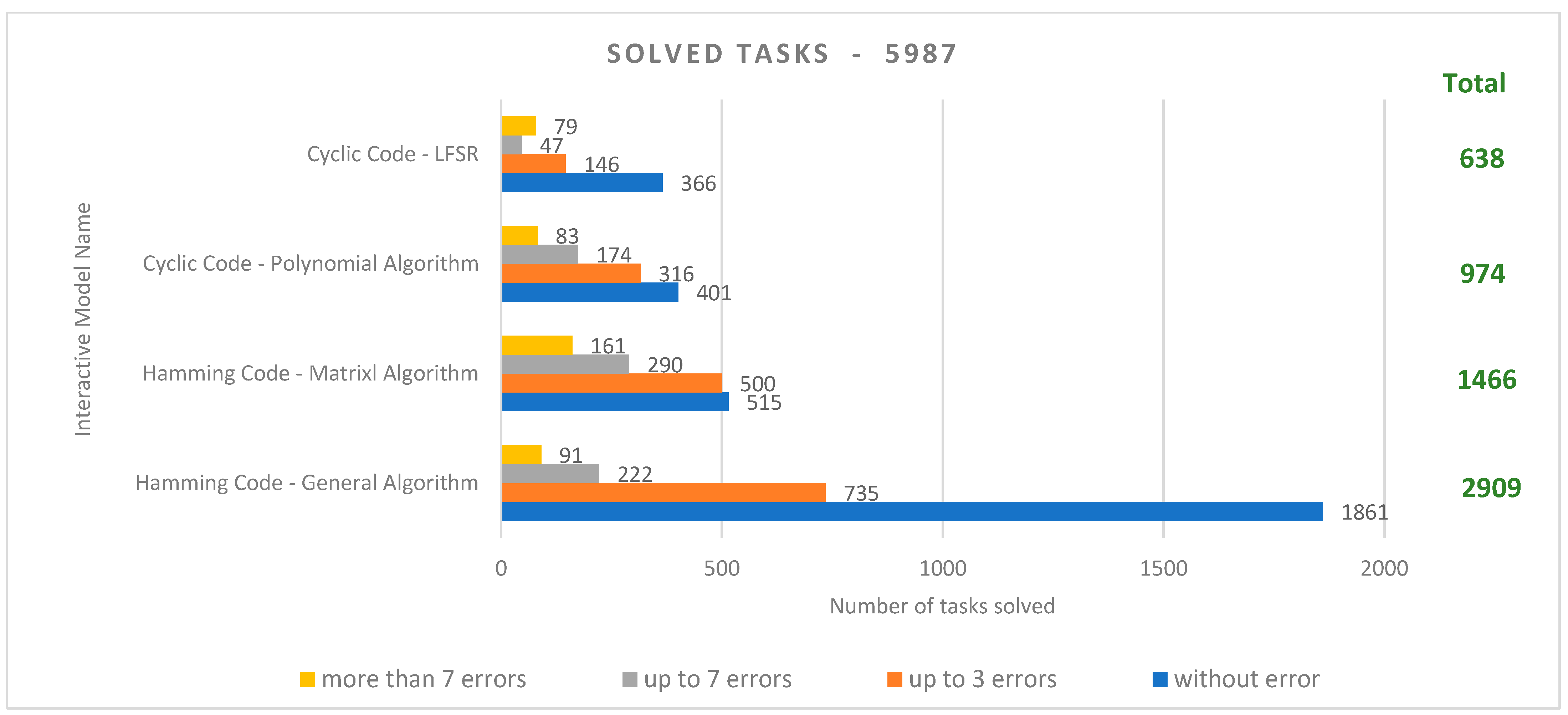
3.3. Analysis of Statistical Information on System Usability
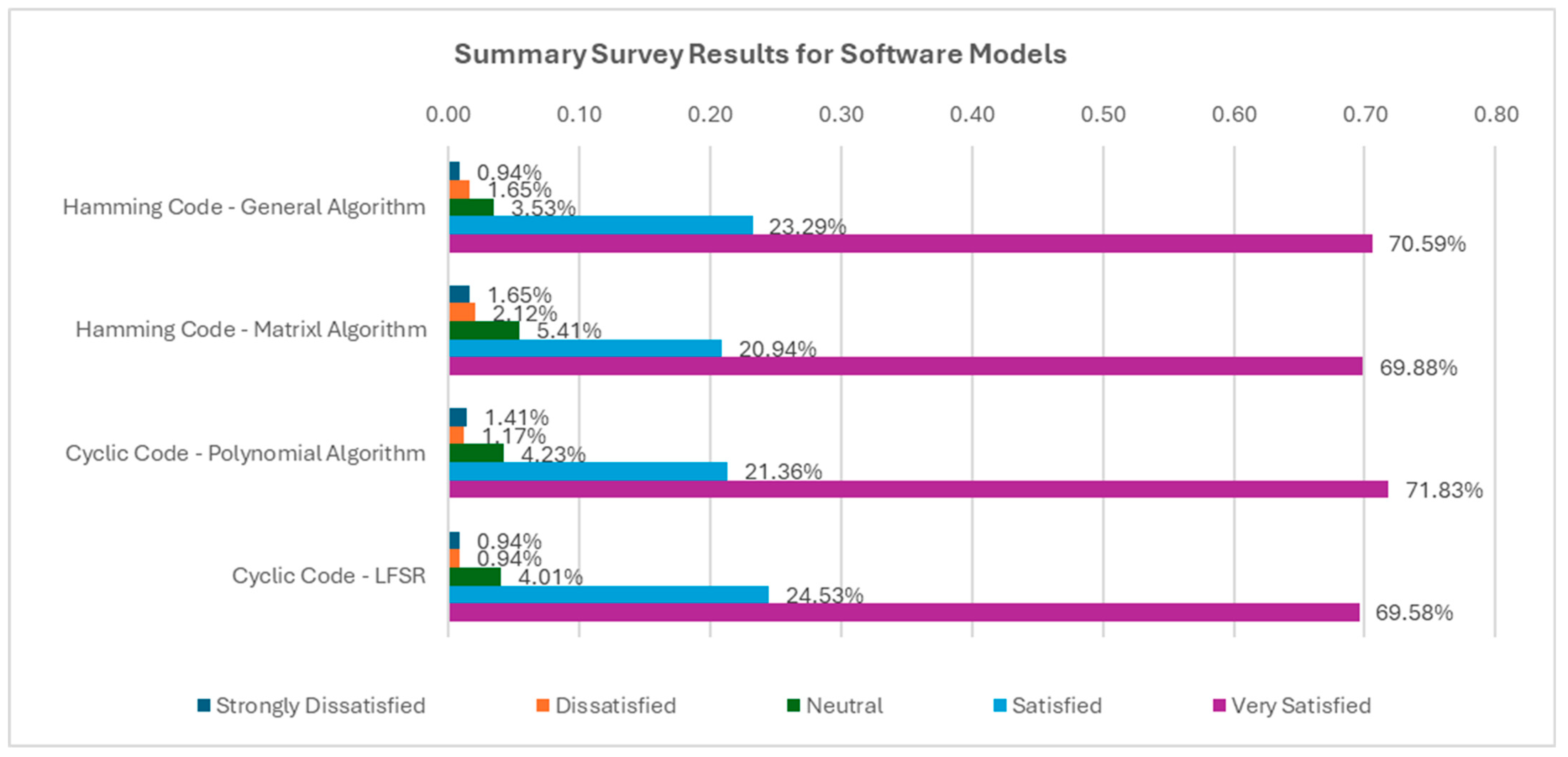
3.4. Analysis of Data from a Survey on Students’ Opinions of the Use of the Virtual Laboratory
4. Discussion
- One of the main advantages recognized by the teachers is the software’s ability to automatically assign personalized tasks to each student. This feature significantly reduces the time required for teachers to prepare materials for exercises, tests, and course assignments.
- A ranking system for the best active students was designed on the recommendation of the teachers, and this has led to a significant increase in the number of solved tasks completed by students. The ranking system has motivated students to solve more tasks, striving to minimize mistakes and improving their ranking.
- Another requirement of the teaching staff was the automated identification of student mistakes and inserting the data for them in the database. This functionality has reduced the time teachers previously spent manually reviewing assignments before the virtual laboratory’s implementation. The review and grading process has been accelerated, facilitating the evaluation of a larger number of students in a shorter period.
- Another important aspect, recommended by the teachers, is that the virtual laboratory ensures a transparent assessment process by automatically verifying results. This eliminates potential subjectivity in grading and guarantees that student evaluations are based on their actual achievements.
- Furthermore, teachers report that the virtual laboratory is valuable for solving more complex tasks (with higher bit-rate information), which were difficult to achieve using traditional written methods.
- Integration in different educational contexts: How the virtual laboratory can be used in different learning situations and environments (for example, in different educational systems or disciplines).
- Scalability: Assessing the virtual lab’s potential to be implemented on a large scale, such as in many schools or universities simultaneously, and whether it can serve a large number of users.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lewis, D.I. The Pedagogical Benefits and Pitfalls of Virtual Tools for Teaching and Learning Laboratory Practices in the Biological Sciences; The Higher Education Academy, STEM, 2014; Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=aa4c7290fbf0301cbbfc394f6085cd12692f5519 (accessed on 2 September 2024).
- Achuthan, K.; Francis, S.P.; Diwakar, S. Augmented reflective learning and knowledge retention perceived among students in classrooms involving virtual laboratories. Educ. Inf. Technol. 2017, 22, 2825–2855. [Google Scholar] [CrossRef]
- Achuthan, K.; Kolil, V.K.; Diwakar, S. Using virtual laboratories in chemistry classrooms as interactive tools towards modifying alternate conceptions in molecular symmetry. Educ. Inf. Technol. 2018, 23, 2499–2515. [Google Scholar] [CrossRef]
- Pastor, R. Online laboratories as a cloud service developed by students. In Proceedings of the IEEE Frontiers in Education Conference (FIE), Oklahoma City, OK, USA, 23–26 October 2013. [Google Scholar]
- Peidró, A.; Reinoso, O.; Gil, A.; Marín, J.M.; Payá, L. A virtual laboratory to simulate the control of parallel robots. IFAC-PapersOnLine 2015, 48, 19–24. [Google Scholar] [CrossRef]
- Valdez, M.; Ferreira, C.M.; Barbosa, F.P.M. 3D Virtual Laboratory for Teaching Circuit Theory—A Virtual Learning Environment (VLE). In Proceedings of the 51st International Universities’ Power Engineering Conference, Coimbra, Portugal, 6–9 September 2016. [Google Scholar] [CrossRef]
- Chao, J.; Chiu, J.L.; DeJaegher, C.J.; Pan, E.A. Sensor-augmented virtual labs: Using physical interactions with science simulations to promote understanding of gas behaviour. J. Sci. Educ. Technol. 2016, 25, 16–33. [Google Scholar] [CrossRef]
- Booth, C.; Cheluvappa, R.; Bellinson, Z.; Maguire, D.; Zimitat, C.; Abraham, J.; Eri, R. Empirical evaluation of a virtual laboratory approach to teach lactate dehydrogenase enzyme kinetics. Ann. Med. Surg. 2016, 8, 6–13. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, A.; Nordin, M.K.; Saaid, M.F.; Johari, J.; Kassim, R.A.; Zakaria, Y. Remote control temperature chamber for virtual laboratory. In Proceedings of the IEEE 9th International Conference on Engineering Education (ICEED), Kanazawa, Japan, 9–10 November 2017; pp. 206–211. [Google Scholar]
- Erdem, M.B.; Kiraz, A.; Eski, H.; Çiftçi, Ö.; Kubat, C. A conceptual framework for cloud-based integration of Virtual laboratories as a multi-agent system approach. Comput. Ind. Eng. 2016, 102, 452–457. [Google Scholar] [CrossRef]
- Hashemipour, M.; Manesh, H.F.; Bal, M. A modular virtual reality system for engineering laboratory education. Comput. Appl. Eng. Educ. 2011, 19, 305–314. [Google Scholar] [CrossRef]
- Budai, T.; Kuczmann, M. Towards a modern, integrated virtual laboratory system. Acta Polytech. Hung. 2018, 15, 191–204. [Google Scholar] [CrossRef]
- Trnka, P.; Vrána, S.; Šulc, B. Comparison of Various Technologies Used in a Virtual Laboratory. IFAC-PapersOnLine 2016, 49, 144–149. [Google Scholar] [CrossRef]
- Ren, W.; Jin, N.; Wang, T. An Interdigital Conductance Sensor for Measuring Liquid Film Thickness in Inclined Gas-Liquid Two-Phase Flow. IEEE Trans. Instrum. Meas. 2024, 73, 9505809. [Google Scholar] [CrossRef]
- Okoyeigbo, O.; Agboje, E.; Omuabor, E.; Samson, U.A.; Orimogunje, A. Design and implementation of a java based virtual laboratory for data communication simulation. Int. J. Electr. Comput. Eng. (IJECE) 2020, 10, 5883–5890. [Google Scholar] [CrossRef]
- Erder, B.; Akar, A. Remote accessible laboratory for error controlled coding techniques with the labview software. Procedia-Soc. Behav. Sci. 2010, 2, 372–377. [Google Scholar] [CrossRef][Green Version]
- Ersoy, M.; Kumral, C.D.; Çolak, R.; Armağan, H.; Yiğit, T. Development of a server-based integrated virtual laboratory for digital electronics. Comput. Appl. Eng. Educ. 2022, 30, 1307–1320. [Google Scholar] [CrossRef]
- Mertler, C.A. (Ed.) The Wiley Handbook of Action Research in Education; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Chatzopoulos, A.; Papoutsidakis, M.; Kalogiannakis, M.; Psycharis, S. Action Research Implementation in Developing an Open Source and Low Cost Robotic Platform for STEM Education. Int. J. Comput. Appl. 2019, 178, 33–46. [Google Scholar] [CrossRef]
- Chatzopoulos, A.; Kalogiannakis, M.; Papadakis, S.; Papoutsidakis, M. A novel, modular robot for educational robotics developed using action research evaluated on Technology Acceptance Model. Educ. Sci. 2022, 12, 274. [Google Scholar] [CrossRef]
- Dehalwar, K.; Sharma, S. Fundamentals of Research Writing and Uses of Research Methodologies; Edupedia Publications Pvt Ltd.: New Delhi, India, 2023. [Google Scholar] [CrossRef]
- Kapilan, N.; Vidhya, P.; Gao, X.Z. Virtual laboratory: A boon to the mechanical engineering education during COVID-19 pandemic. High. Educ. Future 2021, 8, 31–46. [Google Scholar] [CrossRef]
- Kemmis, S.; McTaggart, R.; Nixon, R. The Action Research Planner: Doing Critical Participatory Action Research; Springer: Singapore, 2014. [Google Scholar]
- Pressman, R.S. Software Engineering: A Practitioner’s Approach; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Atkinson, C.; Weeks, D.C.; Noll, J. The design of evolutionary process modeling languages. In Proceedings of the 11th Asia-Pacific Software Engineering Conference, Busan, Republic of Korea, 30 November–3 December 2004; pp. 73–82. [Google Scholar] [CrossRef]
- Bell, E.; Thayer, T. Software requirements: Are they really a problem? In Proceedings of the 2nd International Conference on Software Engineering (ICSE), San Francisco, CA, USA, 13–15 October 1976; IEEE Computer Society Press: Washington, DC, USA, 1976; pp. 61–68. [Google Scholar]
- Field, A. Discovering Statistics Using IBM SPSS Statistics; Sage: Newcastle upon Tyne, UK, 2013. [Google Scholar]
- Mohammed, A.; Shayib, A. Applied Statistics, 1st ed.; Bookboon: London, UK, 2013; ISBN 978-87-403-0493-0. [Google Scholar]
- Stevens, J.P. Applied Multivariate Statistics for the Social Sciences, 5th ed.; Routledge: New York, NY, USA, 2012. [Google Scholar]
- Illowsky, B.; Dean, S. Introductory Statistics; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Gray, C.D.; Kinnear, P.R. IBM SPSS Statistics 19 Made Simple; Psychology Press: Hove, UK, 2012. [Google Scholar]
- Durlak, J.A. How to select, calculate, and interpret effect sizes. J. Pediatr. Psychol. 2009, 34, 917–928. [Google Scholar] [CrossRef] [PubMed]



| Average Grade from the Previous Two Semesters | ||||
|---|---|---|---|---|
| Group | Statistic | Std. Error | ||
| Control | Mean | 4.5829 | 0.10109 | |
| 95% Confidence Interval for Mean | Lower Bound | 4.3805 | ||
| Upper Bound | 4.7852 | |||
| 5% Trimmed Mean | 4.5778 | |||
| Median | 4.5000 | |||
| Variance | 0.603 | |||
| Std. Deviation | 0.77649 | |||
| Minimum | 3.00 | |||
| Maximum | 6.00 | |||
| Range | 3.00 | |||
| Interquartile Range | 1.34 | |||
| Skewness | 0.209 | 0.311 | ||
| Kurtosis | −0.878 | 0.613 | ||
| Experimental | Mean | 4.6810 | 0.08408 | |
| 95% Confidence Interval for Mean | Lower Bound | 4.5127 | ||
| Upper Bound | 4.8493 | |||
| 5% Trimmed Mean | 4.6699 | |||
| Median | 4.6700 | |||
| Variance | 0.417 | |||
| Std. Deviation | 0.64586 | |||
| Minimum | 3.20 | |||
| Maximum | 6.00 | |||
| Range | 2.80 | |||
| Interquartile Range | 1.00 | |||
| Skewness | 0.131 | 0.311 | ||
| Kurtosis | −0.554 | 0.613 | ||
| One-Sample Kolmogorov–Smirnov Test a | ||
|---|---|---|
| Average Grade from the Previous Two Semesters | ||
| N | 59 | |
| Normal Parameters b,c | Mean | 4.5829 |
| Std. Deviation | 0.77649 | |
| Most Extreme Differences | Absolute | 0.102 |
| Positive | 0.102 | |
| Negative | −0.072 | |
| Test Statistic | 0.102 | |
| Asymp. Sig. (2-tailed) | 0.200 d,e | |
| One-Sample Kolmogorov–Smirnov Test a | ||
|---|---|---|
| Average Grade from the Previous Two Semesters | ||
| N | 59 | |
| Normal Parameters b,c | Mean | 4.6810 |
| Std. Deviation | 0.64586 | |
| Most Extreme Differences | Absolute | 0.096 |
| Positive | 0.094 | |
| Negative | −0.096 | |
| Test Statistic | 0.096 | |
| Asymp. Sig. (2-tailed) | 0.200 d,e | |
| Independent Samples Test | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Levene’s Test for Equality of Variances | t-Test for Equality of Means | |||||||||
| F | Sig. | t | df | Sig. (2-Tailed) | Mean Difference | Std. Error Difference | 95% Confidence Interval of the Difference | |||
| Lower | Upper | |||||||||
| Average Grade from the Previous Two Semesters | Equal variances assumed | 2.571 | 0.112 | −0.746 | 116 | 0.457 | −0.09814 | 0.13149 | −0.35857 | 0.16230 |
| Equal variances not assumed | −0.746 | 112.275 | 0.457 | −0.09814 | 0.13149 | −0.35866 | 0.16239 | |||
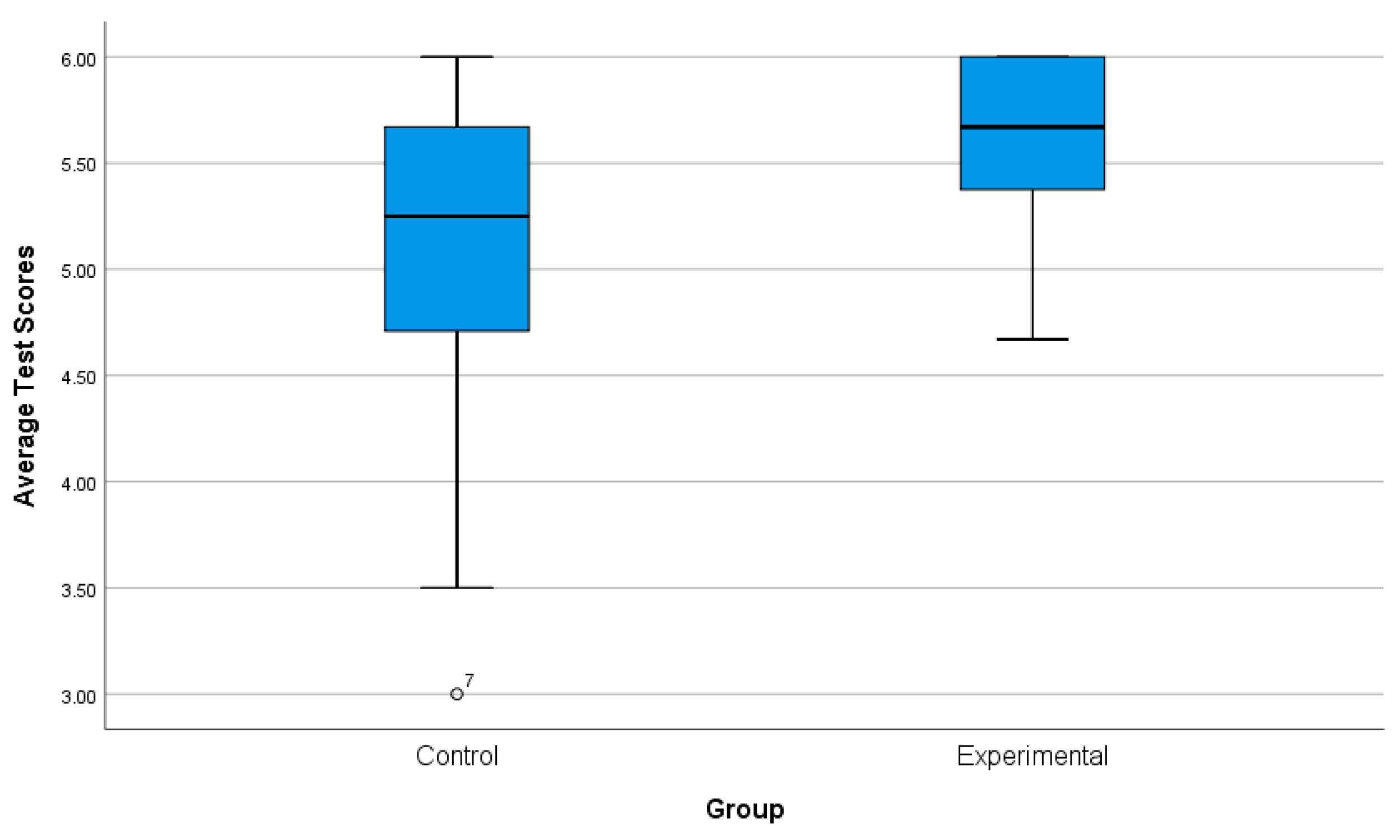
| Average Test Scores | ||||
|---|---|---|---|---|
| Group | Statistic | Std. Error | ||
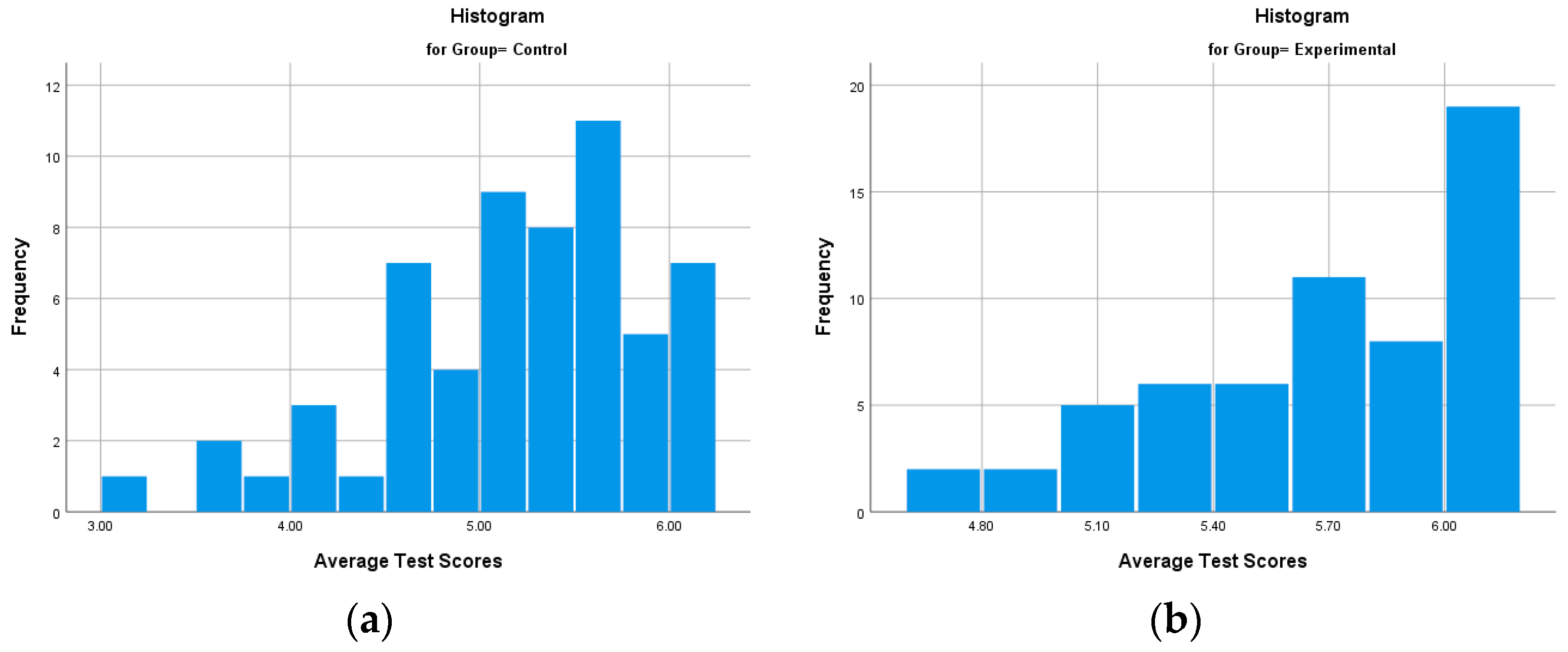
| Control | Mean | 5.1371 | 0.09150 | |
| 95% Confidence Interval for Mean | Lower Bound | 4.9540 | ||
| Upper Bound | 5.3203 | |||
| 5% Trimmed Mean | 5.1865 | |||
| Median | 5.2500 | |||
| Variance | 0.494 | |||
| Std. Deviation | 0.70284 | |||
| Minimum | 3.00 | |||
| Maximum | 6.00 | |||
| Range | 3.00 | |||
| Interquartile Range | 1.00 | |||
| Skewness | −0.899 | 0.311 | ||
| Kurtosis | 0.509 | 0.613 | ||
| Experimental | Mean | 5.6400 | 0.04780 | |
| 95% Confidence Interval for Mean | Lower Bound | 5.5443 | ||
| Upper Bound | 5.7357 | |||
| 5% Trimmed Mean | 5.6710 | |||
| Median | 5.6700 | |||
| Variance | 0.135 | |||
| Std. Deviation | 0.36713 | |||
| Minimum | 4.67 | |||
| Maximum | 6.00 | |||
| Range | 1.33 | |||
| Interquartile Range | 0.67 | |||
| Skewness | −0.962 | 0.311 | ||
| Kurtosis | 0.229 | 0.613 | ||
| One-Sample Kolmogorov–Smirnov Test a | ||
|---|---|---|
| Average Test Scores | ||
| N | 59 | |
| Normal Parameters b,c | Mean | 5.1371 |
| Std. Deviation | 0.70284 | |
| Most Extreme Differences | Absolute | 0.132 |
| Positive | 0.110 | |
| Negative | −0.132 | |
| Test Statistic | 0.132 | |
| Asymp. Sig. (2-tailed) | 0.012 d | |
| One-Sample Kolmogorov–Smirnov Test a | ||
|---|---|---|
| Average Test Scores | ||
| N | 59 | |
| Normal Parameters b,c | Mean | 5.6400 |
| Std. Deviation | 0.36713 | |
| Most Extreme Differences | Absolute | 0.177 |
| Positive | 0.163 | |
| Negative | −0.177 | |
| Test Statistic | 0.177 | |
| Asymp. Sig. (2-tailed) | 0.000 d | |
| Ranks | ||||
|---|---|---|---|---|
| Group | N | Mean Rank | Sum of Ranks | |
| Average Test Scores | Control | 59 | 46.14 | 2722.00 |
| Experimental | 59 | 72.86 | 4299.00 | |
| Total | 118 | |||
| Test Statistics a | |
|---|---|
| Average Test Scores | |
| Mann–Whitney U | 952.000 |
| Wilcoxon W | 2722.000 |
| Z | −4.282 |
| Asymp. Sig. (2-tailed) | 0.000 |
| Initial State Comparison | Final State Comparison | |
|---|---|---|
| Distribution of data (Kolmogorov–Smirnov Test) | Control group—normal distribution; Experimental group—normal distribution; | Control group—does not follow a normal distribution; Experimental group—does not follow a normal distribution. |
| Test type | Parametric test for two independent samples: -t-test for equality of means; -Levene’s test for equality of variances. | Non-parametric test for two independent samples: Mann–Whitney rank test |
| Result (Hypothesis) | H0: There is no statistically significant difference between the two groups | H1: There is a significant difference in mean scores (average grades) |
| Effect Sizes (Cohen′s d) | Small effect (−0.137) | Big effect (−0.897) |
| Summary | There is an equal start for the control and experimental groups at the beginning of the experiment. | The success rate of the experimental group is higher than the success rate of the control group at the end of the experiment. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aliev, Y.; Ivanova, G.; Borodzhieva, A. Design and Research of a Virtual Laboratory for Coding Theory. Appl. Sci. 2024, 14, 9546. https://doi.org/10.3390/app14209546
Aliev Y, Ivanova G, Borodzhieva A. Design and Research of a Virtual Laboratory for Coding Theory. Applied Sciences. 2024; 14(20):9546. https://doi.org/10.3390/app14209546
Chicago/Turabian StyleAliev, Yuksel, Galina Ivanova, and Adriana Borodzhieva. 2024. "Design and Research of a Virtual Laboratory for Coding Theory" Applied Sciences 14, no. 20: 9546. https://doi.org/10.3390/app14209546
APA StyleAliev, Y., Ivanova, G., & Borodzhieva, A. (2024). Design and Research of a Virtual Laboratory for Coding Theory. Applied Sciences, 14(20), 9546. https://doi.org/10.3390/app14209546








