Abstract
Coiled tubing has been widely used in oilfield development because it can significantly improve oil well productivity and recovery efficiency. However, with the increase in fracturing, drilling, and sand-washing operations, the erosion of coiled tubing walls caused by solid particles has become one of the main failure modes. To accurately predict the erosion rate of coiled tubing, this study studied the influence law of erosion rate through experiments, screened the main influencing factors of erosion rate by grey relational analysis (GRA), and established a back-propagation neural network (BPNN) model optimized by the sparrow search algorithm (SSA) to predict the erosion rate. The results show that the main influencing factors for coiled tubing erosion rate are impact velocity, impact angle, and sand concentration. In addition, the SSA-BPNN model shows a high goodness of fit (R) and a good fit with the experimental data. The SSA-BPNN model underwent standard statistical validation tests, effectively predicting the erosion rate of coiled tubing with a high coefficient of determination and low errors, demonstrating a robust consistency between predicted and actual values. This study is of great significance to oilfield engineers, pipeline designers, and oilfield developers, and provides effective support for optimizing oilfield development and pipeline maintenance. The main users include oil companies, engineering consulting institutions and related industry personnel, and may also attract the interest of scientific research institutions and academia, providing a useful reference for the technological progress of the oil industry.
1. Introduction
Coiled tubing, characterized by its compact footprint, convenient relocation and installation, reservoir protection, enhanced production, and high operational efficiency, is extensively utilized in various domains, including well intervention, drilling, logging, well testing, oil production, and pipeline transportation, as depicted in Figure 1. Erosion refers to the phenomenon during which the solid particles contained in the fluid in high-speed flow impact the wall surface and cause wall damage. During the production of oil and gas fields, there are often high-pressure and high-flow-rate solid-containing fluids, which are prone to erosion when flowing through the coiled tubing [1,2], resulting in thinning of the coiled tubing wall [3], as visually depicted in Figure 2. This thinning process not only compromises the tubing’s strength but also reduces its service life. Through investigation, Jia et al. [4] showed that erosion-caused coiled tubing failure accounted for about 8.6%, and conveying sand was one of the main failure modes. By calculating the rate of impact thinning, the damage of erosion to coiled tubing wall is evaluated, which provides a basis for implementing effective protection and management measures to prolong the service life of coiled tubing.

Figure 1.
Coiled tubing operations site.

Figure 2.
Erosion leads to thinning of coiled tubing wall.
Significant progress has been made by numerous scholars in the study of erosion problems. Cui et al. [5] and Cheng et al. [6] showed that the erosion rate increased with the increase in flow velocity, and there was a critical impact angle to make the erosion rate reach its maximum value. Zhou et al. [7] studied the phenomenon of solid–liquid swirl erosion in pipelines by using a circulating loop system and a variety of experimental methods. They determined that velocity, sand, and concentration were the main influencing factors of pipeline erosion and established a highly fitted regression equation to predict erosion behavior. Xie et al. [8] used high-speed camera technology and a scanning electron microscope to capture sand movement and microscopic erosion images and estimated the erosion rate by the weight loss method.
Advances in computational fluid dynamics (CFD) technology provide a powerful tool for pipeline erosion research. In multiphase liquid–solid simulations, solid particles can be simulated with Eulerian [9] or Lagrangian approaches [10]. The choice of the most correct approach depends on the type of application and the variables involved, such as turbulence or solid particle concentration. Sedrez et al. [11] used the Euler–Lagrange method with the Reynolds stress model for turbulence and the Eulerian multiphase model to study pipeline erosion in oil and gas production, finding that higher mixture velocities led to increased erosion in both liquid–sand and multiphase systems. Wang et al. [12] utilized the RNG k-ε turbulence model and the discrete phase model (DPM) for a comprehensive simulation of erosion processes. The analysis focused on particle erosion mechanisms, the formulation of erosion laws, and the validation of simulation accuracy across varying angles. Zhu et al. [13] investigated reservoir section casing erosion during gas recovery with gas–solid two-phase flow experiments and simulations. Bilal et al. [14] conducted CFD simulations on 90° elbows with various curvature radii and a 45° bend configuration. Comparison with experimental data indicated consistent erosion patterns and maximum erosion locations. Liu et al. [15] employed a Lagrangian-based CFD model to investigate erosion wear on coiled tubing, revealing that severe erosion on curved pipes, particularly at the pipe-casing gap, intensified with higher mass flow rates and sensitivity to sand size, was expedited by increased injection rates, and moderated by higher fluid viscosity. Cao et al. [16] investigated erosion on the inner walls of spiral curved coiled tubing using experimental and numerical simulation methods. The study revealed that higher flow rates worsened erosion, larger sand diameters and pitches decreased erosion rates, and smaller pitches led to a more even erosion distribution. Lai et al. [17] used a two-way coupled Eulerian–Lagrangian approach, merging Grant and Tabakoff’s reflection model with the erosion model from the Erosion/Corrosion Research Center, to predict erosion rates and patterns in solid particle erosion within a centrifugal pump for liquid–solid flow. Shah et al. [18] analyze pipeline erosion in liquid–solid flow through coiled tubing using CFD, emphasizing the impact of factors like flow rate, slurry concentration, proppant characteristics, and fluid viscosity. Zhao et al. [19] used an Eulerian–Lagrangian approach to examine the erosion of four elbows in series, finding that erosion behavior was affected by connection length, particle diameter, curvature radius, and varying sensitivities to particle size among the elbows. Li et al. [20] used the Euler–Lagrange method to analyze gas–solid two-phase flow, comparing one-way coupled DPM with four-way coupled DDPM. Their study revealed that DDPM accurately predicts erosion distribution, showing that 50 μm particles experience erosion rates 8.32 times higher than 10 μm particles at similar gas transmission rates. Hong et al. [21] used the CFD-DPM model in the Lagrange coordinate system to investigate the erosion behavior of different pipeline structures under various flow conditions. Ahn et al. [22] utilized the CFD-DPM model in the Lagrange coordinate system to design an optimized pipeline structure, achieving a significant improvement with an 80% reduction in turbulent dissipation rate and a 99.2% decrease in erosion wear rate.
The rapid development of machine learning and intelligent algorithms has brought great impetus to the study of solid–liquid erosion. Intelligent algorithms such as neural networks, extreme learning machine, and their optimization methods have achieved remarkable results in this field. Pandya et al. [23] developed an improved erosion prediction model combining CFD and machine learning. Through experiments and optimization, the prediction error of the erosion rate was reduced from more than 40% to less than 10%. Shamshirband et al. [24] have shown that the adaptive neuro-fuzzy inference system (ANFIS) model has high accuracy and reliability in predicting erosion. Deng et al. [25] used CFD to analyze the erosion of slot screen and established a life prediction model based on the BP neural network. The prediction results of the model applied to the actual conditions of Bohai Bay are consistent with the actual situation. Wang et al. [26] proposed a genetic algorithm-optimized extreme learning machine (GA-ELM) method to predict the erosion rate and residual life of defective elbows. Zangenehmadar et al. [27] have shown that the ANN model is accurate and robust in predicting the remaining useful life of the water pipe network. Shaik et al. [28] developed a feedforward back-propagation neural network (FFBPN) to predict the status of crude oil pipelines. The research results verify the robustness of the FFBPN model and find that the performance of the FFBPN is better than those of the previous methods. One year later, Shaik et al. [29] proposed another intelligent model and achieved good prediction results.
In summary, current research on solid–liquid two-phase erosion and wear mainly focuses on the outcomes of erosion. The effects of various variables on erosion rates are primarily studied using numerical simulation methods, with experimental methods also exploring the microscopic morphology of erosion based on these simulations. Intelligent prediction methods, compared to traditional experimental approaches, save significant experimental work and improve efficiency. They better capture the complex factors involved in solid–liquid erosion processes and enhance accuracy compared to numerical simulation methods. Although some predecessors have conducted research in intelligent prediction methods, the field still lacks maturity, with a limited scope and room for improving accuracy. Therefore, to enhance predictive accuracy, this study’s model is based on SSA to optimize BPNN. Through the training algorithm, the model fitting degree and prediction accuracy reach 0.99, which can accurately predict the erosion rate of coiled tubing. This model fills the gap in intelligent algorithms regarding coiled tubing erosion, offering guidance for operations like hydraulic sandblasting on coiled tubing.
2. Experimental
2.1. Experimental Device and Processes
The coiled tubing erosion experiment was carried out on the self-made jet erosion test bench. The test bench was composed of a flow control system, a stirring system, a jet chamber, and other main parts. The schematic diagram is shown in Figure 3, and the physical diagram is shown in Figure 4.
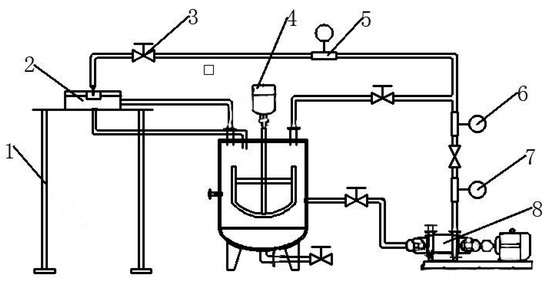
Figure 3.
Erosion test equipment schematic diagram. 1. Test rig; 2. Nozzle; 3. Control valve; 4. Liquid mixer; 5. Electromagnetic flow meter; 6. Temperature sensor; 7. Pressure sensor; 8. Mortar pump.

Figure 4.
Erosion test equipment physical map.
The steps of the coiled tubing erosion experiment were as follows:
- (1)
- Multiple sets of samples were cut from Φ50.8 mm × 4.4 mm coiled tubing with dimensions of 20 mm × 20 mm × 2 mm.
- (2)
- Unique identification numbers were assigned to the samples and they were weighed using a balance with a capacity of 100 g and an accuracy of 0.1 mg.
- (3)
- The samples were secured in the fixture and distance and angle were adjusted accordingly.
- (4)
- A 1 wt% KCl aqueous solution was poured into the sand-mixing barrel.
- (5)
- The mortar pump was started and the rotation speed was adjusted.
- (6)
- The 40–70 mesh silica sand was gradually added to achieve a sand concentration of 15–75 kg/m3.
- (7)
- The frequency converter was slowly adjusted to reach the predetermined impact velocity.
- (8)
- After the experiment was completed, the samples were removed, cleaned, and reweighed.
2.2. Experimental Results
By simulating the actual situation of coiled tubing solid–liquid erosion, the surface of the sample was impacted at a flow rate of 6.63 m/s, 13.27 m/s, 19.90 m/s, and 26.54 m/s. The erosion time was 2 h, the sand concentration was 50 kg/m3, and the jet injection angle was 30°, 45°, 60°, and 90°. The erosion pattern of the coiled tubing sample was obtained, as shown in Figure 5.
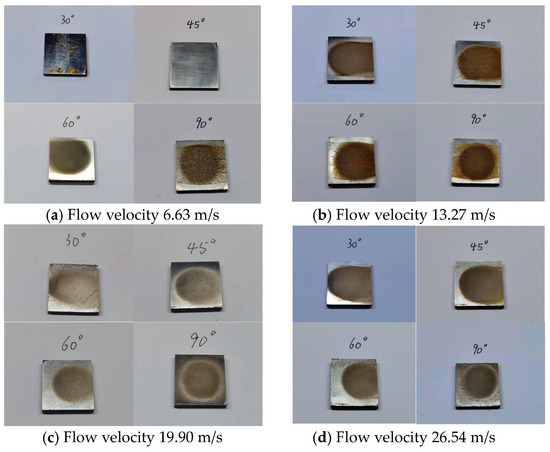
Figure 5.
Erosion morphology of coiled tubing sample.
After erosion, all the coiled tubing samples had a visibly damaged appearance which was scratched and washed by particles. The common erosion morphology of the erosion center was that the sand particles repeatedly impacted to form a clear and identifiable pit, mainly scratches. The damage of the test sample mainly included the impact of the normal component of the impact velocity of the sand on the test sample, and the scratches that had a long time of contact with the surface of the coiled tubing sample for the sand with a small normal velocity component.
The observation of the coiled tubing erosion test in solid–liquid two-phase flow showed that the erosion phenomenon on the surface of the coiled tubing sample was mainly caused by multi-particle impact. The erosion damage degree of coiled tubing surface varied with the impact angle. In addition, with the change in impact velocity, the erosion damage of the pipeline surface also differed. The weight loss method can be used to calculate the weight loss of coiled tubing samples under different conditions, so as to determine the erosion rate of the pipe wall, as shown in Table 1. The results show that the erosion rate increases with the increase in impact velocity between 0.04 mm/h and 0.1 mm/h. It is worth noting that the erosion rate of coiled tubing reached a peak near the erosion angle of 45°.

Table 1.
Erosion weight loss and erosion rate of coiled tubing samples.
A series of erosion experiments were conducted in this study to investigate the correlation between erosion rate and impact angle, impact velocity, sand diameter, and sand concentration. The experimental findings are summarized as follows.
Figure 6 showed the erosion rate changes in the coiled tubing samples at different impact velocities. Under the four impact velocities, the samples demonstrated a trend of initially increasing, then decreasing, and ultimately stabilizing the erosion rate. At an impact angle of 45°, the erosion rate of the sample reaches its maximum. The analysis suggested that the most significant erosion-thinning effect occurred due to the equality of shear and normal stress at a 45° impact angle.
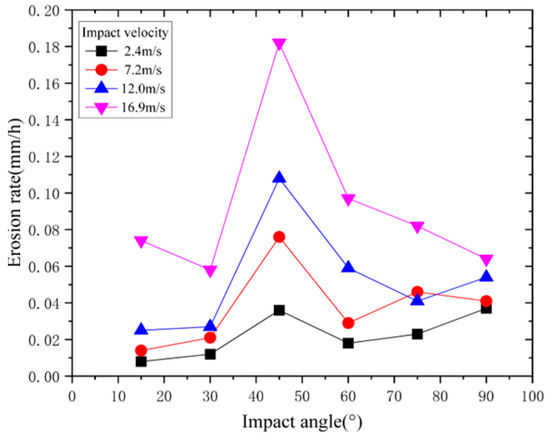
Figure 6.
Relationship between impact angle and coiled tubing erosion rate (under different impact velocities).
Figure 7 shows the erosion rate changes in the coiled tubing samples at different impact angles. Under the six impact angles, the erosion rate showed good consistency with the impact velocity, exhibiting a gradual increase as the velocity increased. The greatest increase in erosion rate was observed when the velocity increased from 12.0 m/s to 16.9 m/s. The analysis suggested that, as the impact velocity increased, the kinetic energy of the sand particles increased, resulting in stronger cutting and impact actions, leading to greater damage to the coiled tubing.
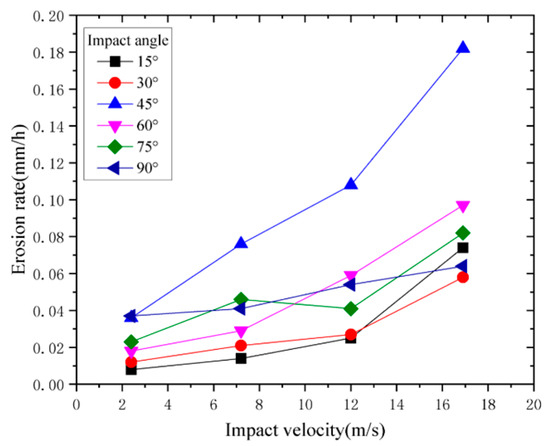
Figure 7.
Relationship between impact velocity and coiled tubing erosion rate (under different impact angles).
Figure 8 shows the erosion rate changes in coiled tubing samples at different sand concentrations. Within the concentration range of 30–45 kg/m3, the erosion rate increased with an increase in sand concentration. In the range of 45–60 kg/m3, the erosion rate decreased with an increase in sand concentration. However, within the concentration range of 60–75 kg/m3, the erosion rate significantly increased again with an increase in sand concentration. The analysis showed that, under normal circumstances, as the concentration of sand particles increased, the impact energy and cutting action of the particles intensified, resulting in an increase in erosion rate. However, within certain concentration ranges, a phenomenon known as the “shielding effect” [30] may occur. This effect involves an increase in collisions between sand particles, leading to enhanced mutual blocking and shielding effects. As a result, some of the impact energy is dispersed, reducing the direct impact energy acting on the surface of the sample and resulting in a decrease in erosion rate. With further increases in concentration, the surface structure of the sample undergoes destruction, leading to heightened intensity in the impact between the sand particles and the surface. This resurgence in impact energy and cutting action reclaimed its dominant role, resulting in a substantial subsequent increase in the erosion rate.
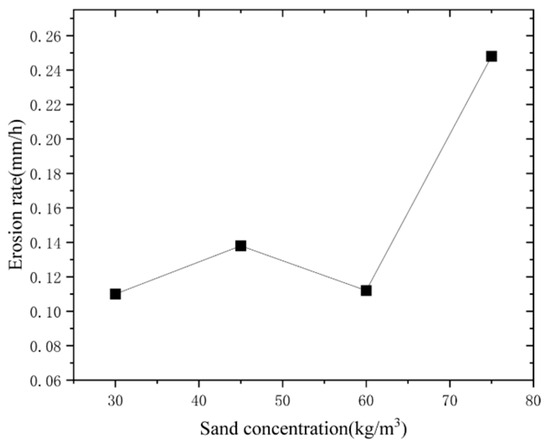
Figure 8.
Relationship between sand concentration and coiled tubing erosion rate.
Figure 9 shows the erosion rate changes in coiled tubing samples at different sand diameters. As the sand particle diameter decreased (i.e., with an increase in mesh size), the erosion rate exhibits a trend of initially increasing and then decreasing. The maximum erosion rate was observed with 80-mesh sand particles. The analysis suggested that there existed a critical threshold in the correlation between sand particle diameter and erosion rate. When the diameter was below the critical threshold, larger sand particles exhibited higher impact energy, stronger cutting action, and increased particle accumulation effects, resulting in an increased erosion rate. Conversely, when the diameter exceeded the critical threshold, the larger sand particle size led to a reduction in the number of particles, decreasing the frequency of material impact and consequently reducing the erosion rate.
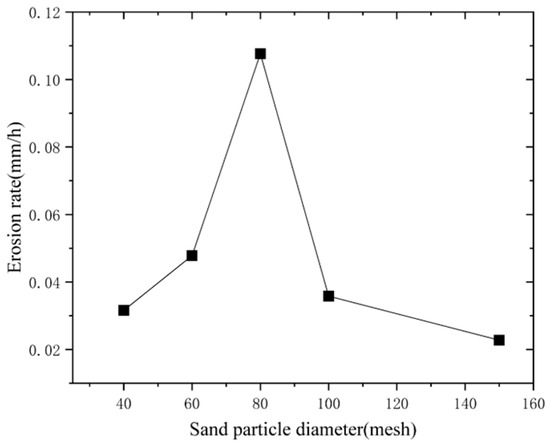
Figure 9.
Relationship between sand diameter and coiled tubing erosion rate.
3. GRA of Influencing Factors of Coiled Tubing Erosion Rate
GRA is a special analysis method for solving multi-factor and nonlinear problems [31]. It overcomes the limitations of mathematical and statistical methods in terms of sample requirements by describing the strength, magnitude, and order of relationships among factors based on sample data. Liao et al. [32] employed GRA to identify potential factors with greater influence on prediction, thereby reducing computational complexity. Specifically, GRA is utilized to select the key controlling factors as inputs for the model, and the calculation steps are as follows [33]:
- (1)
- Taking the erosion rate as the reference sequence, the impact angle, impact velocity, sand diameter, and sand concentration are used as the comparison sequence.
- (2)
- Perform dimensionless processing.
- (3)
- Calculate the relational coefficient between the comparison sequence xi and the reference sequence x0, as shown in Equation (1), where i is the index of features, i = 1, 2, ..., m, indicating different features; k is the index of samples, k = 1, 2, ..., n, representing distinct samples; [0, 1] is the resolution coefficient, usually 0.5.
- (4)
- Calculate the relational degree of the ith feature, as shown in Equation (2), where n denotes the total number of samples.
GRA is employed to analyze factors including impact angle, impact velocity, sand diameter, and sand concentration in the experimental data of solid–liquid erosion of coiled tubing, as shown in Table 2. During the erosion process of coiled tubing, the degree of influence on the erosion rate varies significantly among different factors. The impact velocity is determined to be the most critical influencing factor, followed by the impact angle and sand concentration, while the influence of sand diameter is relatively small. The analysis suggests that an increase in impact velocity significantly enhances the kinetic energy of the sand particles, intensifying their cutting and impact actions, thereby exacerbating the erosion intensity. The impact angle and sand concentration directly affect the contact mode and impact strength between the sand and pipeline surface and then affect the erosion degree. Although the sand particle diameter will affect the number of sand particles, its influence on erosion has no obvious law.

Table 2.
Summary of GRA results.
4. Methodology
4.1. Basic Principle of BPNN
ANN performs well in dealing with complex linear and nonlinear problems. Among them, BPNN is a widely used multi-layer feedforward network [34,35], which is trained by an error back-propagation algorithm with high efficiency and accuracy [36]. Its working principle is based on the gradient descent method. By repeatedly adjusting the weight and threshold of the network, the mean squared error (MSE) between the network output and the target output is gradually reduced. The BPNN is composed of an input layer, one or more hidden layers, and an output layer. The signal starts to propagate from the input layer, and after the processing and transformation of the hidden layer, it ultimately affects the output results of the output layer.
The training process for BPNN includes two stages: learning and working. During the learning stage, the training sample data are repeatedly trained and learned, primarily by adjusting the weights of the output layer and the hidden layer using feedback from the output data error signal. The working stage occurs after the completion of the learning stage, where the trained network is utilized to predict new input data.
4.2. Basic Principle of SSA
The SSA is a new optimization algorithm based on swarm intelligence proposed in 2020 [37]. It simulates sparrow foraging and anti-predation behavior and uses the discoverer–follower model and detection and early warning mechanisms to achieve the goal of foraging optimization and avoiding danger. In the SSA, the discoverer searches for food on behalf of the entire sparrow population and provides the foraging direction to all followers. Some followers will compete with the discoverer for food, allowing the population to search for resources more comprehensively. When faced with the threat of predation, the sparrows on the edge of the population need to adjust their position to find a safe area, while the sparrows in the center are close to their neighbors to reduce the danger.
In the SSA, the population is divided into discoverers, followers, and sentinels in specific proportions, with everyone’s position representing a solution in the problem’s solution space. Follower individuals dynamically adjust their positions based on the movements of discoverer individuals. The follower’s main role is to follow the discoverers’ lead and engage in foraging behaviors, searching for food in the designated directions and regions. Sentinels, on the other hand, perform anti-predation behaviors by monitoring the vicinity of the foraging areas.
The discoverer looks for food for the entire sparrow group and points out the direction of food locations for followers. Therefore, the range of finders looking for food is much larger than that of followers. After many calculations, the location of the discoverer is described as shown in Equation (3), where t is the current number of iterations, itermax is the maximum number of iterations and is a constant, Xi,j is the specific position of the ith sparrow on the jth dimension, a is a random constant with a value in the range of 0–1, R2 and ST are the threshold and safety value when danger is detected, Q is a random constant whose value range is in its normal distribution interval, and L is a 1 × d matrix, where d denotes the dimension of the problem. All the elements of the matrix L are valued at constant 1.
Once the followers become aware that the discoverer has found a more promising food area, they swiftly depart from their current location. The description of the follower location update is shown in Equation (4), where XP is the most favorable location area for the discoverer, Xworst is the worst location area where the discoverer is currently located, and A is a matrix with an element of −1 or 1, which is obtained by transposition and inverse operations after random assignment. When i is greater than half of the total number of sparrows, the ith sparrow with a lower fitness value is not involved in foraging. At this time, these sparrows need to find areas where they can obtain more energy to perform foraging behavior.
It is assumed that one-tenth to one-fifth of the total number of individuals in the sample can perceive the threat and randomly generate their positions in the population. The location description of the alerter is shown in Equation (5), where, Xbest is the best location area for the current sparrow; is the learning step length, assuming that it is a random number that conforms to the normal distribution, with an expected value of 0 and a standard deviation of 1; K is the step size control parameter, and the value range is from −1 to 1, which represents the direction of sparrow individual transfer; the value of K is related to the fitness value fi of the current sparrow individual; and fw is the fitness value of the current sparrow individual as the best or the worst.
4.3. SSA-BPNN Model
The BPNN has resolved numerous application problems, but as its scope of application expands, it has also revealed drawbacks such as slow convergence speed and susceptibility to local optima [38,39]. The SSA has good global search and local development capabilities. By combining the SSA with the BPNN, the advantages of both can be fully utilized. On the one hand, using the powerful generalization mapping ability of the BPNN, the SSA is used to optimize the weight and threshold of the BPNN to improve its convergence speed and global search ability and obtain more accurate results.
The main implementation components of the SSA-BPNN model include the following:
- (1)
- Determine the structure of the BPNN according to the functional requirements.
- (2)
- The SSA is used to optimize the weight and threshold of the BPNN, and the initial optimal parameters are obtained.
- (3)
- The optimized optimal weights and thresholds are given to the BPNN to keep the network structure unchanged. Then, the optimized network is verified by experimental data.
The specific model framework is shown in Figure 10.
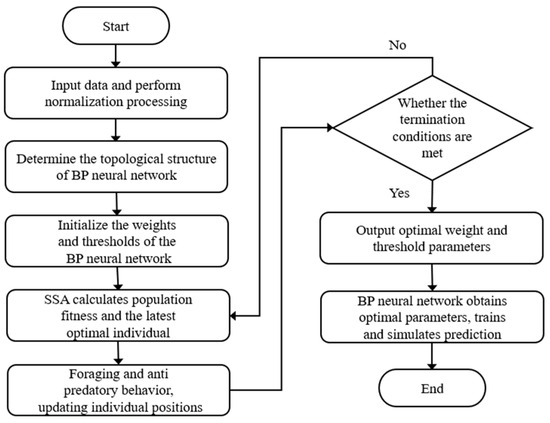
Figure 10.
SSA-BPNN flowchart.
5. Case Analysis
5.1. Data Selection
Using MATLAB R2022b to develop the SSA-BPNN model, the main parameters of the SSA-BPNN model, the transfer function of each layer, and the design of the learning algorithm are shown in Table 3.

Table 3.
Main parameter settings of SSA-BPNN.
For the SSA-BPNN model, the correctness and comprehensiveness of the learning samples are the keys to predicting success or failure. In this study, the experimental results of the coiled tubing erosion rate and the data of reference [40,41] are selected. The exhaust volume sand ratio, impact velocity, sand diameter, and sand mass flow are used as the input parameters of the learning sample, and the erosion rate is used as the output parameters of the learning sample. The specific parameters are shown in Table 4. The first 80% of the experimental data were trained based on the SSA-BPNN model, and the last 20% of the experimental data were used to verify the trained model, and the results were accurate.

Table 4.
Coiled tubing erosion rate parameters.
5.2. Results Analysis
In MATLAB for SSA-BPNN analysis, the evaluation criteria typically include the MSE and R [28]. A smaller MSE value and an R value closer to 1 indicate a better training outcome, reflecting a more effective model fitting.
Figure 11 is the regression analysis diagram of the SSA-BPNN model, showing the network prediction (output) of the response (target) of the training set, the validation set, and the test set. From Figure 11, it is evident that the average goodness of fit for the SSA-BPNN coiled tubing erosion model is 0.9998, indicating a high level of fit. This high goodness of fit suggests that the SSA-BPNN model demonstrates excellent predictive performance.
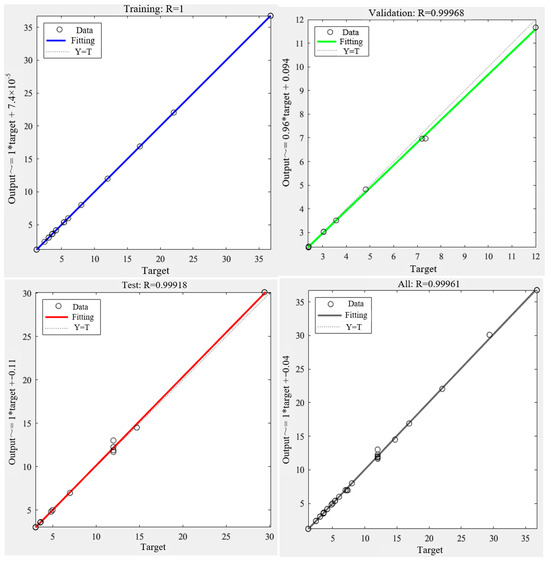
Figure 11.
Training, testing, validation, and overall R = 0.9996 obtained for training dataset.
Figure 12 illustrates the relationship between the gradient of the training data and the MSE. The SSA-BPNN model exhibited excellent validation performance, reaching its minimum MSE value of 0.035258 at epoch 100. This signifies the model’s strong predictive capabilities and effectiveness.
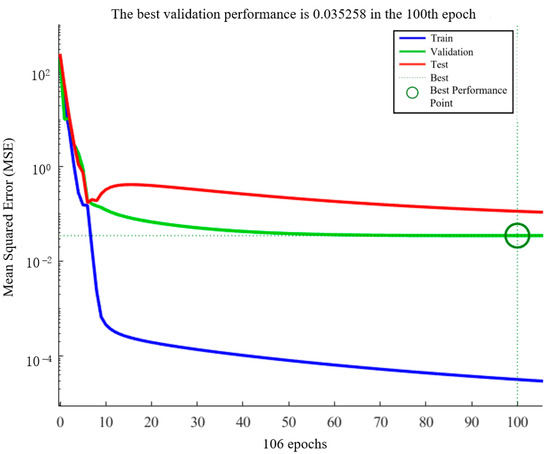
Figure 12.
The relationship between the gradient and the MSE of the training data.
Figure 13 shows the comparison between the actual value and the predicted value. The root mean square error (RMSE) between the actual data and the predicted data is 1.25 × 10−6, which has good consistency.
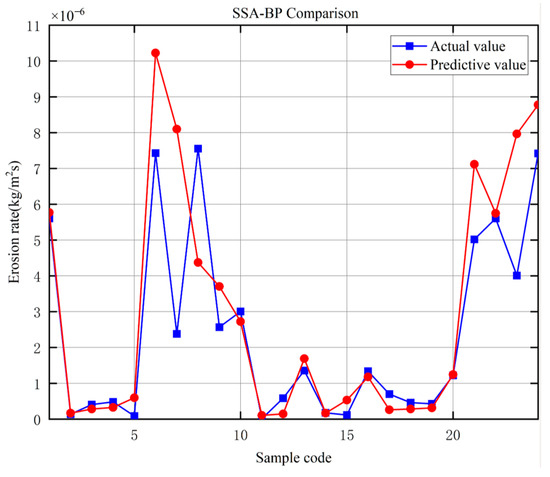
Figure 13.
Comparison chart of erosion rate predicted by SSA-BPNN.
To further assess the model’s accuracy, standard statistical validation tests were conducted on the SSA-BPNN model, including the coefficient of determination (r2), reduced chi-square (X2), RMSE, mean bias error (MBE), and mean percentage error (MPE) [42]. Throughout the training, testing, and validation phases, the goodness of fit between experimental measurements and model calculations is reflected in the SSA-BPNN performance, specifically in predicting the erosion rate parameter, as presented in Table 5. The SSA-BPNN accurately predicts coiled tubing erosion rates with a high coefficient of determination and minimal errors, showcasing a strong alignment between predicted and actual values.

Table 5.
The verification of the SSA-BPNN models.
Through the test of the SSA-BPNN model and error analysis and discussion, it is found that the SSA-BPNN model has high prediction accuracy and fitting degree, which can link the nonlinear relationship between coiled tubing erosion rate and influencing factors well while accurately and quickly predicting coiled tubing erosion rate.
6. Conclusions
Accurate prediction of the coiled tubing erosion rate plays an important role in prolonging and improving the effective service life of coiled tubing. In this study, the influence of different factors on the erosion rate of coiled tubing was studied from the experiment, and the input index of the model was determined by GRA. At the same time, the SSA is innovatively proposed to optimize the BPNN, and a prediction model of coiled tubing erosion rate is constructed. There are five main conclusions.
- (1)
- Based on the experimental results, it is evident that the maximum erosion rate of the coiled tubing occurs at a 45° impact angle.
- (2)
- According to the GRA results, the impact velocity, impact angle, and sand concentration of the sand-carrying fluid have a strong influence on the erosion rate of coiled tubing, and the impact velocity has the greatest influence on the erosion rate of coiled tubing.
- (3)
- The SSA-BPNN model is reliable in predicting the erosion rate of coiled tubing, which can provide guidance for coiled tubing hydraulic sand blasting operation.
- (4)
- This method can provide a reference for the erosion rate of coiled tubing. In the future, influence factors such as the defect size and working conditions of coiled tubing can be considered.
- (5)
- The feature selection of the model is limited, because only five influencing parameters are selected as input parameters to predict the erosion rate of coiled tubing. This indicates that the influence of other parameters on the erosion rate may not be considered, which makes the model unable to fully explain the complexity of the erosion rate. In future model optimization, it is recommended to expand the scope of the dataset and consider a wider range of impact parameters.
Author Contributions
Conceptualization, Y.C.; Methodology, Y.C.; Software, F.F. and G.W.; Validation, G.W.; Formal analysis, G.W. and Y.H.; Investigation, W.Z.; Resources, W.Z.; Data curation, F.F.; Writing—original draft, Y.C.; Writing—review & editing, F.F.; Visualization, F.F.; Supervision, W.Z. and Y.H.; Project administration, Y.C.; Funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, under grant number 52374039 and 52274006, the Natural Science Basic Research Program of Shaanxi, under grant number 2023-JC-YB-337. And the APC was funded by Yinping Cao.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jiang, G.C.; Li, Y.Z.; He, Y.B.; Dong, T.F.; Sheng, K.M.; Sun, Z. Subsection and Superposition Method for Reservoir Formation Damage Evaluation of Complex-Structure Wells. Pet. Sci. 2023, 20, 1843–1856. [Google Scholar] [CrossRef]
- Wang, Z.H.; Xu, Y.F.; Khan, N.; Zhu, C.L.; Gao, Y.H. Effects of the Surfactant, Polymer, and crude oil properties on the formation and stabilization of oil-based foam liquid films: Insights from the microscale. J. Mol. Liq. 2023, 373, 121194. [Google Scholar] [CrossRef]
- Xu, A.R.; Dou, Y.H.; Feng, C.X.; Zheng, J.; Cui, X.K. Coiled Tubing Erosion Prediction and Fracturing Fluid Parameters Optimization During Hydraulic Jet Fracturing. J. Fail. Anal. Prev. 2022, 22, 1276–1292. [Google Scholar] [CrossRef]
- Jia, P.; Zhu, X.X.; Xue, S.F.; Fang, J. Numerical Simulation on Coiled Tubing Erosion During Hydraulic Fracturing. J. Fail. Anal. Prev. 2020, 20, 1928–1938. [Google Scholar] [CrossRef]
- Cui, L.; Li, Z.; Dou, Y.H. Erosion–Corrosion Behavior of 20Cr Steel in Corrosive Solid–Liquid Two-Phase Flow Conditions. J. Fail. Anal. Prev. 2018, 18, 640–646. [Google Scholar] [CrossRef]
- Cheng, J.R.; Li, Z.; Zhang, N.S.; Dou, Y.H.; Cui, L. Experimental Study on Erosion-Corrosion of TP140 Casing Steel and 13Cr Tubing Steel in Gas–Solid and Liquid–Solid Jet Flows Containing 2 wt % NaCl. Materials 2019, 12, 358. [Google Scholar] [CrossRef]
- Zhou, H.; Ji, Q.F.; Liu, W.; Ma, H.Y.; Lei, Y.; Zhu, K.Q. Experimental Study on Erosion-Corrosion Behavior of Liquid–Solid Swirling Flow in Pipeline. Mater. Des. 2022, 214, 110376. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Cao, X.W.; Li, Q.P.; Yao, H.Y.; Qin, R.; Sun, X. Experimental Study on Particle Movement and Erosion Behavior of the Elbow in Liquid-Solid Flow. Heliyon 2023, 9, e21275. [Google Scholar] [CrossRef]
- Beccati, N.; Ferrari, C.; Parma, M.; Semrrin, M. Euerian Multi-Phase CFD model for predicting the performance of a centrifugal dredge pump. Int. J. Comp. Meth. Exp. Meas. 2019, 7, 316–326. [Google Scholar]
- Marinack, M.C., Jr.; Mpagazehe, J.N.; Higgs, C.F., III. An Eulerian, lattice-based cellular automata approach for modeling multiphase flows. Powder Technol. 2012, 221, 47–56. [Google Scholar] [CrossRef]
- Sedrez, T.A.; Shirazi, S.A.; Rajkumar, Y.R.; Sambath, K.; Subramani, H.J. Experiments and CFD Simulations of Erosion of a 90° Elbow in Liquid-Dominated Liquid-Solid and Dispersed-Bubble-Solid Flows. Wear 2019, 426–427, 570–580. [Google Scholar] [CrossRef]
- Wang, G.; Gao, Q.F.; Kou, L.Y.; Zhang, P.; Wang, W.H.; Deng, J.F.; Zhu, X.J. Study on Liquid-Solid Jet Erosion Characteristics of 316L Stainless Steel. J. Mech. Sci. Technol. 2023, 37, 1871–1882. [Google Scholar] [CrossRef]
- Zhu, X.H.; Peng, P.; Jing, J.; Song, W. Research on Casing Erosion in Reservoir Section of Gas Storage Wells Based on Gas-Solid Two-Phase Flow. Eng. Fail. Anal. 2022, 142, 106688. [Google Scholar] [CrossRef]
- Bilal, F.S.; Sedrez, T.A.; Shirazi, S.A. Experimental and CFD Investigations of 45 and 90 Degrees Bends and Various Elbow Curvature Radii Effects on Solid Particle Erosion. Wear 2021, 476, 203646. [Google Scholar] [CrossRef]
- Liu, S.H.; Zhang, Y.W.; Tu, Y.L. Erosion Wear Law of Coiled Tubing Outer Wall. China Powder Sci. Technol. 2016, 22, 80–83. [Google Scholar]
- Cao, Y.P.; Chen, Z.T.; Dou, Y.H.; Zheng, J.; Kang, Z.F. Erosion Factor Analysis of Coiled Tubing with Helical Buckling. China Pet. Mach. 2023, 51, 143–148+156. [Google Scholar]
- Lai, F.; Wang, Y.; EI-Shahat, S.A.; Li, G.J.; Zhu, X.Y. Numerical Study of Solid Particle Erosion in a Centrifugal Pump for Liquid–Solid Flow. J. Fluid. Eng. 2019, 141, 121302. [Google Scholar] [CrossRef]
- Shah, S.N.; Jain, S. Coiled Tubing Erosion During Hydraulic Fracturing Slurry Flow. Wear 2008, 264, 279–290. [Google Scholar] [CrossRef]
- Zhao, X.Y.; Cao, X.W.; Xie, Z.Q.; Cao, H.G.; Wu, C.; Bian, J. Numerical Study on the Particle Erosion of Elbows Mounted in Series in the Gas-Solid Flow. J. Nat. Gas. Sci. Eng. 2022, 99, 104423. [Google Scholar] [CrossRef]
- Li, B.C.; Zeng, M.; Wang, Q.W. Numerical Simulation of Erosion Wear for Continuous Elbows in Different Directions. Energies 2022, 15, 1901. [Google Scholar] [CrossRef]
- Hong, B.Y.; Li, Y.B.; Li, X.P.; Ji, S.P.; Yu, Y.F. Numerical Simulation of Gas-Solid Two-Phase Erosion for Elbow and Tee Pipe in Gas Field. Energies 2021, 14, 6609. [Google Scholar] [CrossRef]
- Ahn, J.H.; Asif, R.; Lee, H.W.; Hwang, I.J.; Hu, J.W. Design and Material Optimization of Oil Plant Piping Structure for Mitigating Erosion Wear. Appl. Sci. 2024, 14, 5234. [Google Scholar] [CrossRef]
- Pandya, D.A.; Dennis, B.H.; Russell, R.D. A Computational Fluid Dynamics Based Artificial Neural Network Model to Predict Solid Particle Erosion. Wear 2017, 378–379, 198–210. [Google Scholar] [CrossRef]
- Shamshirband, S.; Malvandi, A.; Karimipour, A.; Goodarzi, M.; Afrand, M.; Petković, D.; Mahmoodian, N. Performance Investigation of Micro- and Nano-Sized Particle Erosion in a 90° Elbow Using an ANFIS Model. Powder Technol. 2015, 284, 336–343. [Google Scholar] [CrossRef]
- Deng, F.H.; Deng, Z.Q.; Liang, H.; Wang, L.H.; Hu, H.T.; Xu, Y. Life Prediction of Slotted Screen Based on Back-Propagation Neural Network. Eng. Fail. Anal. 2021, 119, 104909. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, C.; Li, Y.L.; Liu, Y.C. Numerical Simulation of Erosion Characteristics and Residual Life Prediction of Defective Pipelines Based on Extreme Learning Machine. Energies 2022, 15, 3750. [Google Scholar] [CrossRef]
- Zangenehmadar, Z.; Moselhi, O. Assessment of Remaining Useful Life of Pipelines Using Different Artificial Neural Networks Models. J. Perform. Constr. Facil. 2016, 30, 04016032. [Google Scholar] [CrossRef]
- Shaik, N.B.; Pedapati, S.R.; Taqvi, S.A.A.; Othman, A.R.; Dzubir, F.A.A. A Feed-Forward Back Propagation Neural Network Approach to Predict the Life Condition of Crude Oil Pipeline. Processes 2020, 8, 661. [Google Scholar] [CrossRef]
- Shaik, N.B.; Pedapati, S.R.; Othman, A.R.; Bingi, K.; Dzubir, F.A.A. An Intelligent Model to Predict the Life Condition of Crude Oil Pipelines Using Artificial Neural Networks. Neural. Comput. Appl. 2021, 33, 14771–14792. [Google Scholar] [CrossRef]
- Macchini, R.; Bradley, M.S.A.; Deng, T. Influence of particle size, density, particle concentration on bend erosive wear in pneumatic conveyors. Wear 2013, 1–2, 21–29. [Google Scholar] [CrossRef]
- Huang, C.H.; Chang, H.Y.; Yang, C.H. A Novel Grey-Based Feature Ranking Method for Feature Subset Selection. J. Chin. Inst. Eng. 2021, 33, 14771–14792. [Google Scholar]
- Liao, K.X.; Yao, Q.K.; Wu, X.; Jia, W.L. A Numerical Corrosion Rate Prediction Method for Direct Assessment of Wet Gas Gathering Pipelines Internal Corrosion. Energies 2012, 5, 3892–3907. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, X.M.; Zhang, Y.M.; Zheng, Y.X.; Wang, T.Y. Gray Correlation Analysis of Factors Influencing Compressive Strength and Durability of Nano-SiO2 and PVA Fiber Reinforced Geopolymer Mortar. Nanotechnol. Rev. 2022, 11, 3195–3206. [Google Scholar] [CrossRef]
- Han, Y.L. Artificial Neural Network Technology as a Method to Evaluate the Fatigue Life of Weldments with Welding Defects. Int. J. Press. Vessels. Pip. 1995, 63, 205–209. [Google Scholar] [CrossRef]
- Nasiri, N.; Khosravani, M.R.; Weinberg, K. Fracture Mechanics and Mechanical Fault Detection by Artificial Intelligence Methods: A review. Eng. Fail. Anal. 2017, 81, 270–293. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Xue, J.K.; Shen, B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Hamey, L.G.C. XOR has No Local Minima: A Case Study in Neural Network Error Surface Analysis. Neural. Netw. 1998, 11, 669–681. [Google Scholar] [CrossRef]
- Nitta, T. Local Minima in Hierarchical Structures of Complex-Valued Neural Networks. Neural. Netw. 2013, 43, 1–7. [Google Scholar] [CrossRef]
- Cheng, J.R.; Yang, X.T.; Li, Z. Numerical simulation of Erosion for API Round Thread Connection in a Solid-liquid Two-phase Flow. China Pet. Mach. 2013, 34, 1067–1071. [Google Scholar]
- Cui, L.; Yang, Y.Q.; Li, J.W.; Li, M.F.; Chang, W.Q.; Cheng, J.R. Study on the Erosion Performance of QT1100 Coiled Tubing Steel in Liquid-Solid Two-phase Flow. China Pet. Mach. 2024, 10, 1–9. [Google Scholar]
- Vasić, M.V.; Jantunen, H.; Mijatović, N.; Nelo, M.; Velasco, P.M. Influence of coal ashes on fired clay brick quality: Random forest regression and artificial neural networks modeling. J. Clean. Product. 2023, 407, 137153. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).