Finite-Time Pinning Event-Triggered Control for Bipartite Consensus of Hybrid-Order Heterogeneous Multi-Agent Systems with Antagonistic Links
Abstract
1. Introduction
- 1.
- The finite-time consensus problem for heterogeneous multi-agent systems with mixed-order dynamics under cooperative–competitive interactions is addressed. To the authors’ knowledge, there is scarce literature simultaneously considering the heterogeneity and finite convergence of multi-agent systems. Moreover, this paper achieves finite-time consensus in systems communicated under a signed directed graph.
- 2.
- An innovative pinning event-triggered control protocol is designed for the proposed multi-agent system to achieve finite-time consensus. On one hand, pinning control is adopted to constrain those agents with zero in-degree to avoid unnecessary communication; on the other hand, event-triggered control is employed to save communication bandwidth. The control protocol proposed in this paper enhances the convergence performance of the system and prolongs the lifespan of the control devices.
- 3.
- The control protocol designed in this paper breaks the communication barrier between first-order agents and second-order agents, enabling communication between hybrid-order agents.
2. Preliminaries and Problem Formulation
2.1. Preliminaries on Signed Digraph Theory
2.2. Preliminaries on Technical Lemmas
2.3. Problem Formulation
3. Main Results
3.1. Design of Event-Triggered Control Protocol
3.2. Consensus Analysis
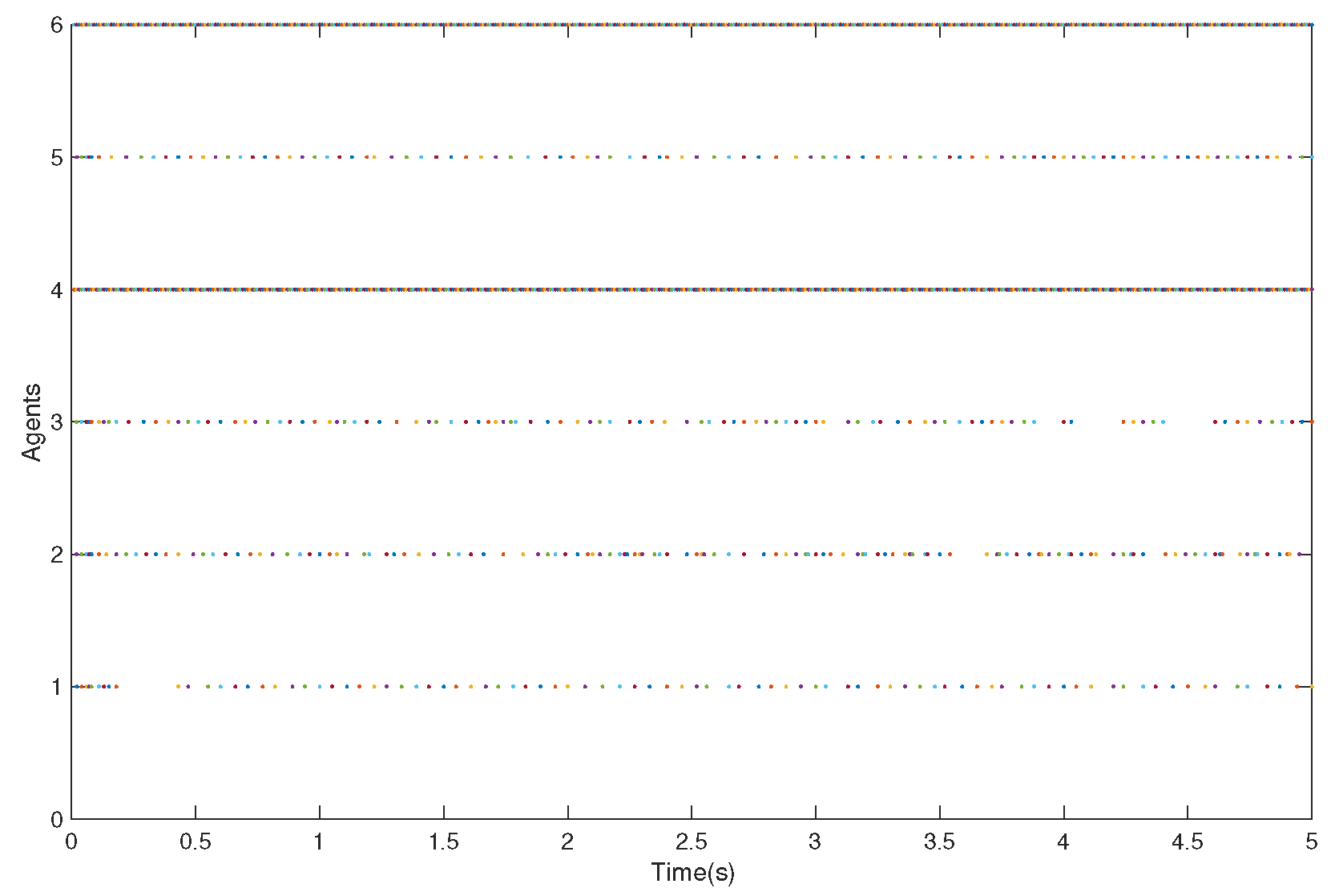
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, S.; Yu, J. Fault detection and time-varying formation control for nonlinear multi-agent systems with Markov switching topology. Inf. Sci. 2023, 649, 119657. [Google Scholar] [CrossRef]
- Liu, G. A Q-Learning-based distributed routing protocol for frequency-switchable magnetic induction-based wireless underground sensor networks. Future Gener. Comput. Syst. 2023, 139, 253–266. [Google Scholar] [CrossRef]
- Zhou, M.; Wan, Z.; Wang, H.; Wen, M.; Wu, R.; Wen, Y.; Yang, Y.; Yu, Y.; Wang, J.; Zhang, W. Malib: A parallel framework for population-based multi-agent reinforcement learning. J. Mach. Learn. Res. 2023, 24, 1–12. [Google Scholar]
- Zeng, C.; Wang, X.; Zeng, R.; Li, Y.; Shi, J.; Huang, M. Joint optimization of multi-dimensional resource allocation and task offloading for QoE enhancement in Cloud-Edge-End collaboration. Future Gener. Comput. Syst. 2024, 155, 121–131. [Google Scholar] [CrossRef]
- Bao, G.; Ma, L.; Yi, X. Recent advances on cooperative control of heterogeneous multi-agent systems subject to constraints: A survey. Syst. Sci. Control Eng. 2022, 10, 539–551. [Google Scholar] [CrossRef]
- Lu, M.; Wu, J.; Zhan, X.; Han, T.; Yan, H. Consensus of second-order heterogeneous multi-agent systems with and without input saturation. ISA Trans. 2022, 126, 14–20. [Google Scholar] [CrossRef]
- Shi, Y.; Yan, H.; Chen, S.; Zhan, X.; He, L. Distributed event-triggered consensus control for leaderless heterogeneous multiagent systems. J. Frankl. Inst. 2020, 357, 3219–3234. [Google Scholar] [CrossRef]
- Gao, R.; Yang, G.H. Resilient cluster consensus for discrete-time high-order multi-agent systems against malicious adversaries. Automatica 2024, 159, 111382. [Google Scholar] [CrossRef]
- Hu, X.; Xiong, Y.; Zhang, Z.; Li, C. Consensus of a new multi-agent system via multi-task, multi-control mechanism and multi-consensus strategy. Neurocomputing 2024, 584, 127586. [Google Scholar] [CrossRef]
- Tang, F.; Wang, H.; Zhang, L.; Xu, N.; Ahmad, A.M. Adaptive optimized consensus control for a class of nonlinear multi-agent systems with asymmetric input saturation constraints and hybrid faults. Commun. Nonlinear Sci. Numer. Simul. 2023, 126, 107446. [Google Scholar] [CrossRef]
- Chen, L.; Tong, S. Observer-Based Adaptive Fuzzy Consensus Control of Nonlinear Multiagent Systems Encountering Deception Attacks. IEEE Trans. Ind. Inform. 2024, 20, 1808–1818. [Google Scholar] [CrossRef]
- Amirkhani, A.; Barshooi, A.H. Consensus in multi-agent systems: A review. Artif. Intell. Rev. 2022, 55, 3897–3935. [Google Scholar] [CrossRef]
- Wang, J.; Yan, Y.; Liu, Z.; Chen, C.P.; Zhang, C.; Chen, K. Finite-time consensus control for multi-agent systems with full-state constraints and actuator failures. Neural Netw. 2023, 157, 350–363. [Google Scholar] [CrossRef]
- Zhou, H.; Sui, S.; Tong, S. Fuzzy adaptive finite-time consensus control for high-order nonlinear multiagent systems based on event-triggered. IEEE Trans. Fuzzy Syst. 2022, 30, 4891–4904. [Google Scholar] [CrossRef]
- Yang, P.; Zhang, A.; Bi, W. Finite-time group consensus for second-order multi-agent systems with input saturation. Neural Process. Lett. 2022, 54, 4211–4228. [Google Scholar] [CrossRef]
- Lu, R.; Wu, J.; Zhan, X.; Yan, H. Finite-time bipartite consensus for second-order nonlinear multi-agent systems under random switching topologies. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 4474–4478. [Google Scholar] [CrossRef]
- Nie, R.; Du, W.; Li, Z.; He, S. Sliding mode-based finite-time consensus tracking control for multi-agent systems under actuator attacks. Inf. Sci. 2023, 640, 118971. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, Z.; Liang, H.; Ahn, C.K. Neural-Network-Based Predefined-Time Adaptive Consensus in Nonlinear Multi-Agent Systems With Switching Topologies. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 9995–10005. [Google Scholar] [CrossRef]
- Jin, N.; Xu, J.; Zhang, H. Distributed Optimal Consensus Control of Multiagent Systems Involving State and Control Dependent Multiplicative Noise. IEEE Trans. Autom. Control 2023, 68, 7787–7794. [Google Scholar] [CrossRef]
- Atallah, M.; Okasha, M.; Dief, T.N.; Jallad, A.H. Optimal consensus control for multi-satellite assembly in elliptic orbit with input saturation. Acta Astronaut. 2023, 208, 82–90. [Google Scholar] [CrossRef]
- Sang, J.; Ma, D.; Zhou, Y. Group-Consensus of Hierarchical Containment Control for Linear Multi-Agent Systems. IEEE/CAA J. Autom. Sin. 2023, 10, 1462–1474. [Google Scholar] [CrossRef]
- Zhu, F.; Zhao, Y.; Fu, Y.; Dinh, T.N. Observer-Based Output Consensus Control Scheme for Strict-Feedback Nonlinear Multi-Agent Systems With Disturbances. IEEE Trans. Netw. Sci. Eng. 2023, 11, 2621–2631. [Google Scholar] [CrossRef]
- Li, X.; Yu, Z.; Li, Z.; Wu, N. Group consensus via pinning control for a class of heterogeneous multi-agent systems with input constraints. Inf. Sci. 2021, 542, 247–262. [Google Scholar] [CrossRef]
- Liu, D.; Ye, D.; Zhao, X.G. Fully distributed secure state estimation for nonlinear multi-agent systems against DoS attacks: An edge-pinning-based method. IEEE Trans. Autom. Sci. Eng. 2023, 21, 4237–4246. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, C.; Zhao, D.; Sun, B.; Li, Y. Event-triggered consensus control of continuous-time stochastic multi-agent systems. Automatica 2022, 137, 110022. [Google Scholar] [CrossRef]
- Du, S.; Sheng, H.; Ho, D.W.C.; Qiao, J. Secure Consensus of Multiagent Systems With DoS Attacks via Fully Distributed Dynamic Event-Triggered Control. IEEE Trans. Syst. Man, Cybern. Syst. 2023, 53, 6588–6597. [Google Scholar] [CrossRef]
- Ahmed, I.; Rehan, M.; Iqbal, N. A novel exponential approach for dynamic event-triggered leaderless consensus of nonlinear multi-agent systems over directed graphs. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 1782–1786. [Google Scholar] [CrossRef]
- Mu, R.; Wei, A.; Li, H.; Yue, L. Leader-following consensus for multi-agent systems with actuator faults via adaptive event-triggered control. J. Frankl. Inst. 2021, 358, 1327–1349. [Google Scholar] [CrossRef]
- Liu, F.; Song, Q.; Wen, G.; Lu, J.; Cao, J. Bipartite synchronization of Lur’e network under signed digraph. Int. J. Robust Nonlinear Control 2018, 28, 6087–6105. [Google Scholar] [CrossRef]
- Zhao, L.; Jia, Y.; Yu, J. Adaptive finite-time bipartite consensus for second-order multi-agent systems with antagonistic interactions. Syst. Control Lett. 2017, 102, 22–31. [Google Scholar] [CrossRef]
- Hu, A.; Wang, Y.; Cao, J.; Alsaedi, A. Event-triggered bipartite consensus of multi-agent systems with switching partial couplings and topologies. Inf. Sci. 2020, 521, 1–13. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, J.; Zhang, Y.; Xu, Y. Event-triggered bipartite consensus for high-order multi-agent systems with input saturation. Neurocomputing 2020, 379, 284–295. [Google Scholar] [CrossRef]
- Xiao, Y.; Xie, H.; Zhao, N. Couple-group consensus of heterogeneous nonlinear multi-agent systems with cooperative–competitive interactions and input saturation. Chaos Solitons Fractals 2024, 179, 114473. [Google Scholar] [CrossRef]
- Altafini, C. Consensus problems on networks with antagonistic interactions. IEEE Trans. Autom. Control 2012, 58, 935–946. [Google Scholar] [CrossRef]
- Gan, Q.; Xiao, F.; Sheng, H. Fixed-time outer synchronization of hybrid-coupled delayed complex networks via periodically semi-intermittent control. J. Frankl. Inst. 2019, 356, 6656–6677. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, G. Event-triggered fixed-time cooperative tracking control for uncertain nonlinear second-order multi-agent systems under directed network topology. J. Frankl. Inst. 2020, 357, 3345–3364. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, Y.; Chang, Q.; Xu, X. Intermittent event-triggered control for finite-time bipartite consensus of second-order multi-agent systems. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2022, 236, 1255–1273. [Google Scholar] [CrossRef]
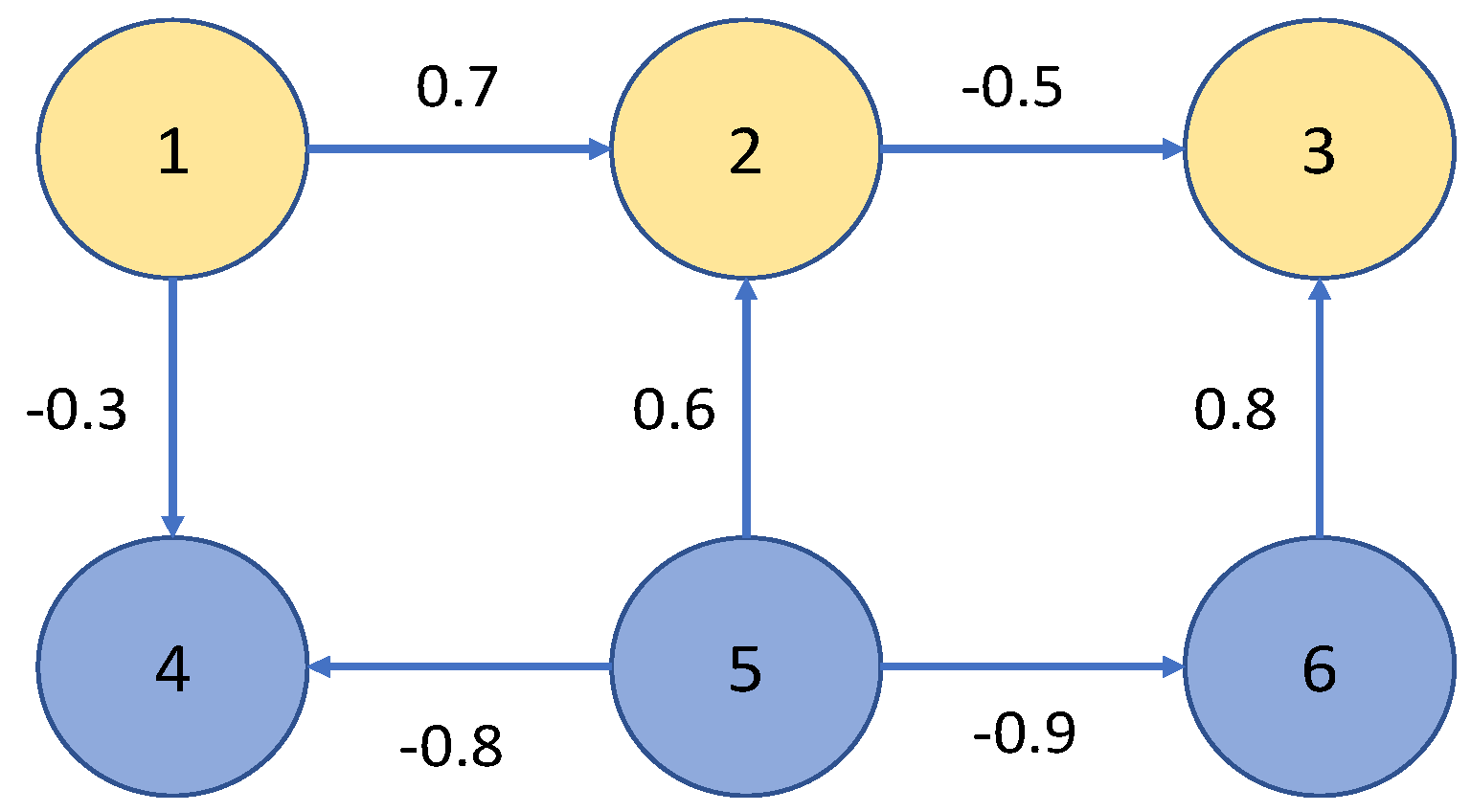

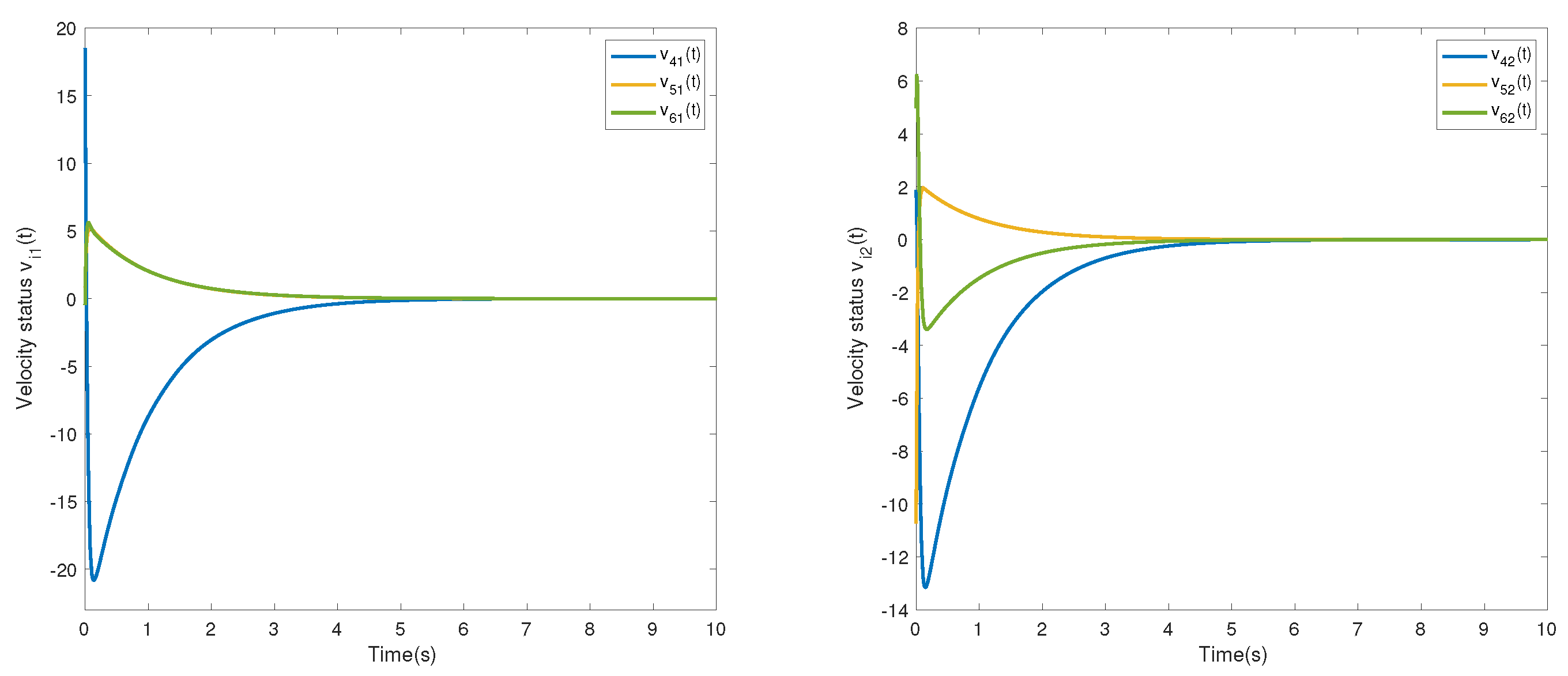
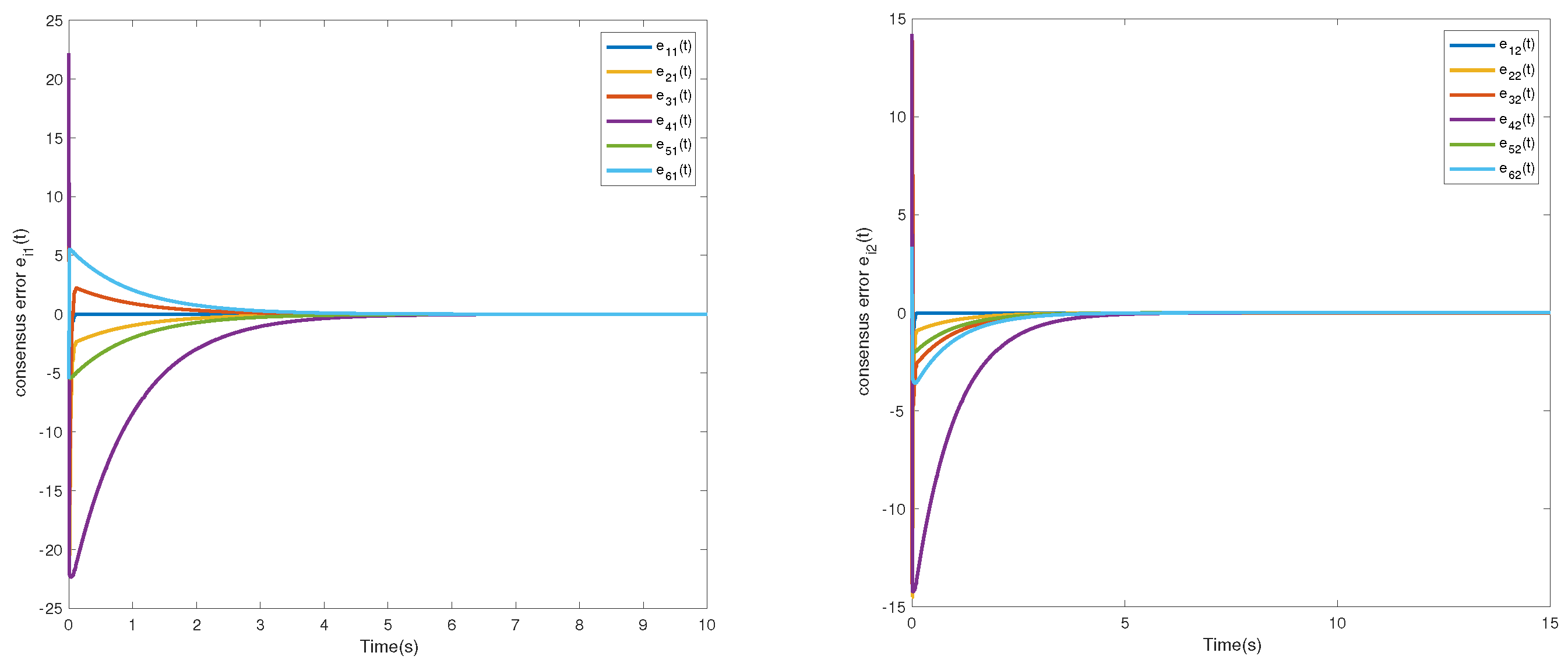
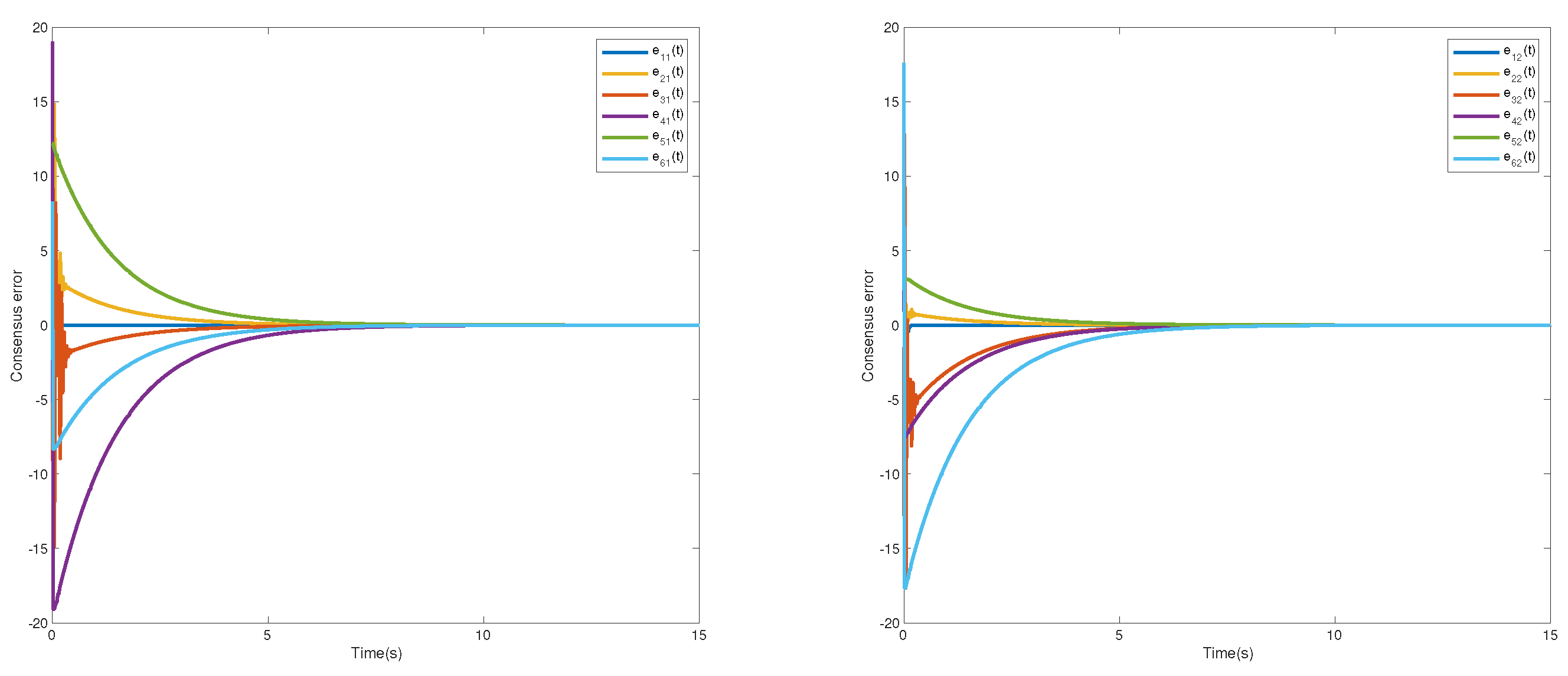
| p | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
| q | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 |
| T | 11.7619 | 8.2652 | 8.4175 | 8.7881 | 9.5253 | 10.4416 | 11.4578 | 12.5351 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Yang, Y.; Qing, N. Finite-Time Pinning Event-Triggered Control for Bipartite Consensus of Hybrid-Order Heterogeneous Multi-Agent Systems with Antagonistic Links. Appl. Sci. 2024, 14, 9468. https://doi.org/10.3390/app14209468
Yu X, Yang Y, Qing N. Finite-Time Pinning Event-Triggered Control for Bipartite Consensus of Hybrid-Order Heterogeneous Multi-Agent Systems with Antagonistic Links. Applied Sciences. 2024; 14(20):9468. https://doi.org/10.3390/app14209468
Chicago/Turabian StyleYu, Xiangfeng, Yongqing Yang, and Nengneng Qing. 2024. "Finite-Time Pinning Event-Triggered Control for Bipartite Consensus of Hybrid-Order Heterogeneous Multi-Agent Systems with Antagonistic Links" Applied Sciences 14, no. 20: 9468. https://doi.org/10.3390/app14209468
APA StyleYu, X., Yang, Y., & Qing, N. (2024). Finite-Time Pinning Event-Triggered Control for Bipartite Consensus of Hybrid-Order Heterogeneous Multi-Agent Systems with Antagonistic Links. Applied Sciences, 14(20), 9468. https://doi.org/10.3390/app14209468






