Abstract
There are many uncertainties in the actual use of thermal protection systems (TPSs). In this paper, an interval finite element model of a TPS under transient heat transfer is established by taking the uncertainties of TPSs as interval parameters. An affine interval finite element method (AIFEM) is proposed to study the temperature response bounds of uncertain TPSs under transient heat transfer conditions. Two numerical examples are given to verify the effectiveness and accuracy of the proposed AIFEM by comparison with the Monte Carlo method. The results show that the AIFEM can provide conservative and efficient calculation results in TPS transient heat transfer design with interval parameters.
1. Introduction
Hypersonic aircraft experience severe friction with air when flying at high speed and are subject to extremely severe aerodynamic heat. Thermal protection systems (TPSs) have a significant thermal insulation effect and can ensure that the interior of the aircraft is at a normal operating temperature [1,2,3]. Due to the action of aerodynamic heat, there is a large temperature difference in TPSs, which may affect their stability and strength [4,5]. Therefore, it is necessary to conduct transient heat transfer analysis on TPSs.
In recent years, there have been many studies on TPS transient heat transfer. Wei et al. [6] obtained a TPS with higher service temperature and lower areal density through heat transfer characteristics analysis. Wang et al. [7] found, through transient heat transfer calculations, that TPSs with graded insulation materials can provide lower temperatures and better temperature distribution uniformity. Li et al. [8] designed and manufactured a new type of TPS and conducted a numerical analysis of its heat transfer behavior. Ding et al. [9] studied the effects of porosity, carbon fiber bundle, and pore diameter on the directional heat transfer of TPSs in L-shaped C/C composites.
However, the above studies are all deterministic studies and ignore the impact of uncertain parameters on TPS transient heat transfer. In engineering practice, the practical application of a TPS will have uncertainties in terms of structural material parameters, boundary conditions, thermal loads, and other parameters [10,11]. Currently, there are three commonly used methods for uncertainty analysis: the probability method, the fuzzy method, and the interval method [12,13]. However, in the testing and practical use of TPSs, due to extreme loading conditions, it is often difficult to obtain the probability distribution functions and membership functions required by the first two methods. The interval method only requires the upper and lower bounds and function ranges of the uncertainty parameters, does not require a specific distribution form, and is more suitable for the uncertainty analysis of TPSs [14,15].
At present, interval methods are widely used in uncertainty analysis. Qiu and Elishakoff [16] proposed a subinterval perturbation method, which is more precise than the interval perturbation method. Deng et al. [17] used the interval analysis method and the convex model method to solve the upper and lower bounds of the uncertain TPS temperature response. Sofi et al. [18] proposed an interval field model to study spatially varying uncertain linear elastic structures, and used Abaqus to realize the entire process. Xiang and Shi [19] proposed an element-by-element interval finite element method to solve internal sound fields with uncertain parameters, and finally obtained an accurate and stable interval of sound pressure response. However, the above interval method is not suitable for TPS design, as the temperature response range in TPS design is larger than the actual temperature response range. That is, TPS design tends to be conservative, so conservative methods are needed to solve the temperature response of uncertain TPSs to make the design of TPSs more secure. At the same time, the obtained temperature response range should not be too conservative; that is, the designed temperature response range is much larger than the actual range, which results in a loss of meaning. Degrauwe et al. [20] proposed an affine interval finite element method (AIFEM) to avoid the problem of over-conservatism, and verified through numerical examples that the AIFEM is conservative and can obtain safe and accurate bounds. Since then, the affine interval algorithm has been further developed. He et al. [21] established an interval mass-in-mass acoustic metamaterial model and used the AIFEM to evaluate the dynamic response boundary of the acoustic metamaterial, obtaining conservative results and meeting the engineering requirements.
In order for TPSs to have absolute safety in practical applications, the design of TPSs with interval parameters requires a conservative method. At present, there is no research on the conservative design of uncertain TPSs. Using conservative methods to analyze uncertain TPSs has practical engineering value. The AIFEM is conservative in uncertainty analysis in terms of both statics and dynamics, while avoiding over-conservative problems. Therefore, the AIFEM is applied to transient heat transfer analysis to provide a conservative solution for the design of uncertain TPSs.
Based on this, this paper uses the AIFEM to conduct a conservative analysis of TPSs with interval parameters under transient heat transfer conditions, and the conservative results obtained provide a reference for the design of TPSs. The rest of this article is organized as follows. In Section 2, transient heat transfer equations with interval parameters are introduced. In Section 3, the AIFEM is used to solve the transient heat transfer temperature response boundary with interval parameters. In Section 4, two numerical examples are given to verify the effectiveness and accuracy of the AIFEM through comparison with the Monte Carlo method (MCM). In Section 5, the full text is summarized.
2. Transient Heat Transfer Equations with Interval Parameters
We express the uncertainty parameters b = [b1, b2, …, bk]T in the model as the interval parameters of vector :
where and represent the upper and lower bounds of the interval, respectively, represents the median value of the interval vector, and represents the radius of the interval vector. The median and radius of the interval vector are expressed as follows:
According to heat transfer, the transient heat transfer differential equation for a homogeneous, isotropic material without internal heat source is
where is the thermal conductivity, is the material density, and is the specific heat capacity of the material.
The initial condition for transient heat transfer is
The boundary conditions for transient heat transfer are
where n is the normal vector at the boundary, is the boundary temperature, is the heat flow density on the boundary, h is the convective heat transfer coefficient, is the ambient air temperature, and , , are the bounds of the object Ω.
In the finite element method, the equilibrium equation for transient heat transfer can be expressed as
where C is the heat capacity matrix, K is the heat transfer matrix, T is the temperature vector, and is the temperature load vector.
Therefore, when considering uncertainty parameters, the above equation can be rewritten as a transient heat transfer equation including interval parameters:
where the subscript t is the value at time t.
Use two-point backward differences to replace the differential in Equation (7). That is,
where is the time step.
By performing first-order Taylor series expansion on , , and in Equation (7) at , it can be expressed as
where k is the number of uncertainty parameters.
By substituting Equations (8) and (9) into Equation (7), you can obtain
where is the determined quantity of temperature response at time and is the uncertainty quantity of temperature response at time .
The order is as follows:
Substituting Equation (11) into Equation (10), the interval heat transfer formula at time t can be rewritten as
The above expression can be regarded as the first-order Taylor series expansion of the following expression:
3. Affine Interval Finite Element Method
For the first-order Taylor series expansion for transient heat transfer problems, if the omitted high-order terms are regarded as error terms, the interval heat transfer matrix in Equation (13) can be rewritten into the form of an affine matrix:
where is the error term, is an interval matrix containing the elements , and × is a Hadamard matrix multiplication operation, which involves multiplying the elements of rows and columns corresponding to the matrices of the same dimension.
Let affine matrix be
where
Also, express the inverse of the affine matrix as an affine matrix:
Expand the affine matrix using Neumann series:
Compare Equations (17) and (18) to obtain the linear correlation terms in the affine matrix :
Using conservative estimates, we can obtain
Substituting Equation (20) into Equation (18), the conservative estimate of the error term is
Let ; then, the above expression can be rewritten as
Due to , conservative estimates are used for the higher-order terms in the above equation:
Bringing Equation (23) into Equation (22) yields
When the spectral radius , the error term is
Therefore, the inverse of affine matrix is
If the first-order Taylor series expansion is used and the error term is a zero matrix, the above formula is simplified to
The inverse of the interval heat transfer matrix for transient heat transfer problems is
Then, the temperature response at time t can be expressed as
Substituting Equations (11) and (28) into Equation (29), and using the calculation rules of the affine algorithm, the upper and lower bounds of the temperature response of transient heat transfer can be obtained.
The flow chart for the AIFEM to solve the temperature response interval bounds is shown in Figure 1.
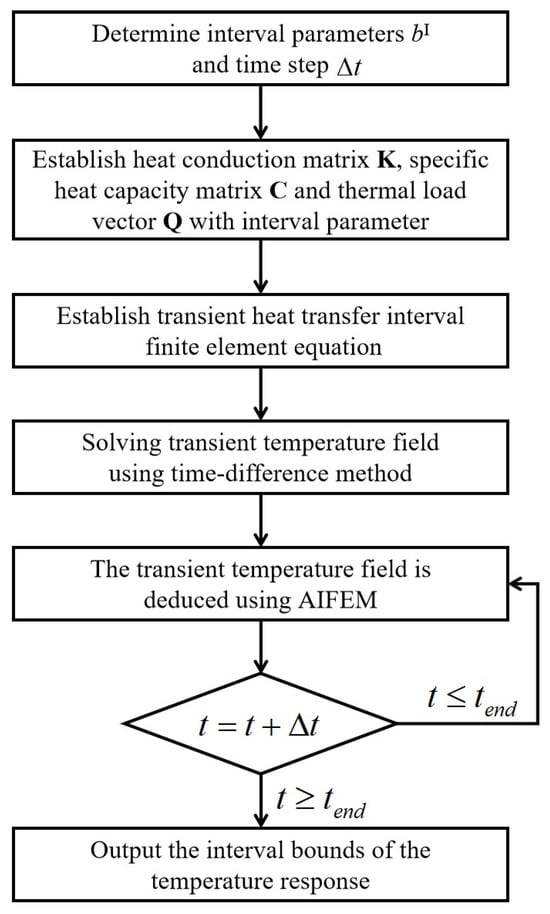
Figure 1.
AIFEM calculation flow chart.
4. Numerical Examples
In this section, two examples are used to verify the effectiveness and accuracy of the AIFEM in transient heat transfer problems. The first example is a two-dimensional thin plate, and the second example is a three-dimensional TPS. In addition, the MCM results with a sample size of 105 are used as exact solutions for the calculation examples for comparison. In this section, Matlab is used to call Abaqus for calculation; Abaqus 6.14 is used to calculate the determined values in the calculation example, and then Matlab R2023a is used to post-process the interval results of the temperature response.
4.1. Plate Model
The two-dimensional plate model shown in Figure 2. The size of the finite element model is 100 mm × 100 mm, with a total of 100 elements, each with a side length of 10 mm and a plate thickness of 1 mm. The density of the structure is ρ = 4000 kg/m3, the specific heat capacity is c = 200 J/(kg·°C), the thermal conductivity coefficient is λ = 10 W/(m·°C), the initial temperature is T0 = 0 °C, the calculation time is 200 s, and the time step is Δt = 1 s. A thermal load of Ts = 200 °C is applied to the left surface of the plate, a heat flow density of qs = 50,000 W/m2 is applied to the upper surface, and the rest of the surface has adiabatic boundary conditions. The temperature gradient is not considered in the thickness direction of the plate. We set the specific heat capacity c and thermal conductivity λ of the material as uncertainty interval parameters, where the uncertainties were 5% and 10%, respectively. The detailed uncertainty interval parameters for the upper bounds (UB) and lower bounds (LB) are shown in Table 1. As shown in Figure 2, three red nodes are used to monitor the temperature field of the board.
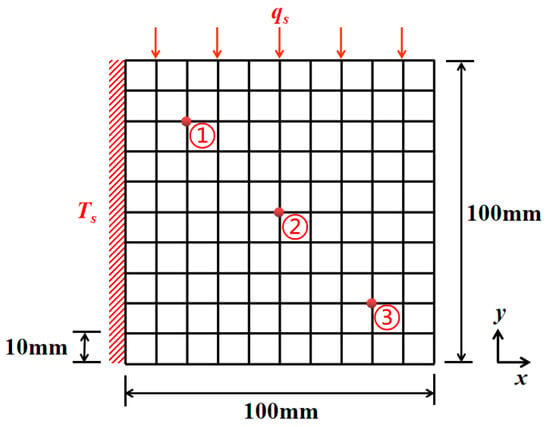
Figure 2.
Plate model: ①, ②, and ③ respectively represent node 1, node 2, and node 3.

Table 1.
Interval parameter bounds of plate model.
The bounds of the temperature response of plates with different uncertainties are shown in Figure 3 and Figure 4. The green dotted line in the figure represents the median value of the temperature response, the red solid line represents the upper and lower bounds of the MCM temperature response, and the blue dashed line represents the upper and lower bounds of the AIFEM temperature response. It can be seen from Figure 3 and Figure 4 that the temperature response boundary of the model predicted by the AIFEM is very close to the MCM, and the change rule is consistent, which demonstrates the rationality of the proposed method. The upper and lower bounds of the temperature response calculated by the AIFEM completely envelop the temperature response of the MCM, exhibiting a certain degree of conservatism. As the uncertainty level increases from 5% to 10%, the range of the model’s temperature response also becomes wider. As time increases, the range of the temperature response gradually increases.
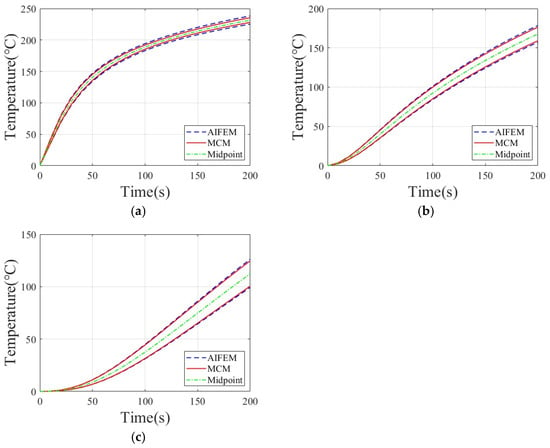
Figure 3.
Plate temperature response at uncertainty level 5%: (a) Node 1; (b) Node 2; (c) Node 3.
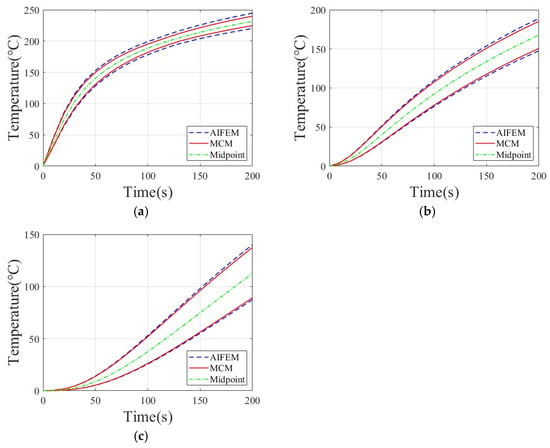
Figure 4.
Plate temperature response at uncertainty level 10%: (a) Node 1; (b) Node 2; (c) Node 3.
Table 2 shows the bounds and relative errors of the temperature response of Node 2 in the plate model at different times. Comparing the AIFEM with the MCM yields relative errors. The relative errors obtained are all less than 3%. When the uncertainty reaches 10%, the AIFEM is still effective for uncertainty analysis. As the uncertainty increases, the relative error increases slightly. The accuracy of the AIFEM was verified by comparing relative errors.

Table 2.
Temperature response bounds and relative error at Node 2 of plate model.
4.2. TPS Model
We selected the three-dimensional structure of a single cell from the TPS model for research, and conducted heat transfer analysis on the main stressed structures, as shown in Figure 5. The size of the finite element model is 100 mm × 100 mm × 40 mm, with a total of 300 elements, each with a side length of 10 mm. The thicknesses of the top face sheet, web, and bottom face sheet are all 5 mm. The TPS model materials all use titanium alloy. The density of the titanium alloy is ρ = 4500 kg/m3, the specific heat capacity is c = 611 J/(kg·°C), the thermal conductivity is λ = 6.8 W/(m·°C), the initial temperature is T0 = 0 °C, the calculation time is 600 s, and the time step is Δt = 1 s. A heat flow density of qs = 1 × 105 W/m2 was applied to the top face sheet of the TPS, and adiabatic boundary conditions were applied around the periphery and underside of the model. The convective heat transfer coefficient is h = 20 W/(m2·K), the ambient temperature is Ta = −80 °C, the surface emissivity of the top face sheet is ε = 0.9, and the Stefan–Boltzmann constant is σ = 5.67 × 10−8 W/(m2·K4). We set the specific heat capacity c, heat conduction coefficient λ, heat flow density qs, and ambient temperature Ta as uncertainty interval parameters, where the uncertainties were 5% and 10%, respectively. The detailed uncertainty interval parameter bounds are shown in Table 3. As shown in Figure 5, three red nodes are used to monitor the temperature field of the TPS. Node 1 is at the connection between the web and the top face sheet, and Nodes 2 and 3 are both on the web.
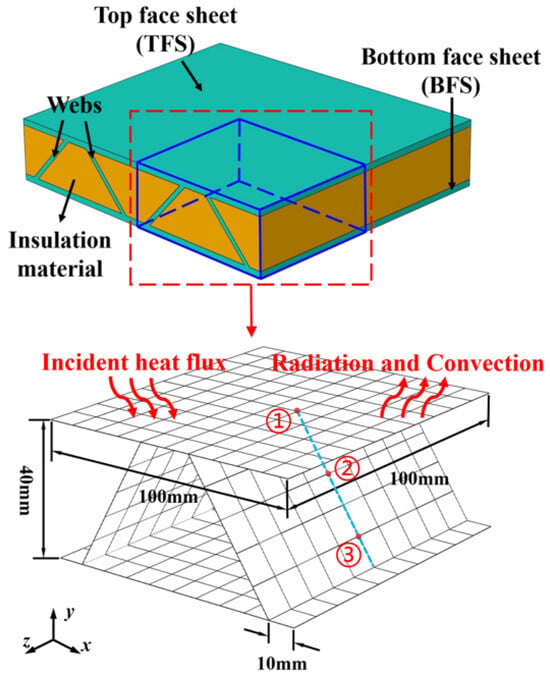
Figure 5.
TPS model: ①, ②, and ③ respectively represent node 1, node 2, and node 3.

Table 3.
Interval parameter bounds of TPS model.
The bounds of the TPS temperature responses with different uncertainties are shown in Figure 6 and Figure 7. It can be seen from Figure 6 and Figure 7 that the obtained interval temperature response boundary has a significant deviation from the median value. As the uncertainty increases, the deviation becomes more obvious. Therefore, it is necessary to analyze the uncertainty of the TPS under transient heat transfer. The TPS temperature response boundary calculated by the AIFEM is consistent with and very close to the boundary change rule of the MCM, which proves the rationality of the AIFEM. The temperature response boundary of the AIFEM calculations is wider, completely enveloping the temperature response of the MCM calculations. The AIFEM is conservative and can provide a safer theoretical solution for the design of TPSs under transient heat transfer conditions. As the uncertainty increases from 5% to 10%, the temperature response range of the TPS becomes wider. As time increases, the range of the TPS temperature response gradually increases.
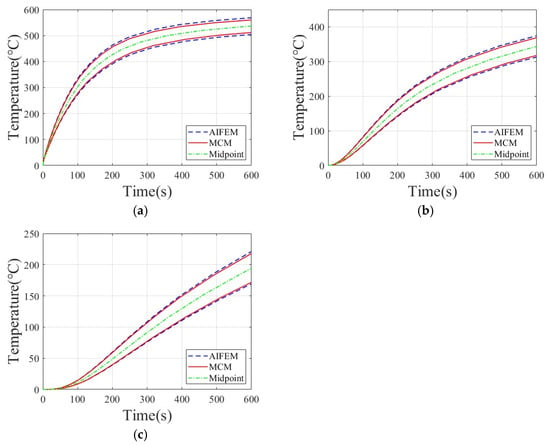
Figure 6.
TPS temperature response at uncertainty level 5%: (a) Node 1; (b) Node 2; (c) Node 3.
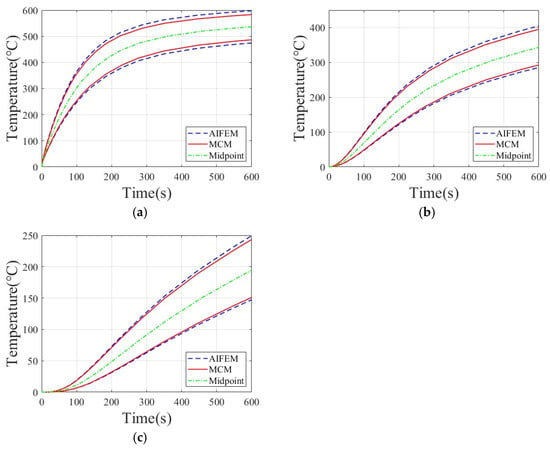
Figure 7.
TPS temperature response at uncertainty level 10%: (a) Node 1; (b) Node 2; (c) Node 3.
Table 4 shows the bounds and relative errors of the temperature response of Node 2 at different times in the TPS model. As the uncertainty and time increase, the AIFEM’s relative error increases slightly. When the uncertainty reaches 10%, the maximum error of the AIFEM is 3.08%, and the AIFEM is still valid for uncertainty analysis. The accuracy of the AIFEM in uncertain TPS transient heat transfer analysis was verified by comparing the relative errors.

Table 4.
Temperature response bounds and relative error at Node 2 of TPS model.
4.3. Comparison of Computing Efficiency between AIFEM and MCM
To illustrate the computational efficiency of the AIFEM and the MCM, Table 5 lists the time consumed by each method in the two examples. The calculations were implemented by MATLAB R2023a on an Intel Core CPU i5-12500H 2.5 GHz. According to Table 5, the AIFEM consumes much less time than the MCM; therefore, the computational efficiency of the AIFEM is much higher than the MCM. The AIFEM reflects more efficient calculation efficiency across different examples. Based on computational efficiency, the AIFEM is a reasonable method to calculate the transient temperature response of TPSs with uncertainties.

Table 5.
Calculation time of two methods.
5. Conclusions
In this paper, the uncertainty of TPSs in transient heat transfer was taken as an interval parameter and verified through a plate model and TPS model. The bounds of the temperature response were obtained using an AIFEM, and compared with the MCM, the effectiveness and accuracy of the AIFEM under transient heat transfer conditions were verified. The main conclusions of this paper are summarized as follows:
- (1)
- The uncertainty of the TPS in the transient heat transfer analysis had a significant impact on its temperature response, so it is necessary to analyze the uncertainty of TPSs.
- (2)
- The temperature response bounds obtained by the AIFEM were wider than those obtained by the MCM, and the AIFEM can generally obtain a more conservative temperature response. The conservative AIFEM is a safe approach in uncertain TPS designs under transient heat transfer conditions.
- (3)
- The temperature response bounds provided by the MCM offered a real solution, but their calculation was very time-consuming. The AIFEM effectively improved the calculation efficiency. From the perspective of calculation efficiency, the AIFEM is a reasonable method to predict the temperature response of uncertain TPSs under transient heat transfer.
- (4)
- Given the uncertainty of TPS design under transient heat transfer conditions, the AIFEM can be used as an efficient and safe method. Next, the authors will try to study the conservatism of uncertain TPS thermal stress based on the AIFEM, and when conservative analysis is needed in other fields, try to use this method for research.
Author Contributions
Conceptualization, X.F. and Z.S.; methodology, X.F. and Z.S.; software, X.F. and Z.Y.; validation, X.F. and Z.Y.; formal analysis, X.F.; investigation, X.F.; resources, X.F.; data curation, X.F. and Z.Y.; writing—original draft preparation, X.F.; writing—review and editing, Z.S.; visualization, X.F.; supervision, Z.S.; project administration, Z.S. and Z.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China (Grant No. 12272172).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Natali, M.; Kenny, J.M.; Torre, L. Science and technology of polymeric ablative materials for thermal protection systems and propulsion devices: A review. Prog. Mater. Sci. 2016, 84, 192–275. [Google Scholar] [CrossRef]
- Uyanna, O.; Najafi, H. Thermal protection systems for space vehicles: A review on technology development, current challenges and future prospects. Acta Astronaut. 2020, 176, 341–356. [Google Scholar] [CrossRef]
- Le, V.T.; San, H.N.; Goo, N.S. Advanced sandwich structures for thermal protection systems in hypersonic vehicles: A review. Compos. Part B-Eng. 2021, 226, 109301. [Google Scholar] [CrossRef]
- Biamino, S.; Antonini, A.; Eisenmenger-Sittner, C.; Fuso, L.; Pavese, M.; Fino, P.; Bauer, E.; Badini, C. Multilayer SiC for thermal protection system of space vehicles with decreased thermal conductivity through the thickness. J. Eur. Ceram. Soc. 2010, 30, 1833–1840. [Google Scholar] [CrossRef]
- Palmer, G.; Kontinos, D.; Sherman, B. Surface Heating Effects of X-33 Vehicle Thermal-Protection-System Panel Bowing. J. Spacecr. Rocket. 1999, 36, 836–841. [Google Scholar] [CrossRef]
- Wei, K.; Cheng, X.; Mo, F.; Wen, W.; Fang, D. Design and analysis of integrated thermal protection system based on lightweight C/SiC pyramidal lattice core sandwich panel. Mater. Des. 2016, 111, 435–444. [Google Scholar] [CrossRef]
- Wang, X.; Wei, K.; Tao, Y.; Yang, X.; Zhou, H.; He, R.; Fang, D. Thermal protection system integrating graded insulation materials and multilayer ceramic matrix composite cellular sandwich panels. Compos. Struct. 2019, 209, 523–534. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, L.; He, R.; Ma, Y.; Zhang, K.; Bai, X.; Xu, B.; Chen, Y. Integrated thermal protection system based on C/SiC composite corrugated core sandwich plane structure. Aerosp. Sci. Technol. 2019, 91, 607–616. [Google Scholar] [CrossRef]
- Ding, C.; Liu, X.; Xie, F.; Du, C.; Wang, Y. Heat transfer and pyrolysis gas flow characteristics of light-weight ablative thermal protection system in the blunt body. Int. J. Therm. Sci. 2023, 186, 108122. [Google Scholar] [CrossRef]
- Rivier, M.; Lachaud, J.; Congedo, P.M. Ablative thermal protection system under uncertainties including pyrolysis gas composition. Aerosp. Sci. Technol. 2019, 84, 1059–1069. [Google Scholar] [CrossRef]
- Brune, A.J.; West, T.K.; Hosder, S. Uncertainty quantification of planetary entry technologies. Prog. Aerosp. Sci. 2019, 111, 100574. [Google Scholar] [CrossRef]
- Moens, D.; Vandepitte, D. Recent advances in non-probabilistic approaches for non-deterministic dynamic finite element analysis. Arch. Comput. Method E. 2006, 13, 389–464. [Google Scholar] [CrossRef]
- Xia, B.; Yu, D. Interval analysis of acoustic field with uncertain-but-bounded parameters. Comput. Struct. 2012, 112, 235–244. [Google Scholar] [CrossRef]
- Moens, D.; Hanss, M. Non-probabilistic finite element analysis for parametric uncertainty treatment in applied mechanics: Recent advances. Finite Elem. Anal. Des. 2011, 47, 4–16. [Google Scholar] [CrossRef]
- Jiang, C.; Fu, C.; Ni, B.; Han, X. Interval arithmetic operations for uncertainty analysis with correlated interval variables. Acta Mech. Sin. 2016, 32, 743–752. [Google Scholar] [CrossRef]
- Qiu, Z.; Elishakoff, I. Antioptimization of structures with large uncertain-but-non-random parameters via interval analysis. Comput. Method Appl. Mech. Eng. 1998, 152, 361–372. [Google Scholar] [CrossRef]
- Deng, Z.; Guo, Z.; Zhang, X. Non-probabilistic set-theoretic models for transient heat conduction of thermal protection systems with uncertain parameters. Appl. Therm. Eng. 2016, 95, 10–17. [Google Scholar] [CrossRef]
- Sofi, A.; Romeo, E.; Barrera, O.; Cocks, A. An interval finite element method for the analysis of structures with spatially varying uncertainties. Adv. Eng. Softw. 2019, 128, 1–19. [Google Scholar] [CrossRef]
- Xiang, Y.; Shi, Z. Interval Analysis of Interior Acoustic Field with Element-By-Element-Based Interval Finite-Element Method. J. Eng. Mech.-ASCE 2021, 147, 04021085. [Google Scholar] [CrossRef]
- Degrauwe, D.; Lombaert, G.; Roeck, G.D. Improving interval analysis in finite element calculations by means of affine arithmetic. Comput. Struct. 2010, 88, 247–254. [Google Scholar] [CrossRef]
- He, F.; Shi, Z.; Zhang, Z.; Qian, D.; Feng, X. Antioptimization of mass-in-mass acoustic metamaterials based on interval analysis. Mech. Syst. Signal Process. 2023, 205, 110855. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).