A Data- and Model-Integrated Driven Method for Recommending the Maximum Safe Braking Deceleration Rates for Trucks on Horizontal Curves
Abstract
1. Introduction
2. Literature Review
2.1. Studies on Vehicle Skidding Based on the Model-Driven Method
2.2. Studies on Vehicle Skidding Based on the Data-Driven Method
- The road geometric design based on the point mass model cannot reflect the truck attributes, nor does it account for the effect of braking maneuvers on truck skidding.
- Researchers have proposed the utilization of the bicycle model to analyze the influence of braking on skid safety in flat curved road segments. However, it still remains a challenge of incorporating the dynamic effects induced by braking into the model without making it unsolvable.
- A relatively comprehensive and uncomplicated model is needed to describe the road–vehicle interaction. When developing this model, it is crucial to consider dynamic changes in brake force distribution, vertical tire load, as well as longitudinal and lateral friction during braking.
- The data-driven method has inherent limitations, often characterized by the elusive “black box” effect. While the method fails to provide a clear understanding of the underlying mechanisms behind braking maneuvers that result in truck skidding, it does contribute to exploring the microcharacteristics of driver braking behavior.
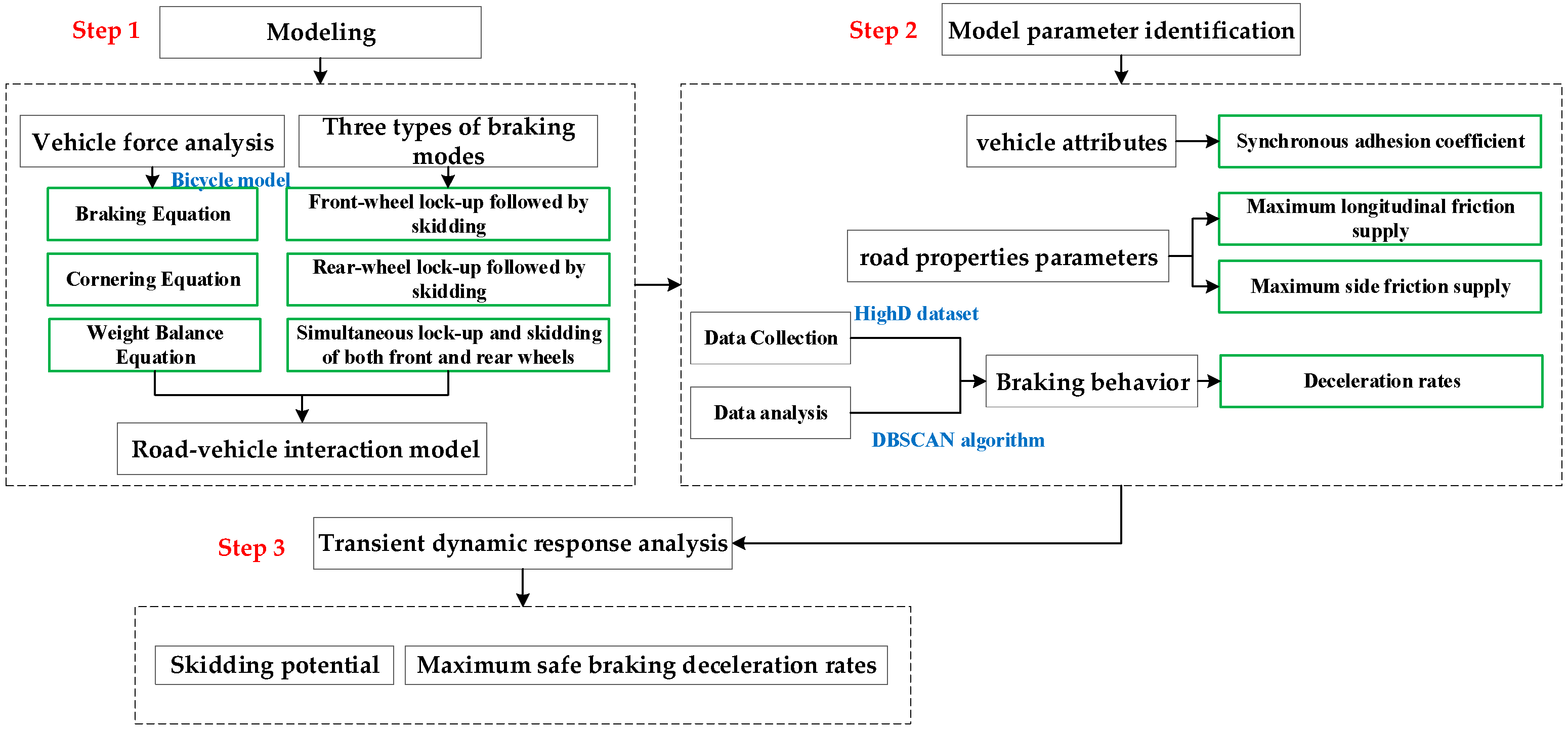
3. Methods
3.1. Road–Vehicle Interaction Model
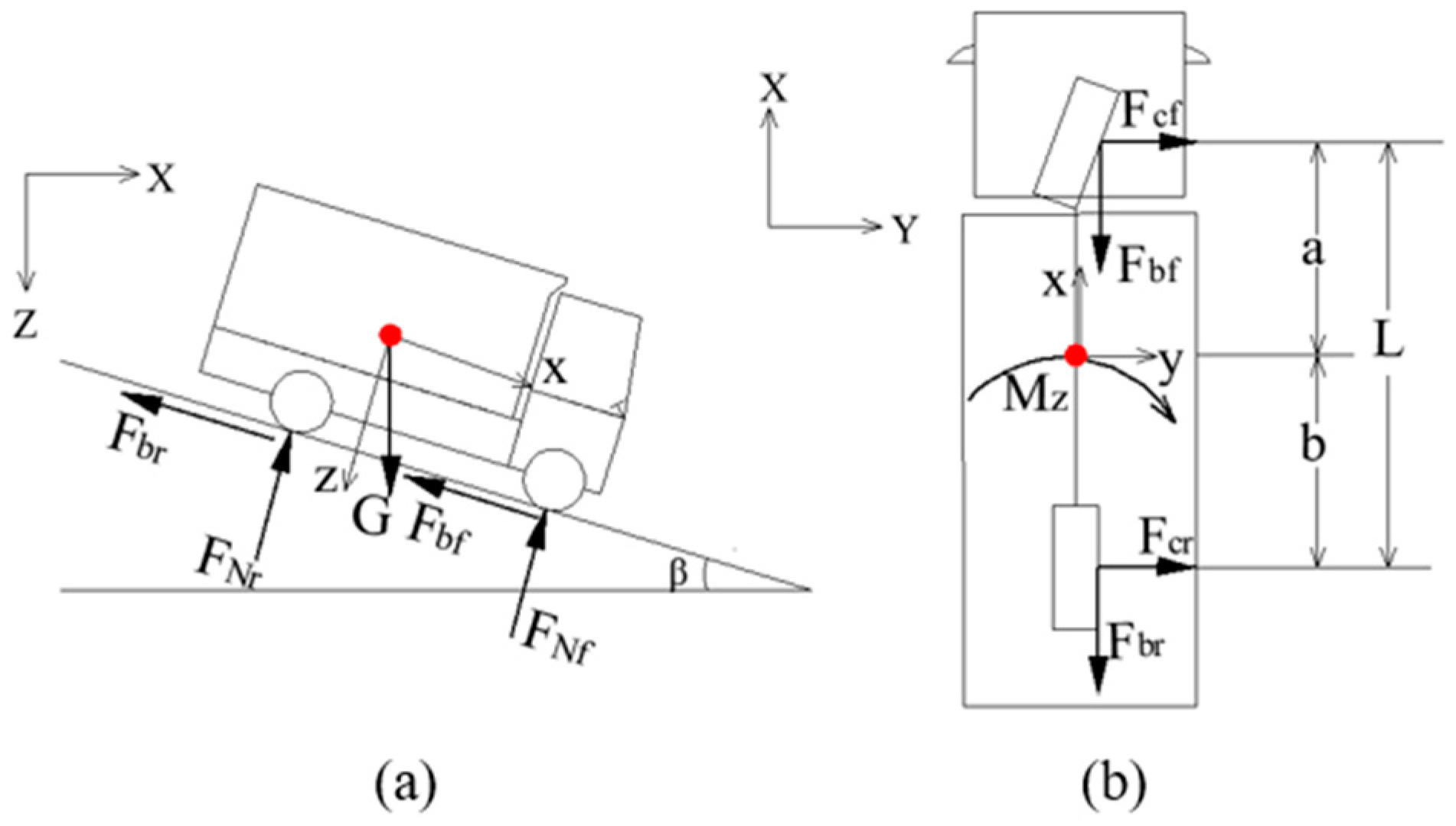
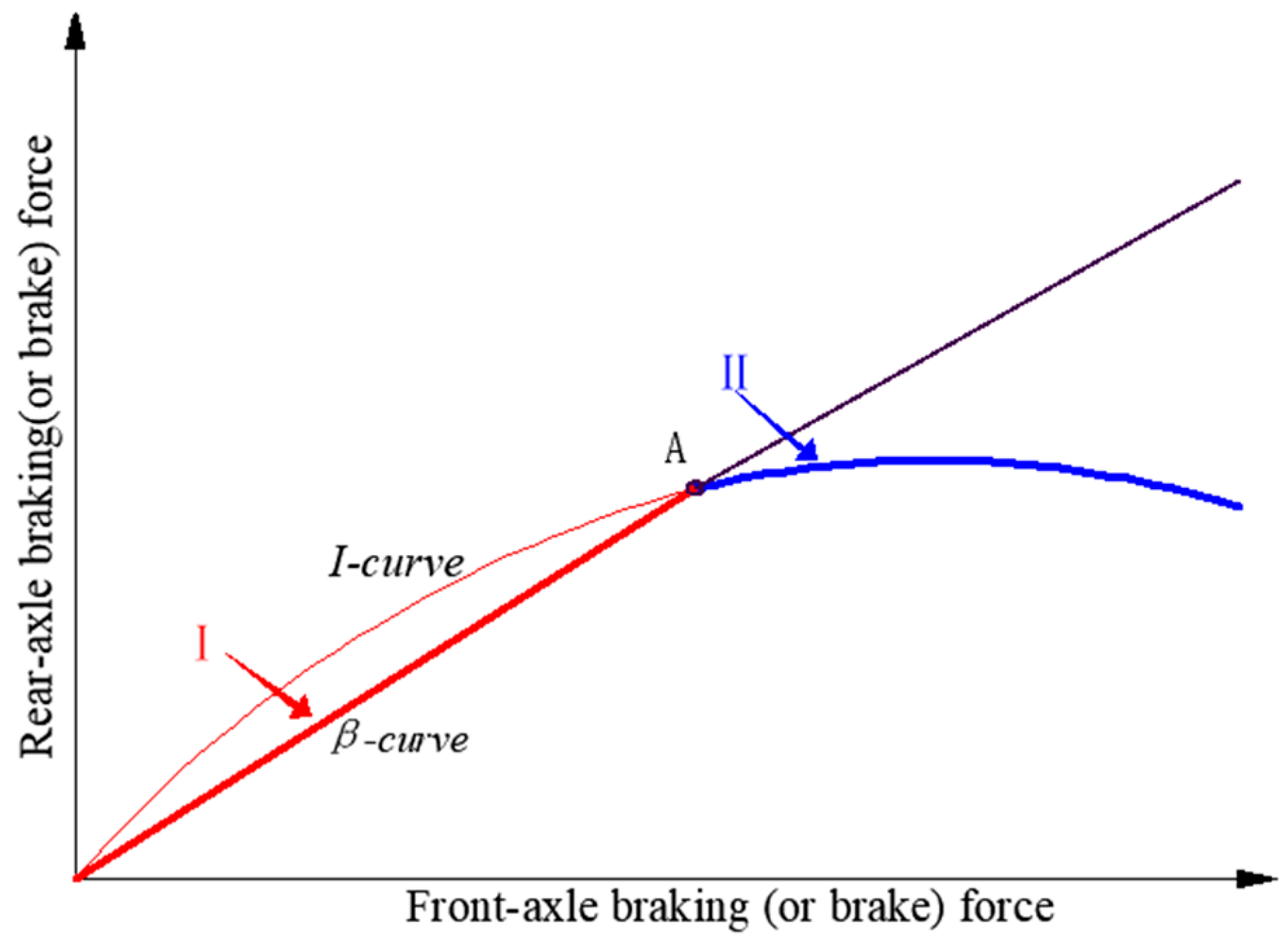
3.1.1. Features and Limitations of the Bicycle Model
- 1.
- Features of the bicycle model
- 2.
- Model analysis
- 3.
- Limitations of the bicycle model
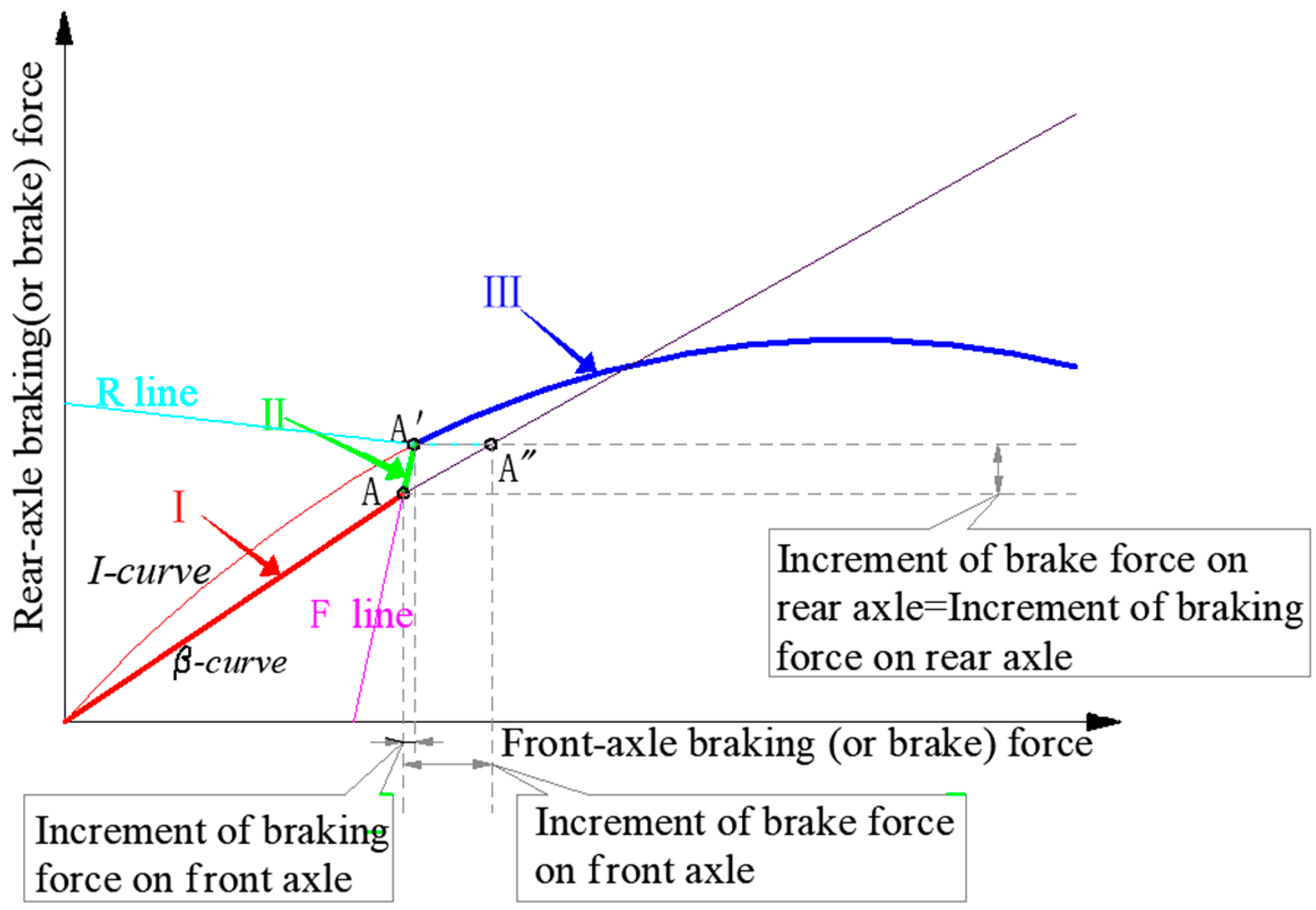
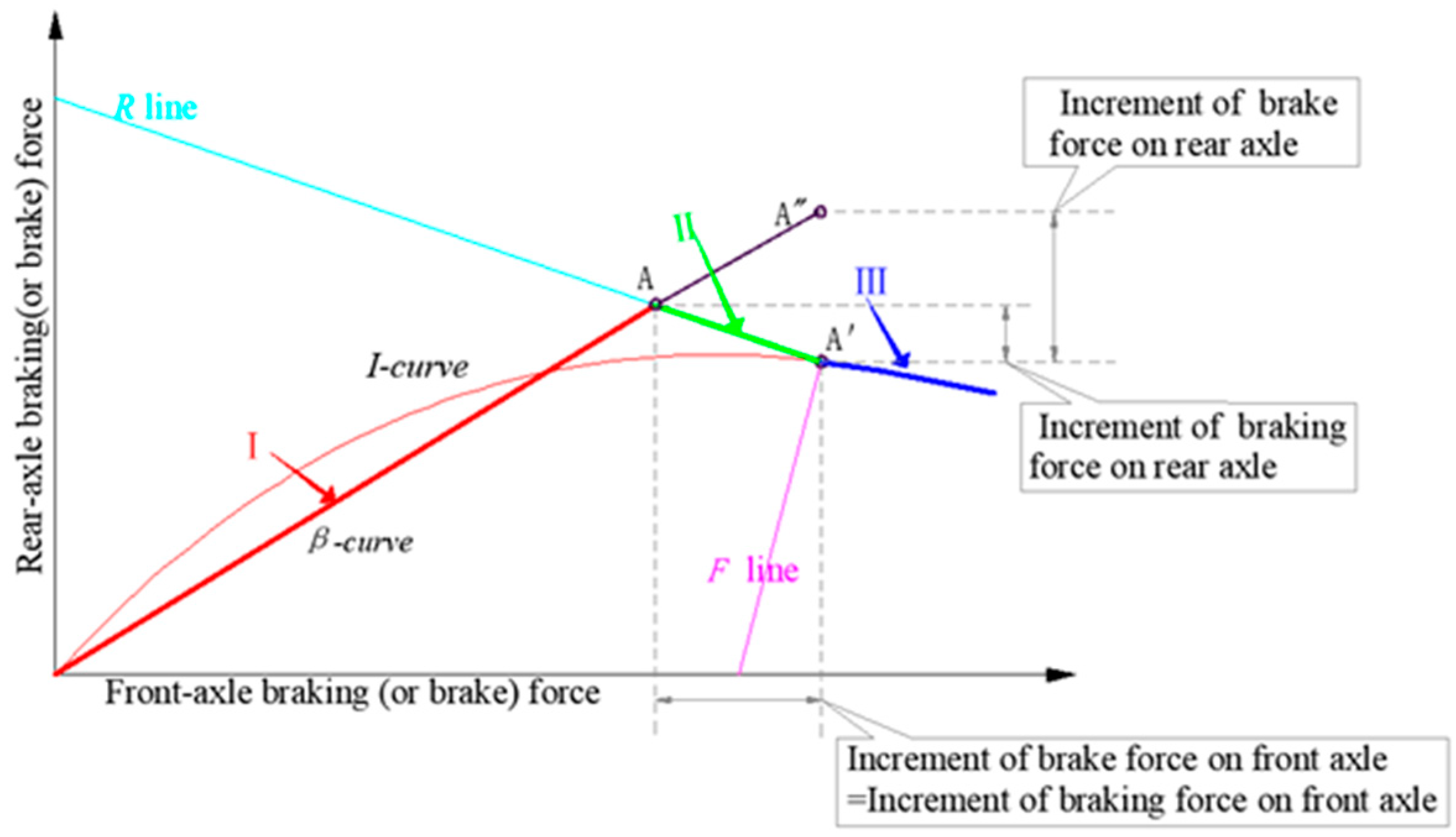
3.1.2. The Road–Vehicle Interaction Model
- 1.
- Truck’s braking characteristics
- : the position of the β-curve lies below the I-curve, implying that during braking, the front wheels consistently experience lock-up before the rear wheels.
- : the position of the β-curve lies above the I-curve, signifying that during braking, the rear wheels consistently experience lock-up before the front wheels.
- : in this scenario, during braking, both the front and rear wheels undergo simultaneous lock-up.
- 2.
- Model development and analysis
- (1)
- Braking mode 1:
- (2)
- Braking mode 2:
- (3)
- Braking mode 3:
3.2. Model Parameter Identification
3.2.1. Identification of Vehicle Attributes and Road Properties Parameters
- 1.
- Synchronous adhesion coefficient ()
- 2.
- Maximum longitudinal friction supply ()
- (1)
- Water film thickness: 0.5 mm, ();
- (2)
- Water film thickness: 1 mm, ();
- (3)
- Water film thickness: 2.5 mm, ().
- 3.
- Maximum side friction supply ()
3.2.2. Identification of Microcharacteristic Parameters of Driver Braking Behavior
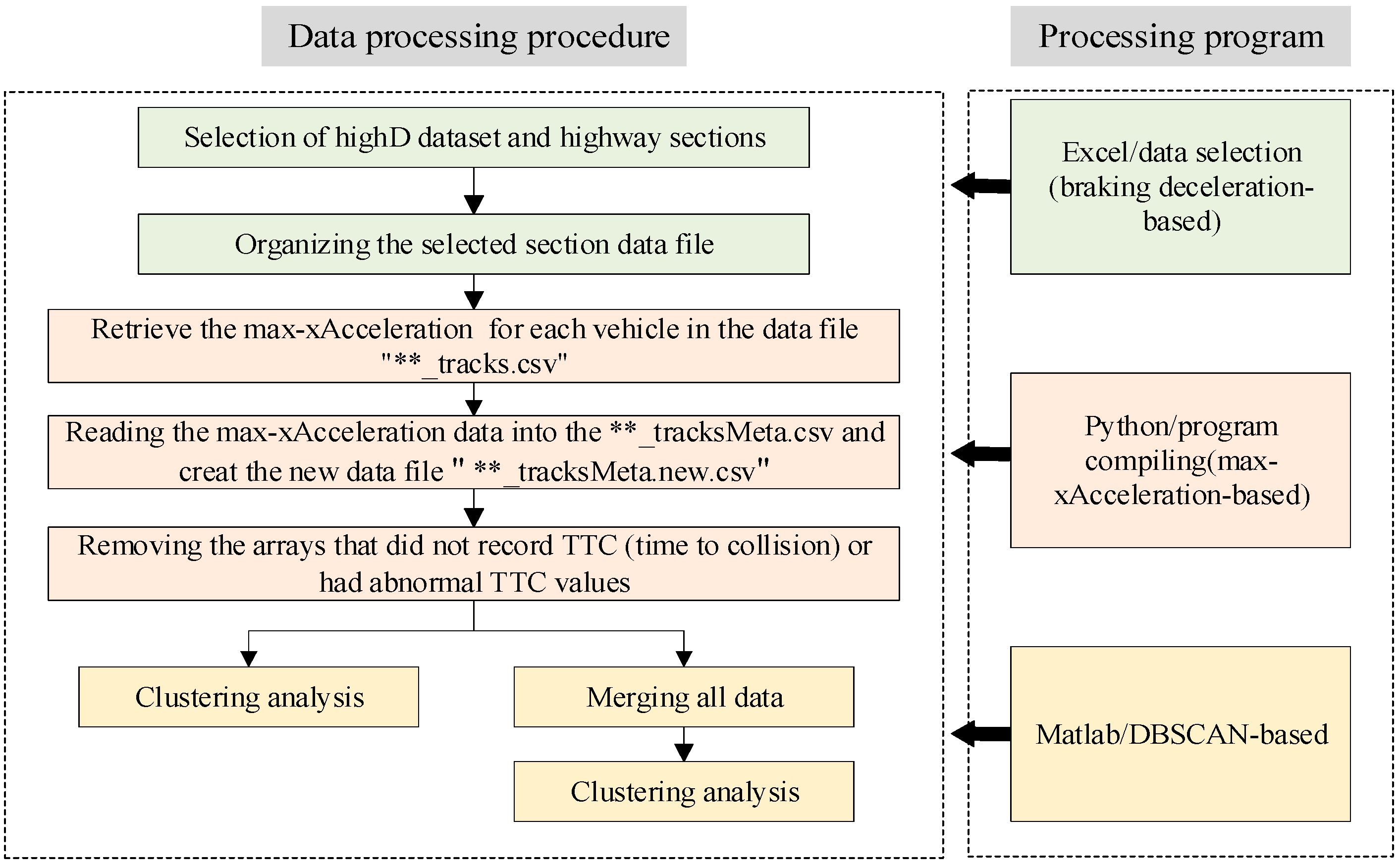
- 1.
- Data Collection
- 2.
- Data Reading and Processing
- (1)
- Utilizing Python programming, the data were compiled based on the data file “**_tracks.csv”. Within the recorded timeframe, the max-xAcceleration (maximum x Acceleration) for each vehicle (corresponding to each ID) was retrieved.
- (2)
- The filtering process is carried out to retain the arrays where the direction of max-xAcceleration is opposite to that of xvelocity.
- (3)
- The retrieved and filtered values of the max-xAcceleration are read into the data file “**_tracksMeta.csv”. A new data file “**_tracksMeta.new.csv” was created.
- (4)
- A further filtering process is conducted. The arrays that did not record TTC (time to collision) or had abnormal TTC values were removed in data file “**_tracksMeta.new.csv”.
- (5)
- Finally, the data file “**_tracksMeta.new.csv” from the eight highway sections were integrated into the data file “all_tracksMeta.csv”.
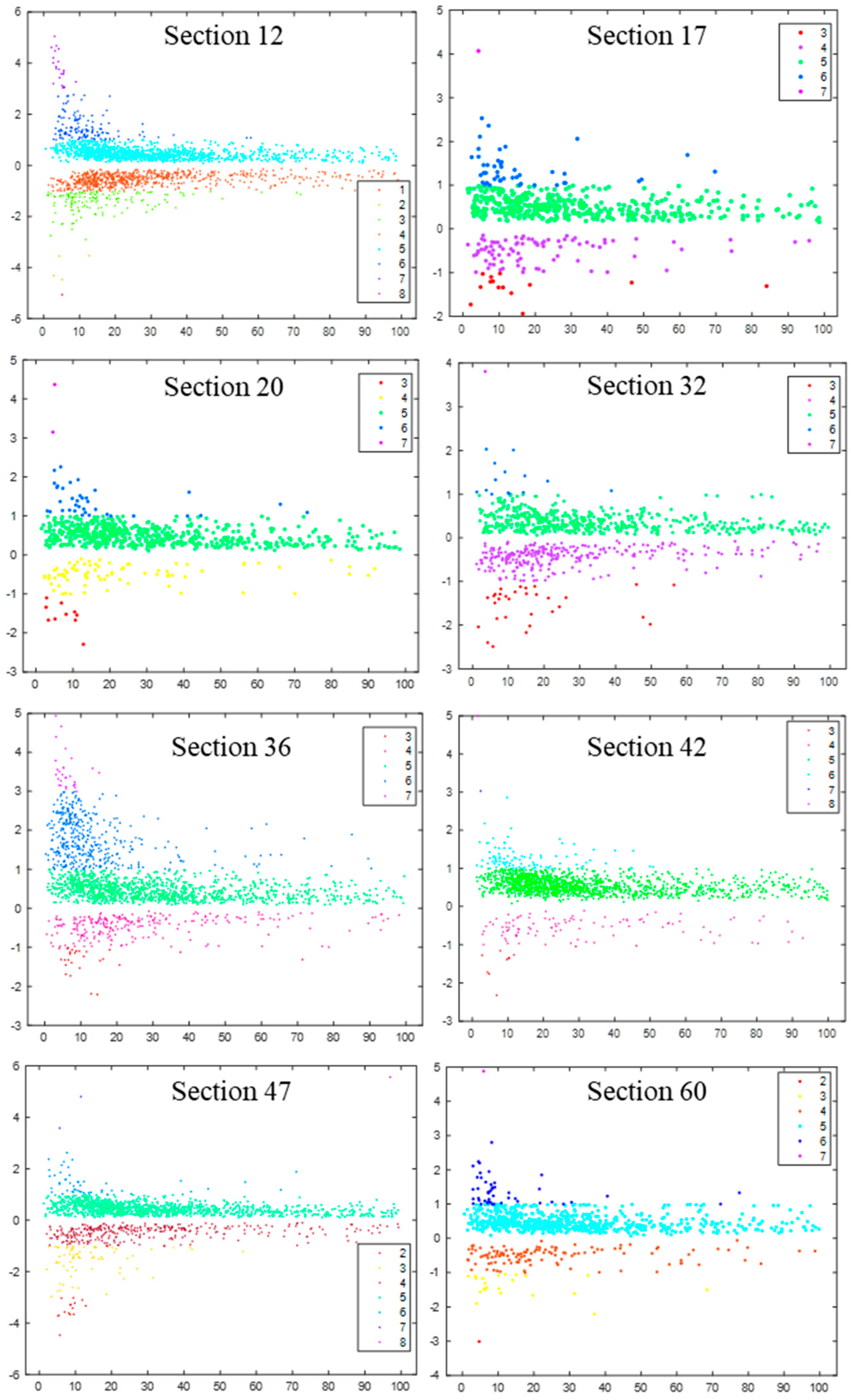
- 3.
- Data Analysis and Parameter Identification.
4. Results
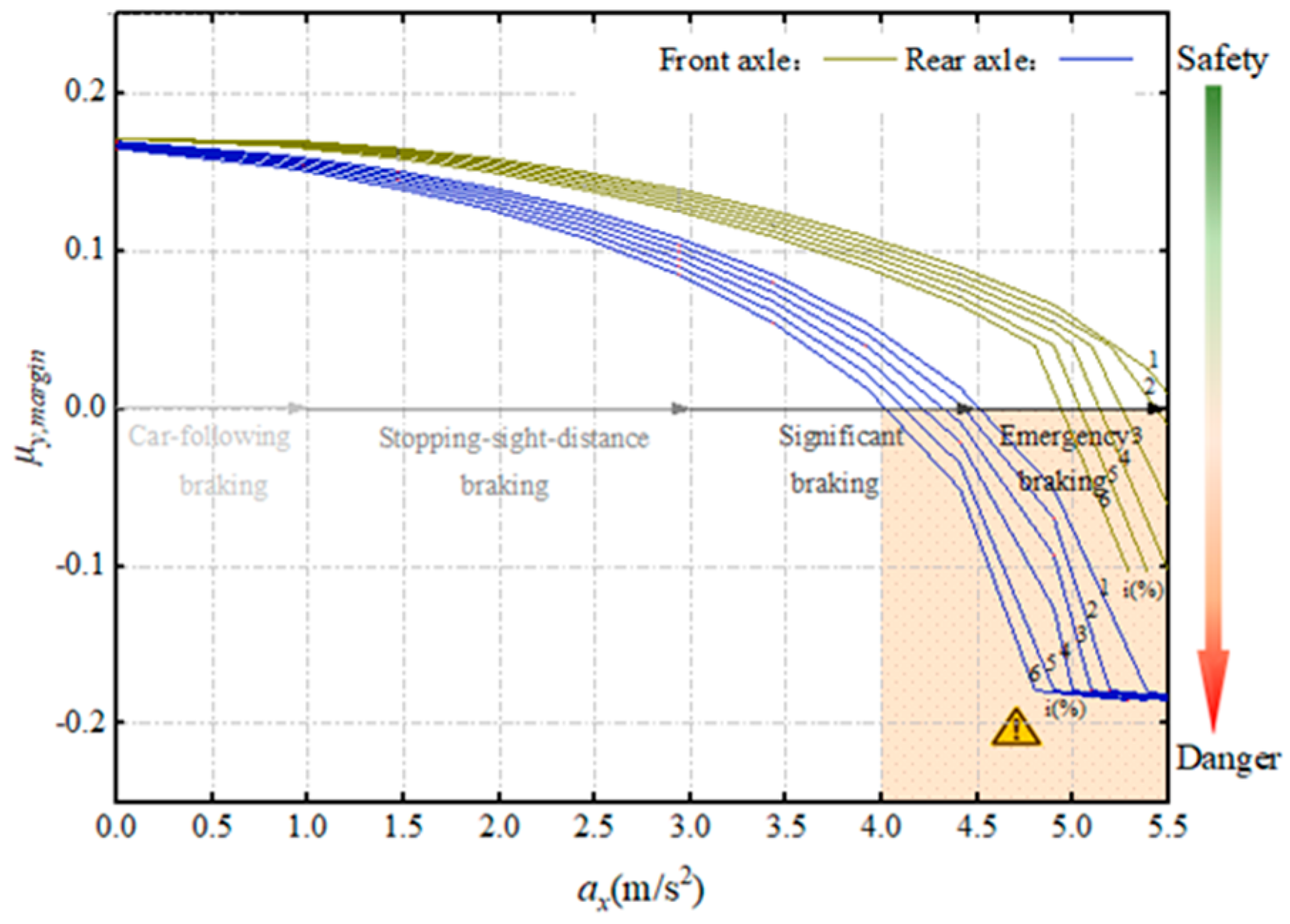
- 1.
- Prediction of truck skidding potential and recommendations of the MSBDRs on horizontal curves with different curve radii. The parameter values in the model are shown in Table 2.
- During braking, there is a higher skidding potential of the rear axle compared to the front axle. In other words, the safety margin against skidding on front axle is met, but that of the rear axle is not necessarily met on horizontal curves during braking.
- The curve radius has an effect on truck skidding. During braking, the smaller the radius of a horizontal curve, the higher the potential of skidding for trucks.
- In addition to emergency braking maneuvers, the horizontal curves designed in accordance with the current road geometry design standards, even with the limit-minimum radius, provide an adequate safety margin against skidding for trucks.
- During emergency braking maneuvers, the horizontal curves designed in accordance with the current road geometry design standards pose a high potential of trucks skidding. The higher the deceleration, the higher the potential of skidding for trucks.
- Therefore, taking into consideration the objective of ensuring safety and mitigating skidding risks, the recommended MSBDR is 4.5 m/s2.
- 2.
- Prediction of truck skidding potential and recommendations of the MSBDRs on horizontal curves with different slopes. The parameter values in the model are shown in Table 3.
- The downgrade has an effect on truck skidding.
- During braking, a horizontal curve with steep slopes is more prone to inducing truck skidding compared to a single horizontal curve. The larger the downgrade rates, the higher the potential of truck skidding.
- During significant and emergency braking maneuvers, trucks traveling on horizontal curves with steep slopes have a higher skidding potential.
- Therefore, the recommended MSBDR is 4 m/s2 on horizontal curves with steep slopes.
- 3.
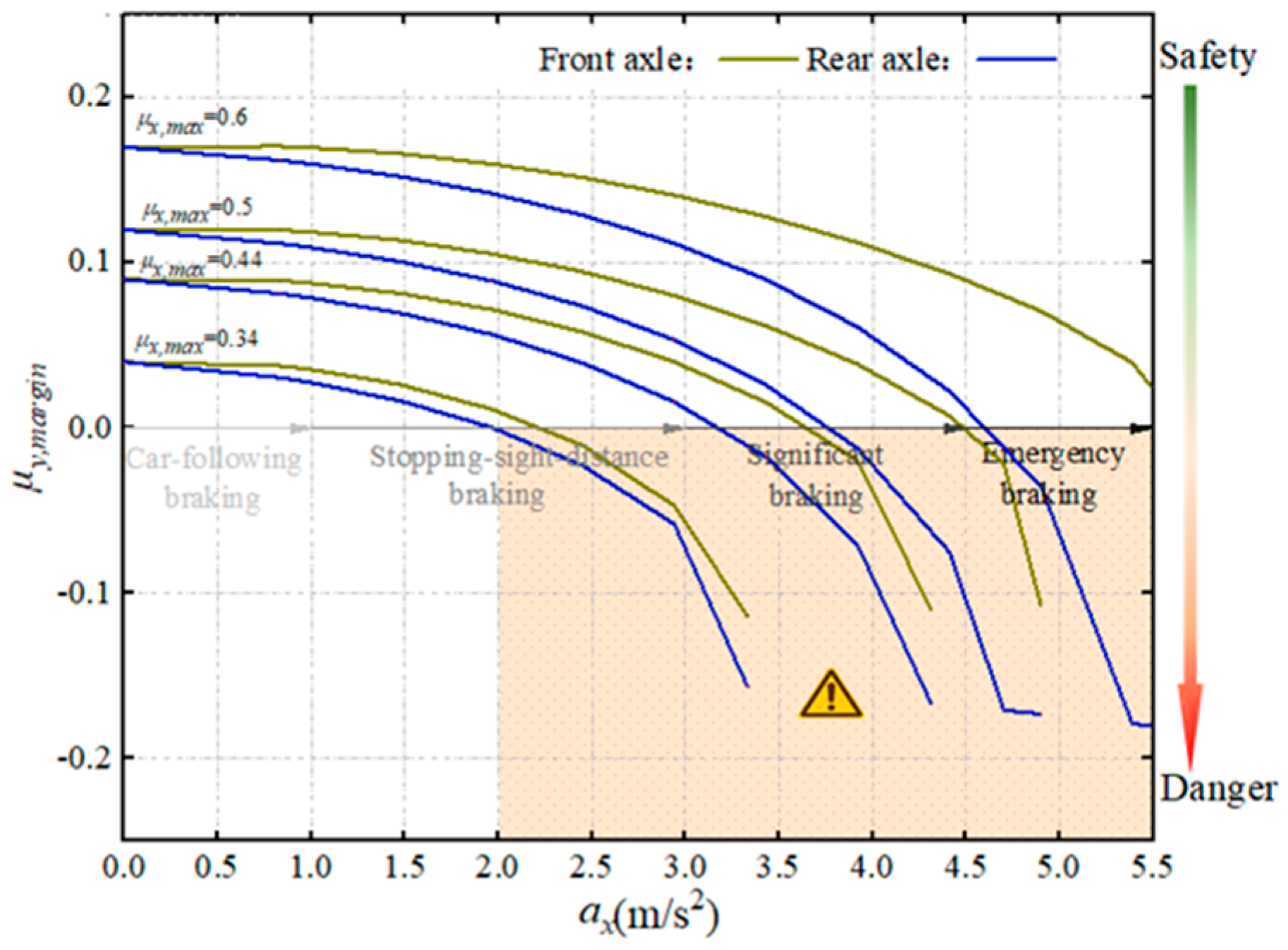
- Prediction of truck skidding potential and recommendations of the MSBDRs on horizontal curves with different friction coefficients. The parameter values in the model are shown in Table 4.
- The friction coefficient has a significant effect on truck skidding.
- The combination of braking and wet road conditions is worse for driving.
- During braking, the lower the friction coefficient, the higher the potential of truck skidding.
- On extremely wet roads (roads with a lower friction coefficient), even during stopping-sight-distance braking maneuvers, there is a higher potential of truck skidding.
- Therefore, the recommended MSBDR is 2 m/s2 on an extremely wet horizontal curve.
- 4.
- Prediction of truck skidding potential and recommendations of the MSBDRs on horizontal curves at different driving speeds. The parameter values in the model are shown in Table 5.
- Driving speed has a significant effect on truck skidding.
- The combination of braking and speeding is worse for driving.
- During braking, the more excessive the speeding, the higher the potential of truck skidding.
- In cases of excessive speeding, during significant and emergency braking maneuvers, there is a higher potential of truck skidding.
- Therefore, the recommended MSBDR is 2 m/s2 at a speed of 20% over the design speed on horizontal curves.
- During braking, there is a higher skidding potential of the rear axle compared to the front axle.
- The present study indicates that the effect of roadway alignment on the potential of truck skidding is very limited during braking.
- Under any driving condition, there is little concern of truck skidding during car-following braking maneuvers; however, there is a high potential of truck skidding during emergency braking maneuvers.
- Under wet road conditions and speeding conditions, there is the potential of truck skidding during sight-distance braking and significant braking.
- In summary, the conditions most prone to causing truck skidding are the emergency braking, the combination of braking and wet road conditions, then the combination of braking and speeding.
- Therefore, the recommended MSBDRs under different conditions are shown in Table 6.
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Key Terms | Symbol | Definitions |
|---|---|---|
| Side friction supply | Friction available between the pavement surface and vehicle tires to prevent skidding in the radial (side) direction, also referred to as the coefficient of side friction. | |
| Maximum side friction supply | The maximum side friction supply is utilized when a vehicle is at the point of impending skid in the radial (side) direction. | |
| Longitudinal friction supply | Friction available between the pavement surface and vehicle tires to prevent skidding in the tangential (longitudinal) direction, also referred to as the coefficient of longitudinal friction. | |
| Maximum longitudinal friction supply | The maximum longitudinal friction supply is utilized when a vehicle is at the point of impending skid in the tangential (longitudinal) direction. | |
| Side friction factor | The unbalanced portion of lateral acceleration or the portion of lateral acceleration that is not balanced by superelevation. The side friction factor represents the vehicle’s need for side friction, also called the side friction demand. | |
| Lateral friction margin | The difference between the available tire–pavement friction and the friction demand of the vehicle as it tracks the curve (i.e., side friction supply ()—side friction factor ()). This friction margin represents the additional lateral acceleration that a vehicle could undergo without skidding. A positive margin indicates that a vehicle can undergo additional lateral acceleration without skidding, while a negative margin indicates that the vehicle tires will skid given the level of friction supplied between the tire and pavement for the condition in question. | |
| Ideal braking force distribution curve | I-curve | A relation curve of braking forces on front and rear axles when front and rear axles are locked at the same time. The further the point on the curve being from the origin, the larger is the maximum longitudinal friction supply. |
| Actual braking force distribution curve | β-curve | In fact, the braking forces on front and rear axles adopt linear distribution. The variation curve of braking forces on front and rear axles is represented as a straight line passing through the origin on the distribution graph. |
| Synchronous adhesion coefficient | The friction coefficient at the intersection of I-curve and β-curve of the vehicle is called the synchronous adhesion coefficient. | |
| F line group | F-line | A series of braking force distribution curves, which represent the variation relationship between the front- and rear-axle braking forces in the case of front-axle lock-up. |
| R line group | R-line | A series of braking force distribution curves, which represent the variation relationship between the front- and rear-axle braking forces in the case of rear-axle lock-up. |
| Braking force | The braking force of the ground acting on the wheel, i.e., the friction between the pavement surface and the tires, whose direction is opposite to the driving direction of the vehicle. | |
| Brake force | The braking force of the brake acting on the wheel, which depends on the brake torque and wheel radius. |
References
- FHWA. Horizontal Curve Safety. 2024. Available online: https://safety.fhwa.dot.gov/roadway_dept/countermeasures/horicurves/ (accessed on 20 July 2024).
- FHWA. Roadway Departure Safety. 2024. Available online: https://safety.fhwa.dot.gov/roadway_dept/ (accessed on 20 July 2024).
- NHTSA. Traffic Safety Facts 2012: A Compilation of Motor Vehicle Crash Data from the Fatality Analysis Reporting System and the General Estimates System; NHTSA: Washington, DC, USA, 2013.
- Furtado, G.; Easa, S.; Abd, E. Vehicle Stability on Combined Horizontal and Vertical Alignments. In Proceedings of the Annual Conference of the Canadian Society of Civil Engineers, Montreal, QC, Canada, 5–8 June 2002. [Google Scholar]
- Choudhari, T.; Maji, A. Modeling driver’s braking and steering behavior along horizontal curves of two-lane rural highways for ADAS applications. Traffic Inj. Prev. 2022, 23, 404–409. [Google Scholar] [CrossRef] [PubMed]
- Petridou, E.; Moustaki, M. Human factors in the causation of road traffic crashes. Eur. J. Epidemiol. 2000, 16, 819–826. [Google Scholar] [CrossRef] [PubMed]
- Gaspar, J.; Brown, T.; Schwarz, C.; Chrysler, S.; Gunaratne, P. Driver Behavior in Forward Collision and Lane Departure Scenarios. In SAE Technical Paper Series; SAE: Warrendale, PA, USA, 2016. [Google Scholar]
- Barnett, J.; Haile, E.R.; Moyer, R.A. Safe Side Friction Factors and Superelevation Design. In Highway Research Board Proceedings; Highway Research Board: Washington, DC, USA, 1937; Volume 16. [Google Scholar]
- Aram, A. Effective Safety Factors on Horizontal Curves of Two-lane Highways. J. Appl. Sci. 2010, 10, 2814–2822. [Google Scholar] [CrossRef][Green Version]
- Ali, Y.; Haque, M.M.; Zheng, Z.; Afghari, A.P. A Bayesian correlated grouped random parameters duration model with heterogeneity in the means for understanding braking behaviour in a connected environment. Anal. Methods Accid. Res. 2022, 35, 100221. [Google Scholar] [CrossRef]
- Sayers, M.W.; Mousseau, C.W.; Gillespie, T.D. Using simulation to learn about vehicle dynamics. Int. J. Veh. Des. 2002, 29, 112–127. [Google Scholar] [CrossRef]
- Li, S.; Li, P.; Yao, Y.; Han, X.; Xu, Y.; Chen, L. Analysis of drivers’ deceleration behavior based on naturalistic driving data. Traffic Inj. Prev. 2020, 21, 42–47. [Google Scholar] [CrossRef]
- AASHTO. A Policy on Geometric Design of Highways and Streets; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2018. [Google Scholar]
- Harwood, D.W.; Mason, J.M.; Glauz, W.D.; Kulakowski, B.T.; Fitzpatrick, K. Truck Characteristics for Use in Highway Design and Operation. Volume II: Appendixes. Final Report; Data collection; Turner-Fairbank Highway Research Center: McLean, VA, USA, 1990. [Google Scholar]
- Harwood, D.W.; Mason, J.M., Jr. Horizontal curve design for passenger cars and trucks. Transp. Res. Rec. 1994, 1445, 22–33. [Google Scholar]
- Harwood, D.W.; Torbic, D.J.; Richard, K.R.; Glauz, W.D.; Elefteriadou, L. Review of Truck Characteristics as Factors in Roadway Design; Nchrp Report; Transportation Research Board: Washington, DC, USA, 2003. [Google Scholar]
- Torbic, D.J.; Donnell, E.T.; Brennan, S.N.; Brown, A.; O’Laughlin, M.K.; Bauer, K.M. Superelevation Design for Sharp Horizontal Curves on Steep Grades. Transp. Res. Rec. J. Transp. Res. Board 2014, 2436, 81–91. [Google Scholar] [CrossRef]
- Chang, T.H. Effect of Vehicles’ Suspension on Highway Horizontal Curve Design. J. Transp. Eng. 2001, 127, 89–91. [Google Scholar] [CrossRef]
- Torbic, D.J.; O’Laughlin, M.K.; Harwood, D.W.; Bauer, K.M.; Bokenkroger, C.D.; Lucas, L.M.; Ronchetto, J.R.; Brennan, S.; Donnell, E.; Brown, A. Superelevation Criteria for Sharp Horizontal Curves on Steep Grades; Transportation Research Board: Washington, DC, USA, 2014. [Google Scholar]
- Brandt, A.; Jacobson, B.; Sebben, S. High speed driving stability of road vehicles under crosswinds: An aerodynamic and vehicle dynamic parametric sensitivity analysis. Veh. Syst. Dyn. 2022, 60, 2334–2357. [Google Scholar] [CrossRef]
- Tang, G.; Ren, C.; Li, C. A Determination Method of Safety Driving Speeds on Different Radii Based on Trucksim. J. Highw. Transp. Res. Dev. 2016, 33, 134–139. [Google Scholar]
- Aly, A.A.; Zeidan, E.-S.; Hamed, A.; Salem, F. An Antilock-Braking Systems (ABS) Control: A Technical Review. Intell. Control. Autom. 2011, 2, 10. [Google Scholar] [CrossRef]
- Allen, K. The Effectiveness of ABS in Heavy Truck Tractors and Trailers; Department of Transportation: Washington, DC, USA, 2010.
- Bin, W.U.; Xichan, Z.H.U.; Jianping, S. Driver Emergency Braking Behavior Based on Naturalistic Driving Data. J. Tongji Univ. 2018, 46, 1514–1519. [Google Scholar]
- Hu, Y.; Li, Y.; Huang, H.; Lee, J.; Yuan, C.; Zou, G. A high-resolution trajectory data driven method for real-time evaluation of traffic safety. Accid. Anal. Prev. 2022, 165, 106503. [Google Scholar] [CrossRef]
- Kurtc, V. Studying car-following dynamics on the basis of the HighD dataset. Transp. Res. Rec. 2020, 2674, 813–822. [Google Scholar] [CrossRef]
- Olleja, P.; Bärgman, J.; Lubbe, N. Can non-crash naturalistic driving data be an alternative to crash data for use in virtual assessment of the safety performance of automated emergency braking systems? J. Saf. Res. 2022, 83, 139–151. [Google Scholar] [CrossRef]
- Hattori, Y.; Ono, E.; Hosoe, S. Optimum vehicle trajectory control for obstacle avoidance problem. IEEE/ASME Trans. Mechatron. 2006, 11, 507–512. [Google Scholar] [CrossRef]
- Abdel-Aty, M.; Cai, Q.; Wu, Y.; Zheng, O. Evaluation of automated emergency braking system’s avoidance of pedestrian crashes at intersections under occluded conditions within a virtual simulator. Accid. Anal. Prev. 2022, 176, 106797. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, Y.; Cafiso, S.D. Automatic Emergency Braking System for Trucks for Two-Wheeler Longitudinal Collision Avoidance. Transp. Res. Rec. 2023, 2677, 565–577. [Google Scholar] [CrossRef]
- MacAdam, C.C. Application of an optimal preview control for simulation of closed-loop automobile driving. IEEE Trans. Syst. Man Cybern. 1981, SMC-11, 393–399. [Google Scholar] [CrossRef]
- Macadam, C.C.; Fancher, P.S.; Segel, L. Side Friction for Superelevation on Horizontal Curves: Volume III—Appendices A–G; Final report, Molecular therapy; Transportation Research Institute (UMTRI): Ann Arbor, MI, USA, 1985. [Google Scholar]
- Kontaratos, M.; Psarianos, B.; Yotis, A. Minimum horizontal curve radius as function of grade incurred by vehicle motion in driving mode. Transp. Res. Rec. 1994, 1445, 86–93. [Google Scholar]
- Bonneson, J.A. Superelevation Distribution Methods and Transition Designs; nchrp Report; Transportation Research Board: Washington, DC, USA, 2000. [Google Scholar]
- Peng, H.; Hu, J.-S. Traction/braking force distribution for optimal longitudinal motion during curve following. Veh. Syst. Dyn. 1996, 26, 301–320. [Google Scholar] [CrossRef]
- Paul, D.; Velenis, E.; Humbert, F.; Cao, D.; Dobo, T.; Hegarty, S. Tyre–road friction μ-estimation based on braking force distribution. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 2030–2047. [Google Scholar] [CrossRef]
- Bergman, W. Theoretical prediction of the effect of traction on cornering force. SAE Trans. 1961, 69, 614–640. [Google Scholar]
- Wong, J.Y. Theory of Ground Vehicles; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Ong, G.P.; Fwa, T.F. Wet-Pavement Hydroplaning Risk and Skid Resistance: Modeling. J. Transp. Eng. 2007, 133, 590–598. [Google Scholar] [CrossRef]
- Peng, J.; Chu, L.; Wang, T.; Fwa, T.F. Analysis of vehicle skidding potential on horizontal curves. Accid. Anal. Prev. 2021, 152, 105960. [Google Scholar] [CrossRef]
- Shaohua, L.; Guiyang, W.; Hesen, W.; Lipeng, Z. Automatic emergency braking/anti-lock braking system coordinated control with road adhesion coefficient estimation for heavy vehicle. IET Intell. Transp. Syst. 2022, 16, 1521–1534. [Google Scholar] [CrossRef]
- Han, L.; Abdel-Aty, M.; Yu, R.; Wang, C. LSTM + Transformer Real-Time Crash Risk Evaluation Using Traffic Flow and Risky Driving Behavior Data. IEEE Trans. Intell. Transp. Syst. 2024. [Google Scholar] [CrossRef]
- Kim, S.; Song, T.-J.; Rouphail, N.M.; Aghdashi, S.; Amaro, A.; Gonçalves, G. Exploring the association of rear-end crash propensity and micro-scale driver behavior. Saf. Sci. 2016, 89, 45–54. [Google Scholar] [CrossRef]
- Jun, J. Potential Crash Exposure Measures Based on GPS-Observed Driving Behavior Activity Metrics; The Georgia Institute of Technology: Atlanta, GA, USA, 2006. [Google Scholar]
- Wang, X.; Zhu, M.; Chen, M.; Tremont, P. Drivers’ rear end collision avoidance behaviors under different levels of situational urgency. Transp. Res. Part C Emerg. Technol. 2016, 71, 419–443. [Google Scholar] [CrossRef]
- Naets, F.; van Aalst, S.; Boulkroune, B.; El Ghouti, N.; Desmet, W. Design and experimental validation of a stable two-stage estimator for automotive sideslip angle and tire parameters. IEEE Trans. Veh. Technol. 2017, 66, 9727–9742. [Google Scholar] [CrossRef]
- Marcillo, P.; Valdivieso Caraguay, Á.L.; Hernández-Álvarez, M. A Systematic Literature Review of Learning-Based Traffic Accident Prediction Models Based on Heterogeneous Sources. Appl. Sci. 2022, 12, 4529. [Google Scholar] [CrossRef]
- Varunjikar, T. Design of Horizontal Curves with Downgrades Using Low-Order Vehicle Dynamics Models. Master’s Thesis, The Pennsylvania State University, University Park, PA, USA, 2011. [Google Scholar]
- Mitschke, M.; Wallentowitz, H. Vehicle Dynamics. Chen Yinsan Yu Qiang Transl; Qinghua University Press: Beijing, China, 2009. [Google Scholar]
- Lamm, R.; Psarianos, B.; Choueiri, E.; Soilemezoglou, G. A practical safety approach to highway geometric design international case studies: Germany, Greece, Lebanon, and the United States. Transp. Res. Circ. 1998, 9, 1–14. [Google Scholar]
- Krajewski, R.; Bock, J.; Kloeker, L.; Eckstein, L. The highD Dataset: A Drone Dataset of Naturalistic Vehicle Trajectories on German Highways for Validation of Highly Automated Driving Systems. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2118–2125. [Google Scholar]
- Li, H. Steering and Handling Simulation of Multi-Axle Heavy-Duty Vehicle. Ph.D. Thesis, Wuhan University of Technology, Wuhan, China, 2013. [Google Scholar]
- Xu, N. Study on the Steady State Tire Model under Combined Conditions; Jilin University: Changchun, China, 2012. [Google Scholar]
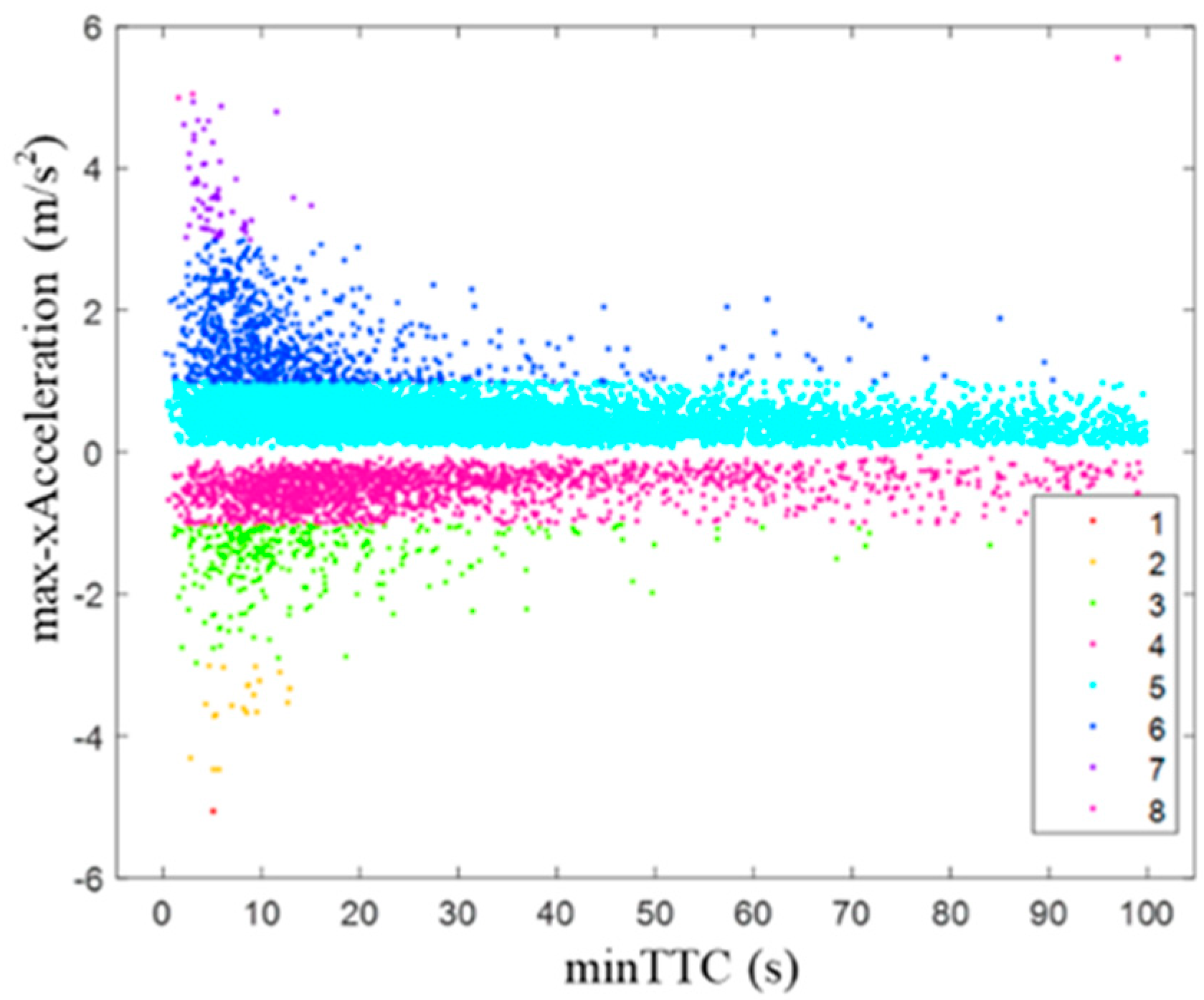


| Classification of Braking Behaviors | Ranges of Deceleration (Algebraic Value) | Unit |
|---|---|---|
| Car-following braking | [0, 1) | m/s2 |
| Stopping-sight-distance braking | [1, 3) | m/s2 |
| Significant braking | [3, 4.5) | m/s2 |
| Emergency braking | [4.5, 5] | m/s2 |
| Influence Factor | Parameter | Symbol | Value | Unit |
|---|---|---|---|---|
| Vehicle | Mass | 30,000 | kg | |
| Height of the CG | 1.8 | m | ||
| Synchronous adhesion coefficient | 0.4 | |||
| Front axle to CG distance | 3.60 | m | ||
| Rear axle to CG distance | 4.25 | m | ||
| Road | Design speed | 120/100/80 | km/h | |
| Radius | 650/400/250 | m | ||
| Superelevation | 8 | % | ||
| Downgrade | 0 | % | ||
| Friction coefficient (tire–pavement) | 0.6 | |||
| Environment | Weather | Dry | ||
| Driver behavior | Speed | 120/100/80 | km/h | |
| Deceleration | 0~5.5 | m/s2 |
| Influence Factor | Parameter | Symbol | Value | Unit |
|---|---|---|---|---|
| Vehicle | Mass | 30,000 | kg | |
| Height of the CG | 1.8 | m | ||
| Synchronous adhesion coefficient | 0.4 | |||
| Front axle to CG distance | 3.60 | m | ||
| Rear axle to CG distance | 4.25 | m | ||
| Road | Design speed | 80 | km/h | |
| Radius | 250 | m | ||
| Superelevation | 8 | % | ||
| Downgrade | 1/2/3/4/5/6 | % | ||
| Friction coefficient (tire–pavement) | 0.6 | |||
| Environment | Weather | Dry | ||
| Driver behavior | Speed | 80 | km/h | |
| Deceleration | 0~5.5 | m/s2 |
| Influence Factor | Parameter | Symbol | Value | Unit |
|---|---|---|---|---|
| Vehicle | Mass | 30,000 | kg | |
| Height of the CG | 1.8 | m | ||
| Synchronous adhesion coefficient | 0.4 | |||
| Front axle to CG distance | 3.60 | m | ||
| Rear axle to CG distance | 4.25 | m | ||
| Road | Design speed | 80 | km/h | |
| Radius | 250 | m | ||
| Superelevation | 8 | % | ||
| Downgrade | 0 | % | ||
| Friction coefficient (tire–pavement) | 0.6/0.5/0.44/0.34 | |||
| Environment | Weather | Dry/wet | ||
| Driver behavior | Speed | 80 | km/h | |
| Deceleration | 0~5.5 | m/s2 |
| Influence Factor | Parameter | Symbol | Value | Unit |
|---|---|---|---|---|
| Vehicle | Mass | 30,000 | kg | |
| Height of the CG | 1.8 | m | ||
| Synchronous adhesion coefficient | 0.4 | |||
| Front axle to CG distance | 3.60 | m | ||
| Rear axle to CG distance | 4.25 | m | ||
| Road | Design speed | 80 | km/h | |
| Radius | 250 | m | ||
| Superelevation | 8 | % | ||
| Downgrade | 0 | % | ||
| Friction coefficient (tire–pavement) | 0.6 | |||
| Environment | Weather | Dry | ||
| Driver behavior | Speed | /1.1/1.2 | km/h | |
| Deceleration | 0~5.5 | m/s2 |
| Condition | Horizontal Curves with a Limit-Minimum-Radius | |||
|---|---|---|---|---|
| Compound condition | / | Steep slopes | Extremely wet road | More than 1.2 |
| MSBDRs (m/s2) | 4.5 | 4.0 | 2.0 | 3.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, T.; Xu, J. A Data- and Model-Integrated Driven Method for Recommending the Maximum Safe Braking Deceleration Rates for Trucks on Horizontal Curves. Appl. Sci. 2024, 14, 9357. https://doi.org/10.3390/app14209357
Xin T, Xu J. A Data- and Model-Integrated Driven Method for Recommending the Maximum Safe Braking Deceleration Rates for Trucks on Horizontal Curves. Applied Sciences. 2024; 14(20):9357. https://doi.org/10.3390/app14209357
Chicago/Turabian StyleXin, Tian, and Jinliang Xu. 2024. "A Data- and Model-Integrated Driven Method for Recommending the Maximum Safe Braking Deceleration Rates for Trucks on Horizontal Curves" Applied Sciences 14, no. 20: 9357. https://doi.org/10.3390/app14209357
APA StyleXin, T., & Xu, J. (2024). A Data- and Model-Integrated Driven Method for Recommending the Maximum Safe Braking Deceleration Rates for Trucks on Horizontal Curves. Applied Sciences, 14(20), 9357. https://doi.org/10.3390/app14209357






