RSTSRN: Recursive Swin Transformer Super-Resolution Network for Mars Images

Abstract

High-resolution optical images will provide planetary geology researchers with finer and more microscopic image data information. In order to maximize scientific output, it is necessary to further increase the resolution of acquired images, so image super-resolution (SR) reconstruction techniques have become the best choice. Aiming at the problems of large parameter quantity and high computational complexity in current deep learning-based image SR reconstruction methods, we propose a novel Recursive Swin Transformer Super-Resolution Network (RSTSRN) for SR applied to images. The RSTSRN improves upon the LapSRN, which we use as our backbone architecture. A Residual Swin Transformer Block (RSTB) is used for more efficient residual learning, which consists of stacked Swin Transformer Blocks (STBs) with a residual connection. Moreover, the idea of parameter sharing was introduced to reduce the number of parameters, and a multi-scale training strategy was designed to accelerate convergence speed. Experimental results show that the proposed RSTSRN achieves superior performance on 2×, 4× and 8×SR tasks to state-of-the-art methods with similar parameters. Especially on high-magnification SR tasks, the RSTSRN has great performance superiority. Compared to the LapSRN network, for 2×, 4× and 8× Mars image SR tasks, the RSTSRN network has increased PSNR values by 0.35 dB, 0.88 dB and 1.22 dB, and SSIM values by 0.0048, 0.0114 and 0.0311, respectively.

1. Introduction

Exploration is the driving force for the development of human civilization and social progress. In the course of human exploration, space exploration can most directly expand the territory of human cognition and is extremely challenging. If we can understand the history of Mars, mankind’s view of the entire solar system may change. By studying the morphological characteristics of the Martian surface, we can gain a deep understanding of the formation and evolution process of the Martian surface and the evolutionary history of Martian geology [1,2,3,4]. Therefore, the primary task of Mars exploration is to obtain global high-resolution optical images.

The earliest global images of Mars were obtained in the early 1970s with a resolution of only 1 km. The Viking 1 and Viking 2 orbiters in the late 1970s obtained global images of Mars with a resolution of 100∼200 m. The Mars Global Surveyor (MGS) and Mars Express have obtained global images of Mars with a resolution of several meters. It took humans 30 years to increase the resolution of images of Mars by hundreds of times. The High-Resolution Imaging Science Experiment (HiRISE) [5,6,7,8,9] of the Mars Reconnaissance Orbiter (MRO) launched in 2005 has further increased the resolution by 10 times, and it obtained Mars remote sensing images with a resolution of up to 0.3 m. HiRISE’s excellent resolution has created many new research topics for planetary geology researchers: how the stratigraphic layers in the interior of Mars are formed; what are the new impact craters on the surface of Mars; what are the dynamic changes on the surface of Mars (such as how sand dunes move). The high-resolution images provided by HiRISE can help researchers explore Martian plates, volcanoes, climate and seasonal effects as well as understand the mysteries of impact crater formation, magma alluvial and glaciation on Mars.

Various physical processes have left rich and colorful patterns on the surface of Mars. High-resolution imaging data can help researchers explore the mysteries of Martian plates, volcanoes, climate, and seasonal effects as well as the formation of impact craters, magma accretion, and glaciation on Mars. However, too high resolution also comes at a cost. On the one hand, the volume of obtained data is too large, and it takes a long time to send it back to the earth due to the limitation of data downlink bandwidth. On the other hand, the field of view is limited, and the images obtained so far only cover about a few percent of the Martian surface.

In order to maximize scientific output, it is necessary to further increase the resolution of acquired images, so image super-resolution (SR) reconstruction techniques have become the best choice. At the same time, the SR will also provide planetary geology researchers with finer and more microscopic image data information so as to open up new research topics and further understand the formation and evolution process of the Martian surface and the evolution history of Martian geology.

The types of surface features on Mars are monotonous with no vegetation or other features except for bare soil and gravel. Compared with natural images, Mars images have more monotonous texture details and equally monotonous color information. This is extremely challenging for image super-resolution reconstruction, because the monotonous image information is difficult for feature learning mechanisms to obtain the high-frequency information required for super-resolution reconstruction.

In this work, we propose a novel Recursive Swin Transformer Super-Resolution Network (RSTSRN) for image SR. The RSTSRN improves upon the LapSRN (Laplacian pyramid Super-Resolution Network) [10] in three aspects: (1) it uses Residual Swin Transformer Block (RSTB) for more effective residual learning; (2) the idea of parameter sharing was introduced to reduce the number of parameters; (3) a multi-scale training strategy was designed to accelerate convergence speed. The shifted windowing scheme (Shifted Window Multi-head Self Attention, SW-MSA) brings greater efficiency. Based on RSTB, high-frequency features contained in images can be fully learned to better reconstruct super-resolution images. Transformer is a model that is completely based on an attention mechanism and does not include convolution. In the multi-head self-attention mechanism, the input is linearly projected onto multiple feature subspaces and processed in parallel by multiple independent attention heads, and then the cascaded result vector is mapped to the final output. We train the RSTSRN model and demonstrate 2×, 4×, and 8× resolution enhancement for images.

2. Related Works

SR algorithms have been applied in different fields, such as remote sensing [11,12,13,14,15], medical image processing [16,17,18], facial recognition [19,20,21], etc. Based on the number of input LR images in the reconstruction process, SR algorithms can be roughly divided into two categories: Multiple-Image SR (MISR) algorithms [22,23,24] and Single-Image SR (SISR) algorithms (also known as learning-based methods) [25,26,27].

2.1. Multiple-Image SR Algorithms

MISR algorithms can fully utilize the basic and non-redundant information contained in each frame of sequential LR images.

The Projection Onto Convex Sets (POCS) algorithm [28,29,30] has the ability to flexibly integrate various spatial observation models, motion models, and degraded models. The POCS algorithm has a strong ability to utilize prior information as well as the ability to maintain details and edges. However, the solution of this type of algorithm is usually not unique, and the reconstruction result has a strong dependence on the initial value. Moreover, the projection process requires a large amount of computation, and the convergence speed is slow. The convergence stability also needs to be further improved. The Iterative Back-Projection algorithm [31,32] is intuitive in theory and easy to implement. However, due to the ill-posed SR reconstruction problem, the solution of the IBP algorithm is not unique. The Maximum A Posteriori (MAP) algorithm [22,33,34,35,36] can fully consider the spatial domain prior information to ensure the stability of the final solution, and it has strong anti-noise performance. However, this type of algorithm has high computational complexity and easily leads to blurred edge details. The hybrid MAP/POCS algorithm [37] considers the convex set constraints and statistical features of the LR image sequence at the same time, thus obtaining the respective advantages of the two algorithms. The quality of the reconstructed image is better than the POCS algorithm and the MAP algorithm but only by using gradient descent optimization methods can convergence be guaranteed.

If the industry wants to fundamentally break through the limitations of MISR algorithms, it still needs to seek new ideas and methods.

2.2. Single-Image SR Algorithms

The basic idea of the SISR algorithm is to obtain the mapping relationship between HR images and LR images through learning, which is used to guide the reconstruction of new HR images. SISR algorithms are further divided into shallow learning-based SR algorithms [11,25,38] and deep learning-based SR algorithms [39,40,41,42].

2.2.1. Shallow Learning-Based SR Algorithms

Classic shallow learning-based algorithms include example-based algorithms [11,25] and sparse-representation-based algorithms [38].

In the reconstruction stage, the example-based algorithm uses the low-frequency information block of the LR image to be reconstructed as an index to search for similar samples in the sample library, and then it uses the high-frequency information corresponding to the matching samples to perform SR reconstruction. This type of algorithm needs to establish a huge sample library, and each LR block needs to search in the sample library, resulting in very high computational complexity. Moreover, due to the mismatching problem of the searched sample blocks, artifacts will be generated at the edges of the reconstructed image blocks, which will seriously affect the reconstruction quality. In order to eliminate artifacts, the reconstruction is performed by overlapping blocks. Averaging high-frequency information of overlapping regions leads to over-smoothed edges in the reconstructed image.

The sparse-representation-based algorithms perform sparse representation on the sample library composed of LR and HR sample image blocks. The sparse coefficients obtained by the corresponding LR block and HR block through their respective dictionaries are relatively similar, thus establishing the connection between LR and HR. This type of algorithm obtains better reconstruction quality, but the sparse coding and reconstruction process require multiple iterations, resulting in high algorithm complexity.

Shallow learning-based algorithms are mainly divided into three stages: feature extraction, learning, and reconstruction. Each stage is independently designed and optimized, and the feature extraction and expressive capabilities of the learning model are limited.

2.2.2. Deep Learning-Based SR Algorithms

The emergence of deep learning technology has made up for the shortcomings of traditional shallow learning algorithms. At present, deep learning-based SR algorithms have become the mainstream algorithms in the industry.

Dong et al. applied the convolutional neural networks to image SR reconstruction for the first time (SR Convolutional Neural Network, SRCNN) [42], and they divided the network into three stages: image block extraction, nonlinear mapping, and image reconstruction, and then these three stages are unified into a CNN (Convolutional Neural Network) framework to realize end-to-end learning from LR images to HR images.

Classic deep learning SR networks include FSRCNN (Fast SRCNN) [43], ESPCN (Efficient Sub-Pixel Convolutional neural Network) [44], VDSR (Very Deep networks for SR) [45], DRCN (Deeply Recursive Convolutional Network) [46], SCN (Sparse-Coding-based Network) [47], DEGREE (Deep Edge Guided REcurrent rEsidual) [48], MemNet (Memory Network) [49], LapSRN [10], DRRN (Deep Recursive Residual Network) [50], SRDenseNet (Super-Resolution Dense convolutional Network) [51], SRGAN (Super-Resolution Generative Adversarial Network) [52], RDN (Residual Dense Network) [53], SwinIR [54], NGswin (N-Gram Swin Trans-former) [55], DAT (Dual Aggregation Transformer) [56], etc.

In recent years, some deep learning-based SR algorithms for Lunar and Mars images have been published and achieved good results [13,27,39,40,57,58,59,60,61]. This provides a useful reference for this work. The author’s team also made some beneficial explorations in the aspect of remote sensing image SR [11,62,63] and carried out research work in several aspects such as network structure and lightweight, loss function and how to realize unsupervised learning. We previously proposed Lightweight Laplacian Pyramid Recursive and Residual Network (LRN) in [64] for Mars images.

3. Materials and Methods

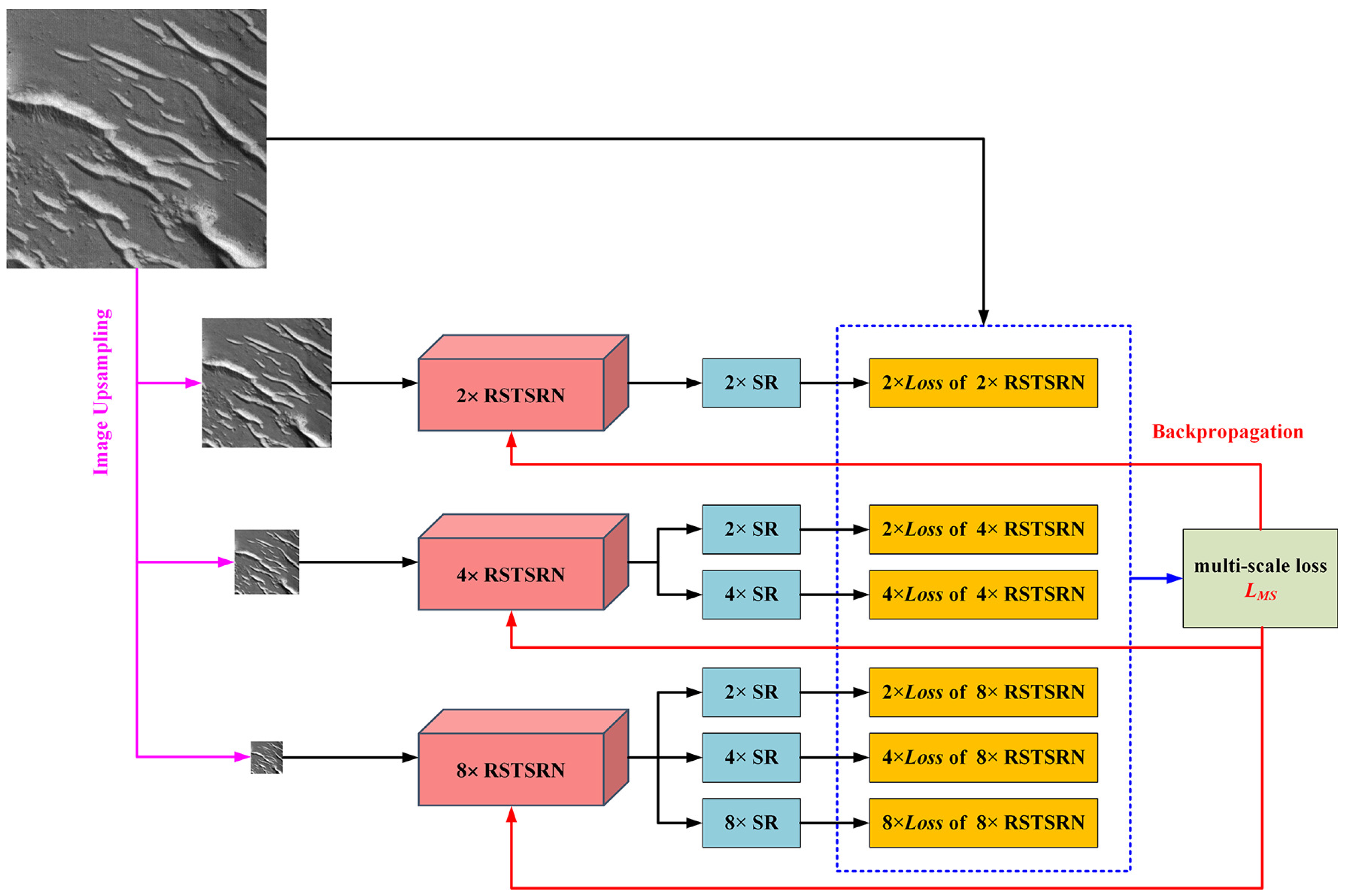
3.1. RSTSRN Architecture

Inspired by the mechanism of parameter sharing and recursive proposed in DRCN [46], we propose a novel Recursive Swin Transformer Super-Resolution Network (RSTSRN) combining the Swin Transformer [65] with the Laplacian Pyramid introduced in the LapSRN. Figure 1 shows our proposed RSTSRN network architecture; our goal is to estimate 2×/4×/8× SR images from an input LR image.

The Residual Image Extraction Block (RIEB) starts from a 3 × 3 convolutional layer, which can be formulated as

$$x_{1sf}=f_{IFE}\left(I_{LR}\right),$$

(1)

where $I_{LR}$ denotes the LR input to the network, $f_{IFE}$ denotes the feature extraction function for $I_{LR}$, and $x_{1sf}$ denotes the feature map extracted from LR.

Then, $x_{1sf}$ passed into the next RSTBs and other layers of the RIEB, as shown in equation

$$I_{2\times \mathrm{R}}=f_{RI}\left(x_{1sf}\right),$$

(2)

$$I_{2\times \mathrm{R}}=f_{RIEB}\left(I_{LR}\right)=f_{RI}\left(f_{IFE}\left(I_{LR}\right)\right),$$

(3)

where $I_{2\times \mathrm{R}}$ denotes the residual image extracted from LR by the first RIEB.

As shown in Figure 1, each RIEB contains 6 RSTBs. RSTB is based on the original RSTB and STB structures that were used in SwinIR [54] and Swin Transformer [65]; we have added the global skip connection that was used within the RIEB, and non-homologous skip connections were used for each RSTB to focus on residual learning. This design reduces the difficulty of learning residual images and improves the convergence efficiency of the network.

After the nonlinear feature mapping, we use the Pixelshuffle layer [44] for up-sampling. The input size of the Pixelshuffle layer is consistent with the size of the LR for each RIEB. The combination of a pair of convolutional layers and a LReLU layer before the Pixelshuffle layer is used to improve the extraction ability of deep features. The convolutional layer after the Pixelshuffle layer is used to improve the reconstruction quality of residual images. The 2×, 4×, and 8× SR image reconstruction processes can be expressed as

$$I_{2\times \mathrm{SR}}=I_{2\times \mathrm{R}}+f_{up}\left(I_{\mathrm{LR}}\right),$$

(4)

$$I_{2\times \mathrm{SR}}=I_{2\times \mathrm{R}}+I_{2\times \mathrm{LR}},$$

(5)

$$I_{4\times \mathrm{SR}}=I_{4\times \mathrm{R}}+f_{up}\left(I_{2\times \mathrm{SR}}\right),$$

(6)

$$I_{4\times \mathrm{SR}}=I_{4\times \mathrm{R}}+I_{4\times \mathrm{LR}},$$

(7)

$$I_{8\times \mathrm{SR}}=I_{8\times \mathrm{R}}+f_{up}\left(I_{4\times \mathrm{SR}}\right),$$

(8)

$$I_{8\times \mathrm{SR}}=I_{8\times \mathrm{R}}+I_{8\times \mathrm{LR}}.$$

(9)

The up-sampling method ($f_{up}$) from $I_{LR}$ to $I_{2\times \mathrm{LR}}$, $I_{2\times \mathrm{SR}}$ to $I_{4\times \mathrm{LR}}$, and $I_{4\times \mathrm{SR}}$ to $I_{8\times \mathrm{LR}}$ is all bicubic interpolation (scale = 2).

In an RSTSRN, the key to generating high-quality SR images is the inference of residual images. The residual image should contain more high-frequency information. Replace up-sampling from $I_{2\times \mathrm{LR}}$ to $I_{4\times \mathrm{LR}}$ and $I_{4\times \mathrm{LR}}$ to $I_{8\times \mathrm{LR}}$ with $I_{2\times \mathrm{SR}}$ to $I_{4\times \mathrm{LR}}$ and $I_{4\times \mathrm{SR}}$ to $I_{8\times \mathrm{LR}}$, respectively; then, the high-frequency information of $I_{2\times \mathrm{SR}}$ and $I_{4\times \mathrm{SR}}$ is better utilized in residual learning.

In an RSTSRN, parameters sharing is designed at two levels: one is between RIEBs and the other is between RSTBs. As shown in Figure 1, the RSTSRN consists of a three-level pyramid structure where each level performs 2× SR tasks with consistent functionality. Therefore, parameter sharing can be carried out between levels, where the convolutional layers, RSTBs, and the Pixelshuffle layer corresponding to each level use the same parameters. RSTBs are the core structure of the RSTSRN network, which is responsible for inferring residual images from shallow features for SR image reconstruction. In an RSTSRN, each RSTB shares the same parameters. However, STBs in RSTB do not share parameters.

3.2. Loss Functions and Multi-Scale Training Strategy

RSTSRN uses the $L_1$ loss function for parameter optimization, which can be formulated as

$$L_S^1={\displaystyle \frac{1}{N}}\sum _{i=1}^N\sum _{j=1}^L|IH{R}_j^i-IS{R}_j^i|,$$

(10)

$$L_{MS}=L_2^1+L_4^1+L_8^1,$$

(11)

where $L_{MS}$ represents the multi-scale loss function, S denotes the scale of the RSTSRN network, N denotes the number of images per batch, L denotes the number of pyramid levels, and $IH{R}_j^i$ and $IS{R}_j^i$ represent the HR image and the SR image, respectively.

We designed a special multi-scale training strategy for the progressive up-sampling framework of the pyramid structure used in an RSTSRN. An 8× RSTSRN network can produce 2×, 4×, and 8× outputs in one forward propagation, while a 4× RSTSRN network can produce 2× and 4× outputs in one forward propagation, each result being a superposition of similar 2× SR reconstruction processes. Multi-scale training refers to simultaneously training three RSTSRN networks with SR scales of 8×, 4×, and 2×. Each forward propagation can produce three 2× outputs, two 4× outputs, and one 8× output. If the final output of three networks (i.e., 8× output of 8× RSTSRN network, 4× output of 4× RSTSRN network, and 2× output of 2× RSTSRN network) has the same spatial resolution; then, three 2× SR results have different spatial resolutions, and the same applies to two 4× SR results. Conducting these tasks simultaneously during training can promote each other and accelerate convergence. The specific approach is to add up the three network loss functions before backpropagation to generate a final multi-scale loss function as shown in Equation (11) and then perform backpropagation parameter optimization for the three RSTSRN networks. The multi-scale training process is shown in Figure 2.

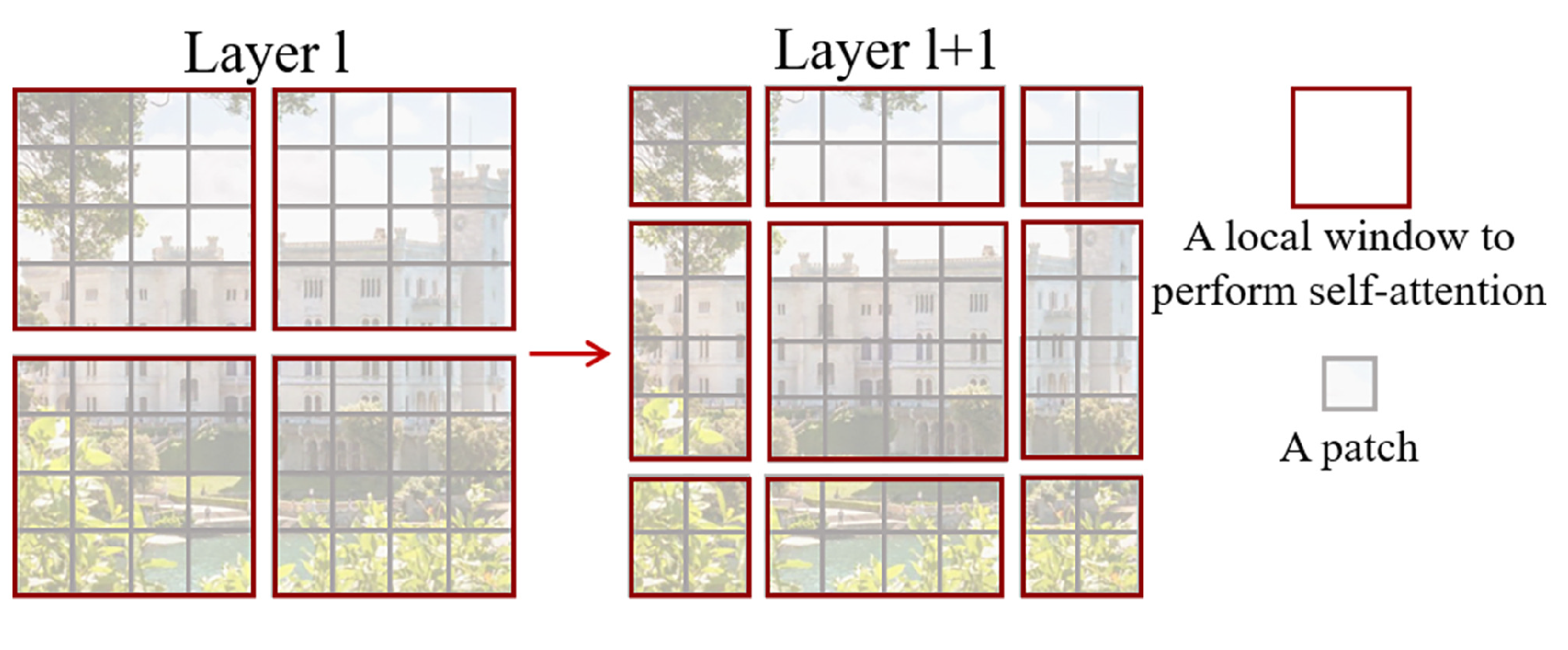
3.3. Shifted Window

This article not only limits the self-attention mechanism to non-overlapping local windows but also enables cross-window attention mechanism applications by shifted windows, improving the efficiency of utilizing window edge information and fully learning high-frequency features contained in images. An illustration of the shifted window approach for computing self-attention is shown in Figure 3 [65]. In layer l, self-attention is computed within each window. In the next layer l+1, the window partitioning is shifted, resulting in new windows. The self-attention computation in the new windows crosses the boundaries of the previous windows in layer l.

3.4. Training and Testing

Our experimental platform is a computer with a CPU of i9-10850K@3.60GHz and a GPU of NVIDIA RTX3090 with 24 GB of GPU memory. The operating system of the experimental platform is Win10, the deep learning framework is Pytorch 1.8, and the CUDA is 12.0.

We first train our network on the DIVerse 2K resolution image dataset (DIV2K) [66] to observe our algorithm’s performance on natural images. We carry out extensive experiments using 5 datasets: Set5 [67], Set14 [68], BSDS100 [69], Urban100 [70] and MANGA109 [71].

We also train our network on 5000 pairs of HiRISE and down-sampled HiRISE cropped samples. The training HR samples (512 × 512) were extracted from ESP_066115_2055 (https://www.uahirise.org/ESP_066115_2055, accessed on 18 March 2022); examples of HiRISE images are shown in Figure 4. The 1500 testing images were extracted from ESP_066194_2100 (https://www.uahirise.org/ESP_066194_2100, accessed on 18 March 2022) and ESP_066828_2050 (https://www.uahirise.org/ESP_066828_2050, accessed on 18 March 2022).

In the training phase, the batch size is set to 20 and the ADAM optimizer is adopted with the setting of ${\beta }_1$ = 0.9, ${\beta }_2$ = 0.999, and $ϵ$ = 10⁻⁸. MultiStep is adopted as the learning rate decay strategy, and the learning rate is initialized to 2 × 10⁻⁴, the multiplication factor is set to 0.5, and the milestones are set to 100,000, 160,000, 180,000, 190,000 and 200,000 iterations.

4. Results

4.1. RSTSRN Results for Natural Images

We compare the proposed RSTSRN with 18 SR algorithms: VDSR [45], DRCN [46], MemNet [49], LapSRN [10], EDSR (Enhanced Deep Super-Resolution) [72], CARN (CAscading Residual Network) [73], D-DBPNs (Dense Deep Back-Projection Networks) [74], MSRN (Multi-Scale Residual Network) [75], IMDN (Information Multi-Distillation Network) [76], AWSRN (Adaptive Weighted Super-Resolution Network) [77], RFDN (Residual Feature Distillation Network) [78], LatticeNet [79], HNCT (Hybrid Network of CNN and Transformer) [80], ELAN (Efficient Long-range Attention Network) [81], ESRT (Efficient Super-Resolution Transformer) [82], SPIN (Super Token Interaction Network) [83], DiVANet (Directional Variance Attention Network) [84] and NGswin [55]. We evaluate the SR images with Peak Signal-to-Noise Ratio (PSNR) and Structural SIMilarity (SSIM) [85].

Table 1. Average PSNR (dB)/SSIM for 2×, 4× and 8× SR. ’Year’ indicates the publication year of each paper. Red indicates the best performance and blue indicates the second best.

Algorithm	Scale	Year	Parameters	Set5 PSNR/SSIM	Set14 PSNR/SSIM	BSDS100 PSNR/SSIM	Urban100 PSNR/SSIM	MANGA109 PSNR/SSIM
Bicubic	2×	-	-	33.66/0.9284	30.34/0.8675	29.57/0.8434	26.88/0.8438	30.82/0.9332
VDSR [45]	2×	2016	665K	37.53/0.9587	33.03/0.9124	31.90/0.8960	30.76/0.9140	37.22/0.9729
DRCN [46]	2×	2016	1774K	37.63/0.9588	33.04/0.9118	31.85/0.8942	30.75/0.9133	37.63/0.9723
MemNet [49]	2×	2017	677K	37.78/0.9597	33.28/0.9142	32.08/0.8978	31.31/0.9195	37.72/0.9740
LapSRN [10]	2×	2017	813K	37.52/0.9581	33.08/0.9109	31.80/0.8949	30.41/0.9112	37.27/0.9745
EDSR [72]	2×	2017	43000K	38.11/0.9601	33.92/0.9195	32.32/0.9013	32.93/0.9351	39.10/0.9773
CARN [73]	2×	2018	1592K	37.76/0.9590	33.52/0.9166	32.09/0.8978	31.51/0.9312	38.36/0.9764
D-DBPN [74]	2×	2018	5819K	38.09/0.9600	33.85/0.9190	32.27/0.9000	32.55/0.9324	38.89/0.9775
MSRN [75]	2×	2018	5930K	38.08/0.9605	33.74/0.9170	32.23/0.9013	32.22/0.9326	38.69/0.9772
IMDN [76]	2×	2019	694K	38.00/0.9605	33.63/0.9177	32.19/0.8996	32.17/0.9283	38.88/0.9774
AWSRN [77]	2×	2019	1397K	38.11/0.9608	33.78/0.9189	32.26/0.9006	32.49/0.9316	38.87/0.9776
RFDN-L [78]	2×	2020	626K	38.08/0.9606	33.67/0.9190	32.18/0.8996	32.24/0.9290	38.95/0.9773
LatticeNet [79]	2×	2020	756K	38.15/0.9610	33.78/0.9193	32.25/0.9005	32.43/0.9302	-
HNCT [80]	2×	2022	356K	38.08/0.9608	33.65/0.9182	32.22/0.9001	32.22/0.9294	38.87/0.9774
ELAN-light [81]	2×	2022	582K	38.17/0.9611	33.94/0.9207	32.30/0.9012	32.76/0.9340	39.11/0.9782
ESRT [82]	2×	2022	677K	38.03/0.9600	33.75/0.9184	32.25/0.9001	32.58/0.9318	39.12/0.9783
SPIN [83]	2×	2023	497K	38.20/0.9615	33.90/0.9215	32.31/0.9015	32.79/0.9340	39.18/0.9784
DiVANet [84]	2×	2023	902K	38.16/0.9612	33.80/0.9195	32.29/0.9012	32.60/0.9325	39.08/0.9775
NGswin [55]	2×	2023	998K	38.05/0.9610	33.79/0.9199	32.27/0.9008	32.53/0.9324	38.97/0.9777
RSTSRN (ours)	2×	-	1830K	38.11/0.9619	33.92/0.9209	32.30/0.9012	32.68/0.9340	39.04/0.9779
Bicubic	4×	-	-	28.43/0.8022	26.10/0.6936	25.97/0.6517	23.14/0.6599	24.91/0.7826
VDSR [45]	4×	2016	665K	31.35/0.8838	28.01/0.7674	27.29/0.7251	25.18/0.7524	28.83/0.8809
DRCN [46]	4×	2016	1774K	31.53/0.8840	28.04/0.7700	27.24/0.7240	25.14/0.7520	28.97/0.8860
MemNet [49]	4×	2017	677K	31.74/0.8893	28.26/0.7723	27.40/0.7281	25.50/0.7630	29.42/0.8942
LapSRN [10]	4×	2017	813K	31.54/0.8856	28.19/0.7720	27.32/0.7280	25.21/0.7560	29.09/0.8900
EDSR [72]	4×	2017	43000K	32.46/0.8968	28.80/0.7876	27.71/0.7420	26.64/0.8033	31.02/0.9148
CARN [73]	4×	2018	1592K	32.13/0.8937	28.60/0.7806	27.58/0.7349	26.07/0.7837	30.36/0.9082
D-DBPN [74]	4×	2018	10291K	32.47/0.8970	28.82/0.7860	27.72/0.7400	26.38/0.7946	30.91/0.9137
MSRN [75]	4×	2018	6078K	32.07/0.8903	28.60/0.7751	27.52/0.7273	26.04/0.7896	30.17/0.9034
IMDN [76]	4×	2019	715K	32.21/0.8948	28.58/0.7811	27.56/0.7353	26.04/0.7838	30.45/0.9075
AWSRN [77]	4×	2019	1587K	32.27/0.8960	28.69/0.7843	27.64/0.7385	26.29/0.7930	30.72/0.9109
RFDN-L [78]	4×	2020	643K	32.28/0.8957	28.61/0.7818	27.58/0.7363	26.20/0.7883	30.61/0.9096
LatticeNet [79]	4×	2020	777K	32.30/0.8962	28.68/0.7830	27.62/0.7367	26.25/0.7873	-
HNCT [80]	4×	2022	372K	32.31/0.8957	28.71/0.7834	27.63/0.7381	26.20/0.7896	30.70/0.9112
ELAN-light [81]	4×	2022	601K	32.43/0.8975	28.78/0.7858	27.69/0.7406	26.54/0.7982	30.92/0.9150
ESRT [82]	4×	2022	751K	32.19/0.8947	28.69/0.7833	27.69/0.7379	26.39/0.7962	30.75/0.9100
SPIN [83]	4×	2023	555K	32.48/0.8983	28.80/0.7862	27.70/0.7415	26.55/0.7998	30.98/0.9156
DiVANet [84]	4×	2023	939K	32.41/0.8973	28.70/0.7844	27.65/0.7391	26.42/0.7958	30.73/0.9119
NGswin [55]	4×	2023	1019K	32.33/0.8963	28.78/0.7859	27.66/0.7396	26.45/0.7963	30.80/0.9128
RSTSRN (ours)	4×	-	1830K	32.63/0.9008	28.89/0.7895	27.77/0.7435	26.78/0.8075	31.40/0.9192
Bicubic	8×	-	-	24.40/0.6045	23.19/0.5110	23.67/0.4808	20.74/0.4841	21.46/0.6138
VDSR [45]	8×	2016	665K	25.73/0.6743	23.20/0.5110	24.34/0.5169	21.48/0.5289	22.73/0.6688
DRCN [46]	8×	2016	1774K	25.93/0.6743	24.25/0.5510	24.49/0.5168	21.71/0.5289	23.20/0.6686
MemNet [49]	-	2017	-	-	-	-	-	-
LapSRN [10]	8×	2017	813K	26.15/0.7028	24.45/0.5792	24.54/0.5293	21.81/0.5555	23.39/0.7068
EDSR [72]	8×	2017	43000K	26.96/0.7762	24.91/0.6420	24.81/0.5985	22.51/0.6221	24.69/0.7841
CARN [73]	-	2018	-	-	-	-	-	-
D-DBPN [74]	8×	2018	23071K	27.21/0.7840	25.13/0.6480	24.88/0.6010	22.73/0.6312	25.14/0.7987
MSRN [75]	8×	2018	6226K	26.59/0.7254	24.88/0.5961	24.70/0.5410	22.37/0.5977	24.28/0.7517
IMDN [76]	-	2019	-	-	-	-	-	-
AWSRN [77]	8×	2019	2348K	26.97/0.7747	24.99/0.6414	24.80/0.5967	22.45/0.6174	24.60/0.7782
RFDN-L [78]	-	2020	-	-	-	-	-	-
LatticeNet [79]	-	2020	-	-	-	-	-	-
HNCT [80]	-	2022	-	-	-	-	-	-
ELAN-light [81]	-	2022	-	-	-	-	-	-
ESRT [82]	-	2022	-	-	-	-	-	-
SPIN [83]	-	2023	-	-	-	-	-	-
DiVANet [84]	-	2023	-	-	-	-	-	-
NGswin [55]	-	2023	-	-	-	-	-	-
RSTSRN (ours)	8×	-	1830K	27.30/0.7895	25.24/0.6498	24.96/0.6045	23.02/0.6458	25.23/0.8022

shows quantitative comparisons for 2×, 4× and 8× SR.

As shown in Table 1, the proposed RSTSRN achieves superior performance (optimal value or near-optimal values) on 2×, 4× and 8× SR tasks to state-of-the-art methods with similar parameters. The RSTSRN obtains the highest PSNR and SSIM values in all five datasets tested at the 4× and 8×SR tasks, and it has a large lead over other algorithms, indicating that our RSTSRN has great performance superiority in the current lightweight methods. We fully verified the effectiveness of RSTB for high-frequency feature learning on high magnification super-resolution reconstruction tasks.

For SR tasks with different multiples, most algorithms will modify the local details of the network model accordingly, and they mainly focus on 2×, 3× and 4× SR tasks. There are relatively few algorithms that focus on the 8 × SR task.

Table 2. Quantitative comparison with the number of parameters of lightweight SR algorithms on multi-scale tasks. ’Year’ indicates the publication year of each paper.

Method	Year	2×	4×	8×	Multi-Scales
VDSR [45]	2016	665 K	665 K	665 K	1995 K
DRCN [46]	2016	1774 K	1774 K	1774 K	5322 K
MemNet [49]	2017	677 K	677 K	-	1354 K
LapSRN [10]	2017	813 K	813 K	813 K	2439 K
CARN [73]	2018	1592 K	1592 K	-	3184 K
AWSRN [77]	2019	1397 K	1587 K	2348 K	5332 K
RSTSRN(ours)	-	1830 K	1830 K	1830 K	1830 K

shows quantitative comparisons with the number of parameters of lightweight SR algorithms on multi-scale tasks. Unlike other lightweight SR reconstruction networks, the RSTSRN uses a progressive up-sampling framework based on the Laplacian image pyramid and an interstage parameter sharing mechanism. Therefore, the same parameter set is used in 2×, 4× and 8× SR tasks, which makes the RSTSRN demonstrate higher lightweight performance in multi-scale reconstruction tasks.

The test results of some algorithms on the benchmark test dataset are as follows. The results of the LapSRN, AWSRN, and D-DBPN with reconstruction capabilities at three scales of 2×, 4×, and 8× are presented. In the comparison of 2× and 4× reconstruction results, a CARN with parameters close to an RSTSRN was selected. In the comparison of 4× reconstruction results, the EDSR with the second-best performance and the largest number of parameters was selected. In the comparison of 4× and 8× reconstruction results, D-DBPN has the second largest number of parameters. In addition, D-DBPN achieved suboptimal results in 8× reconstruction and also achieved good results in 4× reconstruction.

Figure 5 shows the local magnification visual effects of an image named “barbara” in the Set14 dataset at 2×SR. It is obvious that other algorithms except for the RSTSRN and AWSRN have not been able to fully reconstruct the black and white stripes of the scarf in the image. However, the reconstruction results of the AWSRN at the upper end of the enlarged area did not match the original image, so only the RSTSRN completed the complete reconstruction of the area.

Figure 6 shows the visual effect of two local magnifications of an image named “butterfly” in the Set5 dataset at 4× SR. For the first area on the upper right, the notch shape of the white patch in the original image can only be reflected to a certain extent in the SR reconstruction results of the CARN and RSTSRN, while the results of the RSTSRN are closer to the geometric shape of the original image compared to the CARN. For the second region, the shape of the notch in the original image can be reconstructed by most algorithms, but only the reconstruction effect of the RSTSRN can reflect the sharp angle of the notch in the original image. In summary, the RSTSRN demonstrated the best visual performance in the 4× SR reconstruction task of a “butterfly”.

Figure 7 shows the local magnification visual effects of an image named “img_040” in the Urban100 dataset at 8× SR. It is evident that only the RSTSRN has completed the correct reconstruction of this area.

4.2. RSTSRN Results for Mars Image

The natural image reconstruction effect proves the superiority of the RSTSRN. In this subsection, we only compare the proposed RSTSRN with the LapSRN [10].

Table 3. Quantitative comparison of 2×, 4× and 8×SR on Mars remote sensing datasets.

Method	Scale	PSNR/dB	SSIM
Bicubic	2×	34.09	0.8228
LapSRN [10]	2×	34.72	0.8477
RSTSRN(ours)	2×	35.07	0.8525
Bicubic	4×	31.31	0.7124
LapSRN [10]	4×	31.94	0.7396
RSTSRN(ours)	4×	32.82	0.7510
Bicubic	8×	28.60	0.6128
LapSRN [10]	8×	29.23	0.6327
RSTSRN(ours)	8×	30.45	0.6638

shows quantitative comparisons for 2×, 4× and 8× SR.

Compared to the LapSRN network, for the 2×, 4× and 8×SR tasks, the RSTSRN network proposed in this article has increased PSNR values by 0.35 dB, 0.88 dB and 1.22 dB, and SSIM values by 0.0048, 0.0114 and 0.0311, respectively. The objective evaluation indicators have been significantly improved. Figure 8, Figure 9 and Figure 10 show the comparison of subjective visual effects and objective indicators of several Mars images using Bicubic, LapSRN, and RSTSRN algorithms under 2×, 4× and 8× SR reconstruction. It can be seen that the RSTSRN proposed in this article outperforms the prototype algorithm LapSRN in terms of vision. The edge and texture details in the SR reconstructed image of the RSTSRN are clearer and sharper, and the overall details of the SR reconstructed images are closer to the original HR images. The comparative experiment fully verified the effectiveness of RSTB for high-frequency feature learning.

The RSTSRN can not only be used for supporting image analysis to obtain improved scientific understanding of the Martian surface, but it can also be used for supporting existing and future missions. SR images can be employed for a wide range of applications such as the selection of landing sites for future Mars landing missions, the planning of Mars rover exploration paths, and the manned Mars program.

5. Conclusions

In this paper, we introduce a lightweight and efficient image SR reconstruction network RSTSRN based on the Swin Transformer module using the Laplace image pyramid as a framework. The efficiency of the proposed network is mainly due to the following reasons: (1) We use the Laplace image pyramid as the network framework, which breaks the hard 8× SR task into three simple 2× SR tasks so that 8× SR can be performed with a lightweight network RSTSRN. (2) We adopt the parameters-sharing mechanism between the pyramid levels and between the recursive blocks to maintain a low-parameter quantity. (3) We replace the convolution layers with more efficient Swin Transformer modules and adopt the skip connection mechanism to enable the network to achieve higher performance while maintaining low computational complexity.

Despite the positive outcomes of this study, there are some limitations. For example, in terms of the number of parameters, it is still relatively large compared to the latest methods such as SPIN, DiVANet, NGswin, etc., and further lightweight design is needed. To address the limitations of the current work, future research can be conducted in the following directions: one is to further optimize the network structure to further reduce the number of parameters; another is to train and test on more diverse datasets, such as images obtained by ExoMars Trace Gas Orbiter (TGO)’s Color and Stereo Surface Imaging System (CaSSIS) and High-Resolution Imaging Camera (HiRIC) on China’s First Mars Exploration Tianwen-1 Mission to enhance the model’s generalization ability. Through these research approaches, we hope to elevate the super-resolution reconstruction technology for Mars images to a higher level.