Abstract
In this paper, we address the aspect of knapsack balancing in the classic knapsack problem. Recognizing that excessive dispersion in the objective function or constraint coefficients of the optimal solution can be undesirable, we propose, when appropriate, to control this effect through problem multiobjectivization. By multiobjectivization, we mean the addition of one or more objective functions that aim to shift the original problem’s optimal solutions towards Pareto optimal solutions of the multiobjectivized problem, reducing the dispersion of the respective coefficients. We detail how the knapsack balance aspect can be incorporated into the standard knapsack problem model and demonstrate the functionality of this enriched model through illustrative examples.
1. Introduction and Motivation
The knapsack problem is one of the best studied combinatorial optimization problems (see, e.g., [1,2]). It is defined as follows: Given a set of items and a knapsack with a maximal weight C, each item , is characterized by its profit and weight .
A subset of items that together are not heavier than C and provide the highest sum of profits is to be determined. This problem can be formulated as a Linear Binary Programming (LBP) problem as follows:
Many practical decision problems can be modeled as the knapsack problem or one of its variants (see, e.g., [3]). The knapsack problem can also be used as sub-problems of more complex models (see, e.g., [4,5]). As an illustration, let us assume that a farmer models the production of the farm using the knapsack problem. The farm consists of several lots; each lot can accommodate just one crop, yielding a given profit for a given workload. The problem is to assign crops to lots to maximize the total profit under a limited workload budget. To mitigate risks inherent to agriculture, a portfolio of crops rather than a single crop is advisable. Crops yielding small profits may be not very desirable. Prices of crops yielding high profits may vary significantly. Likewise, serving a collection of crops with low and high workload may rise logistic concerns. In consequence, a balanced crop portfolio is of interest, even if portfolio balancing inevitably deteriorates the optimal total profit as compared to the total profit when balancing is not accounted for. Although the problem can be modeled by a more complex, and perhaps more realistic, formulation, the knapsack problem has the advantage to be rather simple. A mechanism to confine the objective function and/or the constraint coefficient dispersion at the optimal solution while retaining the knapsack problem structural simplicity would be of interest.
The example brings us to the issue of knapsack balancing. We can attempt to balance the objective function coefficients, the constraint coefficients, or both at once. In contrast to balancing mechanisms proposed in the literature on combinatorial optimization (see, e.g., [6]), here we propose to balance with the Nash social welfare function that maximizes the product of all quantities that have to be balanced (in the original work of Nash those were individual utilities) ([7]). A distinguishing property of this function is that when the sum of continuous quantities (all positive) is tied to a certain positive value, the maximum of this function is achieved when all quantities are equal.
As seen in Figure 1, function equally assesses all three elements (filled discs), as they all are located on the same contour (the solid line), whereas function differentiates them as they are located on two different contours (dashed lines). Moreover, the latter function has a higher value for the element with than for elements with .
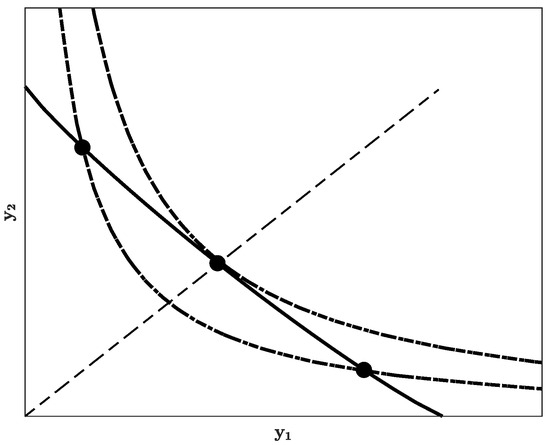
Figure 1.
Properties of functions and .
As shown below, in the context of the knapsack problem, this function has plausible properties, both in terms of balancing and computing.
We approach the problem of knapsack balancing through a multiobjective problem formulation. Multiobjective formulations offer a framework by which some seemingly hidden aspects of underlying decision problems can be incorporated into optimization models. A single-objective optimization model is multiobjectivized by keeping the original objective function and adding new objective functions representing the new aspects that are to be considered. The compromises between the need to optimize the original objective function and the new ones have to be managed using appropriate multiobjective optimization techniques.
The term ’multiobjectivization’ was introduced by Knowles et al. in 2001 ([8]) in the context of evolutionary optimization. Ma et al. ([9]) claim that using multiobjectivization to solve single-objective problems within evolutionary optimization
“can reduce the number of local optima, create new search paths from local optima to global optima, attain more incomparability solutions, and/or improve solution diversity”.
Klamroth and Tind ([10]) discussed reformulations of single-objective problems to multiobjective ones in the context of exact optimization. In [11], multiobjectivization was applied to exploit the specific structure of multiple-choice constraints in the multiple-choice knapsack problem. This idea was further explored in [12].
The main contributions of this article are summarized as follows:
- We introduce knapsack balancing as a new aspect of the knapsack problem.
- We demonstrate how to incorporate the aspect of knapsack balancing into the knapsack problem standard model.
- We provide a formal proof of the correctness of our approach.
- We demonstrate working of the enriched knapsack problem model on illustrative examples.
As discussed in Section 2, knapsack balancing can be interpreted as part of a broader concept of making balanced or fair decisions. This concept was introduced first in the qualitative decision theory (see the reference in the next section) but, to the best of the authors’ knowledge, this paper presents the first fully quantitative treatment of this issue within the context of the knapsack problem.
This article is organized as follows. In Section 2, related works are discussed. Section 3 shows how to incorporate knapsack balancing while staying within the framework of the underlying knapsack problem and mixed-integer linear optimization. In Section 4, we propose a bi-objective formulation of the knapsack problem that accounts for trade-offs between values of the the original knapsack problem objective function and a knapsack balance measure. Section 5 provides illustrative examples, and Section 6 concludes the paper.
2. Related Works
In the literature, there exist many extensions to KP problem formulation (see, e.g., [13,14]). However, the knapsack problem with a product objective function has received limited attention. In a 2018 paper [15], the authors claim that they were the first to consider the knapsack problem with the product objective function. A 2022 survey [13] lists just three papers on this subject, namely [16], where it is shown that the problem is weakly –hard; [15], where mixed-integer linear and nonlinear programming formulations of the problem and a dynamic programming algorithm for its exact solution are presented; and [17], where the first fully polynomial time approximation scheme for the problem was presented. The latter has been recently extended in [18] for a wide class of the knapsack problem generalizations.
It is worth mentioning that the issue of balance of attribute values has emerged in behavioral decision theory early. Simonson ([19]) and Simonson and Tversky ([20]) hypothesize that the attractiveness of an object is enhanced if it is an intermediate object in the choice set and is diminished if it is an extreme object, an effect they call extremeness aversion. The hypothesis is further elaborated in [21,22], where it is argued that an object with equal attribute values will be perceived as the compromise object even when it is not the middle object. The hypotheses are supported by data studies but no formal model is offered.
In [6], the aspect of balance (fairness) in combinatorial optimization is addressed. The authors consider four common measures of the balance of a set of numbers, and in the context of elements of a set balance means elements as equal as possible. Based on case studies, the authors conclude that no measure of balance is systematically better than the others. Some general guidelines on what measure of balance to use depending on the given optimization problem are also presented.
As mentioned, in the literature on the knapsack problem (cf., e.g., [13]), it is argued that a viable option to maximize is to maximize
i.e., to maximize the product of all profits of items selected for the knapsack (see, e.g., [15,18]).
Our inspiration to use function (2) as a tool to address the issue of attribute balance can be referred to the game theory. In that context, Nash ([7]) proposed to use for the value function the product of attribute values, as an option to the sum of attributes. The latter is much more prone to equally assess alternatives with highly scattered attribute values and alternatives with concentrated attribute values than the former (Figure 1).
In the Non-Linear Binary Programming (NLBP) context, function (2) has an equivalent form (cf. [15]):
This equivalency stems from the properties of the exponential function and the fact, that each subset of items is represented by vector , where when , and otherwise, cf. problem (1).
3. Balancing Knapsacks by Objective Function
The knapsack problem with the product objective function is formulated as the following NLBP problem:
In KP, a subset of items with the most balanced profits is sought by means of maximizing . The following example illustrates the effect of item profits balancing at the optimal solution produced by objective function.
Example 1.

We demonstrate the effect of item profits balancing produced by objective function by the example with profits and weights given in Table 1 (), for two values of C (the right-hand side of the constraint), namely and .

Table 1.
Profits and weights of items in Example 1.
To measure the balance of item profits at optimal solutions (), we use the sum of squared deviations from their mean (merits of this function in the context of combinatorial optimization are discussed in, already cited, [6]), namely
where , and mean μ is calculated over .
Remark 1.
is a natural dispersion measure but we cannot use it as an objective function because a. it is nonlinear, b. μ is a function of x, and we intend to stay within the class of mixed-integer linear optimization problems. To this aim, can be only calculated after the optimization terminates.
- . The optimal solution to KP:
- ,
- profits of items selected to :
- ,
- (further on, we round all numbers to the third decimal place).
For comparison, we solve an instance of KP with the same data. The optimal solution to KP:
- ,
- profits of items selected to :
- ,
- .
As one can see, in the terms of , set is more balanced than set (under the same constraint set). On the other hand, since knapsack balancing is made at the cost of a deterioration of the optimal value for KP problem.
- . The optimal solution to KP:
- ,
- profits of items selected to :
- ,
- .
As previously, we solve for comparison KP with the same data.
- The optimal solution to KP:
- ,
- profits of items selected to :
- ,
- .
Again, in the context of measure , set is more balanced than set . On the other hand, .
In general, by solving KP, we obtain the most balanced knapsack, and by solving KP, we obtain the most profitable one. The example shows the existence of a profit–balance trade–off. This naturally leads us to a bi-objective knapsack problem formulation.
4. The Bi-Objective Knapsack Problem with and Objective Functions
4.1. Multiobjective Optimization
In this section, we recall basic facts from multiobjective optimization that are needed in the rest of this work. In particular, we formulate the MultiObjective Programming (MOP) problem, and we recall a method for the derivation of Pareto optimal solutions with the use of the Chebyshev scalarization.
Let , . The MOP problem is defined as follows:
where , , , are objective functions, and “vmax” is the operator of deriving (but not necessarily actually computing!) set N that contains all Pareto optimal solutions x (N is the Pareto optimal set). We say that is Pareto optimal, if for any , , implies . We also say that , , is the outcome of x. Set is called the Pareto front. An element of set is called the Pareto optimal outcome.
According to the well-established result ([24,25,26,27]), x is Pareto optimal (actually, x is properly Pareto optimal, see, e.g., [24,25,26,27]) if and only if it solves the Chebyshev scalarization of problem (6), namely
where , , , , , , and is a positive “sufficiently small” number. We assume that .
The necessity of resorting to the Chebyshev scalarization instead of the simpler and much more popular linear scalarization, i.e., the weighted sum of the objective functions, comes from that the former can derive any Pareto optimal solution, whereas the latter can derive, in general, only a subset of them.
The linearized version of problem (7) has the following form.
In particular, if functions , are linear and the definition of is consistent with the mixed-integer linear class of problems, then the problem (8) remains linear or mixed-integer linear or integer linear. In the following, we will assume that Pareto optimal solutions are computed by solving problem (8) with varying . Given , denotes the Pareto optimal solution designated by , that is a solution to problem (7) with that .
4.2. The Bi-Objective - KP
By analogy to dropping an anchor from a vessel, solving KP (see (1)) is like anchoring its optimal solution to the aspect of maximizing the total profit, while neglecting the balance among item profits. Just as controlled dragging of the anchor can guide a vessel into a more favorable position, it is of interest to investigate the effect of “dragging” the optimal solution of KP towards more balanced ones and observe the effects in the form of trade-offs between these two aspects. To this aim, we formulate the following bi-objective NLBP problem:
As all are positive, one can define function
and formulate the following logarithmic transformation of :
is the bi-objective LBP problem.
Proposition 1.
Pareto optimal sets of problem and problem coincide.
Proof.
Since the logarithmic function is an increasing function, function generates on the same linear order that function does. Hence, function generates on the same partial order that function does. Problems and have the same feasible set , hence their Pareto optimal sets coincide. □
By Proposition 1, the following holds.
Corollary 1.
Given λ, is Pareto optimal solution to problem if and only if it is Pareto optimal solution to problem .
Likewise, we can apply the above consideration to the left-hand side of the constraint, formulating the bi-objective problem:
Function measures the balance of weights of items selected for the knapsack.
As all are positive, one can define function
and formulate the following logarithmic transformation of :
Again, is the bi-objective LBP problem.
Problem is solved with the linearized version (8) of the Chebyshev scalarization (7), and has the form:
where , , , , and is a positive “sufficiently small” number. The counterpart of problem (15) is defined for problem similarly. As seen, the generality of the Chebyshev scalarization (it provides the necessary and sufficient conditions for Pareto optimality of solutions regardless of the form of the problem solved) comes at the cost of solving in addition as many as k (in our case ) optimization problems. Here the additional optimization problems are the knapsack problems that any reasonable mixed-integer solver nowadays solves in a split second for the number of items up to several thousand.
5. Illustrative Examples
In the examples, to solve bi-objective optimization problems, we use the general methodology of multiobjective optimization outlined in Section 4.1.
- Example problems
From the 7th multiple constraint knapsack problem (in the format described under https://people.brunel.ac.uk/%7Emastjjb/jeb/orlib/mknapinfo.html, accessed on 5 May 2024) (5 constraints and 50 items) in the Beasley’s OR–Library (https://people.brunel.ac.uk/%7Emastjjb/jeb/orlib/files/mknap1.txt accessed on 5 May 2024), we derived 5 knapsack problems.
In each such problem, denoted , , the objective function and ith constraint of the original multiple constraint knapsack problem serve as the objective function and the constraint, respectively. Next, each knapsack problem is reformulated as the corresponding problem (see (11)).
- Pareto front approximations
To derive reasonably informative approximations of Pareto fronts to our example problems (11), we use the following set of vectors:
By this definition, , and for all . We assume that ’s are ordered due to the decreasing value of their first component, and each has a corresponding index, resulting from this order. So, , . We also assume that .
Remark 2.
The method to compute Pareto optimal solutions to multiobjective optimization problems applied here can provide, in general, only subsets of Pareto optimal sets, there is no guarantee that all Pareto optimal solutions are derived.
Here, wanting for the illustration to compute as many Pareto optimal solutions as possible, we take advantage of the fact that all instances of problem (11) are solved to optimality in a split second. Thus, the rather large number of λ’s used in the example (in practical terms one can even say extravagantly large) is not an issue.
- Solver
To derive and Pareto optimal solutions for each , we use Gurobi (version 10.0.0) for Microsoft Windows (x64).
Gurobi ([28]) is a general mixed-integer solver, this means it solves linear and quadratic programming problems with integer variables. It is a commercial product but licensed free for any academic user, with all functionalities available under paid licenses.
In our case, the solver is installed on a laptop equipped with an Intel Core i7-7700HQ CPU with 16 GB RAM.
- Results
The results for and are reported in Table 2 and Table 3. The results for , are reported in the Appendix A.

Table 2.
Pareto optimal outcomes to problem stemming from .

Table 3.
Pareto optimal outcomes to problem stemming from .
In these tables, the row with corresponds to the optimal solution of KP, , and the row with corresponds to the optimal solution of KP, .
As observed in many multiobjective combinatorial problems (see, e.g., [29]), multiple vectors can correspond to the same Pareto optimal outcome. Furthermore, this is also the case for our test problems, e.g., for problem (Table 2) the outcomes of Pareto optimal solutions for to are the same as those corresponding to . Repeated Pareto optimal outcomes for are not reported in the tables.
The last column in tables, , contains of profits of items selected to optimal knapsack for . For and , it contains and , respectively.
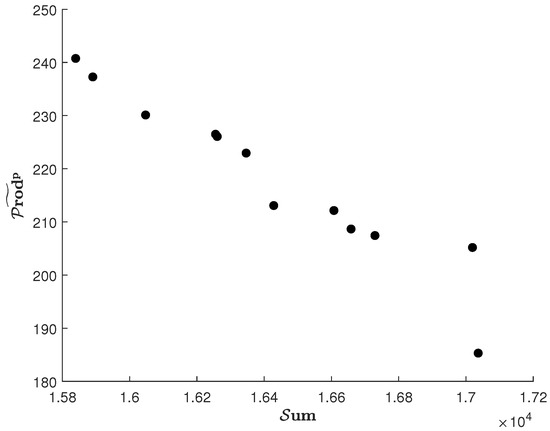
Figure 2.
Pareto optimal outcomes to problem stemming from ; horizontal axis: , vertical axis: .
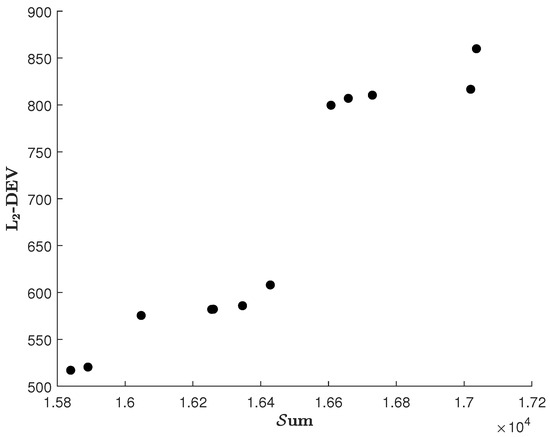
Figure 3.
Pareto optimal outcomes to problem stemming from ; horizontal axis: , vertical axis: .
Figure 2: on the (horizontal axis, the more, the better) and (vertical axis, the more, the better) plane,
Figure 3: on the (horizontal axis, the more, the better) and (vertical axis, the less, the better) plane. Values of have no practical interpretation, so presenting results on the , plane is more reasonable.
6. Conclusions
We have introduced a versatile tool for conducting post-optimal analysis of the classic knapsack problem. Staying within the same class of combinatorial problems as the knapsack problem, namely integer linear optimization, this tool enables us to explore the trade-offs between the optimal value of the underlying problem and the balance of item profits (or item weights). This is achieved through the multiobjectivization of the knapsack problem by adding an auxiliary objective function. The proposed tool therefore makes it possible to identify the decision-maker’s most preferred compromise knapsack. The significance of this development stems from the vast spectrum of practical applications of the knapsack problem and its extensions, as reported in the literature.
Applying the proposed method of knapsack balancing in the context of item profits (or item weights) to other variants of the knapsack problem (e.g., the multidimensional knapsack problem) is rather straightforward, as the only difference would be in feasible sets. For example, in the multiple-choice knapsack problem, balancing can be applied to item profits in selected categories or all categories, as dictated by the decision problem being modeled.
The broader message of this work emphasizes the potential of multiobjectivization for widening the scope of aspects that can be framed into a formal decision-making model. This is a universally valid observation; however, such an opportunity often comes at the cost of increased complexity and computational burden. This in turn often results in limitations of scalability. In this work, we have shown how these challenges can be mitigated through an approach that avoids such limitations.
This article assumes that Pareto optimal solutions are derived using a scalarization technique and exact methods. However, for large-scale instances of knapsack problems where exact solvers cannot determine Pareto optimal solutions in a reasonable time frame, the use of metaheuristics (e.g., the BGA [30] and NSGA-II [31] algorithms) or evolutionary optimization frameworks deriving approximations of the Pareto front (e.g., PKAEO [32]) is a practical alternative.
Author Contributions
I.K.: Conceptualization, Formal analysis, Methodology, Writing—original draft, Writing—review and editing. J.M.: Conceptualization, Software, Formal analysis, Methodology, Writing—original draft, Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Each test instance considered can be reproduced based on its detailed description in the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
The following three tables present Pareto optimal outcomes to problem stemming from knapsack problems , , and , respectively.

Table A1.
Pareto optimal outcomes to problem stemming from .
Table A1.
Pareto optimal outcomes to problem stemming from .
| j | |||||
|---|---|---|---|---|---|
| 0 | – | – | 19,688.000 | 185.824 | 911.322 |
| 1 | 0.995 | 0.005 | 19,688.000 | 185.824 | 911.322 |
| 33 | 0.835 | 0.165 | 19,679.000 | 192.538 | 895.297 |
| 133 | 0.335 | 0.665 | 19,611.000 | 197.179 | 885.795 |
| 153 | 0.235 | 0.765 | 19,576.000 | 200.749 | 877.454 |
| 165 | 0.175 | 0.825 | 19,544.000 | 204.245 | 870.672 |
| 181 | 0.095 | 0.905 | 19,440.000 | 206.909 | 863.358 |
| 186 | 0.070 | 0.930 | 19,380.000 | 207.487 | 862.964 |
| 187 | 0.065 | 0.935 | 19,349.000 | 207.904 | 862.007 |
| 189 | 0.055 | 0.945 | 19,298.000 | 211.076 | 854.957 |
| 197 | 0.015 | 0.985 | 18,503.000 | 214.166 | 840.841 |
| 198 | 0.010 | 0.990 | 18,319.000 | 217.168 | 804.718 |
| 199 | 0.005 | 0.995 | 18,035.000 | 220.275 | 797.057 |
| 200 | – | – | 12,457.000 | 231.887 | 324.431 |

Table A2.
Pareto optimal outcomes to problem stemming from .
Table A2.
Pareto optimal outcomes to problem stemming from .
| j | |||||
|---|---|---|---|---|---|
| 0 | – | – | 19,275.000 | 217.498 | 808.585 |
| 1 | 0.995 | 0.005 | 19,275.000 | 217.498 | 808.585 |
| 9 | 0.955 | 0.045 | 19,274.000 | 220.298 | 802.076 |
| 56 | 0.720 | 0.280 | 19,267.000 | 230.445 | 785.963 |
| 142 | 0.290 | 0.710 | 19,249.000 | 233.242 | 779.847 |
| 188 | 0.060 | 0.940 | 19,155.000 | 236.792 | 773.983 |
| 199 | 0.005 | 0.995 | 18,652.000 | 241.245 | 758.760 |
| 200 | – | – | 18,652.000 | 241.245 | 758.760 |

Table A3.
Pareto optimal outcomes to problem stemming from .
Table A3.
Pareto optimal outcomes to problem stemming from .
| j | |||||
|---|---|---|---|---|---|
| 0 | – | – | 17,955.000 | 192.966 | 854.879 |
| 1 | 0.995 | 0.005 | 17,955.000 | 192.966 | 854.879 |
| 32 | 0.840 | 0.160 | 17,945.000 | 195.628 | 847.210 |
| 41 | 0.795 | 0.205 | 17,942.000 | 196.714 | 846.224 |
| 73 | 0.635 | 0.365 | 17,927.000 | 199.264 | 838.769 |
| 106 | 0.470 | 0.530 | 17,903.000 | 201.056 | 837.178 |
| 120 | 0.400 | 0.600 | 17,888.000 | 203.606 | 829.870 |
| 130 | 0.350 | 0.650 | 17,876.000 | 205.891 | 824.438 |
| 142 | 0.290 | 0.710 | 17,858.000 | 206.750 | 823.668 |
| 155 | 0.225 | 0.775 | 17,819.000 | 211.088 | 814.514 |
| 170 | 0.150 | 0.850 | 17,756.000 | 211.247 | 814.920 |
| 173 | 0.135 | 0.865 | 17,732.000 | 213.909 | 808.021 |
| 184 | 0.080 | 0.920 | 17,600.000 | 228.255 | 591.583 |
| 191 | 0.045 | 0.955 | 17,574.000 | 230.579 | 588.271 |
| 193 | 0.035 | 0.965 | 17,557.000 | 234.877 | 583.480 |
| 195 | 0.025 | 0.975 | 17,517.000 | 242.248 | 575.717 |
| 200 | – | – | 16,137.000 | 246.343 | 511.088 |
References
- Kellerer, H.; Pferschy, U.; Pisinger, D. Knapsack Problems; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Martello, S.; Toth, P. Knapsack Problems: Algorithms and Computer Implementations; John Wiley and Sons: New York, NY, USA, 1990. [Google Scholar]
- Assi, M.; Haraty, R. A survey of the knapsack problem. In Proceedings of the 2018 International Arab Conference on Information Technology (ACIT), Werdanye, Lebanon, 28–30 November 2018; pp. 1–6. [Google Scholar]
- Camargo, V.; Mattiolli, L.; Toledo, F. A knapsack problem as a tool to solve the production planning problem in small foundries. Comput. Oper. Res. 2012, 39, 86–92. [Google Scholar] [CrossRef]
- Mavrotas, G.; Diakoulaki, D.; Kourentzis, A. Selection among ranked projects under segmentation, policy and logical constraints. Eur. J. Oper. Res. 2008, 187, 177–192. [Google Scholar] [CrossRef]
- Olivier, P.; Lodi, A.; Pesant, G. The quadratic multiknapsack problem with conflicts and balance constraints. INFORMS J. Comput. 2021, 33, 949–962. [Google Scholar] [CrossRef]
- Nash, J. Two-person cooperative games. Econometrica 1953, 21, 128–140. [Google Scholar] [CrossRef]
- Knowles, J.; Watson, R.; Corne, D. Reducing local optima in single-objective problems by multi-objectivization. In Evolutionary Multi-Criterion Optimization; Springer: Berlin/Heidelberg, Germany, 2001; pp. 269–283. [Google Scholar]
- Ma, X.; Huang, Z.; Li, X.; Qi, Y.; Wang, L.; Zhu, Z. Multiobjectivization of single-objective optimization in evolutionary computation: A survey. IEEE Trans. Cybern. 2023, 53, 3702–3715. [Google Scholar] [CrossRef]
- Klamroth, K.; Tind, J. Constrained optimization using multiple objective programming. J. Glob. Optim. 2007, 37, 325–355. [Google Scholar] [CrossRef]
- Bednarczuk, E.; Miroforidis, J.; Pyzel, P. A multi-criteria approach to approximate solution of multiple-choice knapsack problem. Comput. Optim. Appl. 2018, 70, 889–910. [Google Scholar] [CrossRef]
- Bednarczuk, E.; Kaliszewski, I.; Miroforidis, J. Approximate solutions to the multiple-choice knapsack problem by multiobjectivization and Chebyshev scalarization. Oper. Res. Decis. 2024; in press. [Google Scholar]
- Cacchiani, V.; Iori, M.; Locatelli, A.; Martello, S. Knapsack problems—An overview of recent advances. Part I: Single knapsack problems. Comput. Oper. Res. 2022, 143, 105692. [Google Scholar] [CrossRef]
- Cacchiani, V.; Iori, M.; Locatelli, A.; Martello, S. Knapsack problems—An overview of recent advances. Part II: Multiple, multidimensional, and quadratic knapsack problems. Comput. Oper. Res. 2022, 143, 105693. [Google Scholar] [CrossRef]
- D’Ambrosio, C.; Furini, F.; Monaci, M.; Traversi, E. On the product knapsack problem. Optim. Lett. 2018, 12, 691–712. [Google Scholar] [CrossRef]
- Halman, N.; Kovalyov, M.; Quilliot, A.; Shabtay, D.; Zofi, M. Bi-criteria path problem with minimum length and maximum survival probability. OR Spectr. 2019, 41, 469–489. [Google Scholar] [CrossRef]
- Pferschy, U.; Schauer, J.; Thielen, C. Approximating the product knapsack problem. Optim. Lett. 2021, 15, 2529–2540. [Google Scholar] [CrossRef]
- Boeckmann, J.; Thielen, C.; Pferschy, U. Approximating single- and multi-objective nonlinear sum and product knapsack problems. Discret. Optim. 2023, 48, 100771. [Google Scholar] [CrossRef]
- Simonson, I. Choice based on reasons: The case of attraction and compromise effects. J. Consum. Res. 1989, 16, 158–174. [Google Scholar] [CrossRef]
- Simonson, I.; Tversky, A. Choice in context: Tradeoff contrast and extremeness aversion. J. Mark. Res. 1992, 29, 281–295. [Google Scholar] [CrossRef]
- Chernev, A. Context effects without a context: Attribute balance as a reason for choice. J. Consum. Res. 2004, 32, 213–223. [Google Scholar] [CrossRef]
- Chernev, A. Extremeness aversion and attribute-balance effects in choice. J. Consum. Res. 2004, 31, 249–263. [Google Scholar] [CrossRef]
- Jacques, I. Mathematics for Economics and Business, 9th ed.; Pearson Education: Harlow, UK, 2018. [Google Scholar]
- Ehrgott, M. Multicriteria Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Kaliszewski, I. Soft Computing for Complex Multiple Criteria Decision Making; Springer: New York, NY, USA, 2006. [Google Scholar]
- Kaliszewski, I.; Miroforidis, J.; Podkopaev, D. Multiple Criteria Decision Making by Multiobjective Optimization—A Toolbox; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Miettinen, K.M. Nonlinear Multiobjective Optimization; Kluwer Academic Publishers: New York, NY, USA, 1999. [Google Scholar]
- GUROBI. 2024. Available online: https://www.gurobi.com/solutions/gurobi-optimizer/ (accessed on 31 September 2024).
- Helfrich, S.; Perini, T.; Halffmann, P.; Halffmann, P.; Bol, N.; Ruzika, S. Analysis of the weighted Tchebycheff weight set decomposition for multiobjective discrete optimization problems. J. Glob. Optim. 2023, 86, 417–440. [Google Scholar] [CrossRef]
- Kabadurmus, O.; Tasgetiren, M.F.; Oztop, H.; Erdogan, M.S. Solving 0-1 bi-objective multi-dimensional knapsack problems using binary genetic algorithm. Heuristics Optim. Learn. Stud. Comput. Intell. 2021, 906, 51–67. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zuo, M.; Gong, D.; Wang, Y.; Ye, X.; Zeng, B.; Meng, F. Process knowledge-guided autonomous evolutionary optimization for constrained multiobjective problems. IEEE Trans. Evol. Comput. 2023, 28, 193–207. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).