Abstract
Infectious disease epidemics have played a crucial role in shaping public health responses, particularly in global health crises. This study emerges as part of the efforts to prepare effective responses to potential future pandemics, leveraging lessons learned during the COVID-19 crisis. The research uses an adapted compartmental epidemiological model and a synthetic multi-agent community to investigate how social variables influence epidemic forecasts in socioeconomically vulnerable regions. Focusing on the simulation of epidemic dynamics in the socio-economically disadvantaged neighbourhood of Ilha Joana Bezerra in Recife, this study examines the impacts of social distancing strategies and other control measures, such as face masks and moderate social isolation. Through the adapted SEPAI3R3O model, which includes compartments for pre-symptomatic and asymptomatic states, this study provides a detailed analysis of disease dynamics in contexts characterised by high social vulnerability. The results underscore the importance of public health policies adapted to socio-economic factors, emphasising the need for continuous preparedness to manage future epidemic threats in vulnerable communities effectively.
1. Introduction
Social factors crucial to health have gained even more importance in recent decades. Advances in knowledge about risk factors and technologies for their mitigation have put disease control in the hands of public health managers. These managers play a fundamental role in deciding how, where, and when to implement new information and technologies, directly impacting who will benefit from them [1]. The growing understanding of epidemiological factors, shaped by the causes and consequences of epidemics, outbreaks, endemics, and pandemics, highlights social factors as significant health risks [2].
With increased knowledge and control, human policies and behaviours shape epidemiological outcomes, affecting existing patterns of disease and death [3]. Historically, social factors had less influence when the understanding of measures for prevention or treatment was limited. However, the effective use of this knowledge has been neglected intellectually and in terms of financial research support [4]. This has resulted in sub-optimal population health. Recognising and leveraging the influence of social factors to achieve optimal health for all can significantly improve global well-being [5].
Public health preparedness has become a critical concept in the face of global health crises, particularly highlighted by recent events such as the COVID-19 pandemic. This concept encompasses the capacity of health systems to anticipate, respond to, and recover from public health emergencies. As the authors of [6] demonstrated in their analysis of the 2022 monkeypox outbreak, clear case definitions and effective contact tracing are crucial components of preparedness, enabling rapid response to emerging threats.
The connection between epidemiology and sociology, proposed in [7], identifies that social phenomena directly influence the emergence and course of diseases. Recent studies, such as [8,9], have shown that poor socio-economic conditions are associated with a higher incidence of infectious diseases such as dengue and tuberculosis.
Given this evidence, could low socio-economic status be a risk factor for COVID-19 and other future epidemics? In study [10], low income was associated with higher rates of chronic health conditions, such as diabetes and heart disease, indicating that people in lower strata are 10% more likely to develop chronic conditions, which could make COVID-19 up to 10 times more deadly [11]. This suggests that social factors influence the proliferation of infectious diseases and increase the likelihood of developing chronic diseases under unfavourable conditions.
In the current coronavirus pandemic, the mortality risk for people in areas with low human development index (HDI) may be up to 10 times higher. A study conducted in São Paulo showed that the most privileged areas had a death rate of 0.7 per 100,000 inhabitants for the 40–44 age group, while in areas with low quality of life this figure rose to 6.7 per 100,000. This study also found that considering all age groups, the rate increased to 8.7 per 100,000. Families in these areas often lack adequate sanitation, clean water and energy and are more vulnerable. With high vulnerability, families tend to conglomerate in a few spaces in peripheral neighbourhoods and favelas, making social isolation more difficult [12].
The present study emerges as part of ongoing efforts to enhance preparedness for potential future pandemics, leveraging lessons learned during the COVID-19 crisis. We investigate how social variables influence epidemic forecasts in socio-economically vulnerable regions, utilising an adapted compartmental epidemiological model (SEPAI3R3O) and a synthetic multi-agent community. We focus on simulating epidemic dynamics in Ilha Joana Bezerra, a socio-economically disadvantaged neighbourhood in Recife, Brazil. This study examines the impact of social distancing strategies and other control measures, such as face masks and moderate social isolation. Through the SEPAI3R3O model, which includes compartments for pre-symptomatic and asymptomatic states, we conduct a detailed analysis of disease dynamics in contexts characterised by high social vulnerability. This approach aligns with the emphasis on comprehensive preparedness strategies highlighted in [6], the authors of which stressed the importance of adapting public health responses to specific outbreak characteristics and local contexts.
Given this evidence, low socio-economic status may be a risk factor for COVID-19 and future epidemics. Studies have indicated that people in lower socio-economic strata are more likely to develop chronic conditions, which can exacerbate the effects of infectious diseases [13]. In the current pandemic, areas with low Human Development Index (HDI) present significantly higher mortality rates [14].
Thus, using an adapted SEIR-based epidemiological model, the simulation developed in this study allows for a detailed analysis of social distancing strategies and their impacts in socially vulnerable scenarios [15]. This model was adjusted to capture the specific socio-economic and demographic nuances of Ilha de Joana Bezerra, with detailed clinical parameters reflecting the various phases of COVID-19 infection and recovery. By focusing on using face masks and 50% adherence to social isolation, the simulation seeks to balance the effectiveness in reducing viral transmission with moderate social and economic impacts [16]. This scenario was chosen for its practical relevance and potential applicability in the studied community, highlighting the importance of mobility for citizens, even during isolation measures [17]. The obtained results reinforce the capacity of the adapted SEIR model to provide valuable insights for formulating more efficient public policies tailored to local scenarios.
The innovative aspect of this research lies in demonstrating how simulations using this new epidemiological model can inform the construction of more efficient public policies. For example, through identifying the most effective social distancing measures, policymakers can prioritise interventions that balance public health needs with economic sustainability. This allows for implementing targeted strategies, such as localised lockdowns or resource allocation, specifically designed to address the unique challenges vulnerable communities face, thereby enhancing overall public health preparedness.
The remainder of this article is organised as follows: Section 2 provides this study’s background and theoretical framework, discussing the SEPAI3R3O model and its relevance to the pandemic. Section 3 describes the multi-agent simulation methodology, detailing the implementation of the SEPAI3R3O model within the agent-based framework. In Section 4, we present the analysis of the results, focusing on the impacts of various social distancing strategies on public health and the economy. Finally, Section 5 concludes the article by summarising the main findings and suggesting directions for future research.
2. Material and Methods
The term “agent” refers to an entity capable of perceiving, thinking, and acting autonomously within a given environment. Bradshaw (1997) defined an agent as “a software entity that operates continuously and autonomously in a particular environment, typically inhabited by other agents, capable of intervening in its environment flexibly and intelligently without requiring constant human intervention” [18].
Agent-based models (ABMs) address the limitations of approaches that overlook individual variations by explicitly considering discrete units or agents with unique characteristics and behavioural rules. These models can represent various entities, such as microorganisms, people, animals, families, or other units that can possess individual attributes. According to [19], some researchers distinguish between individual-based models, where entities follow behavioural rules, and agent-based models, where agents can learn new information from their environment as it changes over time, share information among themselves, and change their behaviours accordingly. However, it was pointed out in [20] that this distinction is becoming less common in the modelling literature. Generally, ABMs aim to gain insights into how system-level outcomes emerge from individual-level behaviours, regardless of how individuals or agents are conceptualised.
At the most fundamental level, these models are composed of three components: a set of agents, the environment, and behaviour rules. Agents exist in an environment, and rules determine how agents interact with each other and the environment throughout a simulation. According to [21], researchers can expand these essential components by increasing their complexity, variety, and number. For example, the world can range from a simple observation to one that includes detailed geographic information, such as realistic topography. Thus, different agents can be modelled, each with its own rules. Additionally, techniques used for agent-based modelling allow for the incorporation of various forms of stochasticity [19].
Based on this premise, several anthropological studies have used agent-based models to explore disease-related processes. Consequently, agent-based models for multi-scale epidemiological issues began to be developed. Some of these studies focused on large urban populations with broad geographic regions [22,23]. In contrast, others modelled hospital infections [24] or even scenarios where the agents are biological components of the immune system [25]. The 1918 pandemic and influenza have been analysed regarding community structure, mobility, and significant social institutions in disease spread [26,27]. Various other diseases and transmission modes have been studied using agent-based models. For example, during the 2014 Ebola outbreak, a team from Virginia Tech, as part of the Ebola forecasting challenge [28], built an agent-based model to provide policy support to decision-makers. The team’s methodology used a synthetic population with consistent demographic attributes and family structure to create the model. Over 24 h, each individual in the synthetic population was assigned a sequence of activities with geographic locations.
Additionally, a social contact network was obtained to consider the duration of co-location, through weighting the co-location of individuals and edges in the network. The disease model was appropriately chosen to translate the edge weights in the social contact network into the probability of edge infection over a day. Thus, the agent-based approach modelled the evolution of the system state by encoding the actions and interactions of individual agents. Bringing this into the context of infectious diseases, the evolution of disease spread can be modelled through the activity patterns and resulting social contacts of individuals, leading to the spread of infection. Consequently, in [29], authors argued for the importance of including human social interactions to model vector-borne or infectious agent diseases rather than simply focusing on spatial factors.
The primary objective of these and other studies in the field of epidemiology is to evaluate the potential of preventive strategies based on proactive actions in susceptible or infected populations [30,31]. Some studies have used models to identify how quarantine and vaccination can effectively control the spread of an infectious disease. In study [32], the effects of various containment measures such as social distancing that included school and workplace closures were observed, and findings indicated the effectiveness of these measures in reducing infectious disease transmission if applied early and continuously. In study [31], the effectiveness of vaccination in different approaches was observed to identify early cases and herd immunity levels in the population. In addition to population control actions, some models have been constructed to analyse individual behaviour changes rather than community-level interventions. For example, in simulations conducted for the influenza epidemic, authors of [33] observed that local transmissions could have been reduced by 25% to 39% if workers had received paid sick leave during the epidemic. Another finding from the simulation was that the severity of an epidemic is directly related to the degree of individual adherence to interventions, such as those mentioned earlier [34].
Thus, considering all of these examples, it is possible to describe that one of the main benefits of agent-based simulation models over statistical or mathematical methods is the enhanced ability to include randomness, individual heterogeneity, and spatial considerations. Therefore, agent-based models can effectively address various epidemiological issues, ranging from prevention recommendations to investigating and understanding the overall disease transmission system under different circumstances or conditions.
2.1. Epidemiological Model: SEPAI3R3O
The literature has extensively discussed the use of compartmental models for studying infectious diseases. The SEIR model, for example, divides the population into susceptible, exposed, infectious, and recovered compartments. Each of these compartments is modelled using a set of differential equations. The model assumes that the population is divided into four groups, represented by the letters in the model name:
- Susceptible (S): People who have not yet been exposed to the virus but are susceptible to contracting it.
- Exposed (E): Individuals who have been in contact with the virus and are carrying the infection but have not yet reached the stage where they can transmit the virus to others. At this stage, they do not show symptoms and are not contagious.
- Infectious (I): People who are infected and are infectious. These people show symptoms and can infect susceptible individuals if they contact them.
- Recovered (R): People who no longer have the virus (either because they have recovered or have died) cannot be infected again.
In the SEIR model, controlling how these groups interact is possible and specifying the average transition time between groups. It is necessary to define entry and exit rates for all these groups, which control how an individual moves from one group to another. As these groups (i.e., stages of the disease/compartments) follow the order of the model (S → E → I → R), the exit rate of the previous group is used as the entry rate for the new group. In the case of the susceptible (S) group, there is no entry rate, as this model assumes that no one can be re-infected. The spread of the virus and the exit rate are controlled by the number of contacts that infected individuals have with susceptible individuals. This is the same rate that defines the entry of new people into the exposed (E) group who have been contaminated but are not yet infectious. The time in this group refers to the disease’s incubation period, and the exit refers to the transition to the infectious group who can transmit the disease to susceptible individuals and usually show symptoms. In the infectious (I) group, the exit rate is controlled by the recovery or death rate; this is commonly known as the case fatality rate (CFR), which is the ratio of deaths caused by the disease to the number of infected people. For the infectious group, it is also necessary to model a contamination rate of susceptible individuals by the infectious ones; the number of new people exposed to the virus also depends on the expected number of new infections generated by an infectious person. This rate is called the primary reproduction number (R0). The recovered (R) group only has an entry rate, as this model considers that there is nowhere else to go once in this group.
In this article, we apply a variation of this model that we call SEPAI3R3O. The numbers added to each compartment indicate that the groups are subdivided into more subgroups; in particular, in this model, we use Exposed (E), Pre-symptomatic (P), Asymptomatic (A), three groups of Infectious (I), and three groups of Recovered (R), in addition to adding a new group called O which represents the deceased. Separating the deceased as a new group is a practice used in other adapted models, as detailed in Section 3, as recovery and death are opposite outcomes for the infected, in addition to the need for analytical interest in both cases.
The model includes the possibility that exposed individuals who have not yet developed symptoms can transmit the virus (“pre-symptomatic transmission”). To model this situation, we added the P class (without symptoms but can transmit). Another common condition is the presence of people who contract the virus but do not show symptoms, for which the A class (asymptomatic individuals) was included. The three groups of Infectious individuals were created to represent three distinct phases of infection: I1, infected individuals with mild symptoms; I2, infected individuals tested due to moderate symptoms (for which they may even be hospitalised); and I3, infected individuals tested with severe symptoms. Following the same logic of the SEIR model, for a person to be hospitalised in severe condition (I3), they must have necessarily passed through the P stage, the I1 stage (infectious but without symptoms and without being tested), and then through the I2 stage (with sufficient symptoms to lead to testing). They only enter the I3 stage if their condition becomes more serious, requiring intensive treatment in a hospital unit. Using this premise, only individuals in the I3 group can die, moving to the O group. This means that in this model, the path for an individual to die is the following: S → P → I2 → I3 → O, S → P → I1 → I2 → I3 → O.
For an individual to move to the recovered (R) group, they must first be in one of the recovering groups (R1, R2, and R3), which represent individuals recovering from the disease at various stages of intensity (i.e., I1, I2, and I3 groups, respectively). The motivation behind creating such groups was the need to consider recovery time based on the severity of the infection, which allows us to model the demand for hospital beds satisfactorily. Therefore, the R1, R2, and R3 groups do not communicate, meaning there are three distinct paths to recovery (R) for an infected person:
- (i.e., faster recovery);
- (i.e., intermediate recovery time);
- (i.e., longer recovery time).
In addition to the subgroups shown above, this model was conceived to consider the under-reporting rate (Psub) of the number of cases as, due to the division of subgroups, there is the possibility of controlling the proportion of people who migrate from I1 to I2 (i.e., cases that show enough symptoms for testing) or who migrate from I1 to R1. Thus, these individuals represent under-reported cases, as they contracted the disease but were never tested. The SEPAI3R3O model is represented in the Figure 1.
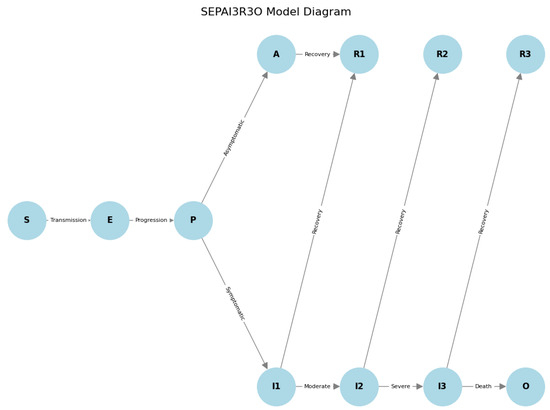
Figure 1.
SEPAI3R3O model diagram illustrating the flow of infection states from Susceptible (S) to Deceased (O), including various stages of infection severity and recovery.
Below are the ordinary differential equations of the model:
where
is the rate at which infected individuals in class come into contact with susceptible individuals and infect them;
is the rate of progression from the exposed class to the infected class;
f is the fraction of all asymptomatic infections.
Parameters represent the transmission rates for different phases of the disease; parameters represent the different recovery rates; u is the mortality rate; and parameters indicate the exit rate from classes E and P, respectively.
The evolution of the medical condition within the model is stochastic, following the probabilities summarised in Table 1. To avoid confusion, we introduce new parameters:

Table 1.
Rates of medical conditions considering hospitalised (), severe (), and death () cases grouped by age. Adapted from data specific to Brazil [35,36].
= 3, 4, 5 represent the percentages of symptomatic cases requiring hospitalisation, cases requiring intensive care and the mortality rate from infection, respectively.
Parameters are crucial in modelling the strain on healthcare systems with a limited capacity. The healthcare infrastructure varies by country but is universally lesser than the total population. Therefore, in each simulation, a critical threshold is set, representing the percentage of the population the healthcare system can manage simultaneously. If the number of hospitalisations and severe cases exceeds this threshold, the model accounts for the unavailability of hospital beds to meet the demand.
Parameters , , and indicate the progression rates from mild to severe infection, from severe to critical infection, and from critical infection to death, respectively. As these rate constants are usually not directly measured in studies, they are related to clinical observations through the following formulas:
—under-reporting rate;
—proportion of cases that move from to ;
—rate of exposure without symptoms or transmission ;
—pre-asymptomatic rate = ;
—transition rate from to ;
—transition rate from to ;
—transition rate from to ;
—transition rate from to ;
—transition rate from to ;
—transition rate from to ;
—fatal cases: mortality rate of recorded cases;
—average recovery time in group ;
—transition rate from group to ;
—average time in group ;
—average time in group ;
—average time in group .
The rates described above are often not directly calculated/measured in studies.
2.2. Multi-Agent Simulation
In the study by Ndaïrou et al. (2020), the COVID-ABS model, an agent-based model grounded in the SEIR framework, was proposed to simulate the dynamics of the COVID-19 pandemic. This innovative model uses agents representing individuals, businesses, and governmental entities, allowing for the analysis of various social distancing strategies and their impacts on public health and the economy.
To utilise the essence of such a model and have more support to prove our research hypothesis, we chose the neighbourhood with the lowest human development index in Recife, Joana Bezerra Island. Located in the heart of Recife, it presents unique characteristics, with a population density of 144.85 per hectare and 12,629 inhabitants. The average nominal monthly household income is BRL 705.83 and 3.5 residents in each of its 3606 households [37].
This study proposes to adapt the COVID-ABS model to reflect this neighbourhood’s socioeconomic and demographic reality. Using the SEPAI3R3O model, we extended the traditional SEIR model to capture the dynamics of COVID-19 in greater detail, incorporating additional states such as pre-symptomatic (P), asymptomatic (A), various levels of infection severity (I1, I2, I3), and recovery (R1, R2, R3), as well as a specific compartment for deaths (O). This simulation considers the pessimistic scenario of the number of cases in this region, even in the face of preventive measures.
Thus, the simulation focused exclusively on mask usage with 50% adherence to social isolation, reflecting a viable strategy that balances efficacy in reducing viral transmission with moderate social and economic impacts. This scenario was chosen due to its practical relevance and potential applicability in the Joana Bezerra Island community, given its specific socio-economic characteristics and based on the artefacts demonstrated in the research questions, where it was possible to show the need for citizen mobility even in social isolation measures.
For the agent-based system model adapted from COVID-ABS in the context of this research, we used the clinical parameters of COVID-19 adapted from the SEPAI3R3O epidemiological model. It was also necessary to re-formulate the types of agents to focus on including social and demographic characteristics that influence the dynamics of disease transmission as follows:
Agent A1—Individuals: In addition to primary attributes such as position, age, epidemiological status, and infection status, we included the variable “Social Vulnerability Level”, which reflects the individual’s exposure to risk factors associated with their socio-economic condition.
Agent A2—Residences: Residences are characterised by their location and family composition and “Housing Conditions”, indicating the adequacy and access to basic services which can affect disease transmission within family units. This new variable was identified after dividing the social strata given the distribution of basic sanitation among neighbourhoods.
Agent A3—Commercial and Service Establishments: These agents consider “Implemented Prevention Measures” such as the availability of sanitation and space for social distancing impacting interactions with Agent A1. These establishments include supermarkets, pharmacies, banks, and other businesses.
Agent A4—Governmental: These represent entities and authorities responsible for implementing public policies, movement restrictions, health measures, and economic support. This type of agent is crucial for simulating the governmental response to the pandemic, such as imposing or relaxing quarantines, vaccination campaigns, and providing financial support to the population.
Agent A5—Health Units: These symbolise hospitals, clinics, and other medical assistance points. These agents are essential for simulating the local healthcare capacity and managing severe cases and COVID-19-related mortality. The interaction of Agent A1 with Agent A5 models the probability of recovery or death based on the severity of the health state and the healthcare system’s capacity.
The model employed for this simulation follows an iterative procedure where T denotes the number of iterations. This model utilises a comprehensive set of input parameters P. These parameters encompass socio-demographic data (Table 2), economic information (Table 3), estimated parameters for COVID-19 (Table 4) and epidemiological factors (Table 5 and Table 6).

Table 2.
Adjusted social and demographic variables for Joana Bezerra Island.

Table 3.
Economic estimates for Joana Bezerra Island, Recife.

Table 4.
Estimated parameters for COVID-19 clinical progression and literature sources.

Table 5.
Additional parameters for COVID-19 clinical progression and literature sources.

Table 6.
Estimated parameters for COVID-19 clinical progression and literature sources.
This information produces response (observable variables) related to the epidemiological or economic effects of the pandemic. Its internal state consists of the union of the internal states of the agents , where and n is the number of agents such that . The Algorithm 1 demonstrates the behaviour of the simulation.
| Algorithm 1 Pseudocode for Agent Simulation |
| Require: P ▹ the set of parameters Require: ▹the number of iterations Ensure: for to T do for each agent in do agent.updateLocation(t, P, ) if agent.isSusceptible() and agent.hasContactWithInfectious() then agent.tryTransitionToExposed(P) end if if agent.isInSomeInfectiousState() then agent.tryUpdatedInfectionStatus(P) for each anotherAgent in do if agent ≠ anotherAgent and agent.canInfect(anotherAgent, P) then agent.infect(anotherAgent) end if end for end if end for summarize() updatePopulationStates() end for |
This pseudocode models the pandemic simulation within the proposed scenario using the SEPAI3R3O model with an agent-based approach. It initialises the agent population based on a set of parameters. Each simulation day involves updating the location of the agents, checking for exposure and infection, allowing interactions that may lead to virus transmission, and finally updating the health status of the agents according to the defined probabilities. The results are summarised at the end of each iteration to reflect changes in population dynamics, such as new infections or recoveries.
All methods of COVID-ABS needed changes. In addition to adding new compartments, the under-reporting rate needed to be included.
This structure allowed for detailed analyses of the effects of social interactions and public health measures on the spread of the disease, explicitly adapting to the context of Joana Bezerra Island and incorporating the complex facets of the SEPAI3R3O model.
2.3. Parameter Estimation
Some parameters from Table 2 and Table 3 were empirically estimated to ensure responses to the epidemiological variables. The percentages of infected agents and immune agents were defined to represent the complete disease dynamics, according to the SEPAI3R3O model.
The parameter related to the population size on Joana Bezerra Island, identified as , assumes significant importance as it directly impacts the execution time of simulations. Meanwhile, the population density of the neighbourhood, calculated using formula , revealed that the 12,629 inhabitants occupy an area of 0.87 km2. This calculation produces a population density of approximately 14,516 inhabitants per km2, highlighting the notable population density in the area in question.
Few studies have used agent-based models to simulate the economic impacts of COVID-19. For example, authors of [64] quantified that a one-month lockdown in Tokyo would lead to a total production loss of 5.3% in Japan’s annual gross domestic product (GDP). Authors of [65] proposed a tool to analyse the pandemic’s health, social, and economic impacts when the government implements a series of interventions, such as school closures, requiring employees to work from home, and providing subsidies to the population. Based on this premise, we surveyed socio-demographic and economic data, such as the total GDP of Joana Bezerra Island, represented by parameter , along with the percentage rates attributed to different economic agents ( for public GDP, for business GDP), which are abstract representations of economic dynamics within a closed local system. The net minimum wage, indicated by , reflects the nominal income after tax deductions, establishing a floor for labour remuneration in the region. On the other hand, the minimum expense, denoted by , corresponds to the estimated cost of a basic set of goods and services necessary for subsistence in the area, reflecting the minimum cost of living for the inhabitants.
These parameters are crucial for understanding the local economic structure and planning policies. The total GDP provides an overview of the region’s economic output. In contrast, the specific rates by type of agent provide insights into the relative contributions of different sectors to the economy. The net minimum wage is an essential indicator of workers’ economic well-being, and the minimum expenses measures the affordability of essential goods and services. Together, these parameters form a basis for detailed economic analyses, thus informing policy and business decisions for Joana Bezerra Island.
2.4. Initialisation
The initialisation was carried out in a two-dimensional environment , where agents are distributed based on the demographic specifications of Joana Bezerra Island. We considered the population density, age distribution, and other demographic parameters to initialise these agents realistically.
Positioning of Agents (A1, A2, A3):
Agents A1: The initial position of agents A1 was determined by the residence location (agents A2) to which they are associated. This reflects a demographic distribution based on the following:
where is the position of the associated agent A2 (residence) and represents a normally distributed variation around the residence position, indicating that the individual is within or near their home.
Agents A2 (residences): The distribution of agents A2 in the environment is based on the demographic density of the studied area. Each agent A2 represents a residence in the neighbourhood, and its position is randomly determined within the environment:
Agents A3 (commercial and service establishments): These are positioned randomly in the environment, reflecting the location of commercial and service establishments on Joana Bezerra Island:
Health State Initialisation (SEPAI3R3O)
Each agent A1 was initialised in one of the states of the SEPAI3R3O model, with most starting in the Susceptible (S) state. The initial proportions of agents in other states (P, A, I1, I2, I3, R1, R2, R3, O) were defined based on prevalence and incidence data for COVID-19 on Joana Bezerra Island, indicated as
where represent the initial percentages of agents in each state of the SEPAI3R3O model.
This table outlines the initial distribution of the population across different health states in the SEPAI3R3O model for Joana Bezerra Island. The values were derived from the data and references of the stated articles, ensuring that the simulation accurately reflected the region’s epidemiological context.
Through this careful initialisation, we addressed various crucial aspects for the realistic modelling of COVID-19 transmission, from the spatial distribution of agents to the initial configuration of their health state according to the specific disease dynamics in the study area. For better understanding, when a person of type A1 is created, they are assigned to a randomly chosen house of type A2. Parameter defines the probability of A1 being economically active/employed. If a person is economically active but not included in group , an employer is randomly chosen among the available A3. We only created a single instance for agents of type A4 and A5.
The age distribution of agent A1 is given by parameter , considering the contact rate parameters and immunity probability .
The social stratum of A1, A2, and A3 is represented by the income distribution listed in Table 7; that is, the share of wealth represented by the GDP parameter . To clarify the wealth distribution process, it is essential to note that the total wealth of the simulation () is not distributed equally among all agents. Instead, it follows a stratified approach that reflects the economic inequality in real-world scenarios, particularly in areas of high social vulnerability such as Joana Bezerra Island. The distribution process occurs as follows:

Table 7.
Income distribution adapted from the World Bank.
- Public Wealth (): 20% of the total GDP is allocated to the government agent (A4), representing public resources and infrastructure.
- Business Wealth (): 40% of the total GDP is distributed among business agents (A3), with variations based on the size and type of each business.
- Individual Wealth (remaining 40%): This portion is distributed among individual agents (A1) following the income distribution adapted from World Bank data, as shown in Table 7.
This stratified distribution ensures that the simulation accurately represents the socio-economic disparities within the community. Individual agents are assigned to these quintiles randomly but in proportions that reflect the area’s overall wealth distribution. It is worth noting that this initial distribution sets the starting conditions for the simulation. As the simulation progresses, these wealth levels may change based on various factors such as economic activities, government policies, and the impact of the pandemic on different sectors of the economy. Through implementing this detailed wealth distribution process, we aim to create a more realistic representation of the economic landscape in Joana Bezerra Island, allowing for more accurate predictions of how different socio-economic groups might be affected by and respond to the pandemic and associated public health measures.
2.5. Simulation Dynamics
Each simulation cycle represents a unit of time of one hour. During each cycle, all agents examine their current state, decide on their actions, and execute them. This may include moving within the environment, interacting with other agents (A1, A2, A3), and updating their health based on the SEPAI3R3O model. This involves contact between A1 agents, commercial interactions between A1 and A3 agents, and payment of taxes to the government agent A4. Below is a flowchart of the simulation dynamics.
Figure 2 illustrates the dynamics of the simulation. Agents follow a decision-making cycle that reflects their health status, economic activity, and social interactions. At the beginning of each cycle, the agent is assessed to determine whether they are alive and their health status. Based on their classification, agents make decisions about their actions, such as going to work, the supermarket, or staying home. Economically active agents assess whether they need to engage with the labour market, which leads them to decide whether to go to work or participate in other activities, such as going to the bank or the pharmacy. The decision regarding contact with other agents is modelled stochastically, considering the risk of contagion and economic and social interactions. If the agent is infected, the simulation checks whether they progress to a more severe stage of the disease or recover: either returning to a recovered state (R1, R2, R3) or succumbing to the illness (O). Each decision is influenced by contextual factors, such as the agent’s level of social vulnerability, which affects their chances of exposure and ability to follow preventive measures.
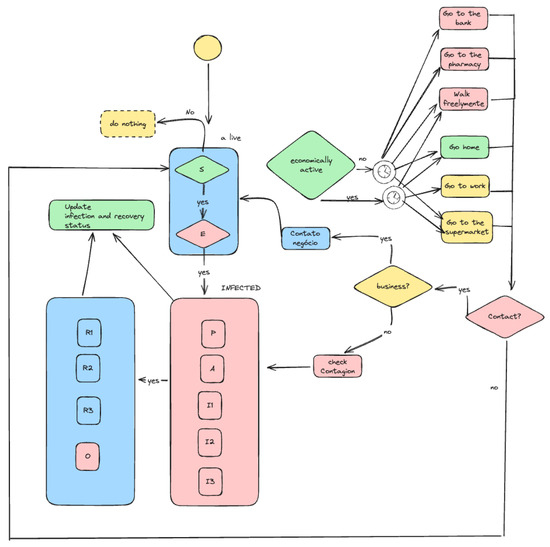
Figure 2.
Simulation dynamics.
2.5.1. Contagion Spread
The simulation of virus propagation uses the granularity of the SEPAI3R3O model, considering specific transmission probabilities to realistically iterate the health states of the agents based on interactions and proximity between susceptible and infected agents.
Following the SEPAI3R3O model, in each simulation, there is an initial percentage of infected and immune individuals ( and , respectively) as well as exposed and pre-symptomatic individuals () and finally the deceased, represented by (percentage of deaths). The remainder of the population consists of susceptible individuals. The rates of medical conditions grouped by age are represented in Table 8.

Table 8.
Rates of medical conditions considering severe infections () and death cases (), grouped by age. Adapted from [66].
The possibility of contagion occurs through the interaction of agents via proximity or contact. Thus, the greater a person’s mobility, the higher the probability of approaching an infected person and becoming infected. Each simulation considers a contagion distance limit , the minimum distance between two agents for viral transmission, and a contagion probability in case of contact.
2.5.2. Economic Transactions
One of the objectives of this study is to simulate the impact on the economy under different types of mobility restrictions imposed by the authorities. In this context, the economic dynamics can be represented by the routines of the different types of agents, as shown in Figure 3.
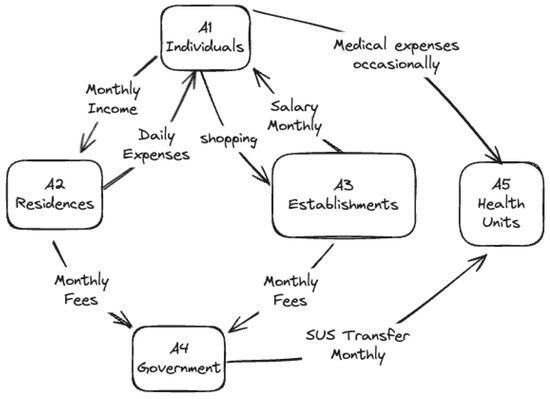
Figure 3.
Economic relations between agents.
In the commercial contact action, which occurs hourly, the agents A1 (individuals) perform economic transactions with A3 (commercial establishments) during their free time, transferring wealth from A1 to A3. The mobility of A1 directly influences these transactions: the more significant the mobility, the higher the spending. Additionally, during a pandemic, these activities are primarily for essential needs, impacting the income of A3. The amount transacted varies according to the social stratum of A1, with higher expenditures occurring in the upper quintiles.
Monthly accounting actions generate regular and systematic recording, monitoring, and economic management between A2, A3, and A4. These activities involve the payment of taxes and salaries, money transfers to suppliers, and assistance to the unemployed. A complete cycle of iterations is required to process all economic transactions.
2.6. Dynamics of A1 Agents (Mobility Patterns)
A1 agents represent individuals in society, and their mobility patterns are modelled considering daily routines such as going home to work, supermarkets, pharmacies, banks, and free movement. The positions of A1 agents are updated based on the following equations, and the dynamic movement simulated of the agent A1 is represented in Table 9.

Table 9.
Agent A1: Movement routines considering the full day and different activities.
- Go home:
- Go to work:
- Go to the supermarket:
- Go to the pharmacy:
- Go to the bank:
- Walk freely:
- Go to the hospital:
2.7. Experimental Methodology
To evaluate our proposed approach, we focused on a specific scenario that reflects a hypothetical social distancing intervention, combining the use of face masks by the entire population with 50% adherence to social isolation. This scenario was selected for its practical relevance and potential for implementation in real-world contexts, balancing public health measures with economic and social impacts.
2.7.1. Scenario Configuration
For a simulation of the scenario described earlier, 35 runs were conducted, each with T = 1440 iterations; this corresponds to a two-month simulation, considering that each iteration represents one hour. This period includes a complete accounting cycle for households, government, and businesses, marked by a salary and tax payment event on the 30th day of each month.
2.7.2. Objectives of Social Interventions
The main objective of social interventions is to minimise the number of deaths (represented by the last compartment ‘O’ in the SEPAI3R3O model), which is directly related to flattening the infection curve (). This implies minimising the infection peak (), defined by equation
and extending the time required to reach this peak (), expressed as
These metrics are essential for analysing the effectiveness of the implemented public health strategies, aiming to control the virus’s spread and minimise individuals’ progression to the most critical infection states, specifically to compartments I3 and O. The main concern is to avoid overloading the healthcare system, ensuring that the number of severe cases and deaths remains below the critical capacity limit of the healthcare system, thus guaranteeing that all patients receive the necessary care without exceeding the capacities of health services. We aim to demonstrate how this behaviour plays out based on the considered pessimistic scenario (using the new model, including the under-reporting rate). In this way, it is possible to compare the different approaches considered in this research, thus increasing the possibilities of analysis for generating efficient public policies.
2.7.3. Simulation Strategy: Masks and Moderate Social Isolation
This scenario combines the universal use of face masks with the adoption of moderate social isolation, where 50% of the population adheres to social distancing. This strategy seeks to balance mitigation of the spread of the virus with maintaining essential social and economic activities, particularly adapting to the conditions and needs of Joana Bezerra Island in Recife.
Joana Bezerra Island, characterised by its high population density and challenging socio-economic conditions, represents a unique scenario where extreme measures such as a complete lockdown may not be viable and sustainable in the long term. Therefore, the choice of this scenario is based on evidence suggesting the effectiveness of mask use and moderate social distancing in reducing viral transmission without completely paralysing community life and the local economy.
To implement this scenario in the SEPAI3R3O model, we adjusted the parameters related to viral transmission and the isolation behaviour of agents. The adjusted parameters were the minimum distance for virus transmission reflecting the effectiveness of mask use and physical distancing; the contagion rate indicating the reduction in transmission probability due to protective measures; and the level of social isolation representing the proportion of the population adhering to isolation.
3. Results
To contextualise the obtained results, it is essential to understand the Division of Recife into socio-economic strata to better understand and manage the distribution of public services and resources. Recife is divided into five strata based on the percentage of Areas of Social Interest (CIS) in each neighbourhood, as shown in Table 10. Joana Bezerra Island is located in Stratum D, which includes neighbourhoods with 35–86% CIS areas.

Table 10.
Division of neighbourhoods by strata.
Stratum D, where Joana Bezerra Island is located, has a total population of 337,155. Joana Bezerra Island specifically represents approximately 4% of this total, with 12,629 inhabitants. This neighbourhood was chosen for the simulation due to its high population density and challenging socio-economic conditions, typical characteristics of areas with greater vulnerability to spreading infectious diseases.
The initial simulation using only the SEPAI3R3O epidemiological model without agents started with 275 infection cases in Stratum D, of which 11 were attributed to Joana Bezerra Island based on the population proportion. After one week, infections increased to 1090 in Stratum D, with 44 cases on Joana Bezerra Island. These values served as the baseline for subsequent simulations incorporating agents. These data are detailed in Table 11 and represented in Figure 4.

Table 11.
Infection data—population of Stratum D and Joana Bezerra Island.
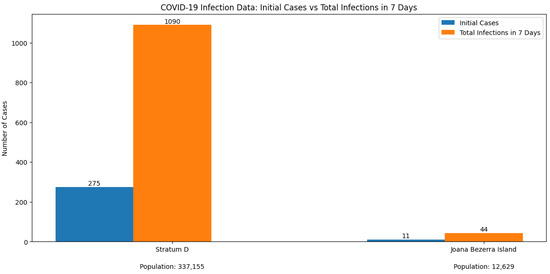
Figure 4.
Infection data—population of Stratum D and Joana Bezerra Island.
A significant reduction in infections was observed when using the SEPAI3R3O epidemiological model combined with agent-based modelling to reflect the local socio-economic reality and the ability to model scenarios. The simulation considering the use of face masks and 50% adherence to social isolation demonstrated a 13% reduction in the number of infections (It). On Joana Bezerra Island, the final number of infections in one week dropped from 44 to 39, while that in two months decreased from 352 to 308, highlighting the effectiveness of the implemented preventive measures, as detailed in Table 12. Figure 5 represents the simulated contagion evolution over 30 and 60 days; in Figure 6, the same data zoomed in lowers values.

Table 12.
Infection case projections on Joana Bezerra Island.
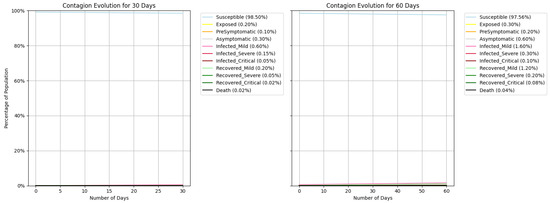
Figure 5.
Simulation execution—contagion evolution with Susceptible line.
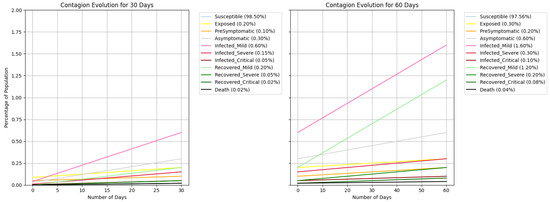
Figure 6.
Simulation execution—contagion evolution without Susceptible line.
In addition to public health impacts, the simulation also revealed positive economic effects. The introduction of agents allowed for a balance in supply consumption, avoiding significant peaks in taxation and contributing to the stabilisation of tax revenue. This indicated an improvement in the population’s purchasing power, despite the initial increase in consumption due to preventive measures.
Combining robust preventive measures with the maintenance of essential activities, this new balance validates the approach adopted for Joana Bezerra Island, offering a sustainable path for pandemic management in areas with high socio-economic difficulties. The results reinforce that proactive actions based on agent simulation lead to a more controlled and less severe scenario than purely reactive measures.
To better measure the simulation’s behaviour for the economic scenario, it was necessary to analyse a more extended simulation period as, in just seven days, it would not be possible to carry out the salary and tax payments process. We simulated for 60 days, as shown in Figure 5 and Figure 6. We could identify the average economic impact on Joana Bezerra Island during this period. Figure 7 demonstrates the three main categories: individuals (represented by the purple line), businesses (red line), and government (blue line). This graph was generated based on the simulation that considered using face masks and moderate adherence to social isolation (50%).
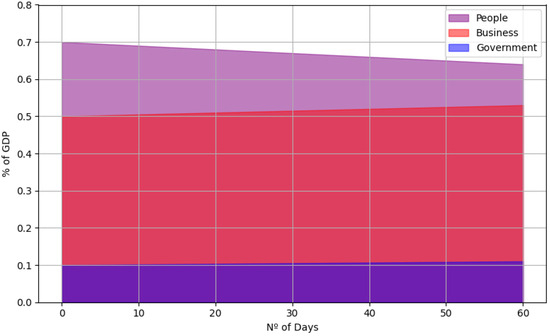
Figure 7.
Average economic impact on Joana Bezerra Island over 60 days.
The purple line, representing individuals, indicates a gradual decrease in the percentage of GDP over time. This behaviour indicates that the population is losing wealth as the pandemic progresses, although the decline is less steep due to the mitigation measures adopted.
On the other hand, the red line, representing businesses, shows a slight and gradual increase in the percentage of GDP. This increase suggests that despite the adversities, businesses maintain a certain level of balance between revenue and expenses, mainly due to adopting preventive measures such as masks and moderate social distancing.
The blue line, representing the government, shows a slight growth trend over the analysed period. Although small, this growth can be attributed to effective government policies and fiscal control during the pandemic, allowing for better public resource management.
These dynamics reflect the importance of public health policies adapted to local socio-economic realities. Although moderate, preventive measures such as masks and social distancing effectively mitigate negative economic impacts for the population and businesses while allowing the government to maintain relative stability.
The detailed analysis of the economic results revealed that adopting these measures can provide a more balanced and sustainable path for managing the pandemic in vulnerable communities such as Joana Bezerra Island. This scenario highlights the need for intervention strategies considering each region’s specific socio-economic conditions, thus providing a more efficient and equitable response to the crisis.
Considerations on Other Scenarios
When analysing the other scenarios, including complete lockdown and vertical isolation, we observed that while such measures may effectively reduce the number of cases and deaths, they are not readily applicable or sustainable in all contexts, especially in areas with high social and economic vulnerability. The choice of the mask-wearing and moderate social isolation scenario reflects a more balanced strategy adapted to local realities, as demonstrated on Joana Bezerra Island.
4. Discussion
This study utilised an agent-based model incorporating the SEPAI3R3O epidemiological framework to simulate the spread of COVID-19 in Joana Bezerra Island, a socioeconomically vulnerable area of Recife, Brazil. The simulation evaluated the impact of moderate preventive measures, specifically universal face mask use and 50% adherence to social isolation, on public health and economic outcomes.
4.1. Interpretation of Key Findings
The simulation results demonstrated a 13% reduction in infections over two months, with cases dropping from 352 to 308. This significant decrease highlights the potential effectiveness of moderate interventions in mitigating disease spread, even in areas with high socioeconomic vulnerability. The findings suggest that a balanced approach to pandemic management can yield positive results without resorting to more extreme measures like complete lockdowns, which may be particularly challenging to implement in vulnerable communities.
From an economic perspective, the simulation revealed a stabilisation in tax revenue and improved the population’s purchasing power. This indicates that the adopted measures struck a balance between controlling the spread of the virus and maintaining essential economic activities. Achieving this balance is crucial in areas like Joana Bezerra Island, where extreme economic disruptions could severely affect the vulnerable population.
Implications for Public Health Policy
The results of this study have several important implications for public health policy, especially in the context of socioeconomically disadvantaged areas.
- Tailored Interventions: The effectiveness of moderate measures in reducing infection rates suggests that public health strategies can be tailored to vulnerable communities’ specific needs and constraints without compromising their efficacy.
- Economic Considerations: The observed economic stability underscores the importance of considering health and economic impacts when designing pandemic response strategies. This is particularly crucial in areas with high levels of informal employment and limited social safety nets.
- Feasibility of Implementation: The focus on universal mask use and moderate social isolation presents a more feasible approach for communities where strict lockdowns may be impractical or economically devastating.
- Data-Driven Decision Making: Using agent-based modelling with detailed epidemiological frameworks like SEPAI3R3O can provide valuable insights for policymakers, allowing for more informed and targeted interventions.
4.2. Unexpected Findings and Explanations
One unexpected finding was the degree of economic stability achieved despite implementing preventive measures. This could be attributed to the model’s incorporation of detailed socioeconomic factors specific to Joana Bezerra Island, such as the high proportion of informal workers and the community’s adaptive economic behaviours. The simulation may have captured the resilience of local economic networks in the face of moderate restrictions, a factor often overlooked in more generalised epidemiological models.
4.3. Study Limitations
This study, while providing valuable insights into the dynamics of COVID-19 transmission in socio-economically vulnerable areas, has several limitations that should be considered when interpreting the results. The SEPAI3R3O model, although more detailed than traditional SEIR models, still simplifies the complex dynamics of COVID-19 transmission. Some nuances of disease progression and transmission may not be fully captured, potentially affecting the accuracy of long-term projections.
A significant limitation is the uncertainty of many of the model’s parameters. Transmission rates (βi), recovery rates (ci), and other vital parameters are based on early estimates from the COVID-19 pandemic. These values may have evolved as our understanding of the virus improved, potentially impacting the model’s accuracy. While this study incorporated some socio-economic factors, it may only capture some of the nuances of social vulnerability that could influence disease spread in highly disadvantaged areas. Another limitation is the use of static parameters for aspects such as social distancing adherence and mask usage, as these behaviours may change over time due to various factors such as pandemic fatigue or changing public health messaging. The under-reporting rate (Psub) is a critical parameter significantly impacting the model’s projections. However, accurately estimating this rate is challenging and may vary over time and across different population segments. Due to the nature of this study and the ongoing pandemic, comprehensive validation of the model against real-world data from Joana Bezerra Island may be limited.
While innovative, the model’s economic aspects still represent a simplified view of complex economic interactions and thus may only capture some of the nuances of economic impact in a highly vulnerable community. Additionally, while the model includes healthcare units (A5), it may not fully capture the complexities of healthcare system capacity and its dynamic nature during a pandemic.
The model makes assumptions about individual behaviours (e.g., mobility patterns and adherence to measures) that may only partially reflect the diversity of behaviours in a real-world setting, especially in socio-economically challenged areas. This study focused primarily on mask usage and moderate social isolation, with other potential interventions or combinations needing to be extensively explored. The two-month simulation period may not capture the long-term dynamics of the pandemic or potential seasonal variations in transmission. While the model was adapted to Joana Bezerra Island, it may not capture fine-grained spatial variations within the neighbourhood that could influence disease spread. Although the model includes age-specific parameters for severe infections and mortality, it may not fully capture all age-related differences in transmission, susceptibility, and social behaviour. Finally, the model does not include the impact of vaccination, which became a crucial factor in the later stages of the pandemic.
Therefore, future studies could address these limitations by incorporating more detailed data, refining parameter estimates, and expanding the model to include a broader range of interventions and socio-economic factors. Despite these limitations, this study provides valuable insights into the potential impacts of public health measures in vulnerable communities. It can serve as a foundation for future research in this critical area.
5. Conclusions
This study developed a simulation using the SEPAI3R3O epidemiological model, specifically adapted to Ilha de Joana Bezerra, demonstrating the effectiveness of moderate preventive measures, such as mask usage and partial adherence to social isolation, in mitigating the negative impacts of the COVID-19 pandemic. The results suggest that, even in scenarios of high socio-economic vulnerability, it is possible to balance reducing viral transmission and maintaining essential economic activities.
The SEPAI3R3O model proposed in this study not only expands the traditional SEIR model but also incorporates a critical level of detail, including pre-symptomatic and asymptomatic states, as well as different severity levels of infections. This granularity allows for a more precise analysis of the transmission and recovery dynamics of COVID-19 in vulnerable communities.
By introducing agents representing individuals (A1), households (A2), commercial and service establishments (A3), governmental entities (A4), and healthcare units (A5) into the model, we enabled the realistic simulation of social and economic interactions. This agent-based approach allowed us to observe how different public health measures affect virus spread and economic impact, highlighting the importance of public policies adapted to specific local conditions.
The results indicate a significant reduction in the number of infections and stabilisation in economic impact. Despite the initial loss of wealth among the population, businesses could maintain a stable level of operation, and the government managed its resources effectively. These findings reinforce the importance of flexible and informed public policies balancing public health and economic activity, even in highly vulnerable communities.
For future work, exploring different intervention scenarios, including variations in adherence rates to social isolation measures and the impact of vaccination campaigns, is recommended. Additionally, incorporating real mobility and social interaction data can provide an even more accurate and reality-adapted simulation, improving the crisis response capability.
Another important point for future research is the long-term analysis of post-pandemic economic and social impacts in evaluating economic recovery and community resilience. Implementing economic and social support strategies for vulnerable populations should be a priority, ensuring that the lessons learned during the pandemic are applied to more effective and inclusive public policies.
Finally, expanding the model to other regions with different socio-economic characteristics can help to validate the applicability of the proposed strategies and provide valuable insights for policy formulation on a national and international scale. The robustness of the SEPAI3R3O model, combined with the flexibility of the agent-based approach, offers a powerful tool for public managers and researchers facing future health crises.
Author Contributions
Conceptualization, C.A.C.d.L.; Software, L.A.S.; Validation, C.A.C.d.L. and L.A.S.; Formal analysis, P.C.d.A.R.T.; Investigation, L.A.S. and P.C.d.A.R.T.; Writing—original draft, L.A.S.; Writing—review & editing, L.A.S. and P.C.d.A.R.T.; Project administration, P.C.d.A.R.T.; Funding acquisition, L.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The simulation code and the artefacts supporting this article’s content are available on GitHub. The repository can be accessed via the following link: https://github.com/clvschaves/agent_search (accessed on 20 September 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Marmot, M. Social Determinants of Health Inequalities. Lancet 2005, 365, 1099–1104. [Google Scholar] [CrossRef]
- Berkman, L.F.; Kawachi, I.; Glymour, M.M. Social Epidemiology; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Galea, S. Macrosocial Determinants of Population Health. Annu. Rev. Public Health 2011, 32, 35–55. [Google Scholar]
- Braveman, P.; Egerter, S.; Williams, D.R. The Social Determinants of Health: Coming of Age. Annu. Rev. Public Health 2011, 32, 381–398. [Google Scholar] [CrossRef]
- Marmot, M.; Friel, S.; Bell, R.; Houweling, T.A.J.; Taylor, S.; on behalf of the Commission on Social Determinants of Health. Closing the Gap in a Generation: Health Equity Through Action on the Social Determinants of Health. Lancet 2008, 372, 1661–1669. [Google Scholar] [CrossRef]
- Guarducci, G.; Porchia, B.R.; Lorenzini, C.; Nante, N. Overview of Case Definitions and Contact Tracing Indications in the 2022 Monkeypox Outbreak. Infez. Med. 2023, 31, 13–19. [Google Scholar] [CrossRef]
- Steudler, F. Sociologie Médicale; U2; Armand Colin: Paris, France, 1972. [Google Scholar]
- de Souza, C.T.V.; Nunes, J.A.; da Hora, D.L.; Erthal, R.M.d.C.; Pimentel, M.I.F.; Pacheco, S.J.B. Social Epidemiology, Education, and Health Promotion in Infectious Disease. J. Trop. Pathol. 2014, 43, 98–104. [Google Scholar] [CrossRef][Green Version]
- Johansen, I.C.; Carmo, R.L.D.; Alves, L.C.; Bueno, M.D.C.D. Environmental and Demographic Determinants of Dengue Incidence in Brazil. Rev. Salud Publica 2018, 20, 346–351. [Google Scholar] [CrossRef]
- Link, B.G. Epidemiological Sociology and the Social Shaping of Population Health. J. Health Soc. Behav. 2008, 49, 367–384. [Google Scholar] [CrossRef]
- Felinto, G.M.; Escosteguy, C.C.; Medronho, R.d.A. Fatores Associados ao Óbito dos Casos Graves de Influenza A(H1N1)pdm09. Cad. Saúde Coletiva 2018, 27, 11–19. [Google Scholar] [CrossRef]
- Mello, D. Risco de Morrer por Coronavírus Varia até 10 vezes Entre Bairros de SP. Agência Brasil. 2020. Available online: https://agenciabrasil.ebc.com.br/saude/noticia/2020-05/risco-de-morrer-por-coronavirus-varia-ate-10-vezes-entre-bairros-de-sp (accessed on 20 December 2023).
- Levy Yeyati, E.; Filippini, F. Social and Economic Impact of COVID-19. 2021. Available online: https://www.brookings.edu/articles/social-and-economic-impact-of-covid-19/ (accessed on 18 July 2024).
- Patel, J.A.; Nielsen, F.B.; Badiani, A.A.; Assi, S.; Unadkat, V.A.; Patel, B.; Ravindrane, R.; Wardle, H. Poverty, Inequality and COVID-19: The Forgotten Vulnerable. Public Health 2020, 183, 110. [Google Scholar]
- Silva, P.C.; Batista, P.V.; Lima, H.S.; Alves, M.A.; Guimarães, F.G.; Silva, R.C. COVID-ABS: An Agent-Based Model of COVID-19 Epidemic to Simulate Health and Economic Effects of Social Distancing Interventions. Chaos Solitons Fractals 2020, 139, 110088. [Google Scholar] [CrossRef]
- Chu, D.K.; Akl, E.A.; Duda, S.; Solo, K.; Yaacoub, S.; Schünemann, H.J.; El-Harakeh, A.; Bognanni, A.; Lotfi, T.; Loeb, M.; et al. Physical Distancing, Face Masks, and Eye Protection to Prevent Person-to-Person Transmission of SARS-CoV-2 and COVID-19: A Systematic Review and Meta-Analysis. Lancet 2020, 395, 1973–1987. [Google Scholar] [CrossRef]
- Bonaccorsi, G.; Pierri, F.; Cinelli, M.; Flori, A.; Galeazzi, A.; Porcelli, F.; Schmidt, A.L.; Valensise, C.M.; Scala, A.; Quattrociocchi, W.; et al. Economic and Social Consequences of Human Mobility Restrictions Under COVID-19. Proc. Natl. Acad. Sci. USA 2020, 117, 15530–15535. [Google Scholar] [CrossRef]
- Bradshaw, J.M.; Dutfield, S.; Benoit, P.; Woolley, J.D. KAoS: Toward an Industrial-Strength Open Agent Architecture. Softw. Agents 1997, 13, 375–418. [Google Scholar]
- Gilbert, N. Agent-Based Models, 1st ed.; SAGE Publications, Inc.: London, UK, 2007. [Google Scholar]
- Railsback, S.F.; Grimm, V. Agent-Based and Individual-Based Modeling: A Practical Introduction; Princeton University Press: Princton, NJ, USA, 2011. [Google Scholar]
- Epstein, J.M.; Axtell, R. Growing Artificial Societies: Social Science from the Bottom Up; Brookings Institution Press: Washington, DC, USA; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Das, T.K.; Savachkin, A.A.; Zhu, Y. A Large-Scale Simulation Model of Pandemic Influenza Outbreaks for Development of Dynamic Mitigation Strategies. IIE Trans. 2008, 40, 893–905. [Google Scholar] [CrossRef]
- Ohkusa, Y.; Sugawara, T. Simulation Model of Pandemic Influenza in the Whole of Japan. Jpn. J. Infect. Dis. 2009, 62, 98–106. [Google Scholar] [CrossRef]
- Hotchkiss, J.R.; Strike, D.G.; Simonson, D.A.; Broccard, A.F.; Crooke, P.S. An Agent-Based and Spatially Explicit Model of Pathogen Dissemination in the Intensive Care Unit. Crit. Care Med. 2005, 33, 168–176; discussion 253–254. [Google Scholar] [CrossRef]
- Segovia-Juarez, J.L.; Ganguli, S.; Kirschner, D. Identifying Control Mechanisms of Granuloma Formation During M. tuberculosis Infection Using an Agent-Based Model. J. Theor. Biol. 2004, 231, 357–376. [Google Scholar] [CrossRef]
- O’Neil, C.A.; Sattenspiel, L. Agent-Based Modeling of the Spread of the 1918–1919 Flu in Three Canadian Fur Trading Communities. Am. J. Hum. Biol. 2010, 22, 757–767. [Google Scholar] [CrossRef]
- Orbann, C.; Dimka, J.; Miller, E.; Sattenspiel, L. Agent-Based Modeling and the Second Epidemiologic Transition. In Modern Environments and Human Health: Revisiting the Second Epidemiologic Transition; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014; pp. 103–122. [Google Scholar] [CrossRef]
- Waldrop, M.M. Special agents offer modeling upgrade. Proc. Natl. Acad. Sci. USA 2017, 114, 7176–7179. [Google Scholar] [CrossRef]
- Reiner, R.C., Jr.; Stoddard, S.T.; Scott, T.W. Socially Structured Human Movement Shapes Dengue Transmission Despite the Diffusive Effect of Mosquito Dispersal. Epidemics 2014, 6, 30–36. [Google Scholar] [CrossRef]
- Atti, M.L.C.; Merler, S.; Rizzo, C.; Ajelli, M.; Massari, M.; Manfredi, P.; Furlanello, C.; Tomba, G.S.; Iannelli, M. Mitigation Measures for Pandemic Influenza in Italy: An Individual Based Model Considering Different Scenarios. PLoS ONE 2008, 3, e1790. [Google Scholar] [CrossRef]
- Eidelson, B.M.L.I. VIR-POX: An Agent-Based Analysis of Smallpox Preparedness and Response Policy. J. Artif. Soc. Soc. Simul. 2004, 7, 1–6. [Google Scholar]
- Milne, G.J.; Kelso, J.K.; Kelly, H.A.; Huband, S.T.; McVernon, J. A Small Community Model for the Transmission of Infectious Diseases: Comparison of School Closure as an Intervention in Individual-Based Models of an Influenza Pandemic. PLoS ONE 2008, 3, e4005. [Google Scholar] [CrossRef]
- Kumar, S.; Grefenstette, J.J.; Galloway, D.; Albert, S.M.; Burke, D.S. Policies to Reduce Influenza in the Workplace: Impact Assessments Using an Agent-Based Model. Am. J. Public Health 2013, 103, 1406–1411. [Google Scholar] [CrossRef]
- Williams, A.D.; Hall, I.M.; Rubin, G.J.; Amlôt, R.; Leach, S. An Individual-Based Simulation of Pneumonic Plague Transmission Following an Outbreak and the Significance of Intervention Compliance. Epidemics 2011, 3, 95–102. [Google Scholar] [CrossRef]
- Dantas, M.N.P.; de Souza, D.L.B.; de Souza, A.M.G.; Aiquoc, K.M.; de Souza, T.A.; Barbosa, I.R. Demand for Hospitalization Services for COVID-19 Patients in Brazil. Rev. Bras. Epidemiol. 2021, 24, e210004. [Google Scholar] [CrossRef]
- da Saúde, M. Boletim Epidemiológico Especial—Doença pelo Coronavírus COVID-19. 2021. Available online: https://www.gov.br/saude/pt-br/centrais-de-conteudo/publicacoes/boletins/epidemiologicos/edicoes/2021 (accessed on 30 May 2021).
- Prefeitura do Recife. Ilha de Joana Bezerra; Prefeitura do Recife: Recife, Brazil, 2024. [Google Scholar]
- SEBRAE. Pesquisa Sobre Micro e Pequenas Empresas; Technical Report; Serviço Brasileiro de Apoio às Micro e Pequenas Empresas: Brasilia, Brazil, 2020. [Google Scholar]
- IBGE. Produto Interno Bruto Dos Municípios; Technical Report; Instituto Brasileiro de Geografia e Estatística: Brasilia, Brazil, 2020. [Google Scholar]
- World Bank. Government Expenditure (% of GDP)—Brazil. 2021. Available online: https://data.worldbank.org/indicator/NE.CON.GOVT.ZS?locations=BR (accessed on 6 April 2021).
- Banco Central do Brasil. Relatório de Economia Bancária; Technical Report; Banco Central do Brasil: Brasilia, Brazil, 2020. [Google Scholar]
- Ministério da Economia. Salário Mínimo. 2021. Available online: https://www12.senado.leg.br/noticias/materias/2021/01/04/ja-esta-em-vigor-novo-salario-minimo-de-r-1.100 (accessed on 20 December 2020).
- DIEESE. Pesquisa Nacional da Cesta Básica de Alimentos; Technical Report; Departamento Intersindical de Estatística e Estudos Socioeconômicos: Sao Paulo, Brazil, 2021. [Google Scholar]
- IBGE. Pesquisa Nacional por Amostra de Domicílios Contínua—PNAD Contínua; Technical Report; Instituto Brasileiro de Geografia e Estatística: Brasilia, Brazil, 2021. [Google Scholar]
- Linton, N.M.; Kobayashi, T.; Yang, Y.; Hayashi, K.; Akhmetzhanov, A.R.; Jung, S.-M.; Yuan, B.; Kinoshita, R.; Nishiura, H. Incubation Period and Other Epidemiological Characteristics of 2019 Novel Coronavirus Infections with Right Truncation: A Statistical Analysis of Publicly Available Case Data. J. Clin. Med. 2020, 9, 538. [Google Scholar] [CrossRef]
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.; Azman, A.S.; Reich, N.G.; Lessler, J. The Incubation Period of 2019-nCoV from Publicly Reported Confirmed Cases: Estimation and Application. medRxiv 2020. [Google Scholar] [CrossRef]
- Yang, P.; Ding, Y.; Xu, Z.; Pu, R.; Li, P.; Yan, J.; Liu, J.; Meng, F.; Huang, L.; Shi, L.; et al. Epidemiological and Clinical Features of COVID-19 Patients with and without Pneumonia in Beijing, China. medRxiv 2020. [Google Scholar] [CrossRef]
- Wang, C.; Liu, L.; Hao, X.; Guo, H.; Wang, Q.; Huang, J.; He, N.; Yu, H.; Lin, X.; Pan, A.; et al. Evolving Epidemiology and Impact of Non-pharmaceutical Interventions on the Outbreak of Coronavirus Disease 2019 in Wuhan, China. medRxiv 2020. [Google Scholar] [CrossRef]
- Sanche, S.; Lin, Y.T.; Xu, C.; Romero-Severson, E.; Hengartner, N.; Ke, R. The Novel Coronavirus, 2019-nCoV, is Highly Contagious and More Infectious Than Initially Estimated. medRxiv 2020. [Google Scholar] [CrossRef]
- Tindale, L.C.; Stockdale, J.E.; Coombe, M.; Garlock, E.S.; Lau, W.Y.V.; Saraswat, M.; Zhang, L.; Chen, D.; Wallinga, J.; Colijn, C. Evidence for Transmission of COVID-19 Prior to Symptom Onset. eLife 2020, 9, e57149. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Zhang, L.; Fan, G.; Xu, J.; Gu, X.; et al. Clinical Features of Patients Infected with 2019 Novel Coronavirus in Wuhan, China. Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef]
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical Course and Risk Factors for Mortality of Adult Inpatients with COVID-19 in Wuhan, China: A Retrospective Cohort Study. Lancet 2020, 395, 1054–1062. [Google Scholar] [CrossRef]
- Xing, L. The Epidemiological Characteristics of an Outbreak of 2019 Novel Coronavirus Diseases (COVID-19) in China. Zhonghua Liu Xing Bing Xue Za Zhi = Zhonghua Liuxingbingxue Zazhi 2020, 41, 145–151. [Google Scholar] [CrossRef]
- Gu, J.; Liang, L.; Song, H.; Kong, Y.; Ma, R.; Hou, Y.; Zhao, J.; Liu, J.; He, N.; Zhang, Y. A Method for Hand-Foot-Mouth Disease Prediction Using GeoDetector and LSTM Model in Guangxi, China. Sci. Rep. 2019, 9, 17928. [Google Scholar] [CrossRef]
- Wu, E.; Villani, J.; Davis, A.; Fareed, N.; Harris, D.R.; Huerta, T.R.; LaRochelle, M.R.; Miller, C.C.; Oga, E.A. Community Dashboards to Support Data-Informed Decision-Making in the HEALing Communities Study. Drug Alcohol Depend. 2020, 217, 108331. [Google Scholar] [CrossRef]
- Verity, R.; Okell, L.C.; Dorigatti, I.; Winskill, P.; Whittaker, C.; Imai, N.; Cuomo-Dannenburg, G.; Thompson, H.; Walker, P.G.T.; Fu, H.; et al. Estimates of the Severity of COVID-19 Disease. medRxiv 2020. [Google Scholar] [CrossRef]
- Russell, T.W.; Hellewell, J.; Jarvis, C.I.; Van Zandvoort, K.; Abbott, S.; Ratnayake, R.; Flasche, S.; Eggo, R.M.; Edmunds, W.J.; Kucharski, A.J.; et al. Estimating the Infection and Case Fatality Ratio for COVID-19 Using Age-Adjusted Data from the Outbreak on the Diamond Princess Cruise Ship. Eurosurveillance 2020, 25, 2000256. [Google Scholar]
- Riou, J.; Hauser, A.; Counotte, M.J.; Althaus, C.L. Adjusted Age-Specific Case Fatality Ratio During the COVID-19 Epidemic in Hubei, China, January and February 2020. medRxiv 2020. [Google Scholar] [CrossRef]
- Mizumoto, K.; Kagaya, K.; Zarebski, A.; Chowell, G. Estimating the Asymptomatic Ratio of 2019 Novel Coronavirus Onboard the Princess Cruises Ship, 2020. medRxiv 2020. [Google Scholar] [CrossRef]
- Nishiura, H.; Kobayashi, T.; Miyama, T.; Suzuki, A.; Jung, S.; Hayashi, K.; Kinoshita, R.; Yang, Y.; Yuan, B.; Akhmetzhanov, A.R.; et al. Estimation of the Asymptomatic Ratio of Novel Coronavirus Infections (COVID-19). medRxiv 2020. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Bao, C.; Zhou, Y.; Ji, H.; Wu, Y.; Shi, Y.; Shen, W.; Bao, J.; Li, J.; Hu, J.; et al. Forecasting Incidence of Hand, Foot and Mouth Disease Using BP Neural Networks in Jiangsu Province, China. BMC Infect. Dis. 2019, 19, 828. [Google Scholar] [CrossRef]
- Tapiwa, G.; Cécile, K.; Dongxuan, C.; Andrea, T.; Christel, F.; Jacco, W.; Niel, H. Estimating the Generation Interval for COVID-19 Based on Symptom Onset Data. medRxiv 2020. [Google Scholar] [CrossRef]
- Li, Y.; Wang, B.; Peng, R.; Zhou, C.; Zhan, Y.; Liu, Z.; Jiang, X.; Zhao, B. Mathematical Modeling and Epidemic Prediction of COVID-19 and Its Significance to Epidemic Prevention and Control Measures. Ann. Infect. Dis. Epidemiol. 2020, 5, 1052. [Google Scholar]
- Inoue, H.; Todo, Y. The Propagation of the Economic Impact through Supply Chains: The Case of a Mega-City Lockdown against the Spread of COVID-19. arXiv 2020, arXiv:2003.14002. [Google Scholar] [CrossRef]
- Dignum, F.; Dignum, V.; Davidsson, P.; Ghorbani, A.; van der Hurk, M.; Jensen, M.; Kammler, C.; Lorig, F.; Ludescher, L.G.; Melchior, A.; et al. Analysing the Combined Health, Social and Economic Impacts of the Coronavirus Pandemic Using Agent-Based Social Simulation. arXiv 2020, arXiv:2004.12809. [Google Scholar]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunubá, Z.; Cuomo-Dannenburg, G.; et al. Report 9: Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand; Technical Report; Imperial College London: London, UK, 2020. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).