Combining CBAM and Iterative Shrinkage-Thresholding Algorithm for Compressive Sensing of Bird Images
Abstract
1. Introduction
2. Dataset
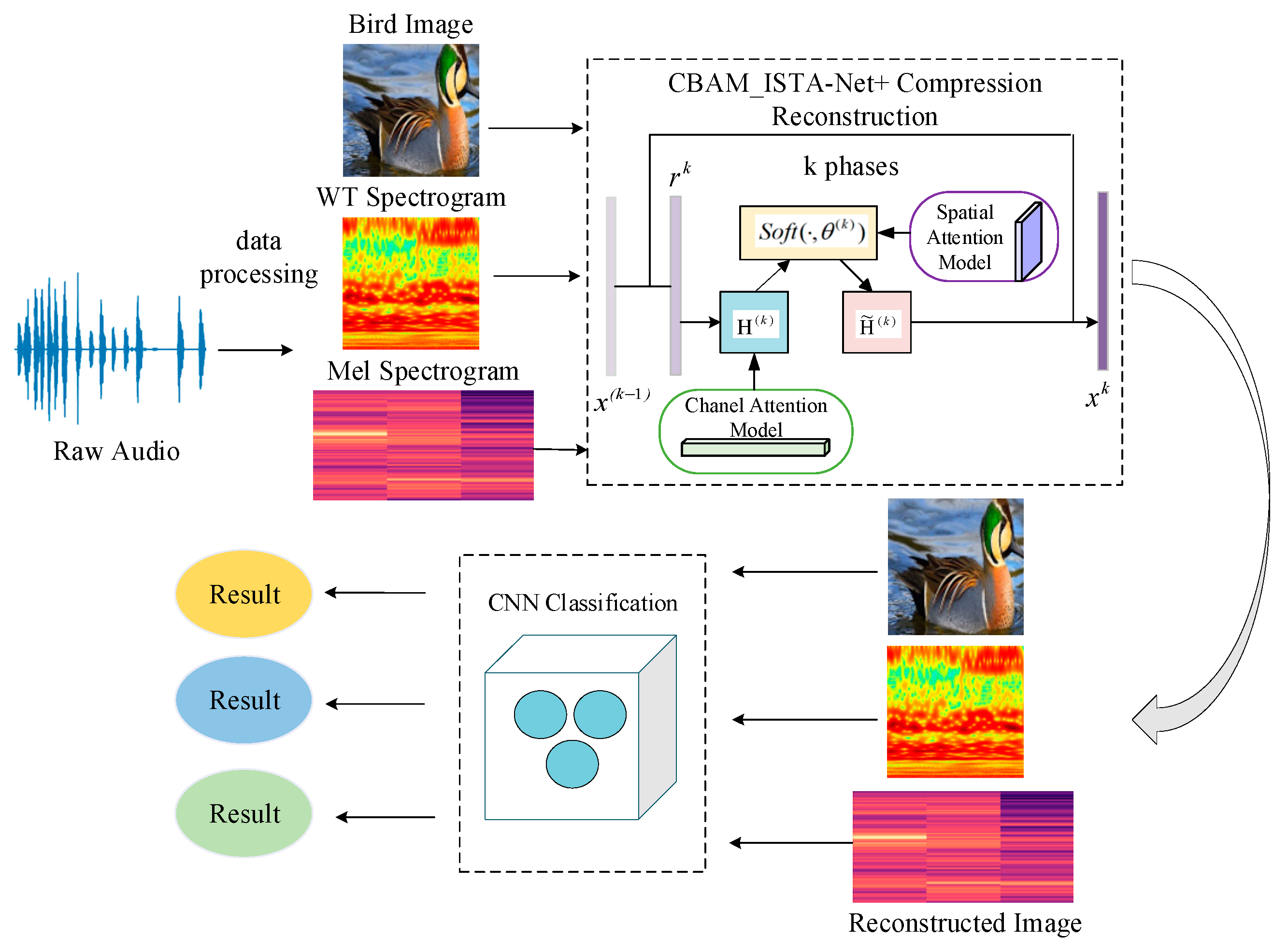
3. Research Method
3.1. Data Preprocessing
3.2. Generation of Audio Spectrograms
3.2.1. Mel Spectrograms
3.2.2. Wavelet Transform
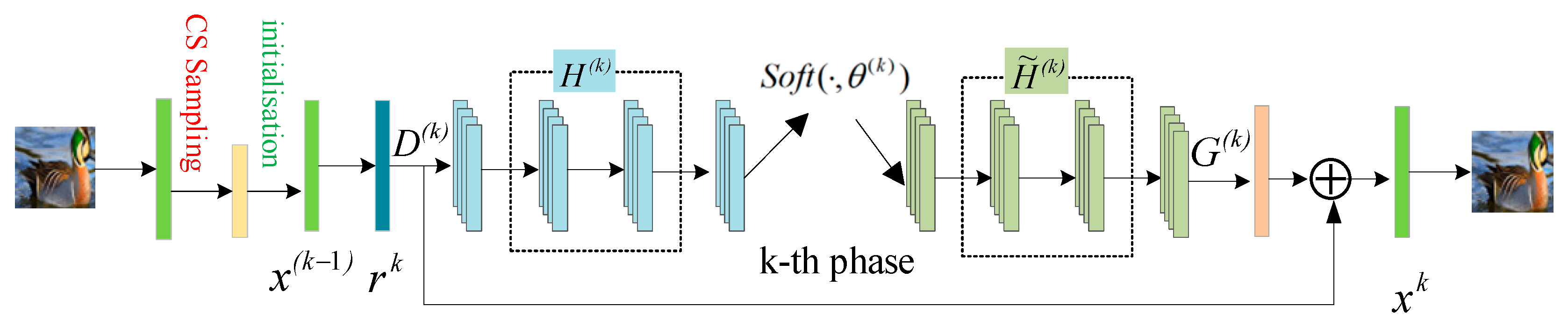
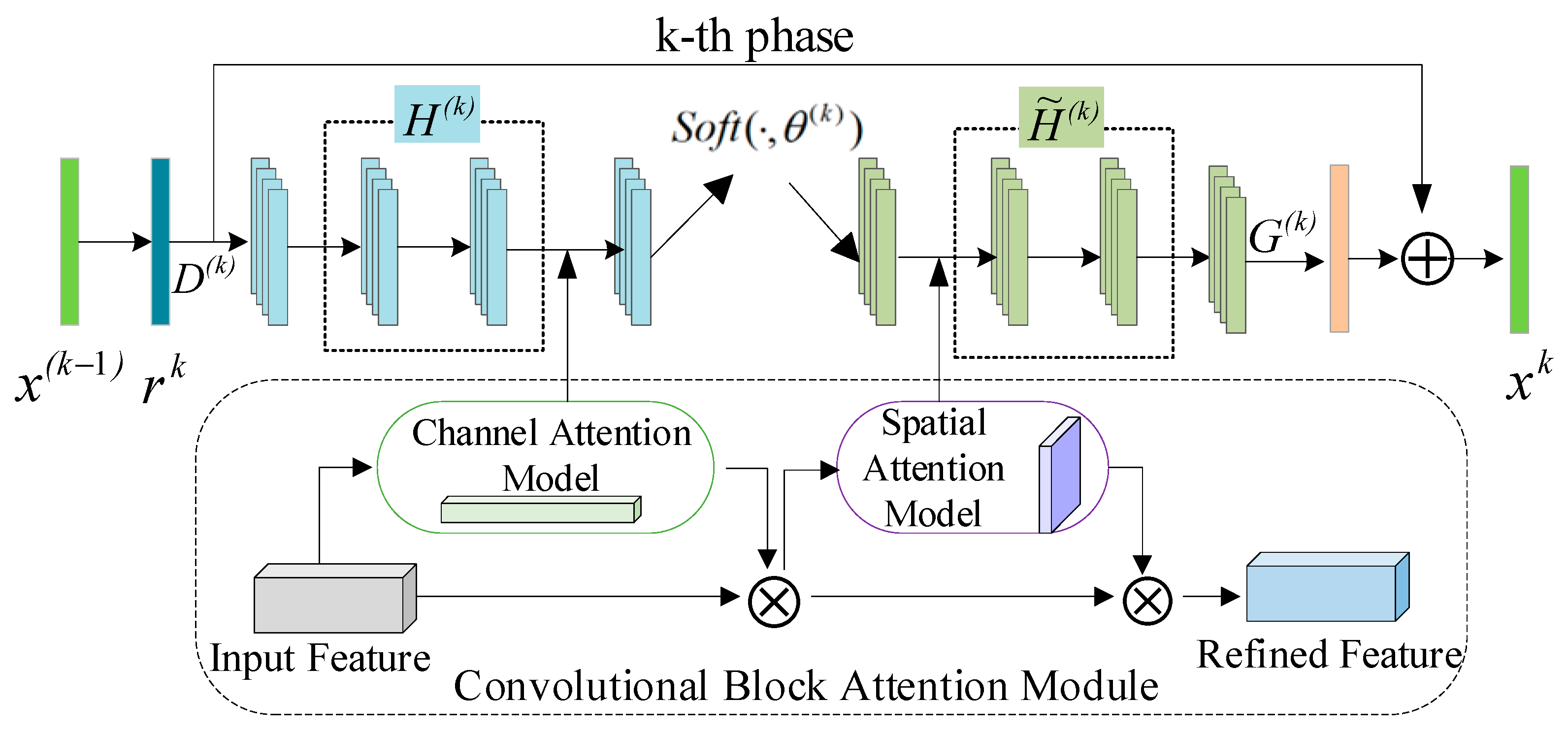
3.3. CBAM_ISTA-Net+ Compression and Reconstruction
3.3.1. Iterative Shrinkage-Thresholding Algorithm Network (ISTA-Net+)
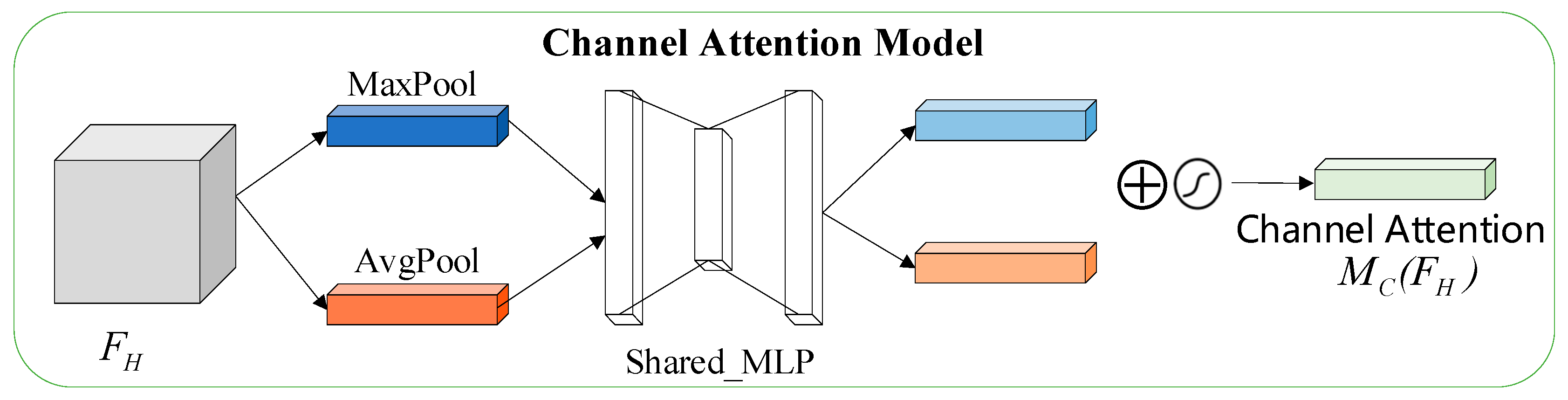
3.3.2. Improved CBAM_ISTA-Net+ Algorithm
- Channel Attention
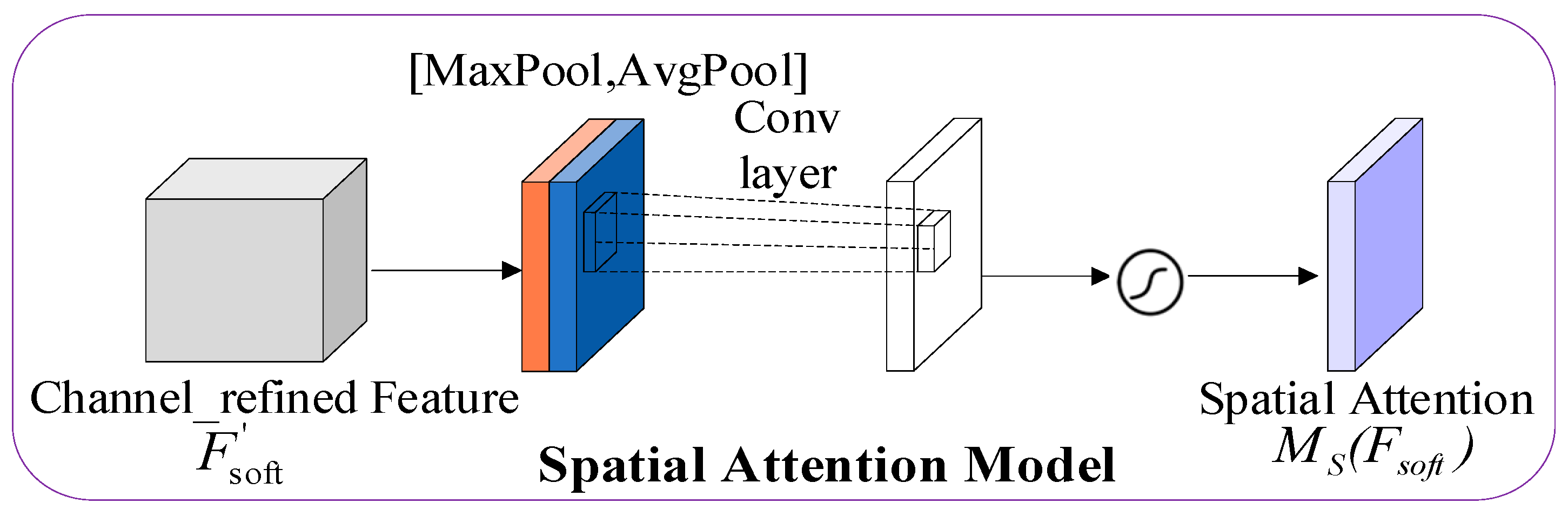
- Spatial Attention
| Algorithm 1: The procedure of CBAM_ISTA+ |
| Input: Output: ; ; 3. for k = 1; k ≤ L do by Formulas (6) and (7); |
| ; 6. Forward propagation convolution to extract deep features , ; ; ; ; 10. Backward propagation convolution ; , and flattened to vector form: ; 12. end; 13. Obtaining reconstruction results . |
4. Experiment and Result Analysis
4.1. Experimental Design and Environment
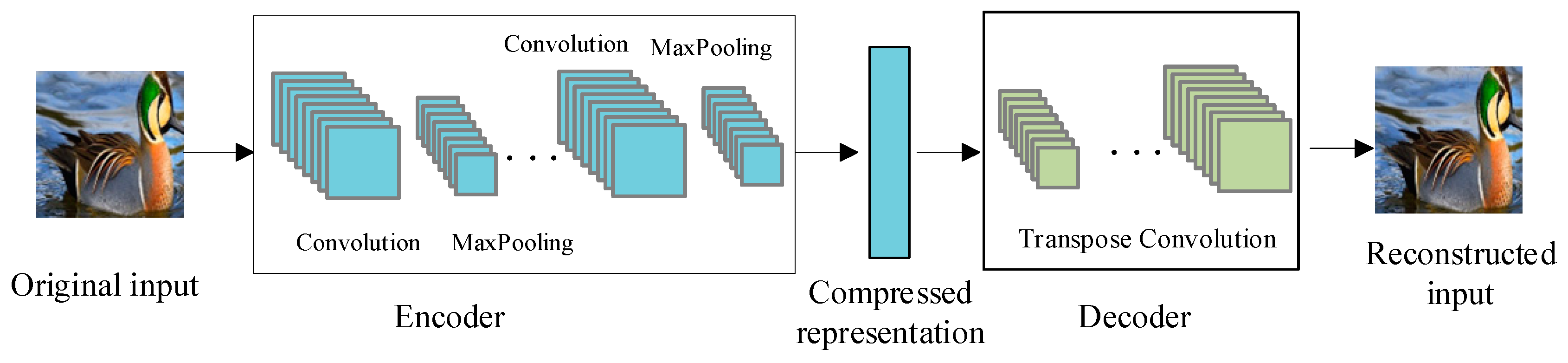
4.1.1. CAE Comparison Experiment
4.1.2. CNN Classification Model Settings
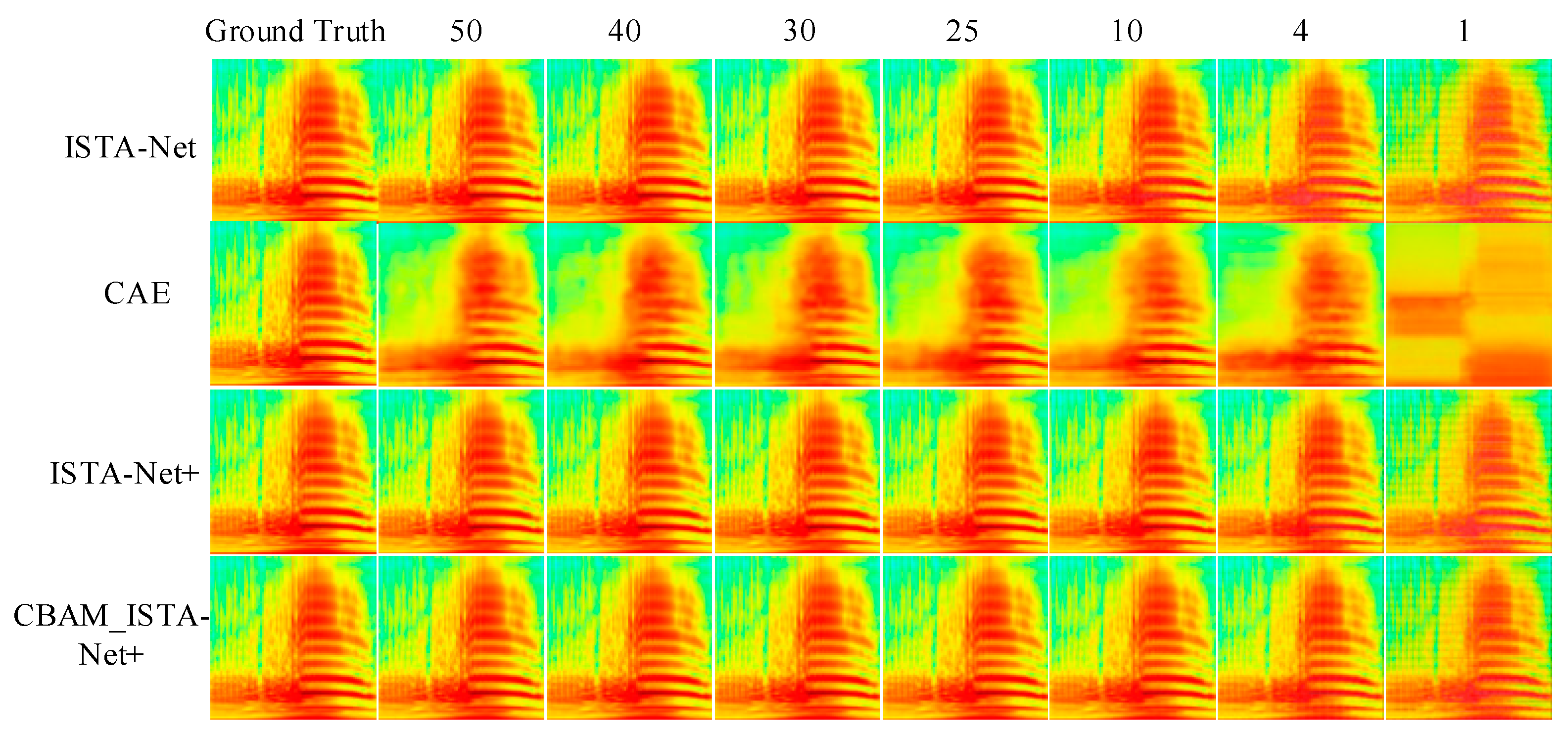
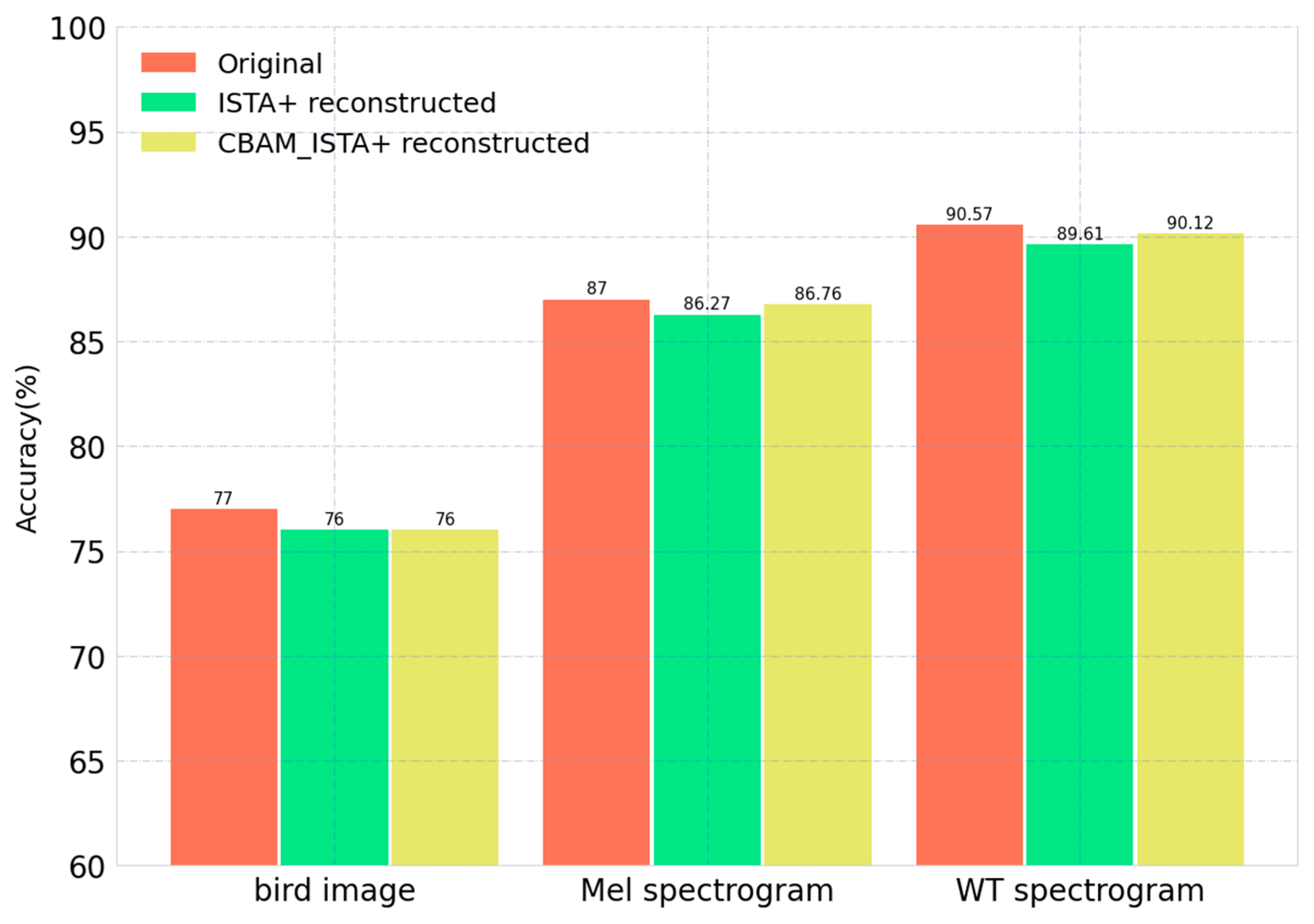
4.2. Result Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cui, J.; Xiao, Z. Progress in bioacoustics monitoring and research of wild vertebrates in China. Biodivers. Sci. 2023, 31, 23023. [Google Scholar] [CrossRef]
- Kahl, S.; Wood, C.M.; Eibl, M.; Klinck, H. BirdNET: A deep learning solution for avian diversity monitoring. Ecol. Inform. 2021, 61, 101236. [Google Scholar] [CrossRef]
- Shonfield, J.; Bayne, E.M. Autonomous recording units in avian ecological research: Current use and future applications. Avian Conserv. Ecol. 2017, 12, 14. [Google Scholar] [CrossRef]
- Hong, Y.; Lu, X.; Zhao, H. Bird diversity and interannual dynamics in different habitats of agricultural landscape in Huanghuai Plain. Acta Ecol. Sin. 2021, 41, 2045–2055. [Google Scholar]
- Candès, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Deng, J.; Ren, G.; Jin, Y.; Ning, W. Iterative weighted gradient projection for sparse reconstruction. Inf. Technol. J. 2011, 10, 1409–1414. [Google Scholar] [CrossRef][Green Version]
- Ji, S.; Xue, Y.; Carin, L. Bayesian compressive sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Mallat, S.G.; Zhang, Z. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef]
- Qin, J.; Li, S.; Needell, D.; Ma, A.; Grotheer, R.; Huang, C.; Durgin, N. Stochastic greedy algorithms for multiple measurement vectors. arXiv 2017, arXiv:1711.01521. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Q.; Amin, M.G. Multi-Task Bayesian compressive sensing exploiting signal structures. Signal Process. 2021, 178, 107804. [Google Scholar] [CrossRef]
- Abdelhay, M.A.; Korany, N.O.; El-Khamy, S.E. Synthesis of uniformly weighted sparse concentric ring arrays based on off-grid compressive sensing framework. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 448–452. [Google Scholar] [CrossRef]
- Gong, Y.; Shaoqiu, X.; Zheng, Y.; Wang, B. Synthesis of multiple-pattern planar arrays by the multitask Bayesian compressive sensing. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 1587–1591. [Google Scholar] [CrossRef]
- Fang, L.; Wang, C.; Li, S.; Rabbani, H.; Chen, X.; Liu, Z. Attention to lesion: Lesion-aware convolutional neural network for retinal optical coherence tomography image classification. IEEE Trans. Med. Imaging 2019, 38, 1959–1970. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Peng, C.; Yu, G.; Zhang, X.; Deng, Y.; Sun, J. Detnet: A backbone network for object detection. arXiv 2018, arXiv:1804.06215. [Google Scholar]
- Pan, Z.; Qin, Y.; Zheng, H.; Hou, L.; Ren, H.; Hu, Y. Block compressed sensing image reconstruction via deep learning with smoothed projected Landweber. J. Electron. Imaging 2021, 30, 041402. [Google Scholar] [CrossRef]
- Zhou, S.; He, Y.; Liu, Y.; Li, C.; Zhang, J. Multi-channel deep networks for block-based image compressive sensing. IEEE Trans. Multimed. 2020, 23, 2627–2640. [Google Scholar] [CrossRef]
- Zhang, X.; Lian, Q.; Yang, Y.; Su, Y. A deep unrolling network inspired by total variation for compressed sensing MRI. Digit. Signal Process. 2020, 107, 102856. [Google Scholar] [CrossRef]
- Kulkarni, K.; Lohit, S.; Turaga, P.; Kerviche, R.; Ashok, A. Reconnet: Non-iterative reconstruction of images from compressively sensed measurements. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 449–458. [Google Scholar]
- Yao, H.; Dai, F.; Zhang, S.; Zhang, Y.; Tian, Q.; Xu, C. Dr2-net: Deep residual reconstruction network for image compressive sensing. Neurocomputing 2019, 359, 483–493. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Yang, Y.; Sun, J.; Li, H.; Xu, Z. ADMM-Net: A deep learning approach for compressive sensing MRI. arXiv 2017, arXiv:1705.06869. [Google Scholar]
- Zhang, J.; Ghanem, B. ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1828–1837. [Google Scholar]
- Shi, W.; Jiang, F.; Liu, S.; Zhao, D. Image compressed sensing using convolutional neural network. IEEE Trans. Image Process. 2019, 29, 375–388. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Liu, Y.; Liu, J.; Wen, F.; Zhu, C. AMP-Net: Denoising-based deep unfolding for compressive image sensing. IEEE Trans. Image Process. 2020, 30, 1487–1500. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Zhang, J. Content-aware scalable deep compressed sensing. IEEE Trans. Image Process. 2022, 31, 5412–5426. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Chen, J.; Liu, Q.; Liu, B.; Guo, G. Dual-path attention network for compressed sensing image reconstruction. IEEE Trans. Image Process. 2020, 29, 9482–9495. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Mou, C.; Wang, S.; Ma, S.; Zhang, J. Optimization-inspired cross-attention transformer for compressive sensing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 6174–6184. [Google Scholar]
- Geng, C.; Jiang, M.; Fang, X.; Li, Y.; Jin, G.; Chen, A.; Liu, F. HFIST-Net: High-throughput fast iterative shrinkage thresholding network for accelerating MR image reconstruction. Comput. Methods Programs Biomed. 2023, 232, 107440. [Google Scholar] [CrossRef]
- Cui, W.; Wang, X.; Fan, X.; Liu, S.; Gao, X.; Zhao, D. Deep Network for Image Compressed Sensing Coding Using Local Structural Sampling. ACM Trans. Multimed. Comput. Commun. Appl. 2024, 20, 1–22. [Google Scholar] [CrossRef]
- Wang, H.; Li, H.; Jiang, X. DMFNet: Deep matrix factorization network for image compressed sensing. Multimed. Syst. 2024, 30, 191. [Google Scholar] [CrossRef]




| Layer | Name | Type | Kernel Size | Stride | Input Size |
|---|---|---|---|---|---|
| 1 | Conv Input | Input Layer | - | - | 224 × 224 × 3 |
| 2 | Conv1 | Convolution2D | 3 × 3 | 1 | 224 × 224 × 3 |
| 3 | Pool1 | MaxPool2D | 2 × 2 | 2 | 112 × 112 × 64 |
| 4 | Conv2 | Convoltion2D | 3 × 3 | 1 | 112 × 112 × 64 |
| 5 | Pool2 | MaxPool2D | 2 × 2 | 2 | 56 × 56 × 128 |
| 6 | - | Flatten | - | - | 56 × 56 × 128 |
| 7 | Fc1 | Linear | - | - | 128 × 56 × 56 |
| 8 | Fc2 | Linear | - | - | 256 |
| 9 | - | Output | - | - |
| Dataset | Methods | CS Ratio | Time | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 50% | 40% | 30% | 25% | 10% | 4% | 1% | GPU | ||
| Bird image | CAE | 21.58 | 21.37 | 21.31 | 21.15 | 20.63 | 19.80 | 16.36 | 0.0039 s |
| ISTA-Net | 32.36 | 30.27 | 28.20 | 27.58 | 22.74 | 20.65 | 17.15 | 0.054 s | |
| ISTA-Net+ | 33.31 | 31.48 | 29.54 | 28.42 | 23.93 | 20.07 | 16.99 | 0.058 s | |
| CBAM_ISTA-Net+ | 33.62 | 31.77 | 29.80 | 28.68 | 24.12 | 20.44 | 17.31 | 0.061 s | |
| Mel spectrogram | CAE | 23.13 | 22.92 | 22.51 | 22.41 | 21.64 | 20.65 | 17.29 | 0.0137 s |
| ISTA-Net | 38.68 | 37.18 | 35.88 | 34.22 | 29.70 | 24.85 | 19.47 | 0.1046 s | |
| ISTA-Net+ | 47.00 | 41.15 | 39.89 | 37.76 | 29.14 | 24.20 | 19.69 | 0.1104 s | |
| CBAM_ISTA-Net+ | 55.76 | 53.58 | 46.27 | 40.40 | 29.67 | 24.68 | 19.84 | 0.079 s | |
| WT spectrogram | CAE | 21.82 | 21.70 | 21.68 | 21.61 | 21.37 | 20.36 | 16.46 | 0.0216 s |
| ISTA-Net | 35.00 | 34.13 | 32.51 | 31.44 | 26.72 | 24.34 | 19.33 | 0.1072 s | |
| ISTA-Net+ | 38.31 | 36.29 | 33.66 | 32.44 | 27.30 | 23.92 | 19.84 | 0.1119 s | |
| CBAM_ISTA-Net+ | 38.59 | 36.41 | 33.89 | 32.63 | 28.70 | 24.09 | 20.51 | 0.1185 s | |
| Dataset | Algorithm | CS Ratio | ||||||
|---|---|---|---|---|---|---|---|---|
| 50% | 40% | 30% | 25% | 10% | 4% | 1% | ||
| Set11 | ISTA-Net [23] | 37.43 | 35.36 | 32.91 | 31.53 | 25.80 | 21.23 | 17.30 |
| ISTA-Net+ | 38.01 | 36.04 | 33.73 | 32.40 | 26.51 | 21.57 | 17.21 | |
| CBAM_ISTA-Net+ | 38.13 | 36.08 | 33.83 | 32.57 | 26.75 | 21.69 | 17.32 | |
| BSD68 | ISTA-Net [23] | 33.60 | 31.85 | 29.93 | 29.07 | 25.02 | 22.12 | 19.11 |
| ISTA-Net+ | 34.01 | 32.17 | 30.34 | 29.29 | 25.32 | 22.38 | 19.03 | |
| CBAM_ISTA-Net+ | 34.12 | 32.27 | 30.39 | 29.36 | 25.45 | 22.42 | 19.09 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, D.; Zhang, Y.; Lv, D.; Lu, J.; Fu, Y.; Li, Z. Combining CBAM and Iterative Shrinkage-Thresholding Algorithm for Compressive Sensing of Bird Images. Appl. Sci. 2024, 14, 8680. https://doi.org/10.3390/app14198680
Lv D, Zhang Y, Lv D, Lu J, Fu Y, Li Z. Combining CBAM and Iterative Shrinkage-Thresholding Algorithm for Compressive Sensing of Bird Images. Applied Sciences. 2024; 14(19):8680. https://doi.org/10.3390/app14198680
Chicago/Turabian StyleLv, Dan, Yan Zhang, Danjv Lv, Jing Lu, Yixing Fu, and Zhun Li. 2024. "Combining CBAM and Iterative Shrinkage-Thresholding Algorithm for Compressive Sensing of Bird Images" Applied Sciences 14, no. 19: 8680. https://doi.org/10.3390/app14198680
APA StyleLv, D., Zhang, Y., Lv, D., Lu, J., Fu, Y., & Li, Z. (2024). Combining CBAM and Iterative Shrinkage-Thresholding Algorithm for Compressive Sensing of Bird Images. Applied Sciences, 14(19), 8680. https://doi.org/10.3390/app14198680





