Abstract
This paper develops the theory of factorial numbers formed by positional number systems with mixed-base factorial number systems. The fundamentals of the theory of factorial numbers are outlined, a method for obtaining them is given, their range is determined, and noise immunity is assessed. The addition and subtraction operations on factorial numbers are considered, and examples of their implementation are given. Methods for transitioning from positional numbers to factorial numbers and back are proposed. Methods are given for converting factorial numbers into permutations and permutations into factorial numbers. The operations of adding and subtracting permutations using factorial numbers are described. The noise immunity of permutations and the ability to detect and correct errors are assessed. The prospects of using permutations formed by factorial numbers for constructing noise-resistant ciphers are shown.
1. Introduction
The development of number systems has a long history, which began with the advent of economic ties between people and the need to count that they caused. For this purpose, non-positional number systems were then used, in which numbers were represented by special symbols (hieroglyphs). Such a number system was, for example, the Roman numbering, which is used to this day. The rules for performing arithmetic operations in non-positional counting were very complex. In Europe, there was even a phrase “enter fractions” when talking about very complex things or events.
The use of non-positional number systems in practice could have continued for a long time, if not for the aggressive campaigns of the Arabs in the Middle Ages, which brought the decimal positional number system from India to Europe. It was extraordinarily simple. It used only an alphabet of numbers, called Arabic, due to the fact that they were brought by the Arabs, and a weighting coefficient for each digit in the form of a power of its number in base 10.
With the advent of decimal positional numbers, the development of positional number systems began, which is still ongoing. First, Leibniz, a 17th century German philosopher and mathematician, added the binary system to the positional decimal number systems for fun and games. Then, positional octal and hexadecimal number systems and others similar to them appeared.
The invention of positional number systems in itself is an amazing phenomenon that has no analogs in the history of mankind. It turned out that even a brilliant person could not create such a simple thing as a decimal positional number system. Only a people could have invented it, and not even everywhere. The Native Americans, for example, never came up with a positional number system, although they came close to it.
However, all these systems, due to their simplicity, could not detect errors in their operation. Therefore, in the 20th century, more complex positional number systems appeared that had this ability, and therefore made it possible to build inherently noise-resistant computer technology. But that is not all. Using these number systems, it became possible to design processors that solve special combinatorial problems with greater speed.
The first of these systems was developed in the mid-20th century. It was the Fibonacci number system that led to a rethinking of the principles of positional counting. A project was proposed to create a noise-resistant Fibonacci computer based on it, which, unfortunately, did not become a reality. It was difficult to make then due to the redundancy of the hardware costs required for its implementation. However, today, when hardware costs do not play such a decisive role as before, a noise-resistant Fibonacci computer is quite possible.
The issue of noise immunity and, accordingly, reliability is important in competing ideas in the field of computer technology, and the higher reliability an idea promises, the more interesting it is. Moreover, today there are no revolutionary ideas in computing, except for the idea of quantum computers. However, quantum computers use ordinary positional calculations and, if they are destined to appear on an industrial scale, will be highly specialized devices. At the same time, Fibonacci computers are universal devices that can replace conventional computers of any complexity, making them much more reliable.
The next noise-resistant number systems were binomial systems, of which there are several classes, but due to their complexity, they are promising today mainly only for solving highly specialized problems, such as information compression and generating various noise-resistant combinatorial codes. Binomial counters are especially valuable because of their noise immunity, speed and, accordingly, reliability. It is also possible to create a noise-resistant binomial processor that would compress binary information.
The factorial number systems discussed in this article arose in the last century. Historically, they are a consequence of the development of polyadic number systems [1,2,3,4]. By their essence, they are noise-resistant like Fibonacci and binomial systems, but they have an advantage over them, which is manifested in the fact that they are able to form permutations.
This is due to the fact that the range of factorial numbers is equal to the factorial of the number of their digits (the length of the number). For example, if the number of digits 0, 1, 2, 3 in factorial numbers is 4, then their quantity will be 4! = 24. But the same quantity of 24 will have permutations of 4 elements. This suggested that each factorial number can be associated with a permutation and vice versa. To implement the specified correspondence, the weight coefficient of each digit of the factorial number had to be equal to the factorial of its number 0!, 1!, 2!, 3!. This condition led to the appearance of a factorial number system.
The ability to obtain permutations based on factorial numbers means that they can be used to solve the traveling salesman problem by sequential search. It is universal, since a large number of combinatorial optimization problems can be reduced to it. Consequently, on the basis of the factorial number system, it is possible to build a specialized processor which is a universal solver of combinatorial problems. In terms of performance, it should surpass any other conventional similar devices that use brute force. The speed of a universal solver can only be surpassed by a quantum computer with its superposition and other quantum effects, which, in its idea, is also aimed at solving brute-force problems. But given its price and reliability, it is too early to talk about its practical use on a mass scale.
Permutations derived from factorial numbers can also find and, if necessary, correct errors in the storage and transmission of messages [5,6,7,8]. Also, permutations formed by factorial numbers, like numbers themselves, can actually be used in cryptography problems simply because they have been used there traditionally since the beginning of the science [9,10,11,12,13,14,15,16,17,18,19,20].
Factorial numbers can be used independently without permutations in problems of combinatorics and computer science. They can be used to build noise-resistant digital devices and automation based on them. The use of factorial numbers for the transmission and storage of binary data is quite promising, since they have a certain level of noise immunity. In addition, they can be gathered from the outputs of specialized factorial devices, such as counting devices, in measuring systems and transmitted to a receiver in such a noise-resistant form.
2. Problem Statement
Based on the above, a vast number of problems related to factorial numbers arise, which shall be considered in this work. These are, first, ways of forming factorial numbers in a random or systematic order, and second, the transition from factorial numbers to their numbers (natural numbers). It is also important to solve the problem of forming permutations based on factorial numbers and converting permutations back into factorial numbers and then into numbers of natural number systems. It is also necessary to obtain algorithms for performing arithmetic operations on factorial numbers and, with their help, corresponding operations on permutations. In addition, it is necessary to study factorial numbers and permutations for noise immunity and the ability to detect and correct errors. The possibility of obtaining noise-resistant ciphers using permutations obtained using factorial numbers should also be considered.
3. Theory of Factorial Numbers
Like any positional number system, the factorial system has a digit value, an alphabet of numbers and weighting coefficients for each digit. In terms of complexity, it is approximately the same as decimal. The difference is that the maximum value of each digit of a factorial number is equal to the number of that digit. If it is, for example, the hundredth digit, then the maximum value for it will be equal to 100, and the number of all digits in the number, considering the zero digit, will be equal to 101. The weighting coefficient in this case is 100! = 100 × 99 × … × 1. The preceding 99-th digit will have a maximum value of 99 and a weight of 99!. And so it goes further until the zero digit, the weight of which is 0! = 1. All these features of factorial number systems are shown by Equation (1) for the numerical factorial function. The weights of the factorial numbers in it increase according to a dependence close to exponential.
A factorial number is a positional n-digit number F = , where x is the number of the i-th digit, [3,4], for which the numerical function is
In this case, the expression i! = i × (i − 1) × … × 1 is called the factorial of i. Then, for example, 4! = 4 × 3 × 2 × 1 = 24.
In other words, the number F is written as a sequence of n digits, starting with the zero digit. It is assumed that the number i, i = 0, 1, …, n − 1, corresponds to the weight i!. The number of digits in the numbers of the factorial number system, as Equation (1) shows, is not related to the factorials. It increases linearly. For the zero digit there is one—“0”, for the first digit there are two—“0” and “1”, for the second three—“0”, “1”, “2” and so on. These numbers are easily converted into binary numbers, and then all processing of information presented in factorial numbers occurs in binary codes.
For example, the six-digit factorial number N = 3 4 0 0 1 0 is represented using a numeric function as F = 3 × 5! + 4 × 4! + 0 × 3! + 0 × 2! + 1 × 1! + 0 × 0! = 360 + 96 + 0 + 0 + 1 + 0 = 457.
For the theory and practical application of factorial numbers, what matters is the minimum Fmin and maximum Fmax value of the number F, as well as the range of representation of the numbers P. The minimum factorial number will be when in (1) all xi = 0. Accordingly, F = Fmin = 0 ∙ (n − 1)! + … + 0 ∙ 1! + 0 ∙ 0! = 0.
The maximum factorial number F = Fmax will be when in (1) all xi = i, i = 0, 1, …, n – 1, since, as follows from Expression (1), any deviation of the values of the numbers xi from the values of i downward will lead to a decrease in the number F.
Theorem 1.
Maximum number in n-digit factorial number system Fmax = n! − 1.
Proof of Theorem 1.
Consider a function F in which xi = i, i = 0, 1, …, n – 1. Then, given the equality we get The theorem has been proven. □
Consequence 1.
Since the maximum factorial number Fmax = n! – 1, then, starting from 0, the range of representable factorial numbers P = Fmax + 1 = n! – 1 + 1 = n!.
Thus, the maximum factorial number with n = 6 digits Fmax = 5 × 5! + 4 × 4! + 3 × 3! + 2 × 2! + 1 × 1! + 0 × 0! = 600 + 96 + 18 + 4 + 1 + 0 = 719, and the range of factorial numbers of the corresponding number system, considering 0, P = 719 + 1 = 6! = 720.
An important feature of the factorial number system that makes it attractive for computing is that it is noise-resistant. This follows from the fact that factorial numbers form a subset of the allowed combinations of the original (base) set. Other combinations that are not factorial numbers will be forbidden. For example, a four-digit factorial number system has 4! = 24 factorial numbers, and the base number of combinations of the original set is 44 = 256. Forbidden combinations will be 256 − 24 = 232. Assuming that the transition of a factorial number both into itself and any of the forbidden combinations is equally probable, the probability of detecting an error, provided that all factorial numbers appear with equal probability, will be equal to 1 − 24/256 = 0.91.
3.1. Enumeration of Factorial Numbers with an Interval Equal to 1
The enumeration of n-digit factorial numbers in the range P in ascending order contains the following steps:
- Starting from the first digit, all the digits of the factorial number F are looked through until a digit xi appears that is different from the value of the digit i = 1, 2, 3, …, n – 1, in which it is located. This digit is increased by one, and the digits of the all low-order digits, starting with digit i – 1, are set to 0. The value of the zero digit is equal to 0.
- If, when viewing all the digits of the number F in the order specified in step 1, the number xi, different from i = 1, 2, 3, …, n – 1, does not appear in them, then F = Fmax. End.
- Step 1 is repeated until each digit xi of the factorial number F is equal i. In this case, F = Fmax. End.
For example, factorial number F = 5 3 3 2 1 0 = 5 × 5! + 3 × 4! + 3 × 3! + 2 × 2! +1 × 1! + 0 × 0! = 695. When increasing, in accordance with the algorithm, the fourth digit of the specified number by one and setting all low-order digits as 0, it is converted into the number 5 4 0 0 0 0 = 5 × 5! + 4 × 4! + 0 × 3! + 0 × 2! +0 × 1! + 0 × 0! = 696. After that, the algorithm generates the number 5 4 0 0 1 0 = 697, then the number 5 4 0 1 0 0 = 698, …, 5 4 3 2 1 0 = 6! − 1 = 719. End.
The proof of the correctness of the considered algorithm is given below. It uses Theorem 1, which proves that for i = 0, 1, …, n – 1, Fmax = (i + 1)! – 1. Then, the appearance in the number F of the first digit on the right xi, , less than its corresponding value i = 1, 2, 3, …, n − 1, will lead to the fact that the corresponding sum of its products preceding digit i will be equal to i! − 1. In this case, adding one to the number xi will lead to an increase in the value of the product it forms to the value and, accordingly, to an increase in the number F by the amount i!. If we now reset all digits of the number F, starting from (i − 1) digit, then since , a new ordinal number F will be obtained with its value increased by one, which is the task of the proposed algorithm. After that, a new cycle of increasing the number F by one begins, similar to the above cycle, with obtaining new ordinal numbers F. Such cycles and new numbers F continue until all n digits of the factorial number are in the order n − 1, n − 2, …, 1, 0, corresponding to the factorial number Fmax. This concludes the algorithm for enumerating factorial numbers.
Below in Table 1, all 4! = 24 four-bit factorial numbers of length n = 4 are presented, obtained in accordance with the given algorithm.

Table 1.
Factorial numbers for n = 4.
3.2. Operations of Addition and Subtraction in the Factorial Number System
When performing addition and subtraction operations in the factorial number system, the rules of the unitary number system are used in the zero digit of numbers, in the first place binary, in the second ternary, etc. [3,4].
Example 1.
Add and subtract the factorial numbers A = 23,110 and B = 12,200.
Solution 1.
.
Verificationn 1:
- 23110<F> = 2∙4! + 3∙3! + 1∙2! + 1∙1! + 0∙0! = 69<10>;12200<F> = 1∙4! + 2∙3! + 2∙2! + 0∙1! + 0∙0! = 40<10>;42010<F> = 4∙4! + 2∙3! + 0∙2! + 1∙1! + 0∙0! = 69<10>+40<10> = 109<10>;10210<F> = 1∙4! + 0∙3! + 2∙2! + 1∙1! + 0∙0! = 69<10>–40<10> = 29<10>.
3.3. Interval Search of Factorial Numbers
Using arithmetic operations of addition and subtraction over factorial numbers allows for solving the problem of enumerating factorial numbers in ascending and descending order for any integer value of the enumeration interval, including one.
The operation of addition with one is that each factorial number can be transformed by adding one into a neighboring number that is one greater. So, for example, after the number F = 3 4 0 0 1 0 = 457<10>, as a result of the operation of its addition with 1, the number 3 4 0 1 0 0 = 458<10> will appear. Then, after it comes the number 3 4 0 1 0 0 + 1 = 3 4 0 1 1 0 = 459<10> and so on until the factorial number 5 4 3 2 1 0 = 719<10>.
Sequential enumeration with an integer greater than one is carried out similarly to addition with one. For example, the first result of adding the factorial number 2 1 1 0 = 15<10> with the number 1 1 0 0 = 8<10> will give the number 2 1 1 0 + 1 1 0 0 = 3 2 1 0 = 3 × 3! + 2 × 2! + 1 × 1! + 0 × 0! = 23<10>. Then, the second addition occurs with the number 8: 3 2 1 0 + 1 1 0 0 = 1 1 0 1 0 = 31<10>.
Enumerating factorial numbers in descending order consists of subtracting the same integer at each step. So, at the first step, 2 2 0 0 − 1 1 0 0 = 1 1 0 0 = 8<10>. At the second step, 1 1 0 0 − 1 1 0 0 = 0 0 0 0 = 0<10>. The subtractive search is completed.
3.4. Converting Factorial Numbers to Natural Numbers and Vice Versa
Converting a factorial number to a natural number is completed using the numeric function for the factorial number system (1).
Example 2.
Convert the factorial number F = 2 3 2 2 0 0 to the number X in the decimal number system.
Solution 2.
.
The transformation of the number X ≥ 1 from the natural number system into the factorial number F occurs in steps, at each of which the quotient obtained in the previous step is divided by one of the divisors 1, 2, …, n − 1 until the quotient becomes less than the divisor. In this case, the first quotient is the number to be translated, which is divided by one. The last quotient and the sequence of remainders from the divisions are written out from right to left. The result will be the required factorial number.
Example 3.
Convert decimal number X = 69 to factorial number F.
Solution 3.
Result 3:
F = 2 3 1 1 0.
Verification 3:
2 × 4! + 3 × 3! + 1 × 2! + 1 × 1! + 0 × 0! = 48 + 18 + 2 + 1 = 69.
3.5. Compression of Factorial Numbers
Factorial numbers have redundancy, since each of them in binary form with uniform encoding contains bits of information. At the same time, the factorial number contains bit. Therefore, during its transmission and storage, compression may be necessary. The data compression ratio S depends on the absolute redundancy of the factorial number and is defined as . For example, with n = 4, the absolute redundancy is bits, and the compression ratio S = 8/5 ≈ 1.745.
Table 2 and the graph in Figure 1 show the absolute redundancy and data compression ratio S as n changes from 2 to 16.

Table 2.
Redundancy and compression of factorial numbers.
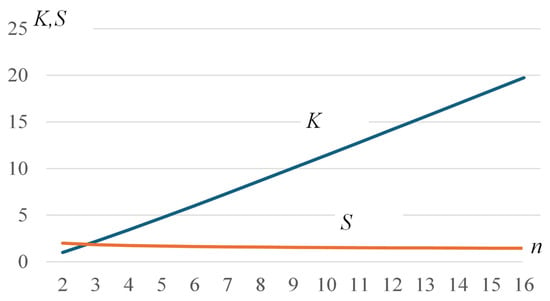
Figure 1.
Redundancy and compression plots of factorial numbers.
3.6. Detecting Errors in Factorial Numbers
Among the factorial numbers F, erroneous numbers may appear during their transmission and storage. They are detected when restrictions on digit values are violated. Thus, the factorial number 2 3 2 1 0 is correct, but the number 2 3 2 2 0 is incorrect since the value of the first digit of this number is two, and it cannot be greater than one.
The restrictions on the values of the digits in the factorial number are distributed unevenly. Thus, only the number 0 can appear in the zero digit. Any other number is a sign of an error. At the same time, in the highest (n − 1)-th digit, all n − 1 numbers are allowed, and therefore errors in it are not detected. Errors in other digits are detected but with different probabilities. Errors in digits of a factorial number can be corrected either by retransmitting them or by additional noise-resistant coding of these digits.
4. Application of Factorial Numbers in Permutation Problems
4.1. Converting Factorial Numbers to Permutations
A permutation is a sequence of different elements (numbers, letters) of finite length n. The number of permutations of length n is equal to the factorial n!. Permutations play an important role in mathematics—for example, there is abstract algebra based on permutations—and in numerous practical applications [5,6,7,8,9,10,11,12,13,21,22,23,24,25,26,27,28,29,30]. The most complex unsolved combinatorial optimization problem to date, known as the traveling salesman problem, is the problem of finding a minimum on a set of permutations [30].
The ability to obtain permutations based on factorial numbers is an important application, although not the only one. In [1,2,3,4,5,22], an algorithm for obtaining permutations based on factorial numbers is described. It follows from the property of permutations, according to which all their elements are different, that accordingly, each subsequent element of the permutation must be different from all previous ones. The algorithm proposed below, which is characterized by greater simplicity and speed, takes into account the property of permutations, according to which the sum of the digits in the permutation is constant and equal to (n × (n − 1))/when obtaining the last element of permutation [6,7,8].
The algorithm contains the following steps:
- The value of the highest n − 1 digit of the factorial number is the first element of the permutation.
- The value of the i-th digit of the factorial number is compared with all the values of the preceding digits of the permutation, and for each new comparison result in which it is equal to or greater than the value with which it is being compared, it is increased by one. The resulting sum of ones forms the i-th element of the permutation.
- The last number of the permutation in the zero digit is found in the form of the difference between the previously known constant sum of n elements of the permutation and the sum of the n − 1 elements of the permutation already received.
For example, if it is necessary to convert the factorial number 3 4 0 0 1 0 into a permutation, then in accordance with the given conversion algorithm, we obtain the permutation 3 5 0 1 4 2. There are no repeating digits in it. The sum of the digits is (6 × 5)/2 = 15. Therefore, the last digit is found as a result of subtracting 15 − 13 = 2.
Table 3 for n = 4 presents all factorial numbers and the permutations obtained from them.

Table 3.
Converting factorial numbers to permutations for n = 4.
4.2. Converting Permutations to Factorial Numbers
The method of transition from a permutation to a factorial number is that the value in the higher digit of the permutation is the value in the higher digit (n − 1) of the factorial number. Any other digit of it is obtained by subtracting from the corresponding value of the permutation a number equal to the number of smaller digits of the permutation standing in front of it on the left. This algorithm works, as can be seen by looking at the factorial numbers in Table 3.
4.3. Converting Permutations to Natural Number Systems and Vice Versa
Such permutation transformation problems often arise when solving combinatorial optimization problems, as well as in the encryption and decryption of messages in problems of cryptography and cryptanalysis [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. They are solved by using the above algorithms to move from permutations to factorial numbers and then from them to numbers of natural number systems. The inverse problem is solved by moving from a natural number to a factorial number and from it to a permutation.
4.4. Permutation Arithmetic
Factorial numbers can be used to perform addition and subtraction operations on permutations. Moreover, they make it possible to perform this on two levels. At the first level, permutations are converted into factorial numbers, and addition or subtraction operations are performed on them. Then the resulting factorial numbers are converted into permutations, representing the final result of the arithmetic operation performed on the permutations. For example, if the permutations 2 1 3 0 and 1 2 0 3 are being added, then their factorial numbers 2 1 1 0 and 1 0 0 0 are obtained, and then the sum is calculated as 2 1 1 0 + 1 0 0 0 = 3 1 1 0. After that, the factorial number 3 1 1 0 is transformed into the permutation 3 1 2 0. This means that the sum of the permutations is 2 1 3 0 + 1 2 0 3 = 3 1 2 0.
The second level is arithmetic operations at the level of natural numbers. Then, after the first level of transformation of permutations into factorial numbers, they are converted to the corresponding numbers of the natural number system and the required arithmetic operations are performed on them. The results of these operations are converted first into factorial numbers and then into permutations, representing the final result of performing arithmetic operations on the original permutations. For example, the permutation 3 1 2 0 is divided by permutation 0 2 3 1. Then, the first level of the division operation contains the factorial permutation numbers 3 1 1 0 and 0 1 1 0. Then, they are converted to the corresponding natural numbers 2, 1 and 3. Dividing the number 21 by 3 gives the number 7, which is converted to the factorial number 1 0 1 0. This number, in turn, according to the algorithm proposed above, is converted into permutation 1 0 3 2. This is the result of dividing permutation 3 1 2 0 by 0 2 3 1.
4.5. Interval Search of Permutations
The presence of the factorial addition and subtraction operations of factorial numbers makes it possible, on this basis, to obtain an enumeration of permutations with different numerical intervals 1, 2, … Such interval search makes it possible, for example, to speed up the solution of mathematical problems when a global minimum or maximum needs to be found. Then, it is possible to quickly reach the segment of the function where the extremum is located and, after that, by changing the size of the interval, find the extremum itself.
The proposed method for interval search of permutations based on the arithmetic of factorial numbers consists of the following steps:
- The first factorial number is arbitrarily set and converted into a permutation.
- According to the rules of factorial arithmetic, the first interval factorial number, with the help of which the search is performed, is added to the original number and converted into a permutation, then the second, etc., until the required permutation is found.
- When the required permutation is obtained, the search for permutations ends.
4.6. Errors in Permutations
A feature of permutations is that the appearance of identical elements in a permutation, for example, two ones or more, is a sign of an error [7]. An indicator of an error can be the original sum of the values of all its digits, which is the same for permutations of equal length. For Table 2, it is equal to six. Violation of this sum in the permutations of Table 2 indicates the presence of an error in them.
Which of the identical elements of the permutation is erroneous is identified in another way, for example, by using XOR checksum for them [31]. There are other more sophisticated methods for detecting and correcting errors based on permutations [7,8].
Detection of errors in permutations is possible because in all possible code combinations generated by n symbols, permutations that form allowed code combinations can be found. The remaining code combinations are forbidden combinations, the appearance of which is a sign of an error.
The number of allowed combinations is determined by the range of permutations P = n! of length n, and the number of forbidden permutations is determined by the difference nn − n!. Using factorial numbers to generate permutations makes it possible to obtain them of almost any length n, which means achieving a high level of noise immunity, which increases with increasing n, as follows from Table 4.

Table 4.
Allowed and forbidden states for permutations.
Table 4 makes it possible to determine the probability of detecting errors in permutations of different lengths, containing from one to eight elements. This thereby makes it possible to select an error-resistant code based on permutations. The probability of detected errors in permutations is defined as follows:
Table 5 shows the values of probability p for values of factorial numbers with bit depth n varying from one to eight.

Table 5.
Probability of detected errors p.
Table 5 and Figure 2 clearly show that as the length of permutations n increases, the probability of detecting errors p tends to 1.
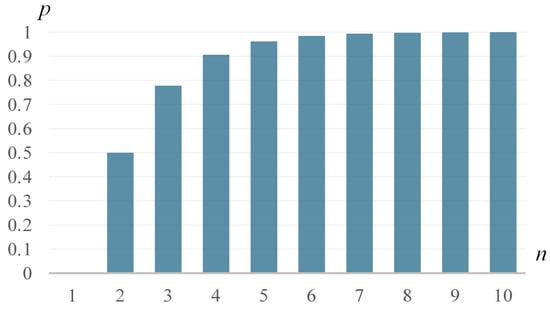
Figure 2.
Graph of the probability of detected errors p as a function of the permutation length n.
4.7. Protecting Information Using Permutations
Permutations containing n elements are capable of encrypting transmitted or stored information and thereby reliably protecting it from unauthorized access by encoding binary messages of at least integer length . In this case, the keys can be permutations of selected elements in permutations of all elements, carried out by factorial numbers [31]. In this case, information protection is combined with its noise-resistant coding, which makes it possible to accomplish both tasks of protection against interference and unauthorized access using permutations. Few codes have these properties today, even though they are useful for practical applications.
5. Conclusions
This work’s study of factorial numbers made it possible to display existing methods for obtaining factorial numbers and simplify them. Evaluating the noise immunity of factorial numbers allows them to be used for the efficient storage and transmission of information. Compressing factorial numbers by numbering them makes it possible to reduce their transmission time and storage capacity. Factorial arithmetic is noise-tolerant and therefore allows for performing arithmetic operations on factorial numbers more reliably.
An important practical application of factorial numbers is the formation of permutations in ascending and descending order with the ability to perform computational operations on them. This allows permutations to be used in many practical applications, such as combinatorial optimization problems or constructing ciphers. In addition, permutations themselves have good noise immunity, and therefore, their practical use makes it possible to effectively detect and, in some cases, correct errors.
A valuable property of factorial numbers is the possibility of enumerating them and, with it, enumerating permutations, both in the case of increasing the factorial numbers by one and adding any other integer, both positive and negative. This gives flexibility and versatility to the problem of enumerating permutations.
Permutations that use factorial numbers for their generation provide good opportunities to hide useful information since they allow binary messages of almost unlimited length to be converted into them. Thus, the probabilities of letters and numbers in the alphabets of input messages are masked. In addition, their secrecy without additional time costs is accompanied by increased noise immunity.
In the future, various restrictions may be introduced on permutations, which will require the introduction of additional restrictions on factorial numbers and, with them, the development of new methods for generating permutations with restrictions.
Author Contributions
Conceptualization, O.B. (Oleksiy Borysenko), O.H. and S.M.; methodology, O.B. (Oleksiy Borysenko) and O.H.; validation, O.B. (Oleksiy Borysenko), S.M. and V.B; data curation, V.B.; writing—original draft preparation, O.B. (Oleksiy Borysenko), O.H. and S.M.; writing—review and editing, O.B. (Oleksiy Borysenko), S.M., O.H., O.B. (Olga Berezhna), A.N., T.S., J.P. and V.B.; visualization, O.H. and S.M.; supervision, O.B. (Oleksiy Borysenko) and J.P.; project administration, J.P.; funding acquisition, J.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the RRF project Latvian Quantum Technologies Initiative Nr. 2.3.1.1.i.0/1/22/I/CFLA/001.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Laisant, C.-A. Sur la numération factorielle, application aux permutations. Bull. De La Société Mathématique De Fr. 1888, 16, 176–183. (In French) [Google Scholar] [CrossRef]
- Janasz, M.; Barańska, B. Factorial number system as an example of substantial learning environment for pre-and in-service teachers of mathematics, Studia ad. Didact. Math. Pertin. 2019, 10, 176–183. [Google Scholar] [CrossRef]
- Borisenko, A.A.; Kalashnikov, V.V.; Kulik, I.A.; Goryachev, A.E. Generation of Permutations Based Upon Factorial Numbers. In Proceedings of the Eighth International Conference on Intelligent Systems Design and Applications, Kaohiung, Taiwan, 26–28 November 2008; pp. 57–61. [Google Scholar] [CrossRef]
- Borysenko, O.A.; Kulyk, I.A.; Horiachev, O.Y. Electronic system for generation of permutations on the basis of factorial numbers. Visnyk Sumdu. Tech. Sci. 2007, 1, 183–188. (In Ukrainian) [Google Scholar]
- Borysenko, O.; Horiachev, O.; Kulyk, I.; Yakovlev, M. Factorial Permutation Generation. In Proceedings of the 2019 IEEE International Scientific-Practical Conference Problems of Infocommunications, Science and Technology (PIC S&T), Kyiv, Ukraine, 8–11 October 2019; pp. 375–378. [Google Scholar] [CrossRef]
- Borysenko, A.A.; Horiachev, O.Y.; Matsenko, S.M.; Kobiakov, O.M. Noise-Immune Codes Based on Permutations. In Proceedings of the 2018 IEEE 9th International Conference on Dependable Systems, Services and Technologies (DESSERT), Kiev, Ukraine, 24–27 May 2018; IEEE: Washington, DC, USA, 2018; pp. 609–612. [Google Scholar]
- Horiachev, O. The detection of errors in permutations. Visnyk Sumdu. Tech. Sci. 2009, 3, 169–174. (In Russian) [Google Scholar]
- Borysenko, O.; Horiachev, O. Methods of error detection and correction in permutations. Inf. Process. Syst. 2013, 109, 171–173. [Google Scholar]
- Faure, E.; Shvidkiy, V.; Shcherba, A. Method of forming reproducible and unpredictable sequence of permutations. Ukr. Sci. J. Inf. Secur. 2014, 20, 253–258. [Google Scholar] [CrossRef]
- Bereg, S.; Malouf, B.; Morales, L.; Stanley, T.; Sudborough, I.H. Using Permutation Rational Functions to Obtain Permutation Arrays with Large Hamming Distance. Des. Codes Cryptogr. 2022, 90, 1659–1677. [Google Scholar] [CrossRef]
- Bereg, S.; Mojica, L.G.; Morales, L.; Sudborough, I.H. Constructing Permutation Arrays Using Partition and Extension. Des. Codes Cryptogr. 2020, 88, 311–339. [Google Scholar] [CrossRef]
- Bereg, S.; Luis, G.; Mojica, L.G.; Morales, L.; Sudborough, I.H. Kronecker Product and Tiling of Permutation Arrays for Hamming Distances. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; IEEE: Washington, DC, USA, 2017; pp. 2198–2202. [Google Scholar] [CrossRef]
- Frankl, P.; Deza, M. On the Maximum Number of Permutations with given Maximal or Minimal Distance. J. Comb. Theory Ser. A 1977, 22, 352–360. [Google Scholar] [CrossRef]
- Dixon, J.D.; Mortimer, B. Permutation Groups. In Graduate Texts in Mathematics; Springer: New York, NY, USA, 1996; Volume 163, 348p, ISBN 978-1-4612-0731-3. [Google Scholar]
- Chu, W.; Colbourn, C.J.; Dukes, P. Constructions for Permutation Codes in Powerline Communications. Des. Codes Cryptogr. 2004, 32, 51–64. [Google Scholar] [CrossRef]
- Janiszczak, I.; Lempken, W.; Östergård, P.R.J.; Staszewski, R. Permutation Codes Invariant under Isometries. Des. Codes Cryptogr. 2015, 75, 497–507. [Google Scholar] [CrossRef]
- Smith, D.H.; Montemanni, R. A New Table of Permutation Codes. Des. Codes Cryptogr. 2012, 63, 241–253. [Google Scholar] [CrossRef]
- Faure, E.; Shcherba, A.; Makhynko, M.; Stupka, B.; Nikodem, J.; Shevchuk, R. Permutation-Based Block Code for Short Packet Communication Systems. Sensors 2022, 22, 5391. [Google Scholar] [CrossRef] [PubMed]
- Faure, E.; Shvydkyi, V.; Shcherba, V. Combined Factorial Coding and Its Properties. Radio Electron. Comput. Sci. Control 2016, 3, 80–86. [Google Scholar] [CrossRef][Green Version]
- Faure, E.; Shcherba, A.; Vasiliu, Y.; Fesenko, A. Cryptographic Key Exchange Method for Data Factorial Coding. In Proceedings of the International Workshop on Cyber Hygiene (CybHyg-2019), Kyiv, Ukraine, 30 November 2019; CEUR Workshop Proceedings; 2020. Volume 2654, pp. 643–664. [Google Scholar]
- Moldovyan, A.A.; Moldovyan, N.A.; Guts, N.D.; Izotov, B.V. Cryptography: High-Speed Ciphers; BKhV-Petersburg: St. Petersburg, Russian, 2002; 244p. (In Russian) [Google Scholar]
- Reingold, E.M.; Nievergelt, J.; Deo, N. Combinatorial Algorithms: Theory and Practice; Prentice-Hall: Englewood Cliffs, NJ, USA, 1977; 433p. [Google Scholar]
- Karim, S.; Ibrahim, H. Starter Set Generation Based on Factorial Numbers for Half Wing of Butterfly Representation. Math. Stat. 2021, 9, 664–668. [Google Scholar] [CrossRef]
- Lénárt, I. Periodic, Irrational and Transcendental Numbers in the Factorial Series. J. Appl. Math. Phys. 2022, 10, 558–575. [Google Scholar] [CrossRef]
- Mezmaz, M.; Leroy, R.; Melab, N.; Tuyttens, D. A Multi-core Parallel Branch-and-Bound Algorithm Using Factorial Number System. In Proceedings of the 2014 IEEE International Parallel & Distributed Processing Symposium (IPDPS), Phoenix, AZ, USA, 19–23 May 2014; pp. 1203–1212. [Google Scholar] [CrossRef]
- Knuth, D.E. The Art of Computer Programming: Volume 2: Seminumerical Algorithms, 3rd ed.; Addison-Wesley: Boston, MA, USA, 2022; 782p. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming: Volume 3: Sorting and Searching, 2nd ed.; Addison-Wesley: Boston, MA, USA, 2022; 800p. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming: Volume 4: Combinatorial Algorithms, Part 1, 1st. ed.; Addison-Wesley Professional: Boston, MA, USA, 2022; 912p. [Google Scholar]
- Patel, D.; Patel, A. Generating the nth Lexicographical Element of a Mathematical k-Permutation Using Permutational Number System. 27 July 2022. Available online: https://ssrn.com/abstract=4174035 (accessed on 20 August 2022). [CrossRef]
- Borisenko, A.A.; Goryachev, A.E. Approach to the traveling salesman problem based on factorial numbers. Actual Probl. Econ. 2009, 10, 150–154. (In Russian) [Google Scholar]
- Borysenko, O.; Horiachev, O.; Berezhna, O.; Matsenko, S.; Novhorodtsev, A. Noise-immune Transfer of Decimal Data with Protection Based on Permutations. In Proceedings of the 2023 IEEE 13th International Conference on Electronics and Information Technologies (ELIT), Lviv, Ukraine, 26–28 September 2023; pp. 1–4. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).