Research on the Gap Effect of Circular Concrete-Filled Steel Tubes Using the Improved Cohesive Zone Model
Abstract
:1. Introduction
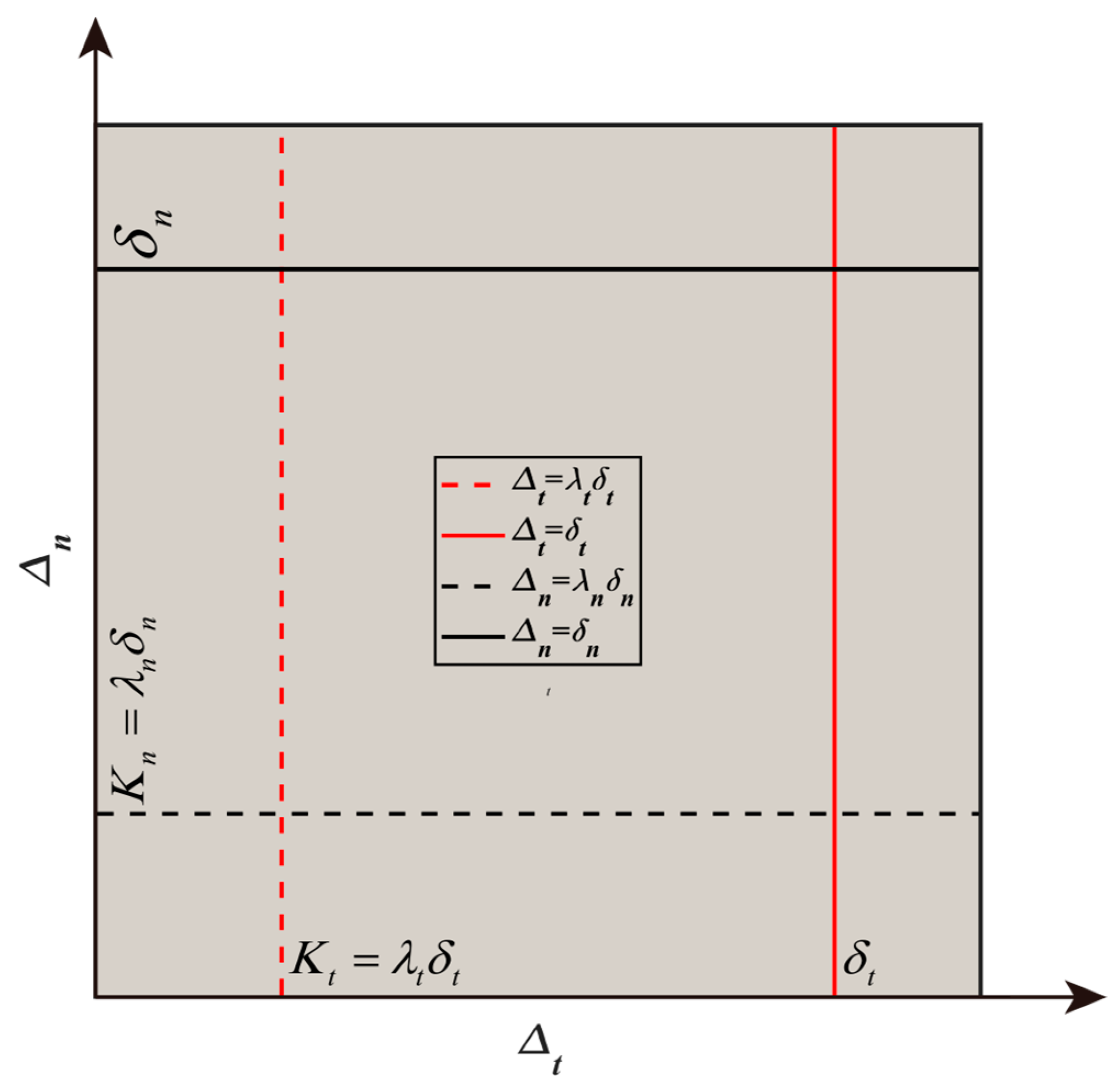
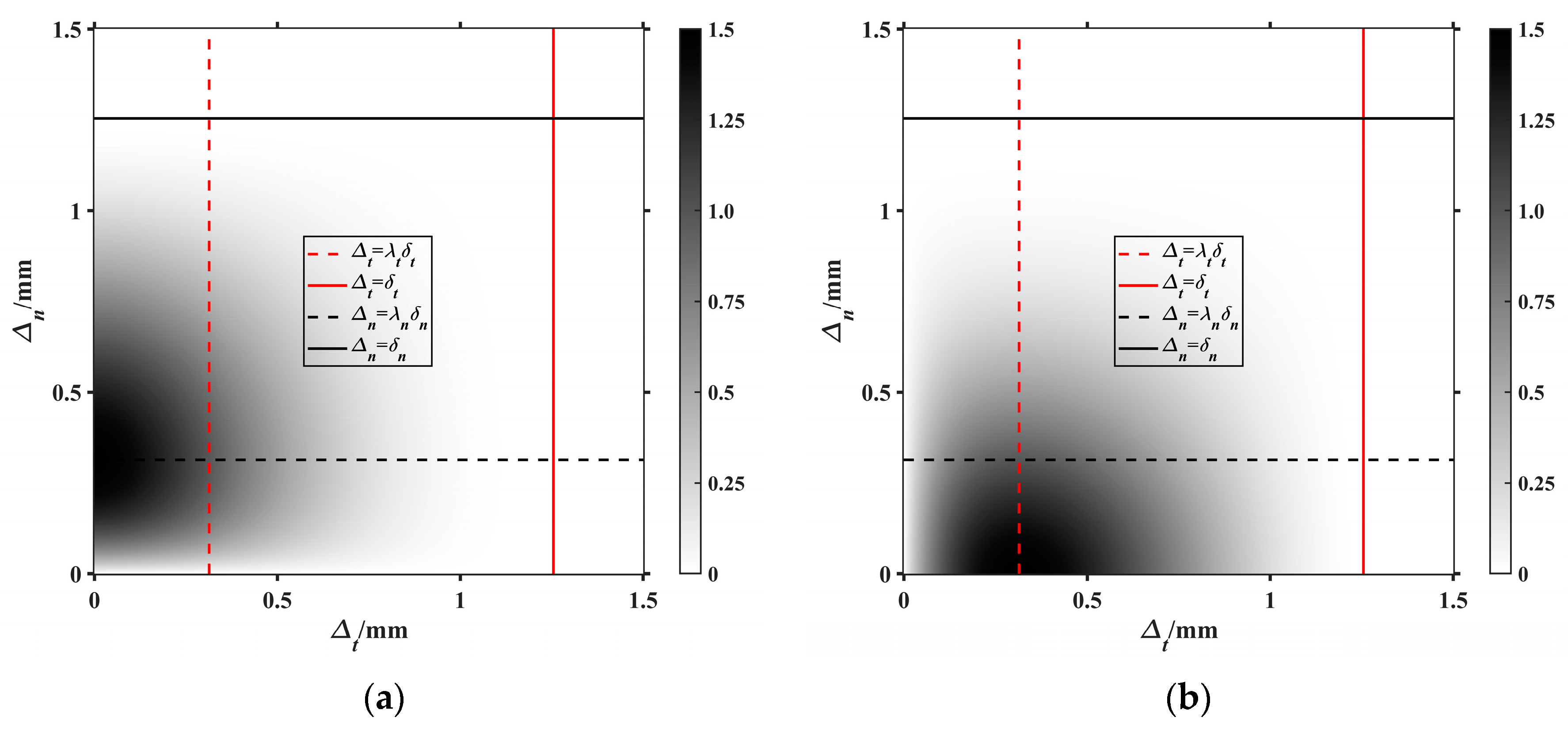
2. Improved Cohesive Model
2.1. Basic Principles
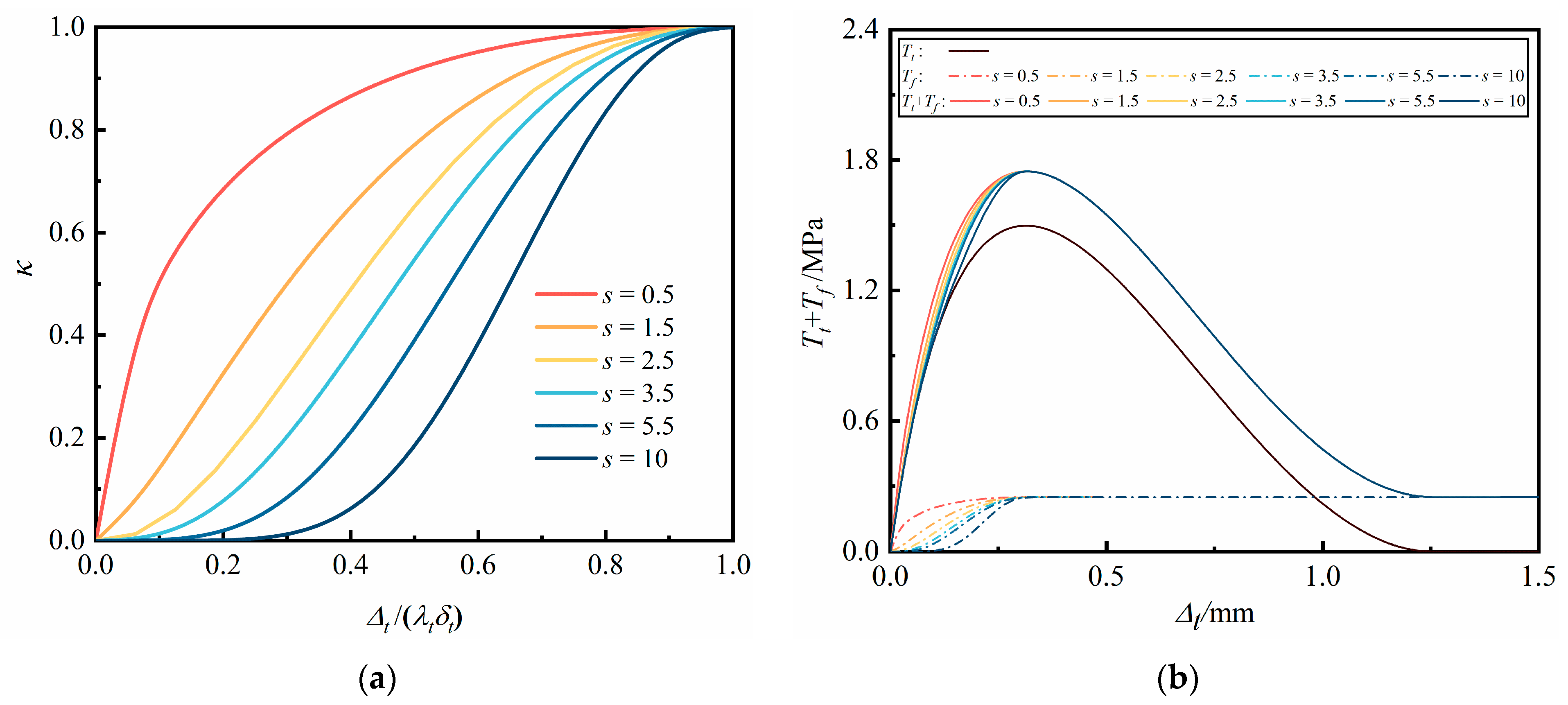
2.2. Friction Model
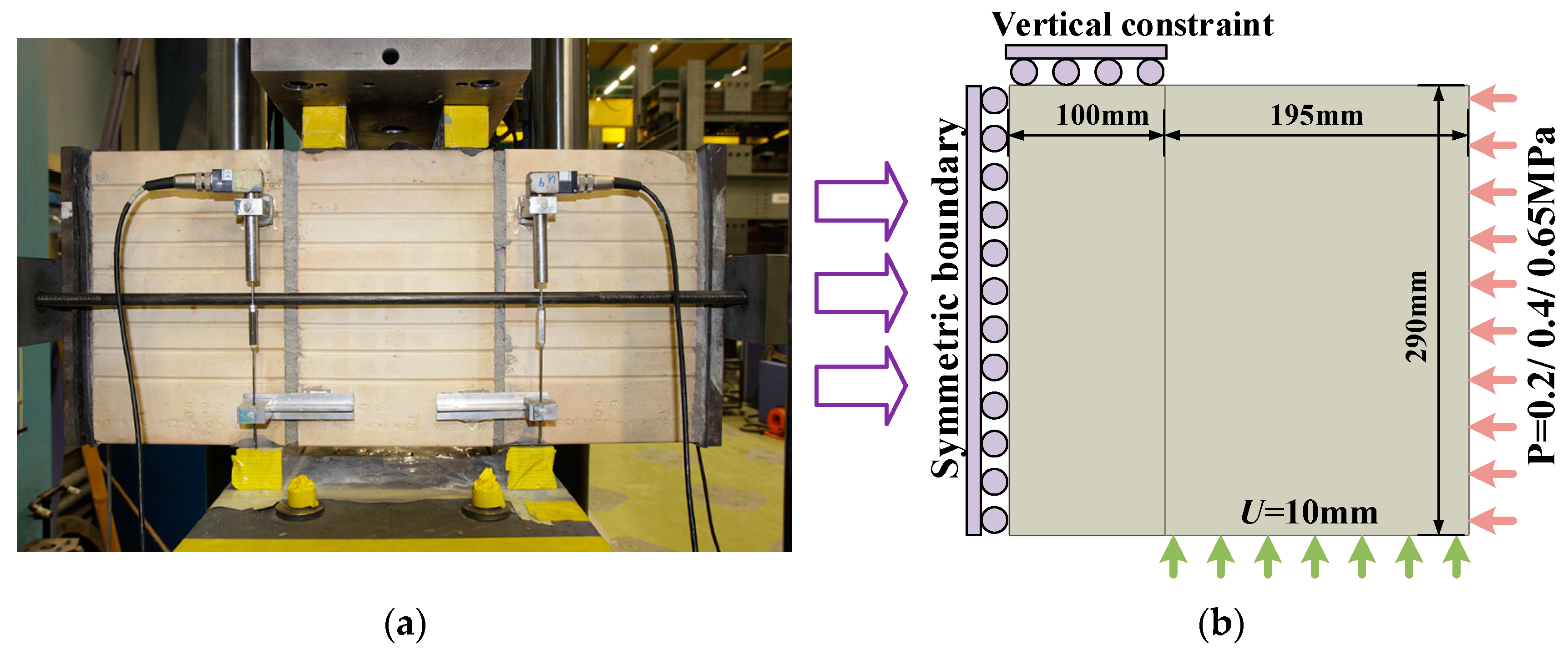
2.3. Numerical Benchmark
3. Analysis of the Flexural Performances of CCFSTs with Gaps
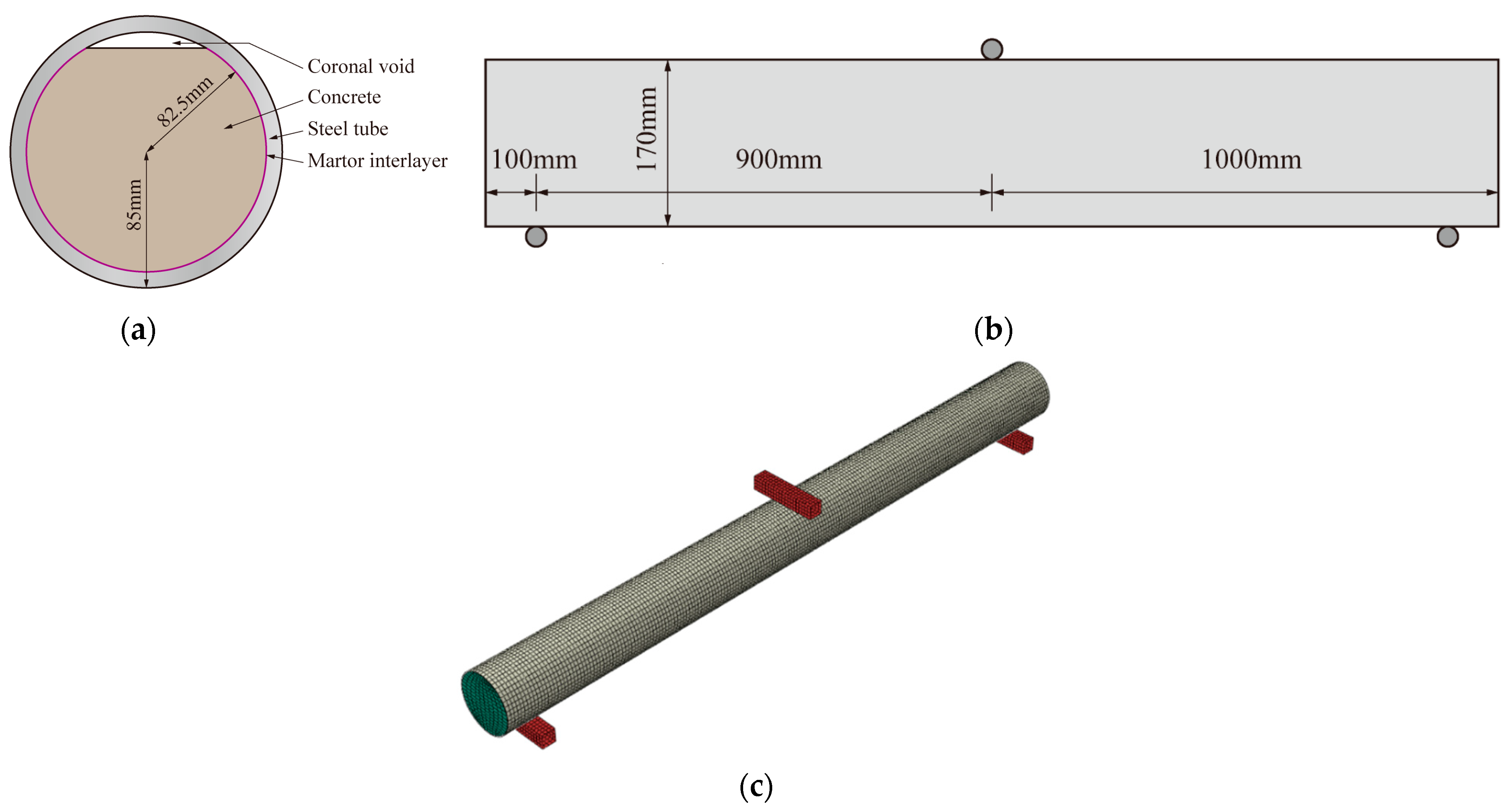
3.1. Numerical Model Configuration
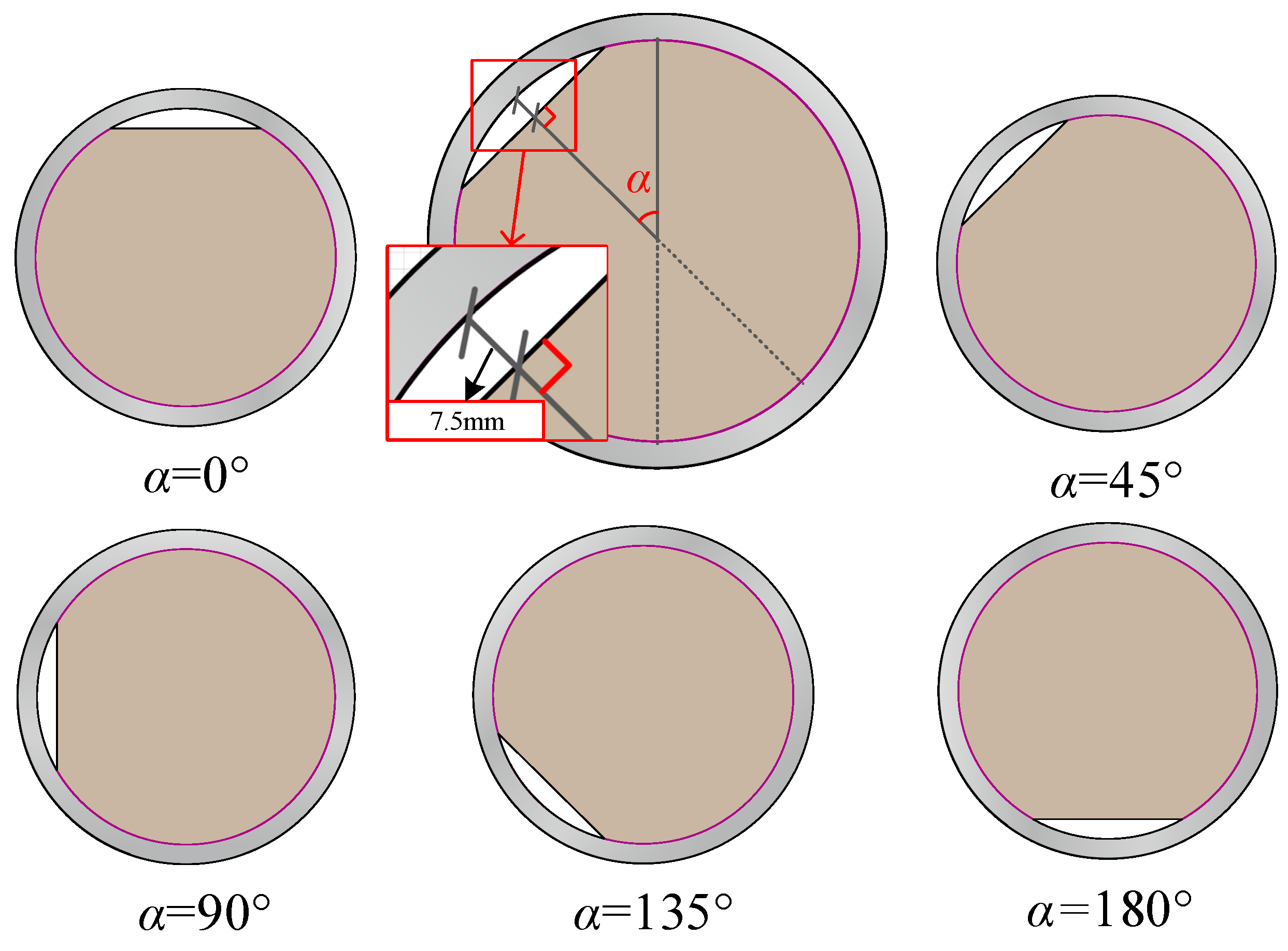
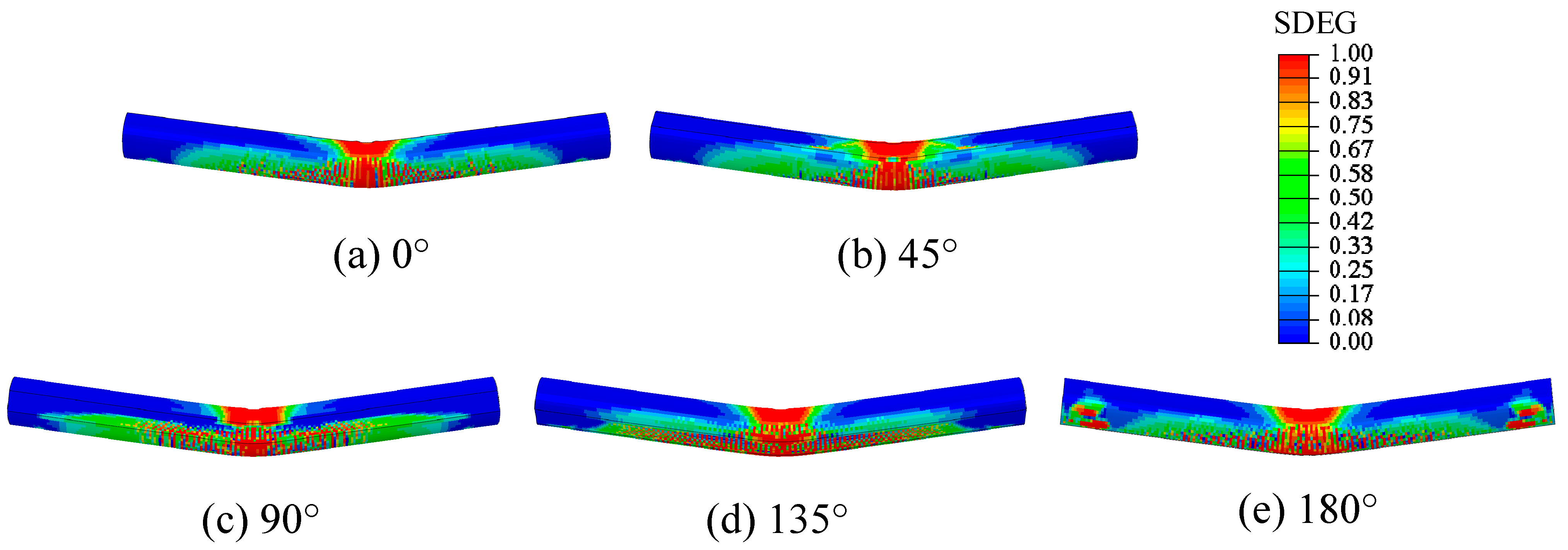
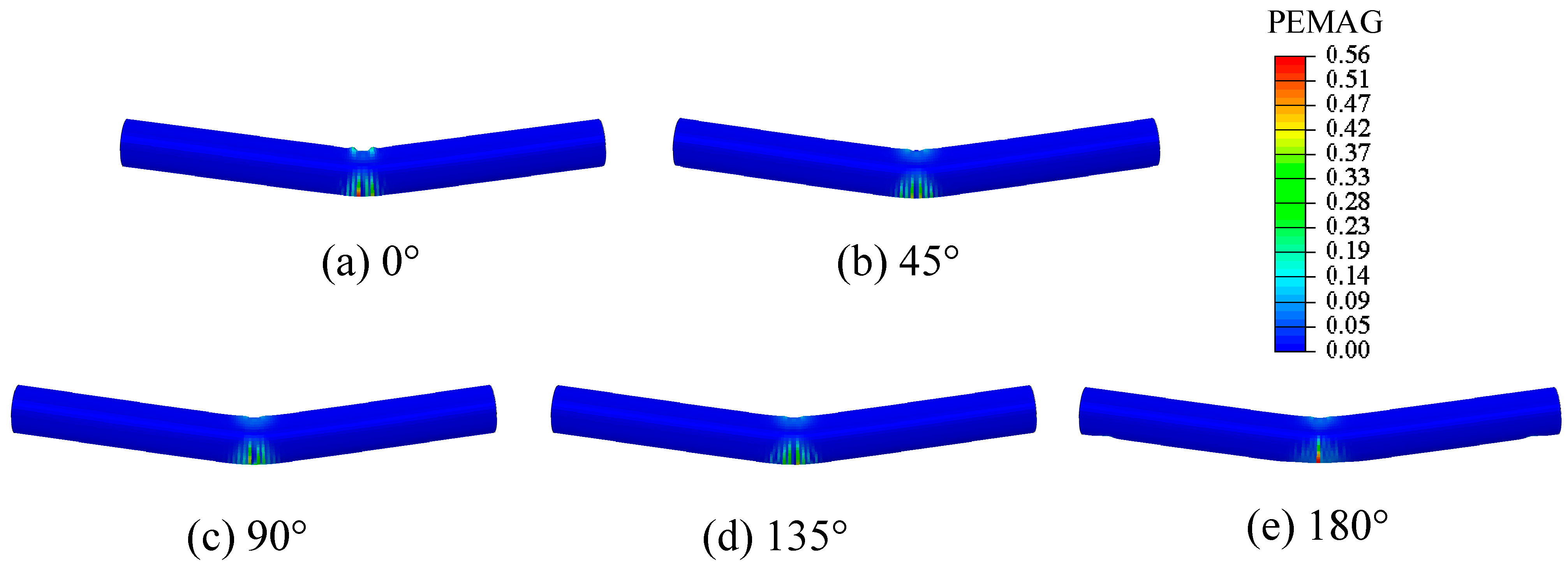
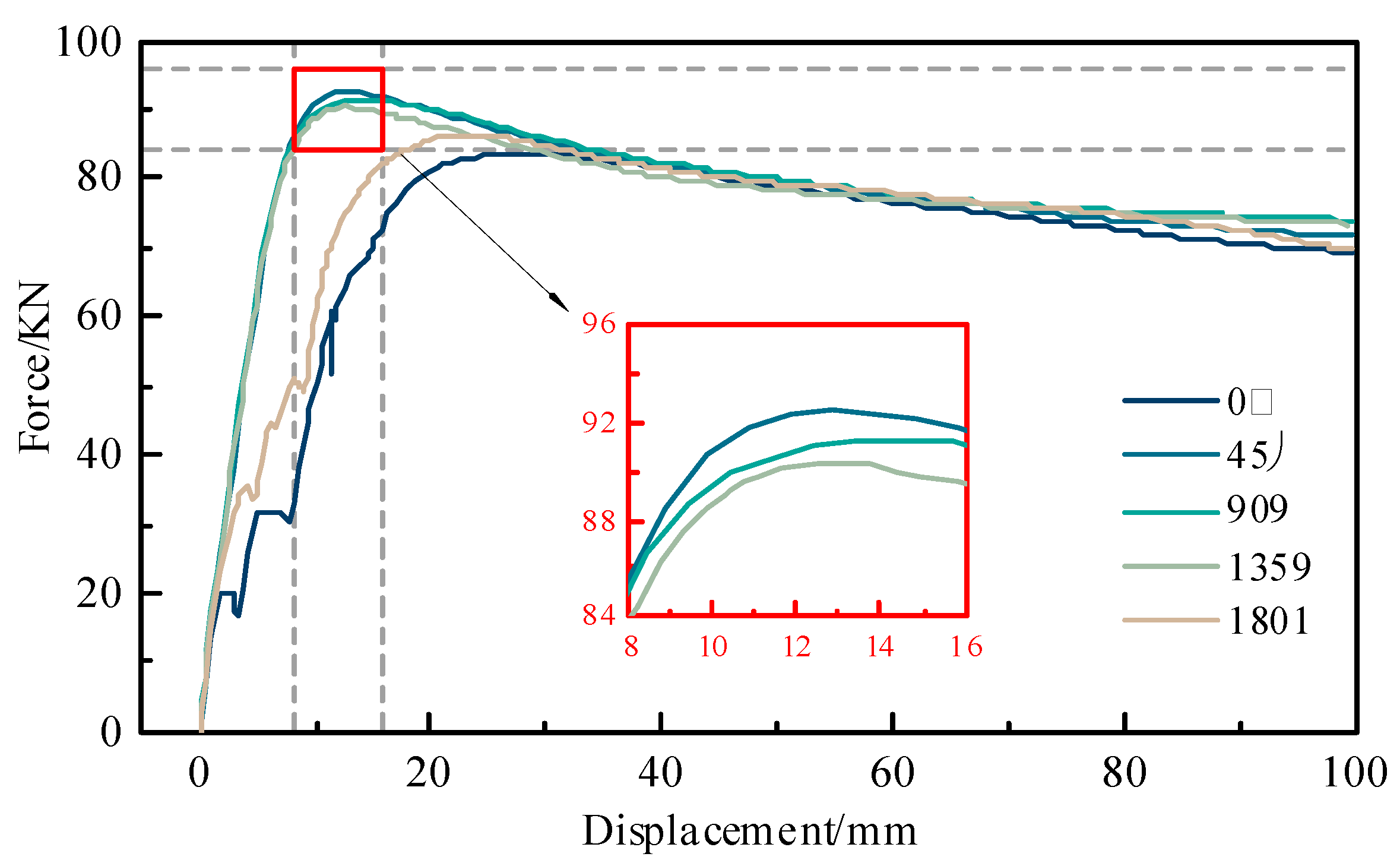
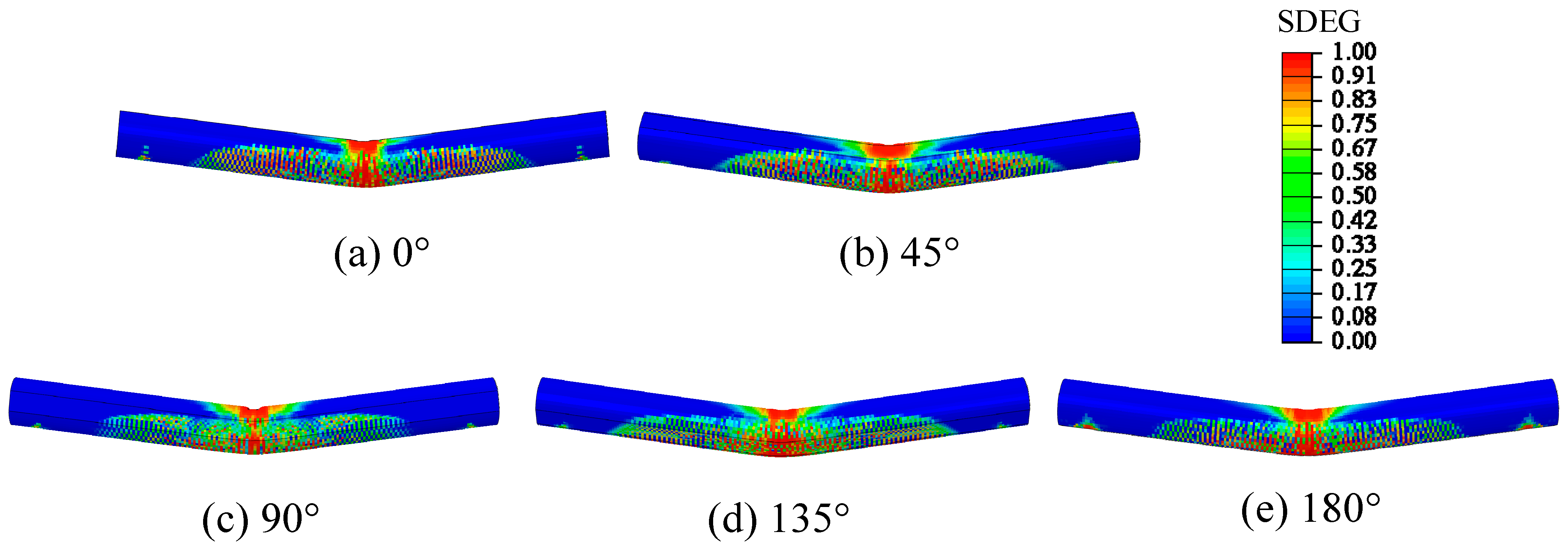
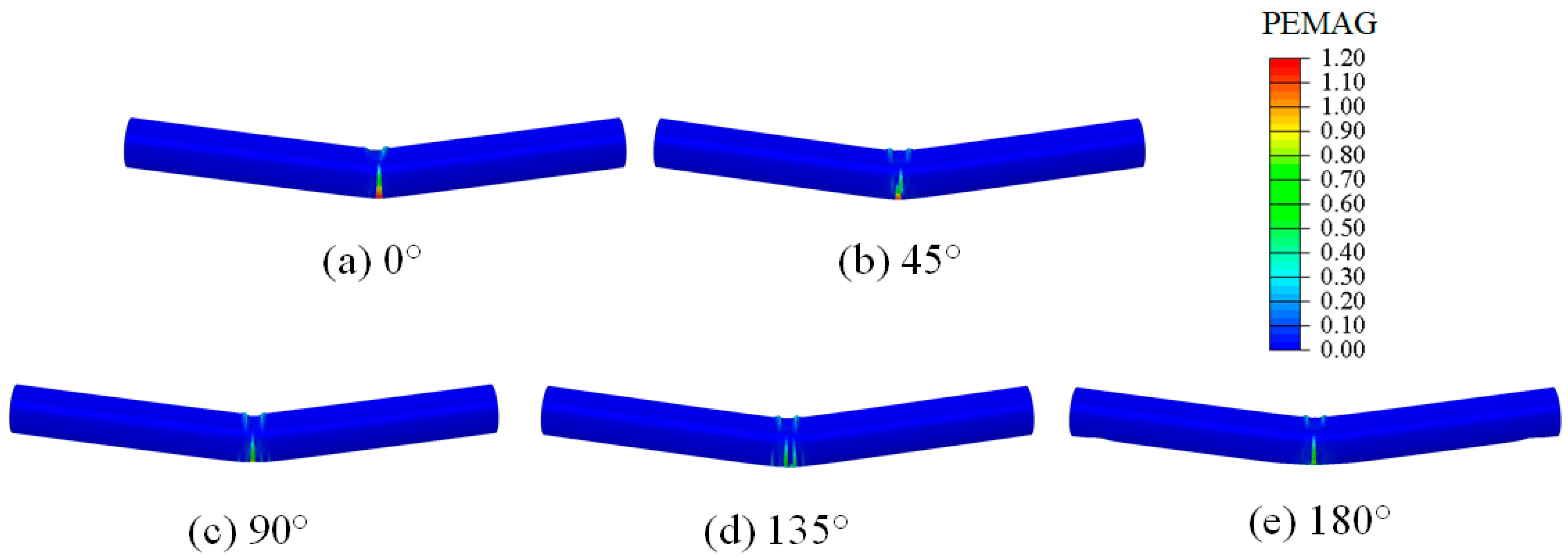
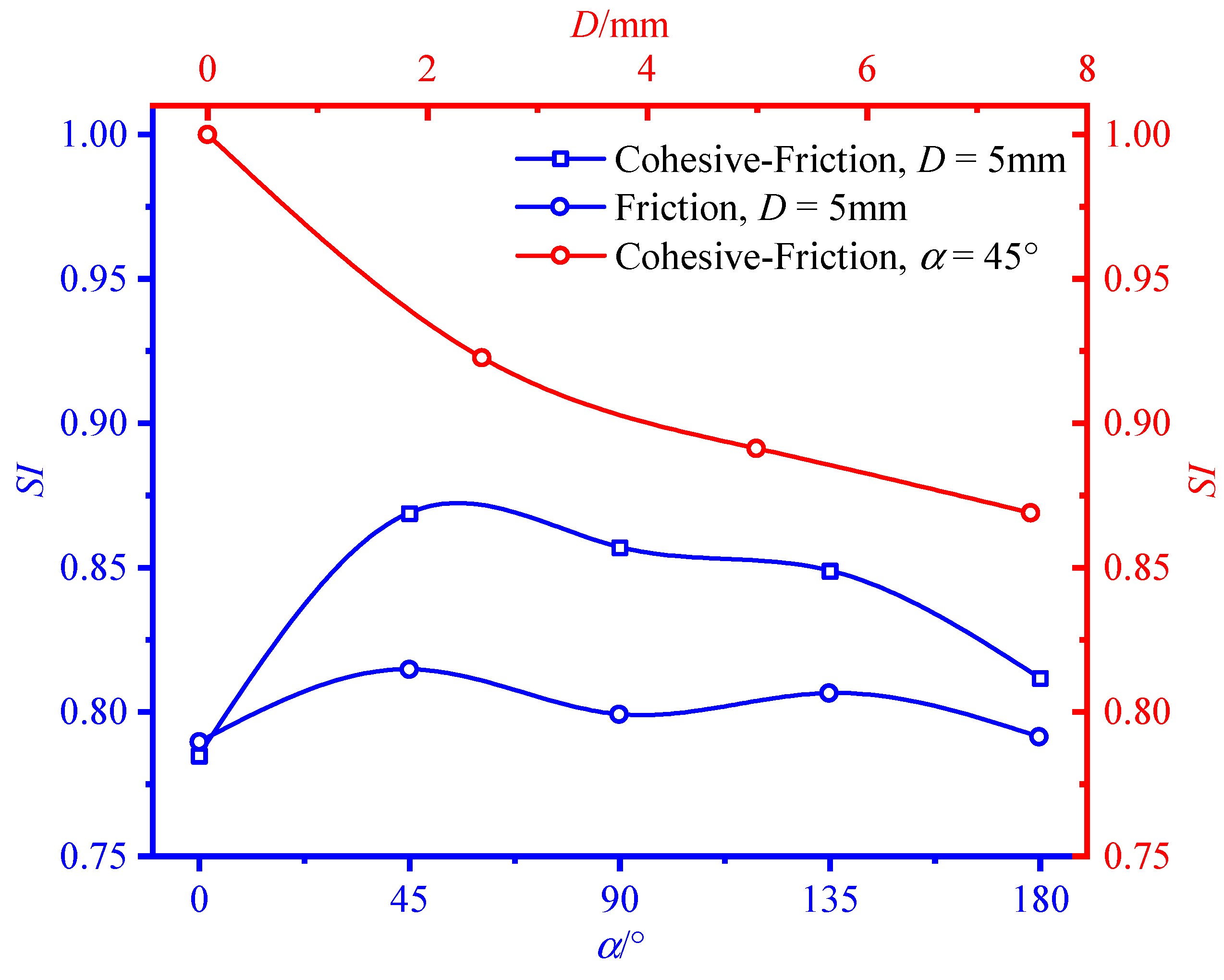
3.2. Effect of the Angle between Loading Direction and Coronal Gap Axis
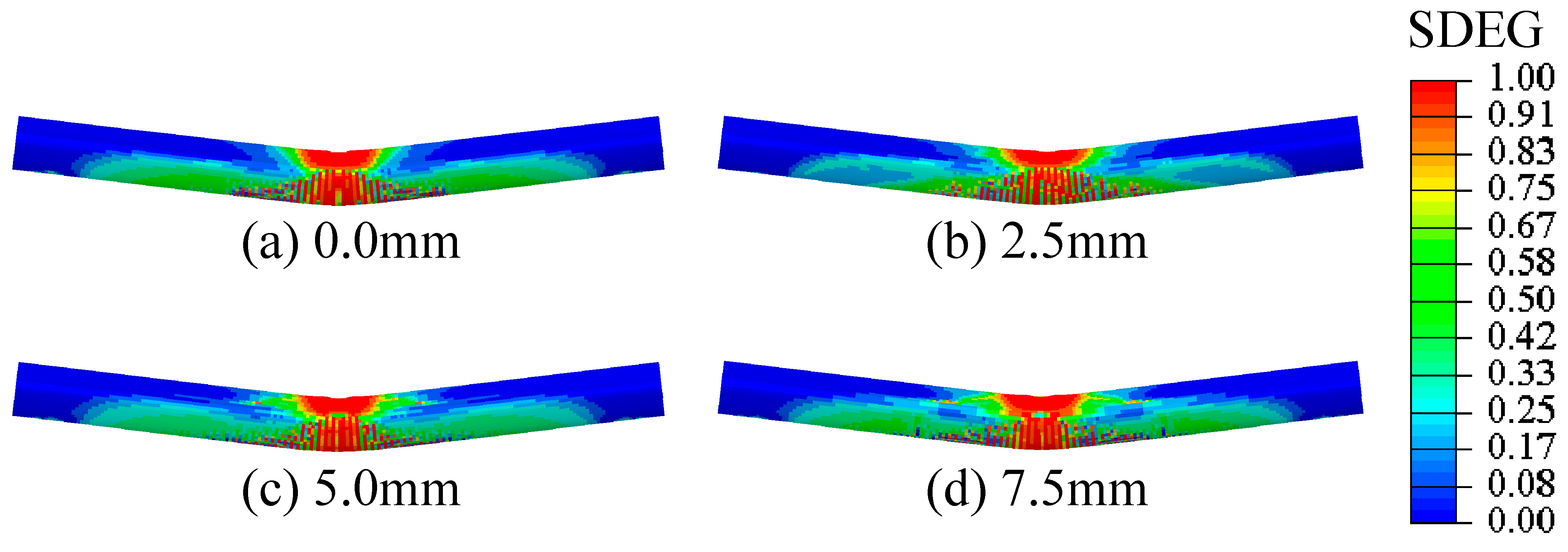
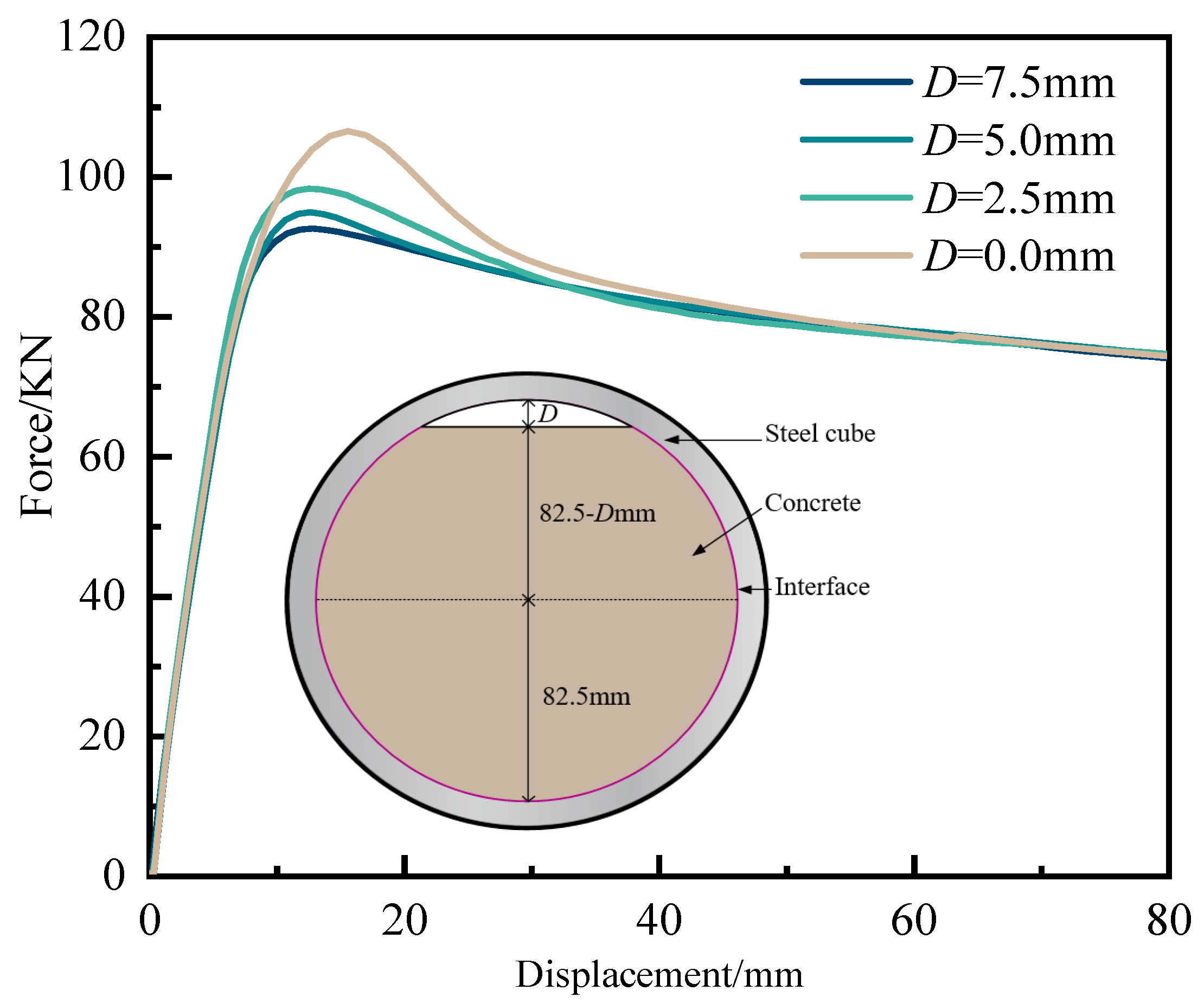
3.3. Effect of the Coronal Gap Height
4. Discussion
5. Conclusions
- (1)
- The improved cohesive interface model can ensure that friction and cohesion peak at the same element deformation. The unified potential function governing the tangential and normal behaviors of an interface can facilitate the mechanical interaction between Mode I and Mode II fractures. Meanwhile, the smooth friction growth function, which was incorporated during the elastic deformation stage, can accurately capture contact pressure and friction force. This approach can also address the issue of excessive invasion between contact surfaces which may lead to incorrect deformation.
- (2)
- By comparing with the classical shear test on the composite masonry structure, we found that the applied model shows the advantage of convenient parameter fitting. Simultaneously, it indicates high accuracy in predicting shear stress and shear displacement. Especially, it is universally applicable under different compressive stress conditions. The predicted shear stress–displacement curves generally fell within the envelope of the experimental data, and the model showed high accuracy in predicting both shear strength and residual strength.
- (3)
- Under three-point bending, when the angle between the loading direction and the coronal gap axis was 0° or 180°, the middle part of the CCFST structure exhibited significantly higher equivalent plastic strains and lower peak bearing forces compared to the other angles. In addition, the CCFST without a mortar interface showed much larger equivalent plastic strains and higher peak bearing forces at the middle part than the CCFST with a mortar interface. In addition, the peak bearing forces decreased as the height of the coronal gap increased from 0.0 mm to 7.5 mm, with the highest forces observed at 0.0 mm and the lowest at 7.5 mm. Given the significant weakening of the structural performance caused by the coronal gap, the SI can be beneficial for the structural design of CCFSTs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, J.L.; Wang, J.J. Concrete-filled steel tube arch bridges in China. Engineering 2018, 4, 143–155. [Google Scholar] [CrossRef]
- Guo, C.; Lu, Z.R. Air void and cap gap composite defects of concrete-filled steel-tube arch bridge transverse brace. J. Perform. Constr. Facil. 2020, 34, 04020073. [Google Scholar] [CrossRef]
- Yu, J.; Gong, B.; Cao, C.; Tang, C. A novel cohesive interlayer model considering friction. Int. J. Solids Struct. 2024, 305, 113049. [Google Scholar] [CrossRef]
- Chen, H.B.; Xu, B.; Zhou, T.M. Multi-scale stress wave simulation for aggregates segregation detection of concrete core in circular CFST coupled with PZT patches. Materials 2018, 11, 1223. [Google Scholar] [CrossRef] [PubMed]
- Liao, F.Y.; Han, L.H.; He, S.H. Behavior of CFST short column and beam with initial concrete imperfection: Experiments. J. Constr. Steel Res. 2011, 67, 1922–1935. [Google Scholar] [CrossRef]
- Rath, S.; Ouchi, M.; Puthipad, N.; Attachaiyawuth, A. Improving the stability of entrained air in self-compacting concrete by optimizing the mix viscosity and air entraining agent dosage. Constr. Build. Mater. 2017, 148, 531–537. [Google Scholar] [CrossRef]
- Liao, F.Y.; Han, L.H.; Zhong, T. Behaviour of CFST stub columns with initial concrete imperfection: Analysis and calculations. Thin-Walled Struct. 2013, 70, 57–69. [Google Scholar] [CrossRef]
- Han, L.H.; An, Y.F. Performance of concrete-encased CFST box stub columns under axial compression. J. Constr. Steel Res. 2014, 93, 62–76. [Google Scholar] [CrossRef]
- Han, L.H.; Ye, Y.; Liao, F.Y. Effects of core concrete initial imperfection on performance of eccentrically loaded CFST columns. J. Struct. Eng. 2016, 142, 04016132. [Google Scholar] [CrossRef]
- Huang, Y.H.; Liu, A.R.; Fu, J.Y.; Pi, Y.L. Experimental investigation of the flexural behavior of CFST trusses with interfacial imperfection. J. Constr. Steel Res. 2017, 137, 52–65. [Google Scholar] [CrossRef]
- Chen, S.; Hou, C.; Zhang, H.; Han, L.H. Structural behaviour and reliability of CFST trusses with random initial imperfections. Thin-Walled Struct. 2019, 143, 106192. [Google Scholar] [CrossRef]
- Huang, Y.H. Mechanism and Effect of Arch Rib Disease and Suspender Replacement for Concrete-Filled Steel Tube Arch Bridges. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2010. [Google Scholar]
- Hola, J.; Sadowski, L.; Schabowicz, K. Nondestructive identification of delaminations in concrete floor toppings with acoustic methods. Autom. Constr. 2011, 20, 799–807. [Google Scholar] [CrossRef]
- Ye, Y.; Li, W.; Liu, X.J.; Guo, Z.X. Behaviour of concrete-filled steel tubes with concrete imperfection under axial tension. Mag. Concr. Res. 2021, 73, 743–756. [Google Scholar] [CrossRef]
- Lu, Z.R.; Guo, C.; Li, G. Air void and ring gap effect on CFST arch bridges dynamic performance. J. Constr. Steel Res. 2020, 177, 106418. [Google Scholar] [CrossRef]
- Zhang, R.L.; Hao, Z.F.; Ma, L.N.; Ning, G.X.; Li, Z.Y.; Gao, F. Influence of defect rate and location of core concrete on the bearing capacity of concrete-filled steel tube. Build. Struct. 2021, 51, 78–84. [Google Scholar] [CrossRef]
- Chao, Z.; Gong, B.; Yue, W.; Xu, X.; Shi, D.; Yang, C.; Hu, T. Experimental study on stress-dependent gas permeability and porosity of artificially cracked cement mortar. Constr. Build. Mater. 2022, 359, 129290. [Google Scholar] [CrossRef]
- Tian, L.M.; Kou, Y.F.; Lin, H.L.; Li, T.J. Interfacial bond-slip behavior between H-shaped steel and engineered cementitious composites (ECCs). Eng. Struct. 2021, 231, 111731. [Google Scholar] [CrossRef]
- Feng, X.; Gong, B.; Liang, Z.; Wang, S.; Tang, C.; Li, H.; Ma, T. Study of the dynamic failure characteristics of anisotropic shales under impact Brazilian splitting. Rock Mech. Rock Eng. 2024, 57, 2213–2230. [Google Scholar] [CrossRef]
- Chen, B.; Gong, B.; Wang, S.; Tang, C. Research on zonal disintegration characteristics and failure mechanisms of deep tunnel in jointed rock mass with strength reduction method. Mathematics 2022, 10, 922. [Google Scholar] [CrossRef]
- Wang, Y.; Gong, B.; Tang, C.; Yang, X. Size effect and lateral pressure effect on the mechanical resistance of columnar jointed basalt. Int. J. Rock Mech. Min. Sci. 2023, 171, 105571. [Google Scholar] [CrossRef]
- Enayatpour, S.; van Oort, E.; Patzek, T. Thermal shale fracturing simulation using the Cohesive Zone Method (CZM). J. Nat. Gas Sci. Eng. 2018, 55, 476–494. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- Haddad, M.; Sepehrnoori, K. XFEM-based CZM for the simulation of 3D multiple-stage hydraulic fracturing in quasi-brittle shale formations. Rock Mech. Rock Eng. 2016, 49, 4731–4748. [Google Scholar] [CrossRef]
- Tvergaard, V. Effect of fiber debonding in a whisker-reinforced metal. Mater. Sci. Eng. A 1990, 125, 203–213. [Google Scholar] [CrossRef]
- Gong, B.; Zhao, T.; Thusyanthan, I.; Tang, C. Modelling rock fracturing by a novel implicit continuous to discontinuous method. Comput. Geotech. 2024, 166, 106035. [Google Scholar] [CrossRef]
- Dehestani, M.; Mousavi, S.S. Modified steel bar model incorporating bond-slip effects for embedded element method. Constr. Build. Mater. 2015, 81, 284–290. [Google Scholar] [CrossRef]
- Jin, L.; Liu, M.J.; Huang, J.Q.; Du, X.L. Mesoscale modelling of bond failure behavior of ribbed steel bar and concrete interface. SCIENTIA SINICA Technol. 2019, 49, 445–454. [Google Scholar] [CrossRef]
- Bolhassani, M.; Hamid, A.A.; Lau, A.C.W.; Moon, F. Simplified micro modeling of partially grouted masonry assemblages. Constr. Build. Mater. 2015, 83, 159–173. [Google Scholar] [CrossRef]
- Zeng, B.; Li, Y.; Noguez, C.C. Modeling and parameter importance investigation for simulating in-plane and out-of-plane behaviors of un-reinforced masonry walls. Eng. Struct. 2021, 248, 113233. [Google Scholar] [CrossRef]
- Sunkpal, M.; Sherizadeh, T. Exploring the deformation mechanics of coal ribs using the distinct element modeling approach. Rock Mech. Rock Eng. 2022, 55, 2879–2898. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, L.; Keer, L.M. Pore pressure cohesive zone modeling of hydraulic fracture in quasi-brittle rocks. Mech. Mater. 2015, 83, 17–29. [Google Scholar] [CrossRef]
- Li, Y.; Deng, J.G.; Liu, W.; Feng, Y. Modeling hydraulic fracture propagation using cohesive zone model equipped with frictional contact capability. Comput. Geotech. 2017, 91, 58–70. [Google Scholar] [CrossRef]
- Li, Y.; Liu, W.; Deng, J.; Yang, Y.; Zhu, H. A 2D explicit numerical scheme-based pore pressure cohesive zone model for simulating hydraulic fracture propagation in naturally fractured formation. Energy Sci. Eng. 2019, 7, 1527–1543. [Google Scholar] [CrossRef]
- Park, K. Potential-Based Fracture Mechanics Using Cohesive Zone and Virtual Internal Bond Modeling. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2009. [Google Scholar]
- Park, K.; Paulino, G.H.; Roesler, J.R. A unified potential-based cohesive model of mixed-mode fracture. J. Mech. Phys. Solids 2009, 57, 891–908. [Google Scholar] [CrossRef]
- Gilormini, P.; Diani, J. Some features of the PPR cohesive-zone model combined with a linear unloading/reloading relationship. Eng. Fract. Mech. 2017, 173, 32–40. [Google Scholar] [CrossRef]
- Oliver, G.L.; Paulino, G.H.; Buttlar, W.G. Fractional calculus derivation of a rate-dependent PPR-based cohesive fracture model: Theory, implementation, and numerical results. Int. J. Fract. 2019, 216, 1–29. [Google Scholar] [CrossRef]
- Yang, J.; Lian, H.; Nugyen, V.P. Study of mixed mode I/II cohesive zone models of different rank coals. Eng. Fract. Mech. 2021, 246, 107611. [Google Scholar] [CrossRef]
- Zhong, Y.; Gao, L.; Cai, X.; An, B.; Zhang, Z.; Lin, J.; Qin, Y. An improved cohesive zone model for interface mixed-mode fractures of railway slab tracks. Appl. Sci. 2021, 11, 456. [Google Scholar] [CrossRef]
- Spring, D.W.; Paulino, G.H. Computational homogenization of the debonding of particle reinforced composites: The role of interphases in interfaces. Comput. Mater. Sci. 2015, 109, 209–224. [Google Scholar] [CrossRef]
- Park, K.; Paulino, G.H. Computational implementation of the PPR potential-based cohesive model in ABAQUS: Educational perspective. Eng. Fract. Mech. 2012, 93, 239–262. [Google Scholar] [CrossRef]
- Spring, D.W.; Paulino, G.H. A growing library of three-dimensional cohesive elements for use in ABAQUS. Eng. Fract. Mech. 2014, 126, 190–216. [Google Scholar] [CrossRef]
- Park, K.; Choi, M.H.; Paulino, G.H. Assessment of cohesive traction-separation relationships in ABAQUS: A comparative study. Mech. Res. Commun. 2016, 78, 71–78. [Google Scholar] [CrossRef]
- Beyer, K.; Abo-El-Ezz, A.; Dazio, A. Quasi-Static Cyclic Tests on Different Types of Masonry Spandrels; Institute of Structural Engineering, Swiss Federal Institute of Technology Zürich: Zürich, Switzerland, 2010; pp. 75–80. [Google Scholar] [CrossRef]
- Beyer, K.; Dazio, A. quasi-static monotonic and cyclic tests on composite spandrels. Earthq. Spectra 2012, 28, 885–906. [Google Scholar] [CrossRef]
- Snozzi, L.; Molinari, J.F. A cohesive element model for mixed mode loading with frictional contact capability. Int. J. Numer. Methods Eng. 2013, 93, 510–526. [Google Scholar] [CrossRef]
- Baek, H.; Park, K. Cohesive Frictional-Contact Model for Dynamic Fracture Simulations under Compression. Int. J. Solids Struct. 2018, 144–145, 86–99. [Google Scholar] [CrossRef]
- Giżejowski, M.; Szczerba, R.; Gajewski, M.; Stachura, Z. Beam-column in-plane resistance based on the concept of equivalent geometric imperfections. Arch. Civ. Eng. 2016, 62, 35–72. [Google Scholar] [CrossRef]
- Ye, F.X.; Zha, X.X.; Wang, H.X. The application of a HHT based ultrasonic detecting method in quality assessment of CFST. Adv. Steel Constr. 2011, 7, 182–191. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modeer, M.; Peterson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture. Cem. Concr. Res. 1976, 6, 773–782. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- American Concrete Institute. Building Code Requirements for Structural Concrete (ACI 318-11) and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 2011. [Google Scholar]
- Papanikolaou, V.K.; Kappos, A.J. Confinement-sensitive plasticity constitutive model for concrete in triaxial compression. Int. J. Solids Struct. 2007, 44, 7021–7048. [Google Scholar] [CrossRef]
- Tao, Z.; Wang, Z.B.; Yu, Q. Finite element modelling of concrete-filled steel stub columns under axial compression. J. Constr. Steel Res. 2013, 89, 121–131. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M. Observed stress-strain behavior of confined concrete. J. Struct. Eng. 1988, 114, 22687. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Kabir, M.I.; Lee, C.K.; Rana, M.M.; Zhang, Y.X. Flexural and bond-slip behaviours of engineered cementitious composites (ECC) encased steel composite beam. J. Constr. Steel Res. 2019, 157, 229–244. [Google Scholar] [CrossRef]
- Dassault Systèmes Abaqus 2016 Online Documentation; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2016; Available online: http://130.149.89.49:2080/v2016/index.html (accessed on 18 December 2017).
- Nasiri, E.; Liu, Y. Development of a detailed 3D FE model for analysis of the in-plane behaviour of masonry infilled concrete frames. Eng. Struct. 2017, 143, 603–616. [Google Scholar] [CrossRef]
- Tao, Z.; Song, T.Y.; Uy, B.; Han, L.H. Bond behavior in concrete-filled steel tubes. J. Constr. Steel Res. 2016, 120, 81–93. [Google Scholar] [CrossRef]
- Wang, Y.F.; Ma, Y.S.; Han, B.; Deng, S.Y. Temperature effect on creep behavior of CFST arch bridges. J. Bridge Eng. 2013, 18, 1397–1405. [Google Scholar] [CrossRef]
- CEN. EN 1994-1-1; Eurocode 4: Design of Composite Steel and Concrete Structures-Part 1.1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004. [CrossRef]



| Parameter | Value |
|---|---|
| Mode I fracture energy, ϕn/MPa∙mm | 0.125 |
| Mode II fracture energy, ϕt/MPa∙mm | 0.45 |
| Normal cohesive strength, σmax/MPa | 0.2295 |
| Tangential cohesive strength, τmax/MPa | 0.2295 |
| Normal initial slope indicator, λn | 0.06 |
| Tangential initial slope indicator, λt | 0.06 |
| Normal shape parameter, α | 5.0 |
| Tangential shape parameter, β | 5.0 |
| Friction shape parameter, s | 1.0 |
| Friction coefficient, μ | 0.77 |
| Parameter | Value |
|---|---|
| Mode I fracture energy, ϕn/MPa∙mm | 0.04 |
| Mode II fracture energy, ϕt/MPa∙mm | 0.4 |
| Normal cohesive strength, σmax/MPa | 0.2 |
| Tangential cohesive strength, τmax/MPa | 1.0 |
| Normal initial slope indicator, λn | 0.25 |
| Tangential initial slope indicator, λt | 0.25 |
| Normal shape parameter, α | 5.0 |
| Tangential shape parameter, β | 5.0 |
| Friction shape parameter, s | 4.0 |
| Friction Coefficient, μ | 0.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Gong, B.; Cao, C. Research on the Gap Effect of Circular Concrete-Filled Steel Tubes Using the Improved Cohesive Zone Model. Appl. Sci. 2024, 14, 8361. https://doi.org/10.3390/app14188361
Yu J, Gong B, Cao C. Research on the Gap Effect of Circular Concrete-Filled Steel Tubes Using the Improved Cohesive Zone Model. Applied Sciences. 2024; 14(18):8361. https://doi.org/10.3390/app14188361
Chicago/Turabian StyleYu, Jiang, Bin Gong, and Chenrui Cao. 2024. "Research on the Gap Effect of Circular Concrete-Filled Steel Tubes Using the Improved Cohesive Zone Model" Applied Sciences 14, no. 18: 8361. https://doi.org/10.3390/app14188361
APA StyleYu, J., Gong, B., & Cao, C. (2024). Research on the Gap Effect of Circular Concrete-Filled Steel Tubes Using the Improved Cohesive Zone Model. Applied Sciences, 14(18), 8361. https://doi.org/10.3390/app14188361







