Abstract
Parkinson’s disease (PD) is a neurodegenerative disorder marked by motor and cognitive impairments. The early prediction of cognitive deterioration in PD is crucial. This work aims to predict the change in the Montreal Cognitive Assessment (MoCA) at years 4 and 5 from baseline in the Parkinson’s Progression Markers Initiative database. The predictors included demographic and clinical variables: motor and non-motor symptoms from the baseline visit and change scores from baseline to the first-year follow-up. Various regression models were compared, and SHAP (SHapley Additive exPlanations) values were used to assess domain importance, while model coefficients evaluated variable importance. The LASSOLARS algorithm outperforms other models, achieving lowest the MAE, and , for the fourth- and fifth-year predictions, respectively. Moreover, when trained to predict the average MoCA score change across both time points, its performance improved, reducing its MAE by 19%. Baseline MoCA scores and MoCA deterioration over the first-year were the most influential predictors of PD (highest model coefficients). However, the cumulative effect of other cognitive variables also contributed significantly. This study demonstrates that mid-term cognitive deterioration in PD can be accurately predicted from patients’ baseline cognitive performance and short-term cognitive deterioration, along with a few easily measurable clinical measurements.
1. Introduction
Artificial Intelligence (AI) and machine learning (ML) have revolutionized various sectors, including healthcare, by enabling the analysis of large datasets. Recent studies [1] highlight the transformative impact of big data and AI on healthcare, emphasizing the potential of AI to improve the diagnosis, treatment, and management of diseases through the intelligent analysis of complex datasets.
Parkinson’s disease (PD) is a progressive neurodegenerative disorder characterized by a loss of dopaminergic neurons in the substantia nigra. The cardinal motor symptoms for a PD diagnosis include tremor, rigidity, and bradykinesia [2]. However, cognitive impairment is a common and disabling feature of PD, affecting up to 70% of patients within 10 years of their diagnosis [3]. Some PD patients are more susceptible to an early onset of dementia, but the current lack of clinically validated biomarkers hinders an accurate prognostication of the rate of cognitive decline [4]. Given the substantial impact of PD-associated dementia on independence, caregiver burden, and mortality, there is growing interest in identifying individuals with early-stage PD who are at higher risk of rapid cognitive decline to facilitate intervention studies.
The Montreal Cognitive Assessment (MoCA) test is a widely used screening tool for determining cognitive impairment in PD. It is a brief cognitive assessment that measures multiple cognitive domains, including attention, memory, language, and visuospatial skills. The MoCA has been shown to have high sensitivity and specificity for detecting cognitive impairment in PD [5].
Focusing on PD, ML techniques have advanced significantly in recent years and show promise for predicting cognitive decline over time. Previous studies using ML methods have developed accurate prediction models with high degrees of accuracy, sensitivity, and specificity for mild cognitive impairment and dementia in de novo PD patients, suggesting that ML techniques may have a significant potential to predict cognitive outcomes [6,7]. However, these models relied on the discretization of cognitive outcomes, single-time-point data, and complex multi-modal data, which pose challenges for their scalability in clinical settings (see Section 2 for more information).
In this study, our objective was to predict mid-term cognitive outcomes in early PD patients from the Parkinson’s Progression Markers Initiative (PPMI) [8] cohort using multiple ML methods. To achieve this, we evaluated the effectiveness of several easily measurable demographic and clinical variables at anticipating changes in MoCA scores over the 4 to 5 years following the baseline visit. We relied on baseline and 1-year changes in demographic, cognitive, olfactory, autonomic, neuropsychiatric, sleep disorder, and motor symptoms as predictor variables. Additionally, we assessed the contribution of each category of variable to the prediction, enhancing the model’s transparency and explicability for clinical stakeholders. The implications of this study are significant, as they provide a foundation for identifying patients with early PD who are at higher risk for cognitive decline, enabling timely interventions and better patient management.
The remainder of the paper is structured as follows: in Section 2, we explain open research challenges and how they are addressed in this study. In Section 3, we describe the database, data pre-processing, ML methods, and evaluation metrics used in the experiments. In Section 4, we present the results of the experiments. In Section 5, we compare our findings with those of other studies and discuss the limitations of our work. Finally, in Section 6, we offer some concluding remarks.
2. Related Works
Several studies have addressed the problem of ML for the prediction of cognitive deterioration in patients with early PD. One of the main databases in the field is PPMI, which contains a cohort of recently diagnosed PD participants. This PD cohort is comprised of several subgroups, which include idiopathic PD participants and several genetic PD participants. Idiopathic means that a disease has no identifiable cause; therefore, its evolution is less predictable because there are no defined phenotypes. However, none of the studies specify having selected this subgroup.
In the study by Harvey et al. (2022) [9], a multivariate ML model was developed to predict cognitive impairment and dementia conversion using clinical, biofluid, and genetic/epigenetic measures taken from baseline. The researchers found that clinical variables alone performed best, with only marginal improvements seen when additional data types were included. This indicates that while the inclusion of multi-modal data can enhance prediction, clinical measures remain crucial for accurate forecasts.
Similarly, Gorji and Jouzdani (2024) [10] compared the effectiveness of different cognitive scales, specifically the Montreal Cognitive Assessment (MoCA) and the Movement Disorder Society-Unified Parkinson’s Disease Rating Scale (MDS-UPDRS-I), combined with DAT SPECT imaging and clinical biomarkers in predicting cognitive decline over five years. Their findings revealed that the MoCA was the more effective predictor. Additionally, the incorporation of deep radiomic features from DAT SPECT significantly improved its predictive performance, highlighting the importance of advanced imaging techniques in enhancing the accuracy of predictions.
The research conducted by Salmanpour et al. (2019) [11] focused on optimizing feature selection and machine learning algorithms to predict MoCA scores in PD patients. By using robust predictor algorithms and feature subset selection, they achieved high predictive accuracy with a minimal set of features. This study underscores the importance of feature selection, showing that effective prediction can be accomplished with fewer, well-chosen variables.
Hosseinzadeh et al. (2023) [12] combined handcrafted radiomics, deep features from DAT SPECT, and clinical features to predict cognitive outcomes in PD patients. They found that clinical features were vital for prediction, and the combination of these with imaging features yielded the highest accuracy. This demonstrates the critical role of integrating multi-modal data, but also points to the necessity of identifying which features contribute most to predictive performance.
Almgren et al. (2023) [13] developed a multimodal ML model to predict continuous cognitive decline using clinical test scores, cerebrospinal fluid (CSF) biomarkers, brain volumes from T1-weighted MRI, and genetic variants. The best-performing model combined clinical and CSF biomarkers, suggesting that Alzheimer’s disease-related pathology significantly contributes to cognitive decline in PD. This study highlights the importance of considering biomarkers associated with other neurodegenerative diseases in predicting cognitive outcomes in PD.
Ostertag et al. (2023) [14] approached the prediction of long-term cognitive decline through a Deep Neural Network with transfer learning from Alzheimer’s disease to PD. This model used brain MRI and clinical data, demonstrating that knowledge transfer between neurodegenerative diseases is feasible and can improve prediction in PD. Their results showed that leveraging models pre-trained on related diseases could yield significant predictive power, even when direct data on the target disease are limited.
Despite these advancements, challenges remain. Current studies primarily focus on categorizing PD patients into distinct groups based on their cognitive outcomes. This discrete approach overlooks the continuous nature of cognitive decline, which varies significantly among individuals. There is a need for models that capture these continuous changes, providing a more nuanced understanding of cognitive decline and enabling more tailored and timely interventions.
Furthermore, many studies use a wide range of predictors from different modalities to enhance predictive accuracy. While this approach can improve the precision of predictions, it may hinder the translation of these models into primary care settings due to limited resources and time constraints. Simplifying predictive models to include a small number of easily measurable and objective predictor variables is crucial. This will facilitate the application of these models in primary care settings, ensuring their broader accessibility and utility.
3. Materials and Methods
3.1. Database
The PPMI is a large scale observational study launched in 2010 to identify the biomarkers of PD progression. The PPMI is a collaborative effort between academic institutions, industry partners, and patient advocacy groups, providing valuable insights into the early stages of PD and the potential biomarkers of disease progression. The database is an open access dataset. Data used in the preparation of this manuscript were obtained from the PPMI database (www.ppmi-info.org/data, accessed on 1 August 2024). Study protocol and manuals are available at www.ppmi-info.org/study-design, accessed on 1 August 2024. The data used for this paper were downloaded on December 2021.
We selected demographic variables and motor and non-motor test variables from this database (these are described in Appendix A). Additionally, the MoCA test (adjusted for education) was used. The data used are detailed in Table 1. For our analysis, we employed baseline data (BL) and the deterioration between baseline and first-year measurements (Y1) of motor, sleep, autonomic, cognitive, and neuropsychiatric variables. These variables were transformed to indicate severity (the higher the value, the greater the severity). For the prediction target, we calculated the deterioration of the total MoCA score from BL to year 4 and 5. At year 4, the overall deterioration rate is 44%, with 17% of subjects having a cognitive impairment of at least three MoCA points. At year 5, over 41% of the subjects exhibited some level of deterioration, and almost 20% had a MoCA change of at least three points.

Table 1.
Demographics and clinical characteristics of PD patients.
The PPMI database contains 693 patients with PD, 395 of whom have idiopathic PD. The database was cleaned based on various criteria to ensure the reliability and accuracy of the predictive models. Firstly, only tests performed within a maximum of 6 months from baseline were considered, resulting in the removal of two patients. This was done to ensure the data were collected during the same patient phase, as some tests were performed during the screening phase rather than at baseline. Secondly, for the first-year data, only tests performed within a maximum of 3 months were considered, minimizing variability in the timing of the assessments and leading to the exclusion of 51 patients. Thirdly, patients with missing values in year 4 or 5 for the MoCA variable were removed, resulting in the exclusion of 82 patients. This was necessary to ensure complete data for reliable model training and testing. Finally, the coherence in cognitive status between their MoCA score and an expert medical diagnosis (based on the COGSTATE variable of the database) was assessed. Specifically, five subjects with a MoCA score lower than 21 points (indicating dementia according to the JC Dalrymple-Alford et al. study [15]) but normal expert medical perception were removed, as well as two subjects with no medical perception. These exclusions were made to maintain consistency and accuracy in the cognitive status data used for analysis. After applying these exclusion criteria, the study involved 253 subjects. A summary of the subject selection process can be seen in Figure 1.
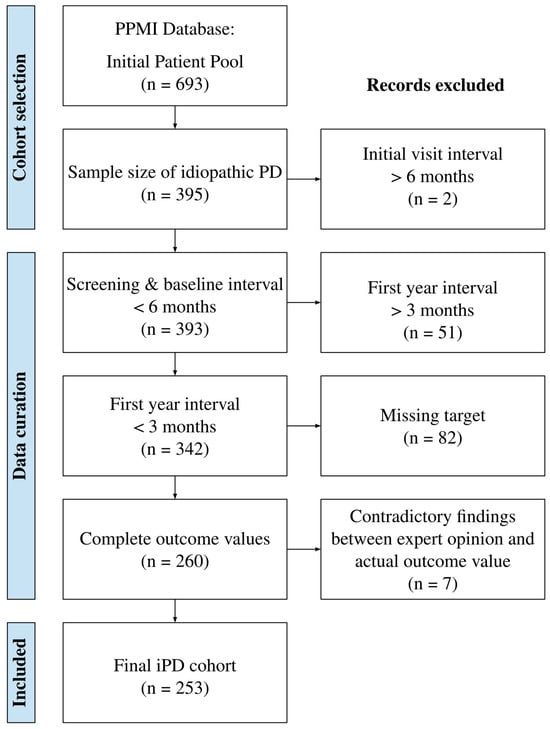
Figure 1.
The database was cleaned according to several criteria: non-idiopathic cases, tests from the same visit performed over an extended interval, a missing value in the prediction target, and cognitive perceptions that were contradictory to an expert’s clinical assessment.
3.2. Pre-Processing
To pre-process the data, we implemented a sophisticated missing value imputation method that uses the patient’s evolution over time to estimate their progression slope. Initially, minimal missing data were observed across the various categories: 1 out of 10 demographic variables, 9 out of 19 baseline variables, and 7 out of 19 first-year variables (used to calculate the Y1 variables), with each missing no more than 0.07% of their data.
For the imputation process, we leveraged the longitudinal nature of our data, using the patients’ progression over time to estimate changes. For example, to impute a missing baseline variable, we considered the patient’s data from subsequent years (year 1 to year 5). For missing first-year variables, we considered the data from the baseline and subsequent years (year 2 to year 5). We calculated the intercept and slope using linear regression on the available data points, and then used these values for imputation.
In cases where a slope could not be established due to insufficient data points (fewer than two), we employed an alternative method involving the mean slope of the five nearest neighbors. This scenario occurred in three instances involving first-year variables. To identify the closest five neighbors, the data were scaled and the distances between points calculated using Euclidean distances. We then averaged the slopes derived from these neighbors, using their data from baseline to year 5. To impute the missing first-year variable, we added the average slope, derived from the nearest neighbors, to the baseline value.
For categorical variables, missing values were imputed by calculating the mode of the variable at that specific time point. This method ensures that our imputation strategy remains consistent and grounded in the underlying data distribution.
Additionally, numerical variables were standardized, and one-hot encoding was applied to categorical variables to bring all the data into the same space.
3.3. Experimental Setup
Five supervised regression algorithms were trained using a two-level stratified 10-fold cross-validation approach. In this setup, the outer 10-fold cross-validation (outer-CV) was employed to evaluate the models, ensuring an unbiased estimation of their performance. For hyperparameter tuning, we implemented a nested, stratified 10-fold cross-validation (inner-CV) within each training fold of the outer-CV. This inner-CV was exclusively used for tuning the hyperparameters, ensuring that the tuning process was isolated from the test data (see Appendix B for more information).
The algorithms used were a linear regression (LR), decision tree (DT), Support Vector Machine (SVM), Least Absolute Shrinkage and Selection Operator with Least Angle Regression (LASSOLARS), and Random Forest (RF). These algorithms were selected to cover a diverse range of modeling techniques, from linear models (LR) to more complex, non-linear models (DT, SVM, RF) and regularized regression methods (LASSOLARS). All these algorithms were implemented using the Python 3.8.10. programming language and the versatile scikit-learn library. A random seed of 0 was used for consistency across the algorithms. To validate the algorithms, as in the work by Salmanpour et al. (2019) [11], we calculated the mean absolute error (MAE) metric between the predicted and actual values.
It is important to include a feature importance analysis to identify which features are most predictive of cognitive deterioration. For this purpose, we used the SHapley Additive exPlanations (SHAP) algorithm (see Appendix C). The advantage of this algorithm is that it allows for the analysis of the importance of groups of variables, categorized according to their domain (as defined in Table 1).
4. Results
The five algorithms were trained to predict the cognitive deterioration (based on the changing score of the MoCA test) of each patient in their fourth and fifth year post diagnosis, using demographic and clinical variables. These algorithms were trained using baseline variables (BL), the deterioration of variables from the baseline to first year (Y1), or a combination of both (BL + Y1).
The results are presented in Figure 2. In total, 30 variables were used for BL and Y1, while 49 variables were used for BL + Y1. In all three cases, the 10 demographic variables and the olfactory variable were common. Overall, the BL + Y1 combination with the LASSOLARS algorithm consistently outperformed the other models, producing the lowest MAEs of and for the fourth- and fifth-year predictions, respectively. Despite having twice as much clinical information, the improvement obtained using BL + Y1 was not significantly large. Additionally, some inconsistencies were observed in the results. While the Y1 data appeared to be more informative than the BL data, with a lower error for the fourth-year prediction of cognitive deterioration (Figure 2a), the opposite was observed for the fifth-year MoCA change prediction (Figure 2b).
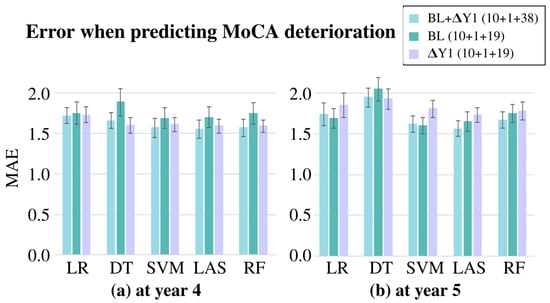
Figure 2.
Mean absolute error (MAE) generated when predicting cognitive deterioration (a) at year 4 and (b) at year 5. The bars represent the mean of the 10 folds, while the lines indicate the standard deviation. The MAE values are estimated using the 5 algorithms and the clinical variables at baseline (BL), the deterioration of the clinical variables from baseline to the first year (Y1), and a combination of both (BL + Y1). The number of predictors used in each analysis is shown in parentheses. Abbreviations: LR = linear regression, DT = decision tree, SVM = Support Vector Machine, LAS = Least Absolute Shrinkage and Selection Operator with Least Angle Regression, RF = Random Forest.
We further analyzed the LASSOLARS algorithm with BL + Y1, as it provided the best results. Figure 3 shows the relationship between the predicted and the actual values. Figure 4 presents a feature importance analysis: part (a) displays the importance of the domains using SHAP values, excluding the MoCA variable from the cognitive domain. The clinical variables at the baseline and their first-year change are grouped accordingly; part (b) extends this view to the importance of the variables through the LASSOLARS coefficients, focusing on those with a mean coefficient greater than 0.1 in any year. The race variable is omitted due to its highly imbalanced distribution and minimal impact on the study’s cases.
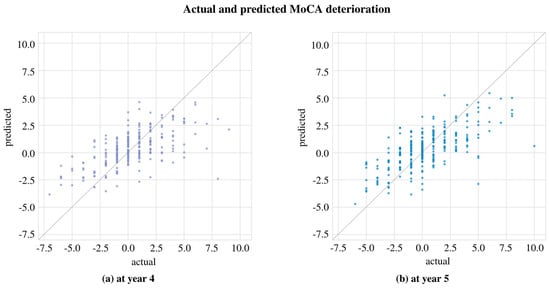
Figure 3.
Relation between predicted and actual cognitive deterioration (a) at year 4 and (b) at year 5. The predictions were obtained from the LASSOLARS model trained with baseline and first-year change data.
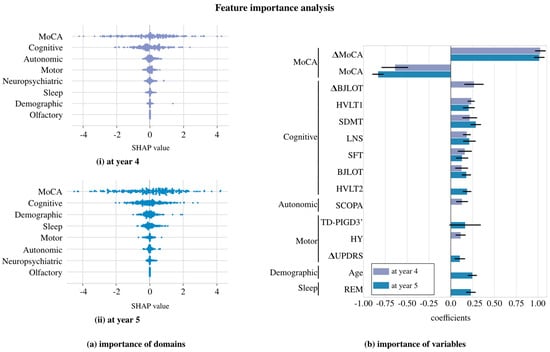
Figure 4.
Feature importance analysis of the LASSOLARS model for predicting cognitive deterioration at year 4 and year 5. (a) Importance of domains: SHAP values are presented, with the domains ordered from the most to least important in predicting deterioration. (b) Importance of variables: This graph displays the coefficients of the most significant variables in the LASSOLARS model. The bars represent the mean of the 10 folds, while the black lines indicate the standard deviation. indicates that this is the first-year change, while all the others are baseline values. Variables are sorted based on their importance in year 4, considering both the domain order established by the SHAP algorithm and the variable order. Abbreviations: HVLT1 = Hopkins Verbal Learning Test-Revised immediate/total recall, HVLT2 = Hopkins Verbal Learning Test-Revised discrimination recognition, TD-PIGD3’ = indeterminate at year 1 in TD-PIGD classification; see the rest in Table 1.
From Figure 4, it is evident that the early MoCA score is the most informative, followed by the cognitive group. The high positive coefficient of MoCA suggests that MoCA deterioration in the first year is a clear indicator of further deterioration in subsequent years. Conversely, the negative coefficient of MoCA indicated that a greater deterioration is probable if the patient shows a high MoCA score at baseline. Interestingly, the olfactory group (UPSIT) appears to be the least informative across both years. However, the importance of the remaining tests is not consistent. For example, when predicting the deterioration at year 4, the first-year change in the BJLOT test and the baseline values of the SCOPA-AUT and HY tests are relevant, but they are not when predicting the deterioration at year 5.
Given the inconsistencies in the variables used for predicting MoCA changes in years 4 and 5, likely due to the intrinsic variability in the test, we trained the LASSOLARS model to predict the mean MoCA deterioration over years 4 and 5 as a surrogate for mid-term cognitive decline. As a result, we achieved a 19% improvement in its MAE (see Table 2).

Table 2.
Mean absolute error (MAE) of the three prediction targets using the LASSOLARS algorithm trained with baseline and first-year change data.
Figure 5 shows the results of this approach. Figure 5a demonstrates that the predictions are closer to the diagonal compared to Figure 3, where individual year 4 and year 5 scores were predicted. In Figure 5b, the SHAP diagram confirms the conclusions obtained from previous steps: the cognitive domain remains the most important, with the MoCA variable providing the most information, while the olfactory domain is the least informative. Finally, Figure 5c shows the order of the most relevant variables. Among the cognitive variables, in addition to the two MoCA variables, the SDMT, HVLT-R immediate/total recall, and LNS at baseline stand out. These tests assess specific domains of cognition.
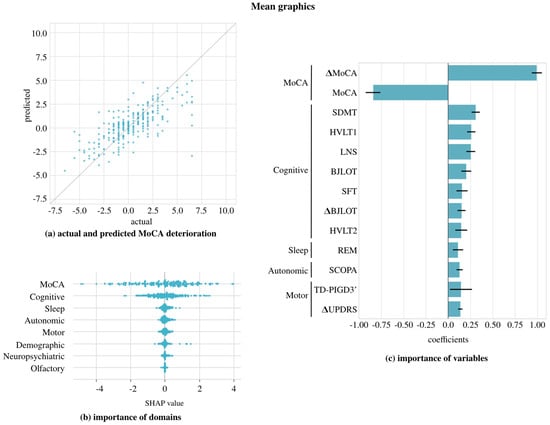
Figure 5.
Mid-term cognitive deterioration (mean between year 4 and year 5) predicted with the LASSOLARS model. Figure (a): the relation between predicted and actual values; Figure (b): the importance of domain by SHAP value; and Figure (c): the most relevant variables ( indicates the first-year change and all the others are baseline values). Abbreviations: HVLT1 = Hopkins Verbal Learning Test-Revised immediate/total recall, HVLT2 = Hopkins Verbal Learning Test-Revised discrimination recognition, TD-PIGD3’ = indeterminate at year 1 in TD-PIGD classification; see the rest in Table 1.
To further analyze how the information provided by different variables differs across years, Figure 6 represents the most relevant variables, ordered by their coefficient, for each of the prediction targets analyzed. Year 4 appears on the left-hand side, year 5 on the right-hand side, and the mean in the middle. Lines connect the same variable between year 4 and the mean, and between year 5 and the mean, with different colors corresponding to different domains. Dashed lines indicate that the corresponding variable is significant in only two of the three target predictions. According to the figure, the MoCA variables are consistently the most important across all prediction targets, with little change between them. Additionally, when variables are relevant for predicting both years 4 and 5, their relevance tends to increase when the target is the mean. Conversely, when a variable is only relevant in two of the three years, its relevance appears to decrease when predicting the mean target.
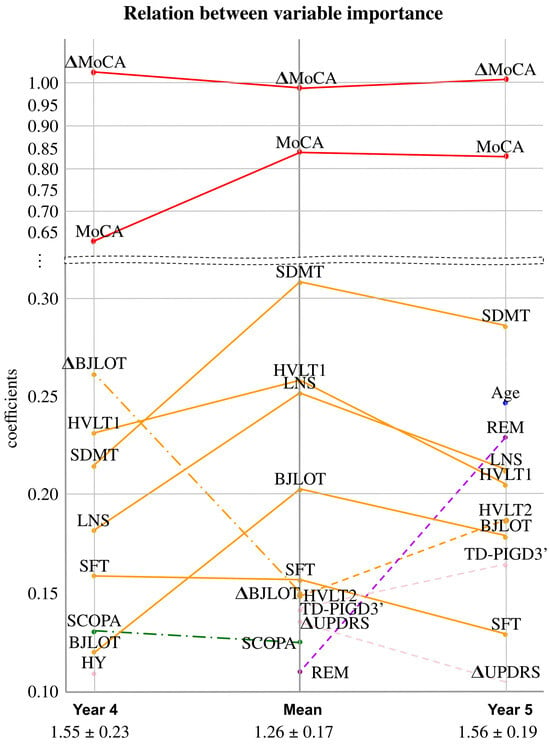
Figure 6.
Relation between the LASSOLARS coefficients used for predicting MoCA deterioration at different time points. The graph is divided into two sections, with the lower section providing a zoomed-in view. Variables with a symbol represent changes in the first year, while those without it represent baseline values. At the bottom of the graph, the mean absolute error (mean ± standard deviation) is displayed. Abbreviations: HVLT1 = Hopkins Verbal Learning Test-Revised immediate/total recall, HVLT2 = Hopkins Verbal Learning Test-Revised discrimination recognition, TD-PIGD3’ = indeterminate at year 1 in TD-PIGD classification; see the rest in Table 1.
5. Discussion
In this study, we used ML techniques to predict mid-term cognitive outcomes in early PD patients, using demographic and clinical variables from the early stages of PD as predictors. We tested several algorithms and selected LASSOLARS, which performed the best based on the MAE metric.
Predicting cognitive decline is of the utmost importance in PD research. While the diagnosis of PD is primarily based on motor symptoms, cognitive impairment is increasingly recognized as a common and often debilitating non-motor symptom of the disease [2]. In fact, up to 70% of PD patients will develop cognitive impairment over the course of the disease [3]. Given that the severity and pattern of cognitive impairment in PD can vary widely between individuals [4], identifying patients at greater risk of cognitive decline is crucial for optimizing patient care and patient stratification for clinical trials.
According to our results, the baseline global cognition (baseline MoCA score) and cognitive decline (MoCA deterioration) after one year were the most determinant factors for predicting mid-term cognitive scores. This aligns with a previous study that found baseline MoCA scores to be highly associated with cognitive profiles at 8 years on in the PPMI cohort [9]. To better understand how different factors collectively influence cognitive deterioration, we conducted a deeper analysis of the relative importance of these variables compared to other clinical variables. Using SHAP values and LASSOLARS coefficients, we assessed the importance of various predictors.
In addition to the baseline MoCA score and one-year MoCA deterioration, other cognitive variables were also relevant for the final prediction. However, the models for year 4 and year 5 did not completely agree on their importance. This inconsistency may be attributed to two reasons: the similar importance of different domains and the potential overfitting of the models to noisy variations in the prediction targets. Indeed, obtaining reliable measurements of cognition for constructing models is challenging due to the inherent noise present in clinical tests. Averaging cognitive scores from multiple time points can help mitigate this issue. In our study, we found that averaging the MoCA scores from years 4 and 5 resulted in lower MAE values than using individual time points. This approach resolves the inconsistencies found in the models fitted to year 4 and 5, reinforcing the importance of the predictors selected by both models—the baseline values of SDMT, HVLT immediate/total recall, LNS, BJLOT, and SFT—and including variables with lower importance levels that were selected by only one of the models—the baseline values of HVLT discrimination recognition, SCOPA, and REM and 1-year deterioration of BJLOT and MDS-UPDRS total.
Several previous studies have attempted to predict cognitive outcomes in PD using ML algorithms [6,7,11]. However, the prevailing trend in the field is to categorize PD patients into distinct groups based on their cognitive outcomes, overlooking the continuous nature of cognitive changes among patients. For instance, Gramotnev et al. (2019) [6] categorized MoCA score changes into severe and mild-to-moderate cognitive impairment, while Nguyen et al. (2020) [7] established a cutoff score of 26/27 for MoCA, creating two categories: normal cognition and mild cognitive impairment (MCI). The use of different criteria for categorizing MoCA scores makes it challenging to compare results across studies. Furthermore, the normative data for the MoCA vary with age [16], making it difficult to establish a universal cutoff value for dichotomizing patients. In contrast, our work leverages continuous MoCA scores to predict cognitive decline in PD, avoiding the pitfalls of discretization and allowing for a more nuanced understanding of cognitive changes.
We identified only a single study that predicted cognitive outcomes using MoCA changes as a continuous variable. In their work, Salmanpour et al. (2019) [11] predicted the MoCA score at year 4 using non-motor data obtained at baseline and at the first year from the PPMI database (n = 184 PD). Their best approach used NSGAII [17] for feature subset selection (selecting six features), combined with LOLIMOT [18] for prediction, achieving a MAE of . When tested on independent data (n = 308 PD), they achieved a MAE of . Using the same cohort of patients, we improved their predictions by obtaining lower MAEs for the year 4 MoCA change () using demographic and clinical variables. In contrast to their results, the LASSOLARS algorithm provided the best results in our work. LASSOLARS has advantages over other algorithms, as it automatically adjusts the number of variables using a regularization method. This feature is particularly useful when dealing with high-dimensional databases, as it identifies a subset of predictors that capture the most relevant information while discarding redundant information.
In contrast, models such as DT and RF showed worse performances, likely due to their sensitivity to the high-dimensional and potentially noisy data. SVM models, while effective in some scenarios, required extensive hyperparameter tuning and were more computationally intensive, making them less practical for clinical implementation. Finally, LR struggled with the high dimensionality of the data and did not incorporate the regularization needed to handle irrelevant or less important variables, leading to less accurate predictions.
This study enhances our understanding of cognitive decline in PD by demonstrating that mid-term cognitive deterioration can be effectively predicted using early short-term changes in MoCA scores. Our results indicate that incorporating baseline variables from specific cognitive domains significantly improves predictive performance. By averaging MoCA scores over multiple time points, our approach offers robust and scalable predictions, reducing inconsistencies and increasing reliability. These findings suggest that early cognitive assessments are crucial for predicting cognitive decline, allowing for timely interventions and better patient management in clinical settings.
To transform these findings into practical clinical applications, several steps must be taken. First, integrating ML models into clinical workflows requires developing user-friendly software tools that can be easily adopted by healthcare providers. These tools should provide clear guidelines on how to input patient data and interpret model predictions. Training and education programs for clinicians will be essential to ensure they understand the utility and limitations of these predictive models. Potential challenges include ensuring the quality and consistency of the input data, as variability in data collection can affect model accuracy. Standardizing data collection protocols across different clinical settings will be necessary to mitigate this issue.
One potential limitation of this study is that the results are based on the PPMI cohort of early-stage PD patients, so caution should be taken when extrapolating the findings to other populations or later stages of PD. Additionally, the exclusion criteria applied during the data cleaning process might impact the generalizability of the study results. Another limitation is that our analyses were based on using clinical data as predictors; incorporating easily obtainable biological specimens such as blood biomarkers could enhance patient stratification and improve clinical practice. Lastly, as the patients’ sex did not prove to be a significant variable, a sex-based analysis was not conducted.
6. Conclusions
This study employed ML techniques to predict mid-term cognitive outcomes in early PD patients using demographic and clinical variables from the PPMI database. Cognitive impairment is a prevalent and highly disabling feature of PD, significantly impacting patients’ quality of life. Certain PD patients are predisposed to experience a more rapid cognitive decline and earlier onset of dementia. However, accurately predicting the rate of cognitive deterioration from the early stages of PD remains a clinical challenge that has not been fully addressed.
The performance of various algorithms was compared, with the LASSOLARS algorithm consistently outperforming others, achieving the lowest MAE for predictions of year 4 and 5 MoCA scores. The importance of the predictors was assessed using SHAP values and LASSOLARS coefficients; revealing that the baseline MoCA score and MoCA deterioration at one-year intervals had the highest coefficients, indicating their significant contributions to mid-term MoCA score predictions. A LASSOLARS model trained to predict the mean MoCA deterioration at year 4 and year 5 demonstrated a 19% improvement in MAE, highlighting its robustness.
In conclusion, our study demonstrates that using a limited number of objective and easily obtainable predictor variables can lead to the accurate prediction of cognitive outcomes in early-stage PD patients, providing a promising avenue for the development of ML models for clinical use. However, this study has some limitations: it is based on the PPMI cohort of early-stage PD patients, so caution is needed when generalizing to other populations or later stages of PD. This analysis relied on clinical data as its predictors, but incorporating biological specimens like blood biomarkers could enhance patient stratification. Additionally, a sex-based analysis was not conducted as sex was not a significant variable.
Author Contributions
Conceptualization, all authors; methodology, M.M.-E., O.A., I.G. (Ibai Gurrutxaga) and J.M.; software, M.M.-E.; validation, I.G. (Iñigo Gabilondo) and A.M.-G.; formal analysis, all authors; investigation, M.M.-E.; resources, I.G. (Iñigo Gabilondo) and I.G. (Ibai Gurrutxaga); data curation, M.M.-E.; writing—original draft preparation, M.M.-E. and A.M.-G.; writing—review and editing, all authors; visualization, M.M.-E.; supervision, J.C.G.-E.; project administration, M.M.-E.; funding acquisition, O.A., J.M. and I.G. (Iñigo Gabilondo). All authors have read and agreed to the published version of the manuscript.
Funding
Maitane Martinez-Eguiluz is the recipient of a predoctoral fellowship from the Basque Government (Grant PRE-2022-1-0204). This work was funded by Grant PID2021-123087OB-I00, MICIU/AEI/10.13039/501100011033, and FEDER, UE (Grant Recipient: Olatz Arbelaitz and Javier Muguerza), as well as the Department of Economic Development and Competitiveness (ADIAN, IT1437-22) of the Basque Government (Grant Recipient: Javier Muguerza).
Institutional Review Board Statement
(1) Approval Code: The PPMI study has been registered on ClinicalTrials.gov with the identifier NCT01141023, which serves as the approval reference for this specific study. (2) Name of the Ethics Committee or Institutional Review Board: The study was approved by the local ethics committees of the participating sites. A list of these sites and their respective ethics committees can be found at https://www.ppmi-info.org/about-ppmi/ppmi-clinical-sites. Participants provided written, informed consent to participate. (3) Date of Approval: The exact date of approval for each site’s ethics committee is not provided in the public domain. (4) Adherence to the Declaration of Helsinki: The study was conducted in accordance with the Declaration of Helsinki and Good Clinical Practice (GCP) guidelines after approval of the local ethics committees of the participating sites. Further information can be found in https://doi.org/10.1002/acn3.644.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Restrictions apply to the availability of these data. Data are available from https://www.ppmi-info.org/ (last accessed on 1 August 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Test and Questionnaires
This section describes the tests and questionnaires used in the study. These are the following:
- The University of Pennsylvania Smell Identification Test (UPSIT) is a standardized test used to evaluate a person’s sense of smell. It consists of 40 microencapsulated odorants embedded in a “scratch and sniff” booklet. The subject must identify each odorant from a list of four possible choices.
- The Movement Disorder Society-Unified Parkinson’s Disease Rating Scale (MDS-UPDRS) is a clinical tool used to assess the motor and non-motor symptoms of PD. It consists of four parts: Part I evaluates non-motor experiences of daily living, Part II assesses motor experiences of daily living, Part III is a motor examination, and Part IV evaluates motor complications related to treatment.
- The Hoehn and Yahr (HY) scale is a system commonly used to describe the progression of PD based on the severity of symptoms. It classifies the disease into five stages, ranging from Stage 1 (unilateral involvement only) to Stage 5 (wheelchair-bound or bedridden unless aided).
- The Rapid Eye Movement Sleep Behavior Disorder Screening Questionnaire (RBDSQ) is used to assess the presence and severity of the Rapid Eye Movement (REM) sleep behavior disorder (RBD), a condition characterized by the absence of normal muscle paralysis during REM sleep, leading to movements and behaviors during sleep that can be harmful. The RBDSQ consists of 10 questions related to RBD symptoms and behaviors, with a score calculated based on the responses.
- The Epworth Sleepiness Scale (ESS) is a questionnaire used to assess a person’s likelihood of falling asleep during various daily activities. The individual rates their likelihood of falling asleep in eight different situations on a scale of 0–3.
- The Scale for Outcomes in Parkinson’s Disease - Autonomic (SCOPA-AUT) is a clinical assessment tool used to evaluate the severity of autonomic dysfunction in PD patients. It consists of 25 items assessing symptoms related to autonomic function, including cardiovascular, gastrointestinal, genitourinary, thermoregulatory, and pupillomotor functions.
- The Hopkins Verbal Learning Test-Revised (HVLT-R) is a neuropsychological test used to assess verbal memory and learning abilities. It involves the presentation of 12 words over three learning trials, followed by a delayed recall trial after 20–30 min and a recognition trial where the patient identifies the previously presented words from a list that includes distractors.
- The Benton Judgement of Line Orientation Test (BJLOT) is a neuropsychological assessment that measures an individual’s ability to perceive and reproduce the orientation of lines in space. The test consists of 30 black-and-white illustrations of line pairs, with the individual asked to match the angles to one of several response options.
- The Semantic Fluency Test (SFT) is a neuropsychological test that assesses a person’s ability to produce words belonging to a specific category, such as animals or fruits.
- Letter Number Sequencing (LNS) is a cognitive assessment test that evaluates an individual’s working memory and attention. The examiner reads a series of alternating letters and numbers aloud, and the individual is then asked to repeat them back in numerical and alphabetical order.
- The Symbol Digit Modalities Test (SDMT) is a neuropsychological test that assesses cognitive processing speed and attention. The subject is given a key that pairs specific numbers with corresponding abstract symbols. They are then presented with a series of symbols and asked to match each symbol to its corresponding number as quickly and accurately as possible within a fixed time frame.
- The State-Trait Anxiety Inventory (STAI) is a psychological assessment tool used to measure anxiety in individuals. The inventory consists of two sets of 20 items each, measuring two different aspects of anxiety: State Anxiety, which refers to an individual’s current feelings of anxiety, and Trait Anxiety, which refers to their general tendency to be anxious across different situations.
- The Geriatric Depression Scale (GDS) is a screening tool used to identify depression in older adults. It consists of 30 yes/no questions that evaluate the presence and severity of depressive symptoms, such as feelings of sadness or worthlessness, a loss of interest in activities, and changes in appetite and sleep patterns.
- The Questionnaire for Impulsive-Compulsive Disorders (QUIP) is a self-administered questionnaire that assesses the presence and severity of symptoms related to impulse control disorders and compulsive behaviors in individuals with PD. The QUIP consists of 19 questions that evaluate the presence of four types of behaviors: pathological gambling, hypersexuality, compulsive buying, and binge eating.
Appendix B. Hyperparameters
Optimizing hyperparameters is crucial for enhancing the performance of ML models. In this study, we used the hyperopt algorithm [19], which is designed for efficient optimization in high-dimensional parameter spaces, to fine-tune the parameters of our models. This process was carried out using the same stratified 10-fold cross-validation approach solely on the training data of the outer-CV, ensuring the robustness and generalizability of our predictive models. Hyperopt facilitates a systematic exploration of the parameter space, replacing traditional, often subjective, manual tuning with a rigorous, reproducible method. By automating the selection of the best parameters, we aimed to achieve optimal model performance and ensure consistency in our results across all algorithmic implementations.
The fmin function from the hyperopt library played a crucial role in managing the optimization process, leveraging the Tree-structured Parzen Estimator (TPE) method—a Bayesian optimization technique well suited to high-dimensional spaces [20]. We defined our loss function as the average MAE, and hyperopt marked the evaluations with STATUS_OK to confirm successful trial completions. Our decision tree model’s hyperparameters were tuned over 500 trials to find the optimal settings, ensuring a thorough exploration of the hyperparameter space defined by dt_space. The trials’ object in the optimization process acts as a comprehensive log, recording the outcomes of each evaluation, including the details of the hyperparameters tested and their corresponding performance metrics.
To enhance the robustness of our approach, we optimized the hyperparameters within each training subset of the outer loop of our cross-validation process. This methodology incorporates two layers of cross-validation: an outer loop to evaluate the model’s performance and an inner loop to optimize the hyperparameters within each training subset of the outer loop. Such a methodical setup reinforces the integrity of our model evaluation, creating more reliable and generalizable results.
For our study, we used the StratifiedKFold function from the sklearn library, setting it to create 10 stratified folds. These samples were arranged in ascending order by their identification number and were not shuffled. Given the continuous nature of our outcome variable, we employed the cut function from the pandas library to categorize this variable into 10 bins of equal width. This categorization was solely for the purpose of creating stratified folds and was not used in the actual training of our models. This stratification process was consistently applied in both the outer and inner loops of our cross-validation to maintain uniformity and integrity in our model evaluation approach.
The LinearRegression function did not require hyperparameter optimization to achieve an optimal performance. Although LinearRegression includes additional hyperparameters, such as fit_intercept, to determine whether an intercept should be calculated, these were not relevant to our specific analysis objectives.
In the LassoLarsCV function, we specified only the cross-validation split through the cv hyperparameter, which was the same setting used for tuning all other algorithms. All other hyperparameters were left at their default values, as this algorithm incorporates its own internal optimization mechanism for estimating regularization parameter alpha.
For the DecisionTreeRegressor function, the following hyperparameters were tuned:
- The function used to evaluate the quality of a split is referred to as the criterion. Its supported criteria include squared_error, which calculates the mean squared error equivalent to the variance reduction and minimizes the L2 loss by using the mean of each terminal node. Another criterion is friedman_mse, which computes the mean squared error while incorporating Friedman’s improvement score for evaluating potential splits. Lastly, absolute_error determines the mean absolute error and minimizes the L1 loss by using the median of each terminal node.
- The maximum depth of the tree (max_depth) specifies how deep the tree can grow. If set to None, the tree will continue to expand until all leaves are pure or until each leaf has fewer than the specified min_samples_split samples (see below). Alternately, the tree depth can be explicitly set to values such as 2, 4, 6, 8, or 10.
- The Max_features hyperparameter determines the number of features to evaluate when identifying the optimal split. If set to None, all features are considered. If set to sqrt, then max_features is the square root of the total number of features.
- The Min_samples_leaf hyperparameter specifies the minimum number of samples that must be present in a leaf node. The possible values were 1, 2, or 4.
- The Min_samples_split hyperparameter defines the minimum number of samples necessary to divide an internal node. The options for this setting were 2, 5, or 10.
The hyperparameters adjusted for the RandomForestRegressor included the number of trees in the forest (n_estimators) as well as those previously specified for the DecisionTreeRegressor. The available options for n_estimators were 100, 200, or 500.
The hyperparameters tuned for the SVR algorithm included:
- The kernel type, which transforms the input data into higher-dimensional spaces. The polynomial kernel, denoted as poly, raises the input features to a specified degree, allowing the SVM to learn complex, non-linear decision boundaries. The Radial Basis Function (RBF) kernel, or rbf, measures the distance between samples in a Gaussian-distributed space, effectively managing non-linear separations even when the data have no clear boundaries. Lastly, the sigmoid kernel mimics the behavior of a neural network’s activation function, transforming the feature space according to a logistic function.
- The kernel coefficient, known as gamma, which has possible values of 1, 0.1, 0.01, and 0.001
- The regularization parameter, referred to as C, with choices of 0.1, 1, 10, and 100.
Appendix C. SHAP
SHAP (SHapley Additive exPlanations) [21] explains machine learning model outputs by assessing each feature’s impact on the model’s prediction. It measures how the presence or absence of a feature affects the prediction, providing a nuanced view of feature importance that includes interactions between features and their distributions across the data.
Developed from a game-theoretic perspective, SHAP is grounded in the principles of Shapley values, a classic method from cooperative game theory used to fairly distribute the payout among players based on their contribution to the whole game. In the context of machine learning, SHAP values assign each feature an “importance” value for a particular prediction, reflecting the contribution of each feature to the prediction relative to a baseline prediction made in the absence of those features.
A positive SHAP value indicates that the variable has a positive influence on the final value, meaning that the MoCA deterioration will be greater. Conversely, a negative SHAP value indicates that the patient will improve their MoCA test value compared to their baseline.
References
- Arshad, H.; Tayyab, M.; Bilal, M.; Akhtar, S.; Abdullahi, A. Trends and Challenges in harnessing big data intelligence for health care transformation. Artif. Intell. Intell. Syst. 2024, 220–240. [Google Scholar] [CrossRef]
- Aarsland, D.; Andersen, K.; Larsen, J.; Lolk, A.; Nielsen, H.; Kragh-Sørensen, P. Risk of dementia in Parkinson’s disease: A community-based, prospective study. Neurology 2001, 56, 730–736. [Google Scholar] [CrossRef] [PubMed]
- Aarsland, D.; Kurz, M.W. The epidemiology of dementia associated with Parkinson’s disease. Brain Pathol. 2010, 20, 633–639. [Google Scholar] [CrossRef] [PubMed]
- Aarsland, D.; Batzu, L.; Halliday, G.M.; Geurtsen, G.J.; Ballard, C.; Ray Chaudhuri, K.; Weintraub, D. Parkinson disease-associated cognitive impairment. Nat. Rev. Dis. Prim. 2021, 7, 47. [Google Scholar] [CrossRef] [PubMed]
- Hoops, S.; Nazem, S.; Siderowf, A.; Duda, J.; Xie, S.; Stern, M.; Weintraub, D. Validity of the MoCA and MMSE in the detection of MCI and dementia in Parkinson disease. Neurology 2009, 73, 1738–1745. [Google Scholar] [CrossRef] [PubMed]
- Gramotnev, G.; Gramotnev, D.K.; Gramotnev, A. Parkinson’s disease prognostic scores for progression of cognitive decline. Sci. Rep. 2019, 9, 17485. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, A.A.; Maia, P.D.; Gao, X.; Damasceno, P.F.; Raj, A. Dynamical role of pivotal brain regions in Parkinson symptomatology uncovered with deep learning. Brain Sci. 2020, 10, 73. [Google Scholar] [CrossRef] [PubMed]
- Marek, K.; Jennings, D.; Lasch, S.; Siderowf, A.; Tanner, C.; Simuni, T.; Coffey, C.; Kieburtz, K.; Flagg, E.; Chowdhury, S.; et al. The Parkinson progression marker initiative (PPMI). Prog. Neurobiol. 2011, 95, 629–635. [Google Scholar] [CrossRef]
- Harvey, J.; Reijnders, R.A.; Cavill, R.; Duits, A.; Köhler, S.; Eijssen, L.; Rutten, B.P.; Shireby, G.; Torkamani, A.; Creese, B.; et al. Machine learning-based prediction of cognitive outcomes in de novo Parkinson’s disease. npj Park. Dis. 2022, 8, 150. [Google Scholar] [CrossRef]
- Gorji, A.; Fathi Jouzdani, A. Machine learning for predicting cognitive decline within five years in Parkinson’s disease: Comparing cognitive assessment scales with DAT SPECT and clinical biomarkers. PLoS ONE 2024, 19, e0304355. [Google Scholar] [CrossRef]
- Salmanpour, M.R.; Shamsaei, M.; Saberi, A.; Setayeshi, S.; Klyuzhin, I.S.; Sossi, V.; Rahmim, A. Optimized machine learning methods for prediction of cognitive outcome in Parkinson’s disease. Comput. Biol. Med. 2019, 111, 103347. [Google Scholar] [CrossRef] [PubMed]
- Hosseinzadeh, M.; Gorji, A.; Fathi Jouzdani, A.; Rezaeijo, S.M.; Rahmim, A.; Salmanpour, M.R. Prediction of Cognitive decline in Parkinson’s Disease using clinical and DAT SPECT Imaging features, and Hybrid Machine Learning systems. Diagnostics 2023, 13, 1691. [Google Scholar] [CrossRef] [PubMed]
- Almgren, H.; Camacho, M.; Hanganu, A.; Kibreab, M.; Camicioli, R.; Ismail, Z.; Forkert, N.D.; Monchi, O. Machine learning-based prediction of longitudinal cognitive decline in early Parkinson’s disease using multimodal features. Sci. Rep. 2023, 13, 13193. [Google Scholar] [CrossRef] [PubMed]
- Ostertag, C.; Visani, M.; Urruty, T.; Beurton-Aimar, M. Long-term cognitive decline prediction based on multi-modal data using Multimodal3DSiameseNet: Transfer learning from Alzheimer’s disease to Parkinson’s disease. Int. J. Comput. Assist. Radiol. Surg. 2023, 18, 809–818. [Google Scholar] [CrossRef] [PubMed]
- Dalrymple-Alford, J.; MacAskill, M.; Nakas, C.; Livingston, L.; Graham, C.; Crucian, G.; Melzer, T.; Kirwan, J.; Keenan, R.; Wells, S.; et al. The MoCA: Well-suited screen for cognitive impairment in Parkinson disease. Neurology 2010, 75, 1717–1725. [Google Scholar] [CrossRef] [PubMed]
- Ojeda, N.; Del Pino, R.; Ibarretxe-Bilbao, N.; Schretlen, D.J.; Pena, J. Montreal Cognitive Assessment Test: Normalization and standardization for Spanish population. Rev. Neurol. 2016, 63, 488–496. [Google Scholar] [CrossRef] [PubMed]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Martínez-Morales, J.; Palacios, E.; Carrillo, G.V. Modeling of internal combustion engine emissions by LOLIMOT algorithm. Procedia Technol. 2012, 3, 251–258. [Google Scholar] [CrossRef]
- Bergstra, J.; Yamins, D.; Cox, D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the International Conference on Machine Learning, PMLR, Atlanta, GA, USA, 17–19 June 2013; pp. 115–123. Available online: https://proceedings.mlr.press/v28/bergstra13.html (accessed on 11 August 2024).
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. Adv. Neural Inf. Process. Syst. 2011, 24, 2546–2554. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).