Ergonomic Assessment of Key Biomechanical Factors in Patient Lifting: Results from a Cross-Sectional Study
Abstract
1. Introduction
2. Materials and Methods
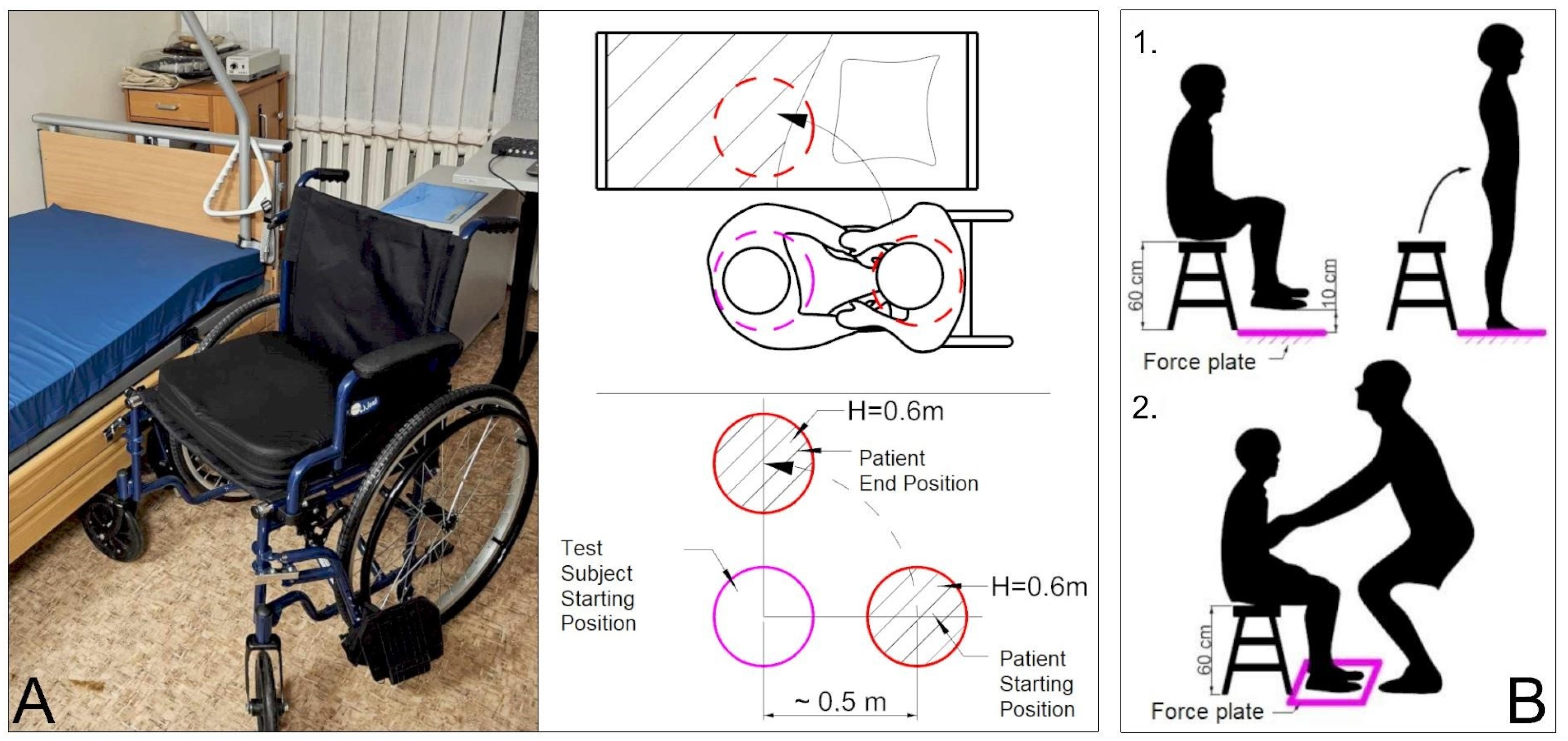
2.1. Test Subject and Research Procedure
- The first scenario simulates a heavily physically disabled person, where patient does not assist the test subject in any way and remains relaxed. Patient’s hands are down.
- The second scenario simulates a patient with ability to move above the waist, where the assistance is provided by the patient placing their hands on the test subject’s shoulders. The patient cannot stand on their own, and the assistance is minimal.
- Similarly to the first scenario, in the third scenario, the patient does not assist at all, but in this case, test subject uses ergonomical belt during the lifting. Patient’s hands are down, and body is relaxed.
- The patient begins by sitting on the chair without touching the force plate, with legs lifted. The measurement commences when the patient stands on the force plate, remains standing for a few seconds, and then returns to a seated position on the chair. This is presented in Figure 2B(1) scenario.
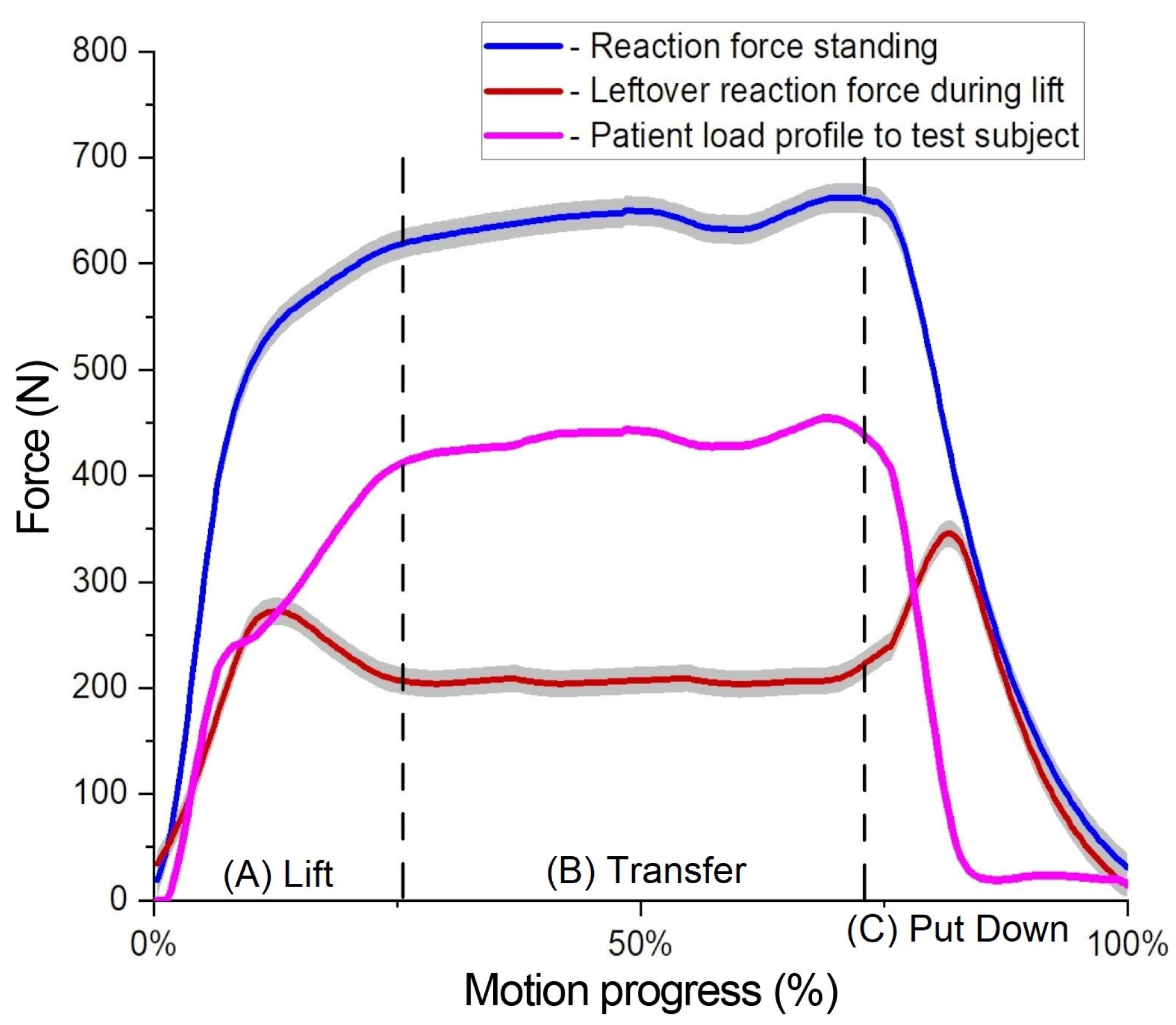
- The second measurement begins with the patient sitting on the chair with their legs touching the force plate. The patient is lifted by the test subject between two surfaces, replicating the main research scenario. Throughout the lift, the patient keeps their legs on the force plate, allowing measurement of the remaining force. This setup enables continuous measurement of the force exerted while the patient’s legs remain in contact with the force plate throughout the lifting motion. This presented in Figure 2B(2) scenario.
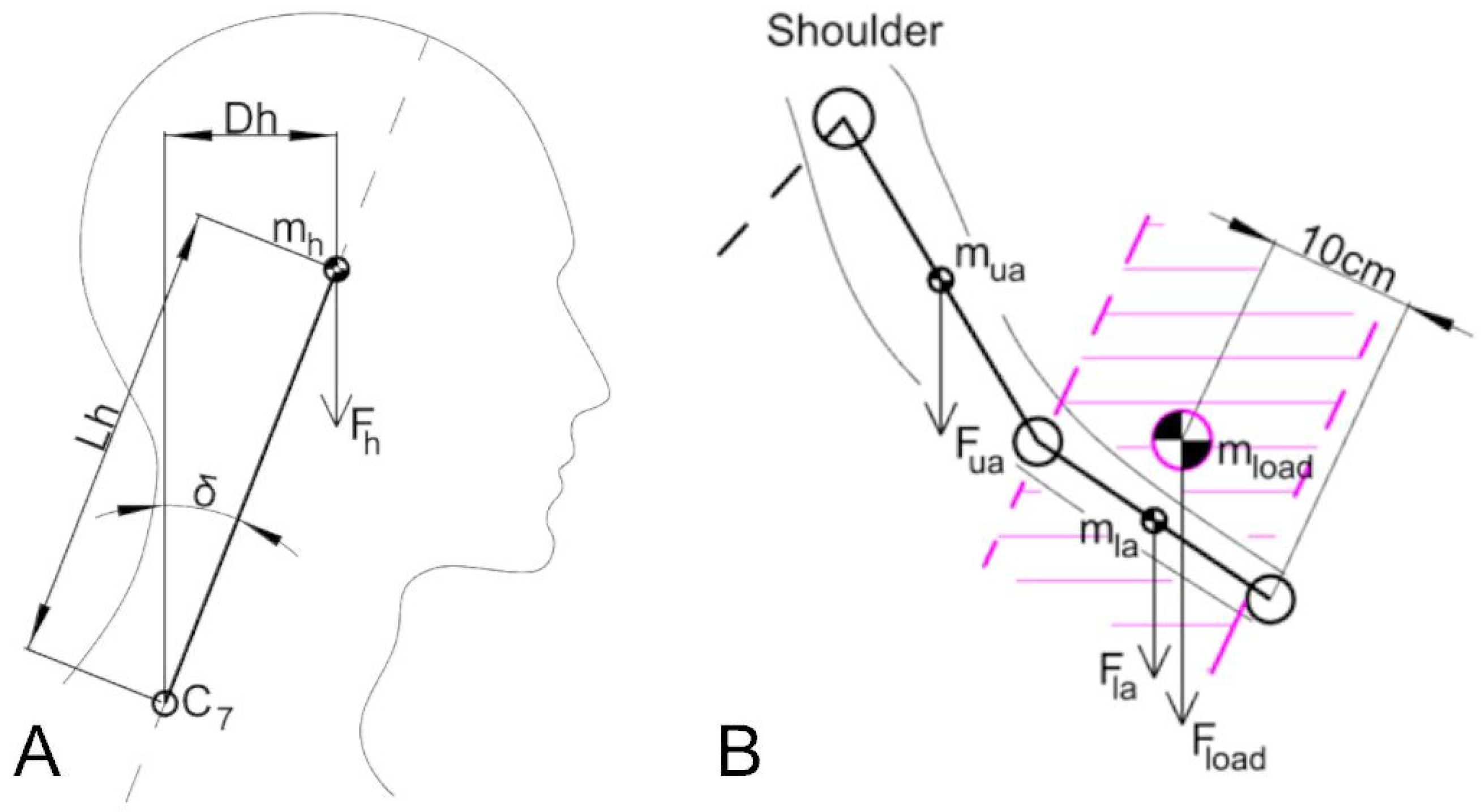
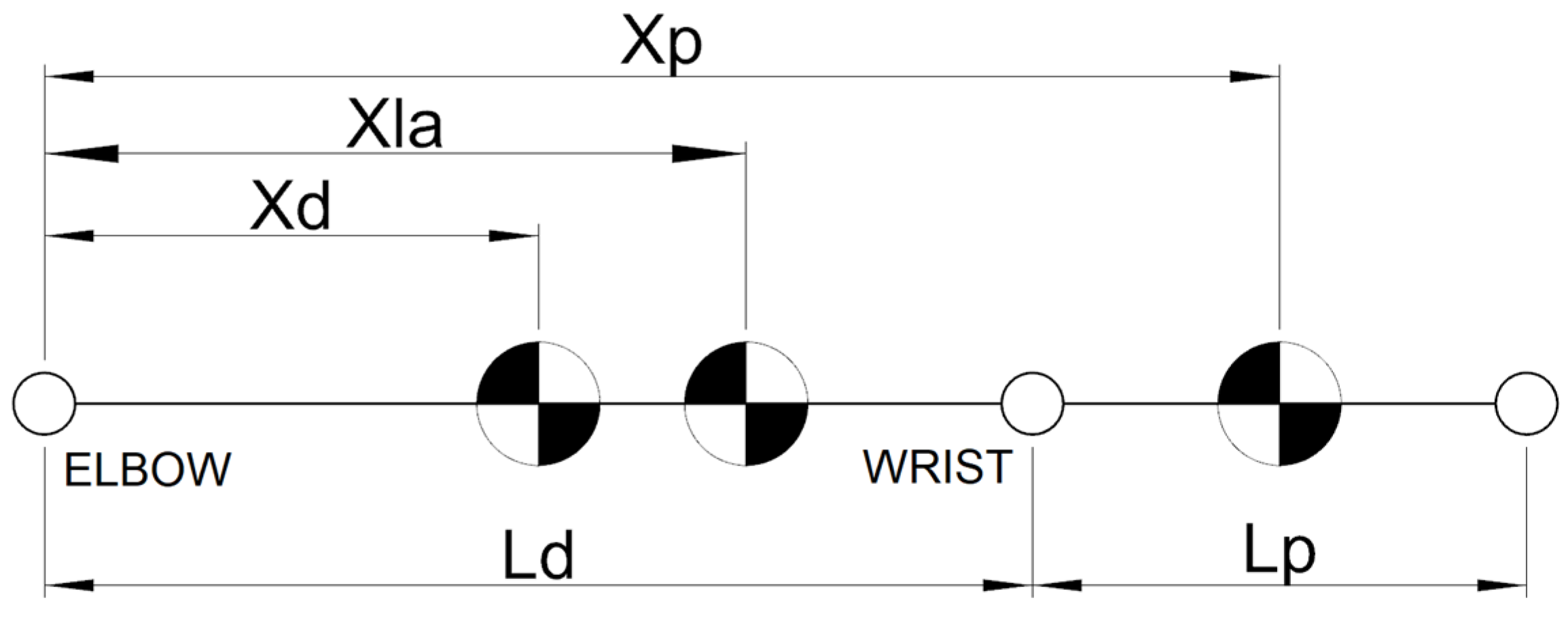
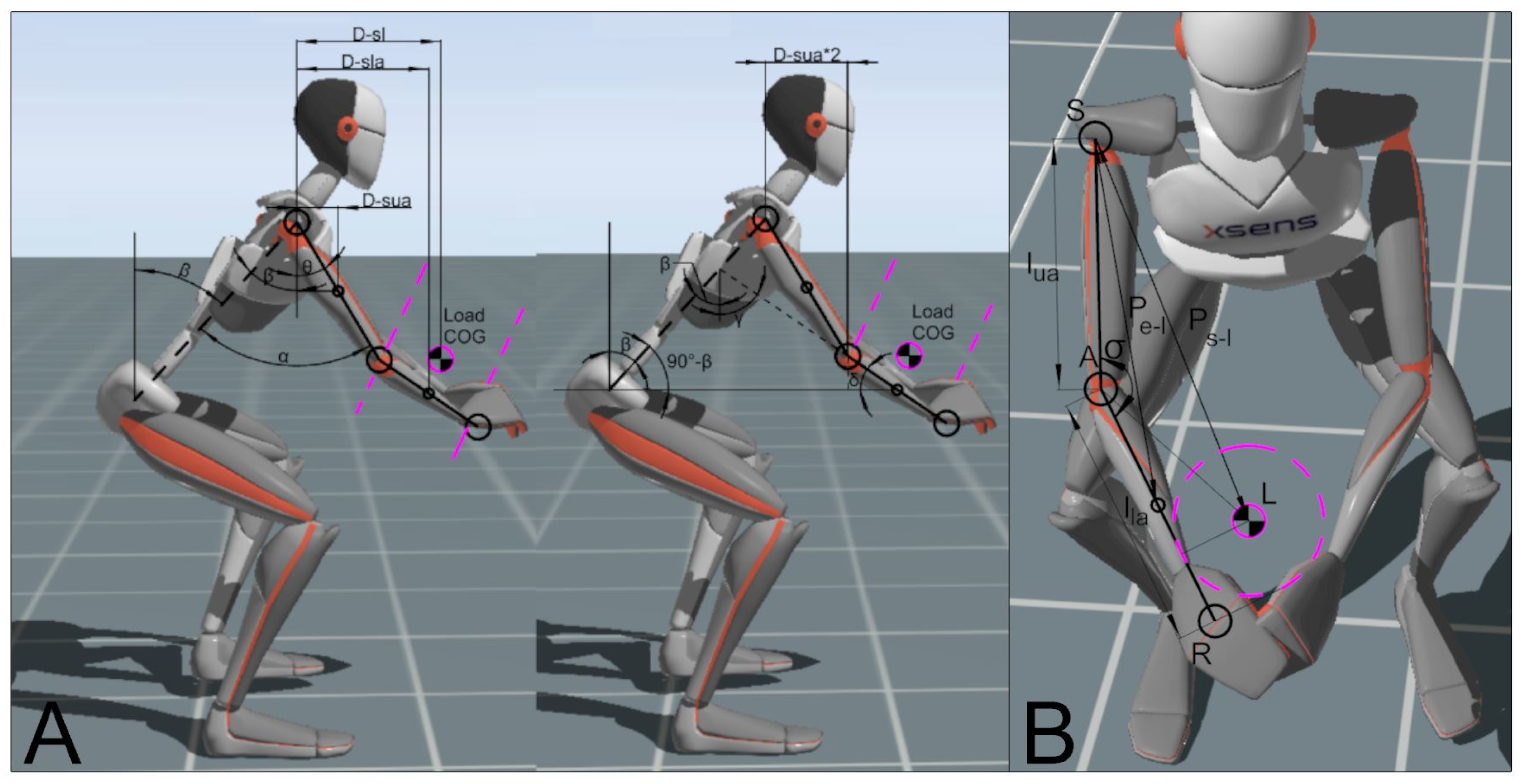
2.2. Mathematical Methods
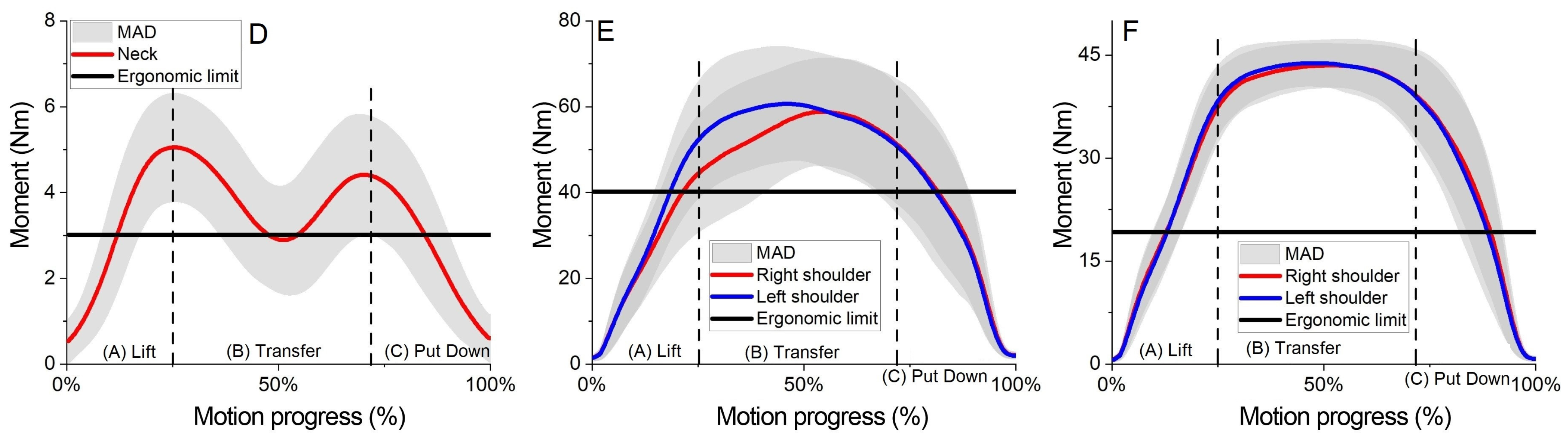
2.3. Ergonomic Boundary Evaluation
3. Results
3.1. Patient Load Force Profile
3.2. Inverse Dynamics Results
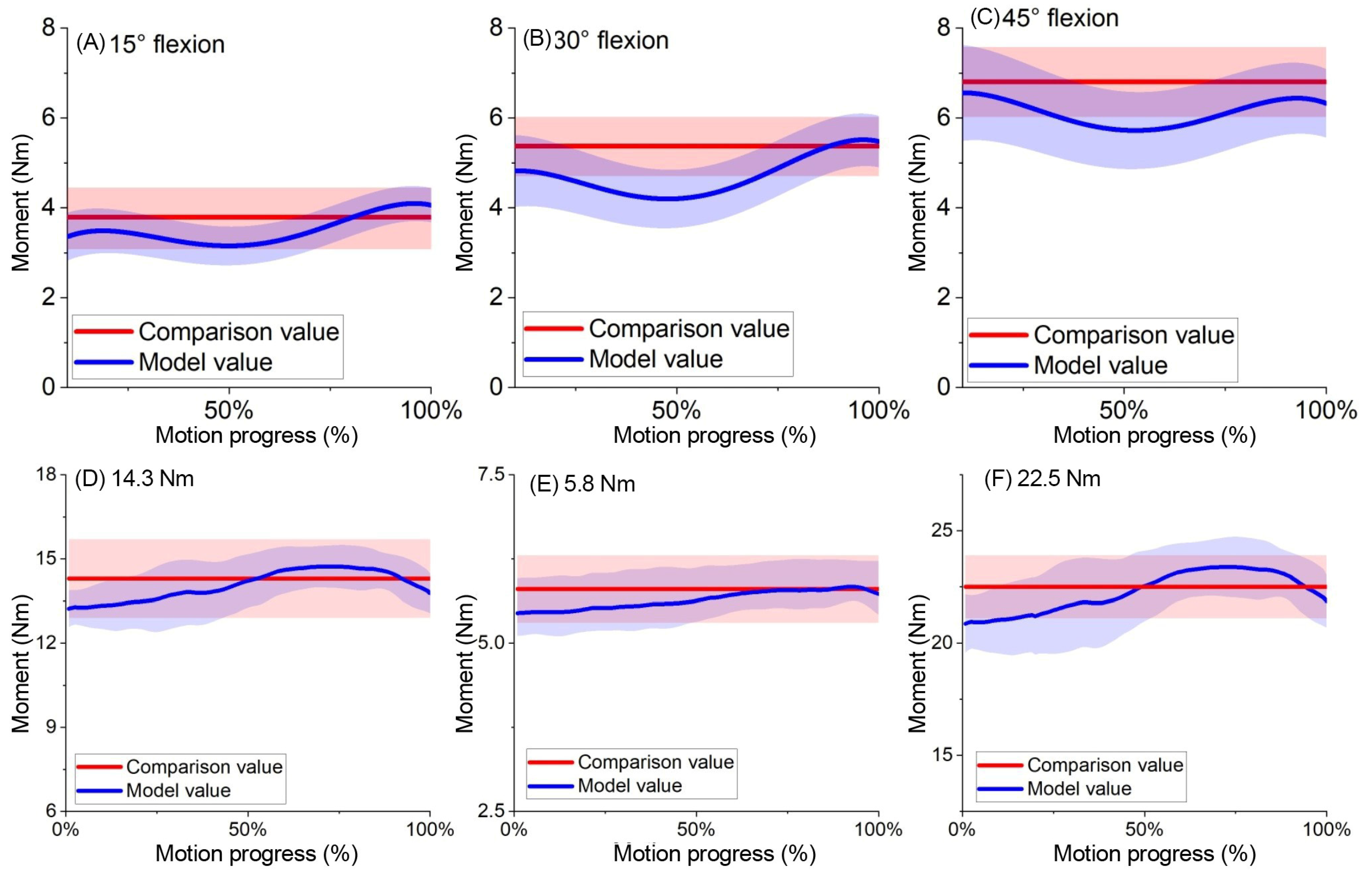
3.3. Model Verification
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Skals, S.; Bláfoss, R.; de Zee, M.; Andersen, L.L.; Andersen, M.S. Effects of load mass and position on the dynamic loading of the knees, shoulders and lumbar spine during lifting: A musculoskeletal modelling approach. Appl. Ergon. 2021, 96, 103491. [Google Scholar] [CrossRef] [PubMed]
- Conforti, I.; Mileti, I.; Del Prete, Z.; Palermo, E. Measuring Biomechanical Risk in Lifting Load Tasks Through Wearable System and Machine-Learning Approach. Sensors 2020, 20, 1557. [Google Scholar] [CrossRef] [PubMed]
- ISO 11228-1; Ergonomics—Manual Handling—Part 1: Lifting, Lowering and Carrying. International Organization for Standardization: Geneva, Switzerland, 2003.
- McAtamney, L.; Corlett, E.N. RULA: A Survey Method for the Investigation of Work-Related Upper Limb Disorders. Appl. Ergon. 1993, 24, 91–99. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, T.; Serranheira, F.; Loureiro, H. Work-related musculoskeletal disorders in primary health care nurses. Appl. Nurs. Res. 2017, 33, 72–77. [Google Scholar] [CrossRef]
- Anap, D.B.; Iyer, C.; Rao, K. Work-related musculoskeletal disorders among hospital nurses in rural Maharashtra, India: A multi-centre survey. Int. J. Res. Med. Sci. 2017, 1, 101–107. [Google Scholar] [CrossRef]
- Ryu, E.; Ye, B.; Yi, Y.; Kim, J. Risk factors of musculoskeletal symptoms in university hospital nurses. Ann. Occup. Environ. Med. 2014, 26, 47. [Google Scholar] [CrossRef]
- Chung, Y.C.; Hung, C.T.; Li, S.F.; Lee, H.M.; Wang, S.G.; Chang, S.C.; Pai, L.W.; Huang, C.N.; Yang, J.H. Risk of musculoskeletal disorder among Taiwanese nurses cohort: A nationwide population-based study. BMC Musculoskelet. Disord. 2013, 14, 144. [Google Scholar] [CrossRef]
- Arvidsson, I.; Gremark Simonsen, J.; Dahlqvist, C.; Axmon, A.; Karlson, B.; Björk, J.; Nordander, C. Cross-sectional associations between occupational factors and musculoskeletal pain in women teachers, nurses and sonographers. BMC Musculoskelet. Disord. 2016, 17, 35. [Google Scholar] [CrossRef]
- Hignett, S.; McAtamney, L. Rapid entire body assessment (REBA). Appl. Ergon. 2000, 31, 201–205. [Google Scholar] [CrossRef] [PubMed]
- David, G.C. Ergonomic methods for assessing exposure to risk factors for work-related musculoskeletal disorders. Occup. Med. 2005, 55, 190–199. [Google Scholar] [CrossRef] [PubMed]
- Buchholz, B.; Paquet, V.; Punnett, L.; Lee, D.; Moir, S. PATH: A work sampling-based approach to ergonomic job analysis for construction and other non-repetitive work. Appl. Ergon. 1996, 27, 177–187. [Google Scholar] [CrossRef] [PubMed]
- Boschman, J.S.; Noor, A.; Lundström, R.; Nilsson, T.; Sluiter, J.K.; Hagberg, M. Relationships between work-related factors and musculoskeletal health with current and future work ability among male workers. Int. Arch. Occup. Environ. Health 2017, 90, 517–526. [Google Scholar] [CrossRef]
- Hani, D.B.; Huangfu, R.; Sesek, R.; Schall, M.C., Jr.; Davis, G.A.; Gallagher, S. Development and validation of a cumulative exposure shoulder risk assessment tool based on fatigue failure theory. Ergonomics 2021, 64, 39–54. [Google Scholar] [CrossRef] [PubMed]
- Ramachandran, H.; Vasudevan, D.; Brahma, A.; Pugazhenthi, S. Estimation of mass moment of inertia of human body, when bending forward, for the design of a self-transfer robotic facility. J. Eng. Sci. Technol. 2016, 11, 166–176. [Google Scholar]
- Hall, S.J. Basic Biomechanics, 6th ed.; McGraw-Hill: Boston, MA, USA, 2012. [Google Scholar]
- van der Helm, F.C.; Veeger, H.E. Quasi-static analysis of muscle forces in the shoulder mechanism during wheelchair propulsion. J. Biomech. 1996, 29, 39–52. [Google Scholar] [CrossRef]
- Cheung, K.; Ma, K.Y.; Cheung, H.H.; Lee, C.H.; Chan, I.M.M.; Cheung, S.T.; Chung, W.Y.; Yeung, S.S.; Lo, W.C. Predictors of work-related mus-culoskeletal symptoms in shoulders among nursing assistants working in nursing homes. PeerJ 2021, 9, e11152. [Google Scholar] [CrossRef] [PubMed]
- Guduru, R.K.R.; Domeika, A.; Obcarskas, L.; Ylaite, B. The Ergonomic Association between Shoulder, Neck/Head Disorders and Sedentary Activity: A Systematic Review. J. Healthc. Eng. 2022, 2022, 5178333. [Google Scholar] [CrossRef]
- Senvaitis, K.; Daunoraviciene, K.; Adomaviciene, A. Biomechanical assessment of critical factors during patient lifting: Shoulder gridle and cumulative moment ergonomic evaluation. Acta Mech. Autom. (AMA) 2024, 18, 323–332. [Google Scholar] [CrossRef]
- Pamuła, H.; Loo, W. Center of Mass Calculator. Available online: https://www.omnicalculator.com/math/center-of-mass (accessed on 27 December 2023).
- Kumar, S.; Narayan, Y. Cumulative spinal load among X-ray technologist: A field study of techniques, frame rate and prediction. Int. J. Ind. Ergon. 2005, 35, 889–903. [Google Scholar] [CrossRef]
- Greenland, K.O.; Merryweather, A.S.; Bloswick, D.S. The effect of lifting speed on cumulative and peak biomechanical loading for symmetric lifting tasks. Saf. Health Work 2013, 4, 105–110. [Google Scholar] [CrossRef]
- Backes, A.; Skejø, S.D.; Gette, P.; Nielsen, R.Ø.; Sørensen, H.; Morio, C.; Malisoux, L. Predicting cumulative load during running using field-based measures. Scand. J. Med. Sci. Sports 2020, 30, 2399–2407. [Google Scholar] [CrossRef]
- Boslaugh, S.; Watters, P.A. Statistics in a Nutshell: A Desktop Quick Reference; O’Reilly Media: Sebastopol, CA, USA, 2008. [Google Scholar]
- Arendra, A.; Akhmad, S.; Lumintu, I. Working tool redesign to reduce ergonomic risk of salt evaporation field workers based on RULA and REBA assessments using esMOCA Instrument. J. Phys. Conf. Ser. 2020, 1477, 022034. [Google Scholar] [CrossRef]
- Zhang, C.; Roossien, C.C.; Verkerke, G.J.; Houdijk, H.; Hijmans, J.M.; Greve, C. Biomechanical Load of Neck and Lumbar Joints in Open-Surgery Training. Sensors 2023, 23, 6974. [Google Scholar] [CrossRef] [PubMed]
- Miller, H.; Rockefeller, K.; Townsend, P. International round table discussion: Do gait belts have a role in safe patient handling programs? Int. J. Safe Patient Handl. Mobil. 2017, 7, 116–121. [Google Scholar]
- Hlavenka, T.M.; Christner, V.F.K.; Gregory, D.E. Neck posture during lifting and its effect on trunk muscle activation and lumbar spine posture. Appl. Ergon. 2017, 62, 28–33. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, R.; Cronin, J.; Faigenbaum, A.; Haff, G.; Howard, R.; Kraemer, W.; Micheli, L.; Myer, G.; Oliver, J. National Strength and Conditioning Association Position Statement on Long-Term Athletic Development. J. Strength Cond. Res. 2016, 30, 1491–1509. [Google Scholar] [CrossRef]
- Ramasamy, Y.; Usman, J.; Razman, R.; Wei, Y.M.; Towler, H.; King, M. A Systematic Review of the Biomechanical Studies on Shoulder Kinematics in Overhead Sporting Motions: Types of Analysis and Approaches. Appl. Sci. 2023, 13, 9463. [Google Scholar] [CrossRef]
- Murray, I.A.; Johnson, G.R. A study of the external forces and moments at the shoulder and elbow while performing everyday tasks. Clin. Biomech. 2004, 19, 586–594. [Google Scholar] [CrossRef]
- Tapanya, W.; Puntumetakul, R.; Swangnetr, M.; Neubert, R.; Boucaut, R. Influence of Neck Flexion Angle on Gravitational Moment and Neck Muscle Activity When Using a Smartphone While Standing. Ergonomics 2021, 64, 900–911. [Google Scholar] [CrossRef]
- Namdari, S.; Yagnik, G.; Ebaugh, D.D.; Nagda, S.; Ramsey, M.L.; Williams, G.R.; Mehta, S. Defining Functional Shoulder Range of Motion for Activities of Daily Living. J. Shoulder Elbow Surg. 2012, 21, 1177–1183. [Google Scholar] [CrossRef]
- Bartolomei, S.; Grillone, G.; Di Michele, R.; Cortesi, M. A Comparison between Male and Female Athletes in Relative Strength and Power Performances. J. Funct. Morphol. Kinesiol. 2021, 6, 17. [Google Scholar] [CrossRef] [PubMed]
- Gallagher, S.; Schall, M.C., Jr. Musculoskeletal Disorders as a Fatigue Failure Process: Evidence, Implications and Research Needs. Ergonomics 2017, 60, 255–269. [Google Scholar] [CrossRef] [PubMed]
- Gallagher, S.; Schall, M.C., Jr.; Sesek, R.F.; Huangfu, R. An Upper Extremity Risk Assessment Tool Based on Material Fatigue Failure Theory: The Distal Upper Extremity Tool (DUET). Hum. Factors 2018, 60, 1205–1217. [Google Scholar] [CrossRef] [PubMed]


| Neck | R. Shoulder | L. Shoulder | R. Elbow | L. Elbow | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean Acc Nm | Moment MAD | Mean Acc Nm | Moment MAD | Mean Acc Nm | Moment MAD | Mean Acc Nm | Moment MAD | Mean Acc Nm | Moment MAD | |
| All pop. n = 396 | 96.66 | 32.49 | 1156.51 | 351.51 | 1211.7 | 373.27 | 890.9 | 206.2 | 776.285 | 171.06 |
| Scenario | ||||||||||
| #1 n = 132 | 103.81 | 33.31 | 1286.58 | 343.99 | 1366.35 | 429.59 | 964.06 | 214.76 | 846.99 | 188.39 |
| #2 n = 132 | 92.20 | 29.95 | 1117.29 | 289.82 | 1196.24 | 318.38 | 855.78 | 180.34 | 734.82 | 149.8 |
| #3 n = 132 | 93.95 | 34.27 | 1065.65 | 381.06 | 1072.51 | 339.11 | 852.89 | 215.93 | 747.05 | 166.44 |
| Age | ||||||||||
| <25 n = 243 | 104.77 | 31.59 | 1166.98 | 324.27 | 1258.59 | 373.28 | 918.52 | 212.67 | 775.20 | 171.15 |
| 25–35 n = 99 | 84.23 | 28.49 | 1103.70 | 313.46 | 1164.99 | 301.67 | 856.52 | 164.62 | 763.53 | 138.86 |
| >50 n = 53 | 82.70 | 31.60 | 1206.20 | 563.30 | 1086.31 | 451.79 | 829.65 | 239.63 | 804.58 | 235.34 |
| Physical level | ||||||||||
| Low n = 126 | 100.20 | 32.60 | 1201.74 | 431.10 | 1238.15 | 444.85 | 905.26 | 246.61 | 812.04 | 216.07 |
| Mid. n = 171 | 81.21 | 27.75 | 1154.55 | 370.84 | 1205.51 | 334.85 | 845.02 | 175.08 | 766.54 | 145.40 |
| High n = 99 | 118.88 | 29.29 | 1207.27 | 373.06 | 1252.46 | 460.54 | 977.76 | 243.67 | 783.86 | 222.65 |
| Tenure | ||||||||||
| <1 year n = 207 | 101.23 | 28.73 | 1104.02 | 332.51 | 1183.23 | 366.27 | 878.32 | 205.93 | 746.71 | 171.78 |
| 1–3 year n = 99 | 100.84 | 36.38 | 1304.80 | 447.16 | 1355.17 | 398.31 | 960.40 | 219.54 | 839.24 | 185.50 |
| >3 year n = 90 | 76.30 | 28.61 | 1114.10 | 280.26 | 1119.36 | 324.65 | 843.40 | 185.56 | 775.06 | 139.52 |
| Gender | ||||||||||
| Man n = 144 | 111.34 | 29.05 | 1131.11 | 302.52 | 1240.81 | 360.21 | 920.27 | 207.16 | 766.97 | 170.18 |
| Woman n = 252 | 88.03 | 31.77 | 1171.02 | 379.07 | 1195.06 | 379.86 | 874.12 | 204.13 | 781.61 | 171.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senvaitis, K.; Adomavičienė, A.; Tomaševič, A.; Kernagytė, R.; Petrauskaitė, A.; Daunoravičienė, K. Ergonomic Assessment of Key Biomechanical Factors in Patient Lifting: Results from a Cross-Sectional Study. Appl. Sci. 2024, 14, 8076. https://doi.org/10.3390/app14178076
Senvaitis K, Adomavičienė A, Tomaševič A, Kernagytė R, Petrauskaitė A, Daunoravičienė K. Ergonomic Assessment of Key Biomechanical Factors in Patient Lifting: Results from a Cross-Sectional Study. Applied Sciences. 2024; 14(17):8076. https://doi.org/10.3390/app14178076
Chicago/Turabian StyleSenvaitis, Karolis, Aušra Adomavičienė, Alina Tomaševič, Radvilė Kernagytė, Ada Petrauskaitė, and Kristina Daunoravičienė. 2024. "Ergonomic Assessment of Key Biomechanical Factors in Patient Lifting: Results from a Cross-Sectional Study" Applied Sciences 14, no. 17: 8076. https://doi.org/10.3390/app14178076
APA StyleSenvaitis, K., Adomavičienė, A., Tomaševič, A., Kernagytė, R., Petrauskaitė, A., & Daunoravičienė, K. (2024). Ergonomic Assessment of Key Biomechanical Factors in Patient Lifting: Results from a Cross-Sectional Study. Applied Sciences, 14(17), 8076. https://doi.org/10.3390/app14178076







