Abstract
This paper introduces an evolutionary algorithm for objective functions defined over clouds of points of varying sizes. Such design variables are modeled as uniform discrete measures with finite support and the crossover and mutation operators of the algorithm are defined using the Wasserstein barycenter. We prove that the Wasserstein-based crossover has a contracting property in the sense that the support of the generated measure is included in the closed convex hull of the union of the two parents’ supports. We introduce boundary mutations to counteract this contraction. Variants of evolutionary operators based on Wasserstein barycenters are studied. We compare the resulting algorithm to a more classical, sequence-based, evolutionary algorithm on a family of test functions that include a wind-farm layout problem. The results show that Wasserstein-based evolutionary operators better capture the underlying geometrical structures of the considered test functions and outperform a reference evolutionary algorithm in the vast majority of the cases. The tests indicate that the mutation operators play a major part in the performances of the algorithms.
1. Introduction and Related Work
1.1. General Context
This work concerns the optimization of functions defined over clouds (or sets) of points. The decision variables are sets of points, , where each point is a d-dimensional vector of continuous numbers, . An important property of such sets is that they are invariant with respect to a change in numbering of the points.
Many functions of practical interest are black-box functions over clouds of points. The example that initiated this work and that will be used as a test problem is the optimization of the layout of a wind farm. The longitude and latitude of the wind turbines is a point; the decision variable is the number and placement of the set of wind turbines. A typical objective is to maximize the average power produced by the wind farm while minimizing the total incurred cost. Such a problem has received a lot of attention lately. For instance, a code to simulate the wind farm and optimize it can be found in [1]. The operations research community has seized the problem of wind-farm layout design [2,3,4], installation [5] and operation [6]. There are other problems related to wind-farm design such as cable routing [7]. Here, we focus on the optimization of the positions, which boil down to optimizing sets of points.
Numerous other problems involve sets of points, such as the positioning of sensors and actuators in a given domain [8], the optimization of an experimental design [9] and optimal uncertainty quantification [10], where critical densities can be seen as set of points, and mixture modeling [11].
The associated optimization problem is formulated in Equation (1). For each variable and for each , varies in a continuous compact domain, , of :
The number of points is an integer bounded by and . Two examples of clouds of points are given in Figure 1. They have different sizes and patterns so that there is no obvious method to define a topology over these sets. The nature of these design variables makes the function F invariant under a permutation of the points in the cloud X. The space of clouds of points is continuous in the sense that each point can move continuously within the domain, but the number of points is an integer, thus a cloud cannot be directly represented as a continuous vector of fixed dimension. In addition, function F is seen as a black-box in the sense that no information related to its convexity and/or smoothness is assumed. These features of the problem make it hard to rely on standard optimization methods, such as gradient-based algorithms. In this article, we propose and investigate an ad hoc evolutionary algorithm [12,13].
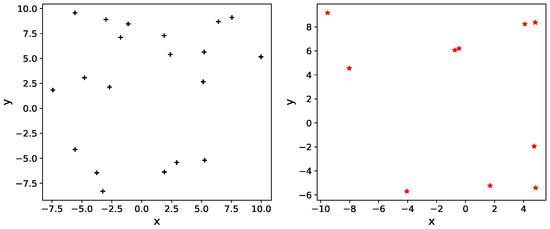
Figure 1.
Two clouds of points for , on the left and on the right.
1.2. Related Work
Although optimization problems over clouds of points are common in real life applications, the literature on algorithms for solving such problems is rarely generic, but it is typically attached to specific applications. We therefore focus on the wind-farm layout problem, which has mainly been tackled by mathematical programming and evolutionary approaches.
1.2.1. Mathematical Programming Techniques
To optimize wind-farm layouts, Pérez et al. [14] proceed in two steps: the number of turbines is chosen a priori, the positions of the turbines are carefully initialized, and then they are locally tuned by mathematical programming techniques in continuous variables, such as those described in [15]. The algorithms suppose that the variables are ordered and they cannot deal with varying size clouds of points.
Mixed integer (non-)linear programming methods can be applied by considering a discretization of the domain with a binary turbine presence/absence variable introduced at each discretization node.
The optimal layout of wind farms is treated in such a way in [16]. The number of wind turbines can vary but the set of possible candidate positions is fixed. The design variables take the form of a graph where the nodes correspond to the positions and the edges to the paths of connection cables between the turbines. Our work, which, beyond wind farms, targets general problems with clouds of points, does not include cable routing variables.
In [17], optimization problems where the decision variables can be compared to a set of positions with a varying size are tackled. The authors discuss formulations where mixed integer linear problems solvers can be employed. Again, binary values encode the presence of turbines, and there are constraints such as a minimal distance between the points of each set. This formulation does not handle continuous point positions.
In mathematical programming, a concept related to variables of varying size is that of cardinality and cardinality constraints, as discussed in [18]. In this family of mixed integer non-linear programming approaches, the interval of possible values for n is divided through inequalities on n and bounds on achievable objective function in the manner of branch-and-bound and cutting-plane methods. Cutting-plane methods are not general and have been derived for specific (linear) problems. Branch-and-bound methods are general but may turn into a comprehensive enumeration of the n values if the bounds are not tight enough.
1.2.2. Evolutionary and Other Stochastic Algorithms
Evolutionary algorithms are very flexible in both the type of problems they can handle and the interfacing with other algorithms they allow. The flexibility comes from the possibility to choose the encoding of the variables and the stochastic variation operators (crossover and mutation) and adapt them to the problem at hand, as theorized with the formula in [19]. These are key reasons for the great interest shown by the computer science community for evolutionary optimization algorithms, as can be seen in [12,13,20]. In the literature, some variants of evolutionary algorithms allow us to deal with the optimization over clouds of points. Instances of recombination and mutation operators for (multi-)sets of discrete elements have been described and put in a formal theory in [21], but these operators do not properly capture the continuous nature of the position vectors. This is further discussed after the presentation of the Wasserstein-based crossovers.
In the work of [22], the number of turbines is fixed and their positions are optimized as continuous variables in a given domain. The authors compare two stochastic methods, a genetic algorithm and an ant colony optimization algorithm. The paper concludes in favor of the ant colony optimization. A similar problem formulation is considered in [23], where a stochastic greedy algorithm perturbs in a continuous manner an initial layout.
Discrete formulations of the wind-farm layout where the possible positions of the turbines are fixed a priori have also been tackled with stochastic methods. A simulated annealing algorithm is used in [24] to find an optimal set of points. A predefined grid of position cells is populated with binary occupied/empty variables.
In both [2,25], the production capacity of a wind farm is maximized while controlling the number of turbines and the land acreage. The layout is represented as a binary vector, optimized by a genetic algorithm.
The article accompanying the development of the TOPFARM tool, [26], compares a sequential linear programming algorithm from [27] to a standard genetic algorithm from [28]. The authors discuss two modelings of the decision variable. The first one maps the functions and decision variables into a linear space to benefit from the efficiency of linear programming. The second approach searches over a predefined grid of the domain. Both methods suppose a fixed number of vectors in the set.
The optimization of a cloud of continuous points is also discussed in [29], where a two-stage genetic algorithm is used to search for an optimal placement. The first stage applies a binary search over possible locations. The number of wind turbines varies during this step. Once a solution in a binary form with a fixed size is obtained, the optimal positions are considered as the centers of cells. The second stage consists of improving this solution, which is used as the initialization for a local continuous search. Our algorithm, which we present soon, has a single step, because no prior information regarding good initial solutions is known and the freezing of the number of points may cause a loss of global optimality.
Ref. [30] also adopts a two stage-method. The first step generates a grid of possible positions, i.e., it performs a discretization of the space. Next, a genetic algorithm is applied where the new variable is a vector containing binary strings. A continuation to this work can be found in [31], where the above genetic algorithm is compared to a particle swarm optimization.
1.3. Contribution of This Work
In this paper, we consider optimization problems where the decision variable is a cloud of points defined in a continuous domain with a varying number of points. We make the following claims:
- A cloud of continuous vectors can be modeled as a uniform discrete measure with finite support.
- This model helps defining a topology in the space of clouds of points using the Wasserstein distance between measures.
- We propose evolutionary crossover and mutation operators relying on the concept of the Wasserstein barycenter.
In Section 2, we introduce crossovers and mutations based on the notion of barycenter using the Wasserstein distance borrowed from optimal transport theory, [32]. In Section 3, we present the baseline algorithm, the test functions and the family of experiments. The results of the experiments, their discussion and a summary of results are included in Section 4. Some perspectives for future work are given in Section 5.
2. Wasserstein Barycenters for the Evolutionary Optimization of Sets
In this work, we consider evolutionary algorithms with a classical ES-() structure, as described in the overview papers [33,34] and summarized in Algorithm 1. Such a search method produces new generations of candidate solutions, which, in our problem, are clouds of continuous vectors, using crossover and/or mutation operations applied to the previous generation. At each iteration, the new generation is made of the best clouds among those of the previous generation and the newly created clouds. This version of ES is elitist in the sense that the best observed solution is always transmitted to the next population. In order to generate new candidate solutions, we introduce in Section 2.2 new crossover and mutation operators that can be applied to clouds of points. We do not fine-tune the different hyper-parameters, such as the population size, the number of generations and the mutation rate. In our implementation, the number of offspring is . Instead, we focus in the rest of the paper on the fundamental definitions of the different operators.
| Algorithm 1 Structure of the ES-() Algorithm |
Input: the population size, the number of iterations, F a function defined over clouds of points, Output: the best cloud of points found and its fitness value;
|
2.1. Fréchet Mean to Wasserstein Barycenter
Recall that is the Dirac measure at . To each cloud of points , we associate the measure . This mapping allows us to reformulate the considered problems as optimizations over the space of discrete uniform measures with a finite support. With this representation, we define crossovers based on the Fréchet mean (a notion developed in [35] for details). We adopt as distance between two measures the Wasserstein distance. Please note that in the literature, this concept is sometimes also called the Kantorovich metric, as in [36]. We remind readers of the following definitions.
Definition 1.
For two measures μ and ν defined over , the Wasserstein distance of order p is defined as follows:
- corresponds to the Euclidean distance between and
- is the set of all probability measures defined over with marginals μ and ν.
Definition 2.
A barycenter () of N measuring
is the minimizer of
, with .
Algorithms to compute this minimum for a fixed size are discussed in [37] and are implemented in the POT Python library [38]. For more information on this topic, specifically with regards to the existence and uniqueness of the barycenter, please refer to [39].
In the following, we consider the Euclidean distance with . We show in Figure 2 an example of such a mean between two clouds of points represented as uniform discrete measures. We can see that the barycenter inherits the shapes of the two clouds. We can demonstrate the following result, that can be interpreted as the contracting or shrinking effect of the Wasserstein barycenter.

Figure 2.
Two initial clouds at the (left, in black) and (right, in red) and their equal weight Wasserstein barycenter (i.e., their mean) in the (middle, in blue).
Theorem 1.
Consider to be the set of discrete measures over with finite support and . Let , and be defined, respectively, as
- ,
- ,
- ,
with the unique minimizer of .
- If the above is verified, we have
The proof for this theorem is provided in Appendix A. This contracting effect, when at work through the Wasserstein-barycenter-based evolutionary operators, can lead to the desertion of the edges of the search space in favor of the center of the space. We propose in the following paragraphs a way to correct this effect.
2.2. Wasserstein-Based Crossover and Mutation Operators
Within the framework of the proposed evolutionary algorithm, we rely on the Wasserstein barycenter in order to define crossover and mutation operators between two clouds of points represented as discrete uniform measures. Both operators are defined in the following paragraphs.
2.2.1. Crossover
Definition 3.
For two measures ( and ), we can compute their crossover with one of the following operators:
- Equal weight crossover: taketo be a new design.
- Random weight crossover: draw random and consideras a new design.
The support’s size of , n, is chosen as follows:
- If , then
- Otherwise, if , generate two crossovers, and , with and
A numerical illustration of the proposed crossover using the Wasserstein barycenter is given in Figure 3. One can notice that the generated clouds of points verify Theorem 1 and inherit the morphology of the parent clouds.
Figure 3.
and are two initial clouds and X represents their equal weight Wasserstein barycenter.
The above crossovers are different from the examples of recombination operators for sets described by Radcliffe in [21] because they act on the clouds as a whole, as opposed to acting on the points of the sets. A consequence is that if two clouds share a point, the Wasserstein-based crossover may move this point in order to minimize global transport, while the genetic set recombination operators will always preserve it (the “respect” property). Fundamentally, the difference is the equivalence class underlying each crossover: in genetic set recombination, the equivalence class is the presence (or absence) of elements (points); in the Wasserstein-based crossover, there is a continuum of elements (the points with their positions), and the equivalence relation is based on the mass of points within sub-regions of the domain. With equivalence classes based on mass of points within regions, the Wasserstein-based crossovers are instances of the very general operators (random respectful recombination —R3— and random transmitting recombination —RTR—) described by Surry and Radcliffe [19].
2.2.2. Mutation
We introduce below the boundary mutation, which includes points located at the border of the domain in order to dilate the clouds and counteract the previously discussed shrinking effect.
Definition 4.
The boundary mutation of a cloud of points is defined as
where is a cloud of points at the domain boundary that can be randomly sampled. In the union , the repetitions of identical points are allowed. To clarify, for a polygon, is the union of points randomly sampled on its sides. For this mutation, the size of the support of is permitted to be equal to the one of .
We also introduce a more general mutation, defined as follows:
Definition 5.
The full domain mutation of a cloud of points is defined as
where is the union of points uniformly sampled in the domain. Its size is chosen randomly with one of the two following schemes:
- in the space of all possible sizes: full size choice
- in with : ternary size choice.
The number of the resulting clouds of points and their supports’ sizes are determined with the same method as the one used in the crossover.
The proposed boundary mutation can be compared to the Levy flight jumps used in particle swarm optimization (PSO) [40]. Both boundary mutation and Levy flights enable large perturbations of the current solutions. When the random weight is almost null, the produced clouds differ a lot from the clouds before the mutation, and similarly, the Levy flights can result in substantial movement of a given particle. Both mechanisms help avoiding premature convergence, which is a risk coming from the contracting crossover and the elitist population replacement. However, the boundary mutation and Levy flights differ substantially:
- The weight is uniformly random, whereas Levy flights jumps occur deterministically in case of prolonged stagnation.
- In the space of clouds, the boundary mutation is focused towards expanding the cloud of points, which is a design choice meant to counteract the effect of crossover, whereas the Levy flights have no preferential direction of perturbation.
Figure 4 illustrates the boundary mutation of an initial cloud (X) on the left and its full domain mutation on the right. With boundary mutation, the points only move slightly and some of them are dilated outside of the initial cloud, whereas the full domain mutation disrupts the cloud more noticeably and in a way less oriented towards the boundary.
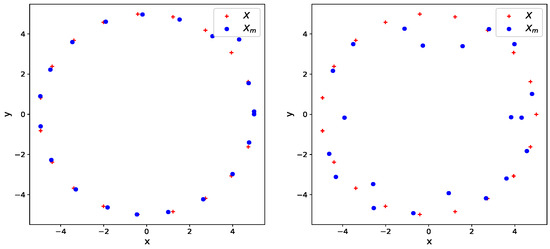
Figure 4.
X and are, respectively, the initial cloud and the cloud mutated with a Wasserstein-based mutation. Boundary mutation on the (left) and full domain mutation on the (right).
If , then . Otherwise, the mutation produces two sets, one with and one with . The two (Boundary and Full Domain) mutations can be arranged in the different ways, as explained below.
2.3. An Alternating Mutation
A first type of mutation based on Wasserstein operators alternates, with a random weight, prob, between the boundary and the full domain mutations. It is detailed in Algorithm 2. prob is the probability to apply a boundary mutation, 1-prob is the probability to apply a full domain mutation.
| Algorithm 2 Alternating Wasserstein mutation |
Input: X cloud to mutate, prob the probability to perform a Boundary mutation Output: The mutated cloud(s)
|
2.4. Successive Boundary and Full Domain Mutations
Boundary mutation and full domain mutation may be called successively in a deterministic fashion. Two alternative ways to weight the barycenters are considered.
2.4.1. Successive Mutations with Independent Random Weights
The first version of the successive mutation considers independent random weights in the mutations and is given in Algorithm 3. The choice of two different weights allows us to differentiate the importance of the two operators.
| Algorithm 3 Independently Weighted (Wasserstein) mutation |
Input: X cloud to mutate Output: The mutated cloud(s);
|
The boundary mutation is executed at the end because it is designed to correct statistically the contracting effect of the Wasserstein barycenter in the bounded domain of the optimization problem.
2.4.2. Successive Mutations with a Single Random Weight
The last mutation follows the same sequential, systematic call to the boundary and full domain operators but considers a single weight for the two operators, as described in Algorithm 4.
| Algorithm 4 Uniquely Weighted (Wasserstein) mutation |
Input: X cloud to mutate Output: The mutated cloud(s);
|
Given a cloud of points X, the number of resulting clouds after a mutation is either one or two. In fact, the boundary mutation always gives a single output, while full domain mutation can give two if the the size of is different from the one of X. By combining crossover and mutation operations, the number of resulting clouds of points after the entire processing of X is between one and four, since two crossovers may occur.
It can be interesting to point out that the full domain mutation with full size choice allows us, in theory, to evaluate any cloud of points X within the boundaries at any given iteration of the optimization procedure. Indeed, with a value of , we obtain that is in the neighborhood of . In the case of ternary size choice, the exploration of any cloud of points may, instead, require several iterations but is still possible. The introduced operators can therefore attain any cloud of points, which asymptotically guarantees a global convergence. Reaching the global optimum through such a random mechanism may be very slow, which is why the proposed algorithm has other features allowing us to speed it up.
3. Numerical Analysis
In this section, we present a baseline algorithm and a set of test functions defined over clouds of points that will allow us to assess the performance of the proposed algorithms.
3.1. A Classical Evolutionary Algorithm Applied to Sets
In order to provide a baseline algorithm, we consider an evolutionary algorithm based on classical operators that, by default, processes sequences of vectors. It can be applied to sets of points with minor modifications, namely, by using the crossover and mutation operators defined below. This algorithm is thought to be a default implementation, serving as a comparison baseline. It is important to note that it does not account for the property of sets of being invariant under point permutation.
3.1.1. Baseline Algorithm Encoding and Crossover
The first step of the algorithm consists of modeling the design variable as an ordered concatenation of points padded with a no-point symbol up to a given maximal cardinality, . The empty points indicate that the size of the set of vectors is not maximal. With such encoding, it is natural to rely on a uniform crossover that randomly switches portions of the sequences corresponding to points between the two parents. The only subtlety being that the no-point symbols are pushed to the right of the sequence to accelerate the convergence towards solutions with an optimal cloud cardinality. The crossover operator is presented in Algorithm 5.
| Algorithm 5 Uniform crossover between sequences |
Input: and Output: their crossover
|
Four examples of uniform crossovers on sequences are given in Figure 5. Contrary to the Wasserstein-based crossovers of Figure 3, the newly generated clouds only contain points drawn from the two parents. In probabilistic terms, the support of the resulting discrete distribution is a subset of the union of the supports of the parent distributions, a mechanism fundamentally different from Wasserstein barycenters.
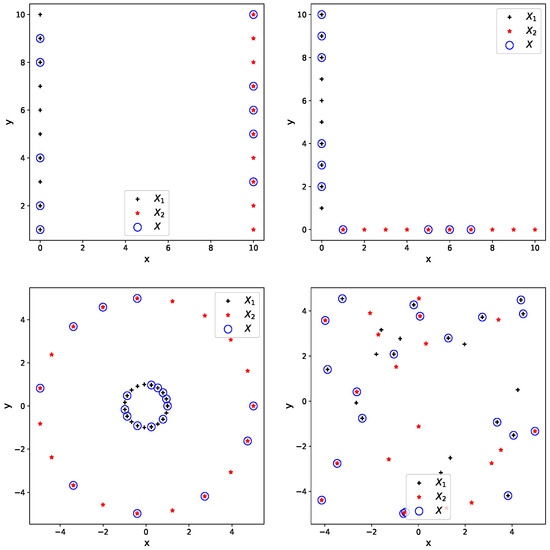
Figure 5.
(black crosses) and (red stars) are two initial clouds, and X (blue circles) represent samples of uniform crossings on sequences.
3.1.2. Mutation
During the mutation, the size of each cloud is changed randomly within the interval bounded by its two nearest integers, and each point is disturbed with an isotropic Gaussian noise. This fairly classical operator, called the Gaussian mutation [41], is detailed in Algorithm 6. In order to avoid obtaining points outside of the domain or with an incoherent cardinality, truncated versions of the discrete law on the cloud size and of the Gaussian perturbations are used. In evolution strategies, the parametrization of the Gaussian mutation standard deviation, , is a key to the optimization dynamics and is sometimes adapted along the search [42]. Here, in the spirit of genetic algorithms, a fixed mutation strength is chosen. More details about are given in Section 3.2.1.
| Algorithm 6 Gaussian mutation |
Input: , Output: A mutation of X
|
We show in Figure 6 the effect of a Gaussian mutation on a given cloud of points, where we can see how all the points are perturbed, as well as the effect of the noise truncation.
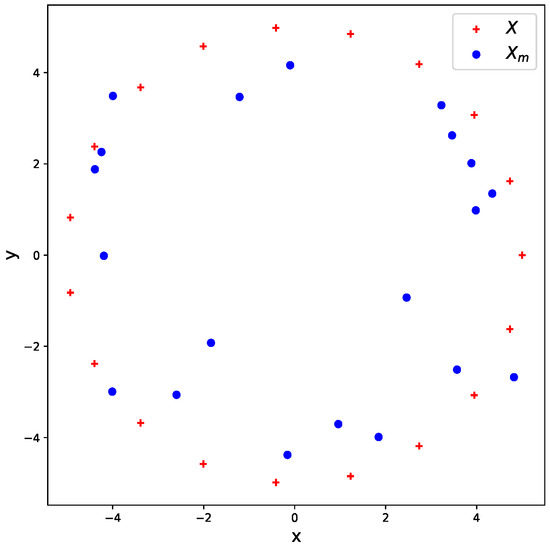
Figure 6.
X (red crosses) and (blue points) are, respectively, the initial cloud and an instance of the mutated cloud with the truncated Gaussian mutation. The value of is 3.333.
The complete algorithm, consistent with the structure outlined in Algorithm 1 and characterized by the uniform crossover on the sequence encoding and the truncated Gaussian mutation, serves as a reference evolutionary algorithm and is referred to as Ref_alg in the remainder of this work.
3.2. Experimental Protocol
In the following paragraphs, we provide some information regarding the numerical experiments that were performed in order to assess the performance of the algorithms.
3.2.1. Algorithms Settings
For all the experiments, the algorithms’ hyperparameters are set as follows:
- We consider square search domains. The length of each side is 100.
- A discretization of step 1 is applied to each side for the sampling on the boundaries for boundary mutation. Continuous alternatives, however, should also work.
- , , .
- The population size is set equal to 10 times the average number of active components in each set, = 300, and the maximum number of iterations of the algorithms is .
- Regarding the choice of , we consider it proportional to , where X and are points sampled uniformly in the domain. The latter quantity is the mean squared distance between two points sampled uniformly in the domain. In a centered-squared domain of side L, we obtain with , the variance of a uniform continuous law. In our case, .
- The default value of prob (Algorithm 2), if not specified, is 0.5.
We denote the proposed evolutionary algorithm, with Wasserstein barycenter-based operators, as Wasserstein-barycenter-based generator evolutionary algorithm (WBGEA). The different versions of this algorithm that we are studying are identified with specific names and presented in Table 1.

Table 1.
Acronyms of the algorithms studied and names of their evolution operators.
Comparing specific versions of these algorithms with each other sheds some light on specific questions. These experiments and the questions addressed are detailed in Table 2.

Table 2.
The different experiments and the associated scientific questions.
The test functions used in order to perform the previously described experiments are presented in Section 3.3.
3.2.2. Performance Metrics
Two performance metrics are observed: the objective function value of the best solution so far and the population diversity. The population diversity allows us to check if all clouds of the population have converged to the same design, which may impair the ability of the search to locate the optimal solution if this convergence is premature. The diversity can be calculated at each iteration in the following way:
where is a population of sets, the associated discrete measures, and is the Wasserstein barycenter of the clouds of pop. The support’s size of is chosen to be the mode of all sizes in pop. As an alternative to the population diversity, one can look at the variance of the objective function values for the clouds in the population. Although it is cheaper to calculate than the diversity, it is more difficult to interpret as its scale depends on the objective function, if the output functions are not normalized. A very flat function would have a low population function variance even if its population is diverse. The population diversity and the best so far objective function provide complementary information. On the one hand, when an evolutionary algorithm has a high performance and a low diversity, it is likely converging towards a global optimum. On the other hand, a low population diversity associated with a poor best objective is a sign that convergence is occurring prematurely to a non-optimal set. Other diversity-performance configurations can occur: for example, a very explorative algorithm maintains by definition a high population diversity, yet it can be high performing if its search operators are biased towards the global optima.
In the numerical experiments reported later, the mean and the standard deviation of both metrics, the best so far objective function and the population diversity are estimated over the 20 repetitions for each algorithm’s variant and each test function.
3.3. Analytical Test Functions
The algorithms described above are tested on several functions taking sets of vectors as inputs. These functions are simplifications of some of the many situations which can be naturally be parameterized as sets of vectors. Wind farms and well fields are two examples, inspiring the wind farm proxy below. Design of experiments can, in some cases, be seen as the optimization of a function taking sets of vectors as inputs, as is the case for the maximin function [43] Finally, the inertia function is also considered. This function can be encountered in multi-component systems such as the accumulated energy or as the regularization term in ridge regression problems. Within the framework of optimization problems, all these test functions need to be maximized.
3.3.1. Wind Farm Proxy
A first family of test functions emulates the energy production of a wind farm. Each wind turbine yields a certain amount of energy which depends on the wake effect caused by neighboring turbines. The inputs are in the form of a cloud of points , with (). Each represents the Cartesian coordinates of a turbine. The test function given below represents the total yield considering all turbines,
Details about the function (representing the gain factor of the turbine due to the wake effect of ) and (a constant representing the maximal yield of a given turbine) may be found in Appendix C. In the remainder of the paper, we use the following notations:
- stands for functions that account for wind coming from a single direction .
- stands for functions modeling the average effect of n wind directions chosen in .
We consider the following test functions: , , , . The function calculates the average production over four directions: 0, 60, 120 (0 is chosen two times). We provide graphical representations of with for the four scenarios in Figure 7. These graphics show the amplitude of the wake interaction between two turbines, depending on their relative position and the direction of the wind. For instance, in the case , we can notice that the scale of the interaction is more important in the direction of the wind and only occurs behind the fixed turbine.
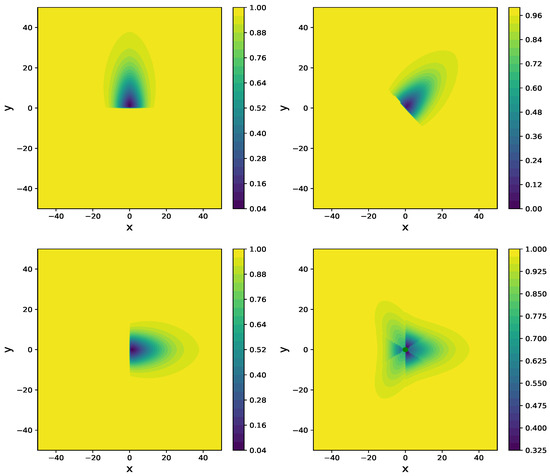
Figure 7.
Representation of with at (top left), (top right), (bottom left), and averaged directions at (bottom right).
is obtained by summing the contribution of each point. We give two examples ( and ) of the function layouts in Figure 8, where nine points are fixed and one is allowed to vary. The values next to the points show their individual contribution to the total production. There is no unit of measure. We can see that the yield of an additional point depends on the direction of the wind and the placement of the existing points. and are just rotations of one another and the interest in keeping both of them is to check the invariance of the algorithms with respect to a rotation of the solution, a property that is not satisfied by all optimization algorithms, as discussed in [44].
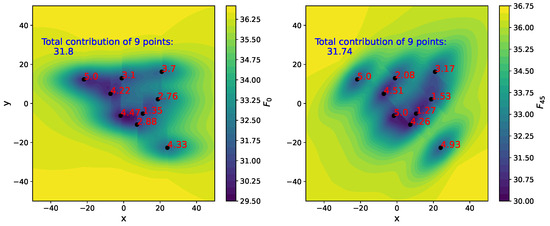
Figure 8.
Representation of and with nine fixed points and one varying. The maximal contribution of a point is fixed to 5.
3.3.2. MinDist Function
Maximizing the smallest distance between points is a popular criterion for designing experiments. It provides another example of a function with a set of vectors as input. We denote a design as with for some . Let us consider our second test function to be
It is noteworthy that, de facto, this function only depends on the values of two components of the input set, namely, the two closest ones, as opposed to the other considered functions that factor in all of the set components.
3.3.3. Inertia Function
Lastly, we consider the function modeling the inertia of a group of points in . For , it is given by
where is the center of mass of the point coordinates, .
The family of test functions have been chosen to offer, a priori, a good diversity of situations: for , one of its global optimum is a cloud where the points are split between the corners of the domain, while takes a space-filling cloud as solution, and the wind-farm functions are maximized by clouds with some alignments that depend on . Samples of good designs are plotted in Figure 9.
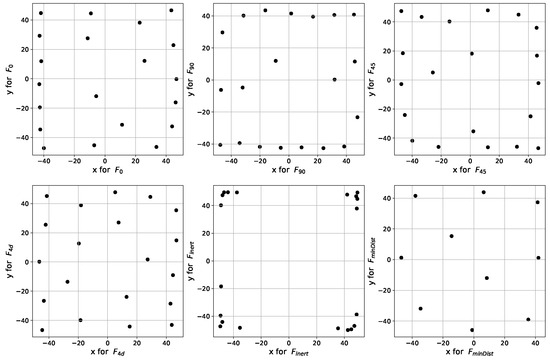
Figure 9.
Best observed designs corresponding, respectively, to the test cases , , , , and (left to right, top to bottom).
3.4. Designs Returned by the Algorithm WBGEA_1t_nc
Figure 9 gathers the best designs found by the WBGEA_1t_nc (Wasserstein-based, ternary mutation of the size, no crossover, as explained in Table 2) variant of the algorithm. These designs are also the best overall observed solutions for the test functions. The best observed solutions correspond to what is produced by a stochastic, evolutionary algorithm after 500 iterations with a population size of and an initial population of 300, which sums up to 150,300 calls to the objective function. They are not fully converged and could be fine tuned by a local search. We have chosen to show these solutions, produced by the evolutionary algorithms without local fine tuning, for a more realistic reporting of their performance. It can be seen that the designs are consistent with the simulated physical phenomena. The points are placed optimally according to the wind directions for the wind-farm functions. For instance, concerning ’s best design, we see that the vertical distances between the points are smaller than the horizontal ones, and there is an alignment of some of the wind turbines at the domain boundary where the wind enters (). The optimal number of points (i.e., turbines) in the set is , as all possible turbines are used to maximize power production. The best observed design for is approximately a rotation of the solution. The solutions to and are not rotations of the solutions or because the square domain is not rotation invariant for these angles. The best designs for have points located in the corners, where they contribute the most to the total inertia. The optimal design for has, logically, points that are spread over all of the domain.
4. Results and Discussions
The series of questions listed in Table 2 are addressed one by one. In order to be brief, concerning wind-farm functions, only the statistics of the performances on are represented. , and have their results presented separately. For each experiment, and for each function, we first discuss the evolution of the current optimum during the optimization iterations and then the evolution of the population diversity.
4.1. Study of a Wasserstein-Based Evolutionary Algorithm
The analysis of Wasserstein evolutionary operators is designed through two series of experiments. The first series studies the implementation of the boundary and full domain mutations; the second is about the sampling of the set size.
4.1.1. Alternating vs. Successive Boundary and Full Domain Mutations
In this experiment, we compare the performances of the three mutations defined in Algorithms 2–4. They are all combined with the crossover defined in (2), and correspond to the algorithms named WBGEA_1, WBGEA_2 and WBGEA_3, respectively. Figure 10, Figure 11 and Figure 12 show (on their lefts) statistics of the best so far objective function values throughout the iterations for the wind farm, the inertia and the point minimum distance cases, respectively. In all of the plots, the implementation WBGEA_1 (which has the alternating mutation) clearly outperforms WBGEA_2 and WBGEA_3 (which have successive mutations). In a more subtle way, WBGEA_2 yields better results than WBGEA_3 in all tests with a compromised speed on . When considering the associated diversity measures in Figure 10, Figure 11 and Figure 12 (on their rights), it is observed that populations in WBGEA_1 always converge faster than those in WBGEA_2 and WBGEA_3. The diversity drops faster with WBGEA_3 than with WBGEA_2 except on .
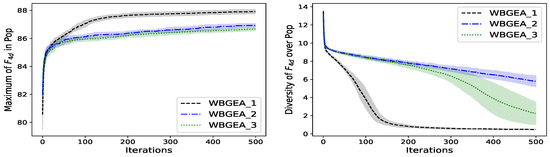
Figure 10.
Alternating vs. Successive Boundary and Full Domain Mutations. The test function is the wind-farm layout problem averaged over 4 directions, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
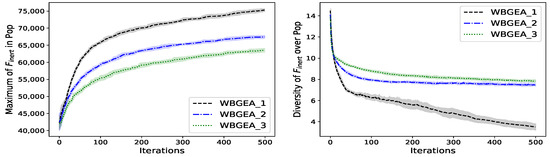
Figure 11.
Alternating vs. Successive Boundary and Full Domain Mutations. The test function is the inertia function, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
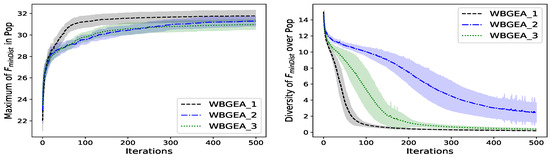
Figure 12.
Alternating vs. Successive Boundary and Full Domain Mutations. The test function is the MinDist function, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
The fact that the boundary and the full domain mutations occur one at a time is the determining advantage of WBGEA_1 over WBGEA_2 and WBGEA_3. If one of the two mutations is detrimental, it will be avoided in fifty percent (prob = 0.5) of the sample cases. The difference between WBGEA_2 and WBGEA_3 follows the same independence idea in a less perceptible way: there will be situations where is large and small, or vice versa, creating some independence between the two mutations. On the contrary, in WBGEA_3, the boundary and full domain mutations are always applied together with the same intensity. These tests suggest a mutation independence principle: for composite mutations made of different types of perturbations, like the boundary and the full domain mutations, the perturbations should be applied independently. The population’s diversity drops faster in WBGEA_1 than in WBGEA_2 and WBGEA_3, suggesting, in conjunction with its better objective values, that WBGEA_1 is more efficiently converging towards the global optima. Conversely, WBGEA_3 is more prone to premature convergence than WBGEA_2, therefore losing diversity faster. With the inertia function, , neither WBGEA_2 nor WBGEA_3 manage to converge: the population diversity plateaus at a relatively high level (about 8).
4.1.2. Handling of Set Size in Mutation: Ternary vs. Full Size
We investigate the role of the size of (Definition 5 for the full domain mutation) in the performances of WBGEA_1. To this aim, the two algorithms compared are WBGEA_1 and WBGEA_1t. In WBGEA_1t, during the full domain mutation, the size of the random cloud is chosen in the triplet composed of the size of the cloud to be mutated and its two nearest integers, while in WBGEA_1, it is chosen in the set of all possible sizes. There is not a great difference in terms of the optimal values returned by the two algorithms except on . Nevertheless, the difference between full and ternary mutations for the size is always to the benefit of the ternary mutation. More details are given in Appendix B. In the following, the ternary mutation, which is more efficient, serves as the default implementation.
4.2. Comparison of Wasserstein and Sequence-Based Operators
4.2.1. Wasserstein-Based vs. Reference Evolutionary Algorithm
In this Section, the default Wasserstein-based algorithm, WBGEA_1t, is compared to the baseline evolutionary algorithm, Ref_alg (Table 1 for the acronyms).
We observe that WBGEA_1t works better than Ref_alg in terms of both convergence speed and final value on the wind-farm problem (Figure 13). Ref_alg, with its classical crossover and Gaussian mutation, is not efficient at learning designs with specific geometrical characteristics such as alignments, which are important in the case of wind farms. The left plot in Figure 14 shows that WBGEA_1t converges faster than Ref_alg on .
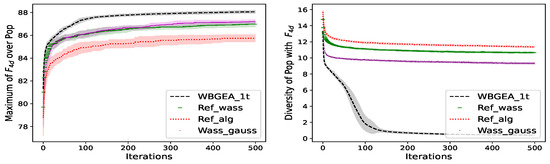
Figure 13.
Wasserstein vs. Classical Evolutionary Operators. The test function is the wind-farm layout problem averaged over 4 directions, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
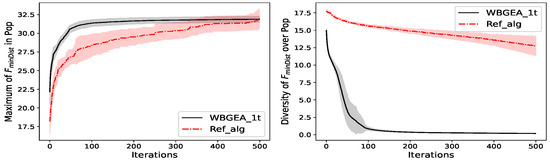
Figure 14.
Wasserstein-Based vs. Reference Evolutionary Algorithm. The test function is the MinDist function, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
As is often seen in the experiments, the behavior of the algorithms is different with the inertia function, . There, as seen on the left plot of Figure 15, Ref_alg outperforms WBGEA_1t. To explain this, another version of WBGEA_1t is tried where the probability to apply the boundary mutation, prob, is raised to 1, which simultaneously prohibits any full domain mutation. The boundary mutation is, of course, adapted to since its optimum has points only on the boundary. WBGEA_1t with only boundary mutations (prob = 1) yields similar final values as Ref_alg, although it converges more slowly (left plot of the Figure 15).
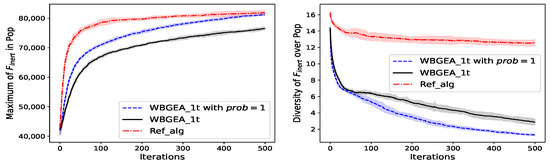
Figure 15.
Wasserstein-Based vs. Reference Evolutionary Algorithm. The test function is the inertia function, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
The diversity of WBGEA_1t decreases to zero more rapidly on the wind farm proxy (right plot of the Figure 13) and (right plot of Figure 14) than on , where the drop is slower (right plot of Figure 15). For these situations, the loss of diversity is associated with a convergence towards a global optimum. For the same reason, increasing the rate of application of the boundary mutation by changing prob from 0.5 to 1 helps in locating global optima and decreases diversity.
Concerning Ref_alg, the diversities of the populations stagnate at a high level for all the test functions (see right plot in Figure 13, Figure 14 and Figure 15). While a convergence of the population to a global optimum induces, by definition, a loss of diversity, the experiment with Ref_alg on function shows that evolutionary algorithms have other long term behaviors: the population remains very diverse, yet the best points approach the optimum consistently throughout repeated runs. The preservation of a high diversity is thought to be an effect of the constant Gaussian mutation strength, , and of the crossover over sequences, which exchange points from the crossed sets.
4.2.2. Wasserstein vs. Classical Evolutionary Operators
In order to better understand the role of the operators, we now invert the mutations of WBGEA_1t and Ref_alg, and the two new obtained algorithms are denoted by Wass_gauss and Ref_wass.
The left plots of Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17 illustrate that in general, the Wasserstein crossover (Equation (2)) outperforms the uniform crossover on sequences (Algorithm 5) when the mutation is the same. Compare Ref_alg to Wass_gauss, which both have a Gaussian mutation, and Ref_wass to WBGEA_1t, which both have an a Wasserstein mutation: the versions with the Wasserstein crossover perform best on all the test functions except . By comparing Ref_wass to Ref_alg, the same graphics demonstrate that, when combined to the uniform crossover, the Wasserstein-based mutation is better than the Gaussian mutation on the wind farm and tests. The performances of WBGEA_1t and Wass_gauss on the left plots of Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17 show that the alternating Wasserstein mutation (Algorithm 2) outdoes the Gaussian mutation (Algorithm 6) when the crossover is Wasserstein-based only on the wind-farm problem.
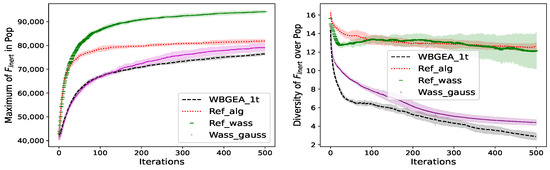
Figure 16.
Wasserstein vs. Classical Evolutionary Operators. The test function is the inertia function, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
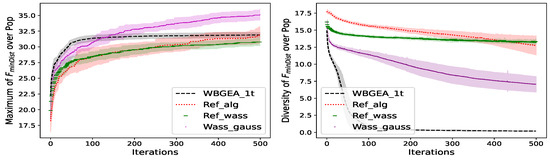
Figure 17.
Wasserstein vs. Classical Evolutionary Operators. The test function is the MinDist function, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
The right plots of Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17 illustrate also that the presence of the classical operators, the uniform crossover on sequences and the Gaussian mutation in the algorithms Ref_alg, Ref_wass and Wass_gauss result in large population diversities on all the test functions. On the contrary, WBGEA_1t, which is based uniquely on Wasserstein operators, has vanishing diversities.
The good results achieved by the algorithms based on Wasserstein operators on the wind farm can be explained by the geometrical properties of their optimal designs: the good solutions for such problems are expected to possess more restrictive geometrical properties, such as regular alignments. On the contrary, the optimal design of has points grouped at the four corners of the domain, which, as will soon be seen, is very favorable to the uniform crossover on sequences. , with its good designs made of points spread over the domain, has an intermediate status made of some alignments for the highest performance solutions but is otherwise sensitive to point local positions.
4.3. Investigating the Role of the Mutation and the Crossover
4.3.1. Role of Crossover
In this section, we investigate the role of crossover, starting from the equal weight crossover, finishing with no crossover and going through a random weight crossover.
- Relaxed Crossover
The crossover used so far has equal weights as in Equation (2) and is compared to the random weight crossover of Equation (3). Having random weights is a form of relaxation in the sense that small and large weights make the crossover result similar to one from the parent cloud. The algorithms with equal and random weight crossovers are denoted WBGEA_1t and WBGEA_1t_rc, respectively.
The left plots of Figure 18, Figure 19 and Figure 20 show that the random weight crossover is more competitive than the equal weight crossover for all the considered test functions, (but on , see Table 3).
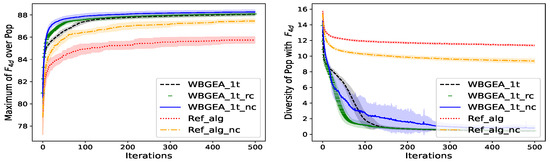
Figure 18.
Relaxed Crossover. The test function is the wind-farm layout problem averaged over 4 directions, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
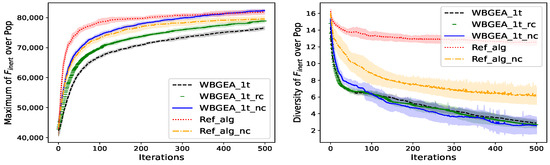
Figure 19.
Relaxed Crossover. The test function is the inertia function, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
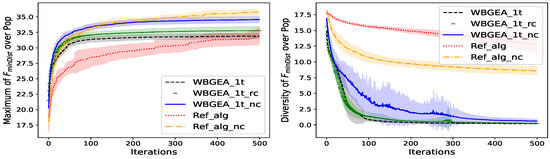
Figure 20.
Relaxed Crossover. The test function is the MinDist function, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.

Table 3.
Mean (with 5 significant digits) ± std. deviation of the best values returned by the algorithms, calculated over 20 independent repetitions for each test function. For each function, the best results are boldfaced.
The superiority of the random weight crossover is related to its ability to produce clouds close to one from their parent when the weight is close to 0 or 1. This allows us to not always destroy the previously selected designs. Such an explanation follows the same line as the mutation independence principle mentioned in Section 4.1.1: because the evolutionary operators may not always lead to better solutions, in particular when applied to already selected high-performing solutions, it is useful to be able to, sometimes, diminish their effect due to randomness.
The evolution of the population diversities of WBGEA_1t_rc and WBGEA_1t on the right of Figure 18, Figure 19 and Figure 20 shows a faster decrease in diversity with the random weight crossover in the wind-farm case, which may be explained by a faster convergence to good solutions. No clear difference in diversity evolution is observed for functions and .
- Absence of Crossover
Variants of the algorithms where no crossover takes place are tested under the names WBGEA_1t_nc and Ref_alg_nc, i.e., they are equipped solely with mutations. We observe on the left of Figure 18, Figure 19 and Figure 20 that the absence of crossover improves the performances of both algorithms, WBGEA_1t and Ref_alg, on all the test functions, with the exception of Ref_alg on . The single Wasserstein mutation (WBGEA_1t_nc) makes the best algorithm for the wind-farm test function. The effect of the crossover on the diversity, as reported on the right of Figure 18, Figure 19 and Figure 20, is different between the uniform crossover on the sequence encoding and the Wasserstein-based crossover. The uniform crossover, through its point shuffling effect, is a provider of diversity. Removing it from the algorithm decreases diversity. The Wasserstein-based crossover replaces pairs of clouds by their barycenter, therefore reducing diversity. Removing it from the algorithm increases diversity, which is visible after about 100 iterations in the wind-farm case. Often, this effect is not as clear with , presumably because removing the crossover from WBGEA_1t makes it converge to the optimum, which contributes to reducing diversity.
4.3.2. Role of the Boundary Mutation
The following results further investigate the role of the boundary mutation within the alternating Wasserstein mutation (Algorithm 2). This mutation carries out a boundary mutation with a probability of prob or a full domain mutation with a probability of 1-prob.
The different values of prob studied are 1, 0.5, 0.1, 0.05 and 0 within the WBGEA_1t_nc algorithm (i.e., there is no crossover).
We observe on the left of Figure 21, Figure 22 and Figure 23 that when we diminish the probability of performing the boundary mutation (prob) from 0.5 to 0, the performances of the algorithms (speed and optimality) decrease on all the test functions. However, a maximal value of prob is not the optimal configuration of WBGEA_1t_nc since when prob = 1, the performance of is inferior to the one with prob = 0.5.
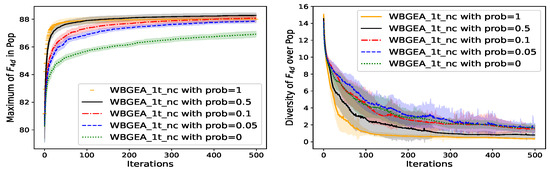
Figure 21.
Role of the Boundary Mutation. The test function is the wind-farm layout problem averaged over 4 directions, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
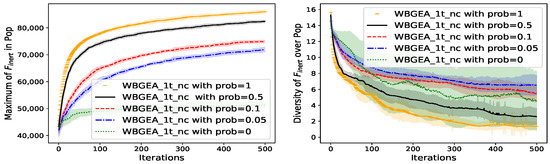
Figure 22.
Role of the Boundary Mutation. The test function is the inertia function, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
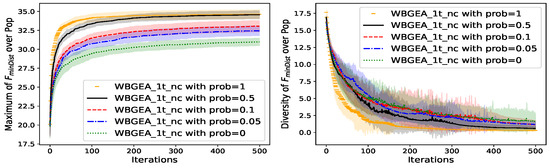
Figure 23.
Role of the Boundary Mutation. The test function is the MinDist function, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
The diversity varies in the opposite way of the performances (right plot of Figure 21, Figure 22 and Figure 23), except for WBGEA_1t_nc with prob = 0 and prob = 1.
The small chances of boundary mutation favor the contracting property stated in Theorem 1 of the Wasserstein barycenter in the full domain mutation. During the latter (full domain mutation), the clouds of points are randomly sampled in the domain and their barycenters are contained in the convex hull of their unions, which contain points in the boundaries with small probabilities. The optimal solutions of the functions making the test cases contain some points neighboring the domain boundaries, which explains why high values of prob favor good performances. Here, the boundary mutation constitutes an essential ingredient in the design of optimal clouds of points.
The increase in diversity with 1-prob comes from the fact that with the shortage of the boundary mutation and the associated increase in full domain mutation, the algorithms bear a closer resemblance to a random research.
4.4. Synthesis
In Table 3, the mean best values plus/minus their standard deviations obtained by each algorithm over 20 repetitions are given. These values are found after 500 iterations with a population size of and an initial population of 300, which sums up to 150,300 calls to the objective function. At such an evaluation budget, the following phenomena take place: on all functions but the inertia, , crossover is counterproductive. stands as an exception with an optimal design made of points symmetrically divided between the corners of the domain, and it benefits from the mixing effect of the classical uniform crossover. Wasserstein-based operators are better at preserving global point structures than sequence based operators and are thus best fitted for problems such as the wind-farm layouts. The smallest distance between points, , is conditioned by individual point positions (as opposed to global structures) and is a good match to the Gaussian mutation. With this in mind, WBGEA_1t_nc yields the best results on the wind-farm test functions. The Gaussian mutation provides (Ref_alg_nc) the best results only on , and Ref_wass is the best contestant for .
The main conclusions, derived from the different experiments, are summarized in Table 4. The following, complementary, general comments should be made.

Table 4.
Summary of experimental questions and conclusions.
4.4.1. Wasserstein-Based Operators
A key result of this study is that when all other components of the algorithms are kept the same, switching from a sequence-based to a Wasserstein-based operator is beneficial. The only exception is the uniform crossover with . We believe that this is related to the conservation of geometrical structure that is allowed by the Wasserstein barycenters underlying the studied evolutionary operators. Figure 2, Figure 3 and Figure 4 illustrate this conservation property.
4.4.2. The Test Suite
The six problems tested give consistent results to the exception of the inertia function, . It is likely that this is because is almost an additive function: it is an additive function provided that the center of inertia of the points, in Equation (6), does not change. Such functions match well with the building blocks assumption of the Schemata Theorem [12], in a manner similar to the royal road functions [45], and benefit from the action of the traditional uniform crossover. The four wind turbine layout problems yield close results. It is confirmed that all the algorithms investigated are rotation invariant as the same statistics (up to the confidence intervals accuracy) are found with and . This is consistent with the operator (Gaussian mutation, Wasserstein barycenters, uniform crossovers) definitions that are all isotropic, i.e., they handle directions in the same way. Results advocating a high rate of use for the boundary mutation show that our test suite is slightly biased towards operators that help putting points on the domain boundary.
4.4.3. On the Random Choice of Operators
The choice of the best evolutionary operators is a difficult problem as it depends in a nonlinear fashion on the objective function and on the search budget [46]. In many ways, it can be considered most of the research in evolutionary computation deals with this question, and the current study is no exception. When it comes to choosing between several operators, the boundary or the full domain mutation, or the equal weight or no crossover, we found that a simple strategy is robust and well-performing, even though it may not be the overall best: choose randomly between the options while allowing each of them to act alone. The alternating mutation applies at random either the boundary or the full domain mutation. The random crossover has effects that range between those of the equal weight crossover and those of no crossover. Such a randomized choice of operator has the advantage of keeping the possibility that each operator contributes to candidate solutions, sometimes without the addition of the effect of the other operators. This constitutes an element of robustness with respect to changing functions and population compositions. It comes at the cost of missing the best operator tuning for a specific task.
4.4.4. Population Diversity: Summary of Results and Visualization
The experimental results present the population diversity, defined in Equation (4), as a complement to the best so far objective function values. The pair of metrics, objective value and population diversity, was anticipated to allow us to discriminate between premature and global convergences. The results have further shown that a variety of scenarios occur in evolutionary optimization: the Wasserstein-based algorithms (WBGEA_…) typically have low population diversities, while sequence-based algorithms (Ref_…) maintain more diverse populations throughout the search.
The objective function impacts the diversity: all versions of algorithms tested, whether Wasserstein or sequence-based, are slow at reducing the diversity when applied to , the inertia function. In the other functions, the diversity of Wasserstein-based optimizers drops to near 0 after about 200 iterations.
Diversity in itself is not indicative of an algorithm’s performance. For example, in Figure 19, looking at , WBGEA_1t_nc and Ref_alg_nc attain comparable objectives but WBGEA_1t_nc and Ref_alg_nc have a low and a high diversity, respectively.
In addition to diversity, the variance of the functions in the populations has been recorded. The information provided by variance is similar to that of diversity, with the additional difficulty created by the varying functions scales. For this reason, we do not report variance results here.
5. Conclusions and Perspectives
We have proposed new evolutionary algorithms made to optimize functions defined over sets of points. The mutation and crossover operators are based on Wasserstein barycenters. The performances of the algorithms were tested on a family of test functions including wind-farm layout emulators. We have proven that the Wasserstein barycenter contracts the points within the convex hull of existing points. To counteract this effect, we have introduced the boundary mutation that biases the Wasserstein barycenters towards the domain boundaries. Our experiments have shown that because Wasserstein-based operators better preserve the geometrical structure of point sets than traditional sequence-based operators, they allow performance gains: replacing a classical operator with its Wasserstein equivalent always improved the search. As a side result, we have found that on our point set test suite, the crossovers are, on average, detrimental to the search. The designs returned by the Wasserstein-based evolutionary algorithm were satisfactory in that they made physical sense: the best wind-farm layouts spread the turbines over the entire design domain and had alignments perpendicular to dominating wind directions; the designs for inertia had points grouped at the corners of the domain; the designs for maximin point distance had uniformly spread points. Of course, these solutions, which were generated by stochastic (evolutionary) optimizers, would benefit from a final fine-tuning with a local search.
This work would benefit from three short term continuations. First, the domain of definition of the points in the set might be non convex. For example, one could consider domains with a hole inside, as happens with overland wind farms. The current operators, through the Wasserstein barycenters, will create points in such a hole and need to be upgraded.
Another continuation is to investigate the effectiveness of the algorithm for clouds of points of dimensions greater than two.
Third, when dealing with computationally expensive functions over point sets, the proposed evolutionary algorithm could be included within a Bayesian optimization algorithm, where it would allow us to optimize the acquisition criteria.
A longer term continuation to this work is to extend it to clouds of colored points. An example would be to optimally select the technology of the wind turbines (the color) within a catalog while optimizing the farm layout.
Author Contributions
Conceptualization, B.S., R.L.R., J.P., M.K. and S.Z.; methodology, B.S., R.L.R. and J.P.; software, B.S.; formal analysis, B.S., R.L.R. and J.P.; writing—original draft preparation, B.S.; writing—review and editing, B.S., R.L.R., J.P., M.K. and S.Z.; visualization, B.S.; supervision, R.L.R., J.P., M.K. and S.Z.; project administration, R.L.R., M.K., J.P. and S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded in part by the French Agence Nationale de la Recherche through the SAMOURAI project, ANR-20-CE46-0013.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
The pseudo-code of the algorithms and the test functions are described in the paper. The hyper-parameters of the algorithms are also given. For any question for future use, please contact authors.
Conflicts of Interest
Authors Julien Pelamatti, Merlin Keller and Sanaa Zannane were employed by the company EDF R&D. The remaining authors declare that the re-search was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
Main notations and abbreviations
| d | Dimension of a vector |
| A compact subset of | |
| The diversity of pop, a population of sets | |
| n, | Size of sets of vectors |
| prob | Probability to perform a boundary mutation |
| A measure associated with a set of points X | |
| The set of discrete measures with finite support | |
| Dirac function | |
| Gaussian mutation variance | |
| Set of n unordered points where and . It will be referred to as a cloud, set or bag of points (or vectors). Compared to an (ordered) list of points, X is invariant with respect to any point permutation because it is a set. | |
| Number of vectors in X |
Appendix A. Proof That the Wasserstein Barycenter Is Contracting
Let be the set of discrete measures over with finite support. Let
Consider the Wasserstein barycenter loss function as follows:
The barycenter stems from the minimization of this loss,
We prove that the points of support of belong to the convex closure of all the points contained in and . The proof works by showing that a point of cannot be outside of the closure, otherwise it yields the absurd result that it is both outside and inside. We start the proof with a complementary lemma that will soon be useful.
Lemma A1.
If C is a convex set of , so is (the adherence of C).
Proof.
Let x and y be two elements of and . There exist two sequences and of C such that and . Therefore, . C being convex, . We have constructed a sequence having its elements in C that tends to ; therefore, . □
is a convex set by definition, since it is the smallest convex set containing the points and . By the above lemma, is convex.
Suppose that there exists a point outside of the closure of the convex set, . equipped with the canonical scalar product (with the associated distance ) is a Hilbert Space and being a non empty, closed convex set, there exists in such that
with denoting the distance, see Theorem 8.3.1 in [47] for the proof. Using the projection property as stated in the Proposition 8.3.5 in [47], we have
Now, let us compare and . We have
Since and , we obtain the following:
Now, consider the discrete measure
We apply the definition of Wasserstein distance as in [48] to the discrete case. Let us denote and the set of matrices with k rows and, respectively, n and m columns. Consider the two following families of matrices: and such that
We introduce the function over :
The right-hand side of the inequality defines a new function over . Therefore, we obtain
By definition,
With the hypothesis of unicity, it means that and , which is a contradiction since we assume that is not in the closure while is. Therefore, cannot be outside of the closure, and Wasserstein barycenters produce clouds that are contracting.
Appendix B. Handling of Set Size in Mutation: Supplementary Results
We observe on the left of Figure A1, Figure A2 and Figure A3 that the convergence of WBGEA_1t is slightly quicker than the one of WBGEA_1 on the wind-farm problem, and on and , respectively. The difference in performance is more noticeable with . The population diversities of the two algorithms computed on the wind-farm function , and have the same appearance, as is shown on the right of Figure A1, Figure A2 and Figure A3: even though the diversity decreases slightly more slowly with WBGEA_1 than with WBGEA_1t, during the first iterations, the final decrease is the same. The results indicate a stagnation in the diversity for all the functions, except for where the decrease continues at 500 iterations.
The diversity measure, as described in Section 3.2.2, is more sensitive to the set sizes than the test functions. It explains the difference between the diversities during the first iterations for the wind farm and functions. The diversity for continues to decrease because the algorithm has not yet converged but progresses towards the optimal solution.
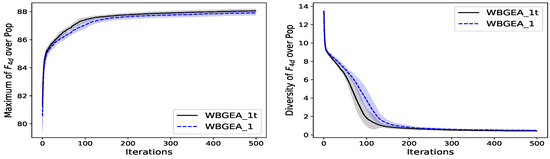
Figure A1.
Handling of Set Size in Mutation. The test function is the wind-farm layout problem averaged over 4 directions, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
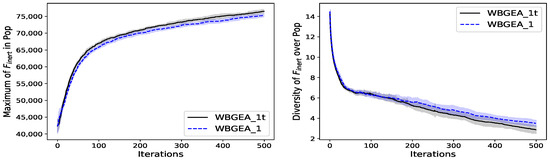
Figure A2.
Handling of Set Size in Mutation. The test function is the inertia function, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
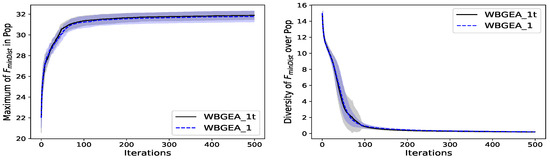
Figure A3.
Handling of Set Size in Mutation. The test function is the MinDist function, . (Left): mean ± std. deviation of the best so far solution. (Right): mean ± std. deviation of the population diversity. Statistics calculated from 20 independent runs.
Appendix C. Details about Wind Farm Proxy
Let the canonical basis of the plane be with and . We denote by the rotation matrix The formula of the wind farm proxy function is given below for a wind in the direction of :
is supposed to be constant, and expresses the penalty factor on the yield of the turbine at that is caused by a turbine at . When the direction of interaction coincides with the x-axis, the interaction loss between rotors at and is
Before explaining , and , we mention that the two terms of are weighted with non-fixed functions depending on the distance between the two points. corresponds to a power gain increasing with the distance between rotors and having a maximum of 1. Its expression is the following:
In regards to the second term, we have
The component quantifies the gain depending on the angle , with the direction of interaction. The result is multiplied with a third function in order to further penalize the proximity between turbines. We have
with , positive parameters and . We can notice that all the terms of Equation (A5) are between 0 and 1, which results in . In order to implement a function modeling the effect of a wind in the direction of (with ), we compute the coordinates of the inputs on the basis and apply the last function on the new inputs (with the new coordinates). The values of , for the three functions defined above are, respectively, 0.15 and 0.5. We choose and for and .
References
- Larsen, G.C.; Réthoré, P.E. TOPFARM—A tool for wind farm optimization. Energy Procedia 2013, 35, 317–324. [Google Scholar] [CrossRef]
- Mosetti, G.; Poloni, C.; Diviacco, B. Optimization of wind turbine positioning in large windfarms by means of a genetic algorithm. J. Wind Eng. Ind. Aerodyn. 1994, 51, 105–116. [Google Scholar] [CrossRef]
- Kusiak, A.; Song, Z. Design of wind farm layout for maximum wind energy capture. Renew. Energy 2010, 35, 685–694. [Google Scholar] [CrossRef]
- Cazzaro, D.; Pisinger, D. Variable neighborhood search for large offshore wind farm layout optimization. Comput. Oper. Res. 2022, 138, 105588. [Google Scholar] [CrossRef]
- Amorosi, L.; Fischetti, M.; Paradiso, R.; Roberti, R. Optimization models for the installation planning of offshore wind farms. Eur. J. Oper. Res. 2024, 315, 1182–1196. [Google Scholar] [CrossRef]
- Zhong, J.; Li, Y.; Wu, Y.; Cao, Y.; Li, Z.; Peng, Y.; Qiao, X.; Xu, Y.; Yu, Q.; Yang, X.; et al. Optimal operation of energy hub: An integrated model combined distributionally robust optimization method with Stackelberg game. IEEE Trans. Sustain. Energy 2023, 14, 1835–1848. [Google Scholar] [CrossRef]
- Bauer, J.; Lysgaard, J. The offshore wind farm array cable layout problem: A planar open vehicle routing problem. J. Oper. Res. Soc. 2015, 66, 360–368. [Google Scholar] [CrossRef]
- Alarie, S.; Audet, C.; Garnier, V.; Le Digabel, S.; Leclaire, L. Snow water equivalent estimation using blackbox optimization. Pac. J. Optim. 2013, 9, 1–21. [Google Scholar]
- Chaloner, K.; Verdinelli, I. Bayesian Experimental Design: A Review. Stat. Sci. 1995, 10, 273–304. [Google Scholar] [CrossRef]
- Stenger, J. Optimal Uncertainty Quantification of a Risk Measurement from a Computer Code. Ph.D. Thesis, Université Paul Sabatier-Toulouse III, Toulouse, France, 2020. [Google Scholar]
- McLachlan, G.J.; Basford, K.E. Mixture Models. Inference and Applications to Clustering; M. Dekker: New York, NY, USA, 1988. [Google Scholar]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Hansen, N.; Arnold, D.V.; Auger, A. Evolution Strategies. In Handbook of Computational Intelligence; Kacprzyk, J., Pedrycz, W., Eds.; Number 871-898; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Pérez, B.; Mínguez, R.; Guanche, R. Offshore wind farm layout optimization using mathematical programming techniques. Renew. Energy 2013, 53, 389–399. [Google Scholar] [CrossRef]
- Byrd, R.H.; Nocedal, J.; Waltz, R.A. K nitro: An integrated package for nonlinear optimization. In Large-Scale Nonlinear Optimization; Springer: Boston, MA, USA, 2006; pp. 35–59. [Google Scholar]
- Fagerfjäll, P. Optimizing Wind Farm Layout: More Bang for the Buck Using Mixed Integer Linear Programming. Master’s Thesis, Chalmers University of Technology and Gothenburg University, Göteborg, Sweden, 2010. Volume 111. [Google Scholar]
- Fischetti, M.; Pisinger, D. Mathematical optimization and algorithms for offshore wind farm design: An overview. Bus. Inf. Syst. Eng. 2019, 61, 469–485. [Google Scholar] [CrossRef]
- Kim, J. Cardinality Constrained Optimization Problems. Ph.D. Dissertation, Purdue University, West Lafayette, IN, USA, 2016. [Google Scholar]
- Surry, P.D.; Radcliffe, N.J. Formal search algorithms + problem characterisations = executable search strategies. In Theory and Principled Methods for the Design of Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2013; pp. 247–270. [Google Scholar]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Radcliffe, N.J. Genetic Set Recombination. In Foundations of Genetic Algorithms; Whitley, L.D., Ed.; Elsevier: Amsterdam, The Netherlands, 1993; Volume 2, pp. 203–219. [Google Scholar] [CrossRef]
- Eroğlu, Y.; Seçkiner, S.U. Design of wind farm layout using ant colony algorithm. Renew. Energy 2012, 44, 53–62. [Google Scholar] [CrossRef]
- Feng, J.; Shen, W.Z. Solving the wind farm layout optimization problem using random search algorithm. Renew. Energy 2015, 78, 182–192. [Google Scholar] [CrossRef]
- Bilbao, M.; Alba, E. Simulated annealing for optimization of wind farm annual profit. In Proceedings of the 2009 2nd International Symposium on Logistics and Industrial Informatics, Linz, Austria, 10–12 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–5. [Google Scholar]
- Grady, S.; Hussaini, M.; Abdullah, M.M. Placement of wind turbines using genetic algorithms. Renew. Energy 2005, 30, 259–270. [Google Scholar] [CrossRef]
- Réthoré, P.E.; Fuglsang, P.; Larsen, G.C.; Buhl, T.; Larsen, T.J.; Madsen, H.A. TOPFARM: Multi-fidelity optimization of wind farms. Wind Energy 2014, 17, 1797–1816. [Google Scholar] [CrossRef]
- Arora, J.S. Introduction to Optimum Design; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Goldberg, D. Genetic Algorithms in Search, Optimization and Machine Learning; Addion Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Song, S.; Li, Q.; Felder, F.A.; Wang, H.; Coit, D.W. Integrated optimization of offshore wind farm layout design and turbine opportunistic condition-based maintenance. Comput. Ind. Eng. 2018, 120, 288–297. [Google Scholar] [CrossRef]
- Pillai, A.C.; Chick, J.; Johanning, L.; Khorasanchi, M.; Pelissier, S. Optimisation of offshore wind farms using a genetic algorithm. Int. J. Offshore Polar Eng. 2016, 26, 225–234. [Google Scholar] [CrossRef]
- Pillai, A.C.; Chick, J.; Johanning, L.; Khorasanchi, M.; Barbouchi, S. Comparison of offshore wind farm layout optimization using a genetic algorithm and a particle swarm optimizer. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Busan, Republic of Korea, 19–24 June 2016; Volume 49972, p. V006T09A033. [Google Scholar]
- Villani, C. Optimal Transport: Old and New; Springer: Berlin/Heidelberg, Germany, 2009; Volume 338. [Google Scholar]
- Sloss, A.N.; Gustafson, S. 2019 evolutionary algorithms review. arXiv 2019, arXiv:1906.08870. [Google Scholar]
- Bartz-Beielstein, T.; Branke, J.; Mehnen, J.; Mersmann, O. Evolutionary algorithms. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2014, 4, 178–195. [Google Scholar] [CrossRef]
- Cao, X. Poincaré Fréchet mean. Pattern Recognit. 2023, 137, 109302. [Google Scholar] [CrossRef]
- Montrucchio, L.; Pistone, G. Kantorovich distance on a finite metric space. arXiv 2019, arXiv:1905.07547. [Google Scholar]
- Cuturi, M.; Doucet, A. Fast computation of Wasserstein barycenters. In Proceedings of the International Conference on Machine Learning, PMLR, Beijing, China, 22–24 June 2014; pp. 685–693. [Google Scholar]
- Flamary, R.; Courty, N.; Gramfort, A.; Alaya, M.Z.; Boisbunon, A.; Chambon, S.; Chapel, L.; Corenflos, A.; Fatras, K.; Fournier, N.; et al. Pot: Python optimal transport. J. Mach. Learn. Res. 2021, 22, 1–8. [Google Scholar]
- Agueh, M.; Carlier, G. Barycenters in the Wasserstein space. SIAM J. Math. Anal. 2011, 43, 904–924. [Google Scholar] [CrossRef]
- Haklı, H.; Uğuz, H. A novel particle swarm optimization algorithm with Levy flight. Appl. Soft Comput. 2014, 23, 333–345. [Google Scholar] [CrossRef]
- Sebag, M.; Ducoulombier, A. Extending population-based incremental learning to continuous search spaces. In Proceedings of the Parallel Problem Solving from Nature—PPSN V, Amsterdam, The Netherlands, 27–30 September 1998; Eiben, A.E., Bäck, T., Schoenauer, M., Schwefel, H.P., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 418–427. [Google Scholar]
- Hansen, N. The CMA evolution strategy: A comparing review. In Towards a New Evolutionary Computation: Advances in the Estimation of Distribution Algorithms; Springer: Berlin/Heidelberg, Germany, 2006; pp. 75–102. [Google Scholar]
- Santner, T.J.; Williams, B.J.; Notz, W.I.; Williams, B.J. The Design and Analysis of Computer Experiments; Springer: New York, NY, USA, 2003; Volume 1. [Google Scholar]
- Hansen, N.; Ros, R.; Mauny, N.; Schoenauer, M.; Auger, A. Impacts of invariance in search: When CMA-ES and PSO face ill-conditioned and non-separable problems. Appl. Soft Comput. 2011, 11, 5755–5769. [Google Scholar] [CrossRef]
- Jansen, T.; Wegener, I. Real royal road functions-where crossover provably is essential. Discret. Appl. Math. 2005, 149, 111–125. [Google Scholar] [CrossRef]
- Consoli, P.A.; Mei, Y.; Minku, L.L.; Yao, X. Dynamic selection of evolutionary operators based on online learning and fitness landscape analysis. Soft Comput. 2016, 20, 3889–3914. [Google Scholar] [CrossRef]
- El, N.; Hassan, H. Topologie Générale et Espaces Normés; ZI des Hauts, no. Édition, 54692; Dunod: Malakoff, France, 2011. [Google Scholar]
- Paty, F.P.; Cuturi, M. Subspace robust Wasserstein distances. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 5072–5081. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).