Machine Learning Regressors to Estimate Continuous Oxygen Uptakes (
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Characteristics
2.2. Data Portion
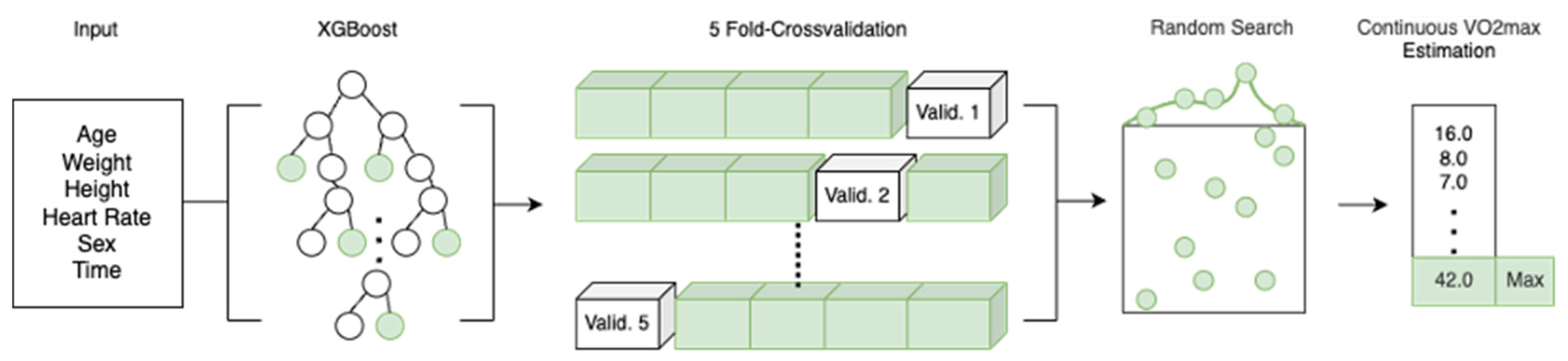
2.3. Modeling
3. Results
3.1. Baseline Participant Characteristics
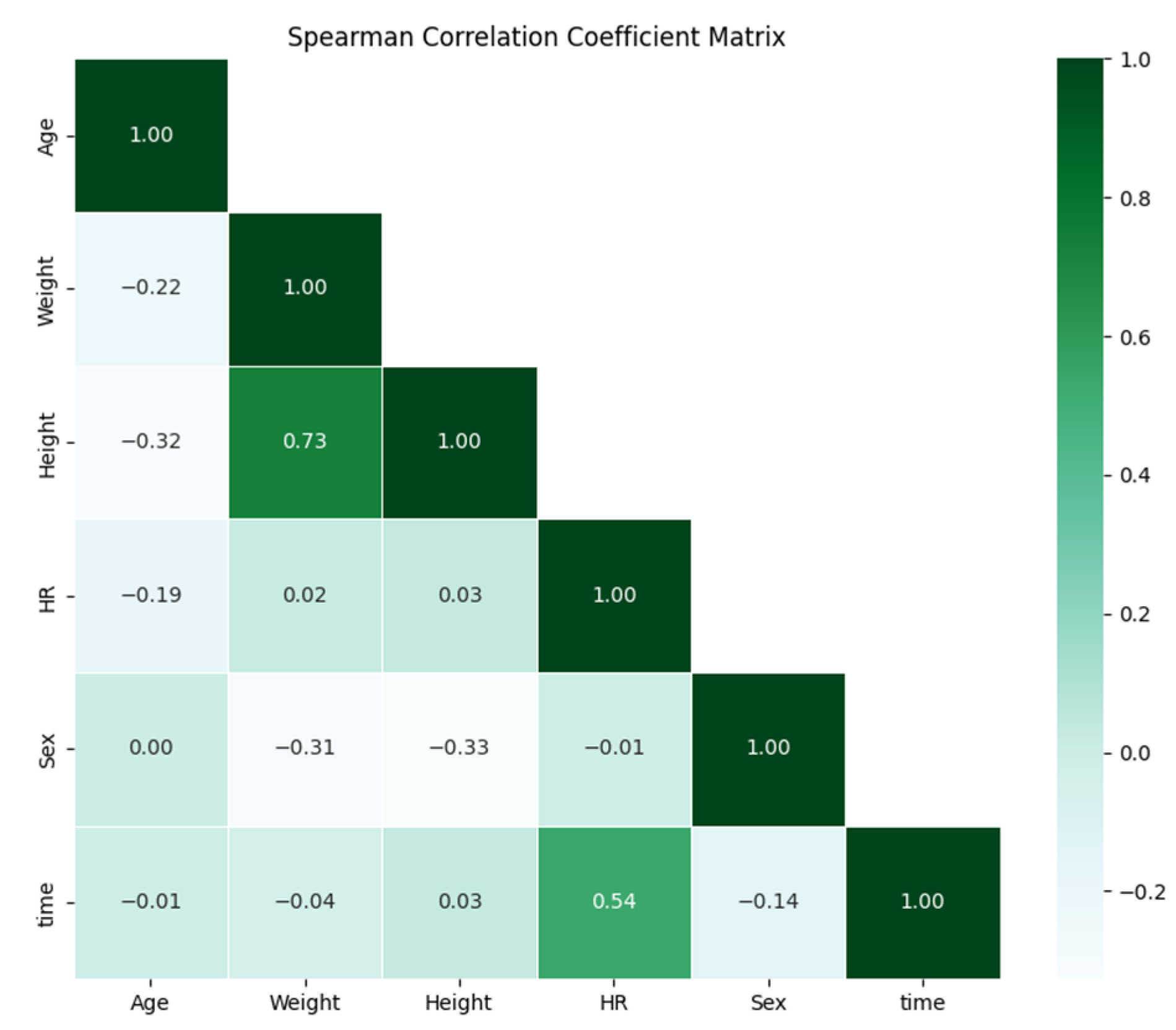
3.2. Parameter Composition
3.3. Continuous Estimation
3.4. Estimation
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Davis, J.M.; Carlstedt, C.J.; Chen, S.C.; Carmichael, M.D.; Murphy, E.A. The Dietary Flavonoid Quercetin Increases VO2max and Endurance Capacity. Int. J. Sport. Nutr. Exerc. Metab. 2010, 20, 56–62. [Google Scholar] [CrossRef]
- Abut, F.; Akay, M.F. Machine Learning and Statistical Methods for the Prediction of Maximal Oxygen Uptake: Recent Advances. Med. Devices Evid. Res. 2015, 8, 369–379. [Google Scholar] [CrossRef]
- Jalili, M.; Nazem, F.; Sazvar, A.; Ranjbar, K. Prediction of Maximal Oxygen Uptake by Six-Minute Walk Test and Body Mass Index in Healthy Boys. J. Pediatr. 2018, 200, 155–159. [Google Scholar] [CrossRef]
- Abut, F.; Akay, M.F.; George, J.D. Developing New VO2max Prediction Models from Maximal, Submaximal and Questionnaire Variables Using Support Vector Machines Combined with Feature Selection. Comput. Biol. Med. 2016, 79, 182–192. [Google Scholar] [CrossRef]
- Squara, P. Matching Total Body Oxygen Consumption and Delivery: A Crucial Objective? Intensiv. Care Med. 2004, 30, 2170–2179. [Google Scholar] [CrossRef]
- Manzoni, C.; Carrard, A.; Fontana, E.; Lemay, M.; Bertschi, M.; Delgado-Gonzalo, R. Towards VO2 Monitoring: Validation of a Heart Rate Based Algorithm. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Republic of Korea, 11–15 July 2017; Volume 2017. [Google Scholar]
- Aouf, M.K.; Seoudy, T.M.; El-Hawsh, G.M. Certain classes of analytic functions defined by integral operators. Electron. J. Math. Anal. Appl. 2015, 3, 245–249. [Google Scholar] [CrossRef]
- Aleppo, G.; Webb, K.M. Continuous Glucose Monitoring Integration in Clinical Practice: A Stepped Guide to Data Review and Interpretation. Diabetes Technol. Soc. 2019, 13, 664–673. [Google Scholar] [CrossRef]
- Vijayan, V.; Connolly, J.; Condell, J.; McKelvey, N.; Gardiner, P. Review of Wearable Devices and Data Collection Considerations for Connected Health. Sensors 2021, 21, 5589. [Google Scholar] [CrossRef] [PubMed]
- Carrier, B.; Helm, M.M.; Cruz, K.; Barrios, B.; Navalta, J.W. Validation of Aerobic Capacity (VO2max) and Lactate Threshold in Wearable Technology for Athletic Populations. Technologies 2023, 11, 71. [Google Scholar] [CrossRef]
- Ashfaq, A.; Cronin, N.J.; Müller, P. Recent Advances in Machine Learning for Maximal Oxygen Uptake (VO2Max) Prediction: A Review. Inform. Med. Unlocked 2022, 28, 100863. [Google Scholar] [CrossRef]
- Alzamer, H.; AbuHmed, T.; Hamad, K. A Short Review on the Machine Learning-Guided Oxygen Uptake Prediction for Sport Science Applications. Electronics 2021, 10, 1956. [Google Scholar] [CrossRef]
- Henriques, J.; Carvalho, P.; Rocha, T.; Paredes, S.; Cabiddu, R.; Trimer, R.; Mendes, R.G.; Borghi-Silva, A.; Kaminsky, L.A.; Ashley, E.A.; et al. A Non-Exercise Based V02max Prediction Using FRIEND Dataset with a Neural Network. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Republic of Korea, 11–15 July 2017; Volume 2017. [Google Scholar]
- Balakarthikeyan, V.; Jais, R.; Vijayarangan, S.; Premkumar, P.S.; Sivaprakasam, M. Heart Rate Variability Based Estimation of Maximal Oxygen Uptake in Athletes Using Supervised Regression Models. Sensors 2023, 23, 3251. [Google Scholar] [CrossRef] [PubMed]
- Rosoł, M.; Petelczyc, M.; Gąsior, J.S.; Młyńczak, M. Prediction of Peak Oxygen Consumption Using Cardiorespiratory Parameters from Warmup and Submaximal Stage of Treadmill Cardiopulmonary Exercise Test. PLoS ONE 2024, 19, e0291706. [Google Scholar] [CrossRef] [PubMed]
- Drinkwater, B.L.; Horvath, S.M.; Wells, C.L. Aerobic Power of Females, Ages 10 to 68. J. Gerontol. 1975, 30, 385–394. [Google Scholar] [CrossRef]
- Jones, N.L.; Makrides, L.; Hitchcock, C.L.; Chypchar, T.; McCartney, N. Normal Standards for an Incremental Progressive Cycle Ergometer Test. Am. Rev. Respir. Dis. 1985, 131, 700–708. [Google Scholar]
- Hansen, J.E.; Sue, D.Y.; Wasserman, K. Predicted Values for Clinical Exercise Testing. Am. Rev. Respir. Dis. 1984, 129, S49–S55. [Google Scholar] [CrossRef]
- Edvardsen, E.; Edvardsen, E.; Hansen, B.H.; Holme, I.; Dyrstad, S.M.; Anderssen, S.A. Reference Values for Cardiorespiratory Response and Fitness on the Treadmill in a 20- to 85-Year-Old Population. Chest 2013, 144, 241–248. [Google Scholar] [CrossRef]
- Mongin, D.; García Romero, J.; Alvero Cruz, J.R. Treadmill Maximal Exercise Tests from the Exercise Physiology and Human Performance Lab of the University of Malaga. Age 2021, 27, 36–32. [Google Scholar] [CrossRef]
- Glass, S.; Dwyer, G.B. ACSM’S Metabolic Calculations Handbook; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2007. [Google Scholar]
- Koutlianos, N.; Dimitros, E.; Metaxas, T.; Cansiz, M.; Deligiannis, A.; Kouidi, E. Indirect Estimation of VO2max in Athletes by ACSM’s Equation: Valid or Not? Hippokratia 2013, 17, 136. [Google Scholar]
- Buttar, K.K.; Saboo, N.; Kacker, S. Measured and Predicted Maximal Oxygen Consumption (VO2max) in Healthy Young Adults: A Cross-Sectional Study. J. Health Sci. Med. Res. 2023, 41, 2022896. [Google Scholar] [CrossRef]
- Fregonezi, G.; Resqueti, V.; Vigil, L.; Calaf, N.; Casan, P. Maximal Oxygen Uptake Cannot Be Estimated from Resting Lung Function and Submaximal Exercise in Patients with Chronic Obstructive Pulmonary Disease. J. Cardiopulm. Rehabil. Prev. 2012, 32, 219–225. [Google Scholar] [CrossRef] [PubMed]
- VENUTM Owner’s Manual. Available online: https://www8.garmin.com/manuals/webhelp/venu/EN-US/Venu_OM_EN-US.pdf (accessed on 10 May 2024).
- Track Your Cardio Fitness Levels. Available online: https://support.apple.com/en-us/108790 (accessed on 26 May 2024).
- Yu, S.; Tian, L.; Liu, Y.; Guo, Y. LSTM-XGBoost Application of the Model to the Prediction of Stock Price. In Artificial Intelligence and Security, Proceedings of the 7th International Conference, ICAIS 2021, Dublin, Ireland, 19–23 July 2021; Sun, X., Zhang, X., Xia, Z., Bertino, E., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2021; Volume 12736. [Google Scholar] [CrossRef]
- Lim, S.; Chi, S. Xgboost Application on Bridge Management Systems for Proactive Damage Estimation. Adv. Eng. Inform. 2019, 41, 100922. [Google Scholar] [CrossRef]
- Joshi, A.; Vishnu, C.; Mohan, C.K.; Raman, B. Application of XGBoost Model for Early Prediction of Earthquake Magnitude from Waveform Data. J. Earth Syst. Sci. 2023, 133, 1–18. [Google Scholar] [CrossRef]
- Lei, T.M.T.; Ng, S.C.W.; Siu, S.W.I. Application of ANN, XGBoost, and Other ML Methods to Forecast Air Quality in Macau. Sustainability 2023, 15, 5341. [Google Scholar] [CrossRef]
- Zivkovic, M.; Tair, M.; Venkatachalam, K.; Bacanin, N.; Hubalovsky, S.; Trojovský, P. Novel Hybrid Firefly Algorithm: An Application to Enhance XGBoost Tuning for Intrusion Detection Classification. PeerJ Comput. Sci. 2022, 8, e956. [Google Scholar] [CrossRef]
- Park, J.Y.; Kim, J.H.; Ryu, D.-H.; Choi, H.Y. Factors Related to Steroid Treatment Responsiveness in Thyroid Eye Disease Patients and Application of SHAP for Feature Analysis with XGBoost. Front. Endocrinol. 2023, 14, 1079628. [Google Scholar] [CrossRef]
- Fang, Z.; Yang, S.; Lv, C.; An, S.; Wu, W. Application of a Data-Driven XGBoost Model for the Prediction of COVID-19 in the USA: A Time-Series Study. BMJ Open 2022, 12, e056685. [Google Scholar] [CrossRef]


| Participants | Age | Equation | |
|---|---|---|---|
| Edvardsen et al. (2013) [19] | n = 759 (394 M/365 F) | 20–85 | Female: (L.min−1) = 3.31 − 0.022 year (mL.kg−1.min−1) = 48.2 − 0.32 year Male: (L.min−1) = 4.97 − 0.033 year (mL.kg−1.min−1) = 60.9 − 0.43 year |
| Jones et al. (1985) [17] | n = 100 (50 M/50 F) | 15–71 | Female: (L.min−1) = −0.624 sex + 0.046 height − 0.021 age − 4.31 Male: (L.min−1) = −0.492 sex + 0.032 height − 0.024 age + 0.019 weight − 3.71 |
| Hansen et at. (1984) [18] | n = 77 (77 M) | 37–74 | Male: (mL.min−1) = weight × (50.75 − 0.372 age) |
| Drinkwater et al. (1975) [16] | n = 109 (109 F) | 10–68 | Female: (L.min−1) = 2.46 − 0.016 age (mL.kg−1.min−1) = 83.663 − 4.114 age + 0.127 age2 − 0.0012 age (mL.kg−1.min−1) = 71.237 − 3.524 age + 0.104 age2 − 0.0010 age (mL.kgLBM−1.min−1) = 90.684 − 3.808 age + 0.118 age2 − 0.0011 age (mL.kgLBM−1.min−1) = 88.99 − 4.459 age + 0.140 age2 − 0.0014 age |
| Training Model (n = 532) | MAE | MSE | RMSE | R2 | RMSLE | MAPE | TT (s) |
|---|---|---|---|---|---|---|---|
| Extreme Gradient Boosting | 0.1834 | 0.0640 | 0.2529 | 0.9996 | 0.0146 | 0.0077 | 0.4600 |
| Light Gradient Boosting Machine | 0.2419 | 0.1274 | 0.3570 | 0.9992 | 0.0169 | 0.0090 | 1.0520 |
| Gradient Boosting Regressor | 0.6158 | 0.6804 | 0.8248 | 0.9959 | 0.0282 | 0.0210 | 3.4760 |
| Linear Regression | 0.8622 | 1.4428 | 1.2011 | 0.9913 | 0.0929 | 0.0407 | 5.3260 |
| AdaBoost Regressor | 2.2091 | 7.4254 | 2.7245 | 0.9551 | 0.1206 | 0.0944 | 2.4900 |
| Cross Validation | MAE | MSE | RMSE | R2 | RMSLE | MAPE | |
| 1 | 0.1297 | 0.0377 | 0.1942 | 0.9998 | 0.0137 | 0.0058 | |
| 2 | 0.1289 | 0.0379 | 0.1947 | 0.9998 | 0.0142 | 0.0057 | |
| 3 | 0.1240 | 0.0335 | 0.1829 | 0.9998 | 0.0129 | 0.0055 | |
| 4 | 0.1265 | 0.0349 | 0.1869 | 0.9998 | 0.0136 | 0.0056 | |
| 5 | 0.1265 | 0.0373 | 0.1933 | 0.9998 | 0.0124 | 0.0055 | |
| Mean | 0.1271 | 0.0363 | 0.1904 | 0.9998 | 0.0134 | 0.0056 | |
| Standard deviation | 0.0020 | 0.0018 | 0.0047 | 0.0000 | 0.0006 | 0.0001 | |
| Test set (n = 154) | MAE | MSE | RMSE | R2 | RMSLE | MAPE | |
| Extreme Gradient Boosting | 0.1793 | 0.1460 | 0.3821 | 0.9991 | 0.0140 | 0.0066 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, D.; Sun, S.
Machine Learning Regressors to Estimate Continuous Oxygen Uptakes (
Hong D, Sun S.
Machine Learning Regressors to Estimate Continuous Oxygen Uptakes (
Hong, Daeeon, and Sukkyu Sun.
2024. "Machine Learning Regressors to Estimate Continuous Oxygen Uptakes (
Hong, D., & Sun, S.
(2024). Machine Learning Regressors to Estimate Continuous Oxygen Uptakes (






