MILP-Based Approach for High-Altitude Region Pavement Maintenance Decision Optimization
Abstract
1. Introduction
1.1. Literature Review
1.2. The Focus of This Study
| Literature | Object Characteristic | Optimization Objective | Model Type | Solution Approach |
|---|---|---|---|---|
| Yu et al. [8] | Project-level; considering greenhouse gas emissions and budget constraints; meeting pavement condition requirements | Greenhouse gas emissions, maintenance costs, pavement condition | Multi-objective nonlinear optimization | Genetic algorithm |
| Zhang et al. [11] | Project-level; constrained budget; meeting pavement condition requirements | Pavement condition | Flowchart | Heuristic algorithm |
| Mahmood et al. [12] | Project-level; meeting pavement condition requirements | Maintenance costs, pavement condition | Multi-objective nonlinear optimization | Improved particle swarm algorithm |
| He and Sun [1] | Network-level; different decision-makers | Benefits for different decision-makers | Mixed-integer programming | Lingo |
| Sun et al. [13] | Network-level; different decision-makers; Pareto optimal solution | Maintenance costs, pavement condition, and environmental impact | Mixed-integer linear programming | Cplex |
| Chen and Wang [14] | Network-level; multiple pavement condition indicators | Maintenance costs, carbon emissions, and energy consumption | Multi-objective optimization | Generalized differential evolution algorithm |
| Lee and Madanat [15] | Network-level; single or multiple budget constraints | Greenhouse gas emission | Single-objective optimization | Lagrangian relaxation |
| Elhadidy et al. [16] | Network-level; Pareto optimal solution | Maintenance costs, pavement condition | Markov-chain, multi-objective optimization | Genetic algorithm-based procedure |
| Fani et al. [17] | Network-level; considering the uncertainty of pavement deterioration and budget deterioration and budget | Pavement condition | Multi-stage stochastic mixed-integer programming | GAMS |
| Lee et al. [18] | Network-level; constrained greenhouse gas emissions | Maintenance costs | Single-objective nonlinear | Two-stage algorithm |
| Li et al. [19] | Network-level; considering dynamic traffic distribution | Maintenance costs, user costs, pavement residual asset value | Multi-stage dynamic programming | Heuristic iterative algorithm |
| FAN and Feng [21] | Network-level; budget uncertainty | Maintenance effectiveness | Stochastic linear programming | Scenario tree-based heuristic algorithm |
| This paper | Network-level; high-altitude region pavement maintenance; monthly maintenance plans; robust solution | Maintenance costs, affected traffic volume, carbon emissions, comfort level, maintenance effectiveness | Mixed-integer linear programming | Gurobi |
- (1)
- For the pavement maintenance decision problem in high-altitude regions, this paper proposes an optimization method for pavement maintenance plans. The initial optimization model constructed considers the typical characteristics of pavement maintenance in high-altitude regions (see Section 2) intending to obtain monthly maintenance plans. By combining the proposed linearization method, the initial nonlinear model is reconstructed into a mixed-integer linear programming (MILP) problem. The composition of the model under five types of decision strategies is discussed (see Section 4.2), responding to the decision- makers’ preferences.
- (2)
- To address the uncertainty of unit maintenance costs, this paper proposes a robust maintenance plan calculation method using a robust optimization method based on the acceptable objective variation range (AOVR). By setting the unit maintenance cost as an interval number, the corresponding optimistic sub-model and pessimistic sub-model are analyzed, and the construction process of the robust optimization model and the process of obtaining robust maintenance plans are discussed.
- (3)
- Combining a specific network-level pavement maintenance decision problem, a case study analysis is conducted. A maintenance decision problem involving 30 road segments is used to discuss the characteristics of different decision strategies; analyze the impact of the number of maintenance workers, annual budget, and minimum pavement condition index (PCI) requirements on decision plans; and discuss the differences among the robust, pessimistic, and optimistic solutions.
2. Problem Formulation
- (1)
- Seasonality characteristics of maintenance work: The duration of cold seasons with low temperatures is long, and some pavements may even be covered with snow for extended periods. To ensure maintenance quality, pavement maintenance should preferably not be conducted in such seasons or months.
- (2)
- Seasonality characteristics of traffic flow: Traffic flow on roads in high-altitude areas is fluctuant. For example, in Lhasa city, Tibet, tourism traffic significantly contributes to overall traffic, with many tourists visiting the city during warmer seasons, especially for self-driving tours. Considering the impact of pavement maintenance on traffic, maintenance should be minimized during high-traffic flow periods.
- (3)
- Fragility characteristics of the ecological environment: High-altitude regions have less vegetation and a more fragile ecological environment compared with lower-altitude areas. Substantial evidence shows that the carbon emission factor is more significant in high-altitude areas compared with other regions [26,27,28,29]. Therefore, the environmental impact of maintenance work needs to be considered.
- (4)
- High-cost characteristics of maintenance work: Due to climate, environment, industrial development, and resource conditions, high-altitude areas are more reliant on maintenance equipment and materials produced in other regions, leading to higher maintenance costs. Manpower costs exhibit similar characteristics.
3. Mathematical Model
3.1. Definition of Symbols
3.2. Constraints
- (1)
- Calculation of the pavement condition index (PCI): The value of PCI is dynamic and influenced by factors such as time, pavement loads, and maintenance work. It ranges from 0 to 100, with higher values indicating better pavement conditions [13]. Let represent the year in which maintenance may be performed, and its calculation formula can be expressed as a piecewise function, that is:
- (2)
- Requirement for PCI value: For pavement technical conditions, different decision-makers have similar requirements, especially desiring that the PCI values of each segment meet the requirement of the minimum value, which can be expressed as:
- (3)
- Calculation of the international roughness index (IRI): IRI is an index used to standardize the evaluation of pavement smoothness, reflecting the level of vibration and bumpiness when traveling on a road [31,32]. Clearly, the better the smoothness, the smaller the IRI, resulting in a better driving experience and a positive impact on traffic safety. Previous studies have shown that IRI is closely related to PCI, indicating that pavement condition affects smoothness. Based on Ref. [31], the relationship between the two can be expressed as:
- (4)
- Requirement for working time: In high-altitude regions, maintenance conditions are generally unfavorable during cold seasons, which tend to last relatively long. Therefore, this paper considers the impact of seasons on maintenance work. Based on this, some months are set as non-maintenance periods, and the corresponding constraint can be expressed as:
- (5)
- Restricted monthly maintenance task: When the number of maintenance workers is limited, the maintenance task that can be completed within a unit of time is also restricted. When scheduling maintenance projects, it is necessary to consider manpower and time requirements. Combining the ceiling function ⌈ ⌉, the man-hours for any segment, and the total number of maintenance workers, the monthly maintenance task can be expressed as:
- (6)
- Limited budget for maintenance: For any given year, decision-makers typically do not want maintenance costs to exceed the annual budget, ensuring that the maintenance plan for each year is carried out within a reasonable funding range. The costs can be calculated based on the maintenance approaches and the maintenance area. The constraint can be expressed as:
- (7)
- Restricted maintenance approaches: The maintenance approach refers to the specific techniques and processes used during pavement maintenance. Based on Assumption 3, each segment can only select one or fewer maintenance approaches within the study period to avoid repeated maintenance and resource wastage. This constraint can be expressed as:
- (8)
- Restricted maintenance frequency: Based on Assumption 4, each segment can undergo maintenance no more than once within the study period to ensure the quality of single-time maintenance and to mitigate the impact on traffic. This constraint can be expressed as:
- (9)
- Coupling of maintenance approach and maintenance frequency: If a segment is not undergoing maintenance, then no maintenance approach is selected for it. This constraint can be expressed as:
- (10)
- Attribute of decision variable: For the attributes of the decision variables in this paper, we further set the following constraints:
3.3. Objective Function
- (1)
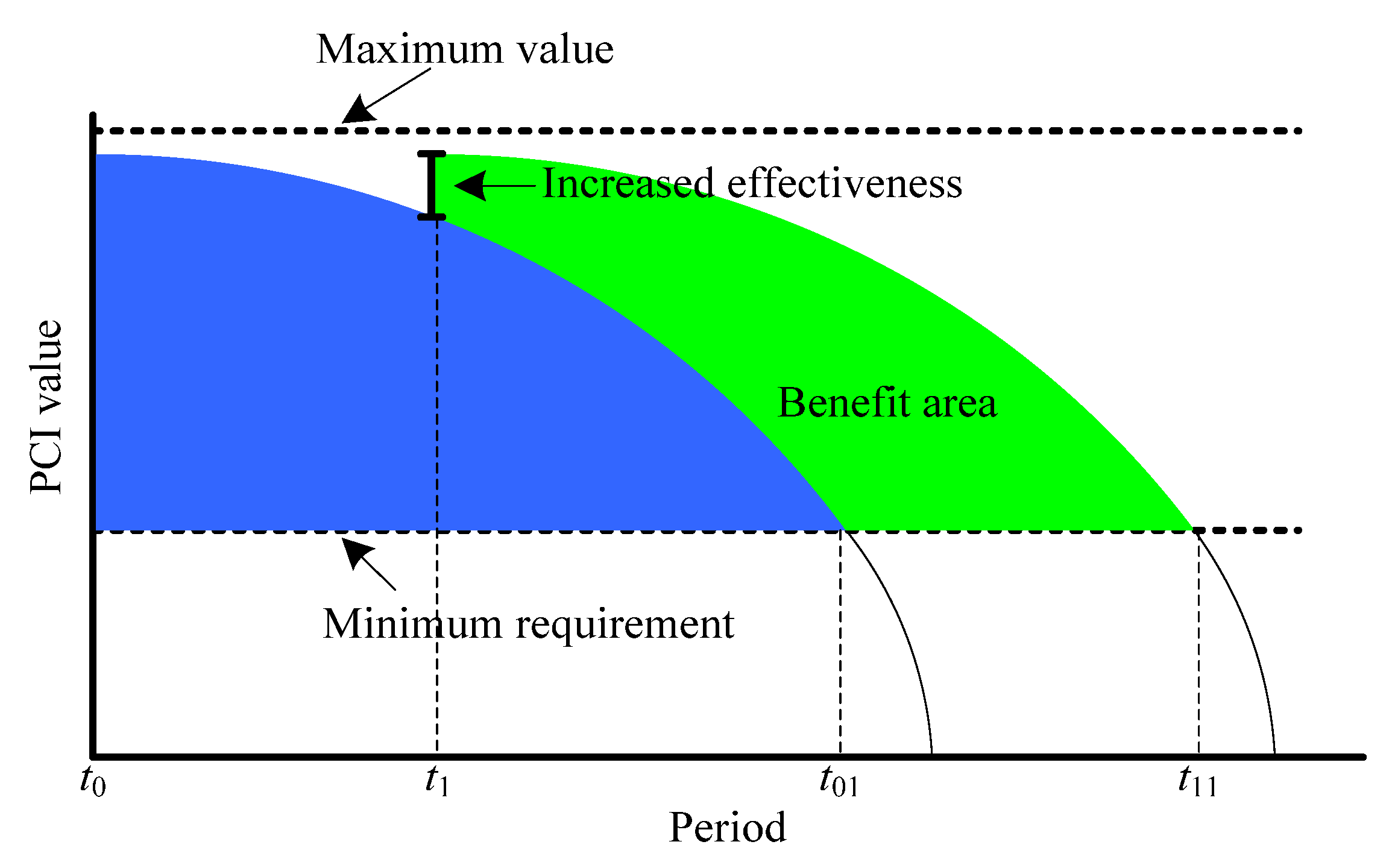
- Maximize maintenance effectiveness: The primary goal of pavement maintenance is to provide better driving conditions for as many users as possible. This means that the decision should consider not only the immediate effects of maintenance (i.e., how is the pavement after maintenance?) but also the overall effectiveness (i.e., how many users can use roads in better condition?). Therefore, this paper uses the product of traffic flow and pavement condition as a decision objective to make maintenance decisions more scientific. Multiplying pavement condition by traffic flow considers that segments with higher traffic flow contribute more to overall effectiveness and, thus, are worth focusing on. This can be expressed as:
- (2)
- Minimize carbon emissions: For pavement maintenance, while improving pavement conditions, there may be environmental impacts, including greenhouse gases, noise, dust, etc. Compared with low-altitude regions, the ecological environment in high-altitude regions is more fragile. Therefore, when formulating pavement maintenance plans for high-altitude regions, these adverse impacts should be given greater consideration. Hence, this paper sets minimizing carbon emissions as an optimization objective, which can be expressed as:
- (3)
- Minimize the affected traffic volume: During pavement maintenance, construction activities inevitably have adverse effects on traffic, especially when traffic flow is high. To reduce the interference of pavement maintenance on traffic, it is necessary to consider traffic management during construction and to schedule maintenance time reasonably. Based on this, this paper constructs an objective function to minimize the impact on traffic, combining the predicted monthly traffic volume, the working hours required for different maintenance methods, and the protection time required after maintenance, specifically expressed as:
- (4)
- Minimizing the roughness index: The international roughness index (IRI) reflects the level of vibration and bumpiness experienced by vehicles traveling on the road [30,32], indicating that roughness affects the comfort of the driving experience. Additionally, roughness has a significant impact on energy consumption, with higher IRI values corresponding to higher energy consumption [32]. Therefore, to meet comfort needs and environmental protection requirements, minimizing IRI value as much as possible can be set as an optimization objective:
- (5)
- Minimize maintenance costs: Minimizing maintenance costs as an optimization objective is a common approach in pavement maintenance decision [3]. The calculation of maintenance costs is related to the maintenance approach and maintenance area, and the corresponding objective function can be expressed as:
4. Model Transformation
4.1. Transformation of Nonlinear Terms
4.2. Transformation of Multi-Objective Functions
5. Case Analysis
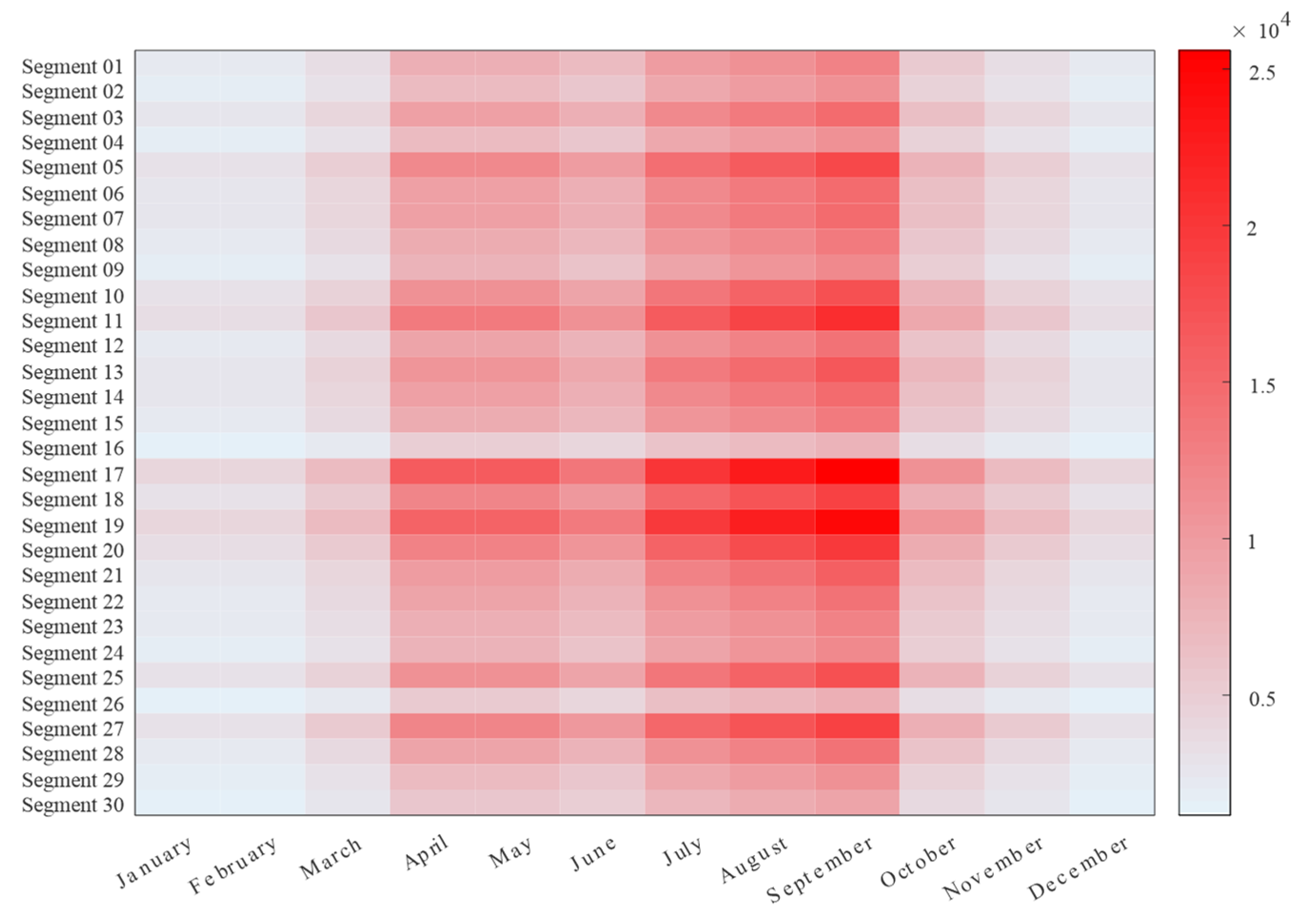
5.1. Case Description
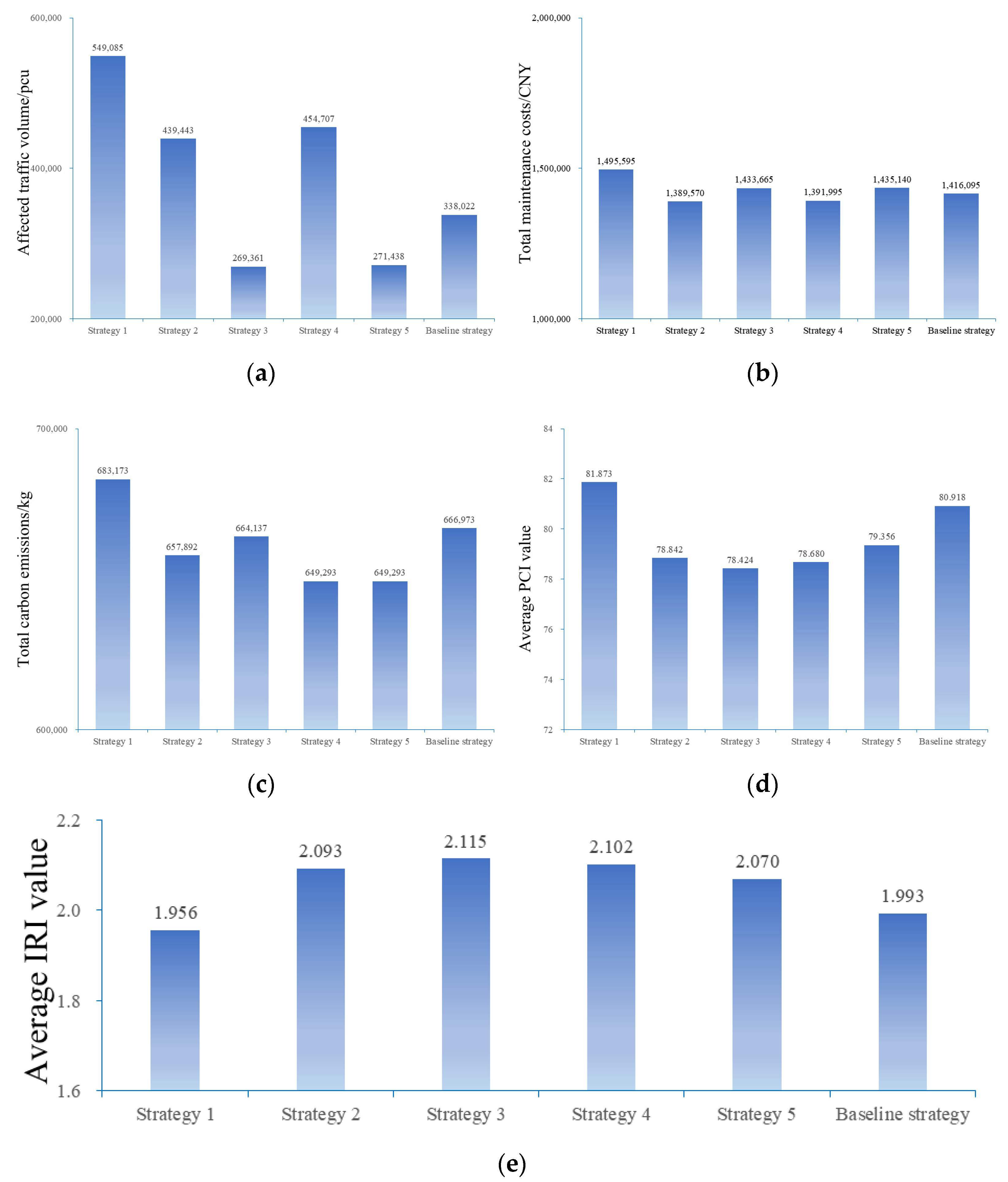
5.2. Result Analysis
6. Extension of the Maintenance Decision Model
6.1. Interval Number
6.2. Optimistic Solution and Pessimistic Solution
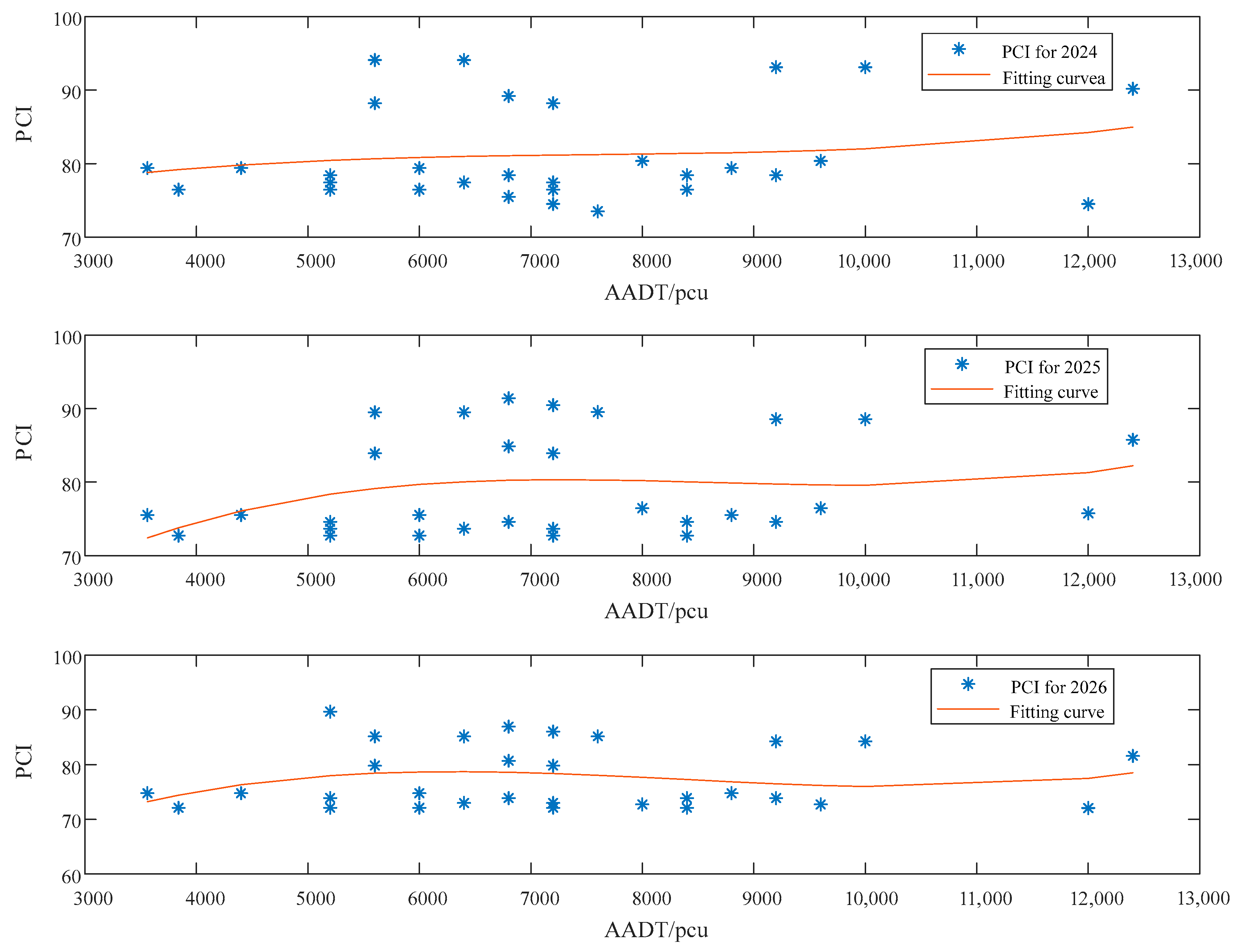
6.3. Robust Solution and Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbols | Meaning | |
|---|---|---|
| Sets | Segments requiring maintenance (indexed by ) | |
| Optional maintenance approaches (indexed by ) | ||
| Years included in the maintenance cycle (indexed by ) | ||
| Months in a year (indexed by ) | ||
| Months suitable for maintenance | ||
| Months unsuitable for maintenance | ||
| Parameters | Average daily traffic volume (pcu) for segment in month of year | |
| The number of days in month of year | ||
| Carbon emissions per square meter (kg/m2) produced by maintenance approach | ||
| The number of protection days required for segment after using maintenance approach | ||
| Cost per square meter (CNY/m2) of using maintenance approach | ||
| Annual maintenance budget (CNY) for year | ||
| Total budget (CNY) for the maintenance cycle | ||
| Maintenance effectiveness (measured in terms of PCI improvement) produced by maintenance approach | ||
| Working hours per square meter (hours/m2) required by maintenance approach | ||
| Initial state (measured in PCI) of segment when making a maintenance decision | ||
| Average PCI required at the network level | ||
| , | The minimum and maximum PCI required at the segment level | |
| , | Used to calculate the PCI state change for segment | |
| , | Used to calculate the IRI state change for segment | |
| The length (meter) of segment requiring maintenance | ||
| The width (meter) of segment requiring maintenance | ||
| The total number of workers involved in maintenance work | ||
| The maximum daily working hours (hours) for workers | ||
| Variables | Whether segment chooses maintenance approach (1 if chosen, 0 otherwise) | |
| Whether maintenance is carried out on segment in month of year (1 if chosen, 0 otherwise) | ||
| The PCI value of segment in year , which is affected by the above two decision variables in the model | ||
| International roughness index (IRI) value of segment in year , which is influenced by | ||
| Auxiliary symbols | The kth sub-objective | |
| The weight of the kth sub-objective | ||
| , | The minimum and maximum values of the kth sub-objective | |
References
- He, Z.; Sun, X. Discrete optimization models and methods for management systems of pavement maintenance and rehabilitation. J. Shanghai Univ. 2010, 14, 217–222. [Google Scholar] [CrossRef]
- Ling, J.; Wang, Z.; Liu, S.; Tian, Y. Preventive Maintenance Decision-Making Optimization Method for Airport Runway Composite Pavements. Appl. Sci. 2024, 14, 3850. [Google Scholar] [CrossRef]
- Pourgholamali, M.; Labi, S.; Sinha, K.C. Multi-objective optimization in highway pavement maintenance and rehabilitation project selection and scheduling: A state-of-the-art review. J. Road Eng. 2023, 3, 239–251. [Google Scholar] [CrossRef]
- Wu, Q.; Li, C.; Xu, P. Comparative Study on the Laboratory and Field Aging Behavior of Asphalt Binders in High-altitude Regions. Technol. Highw. Transp. 2024, 40, 73–81. [Google Scholar]
- Dou, M.; Hu, C.; Duoji, L.; He, Z. Analysis on Surface Troubles of the Qinghai-Tibet Highway. J. Glaciol. Geocryol. 2003, 25, 439–444. [Google Scholar]
- Xu, P.; Zhu, X.; Yao, D.; Shi, C.; Qian, G. Review on intelligent detection and decision of asphalt pavement maintenance. J. Cent. South Univ. (Sci. Technol.) 2021, 52, 2099–2117. [Google Scholar]
- Zhang, X. Research on Intelligent Maintenance Decision Method for the Whole Life Cycle of Road Network Infrastructure. Doctoral Dissertation, Southeast University, Nanjing, China, 2022. (In Chinese). [Google Scholar]
- Yu, B.; Gu, X.; Ni, F.; Guo, R. Multi-objective optimization for asphalt pavement maintenance plans at project level: Integrating performance, cost and environment. Transp. Res. Part D 2015, 41, 64–74. [Google Scholar] [CrossRef]
- Wang, C.H.; Wang, L.J.; Bai, J.H.; Liu, Y.D.; Wang, X.C. Research on Integration Optimization of Asphalt Pavement Preventive Maintenance Timing and Countermeasures During Period. China J. Highw. Transp. 2010, 23, 27–34. [Google Scholar]
- Li, L.; Guan, T. Decision method for preventive maintenance of asphalt pavements considering multiple damage characteristics. J. Shanghai Univ. (Nat. Sci. Ed.) 2022, 28, 689–701. [Google Scholar]
- Zhang, Y.; Shen, A.; Hou, Y. Application of Fund-target Optimization Method in Pavement Maintenance Decision. J. Highw. Transp. Res. Dev. 2018, 35, 34–40. [Google Scholar]
- Mahmood, M.; Mathavan, S.; Rahman, M. A Parameter-free Discrete Particle Swarm Algorithm and Its Application to Multi-objective Pavement Maintenance Schemes. Swarm Evol. Comput. 2018, 43, 69–87. [Google Scholar] [CrossRef]
- Sun, Y.; Hu, M.; Zhou, W.; Xu, W. Multiobjective optimization for pavement network maintenance and rehabilitation programming: A case study in Shanghai, China. Math. Probl. Eng. 2020, 2020, 3109156. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, D. Numerical analysis of a multi-objective maintenance decision model for sustainable highway networks: Integrating the GDE3 method, LCA and LCCA. Energy Build. 2023, 290, 113096. [Google Scholar] [CrossRef]
- Lee, J.; Madanat, S. Optimal policies for greenhouse gas emission minimization under multiple agency budget constraints in pavement management. Transp. Res. Part D 2017, 55, 39–50. [Google Scholar] [CrossRef]
- Elhadidy, A.A.; Elbeltagi, E.E.; Ammar, M.A. Optimum analysis of pavement maintenance using multi-objective genetic algorithms. HBRC J. 2015, 11, 107–113. [Google Scholar] [CrossRef]
- Fani, A.; Golroo, A.; Mirhassani, S.A.; Gandomi, A.H. Pavement maintenance and rehabilitation planning optimisation under budget and pavement deterioration uncertainty. Int. J. Pavement Eng. 2022, 23, 414–424. [Google Scholar] [CrossRef]
- Lee, J.; Madanat, S.; Reger, D. Pavement systems reconstruction and resurfacing policies for minimization of life-cycle costs under greenhouse gas emissions constraints. Transp. Res. Part B 2016, 93, 618–630. [Google Scholar] [CrossRef]
- Li, T.; Zhang, P.; Mao, X. Optimal Decision of Pavement Maintenance Considering the Dynamic Distribution of Traffic Flow. China J. Highw. Transp. 2019, 32, 227–233. [Google Scholar]
- Meng, S.; Shao, Y.; Cao, R.; Wu, S. Multi-objective optimisation of network-level pavement maintenance decisions considering user costs. In Proceedings of the World Transport Conference 2022 (WTC2022); People’s Transportation Press: Beijing, China, 2022; pp. 3333–3341. [Google Scholar]
- Fan, W.; Feng, W. Managing Pavement Maintenance and Rehabilitation Projects under Budget Uncertainties. J. Transp. Syst. Eng. Inf. Technol. 2014, 14, 92–100. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, B. Study on the Tourist Traffic Characteristics of People Entering Tibet and People in the Area. Highlights in Business. Econ. Manag. 2024, 26, 7–14. [Google Scholar]
- Sha, A.; Ma, B.; Wang, H.; Hu, L.; Mao, X.; Zhi, X.; Chen, H.; Liu, Y.; Ma, F.; Liu, Z.; et al. Highway constructions on the Qinghai-Tibet Plateau: Challenge, research and practice. J. Road Eng. 2022, 2, 1–60. [Google Scholar] [CrossRef]
- Suprayoga, G.B.; Bakker, M.; Witte, P.; Spit, T. A systematic review of indicators to assess the sustainability of road infrastructure projects. Eur. Transp. Res. Rev. 2020, 12, 1–15. [Google Scholar] [CrossRef]
- Collier, P.; Kirchberger, M.; Söderbom, M. The cost of road infrastructure in low-and middle-income countries. World Bank Econ. Rev. 2016, 30, 522–548. [Google Scholar] [CrossRef]
- CJJ36-2016; Technical Specification for Urban Road Maintenance. China Construction Industry Press: Beijing, China, 2016. (In Chinese)
- Jiang, Z.; Wu, L.; Niu, H. Investigating the impact of high-altitude on vehicle carbon emissions: A comprehensive on-road driving study. Sci. Total Environ. 2024, 918, 170671. [Google Scholar] [CrossRef] [PubMed]
- Giraldo, M.; Huertas, J.I. Real emissions, driving patterns and fuel consumption of in-use diesel buses operating at high altitude. Transp. Res. Part D 2019, 77, 21–36. [Google Scholar] [CrossRef]
- Qi, Z.; Gu, M.; Cao, J.; Zhang, Z.; You, C.; Zhan, Y.; Ma, Z.; Huang, W. The Effects of Varying Altitudes on the Rates of Emissions from Diesel and Gasoline Vehicles Using a Portable Emission Measurement System. Atmosphere 2023, 14, 1739. [Google Scholar] [CrossRef]
- JTG 5110-2023; Technical Standard for Highway Maintenance. People’s Transportation Press: Beijing, China, 2023. (In Chinese)
- Hasibuan, R.-P.; Surbakti, M.-S. Study of Pavement Condition Index (PCI) relationship with International Roughness Index (IRI) on Flexible Pavement. MATEC Web Conf. 2019, 258, 03019. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, Z. Analysis on Reconstructed Highway User Fuel Consumption Model and Calculation Method Based on Pavement Roughness. J. Highw. Transp. Res. Dev. 2021, 38, 132–138. [Google Scholar]
- Chinneck, J.W.; Ramadan, K. Linear programming with interval coefficients. J. Oper. Res. Soc. 2000, 51, 209–220. [Google Scholar] [CrossRef]
- Li, M.; Gabriel, S.A.; Shim, Y.; Azarm, S. Interval uncertainty-based robust optimization for convex and non-convex quadratic programs with applications in network infrastructure planning. Netw. Spat. Econ. 2011, 11, 159–191. [Google Scholar] [CrossRef]



| Road Type | Excellent | Good | Qualified | Unqualified |
|---|---|---|---|---|
| Expressway | [90, 100] | [75, 90) | [65, 75) | [0, 65) |
| Main/secondary roads | [85, 100] | [70, 85) | [60, 70) | [0, 60) |
| Branch roads | [80, 100] | [65, 80) | [60, 65) | [0, 60) |
| Case | |||
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 1 | 0 | 0 |
| 4 | 1 | 1 | 1 |
| Case | |||
|---|---|---|---|
| 1 | 0 | 0 | |
| 2 | 1 |
| Strategy | Objective | Weight Ranges | ||||
|---|---|---|---|---|---|---|
| 1 | Optimize maintenance effectiveness | >0 | =0 | =0 | >0 | =0 |
| 2 | Optimize cost savings | =0 | =0 | =0 | =0 | >0 |
| 3 | Optimize affected traffic volume | =0 | =0 | >0 | =0 | =0 |
| 4 | Optimize environmental protection | =0 | >0 | =0 | =0 | =0 |
| 5 | Balance all the above considerations | >0 | >0 | >0 | >0 | >0 |
| Segment | Length/m | Width/m | AADT | Initial PCI | Segment | Length/m | Width/m | AADT | Initial PCI |
|---|---|---|---|---|---|---|---|---|---|
| 01 | 180 | 4.5 | 6000 | 78 | 16 | 810 | 3.5 | 3560 | 81 |
| 02 | 190 | 3.5 | 5200 | 80 | 17 | 220 | 3 | 12,400 | 82 |
| 03 | 400 | 4 | 7200 | 79 | 18 | 320 | 3.5 | 9200 | 75 |
| 04 | 260 | 3.5 | 5200 | 78 | 19 | 100 | 3 | 12,000 | 76 |
| 05 | 300 | 4 | 8800 | 81 | 20 | 80 | 4 | 9600 | 82 |
| 06 | 320 | 3 | 7200 | 78 | 21 | 920 | 3.5 | 7600 | 75 |
| 07 | 280 | 3 | 7200 | 81 | 22 | 610 | 3 | 6800 | 77 |
| 08 | 90 | 3.5 | 6400 | 76 | 23 | 230 | 3.5 | 6000 | 81 |
| 09 | 70 | 3 | 5600 | 81 | 24 | 340 | 4 | 5600 | 76 |
| 10 | 288 | 3 | 8400 | 78 | 25 | 550 | 4.5 | 8400 | 80 |
| 11 | 165 | 4.5 | 10,000 | 75 | 26 | 290 | 3 | 3840 | 78 |
| 12 | 180 | 3.5 | 6800 | 80 | 27 | 280 | 3.5 | 9200 | 80 |
| 13 | 580 | 3 | 8000 | 82 | 28 | 650 | 3.5 | 6800 | 77 |
| 14 | 620 | 3 | 7200 | 76 | 29 | 280 | 3 | 5200 | 79 |
| 15 | 750 | 4 | 6400 | 79 | 30 | 660 | 3 | 4400 | 81 |
| Approach | Working Hours (hours/m²) | Carbon Emissions (kg/m²) | Protection Days | Cost (CNY/m²) | Effectiveness |
|---|---|---|---|---|---|
| 1 | 0.2 | 8 | 1 | 10 | 3 |
| 2 | 0.5 | 15 | 2 | 25 | 5 |
| 3 | 0.75 | 32 | 2 | 100 | 20 |
| 4 | 1 | 50 | 3 | 200 | 30 |
| 5 | 1.5 | 80 | 3 | 400 | 45 |
| Strategy | Objective | Weights | ||||
|---|---|---|---|---|---|---|
| 1 | Optimize maintenance effectiveness | 0.5 | 0 | 0 | 0.5 | 0 |
| 2 | Optimize cost savings | 0 | 0 | 0 | 0 | 1 |
| 3 | Optimize affected traffic volume | 0 | 0 | 1 | 0 | 0 |
| 4 | Optimize environmental protection | 0 | 1 | 0 | 0 | 0 |
| 5 | Balance all the above considerations | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| Baseline | Optimize effectiveness and minimize cost | 0.5 | 0 | 0 | 0 | 0.5 |
| Segment | Baseline Strategy | Strategy 5 | PCI Values Based on Strategy 5 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Approach | Year | Month | Approach | Year | Month | 2024 | 2025 | 2026 | |
| 1 | 1 | 3 | 1 | 1 | 3 | 10 | 76.455 | 72.727 | 72.120 |
| 2 | 1 | 1 | 5 | 1 | 3 | 10 | 78.416 | 74.592 | 73.894 |
| 3 | 1 | 2 | 12 | 1 | 3 | 10 | 77.436 | 73.659 | 73.007 |
| 4 | 1 | 3 | 3 | 1 | 3 | 10 | 76.455 | 72.727 | 72.120 |
| 5 | 1 | 3 | 6 | 1 | 3 | 10 | 79.396 | 75.524 | 74.781 |
| 6 | 1 | 3 | 9 | 1 | 3 | 10 | 76.455 | 72.727 | 72.120 |
| 7 | 3 | 1 | 1 | 3 | 1 | 10 | 88.218 | 83.915 | 79.823 |
| 8 | 3 | 1 | 3 | 3 | 1 | 10 | 94.099 | 89.510 | 85.144 |
| 9 | 3 | 1 | 7 | 3 | 1 | 10 | 88.218 | 83.915 | 79.823 |
| 10 | 3 | 1 | 6 | 1 | 3 | 10 | 76.455 | 72.727 | 72.120 |
| 11 | 3 | 1 | 3 | 3 | 1 | 10 | 93.119 | 88.577 | 84.257 |
| 12 | 1 | 1 | 1 | 1 | 3 | 10 | 78.416 | 74.592 | 73.894 |
| 13 | 1 | 3 | 11 | None | None | None | 80.376 | 76.456 | 72.727 |
| 14 | 3 | 2 | 2 | 3 | 2 | 6 | 74.495 | 90.466 | 86.054 |
| 15 | 1 | 3 | 11 | 1 | 3 | 10 | 77.436 | 73.659 | 73.007 |
| 16 | 1 | 3 | 9 | 1 | 3 | 6 | 79.396 | 75.524 | 74.781 |
| 17 | 3 | 1 | 1 | 3 | 1 | 10 | 90.178 | 85.780 | 81.597 |
| 18 | 3 | 1 | 11 | 3 | 1 | 10 | 93.119 | 88.577 | 84.257 |
| 19 | 3 | 1 | 4 | 2 | 2 | 10 | 74.495 | 75.763 | 72.068 |
| 20 | 3 | 1 | 2 | None | None | None | 80.376 | 76.456 | 72.727 |
| 21 | 3 | 2 | 1 | 3 | 2 | 10 | 73.515 | 89.534 | 85.167 |
| 22 | 3 | 1 | 2 | 3 | 1 | 10 | 89.198 | 84.848 | 80.710 |
| 23 | 1 | 2 | 9 | 1 | 3 | 10 | 79.396 | 75.524 | 74.781 |
| 24 | 2 | 2 | 11 | 3 | 1 | 6 | 94.099 | 89.510 | 85.144 |
| 25 | 1 | 3 | 4 | 1 | 3 | 10 | 78.416 | 74.592 | 73.894 |
| 26 | 3 | 3 | 4 | 1 | 3 | 6 | 76.455 | 72.727 | 72.120 |
| 27 | 1 | 1 | 12 | 1 | 3 | 10 | 78.416 | 74.592 | 73.894 |
| 28 | 2 | 2 | 2 | 3 | 2 | 10 | 75.475 | 91.398 | 86.941 |
| 29 | 3 | 2 | 6 | 3 | 3 | 10 | 77.436 | 73.659 | 89.671 |
| 30 | 1 | 3 | 10 | 1 | 3 | 6 | 79.396 | 75.524 | 74.781 |
| Segment | Approach | Segment | Approach | Segment | Approach |
|---|---|---|---|---|---|
| 1 | 1 | 11 | 3 | 21 | 3 |
| 2 | 1 | 12 | 1 | 22 | 3 |
| 3 | 1 | 13 | none | 23 | 1 |
| 4 | 1 | 14 | 3 | 24 | 3 |
| 5 | 1 | 15 | 1 | 25 | 1 |
| 6 | 1 | 16 | 1 | 26 | 1 |
| 7 | 3 | 17 | 3 | 27 | 1 |
| 8 | 3 | 18 | 3 | 28 | 3 |
| 9 | 3 | 19 | 2 | 29 | 3 |
| 10 | 1 | 20 | none | 30 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bo, W.; Qian, Z.; Yu, B.; Ren, H.; Yang, C.; Zhao, K.; Zhang, J. MILP-Based Approach for High-Altitude Region Pavement Maintenance Decision Optimization. Appl. Sci. 2024, 14, 7670. https://doi.org/10.3390/app14177670
Bo W, Qian Z, Yu B, Ren H, Yang C, Zhao K, Zhang J. MILP-Based Approach for High-Altitude Region Pavement Maintenance Decision Optimization. Applied Sciences. 2024; 14(17):7670. https://doi.org/10.3390/app14177670
Chicago/Turabian StyleBo, Wu, Zhendong Qian, Bo Yu, Haisheng Ren, Can Yang, Kunming Zhao, and Jiazhe Zhang. 2024. "MILP-Based Approach for High-Altitude Region Pavement Maintenance Decision Optimization" Applied Sciences 14, no. 17: 7670. https://doi.org/10.3390/app14177670
APA StyleBo, W., Qian, Z., Yu, B., Ren, H., Yang, C., Zhao, K., & Zhang, J. (2024). MILP-Based Approach for High-Altitude Region Pavement Maintenance Decision Optimization. Applied Sciences, 14(17), 7670. https://doi.org/10.3390/app14177670







