An Optimization Method for Location-Routing of Cruise Ship Cabin Materials Considering Obstacle Blocking Effects
Abstract
:1. Introduction
2. Mathematical Model of the BE-LRP
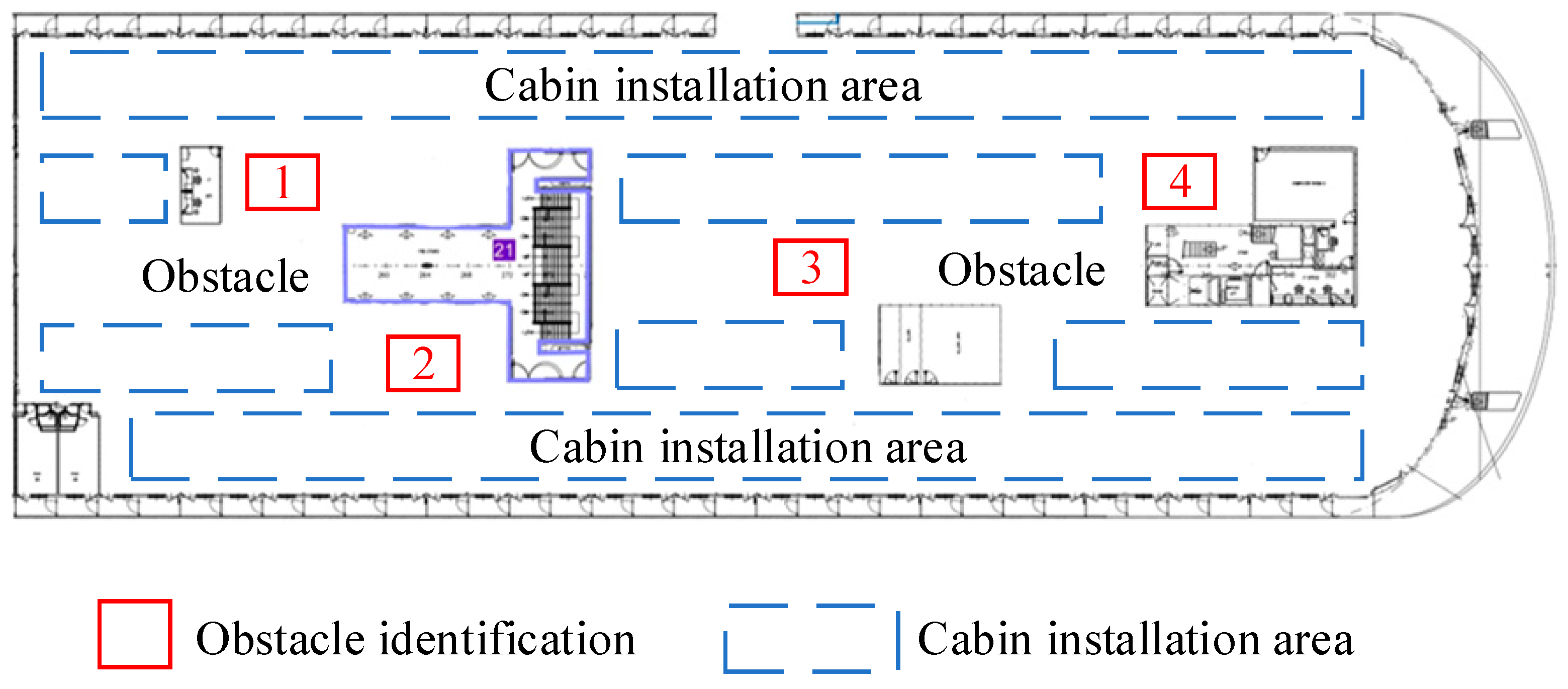
2.1. Description of the BE-LRP
2.2. Model Assumptions and Variable Definitions
2.3. Model Building
3. Blocked Distance Estimation
3.1. Gaussian Process Regression
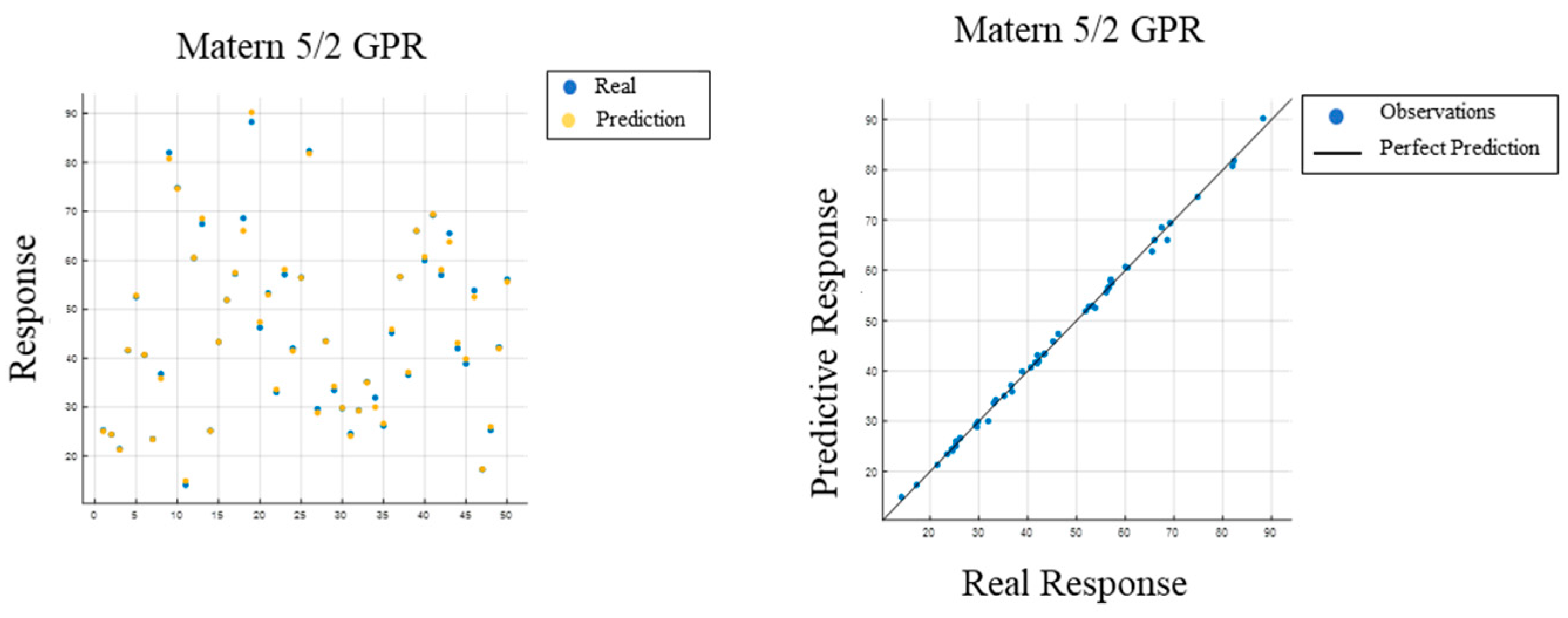
3.2. Blocked Distance Prediction Based on Gaussian Process Regression
4. Hybrid Algorithm Design
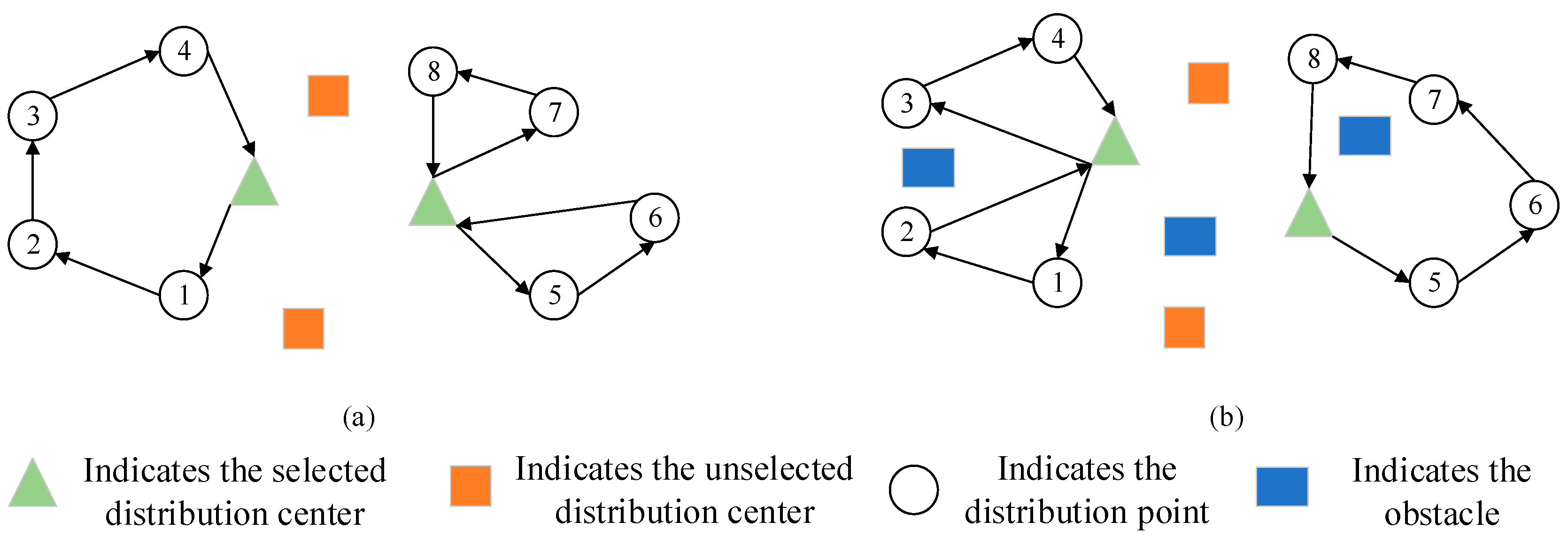
4.1. Handling of Obstacle Blocking Effects
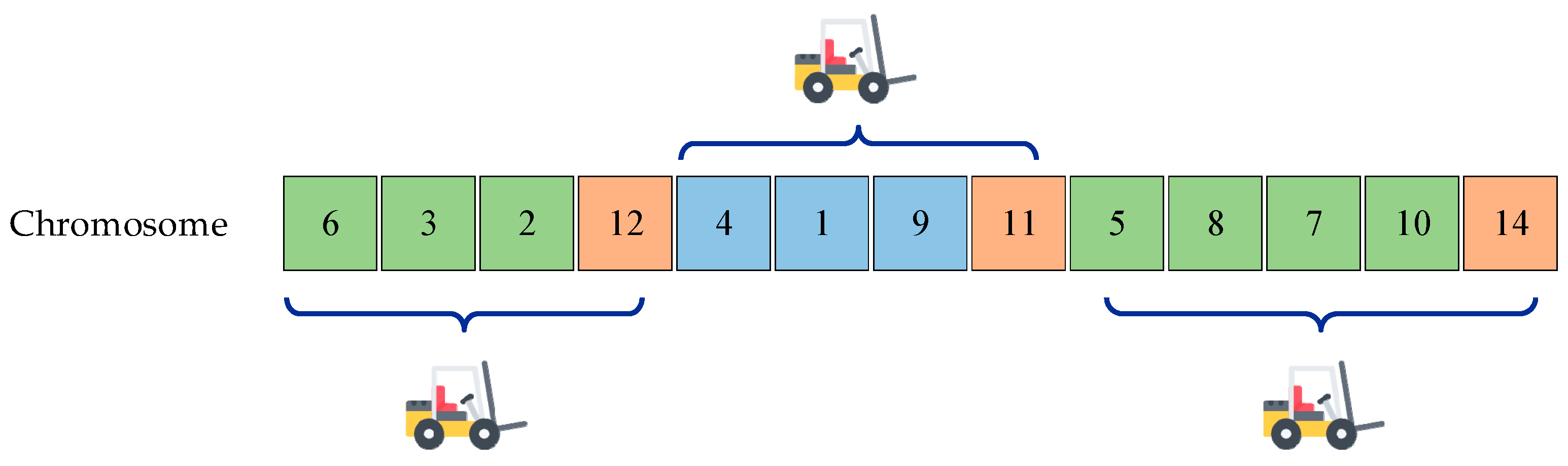
4.2. Encoding Method
4.3. Initial Solution Generation
4.4. Non-Dominated Sorting and Congestion Calculation
| Algorithm 1: Fast Non-Dominated Sorting | |
| Input: | Population P |
| Output: | Pareto rank |
| 1: | Calculate the number of dominant individuals Ni and the combination of dominant individuals Si for each individual in population P |
| 2: | rank = 1 |
| 3: | While P is not empty DO |
| 4: | Form a set F of individuals with Ni = 0 and label the non-dominant |
| 5: | level as rank; For i ∈ F DO |
| 6: | For l ∈ Si DO |
| 7: | Nl = Nl−1 |
| 8: | End For |
| 9: | End For |
| 10: | New population P |
| 11: | rank = rank + 1 |
| 12: | End While |
| Algorithm 2: Congestion Calculation | |
| Input: | Population P |
| Output: | Congestion C |
| 1: | Calculate each objective function f of an individual and calculate the non-dominated rank |
| 2: | For rank = 1: max_rank DO |
| 3: | Take individuals with a non-dominant rank to form a set F |
| 4: | For i ∈ F DO |
| 5: | For each f DO |
| 6: | Sort according to f, the maximum and minimum C are infinite |
| 7: | Ci = Ci + (f(i + 1) − f(i − 1))/(fmax − fmin) |
| 8: | End For |
| 9: | End For |
| 10: | rank = rank + 1 |
| 11: | End For |
4.5. Selection, Crossover, and Mutation
4.5.1. Selection Operation
4.5.2. Crossover Operation
4.5.3. Mutation Operation
5. Result and Discussion
5.1. Instance Validation Conditions
5.2. Optimization Results and Analysis
5.3. Managerial Insights Analysis
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cerveny, L.K.; Miller, A.; Gende, S. Sustainable Cruise Tourism in Marine World Heritage Sites. Sustainability 2020, 12, 611. [Google Scholar] [CrossRef]
- Chen, Q.; Ge, Y.-E.; Lau, Y.; Dulebenets, M.A.; Sun, X.; Kawasaki, T.; Mellalou, A.; Tao, X. Effects of COVID-19 on Passenger Shipping Activities and Emissions: Empirical Analysis of Passenger Ships in Danish Waters. Marit. Policy Manag. 2023, 50, 776–796. [Google Scholar] [CrossRef]
- Yip, T.L.; Lau, Y.; Kanrak, M. Social Transformation in the Cruise Industry during the COVID-19 Pandemic. Front. Mar. Sci. 2023, 10, 1179624. [Google Scholar] [CrossRef]
- Jiao, Y.; Dulebenets, M.A.; Lau, Y. Cruise Ship Safety Management in Asian Regions: Trends and Future Outlook. Sustainability 2020, 12, 5567. [Google Scholar] [CrossRef]
- Wang, J.; Yin, J.; Khan, R.U.; Wang, S.; Zheng, T. A Study of Inbound Logistics Mode Based on JIT Production in Cruise Ship Construction. Sustainability 2021, 13, 1588. [Google Scholar] [CrossRef]
- Salhi, S.; Nagy, G. Consistency and Robustness in Location-Routing. Stud. Locat. Anal. 1999, 13, 3–19. [Google Scholar]
- Drexl, M.; Schneider, M. A Survey of Variants and Extensions of the Location-Routing Problem. Eur. J. Oper. Res. 2015, 241, 283–308. [Google Scholar] [CrossRef]
- Mara, S.T.W.; Kuo, R.J.; Asih, A.M.S. Location-routing Problem: A Classification of Recent Research. Int. Trans. Oper. Res. 2021, 28, 2941–2983. [Google Scholar] [CrossRef]
- Ghaffari-Nasab, N.; Jabalameli, M.S.; Aryanezhad, M.B.; Makui, A. Modeling and Solving the Bi-Objective Capacitated Location-Routing Problem with Probabilistic Travel Times. Int. J. Adv. Manuf. Technol. 2013, 67, 2007–2019. [Google Scholar] [CrossRef]
- Yu, V.F.; Lin, S.-W.; Lee, W.; Ting, C.-J. A Simulated Annealing Heuristic for the Capacitated Location Routing Problem. Comput. Ind. Eng. 2010, 58, 288–299. [Google Scholar] [CrossRef]
- Ting, C.-J.; Chen, C.-H. A Multiple Ant Colony Optimization Algorithm for the Capacitated Location Routing Problem. Int. J. Prod. Econ. 2013, 141, 34–44. [Google Scholar] [CrossRef]
- Validi, S.; Bhattacharya, A.; Byrne, P.J. A Case Analysis of a Sustainable Food Supply Chain Distribution System—A Multi-Objective Approach. Int. J. Prod. Econ. 2014, 152, 71–87. [Google Scholar] [CrossRef]
- Marinakis, Y. An Improved Particle Swarm Optimization Algorithm for the Capacitated Location Routing Problem and for the Location Routing Problem with Stochastic Demands. Appl. Soft Comput. 2015, 37, 680–701. [Google Scholar] [CrossRef]
- Lopes, R.B.; Ferreira, C.; Santos, B.S. A Simple and Effective Evolutionary Algorithm for the Capacitated Location–Routing Problem. Comput. Oper. Res. 2016, 70, 155–162. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, Y.; Liu, X.-F. A Novel Hybrid Genetic Algorithm for the Location Routing Problem with Tight Capacity Constraints. Appl. Soft Comput. 2019, 85, 105760. [Google Scholar] [CrossRef]
- Hof, J.; Schneider, M.; Goeke, D. Solving the Battery Swap Station Location-Routing Problem with Capacitated Electric Vehicles Using an AVNS Algorithm for Vehicle-Routing Problems with Intermediate Stops. Transp. Res. Part B Methodol. 2017, 97, 102–112. [Google Scholar] [CrossRef]
- Quintero-Araujo, C.L.; Guimarans, D.; Juan, A.A. A Simheuristic Algorithm for the Capacitated Location Routing Problem with Stochastic Demands. J. Simul. 2021, 15, 217–234. [Google Scholar] [CrossRef]
- Wu, Y.; Qureshi, A.G.; Yamada, T. Adaptive Large Neighborhood Decomposition Search Algorithm for Multi-Allocation Hub Location Routing Problem. Eur. J. Oper. Res. 2022, 302, 1113–1127. [Google Scholar] [CrossRef]
- Carrasco Heine, O.F.; Demleitner, A.; Matuschke, J. Bifactor Approximation for Location Routing with Vehicle and Facility Capacities. Eur. J. Oper. Res. 2023, 304, 429–442. [Google Scholar] [CrossRef]
- Galindres, L.F.; Guimarães, F.G.; Gallego-Rendón, R.A. Multi-Objective Sustainable Capacitated Location Routing Problem Formulation in Sustainable Supply-Chain Management. Eng. Optim. 2023, 55, 526–541. [Google Scholar] [CrossRef]
- Ponboon, S.; Qureshi, A.G.; Taniguchi, E. Branch-and-Price Algorithm for the Location-Routing Problem with Time Windows. Transp. Res. Part E Logist. Transp. Rev. 2016, 86, 1–19. [Google Scholar] [CrossRef]
- Koç, Ç.; Bektaş, T.; Jabali, O.; Laporte, G. The Fleet Size and Mix Location-Routing Problem with Time Windows: Formulations and a Heuristic Algorithm. Eur. J. Oper. Res. 2016, 248, 33–51. [Google Scholar] [CrossRef]
- Basirati, M.; Akbari Jokar, M.R.; Hassannayebi, E. Bi-Objective Optimization Approaches to Many-to-Many Hub Location Routing with Distance Balancing and Hard Time Window. Neural Comput. Appl. 2020, 32, 13267–13288. [Google Scholar] [CrossRef]
- Alamatsaz, K.; Ahmadi, A.; Mirzapour Al-e-hashem, S.M.J. A Multiobjective Model for the Green Capacitated Location-Routing Problem Considering Drivers’ Satisfaction and Time Window with Uncertain Demand. Env. Sci. Pollut. Res. 2022, 29, 5052–5071. [Google Scholar] [CrossRef]
- Tasouji Hassanpour, S.; Ke, G.Y.; Zhao, J.; Tulett, D.M. Infectious Waste Management during a Pandemic: A Stochastic Location-Routing Problem with Chance-Constrained Time Windows. Comput. Ind. Eng. 2023, 177, 109066. [Google Scholar] [CrossRef] [PubMed]
- Maghfiroh, M.F.N.; Yu, V.F.; Redi, A.A.N.P.; Abdallah, B.N. A Location Routing Problem with Time Windows Consideration: A Metaheuristics Approach. Appl. Sci. 2023, 13, 843. [Google Scholar] [CrossRef]
- Nguyen, V.-P.; Prins, C.; Prodhon, C. A Multi-Start Iterated Local Search with Tabu List and Path Relinking for the Two-Echelon Location-Routing Problem. Eng. Appl. Artif. Intell. 2012, 25, 56–71. [Google Scholar] [CrossRef]
- Nguyen, V.-P.; Prins, C.; Prodhon, C. Solving the Two-Echelon Location Routing Problem by a GRASP Reinforced by a Learning Process and Path Relinking. Eur. J. Oper. Res. 2012, 216, 113–126. [Google Scholar] [CrossRef]
- Ben Mohamed, I.; Klibi, W.; Sadykov, R.; Şen, H.; Vanderbeck, F. The Two-Echelon Stochastic Multi-Period Capacitated Location-Routing Problem. Eur. J. Oper. Res. 2023, 306, 645–667. [Google Scholar] [CrossRef]
- Nucamendi-Guillén, S.; Martínez-Salazar, I.; Khodaparasti, S.; Bruni, M.E. New Formulations and Solution Approaches for the Latency Location Routing Problem. Comput. Oper. Res. 2022, 143, 105767. [Google Scholar] [CrossRef]
- Warsame, Y. Integrating Location-Routing with Task and Motion Planning. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; IEEE: New York, NY, USA, 2020; pp. 329–334. [Google Scholar]
- Wang, Y.; Sun, Y.; Guan, X.; Fan, J.; Xu, M.; Wang, H. Two-Echelon Multi-Period Location Routing Problem with Shared Transportation Resource. Knowl.-Based Syst. 2021, 226, 107168. [Google Scholar] [CrossRef]
- Erke, S.; Bin, D.; Yiming, N.; Qi, Z.; Liang, X.; Dawei, Z. An Improved A-Star Based Path Planning Algorithm for Autonomous Land Vehicles. Int. J. Adv. Robot. Syst. 2020, 17, 172988142096226. [Google Scholar] [CrossRef]
- Li, C.; Huang, X.; Ding, J.; Song, K.; Lu, S. Global Path Planning Based on a Bidirectional Alternating Search A* Algorithm for Mobile Robots. Comput. Ind. Eng. 2022, 168, 108123. [Google Scholar] [CrossRef]
- Lin, M.; Yuan, K.; Shi, C.; Wang, Y. Path Planning of Mobile Robot Based on Improved A* Algorithm. In Proceedings of the Control & Decision Conference, Chongqing, China, 28–30 May 2017. [Google Scholar]
- Gopinath, K.G.S.; Pal, S.; Tambe, P. Prediction of Hardness and Fracture Toughness in Liquid-Phase-Sintered Alumina System Using Gaussian Process Regression and Minimax Probability Machine Regression. Mater. Today Proc. 2018, 5, 12223–12232. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Chen, M.; Tan, Y. SF-FWA: A Self-Adaptive Fast Fireworks Algorithm for Effective Large-Scale Optimization. Swarm Evol. Comput. 2023, 80, 101314. [Google Scholar] [CrossRef]
- Dulebenets, M.A. An Adaptive Polyploid Memetic Algorithm for Scheduling Trucks at a Cross-Docking Terminal. Inf. Sci. 2021, 565, 390–421. [Google Scholar] [CrossRef]
- Singh, E.; Pillay, N. A Study of Ant-Based Pheromone Spaces for Generation Constructive Hyper-Heuristics. Swarm Evol. Comput. 2022, 72, 101095. [Google Scholar] [CrossRef]
- Singh, P.; Pasha, J.; Moses, R.; Sobanjo, J.; Ozguven, E.E.; Dulebenets, M.A. Development of Exact and Heuristic Optimization Methods for Safety Improvement Projects at Level Crossings under Conflicting Objectives. Reliab. Eng. Syst. Saf. 2022, 220, 108296. [Google Scholar] [CrossRef]
- Dulebenets, M.A. A Diffused Memetic Optimizer for Reactive Berth Allocation and Scheduling at Marine Container Terminals in Response to Disruptions. Swarm Evol. Comput. 2023, 80, 101334. [Google Scholar] [CrossRef]




| Set | Definition |
| Set of distribution centers, | |
| Set of cabin positions, | |
| Set of delivery vehicles, | |
| Ordered set of delivery service routes, | |
| Set of vehicles for cabin service | |
| Set of service cabins in the nth route for the vehicle k, | |
| Parameter | Definition |
| Loading capacity of vehicle k | |
| Speed of vehicle k | |
| Storage capacity of distribution centers, | |
| Material demand for cabins, | |
| Number of service routes for car k, | |
| The total number of cabins in the delivery area | |
| Cabin serviced by car k on route n, | |
| Number of vehicles serving all cabins, | |
| Variable | Definition |
| The distance between distribution center i or cabin c and d, | |
| Obstacle blocking influence coefficient, | |
| Time window for cabin j, | |
| The time when the vehicle k leaves the distribution center i on the nth route, , | |
| The time when the vehicle k arrives the distribution center i or cabin j on the nth route, , | |
| Decision Variable | Definition |
| If the vehicle k is on the nth route from the distribution center or cabin i to j, , otherwise , , | |
| If the vehicle k goes from the distribution center i to the cabin j, , otherwise , , , | |
| If the vehicle has a service cabin, , otherwise , | |
| If distribution center i is selected as cabin service, , otherwise , | |
| If distribution center i is selected as cabin j service, , otherwise , , |
| Kernel Type | R2 | RMSE | MSE | MAE |
|---|---|---|---|---|
| Exponential | 0.99 | 2.2466 | 5.0474 | 1.3839 |
| Matern5/2 | 1.00 | 0.8233 | 0.67782 | 0.58186 |
| Square exponential | 1.00 | 0.81744 | 0.66821 | 0.5826 |
| Number | Distribution Center | Distribution Route | Number of Vehicles | Distance (m) |
|---|---|---|---|---|
| Test-01A | DC1 | 8-5; 10-12-16; 9-4 | 10 | 297.166 |
| DC2 | 7-11-13; 6-3-2-1 | |||
| DC4 | 22-24-25; 20-19 | |||
| DC5 | 23-17; 21-18; 15-14 | |||
| Test-01B | DC1 | 8-5; 10-12-16; 9-4 | 11 | 268.431 |
| DC2 | 7-11-13; 6-3-2-1 | |||
| DC4 | 17; 22-24; 20-19 | |||
| DC5 | 23-25; 21-18; 15-14 | |||
| Test-01C | DC1 | 8-5; 10-12-16; 9-4 | 12 | 267.611 |
| DC2 | 7; 11-13; 6-3-2-1 | |||
| DC4 | 17; 22-24; 20-19 | |||
| DC5 | 23-25; 21-18; 15-14 |
| Number | Distribution Center | Distribution Route | Number of Vehicles | Distance (m) |
|---|---|---|---|---|
| Test-01A | DC1 | 5-1; 9-4 | 10 | 282.322 |
| DC2 | 8-10-14; 7-3-2-6 | |||
| DC3 | 15-18; 12-16-17 | |||
| DC4 | 20-21; 22;24 | |||
| DC5 | 19-13-11; 23-25 | |||
| Test-01B | DC1 | 5-1; 9-4 | 11 | 259.177 |
| DC2 | 8-10-14; 7-3-2-6 | |||
| DC3 | 15-18; 12; 17-13-11 | |||
| DC4 | 22-24; 21 | |||
| DC5 | 19-20-16; 23-25 | |||
| Test-01C | DC1 | 9; 5-1; 4 | 12 | 257.177 |
| DC2 | 8-10-14; 7-3-2-6 | |||
| DC3 | 15-18; 12; 17-13-11 | |||
| DC4 | 22-24; 21 | |||
| DC5 | 19-20-16; 23-25 |
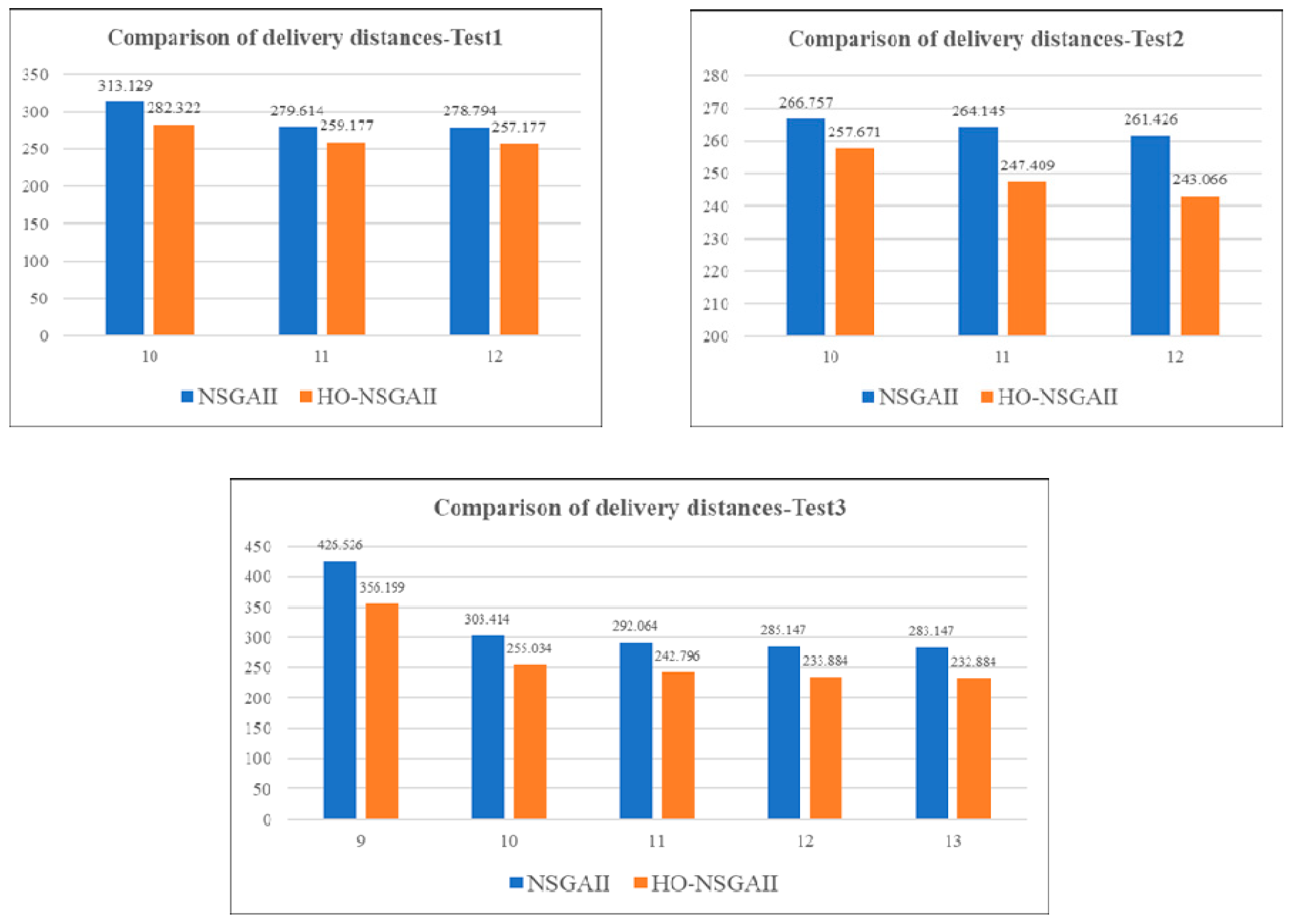
| NSGAII | HO-NSGAII | Distance Gap | Optimization Rate | |||||
|---|---|---|---|---|---|---|---|---|
| m | D1 | D2 | m | D3 | D4 | |||
| Test01 | 10 | 297.166 | 313.129 | 10 | 282.322 | 282.322 | 30.807 | 9.8% |
| 11 | 268.431 | 279.614 | 11 | 259.177 | 259.177 | 20.437 | 7.3% | |
| 12 | 267.611 | 278.794 | 12 | 257.177 | 257.177 | 21.617 | 7.8% | |
| Test02 | 10 | 264.747 | 266.757 | 10 | 257.671 | 257.671 | 9.086 | 3.4% |
| 11 | 260.156 | 264.145 | 11 | 247.409 | 247.409 | 16.736 | 6.3% | |
| 12 | 258.336 | 261.426 | 12 | 243.066 | 243.066 | 18.36 | 7.0% | |
| Test03 | 9 | 396.447 | 426.526 | 9 | 356.199 | 356.199 | 70.327 | 16.4% |
| 10 | 293.853 | 303.414 | 10 | 255.034 | 255.034 | 48.38 | 15.9% | |
| 11 | 282.503 | 292.064 | 11 | 242.796 | 242.796 | 49.268 | 16.8% | |
| 12 | 275.586 | 285.147 | 12 | 233.884 | 233.884 | 51.263 | 17.9% | |
| 13 | 273.586 | 283.147 | 13 | 232.884 | 232.884 | 50.263 | 17.8% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Huang, W.; Wu, X.; Dong, R.; Lin, P. An Optimization Method for Location-Routing of Cruise Ship Cabin Materials Considering Obstacle Blocking Effects. Appl. Sci. 2024, 14, 7510. https://doi.org/10.3390/app14177510
Li J, Huang W, Wu X, Dong R, Lin P. An Optimization Method for Location-Routing of Cruise Ship Cabin Materials Considering Obstacle Blocking Effects. Applied Sciences. 2024; 14(17):7510. https://doi.org/10.3390/app14177510
Chicago/Turabian StyleLi, Jinghua, Wenhao Huang, Xiaoyuan Wu, Ruipu Dong, and Pengfei Lin. 2024. "An Optimization Method for Location-Routing of Cruise Ship Cabin Materials Considering Obstacle Blocking Effects" Applied Sciences 14, no. 17: 7510. https://doi.org/10.3390/app14177510
APA StyleLi, J., Huang, W., Wu, X., Dong, R., & Lin, P. (2024). An Optimization Method for Location-Routing of Cruise Ship Cabin Materials Considering Obstacle Blocking Effects. Applied Sciences, 14(17), 7510. https://doi.org/10.3390/app14177510





