Secure Beamforming Design for UAV-Empowered Integrated Sensing and Communication

Abstract

Integrated sensing and communication (ISAC) systems assisted by unmanned aerial vehicles (UAVs) are susceptible to eavesdropping, making secure information transmission a critical area of research. We propose a joint optimization algorithm to improve the security of UAV-assisted ISAC systems through coordinated adjustments of transmit beamforming and UAV position. The optimization problem aims to minimize the maximum eavesdropping signal-to-interference-plus-noise ratio (SINR) across multiple legitimate users while adhering to three distinct constraints: service quality for legitimate users, sensing requirements for detecting eavesdroppers, and limitations on system transmit power. To address the non-convex optimization challenge effectively, the problem is decomposed into sub-problems focusing on the optimization of transmit beamforming and UAV position. These sub-problems are solved using semidefinite relaxation (SDR), the Dinkelbach method, and successive convex approximation (SCA), with iterative alternation achieving optimal values for the transmit beamforming and UAV position while also proving the convergence of the algorithm. Lastly, simulation results illustrate that the proposed algorithm markedly improves the system’s security performance while preserving its communication and sensing capabilities.

1. Introduction

Amid the rapid advancement of wireless networks, the need for efficient information transmission within the communications sector is consistently intensifying [1,2]. However, with the booming development of the Internet of Things (IoT), communication systems, such as autonomous driving and telemedicine, are required not only to meet traditional needs but also to possess advanced sensing capabilities. This dual demand has made spectrum resources increasingly scarce [3,4]. To address the combined needs of communication and sensing in future wireless systems, researchers have begun to explore the possibility of jointly designing sensing and communication systems to enhance spectral efficiency and reduce hardware costs [5].

At the same time, advancements in multi-antenna and beamforming technologies have brought significant attention to their applications in both sensing and communication [6,7,8,9]. The integration of these technologies has unveiled new opportunities for advancing ISAC systems. In [6], an optimization algorithm was proposed to maximize the mutual information of radar systems. This study also analyzed how the distance to radar targets affects communications and the perceptual performance impact on communication users. Utilizing reconfigurable intelligent surfaces (RIS) can further enhance the performance of ISAC systems [9,10]. In [9], optimizations for two types of RIS were explored: one dedicated to communication and another supporting both communication and sensing. The research entailed adjustments to the transmitting beamforming of the multi-antenna base station and the phase shifts of the RIS.

Due to the significant strides made in UAV technology, they have become a highly promising aerial platform within ISAC systems, offering new solutions to overcome the limitations of traditional ground networks. The introduction of highly mobile and flexible UAVs enables ISAC systems to exhibit superior performance in specific scenarios. Optimization challenges for UAVs in both hovering and flying states were explored, with a focus on the joint design of UAV trajectories and beamforming weights to enhance the ISAC system’s performance [11]. Considering the potential impact of sensed signal reception on the communication signal-to-noise ratio, a time-division sensing mechanism was proposed [12]. This mechanism allows the flexible allocation of UAV sensing times, enabling sensing and communication to occur non-simultaneously. By jointly optimizing UAV flight trajectories, beamforming weights, and user reception weights, the communication performance of the system has been further enhanced. In the aforementioned system, UAVs act as base stations. In [13], UAVs were utilized as relays, with the information age serving as a performance metric. The research minimized this metric by alternately optimizing UAV trajectories, transmit power, and service times, thereby enhancing communication and sensing coverage, as well as overall ISAC system performance. A multi-UAV-assisted ISAC system, where UAVs transmit information to moving ground users while simultaneously sensing them [14]. In [15], the deployment of multiple UAVs to transmit dual-function signals for both communication and location tracking of ground users was discussed. In contrast to [14], this study utilized an extended Kalman filter to accurately estimate and predict the time delays and Doppler shifts in the reflected signals from targets, which ensures precise target tracking.

As ISAC systems rapidly evolve, although their communication and sensing capabilities are increasingly robust, the openness of wireless communication media has raised security concerns, particularly regarding the physical layer security (PLS) of ISAC systems [16]. Artificial noise (AN) is utilized to disrupt eavesdroppers, aiming to maximize the power of AN given that the base station is unaware of the eavesdropper’s channel state, which hinders eavesdropping while maintaining robust communication and sensing performance [17,18]. RIS is employed to optimize transmission beamforming weights and phase shifts, aiming to maximize the perceptual beam pattern gain irrespective of the eavesdropper’s channel state knowledge [19].

Research on the security of UAV-assisted ISAC systems has just begun. In [20], the Stackelberg game model was utilized to analyze the power strategy game between UAVs and eavesdroppers, considering scenarios where the eavesdropper’s channel state is both known and unknown. A distance-based UAV positioning optimization strategy aimed at maximizing the number of users receiving secure communication services was conducted in [21]. However, ref. [20] focused solely on a single-antenna model, whereas [21] implemented maximum ratio combining for transmit beamforming. Addressing the scenario in which multiple eavesdropping targets and communication users coexist, this paper proposes a joint optimization algorithm for UAV transmit beamforming and position. The algorithm employs the SDR and SCA methods for iterative optimization. We seek to minimize the maximum eavesdropping SINR while maintaining communication performance for users and sensing accuracy for targets, thereby bolstering the system’s security. The principal contributions of this paper are outlined as follows:

(1)

Given the security concerns of the UAV-assisted ISAC system, we tackle the challenge of detecting eavesdroppers while facilitating communication with legitimate users. Under the constraints of transmit power, legitimate communication quality of service, and sensing beam pattern gain, the problem is formulated as a joint optimization of UAV positioning and communication and sensing beamforming, aiming to minimize the maximum eavesdropping SINR.

(2)

Owing to the coupling between UAV communication and sensing beamforming, coupled with the intricate relationship between UAV positioning and steering vectors, the problem is inherently non-convex. To address this, the problem is decomposed into two sub-problems: beamforming optimization and UAV positioning optimization. For the UAV positioning sub-problem, a SCA algorithm, leveraging the first-order Taylor expansion, is employed to transform the non-convex problem into a convex one. This problem is subsequently resolved using the CVX toolbox.

(3)

For the beamforming optimization sub-problem, the max-min problem is addressed by introducing slack variables, and the fractional optimization problem is solved using the Dinkelbach method. The optimal beamforming is then determined using the semidefinite relaxation algorithm by ignoring the rank-one constraint and solving through eigenvalue decomposition. Simulation results indicate that the proposed algorithm substantially improves the security performance of the ISAC system, concurrently maintaining robust communication and sensing capabilities.

This paper is structured as follows: Section 2 outlines the system model and the problem formulation; Section 3 details the joint optimization algorithm; Section 4 provides an analysis of the simulation results and performance; and Section 5 offers the conclusions. For ease of reference, essential notations employed in this paper are compiled in

Table 1. Key notations.

Symbol	Definitions	Symbol	Definitions
$N$	Number of antennas	$\mathit{x}$	Transmitted signal of the UAV
$K$,$J$	Number of users and eavesdroppers	$P_{\max }$	Maximum transmit power
$s_k^c$, $s_n^r$	Communication signal and sensing signal	$\mathit{q}$, ${\mathit{u}}_k$, ${\mathit{e}}_j$	Location of UAV, user k and eavesdropper $j$
${\mathit{\omega }}_k^c$, ${\mathit{\omega }}_n^r$	Beamforming vector	${\mathit{h}}_k\left(\mathit{q},{\mathit{u}}_k\right)$	Communication channel from the UAV to the user $k$
$\mathit{a}\left(\mathit{q},{\mathit{u}}_k\right)$	Beamforming steering vector	${\mathit{g}}_j\left(\mathit{q},{\mathit{e}}_j\right)$	Eavesdropping channel
$n_k$, $z_e$	Additive white Gaussian noise	${\sigma }_k^2$, ${\sigma }_e^2$	Noise power spectral density
$\varsigma \left(\theta \left(\mathit{q},{\mathit{e}}_j\right)\right)$	Beam pattern gain	${\Gamma }_k^{\mathrm{com}}$, ${\Gamma }_e^{\mathrm{sen}}$	Threshold of communication and sensing
$A$, $B$, $c_{j,k}$	Slack variables	$R$	Trust region radius

.

2. System Model and Problem Formulation

As illustrated in Figure 1, we explore a UAV-assisted ISAC system comprising a UAV that serves as a dual-function base station, legitimate users, and potential eavesdropping targets. The UAV is equipped with an $N$-antenna uniform linear array (ULA), enabling simultaneous communication with $K\ge 1$ single-antenna users on the ground while detecting $J$ single-antenna eavesdroppers also located on the ground.

2.1. Communication Model

We consider a scenario in which the UAV transmits information signals to legitimate users while simultaneously sending sensing signals to detect eavesdroppers. We employ two different signals for communication and sensing. Let $s_k^c$ denote the desired communication signal sent by the UAV to the legitimate user $k$, ${\mathit{\omega }}_k^c\in {ℂ}^{N\times 1}$ denote the corresponding communication beamforming vector, $s_n^r$ denote the dedicated radar sensing signal sent by the UAV, ${\mathit{\omega }}_n^r\in {ℂ}^{N\times 1}$ and denote the corresponding sensing beamforming vector. The transmitted signal of the UAV is then given by [12,19]:

$$\mathit{x}={\displaystyle \sum _{k=1}^K{\mathit{\omega }}_k^c{s}_k^c+{\displaystyle \sum _{n=1}^N{\mathit{\omega }}_n^r{s}_n^r}}$$

(1)

Assuming, without loss of generality, that both the communication signal $s_k^c,\forall k$ and the sensing signal $s_n^r,\forall n$ are independent and identically distributed complex Gaussian random variables with zero mean and unit variance, i.e., $s_k^c\sim \mathcal{C}\mathcal{N}\left(0,1\right)$ [18]. Therefore, the average transmit power of the UAV is $\mathbb{E}\left({‖\mathit{x}‖}^2\right)={\sum }_{k=1}^K{‖{\mathit{\omega }}_k^c‖}^2+{\sum }_{n=1}^N{‖{\mathit{\omega }}_n^r‖}^2$. Assuming the maximum transmit power of the UAV is $P_{\max }$, the UAV transmit power constraint can be expressed as:

$${\sum }_{k=1}^K{‖{\mathit{\omega }}_k^c‖}^2+{\sum }_{n=1}^N{‖{\mathit{\omega }}_n^r‖}^2\le P_{\max }$$

(2)

We consider a three-dimensional (3D) Cartesian coordinate system, assuming the UAV flight altitude is $H$ meters. The position of the UAV is denoted as $\left(x,y,H\right)$, $\mathit{q}=\left(x,y\right)$ representing its horizontal position. The position of the legitimate user $k$ is fixed at $\left(x_k,y_k,0\right)$, ${\mathit{u}}_k=\left(x_k,y_k\right)$ representing its horizontal position, and the position of the $j$-th eavesdropper is fixed at $\left(x_{e,j},y_{e,j},0\right)$, ${\mathit{e}}_j=\left(x_{e,j},y_{e,j}\right)$ representing its horizontal position. Due to the relatively high deployment altitude of the UAV, there exists a strong Line of Sight (LOS) link between the UAV and each user. Therefore, we model the channel as an LOS channel.

The LOS communication channel from the UAV to the user $k$ is given by:

$$\begin{array}{ll}{\mathit{h}}_k\left(\mathit{q},{\mathit{u}}_k\right)& =\sqrt{\beta d^{-2}\left(\mathit{q},{\mathit{u}}_k\right)}\mathit{a}\left(\mathit{q},{\mathit{u}}_k\right)\\ & =\sqrt{{\displaystyle \frac{\beta }{H^2+{‖\mathit{q}-{\mathit{u}}_k‖}^2}}}\mathit{a}\left(\mathit{q},{\mathit{u}}_k\right)\end{array}$$

(3)

where ${\mathit{h}}_k\left(\mathit{q},{\mathit{u}}_k\right)\in {ℂ}^{N\times 1}$, $\beta$ represents the signal power attenuation gain at the reference distance $d_0=1\mathrm{m}$, $d\left(\mathit{q},{\mathit{u}}_k\right)=\sqrt{H^2+{‖\mathit{q}-{\mathit{u}}_k‖}^2}$ represents the distance between the UAV and the user $k$, and $\mathit{a}\left(\mathit{q},{\mathit{u}}_k\right)\in {ℂ}^{N\times 1}$ represents the beamforming steering vector of the UAV toward the user $k$, which can be expressed as:

$$\mathit{a}\left(\mathit{q},{\mathit{u}}_k\right)={\left[1,\exp \left(j{\displaystyle \frac{2\pi d^{\mathit{a}rr}}{\lambda }}\cos \theta \left(\mathit{q},{\mathit{u}}_k\right)\right),\dots ,\exp \left(j{\displaystyle \frac{2\pi d^{\mathit{a}rr}}{\lambda }}\left(N-1\right)\cos \theta \left(\mathit{q},{\mathit{u}}_k\right)\right)\right]}^{\mathrm{T}}$$

(4)

where $d^{\mathit{a}rr}$ represents the distance between two adjacent antennas in the linear array, $\lambda$ represents the wavelength of the carrier signal, typically $d^{\mathit{a}rr}=\lambda /2$. $\cos \theta \left(\mathit{q},{\mathit{u}}_k\right)$ denotes the cosine of the Angle of Departure (AoD) for the user $k$, given by:

$$\cos \theta \left(\mathit{q},{\mathit{u}}_k\right)={\displaystyle \frac{H}{\sqrt{H^2+{‖\mathit{q}-{\mathit{u}}_k‖}^2}}}$$

(5)

The signal received by the legitimate user $k$ can be expressed as:

$$\begin{array}{ll}{y}_k& ={\mathit{h}}_k^{\mathrm{H}}\left(\mathit{q},{\mathit{u}}_k\right)\mathit{x}+n_k\\ & =\underset{\mathrm{desired}k\text{-}\mathrm{th}\mathrm{user}\mathrm{signal}}{\underbrace{{\mathit{h}}_k^{\mathrm{H}}\left(\mathit{q},{\mathit{u}}_k\right){\mathit{\omega }}_k^c{s}_k^c}}+\underset{\mathrm{interference}\mathrm{signals}\mathrm{from}\mathrm{other}\mathrm{users}}{\underbrace{{\displaystyle \sum _{i=1,i\ne k}^K{\mathit{h}}_k^{\mathrm{H}}\left(\mathit{q},{\mathit{u}}_k\right){\mathit{\omega }}_i^c{s}_i^c}}}\\ & +\underset{\mathrm{sensing}\mathrm{interference}\mathrm{signal}}{\underbrace{{\displaystyle \sum _{n=1}^N{\mathit{h}}_k^{\mathrm{H}}\left(\mathit{q},{\mathit{u}}_k\right){\mathit{\omega }}_n^r{s}_n^r}}}+\underset{\mathrm{AWGN}}{\underbrace{n_k}}\end{array}$$

(6)

where $n_k\sim \mathcal{C}\mathcal{N}\left(0,{\sigma }_k^2\right)$ represents the additive white Gaussian noise (AWGN) received by the user $k$. From (6), it can be observed that the user $k$ receives not only its desired communication signal but also the communication signals from other users, the sensing signals, and the additive noise. Therefore, the SINR for the user $k$ can be expressed as:

$${\mathrm{SIN}\mathrm{R}}_k={\displaystyle \frac{{\left|{\mathit{h}}_k^{\mathrm{H}}\left(\mathit{q},{\mathit{u}}_k\right){\mathit{\omega }}_k^c\right|}^2}{{\left|{\displaystyle \sum _{i=1,i\ne k}^K{\mathit{h}}_k^{\mathrm{H}}\left(\mathit{q},{\mathit{u}}_k\right){\mathit{\omega }}_i^c}\right|}^2+{\left|{\displaystyle \sum _{n=1}^N{\mathit{h}}_k^{\mathrm{H}}\left(\mathit{q},{\mathit{u}}_k\right){\mathit{\omega }}_n^r}\right|}^2+{\sigma }_k^2}}$$

(7)

Analogous to the signal received by legitimate users, the expression for the signal intercepted by the $j$-th eavesdroppers is as follows:

$$\begin{array}{ll}{y}_{e,j}& ={\displaystyle \sum _{i=1}^K{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_i^c{s}_i^c}+{\displaystyle \sum _{n=1}^N{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_n^r{s}_n^r}+z_e\\ & =\underset{\mathrm{eavesdropped}\mathrm{signal}}{\underbrace{{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_k^c{s}_i^c}}+\underset{\mathrm{interference}\mathrm{signals}\mathrm{from}\mathrm{other}\mathrm{users}}{\underbrace{{\displaystyle \sum _{i=1,i\ne k}^K{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_i^c{s}_i^c}}}\\ & +\underset{\mathrm{sensing}\mathrm{interference}\mathrm{signal}}{\underbrace{{\displaystyle \sum _{n=1}^N{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_n^r{s}_n^r}}}+\underset{\mathrm{AWGN}}{\underbrace{z_e}}\end{array}$$

(8)

where ${\mathit{g}}_j\left(\mathit{q},{\mathit{e}}_j\right)=\sqrt{\beta d^{-2}\left(\mathit{q},{\mathit{e}}_j\right)}\mathit{a}\left(\mathit{q},{\mathit{e}}_j\right)\in {ℂ}^{N\times 1}$ represents the eavesdropping channel, $d\left(\mathit{q},{\mathit{e}}_j\right)$ represents the distance between the UAV and the eavesdropper $j$, and $\mathit{a}\left(\mathit{q},{\mathit{e}}_j\right)$ represents the beamforming steering vector of the UAV toward the eavesdropper $j$, with an expression similar to (4). $z_e\sim \mathcal{C}\mathcal{N}\left(0,{\sigma }_e^2\right)$ represents the AWGN received by the eavesdropper. Therefore, SINR for the eavesdropper $j$ listening to the user $k$ can be expressed as:

$${\mathrm{SIN}\mathrm{R}}_{j,k}^e={\displaystyle \frac{{\left|{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_k^c\right|}^2}{{\left|{\displaystyle \sum _{i=1,i\ne k}^K{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_i^c}\right|}^2+{\left|{\displaystyle \sum _{n=1}^N{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_n^r}\right|}^2+{\sigma }_e^2}}$$

(9)

To safeguard the communication security of the ISAC system, it is essential to minimize the maximum eavesdropping SINR while maintaining effective communication between the UAV and legitimate users.

2.2. Sensing Model

The entire sensing process of the UAV is divided into two stages. In the first stage, the UAV emits an omnidirectional scanning signal that can detect multiple users, including both legitimate and illegitimate ones. The UAV distinguishes between legitimate users and eavesdroppers through three scenarios:

(1)

Several legitimate users will actively transmit signals to the UAV, providing their identity and location information. The UAV authenticates this information, and if it passes, the users are confirmed as legitimate. Otherwise, they are considered eavesdroppers.

(2)

The UAV then sends an authentication request to the remaining users. Some users will respond to the authentication request, and the UAV will authenticate this information; if it passes, they are identified as legitimate users. Otherwise, they are considered eavesdroppers.

(3)

If a user neither actively transmits identity information nor responds to the UAV authentication request, the UAV considers them an eavesdropper.

In the second stage, to ensure secure communication and further sense the eavesdroppers, the UAV employs beamforming technology. We formulate an optimization problem aimed at minimizing the maximum eavesdropping SINR while satisfying the communication threshold for legitimate users, the sensing threshold for the target, and the power budget. This approach is designed to maximize the system’s security performance.

However, with the method described above, we cannot distinguish between actual eavesdroppers and non-responding users, such as regular people who are neither system users nor eavesdroppers, as they do not interact with the system. This limitation can result in false alarms.

In the second stage, the composite signals transmitted by the UAV are reflected by the sensing target. Analyzing these reflected signals enables the estimation of relevant target information. The power of the reflected signals can be determined by calculating the beam pattern gain from the UAV directed toward the target, combined with the path loss. Given the requirement for the UAV to sense the presence of the eavesdropper, we employ the beam pattern gain in the eavesdropper’s direction as the metric for sensing performance [22]. In this paper, the communication and sensing signals transmitted by the UAV are jointly utilized for the sensing function. Therefore, for any sensing angle $\theta \left(\mathit{q},{\mathit{e}}_j\right)\in \left[-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}}\right]$, the beam pattern gain $\varsigma \left(\theta \left(\mathit{q},{\mathit{e}}_j\right)\right)$ can be expressed as:

$$\begin{array}{l}\varsigma \left(\theta \left(\mathit{q},{\mathit{e}}_j\right)\right)=\mathbb{E}\left({\left|{\mathit{a}}^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right)\mathit{x}\right|}^2\right)\\ ={\mathit{a}}^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right)\left({\displaystyle \sum _{k=1}^K{\mathit{\omega }}_k^c{\mathit{\omega }}_k^c{\hspace{0.25em}}^{\mathrm{H}}}+{\displaystyle \sum _{n=1}^N{\mathit{\omega }}_n^r{\mathit{\omega }}_n^r{\hspace{0.25em}}^{\mathrm{H}}}\right)\mathit{a}\left(\mathit{q},{\mathit{e}}_j\right)\end{array}$$

(10)

The power of the signals reflected from the sensing target to the UAV, incorporating path loss, is described by $(10)$ and the distance between the two. Detailed computational constraints are provided in constraint $\mathrm{C}2$.

2.3. Problem Formulation

From Equations (7), (9) and (10), it can be observed that the UAV communication and sensing beamforming (${\mathit{\omega }}_k^c,\forall k\mathrm{and}{\mathit{\omega }}_n^r,\forall n$) and its position ($\mathit{q}$) collectively influence the system’s communication and sensing functionalities. Furthermore, the presence of an eavesdropper means these variables also significantly impact the system’s security.

Therefore, we propose a joint optimization of the UAV communication and sensing beamforming (${\mathit{\omega }}_k^c,\forall k\mathrm{and}{\mathit{\omega }}_n^r,\forall n$) and the UAV position ($\mathit{q}$), aiming to minimize the maximum eavesdropper SINR while adhering to the QoS requirements of legitimate users, meeting the sensing metric constraints for the eavesdropper, and complying with the UAV transmit power limitations. Consequently, the optimization problem is formulated as follows:

$$\begin{array}{l}\mathrm{P}1:\underset{{\mathit{\omega }}_k^c,{\mathit{\omega }}_n^r,\mathit{q}}{\min }\underset{j,k}{\max }({\mathrm{SIN}\mathrm{R}}_{j,k}^e={\displaystyle \frac{{\left|{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_k^c\right|}^2}{{\left|{\displaystyle \sum _{i=1,i\ne k}^K{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_i^c}\right|}^2+{\left|{\displaystyle \sum _{n=1}^N{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_n^r}\right|}^2+{\sigma }_e^2}})\\ \mathrm{s}.\mathrm{t}. \mathrm{C}1: {\mathrm{SIN}\mathrm{R}}_k={\displaystyle \frac{{\left|{\mathit{h}}_k^{\mathrm{H}}\left(\mathit{q},{\mathit{u}}_k\right){\mathit{\omega }}_k^c\right|}^2}{{\left|{\displaystyle \sum _{i=1,i\ne k}^K{\mathit{h}}_k^{\mathrm{H}}\left(\mathit{q},{\mathit{u}}_k\right){\mathit{\omega }}_i^c}\right|}^2+{\left|{\displaystyle \sum _{n=1}^N{\mathit{h}}_k^{\mathrm{H}}\left(\mathit{q},{\mathit{u}}_k\right){\mathit{\omega }}_n^r}\right|}^2+{\sigma }_k^2}}\ge {\Gamma }_k^{\mathrm{com}},\forall k\\ \mathrm{C}2:\varsigma \left(\theta \left(\mathit{q},{\mathit{e}}_j\right)\right)= {\mathit{a}}^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right)\left({\displaystyle \sum _{k=1}^K{\mathit{\omega }}_k^c{\mathit{\omega }}_k^c{\hspace{0.25em}}^{\mathrm{H}}}+{\displaystyle \sum _{n=1}^N{\mathit{\omega }}_n^r{\mathit{\omega }}_n^r{\hspace{0.25em}}^{\mathrm{H}}}\right)\mathit{a}\left(\mathit{q},{\mathit{e}}_j\right)\ge d^2\left(\mathit{q},{\mathit{e}}_j\right){\Gamma }_e^{\mathrm{sen}},\forall j\\ \mathrm{C}3:{\sum }_{k=1}^K{‖{\mathit{\omega }}_k^c‖}^2+{\sum }_{n=1}^N{‖{\mathit{\omega }}_n^r‖}^2\le P_{\max }\end{array}$$

(11)

where ${\Gamma }_k^{\mathrm{com}}$ represents the minimum SINR threshold required for the legitimate user $k$ to satisfy the communication quality of service, and ${\Gamma }_e^{\mathrm{sen}}$ represents the sensing threshold. The constraint $\mathrm{C}1$ stipulates the QoS requirement of UAV and legitimate user $k$ communication, constraint $\mathrm{C}2$ indicates that the beam pattern gain of the UAV toward the eavesdropper $j$ must be greater than the product of the sensing threshold ${\Gamma }_e^{\mathrm{sen}}$ and the square of the distance between the UAV and the eavesdropper $j$, and constraint $\mathrm{C}3$ ensures that the power of the signal transmitted by the UAV must not exceed the maximum transmit power $P_{\max }$.

The objective function and constraint $\mathrm{C}1$ in problem $\mathrm{P}1$ are quadratic fractional form, and the steering vector $\mathit{a}\left(\mathit{q},{\mathit{e}}_j\right)$ in constraint $\mathrm{C}2$ is highly coupled with the variable $\mathit{q}$. Additionally, ${\mathit{\omega }}_k^c,\forall k\mathrm{and}{\mathit{\omega }}_n^r,\forall n$ are also highly coupled, rendering problem $\mathrm{P}1$ a highly non-convex problem which is challenging to solve directly. To solve $\mathrm{P}1$, we decompose it into two subproblems: beamforming optimization and UAV positioning optimization. These subproblems are solved iteratively to obtain a suboptimal solution.

3. Joint Optimization Algorithm

In this section, we use an alternating iterative method to solve problem $\mathrm{P}1$. First, we fix the UAV position and introduce slack variables to solve for the optimal transmitting beamforming ${\mathit{\omega }}_k^c,\forall k$ and ${\mathit{\omega }}_n^r,\forall n$ using the Dinkelbach method. Then, with the transmitting beamforming fixed, we use the SCA algorithm to find the optimal position $\mathit{q}$. This process is iteratively repeated until convergence is achieved.

3.1. Transmit Beamforming Optimization

Given the UAV position $\mathit{q}$, the optimization subproblem for the beamforming ${\mathit{\omega }}_k^c,\forall k$ and ${\mathit{\omega }}_n^r,\forall n$ can be formulated as:

$$\begin{array}{l}\mathrm{P}2:\underset{{\mathit{\omega }}_k^c,{\mathit{\omega }}_n^r}{\min }\underset{j,k}{\max }\left({\mathrm{SIN}\mathrm{R}}_{j,k}^e\right)\\ \mathrm{s}.\mathrm{t}.\mathrm{C}1,\mathrm{C}2,\mathrm{C}3\end{array}$$

(12)

Notice that problem $\mathrm{P}2$ is an MM (minorize maximization) problem. To simplify the solution, we introduce an auxiliary variable $A$, transforming the MM problem into a minimization problem. The reformulated problem $\mathrm{P}2$ is expressed as:

$$\begin{array}{l}\mathrm{P}3:\underset{{\mathit{\omega }}_k^c,{\mathit{\omega }}_n^r,A}{\min }A\\ \mathrm{s}.\mathrm{t}{.\mathrm{C}4:\mathrm{SIN}\mathrm{R}}_{j,k}^e={\displaystyle \frac{{\left|{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_k^c\right|}^2}{{\left|{\displaystyle \sum _{i=1,i\ne k}^K{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_i^c}\right|}^2+{\left|{\displaystyle \sum _{n=1}^N{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_n^r}\right|}^2+{\sigma }_e^2}}\le A,\forall j,k\\ \mathrm{C}1,\mathrm{C}2,\mathrm{C}3\end{array}$$

(13)

This is a minimization problem, but due to the single fractional constraint $\mathrm{C}4$ and non-convex constraints $\mathrm{C}1$ and $\mathrm{C}2$, problem $\mathrm{P}3$ remains difficult to solve. Noticing that problem $\mathrm{P}3$ has a similar fractional programming form to those in [10,17], we can apply the Dinkelbach transformation to convert it into a solvable form, i.e., transforming the fractional constraint into a polynomial expression. By introducing an auxiliary variable $c_{j,k}$, constraint $\mathrm{C}4$ is rewritten as:

$${\left|{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_k^c\right|}^2-c_{j,k}\left({\left|{\displaystyle \sum _{i=1,i\ne k}^K{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_i^c}\right|}^2+{\left|{\displaystyle \sum _{n=1}^N{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_n^r}\right|}^2+{\sigma }_e^2\right)\le A,\forall j,k$$

(14)

The auxiliary variable $c_{j,k}$ essentially represents the eavesdropping SINR of the eavesdropper $j$ for the user $k$ [17], and it can be updated using the transmit beamforming ${\mathit{\omega }}_k^c,\forall k$ and ${\mathit{\omega }}_n^r,\forall n$. When the transmit beamforming is given, the optimal $c_{j,k}^{*}$ can be expressed as:

$$c_{j,k}^{\ast }={\displaystyle \frac{{\left|{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_k^c\right|}^2}{{\left|{\displaystyle \sum _{i=1,i\ne k}^K{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_i^c}\right|}^2+{\left|{\displaystyle \sum _{n=1}^N{\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_n^r}\right|}^2+{\sigma }_e^2}},\forall j,k$$

(15)

It can be seen that constraints $\mathrm{C}1$, $\mathrm{C}2$, and $\mathrm{C}3$ contain quadratic variables ${\mathit{\omega }}_k^c,\forall k$ and ${\mathit{\omega }}_n^r,\forall n$, making the problem difficult to handle. Therefore, we adopt the SDR method. We define ${\mathit{W}}_k^c\triangleq {\mathit{\omega }}_k^c{\mathit{\omega }}_k^c{\hspace{0.25em}}^{\mathrm{H}},\forall k$ and ${\mathit{W}}_n^r\triangleq {\mathit{\omega }}_n^r{\mathit{\omega }}_n^r{\hspace{0.25em}}^{\mathrm{H}},\forall n$, with the rank-one constraint expressed as:

$$\begin{array}{l}\mathrm{Rank}\left({\mathit{W}}_k^c\right)=1,\forall k\\ \mathrm{Rank}\left({\mathit{W}}_n^r\right)=1,\forall n\end{array}$$

(16)

Problem $\mathrm{P}3$ can be transformed into:

$$\begin{array}{l}\mathrm{P}4:\underset{{\mathit{W}}_k^c,{\mathit{W}}_n^r,A}{\min }A\\ \mathrm{s}.\mathrm{t}.\mathrm{C}5:\mathrm{tr}\left({\mathit{g}}_j\left(\mathit{q},{\mathit{e}}_j\right){\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{W}}_k^c\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}-c_{j,k}\left({\displaystyle \sum _{i=1,i\ne k}^K\mathrm{tr}\left({\mathit{g}}_j\left(\mathit{q},{\mathit{e}}_j\right){\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{W}}_i^c\right)}+{\displaystyle \sum _{n=1}^N\mathrm{tr}\left({\mathit{g}}_j\left(\mathit{q},{\mathit{e}}_j\right){\mathit{g}}_j^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{W}}_n^r\right)}+{\sigma }_e^2\right)\le A,\forall j,k\\ \mathrm{C}6:{\displaystyle \frac{\mathrm{tr}\left({\mathit{h}}_k\left(\mathit{q},{\mathit{u}}_k\right){\mathit{h}}_k^{\mathrm{H}}\left(\mathit{q},{\mathit{u}}_k\right){\mathit{W}}_k^c\right)}{{\displaystyle \sum _{i=1,i\ne k}^K\mathrm{tr}\left({\mathit{h}}_k\left(\mathit{q},{\mathit{u}}_k\right){\mathit{h}}_k^{\mathrm{H}}\left(\mathit{q},{\mathit{u}}_k\right){\mathit{W}}_i^c\right)}+{\displaystyle \sum _{n=1}^N\mathrm{tr}\left({\mathit{h}}_k\left(\mathit{q},{\mathit{u}}_k\right){\mathit{h}}_k^{\mathrm{H}}\left(\mathit{q},{\mathit{u}}_k\right){\mathit{W}}_n^r\right)}+{\sigma }_k^2}}\ge {\Gamma }_k^{\mathrm{com}},\forall k\\ \mathrm{C}7:{\mathit{a}}^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right)\left({\displaystyle \sum _{k=1}^K{\mathit{W}}_k^c}+{\displaystyle \sum _{n=1}^N{\mathit{W}}_n^r}\right)\mathit{a}\left(\mathit{q},{\mathit{e}}_j\right)\ge d^2\left(\mathit{q},{\mathit{e}}_j\right){\Gamma }_e^{\mathrm{sen}},\forall j\\ \mathrm{C}8:{\displaystyle \sum _{k=1}^K\mathrm{tr}\left({\mathit{W}}_k^c\right)}+{\displaystyle \sum _{n=1}^N\mathrm{tr}\left({\mathit{W}}_n^r\right)}\le P_{\max }\\ \mathrm{C}9:\mathrm{rank}\left({\mathit{W}}_k^c\right)\le 1,\forall k\\ \mathrm{C}10:\mathrm{rank}\left({\mathit{W}}_n^r\right)\le 1,\forall n\end{array}$$

(17)

Ignoring the rank-one constraint, problem $\mathrm{P}4$ becomes a SDR problem, which we solve using the CVX toolbox. Since the rank-one constraint is ignored, we perform eigenvalue decomposition to obtain ${\mathit{\omega }}_k^c,\forall k$ and ${\mathit{\omega }}_n^r,\forall n$, and check if their ranks are one. If not, Gaussian randomization is applied to convert the high-rank solution of problem $\mathrm{P}4$ into a feasible rank-one solution. The details are shown in Algorithm 1.

Algorithm 1: UAV transmit beamforming optimization

Input: ${\mathit{u}}_k$, ${\mathit{e}}_j$, $\mathit{q}$, $P_{\max }$, ${\Gamma }_k^{\mathrm{com}}$, ${\Gamma }_e^{\mathrm{sen}}$ Output: ${\mathit{\omega }}_k^c,\forall k$ and ${\mathit{\omega }}_n^r,\forall n$ 1. Given the initial value $c_{j,k},\forall j,k$, set the minimum increment ${\epsilon }_{\min }$. 2. Repeat: 3.   Solve the optimization problem $\mathrm{P}4$ to obtain ${\mathit{W}}_k^c,\forall k$, ${\mathit{W}}_n^r,\forall n$. 4.   Perform EVD decomposition on ${\mathit{W}}_k^c,\forall k$ and ${\mathit{W}}_n^r,\forall n$ to obtain ${\mathit{\omega }}_k^c,\forall k$ and ${\mathit{\omega }}_n^r,\forall n$. 5.    Update $c_{j,k},\forall j,k$ according to Equation (15). 6. Until: The objective function increment is less than ${\epsilon }_{\min }$.

3.2. UAV Position Optimization

After determining the transmitting beamforming ${\mathit{\omega }}_k^c,\forall k$ and ${\mathit{\omega }}_n^r,\forall n$, the optimization subproblem for the UAV position $\mathit{q}$ can be formulated as:

$$\begin{array}{l}\mathrm{P}5:\underset{\mathit{q}}{\min }\underset{j,k}{\max }\left({\mathrm{SIN}\mathrm{R}}_{j,k}^e\right)\\ s.t.\mathrm{C}1,\mathrm{C}2\end{array}$$

(18)

where, from Equations $\left(4\right)$ and $\left(5\right)$, it is observed that the beamforming steering vector $\mathit{a}\left(\mathit{q},{\mathit{u}}_k\right)$ is non-linearly related and highly coupled with the optimization variable $\mathit{q}$, making problem $\mathrm{P}5$ challenging to solve. Therefore, we adopt the SCA algorithm based on the trust region method [11].

Similarly, to address the MM problem, an auxiliary variable $B$ is introduced, reformulating problem $\mathrm{P}5$ as:

$$\begin{array}{l}\mathrm{P}6:\underset{\mathit{q},B}{\min }B\\ \mathrm{s}.\mathrm{t}{.\mathrm{C}11:\mathrm{SIN}\mathrm{R}}_{j,k}^e={\displaystyle \frac{{\left|{\mathit{a}}^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right){\mathit{\omega }}_k^c\right|}^2}{{\displaystyle \sum _{\begin{array}{l}i=1,\\ i\ne k\end{array}}^K{\left|{\mathit{a}}^{\mathrm{H}}(\mathit{q},{\mathit{e}}_j){\mathit{\omega }}_i^c\right|}^2+{\displaystyle \sum _{n=1}^N{\left|{\mathit{a}}^{\mathrm{H}}(\mathit{q},{\mathit{e}}_j){\mathit{\omega }}_n^r\right|}^2+\frac{{\sigma }_e^2}{\beta }{d}^2(\mathit{q},{\mathit{e}}_j)}}}}\le B,\forall j,k\\ {\mathrm{C}12:\mathrm{SIN}\mathrm{R}}_k={\displaystyle \frac{{\left|{\mathit{a}}^{\mathrm{H}}\left(\mathit{q},{\mathit{u}}_k\right){\mathit{\omega }}_k^c\right|}^2}{{\displaystyle \sum _{\begin{array}{l}i=1,\\ i\ne k\end{array}}^K{\left|{\mathit{a}}^{\mathrm{H}}(\mathit{q},{\mathit{u}}_k){\mathit{\omega }}_i^c\right|}^2+{\displaystyle \sum _{n=1}^N{\left|{\mathit{a}}^{\mathrm{H}}(\mathit{q},{\mathit{u}}_k){\mathit{\omega }}_n^r\right|}^2+\frac{{\sigma }_k^2}{\beta }{d}^2(\mathit{q},{\mathit{u}}_k)}}}}\ge {\Gamma }_k^{\mathrm{com}},\forall k\\ \mathrm{C}13:{\mathit{a}}^{\mathrm{H}}\left(\mathit{q},{\mathit{e}}_j\right)\left({\displaystyle \sum _{k=1}^K{\mathit{\omega }}_k^c{\mathit{\omega }}_k^c{\hspace{0.25em}}^{\mathrm{H}}}+{\displaystyle \sum _{n=1}^N{\mathit{\omega }}_n^r{\mathit{\omega }}_n^r{\hspace{0.25em}}^{\mathrm{H}}}\right)\mathit{a}\left(\mathit{q},{\mathit{e}}_j\right)\ge d^2\left(\mathit{q},{\mathit{e}}_j\right){\Gamma }_e^{\mathrm{sen}},\forall j\end{array}$$

(19)

For convenience, let ${\mathit{W}}_i^c={\mathit{\omega }}_i^c{\mathit{\omega }}_i^c{\hspace{0.25em}}^{\mathrm{H}}$, ${\mathit{W}}_i^r={\mathit{\omega }}_i^r{\mathit{\omega }}_i^r{\hspace{0.25em}}^{\mathrm{H}}$, $\mathit{G}={\displaystyle \sum _{k=1}^K{\mathit{\omega }}_k^c{\mathit{\omega }}_k^c{\hspace{0.25em}}^{\mathrm{H}}}+{\displaystyle \sum _{n=1}^N{\mathit{\omega }}_n^r{\mathit{\omega }}_n^r{\hspace{0.25em}}^{\mathrm{H}}}$. Thus, we represent the $a$ row and $b$ column of ${\mathit{W}}_i^c$, ${\mathit{W}}_i^r$ and $G$ as ${\left[{\mathit{W}}_i^c\right]}_{a,b}$, ${\left[{\mathit{W}}_i^r\right]}_{a,b}$ and ${\left[\mathit{G}\right]}_{a,b}$, respectively, with their magnitudes denoted as $\left|{\left[{\mathit{W}}_i^c\right]}_{a,b}\right|$, $\left|{\left[{\mathit{W}}_i^r\right]}_{a,b}\right|$ and $\left|{\left[\mathit{G}\right]}_{a,b}\right|$, and their phases as ${\theta }_{a,b}^{{\mathit{W}}_i^c}$, ${\theta }_{a,b}^{{\mathit{W}}_i^r}$ and ${\theta }_{a,b}^{\mathit{G}}$. Constraints $\mathrm{C}11$ and $\mathrm{C}12$ are in fractional form and are transformed into polynomial forms. The following procedures are applied to constraints $\mathrm{C}11$, $\mathrm{C}12$, and $\mathrm{C}13$:

• The left and right sides of $\mathrm{C}11$ are taken as the base-2 logarithm, reformulated as:

  $$\begin{array}{l}{\log }_2\eta \left({\mathit{W}}_k^c,d\left(\mathit{q},{\mathit{e}}_j\right)\right)\\ -{\log }_2\left.\left({\displaystyle \sum _{i=1,i\ne k}^K\eta \left.\left({\mathit{W}}_i^c,d(\mathit{q},{\mathit{e}}_j)\right.\right)}\right.+{\displaystyle \sum _{n=1}^N\mu \left(\left.{\mathit{W}}_n^r,d(\mathit{q},{\mathit{e}}_j)\right)\right.}+{\displaystyle \frac{{\sigma }_e{\hspace{0.25em}}^2}{\beta }}{d}^2(\mathit{q},{\mathit{e}}_j)\right)\le {\log }_2(B)\end{array}$$

  (20)

  where

  $$\begin{array}{ll}\eta \left({\mathit{W}}_k^c,d\left(\mathit{q},{\mathit{e}}_j\right)\right)& ={\left|{\mathit{a}}^{\mathrm{H}}(\mathit{q},{\mathit{e}}_j){\mathit{\omega }}_k^c\right|}^2\\ & ={\displaystyle \sum _{\alpha =1}^N{[{\mathit{W}}_k^c]}_{\alpha ,\alpha }+2{\displaystyle \sum _{a=1}^N{\displaystyle \sum _{b=a+1}^N\left|{[{\mathit{W}}_k^c]}_{a,b}\right|}}}\cos \left.\left({\theta }_{a,b}^{{\mathit{W}}_k^c}+\pi (b-a){\displaystyle \frac{H}{d(\mathit{q},{\mathit{e}}_j)}}\right.\right)\end{array}$$

  (21)

  $$\begin{array}{ll}\mu \left.\left({\mathit{W}}_n^r,d(\mathit{q},{\mathit{e}}_j)\right.\right)& ={\left|{\mathit{a}}^{\mathrm{H}}(\mathit{q},{\mathit{e}}_j){\mathit{\omega }}_n^r\right|}^2\\ & ={\displaystyle \sum _{\alpha =1}^N{[{\mathit{W}}_n^r]}_{\alpha ,\alpha }+2{\displaystyle \sum _{a=1}^N{\displaystyle \sum _{b=a+1}^N\left|{[{\mathit{W}}_n^r]}_{a,b}\right|}}}\cos \left.\left({\theta }_{a,b}^{{\mathit{W}}_n^r}+\pi (b-a){\displaystyle \frac{H}{d(\mathit{q},{\mathit{e}}_j)}}\right.\right)\end{array}$$

  (22)

The proofs for $\left(21\right)$ and $\left(22\right)$ can be referred to in reference [11]. At this point, the left-hand side of the inequality constraint $(20)$ exhibits non-convexity with respect to the optimization variable $\mathit{q}$. We implement the SCA algorithm. In the $l$-th iteration, the left-hand side of the inequality is linearized through a first-order Taylor expansion at the local point ${\mathit{q}}^{\left(l\right)}$, and the inequality constraint is subsequently approximated as follows:

$$C_{j,k}^{\left(l\right)}+{\mathit{D}}_{j,k}^{\left(l\right)}{\hspace{0.25em}}^{\mathrm{H}}\left(\mathit{q}-{\mathit{q}}^{\left(l\right)}\right)\le {\log }_2\left(B\right)$$

(23)

where $C_{j,k}^{\left(l\right)}$ is obtained from (20) during the $l$-th iteration, while ${\mathit{D}}_{j,k}^{\left(l\right)}$ is derived from the $l$-th iteration of the derivative of (20) with respect to the variable ${\mathit{q}}^{(l)}$. $\mathit{\varphi }\left({\mathit{W}}_k^c,d\left({\mathit{q}}^{\left(l\right)},{\mathit{e}}_j\right)\right)$ and $\mathit{\delta }\left({\mathit{W}}_n^r,d\left({\mathit{q}}^{(l)},{\mathit{e}}_j\right)\right)$ respectively denote the derivatives of $\eta \left.\left({\mathit{W}}_k^c,d({\mathit{q}}^{(l)},{\mathit{e}}_j)\right.\right)$ and $\mu \left(\left.{\mathit{W}}_n^r,d({\mathit{q}}^{(l)},{\mathit{e}}_j)\right)\right.$ with respect to the variable ${\mathit{q}}^{\left(l\right)}$.

$$\begin{array}{ll}{C}_{j,k}^{(l)}& ={\log }_2\left(\left.\eta \left.\left({\mathit{W}}_k^c,d({\mathit{q}}^{(l)},{\mathit{e}}_j)\right.\right)\right)\right.\\ & -{\log }_2\left.\left({\displaystyle \sum _{\begin{array}{l}i=1,\\ i\ne k\end{array}}^K\eta \left(\left.{\mathit{W}}_i^c,d({\mathit{q}}^{(l)},{\mathit{e}}_j)\right)\right.+{\displaystyle \sum _{n=1}^N\mu \left(\left.{\mathit{W}}_n^r,d({\mathit{q}}^{(l)},{\mathit{e}}_j)\right)\right.}}+{\displaystyle \frac{{\sigma }_e^2}{\beta }}{d}^2({\mathit{q}}^{(l)},{\mathit{e}}_j)\right.\right)\end{array}$$

(24)

$$\begin{array}{ll}{\mathit{D}}_{j,k}^{(l)}& ={\displaystyle \frac{{\log }_2(e)}{f_{j,k}}}\left(\mathit{\varphi }\left({\mathit{W}}_k^c,d\left({\mathit{q}}^{\left(l\right)},{\mathit{e}}_j\right)\right)\right)\\ & -{\displaystyle \frac{{\log }_2(e)}{g_{j,k}}}\left({\displaystyle \sum _{i=1.i\ne k}^K\mathit{\varphi }\left({\mathit{W}}_i^c,d\left({\mathit{q}}^{\left(l\right)},{\mathit{e}}_j\right)\right)}+{\displaystyle \sum _{n=1}^N\mathit{\delta }\left({\mathit{W}}_n^r,d\left({\mathit{q}}^{(l)},{\mathit{e}}_j\right)\right)}+2{\displaystyle \frac{{\sigma }_e^2}{\beta }}\left({\mathit{q}}^{(l)}-{\mathit{e}}_j\right)\right)\end{array}$$

(25)

$$\begin{array}{ll}\mathit{\varphi }\left({\mathit{W}}_k^c,d\left({\mathit{q}}^{\left(l\right)},{\mathit{e}}_j\right)\right)& ={\displaystyle \sum _{a=1}^N{\displaystyle \sum _{b=a+1}^{N}2\pi \left|{\left[{\mathit{W}}_k^c\right]}_{a,b}\right|}}\sin \left({\theta }_{a,b}^{{\mathit{W}}_k^c}+\pi \left(b-a\right){\displaystyle \frac{H}{d\left({\mathit{q}}^{\left(l\right)},{\mathit{e}}_j\right)}}\right){\displaystyle \frac{H\left(b-a\right)}{d^3\left({\mathit{q}}^{(l)},{\mathit{e}}_j\right)}}\\ & \times \left({\mathit{q}}^{(l)}-{\mathit{e}}_j\right)\end{array}$$

(26)

$$\begin{array}{ll}\mathit{\delta }\left({\mathit{W}}_n^r,d\left({\mathit{q}}^{(l)},{\mathit{e}}_j\right)\right)& ={\displaystyle \sum _{a=1}^N{\displaystyle \sum _{b=a+1}^{N}2\pi \left|{\left[{\mathit{W}}_n^r\right]}_{a,b}\right|\sin \left({\theta }_{a,b}^{{\mathit{W}}_n^r}+\pi \left(b-a\right)\frac{H}{d\left({\mathit{q}}^{(l)},{\mathit{e}}_j\right)}\right)\frac{H(b-a)}{d^3\left({\mathit{q}}^{(l)},{\mathit{e}}_j\right)}}}\\ & \times \left({\mathit{q}}^{(l)}-{\mathit{e}}_j\right)\end{array}$$

(27)

Within the derivative calculation of the logarithmic function, $f_{j,k}$ and $g_{j,k}$ are introduced as the denominators, respectively represented as:

$$f_{j,k}=\eta \left.\left({\mathit{W}}_k^c,d({\mathit{q}}^{(l)},{\mathit{e}}_j)\right.\right)$$

(28)

$$g_{j,k}={\displaystyle \sum _{\begin{array}{l}i=1,\\ i\ne k\end{array}}^K\eta \left(\left.{\mathit{W}}_i^c,d({\mathit{q}}^{(l)},{\mathit{e}}_j)\right)\right.+{\displaystyle \sum _{n=1}^N\mu \left(\left.{\mathit{W}}_n^r,d({\mathit{q}}^{(l)},{\mathit{e}}_j)\right)\right.}}+{\displaystyle \frac{{\sigma }_e^2}{\beta }}{d}^2({\mathit{q}}^{(l)},{\mathit{e}}_j)$$

(29)

At this point, the inequality constraint $\left(23\right)$ becomes convex regarding the optimization variable $\mathit{q}$ and auxiliary variable $B$;

2.

Convert the inequality constraint $\mathrm{C}12$ into a polynomial form:

$${\left|{\mathit{a}}^{\mathrm{H}}(\mathit{q},{\mathit{u}}_k){\mathit{\omega }}_k^c\right|}^2-{\Gamma }_k^{\mathrm{com}}\left({\displaystyle \sum _{\begin{array}{l}i=1,\\ i\ne k\end{array}}^K{\left|{\mathit{a}}^{\mathrm{H}}(\mathit{q},{\mathit{u}}_k){\mathit{\omega }}_i^c\right|}^2+{\displaystyle \sum _{n=1}^N{\left|{\mathit{a}}^{\mathrm{H}}(\mathit{q},{\mathit{u}}_k){\mathit{\omega }}_n^r\right|}^2+\frac{{\sigma }_k^2}{\beta }{d}^2(\mathit{q},{\mathit{u}}_k)}}\right)\ge 0$$

(30)

For simplicity of expression, $\left(30\right)$ can be rewritten as:

$$\begin{array}{l}\eta \left.\left({\mathit{W}}_k^c,d(\mathit{q},{\mathit{u}}_k)\right.\right)\\ -{\Gamma }_k^{\mathrm{com}}\left({\displaystyle \sum _{i=1,i\ne k}^K\eta \left.\left({\mathit{W}}_i^c,d(\mathit{q},{\mathit{u}}_k)\right.\right)}+{\displaystyle \sum _{n=1}^N\mu \left(\left.{\mathit{W}}_n^r,d(\mathit{q},{\mathit{u}}_k)\right)\right.}+{\displaystyle \frac{{\sigma }_k^2}{\beta }}{d}^2(\mathit{q},{\mathit{u}}_k)\right)\ge 0\end{array}$$

(31)

Similarly, given the non-convex nature of the inequality with respect to the optimization variable $\mathit{q}$, the left-hand side is linearized via a first-order Taylor expansion at the local point ${\mathit{q}}^{\left(l\right)}$. The constraint $\left(31\right)$ can be approximated as follows:

$$I_k^{(l)}+{\mathit{J}}_k^{(l)}{\hspace{0.25em}}^{\mathrm{H}}\left(\mathit{q}-{\mathit{q}}^{\left(l\right)}\right)\ge 0,\forall k$$

(32)

where

$$\begin{array}{ll}{I}_k^{\left(l\right)}& =\eta \left.\left({\mathit{W}}_k^c,d({\mathit{q}}^{\left(l\right)},{\mathit{u}}_k)\right.\right)\\ & -{\Gamma }_k^{\mathrm{com}}\left({\displaystyle \sum _{i=1,i\ne k}^K\eta \left.\left({\mathit{W}}_i^c,d({\mathit{q}}^{\left(l\right)},{\mathit{u}}_k)\right.\right)}+{\displaystyle \sum _{n=1}^N\mu \left(\left.{\mathit{W}}_n^r,d({\mathit{q}}^{\left(l\right)},{\mathit{u}}_k)\right)\right.}+{\displaystyle \frac{{\sigma }_k^2}{\beta }}{d}^2({\mathit{q}}^{\left(l\right)},{\mathit{u}}_k)\right)\end{array}$$

(33)

$$\begin{array}{ll}{\mathit{J}}_k^{(l)}& =\mathit{\varphi }\left({\mathit{W}}_k^c,d\left({\mathit{q}}^{\left(l\right)},{\mathit{u}}_k\right)\right)\\ & -{\Gamma }_k^{\mathrm{com}}\left({\displaystyle \sum _{i=1.i\ne k}^K\mathit{\varphi }\left({\mathit{W}}_i^c,d\left({\mathit{q}}^{\left(l\right)},{\mathit{u}}_k\right)\right)}+{\displaystyle \sum _{n=1}^N\mathit{\delta }\left({\mathit{W}}_n^r,d\left({\mathit{q}}^{(l)},{\mathit{u}}_k\right)\right)}+2{\displaystyle \frac{{\sigma }_k^2}{\beta }}\left({\mathit{q}}^{(l)}-{\mathit{u}}_k\right)\right)\end{array}$$

(34)

3.

The inequality constraint $\mathrm{C}13$ can be reformulated as:

$${\displaystyle \sum _{\alpha =1}^N{[\mathit{G}]}_{\alpha ,\alpha }+2{\displaystyle \sum _{a=1}^N{\displaystyle \sum _{b=a+1}^N\left|{[\mathit{G}]}_{a,b}\right|}}}\cos \left.\left({\theta }_{a,b}^{\mathit{G}}+\pi (b-a){\displaystyle \frac{H}{d(\mathit{q},{\mathit{e}}_j)}}\right.\right)\ge {\Gamma }_e^{\mathrm{sen}}{d}^2(\mathit{q},{\mathit{e}}_j)$$

(35)

Similarly, by conducting a first-order Taylor expansion at the local point ${\mathit{q}}^{\left(l\right)}$, the inequality constraint is approximated as follows:

$$U_j^{{\hspace{0.25em}}^{(l)}}+{\mathit{V}}_j^{{\hspace{0.25em}}^{(l)}}{\hspace{0.25em}}^{\mathrm{H}}\left(\mathit{q}-{\mathit{q}}^{(l)}\right)\ge {\Gamma }_e^{\mathrm{sen}}\left(H^2+{‖\mathit{q}-{\mathit{e}}_j‖}^2\right)$$

(36)

where

$$U_j^{{\hspace{0.25em}}^{\left(l\right)}}=\eta \left(\mathit{G},d\left({\mathit{q}}^{\left(l\right)},{\mathit{e}}_j\right)\right)$$

(37)

$${\mathit{V}}_j^{{\hspace{0.25em}}^{(l)}}=\mathit{\varphi }\left(\mathit{G},d\left({\mathit{q}}^{\left(l\right)},{\mathit{e}}_j\right)\right)$$

(38)

Based on the transformation of the above three constraints, the three inequality constraints $\mathrm{C}11$, $\mathrm{C}12$, and $\mathrm{C}13$ of problem $\mathrm{P}6$ are approximated as $\left(23\right)$, $\left(32\right)$, and $\left(36\right)$, respectively. To ensure the accuracy of the SCA algorithm, we consider that the change in position between two consecutive iterations is less than $R^{\left(l\right)}$, i.e., $‖{\mathit{q}}^{(l)}-{\mathit{q}}^{(l-1)}‖\le R^{(l)}$.

Building on the aforementioned approach, problem $\mathrm{P}6$ in the $l$-th iteration can be transformed into an approximate convex problem $\mathrm{P}7.l$:

$$\begin{array}{l}\mathrm{P}7.l:\underset{\mathit{q},B}{\min }B\\ \mathrm{s}.\mathrm{t}.\mathrm{C}14:C_{j,k}^{(l)}+{\mathit{D}}_{j,k}^{(l)}{\hspace{0.25em}}^{\mathrm{H}}\left(\mathit{q}-{\mathit{q}}^{(l)}\right)\le {\log }_2(B),\forall j,k\\ C15:I_k^{(l)}+{\mathit{J}}_k^{(l)}{\hspace{0.25em}}^{\mathrm{H}}\left(\mathit{q}-{\mathit{q}}^{(l)}\right)\ge 0,\forall k\\ C16:U_j^{{\hspace{0.25em}}^{(l)}}+{\mathit{V}}_j^{{\hspace{0.25em}}^{(l)}}{\hspace{0.25em}}^{\mathrm{H}}\left(\mathit{q}-{\mathit{q}}^{(l)}\right)\ge {\Gamma }_e^{\mathrm{sen}}\left(H^2+{‖\mathit{q}-{\mathit{e}}_j‖}^2\right),\forall j\\ C17: ‖\mathit{q}-{\mathit{q}}^{(l-1)}‖\le R^{(l)}\end{array}$$

(39)

Theoretically, setting the trust region radius $R^{\left(l\right)}$ sufficiently small can always ensure the convergence of the iterative process [11]. In practice terms, if the solution of problem $\mathrm{P}7.l$ after a certain iteration does not reduce the objective value of problem $\mathrm{P}5$ compared to the previous iteration, the trust region radius is halved, i.e., $R^{\left(l\right)}=R^{\left(l\right)}/2$, and then problem $\mathrm{P}7.l$ is solved again. If the trust region radius $R^{\left(l\right)}$ decreases below a predetermined threshold $R_{\min }$, the iterative process stops. The detailed procedure is outlined in Algorithm 2.

Algorithm 2: UAV position optimization

Input: ${\mathit{\omega }}_k^c,\forall k$, ${\mathit{\omega }}_n^r,\forall n$, ${\sigma }_k^2$, ${\sigma }_e^2$, $P_{\max }$, ${\mathit{u}}_k$, ${\mathit{e}}_j$, ${\Gamma }_k^{\mathrm{com}}$, ${\Gamma }_e^{\mathrm{sen}}$ Output: $\mathit{q}$ 1. Initialize iteration count $l=1$ and ${\mathit{q}}^{\left(0\right)}$, setting the minimum trust region radius $R_{\min }$. 2. Repeat: 3.   Solve the optimization problem $\mathrm{P}7.l$ to obtain ${\mathit{q}}^{\left(l\right)\ast }$. 4.   If the objective function value decreases, then 5.      ${\mathit{q}}^{\left(l\right)}={\mathit{q}}^{\left(l\right)\ast }$, $l=l+1$. 6.   else 7.    $R^{\left(l\right)}=R^{\left(l\right)}/2$. 8.   end if 9. Until $R^{\left(l\right)}<R_{\min }$

3.3. Joint Beamforming and UAV Positioning Optimization

As detailed in Algorithm 3, the proposed alternating iterative algorithm for the UAV-assisted ISAC system repeatedly optimizes the joint beamforming and UAV positioning until the objective function converges or the prescribed maximum number of iterations is reached.

Algorithm 3: Joint beamforming and UAV positioning optimization

Input: ${\sigma }_k^2$, ${\sigma }_e^2$, $P_{\max }$, ${\mathit{u}}_k$, ${\mathit{e}}_j$, ${\Gamma }_k^{\mathrm{com}}$, ${\Gamma }_e^{\mathrm{sen}}$, $o_{\max }$ Output: ${\mathit{\omega }}_k^c,\forall k$, ${\mathit{\omega }}_n^r,\forall n$ and ${\mathit{q}}^{\ast }$ 1. Initialize iteration count $o=1$, ${\mathit{q}}^{\left(0\right)}$. 2. Repeat: 3.   Given the initial UAV position ${\mathit{q}}^{\left(o-1\right)}$, update ${\mathit{\omega }}_k^c{\hspace{0.25em}}^{\left(o\right)},\forall k$ and ${\mathit{\omega }}_n^r{\hspace{0.25em}}^{\left(o\right)},\forall n$ using Algorithm 1. 4.   Given the transmitting beamforming ${\mathit{\omega }}_k^c{\hspace{0.25em}}^{\left(o\right)},\forall k$ and ${\mathit{\omega }}_n^r{\hspace{0.25em}}^{\left(o\right)},\forall n$, update ${\mathit{q}}^{\left(o\right)}$ using Algorithm 2. 5.   $o=o+1$. 6. Until: the objective function value of $\mathrm{P}1$ converges or $o>o_{\max }$.

Subsequently, we examine the convergence and computational complexity of the iterative optimization algorithm for beamforming and UAV positioning.

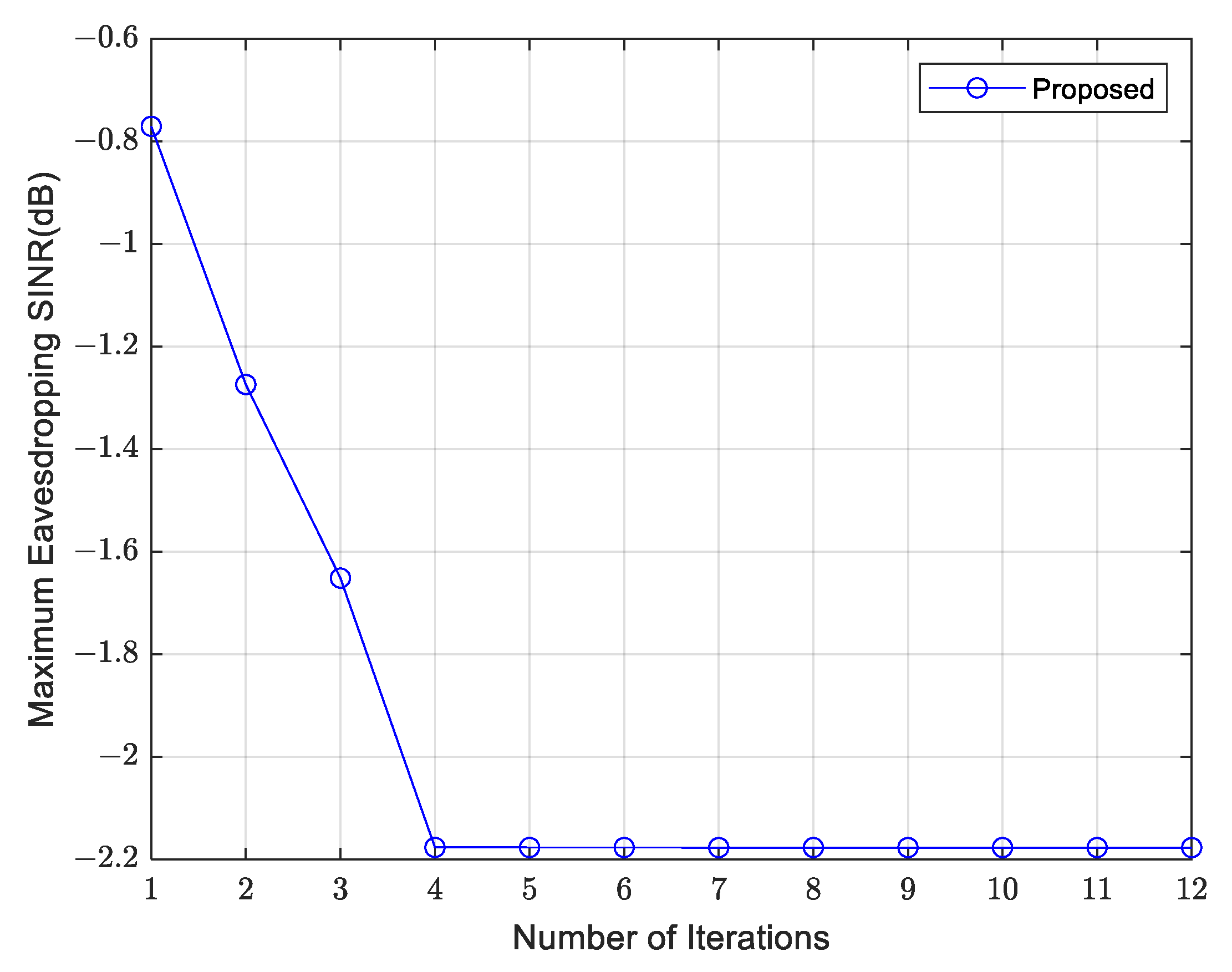
• Convergence: Define ${\mathit{\omega }}_k^c{\hspace{0.25em}}^{\left(l\right)},\forall k$, ${\mathit{\omega }}_n^r{\hspace{0.25em}}^{\left(l\right)},\forall n$, and ${\mathit{q}}^{\left(l\right)}$ as the $l$-th iteration solutions of Algorithm 3, and let the objective function of problem $\mathrm{P}1$ be denoted as $f\left({\mathit{\omega }}_k^c{\hspace{0.25em}}^{\left(l\right)},{\mathit{\omega }}_n^r{\hspace{0.25em}}^{\left(l\right)},{\mathit{q}}^{\left(l\right)}\right)$. In Step 3 of Algorithm 3, by fixing ${\mathit{q}}^{\left(l\right)}$, we obtain ${\mathit{\omega }}_k^c{\hspace{0.25em}}^{\left(l+1\right)},\forall k$ and ${\mathit{\omega }}_n^r{\hspace{0.25em}}^{\left(l+1\right)},\forall n$, thus:

  $$f\left({\mathit{\omega }}_k^c{\hspace{0.25em}}^{\left(l+1\right)},{\mathit{\omega }}_n^r{\hspace{0.25em}}^{\left(l+1\right)},{\mathit{q}}^{\left(l\right)}\right)\le f\left({\mathit{\omega }}_k^c{\hspace{0.25em}}^{\left(l\right)},{\mathit{\omega }}_n^r{\hspace{0.25em}}^{\left(l\right)},{\mathit{q}}^{\left(l\right)}\right)$$

  (40)

Similarly, in Step 4 of Algorithm 3, we obtain:

$$f\left({\mathit{\omega }}_k^c{\hspace{0.25em}}^{\left(l+1\right)},{\mathit{\omega }}_n^r{\hspace{0.25em}}^{\left(l+1\right)},{\mathit{q}}^{\left(l+1\right)}\right)\le f\left({\mathit{\omega }}_k^c{\hspace{0.25em}}^{\left(l+1\right)},{\mathit{\omega }}_n^r{\hspace{0.25em}}^{\left(l+1\right)},{\mathit{q}}^{\left(l\right)}\right)$$

(41)

In summary, we can deduce:

$$f\left({\mathit{\omega }}_k^c{\hspace{0.25em}}^{\left(l+1\right)},{\mathit{\omega }}_n^r{\hspace{0.25em}}^{\left(l+1\right)},{\mathit{q}}^{\left(l+1\right)}\right)\le f\left({\mathit{\omega }}_k^c{\hspace{0.25em}}^{\left(l\right)},{\mathit{\omega }}_n^r{\hspace{0.25em}}^{\left(l\right)},{\mathit{q}}^{\left(l\right)}\right)$$

(42)

This demonstrates that the value of the objective function remains non-increasing throughout the iterative process, thereby guaranteeing the convergence of the alternating iterative optimization algorithm.

2.

Complexity: In Algorithm 3, we solve all subproblems using CVX. The first subproblem is a SDR problem, and the second subproblem is a SCA problem. The algorithmic complexities of the two subproblems are $\mathcal{O}\left(L\log \left(1/ϵ\right){\left(2K+N\right)}^{3.5}\right)$ and $\mathcal{O}\left(L{\left(2K+2\right)}^3\right)$, respectively [12], where $L$ denotes the number of iterations required for the algorithm to achieve convergence, and $ϵ$ represents the convergence accuracy of the algorithm. Consequently, the worst-case computational complexity of Algorithm 3 is $\mathcal{O}\left(L\log \left(1/ϵ\right){\left(2K+N\right)}^{3.5}+L{\left(2K+2\right)}^3\right)$.

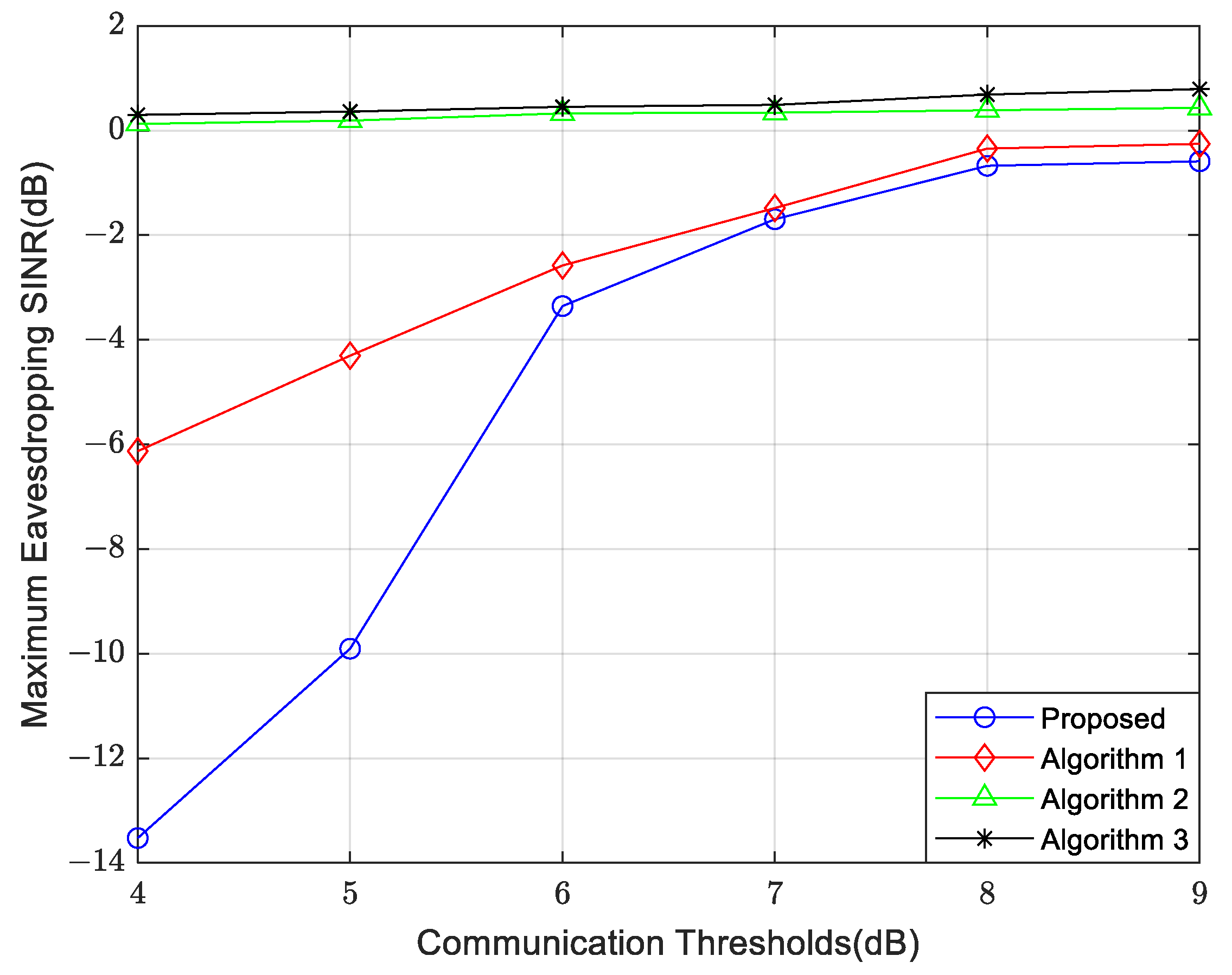
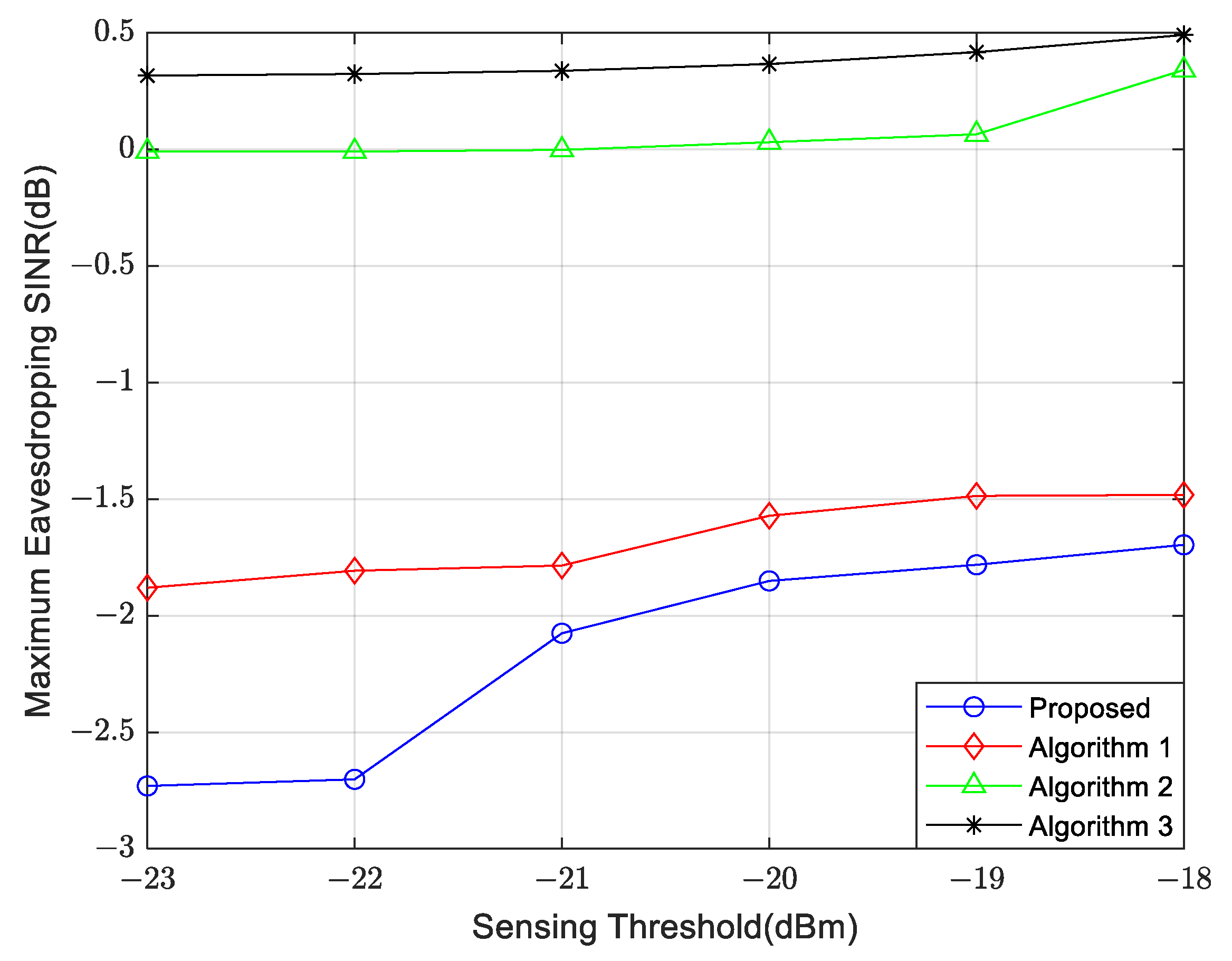
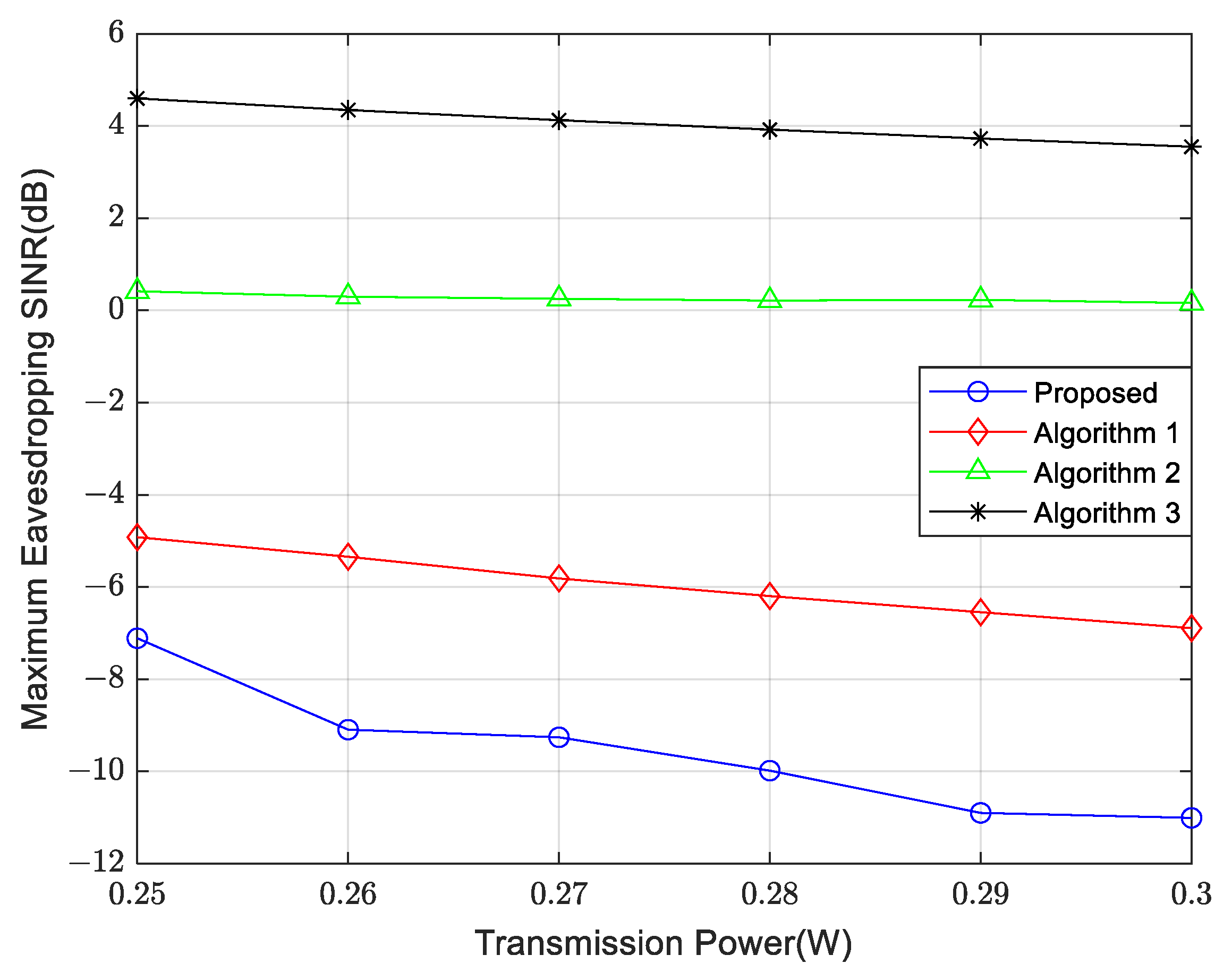
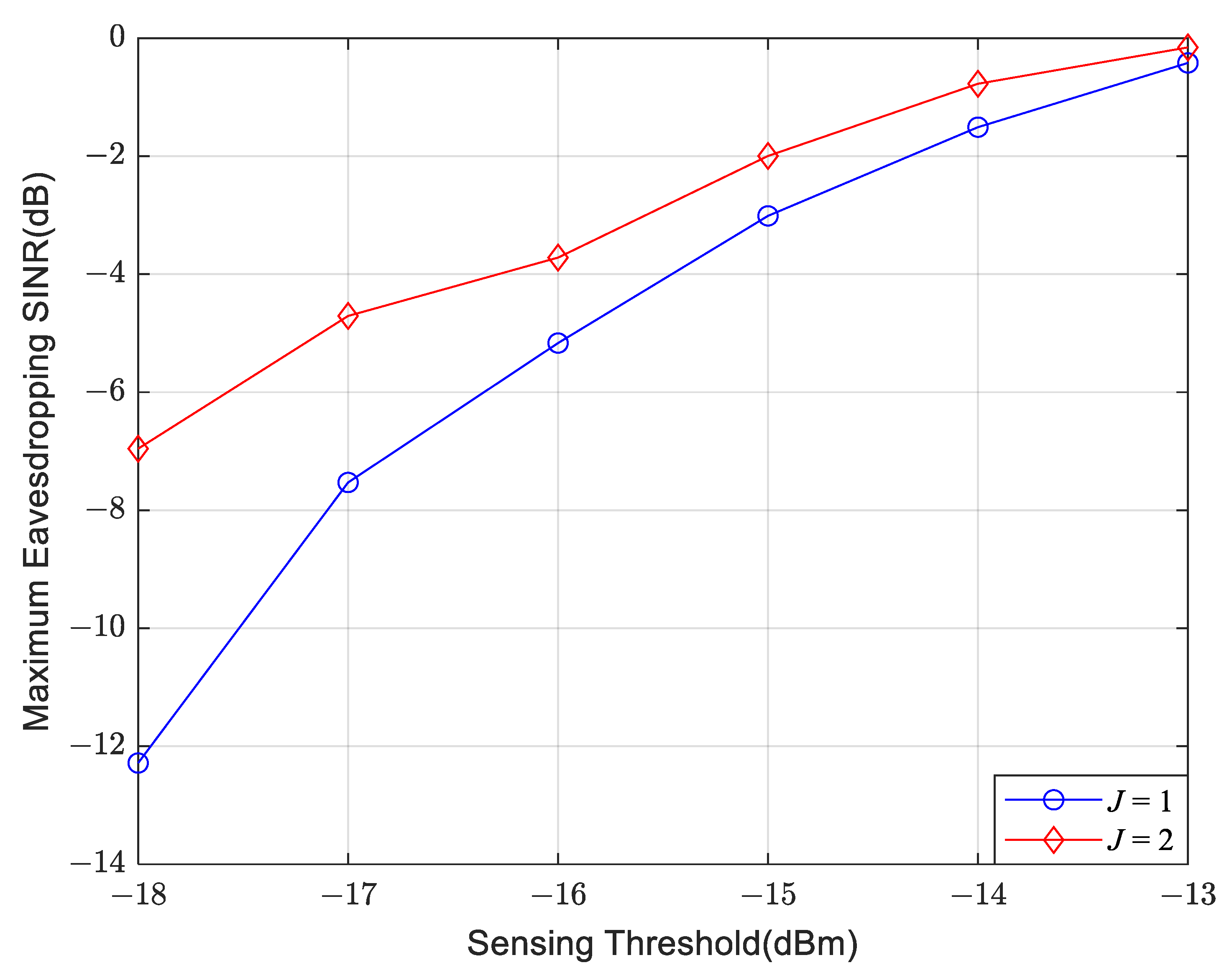
4. Simulation Results and Performance Analysis

To validate the efficacy of the proposed algorithm, MATLAB simulations were conducted. In the simulation, we consider a 1 km × 1 km area, with $K=2$ legitimate ground communication users. We first conduct simulations for the $J=1$ single eavesdropper scenario and then extend our analysis to the case of multiple eavesdroppers. We begin by examining the single eavesdropper scenario. The legitimate users are located at $\left(700,400,0\right)$ and $\left(800,600,0\right)$, and the single eavesdropper is located at $\left(150,500,0\right)$. Unless otherwise specified, the UAV flight altitude is $H=100\mathrm{m}$, the maximum transmit power is $P_{\max }=0.3\mathrm{W}$, and it has four antennas. The communication threshold for all legitimate users is ${\Gamma }_k^{\mathrm{com}}=7\mathrm{dB}$, and the beam pattern gain threshold is ${\Gamma }_e^{\mathrm{sen}}=-18\mathrm{dBm}$. The received noise power for each legitimate user and the eavesdropper is set to ${\sigma }_k^2={\sigma }_e^2=-110\mathrm{dbm}$, and the channel power gain at the reference distance $d_0=1\mathrm{m}$ is $\beta =-60\mathrm{dB}$.

To assess the performance of the proposed algorithm, it is benchmarked against the following three algorithms:

• Comparison Algorithm 1: Only optimize the UAV transmit beamforming without optimizing the UAV position.
• Comparison Algorithm 2: In this algorithm, the UAV transmitted signal contains only communication signals without dedicated sensing signals. Similar to Algorithm 1, it optimizes both the UAV transmit beamforming and the UAV position.
• Comparison Algorithm 3: The UAV transmitted signal contains only communication signals without dedicated sensing signals. It optimizes the UAV transmit beamforming but not the UAV position.

Figure 2 illustrates the convergence behavior of the proposed algorithm. It is evident that the maximum eavesdropping SINR decreases rapidly with the number of iterations, achieving convergence by the fourth iteration.

Figure 3 shows the variation of the maximum eavesdropping SINR with increasing communication thresholds for legitimate users, where the sensing threshold is $-18 \mathrm{dBm}$. The figure clearly demonstrates that the maximum eavesdropping SINR increases monotonically with the communication threshold. This is because the increase in the communication threshold leads to a higher demand for communication resources, which, under the condition of an unchanged sensing threshold, inevitably reduces the system’s security. Furthermore, in Figure 3, the data clearly indicate that the proposed algorithm surpasses the other three algorithms in terms of security performance. By comparing the proposed algorithm with Algorithm 1, it can be seen that optimizing the UAV position reduces the maximum eavesdropping SINR and improves the system’s security performance. By comparing the proposed algorithm with Algorithm 2, it can be seen that although the dedicated sensing signal transmitted by the UAV affects the communication SINR of legitimate users, it can more effectively improve the system’s security under the premise of ensuring sensing performance. This is because dedicated sensing signals more easily meet the system’s sensing requirements, thereby allocating resources to ensure system security. As the communication threshold increases, the performance differential between the proposed algorithm and the comparison algorithms narrows over time. This occurs as the elevated communication threshold restricts the UAV positional freedom, consequently reducing the performance disparity between the proposed algorithm and Algorithm 1. Algorithm 3 exhibits the highest eavesdropping SINR because it solely optimizes beamforming for communication signals without incorporating specialized sensing signals or optimizing UAV positions. Consequently, its eavesdropping SINR is higher compared to other algorithms.

Figure 4 shows the variation of the maximum eavesdropping SINR with increasing sensing thresholds, where the communication threshold is $7 \mathrm{dB}$. The figure clearly demonstrates that with an increasing sensing threshold, the maximum eavesdropping SINR rises monotonically while the performance disparity between the proposed algorithm and Algorithm 1 diminishes. Using dedicated sensing signals and optimizing the UAV position can significantly improve the system’s security performance.

Figure 5 illustrates the relationship between the maximum eavesdropping SINR and the UAV transmit power, where the communication threshold is $5 \mathrm{dB}$ and the sensing threshold is $-20 \mathrm{dBm}$. The figure clearly indicates that the maximum eavesdropping SINR decreases monotonically as the UAV transmit power increases. As the UAV transmit power increases, the system, while ensuring communication and sensing performance, allocates more resources to improve the system’s security performance. This causes the maximum eavesdropping SINR to decrease monotonically with increasing transmit power.

Figure 6 illustrates the correlation between the maximum eavesdropping SINR and the number of antennas, where the communication threshold is $8 \mathrm{dB}$, the sensing threshold is $-18 \mathrm{dBm}$, and the UAV transmit power is $0.3\mathrm{W}$. The figure clearly demonstrates that once the number of antennas surpasses 16, the rate at which the maximum eavesdropping SINR decreases begins to diminish. This is because a radar system with 16 antennas has sufficient spatial degrees of freedom to provide adequate signal processing capability; therefore, more antennas do not significantly lower the maximum eavesdropping SINR. Furthermore, the performance gap in terms of the maximum eavesdropping SINR between the proposed algorithm and the comparison algorithms increases with the number of antennas. This is because the additional antennas provide more spatial degrees of freedom, increasing the UAV positional freedom and making the UAV position more impactful on the system’s security performance.

Next, we simulate the multiple eavesdroppers scenario, with $J=2$ eavesdroppers and $K=2$ legitimate users. Building on the single eavesdropper scenario, the second eavesdropper is located at $\left(300,650,0\right)$. The UAV is equipped with $N=8$ antennas, and its maximum transmit power is set to $P_{\max }=0.25\mathrm{W}$. Figure 7 shows the variation of the maximum eavesdropping SINR with increasing communication thresholds for legitimate users, where the sensing threshold is $-13 \mathrm{dBm}$. It can be observed that the maximum eavesdropping SINR for multiple eavesdroppers is always greater than that for a single eavesdropper. This is because multiple eavesdroppers require the UAV to sense multiple targets, consuming more system resources. Additionally, multiple eavesdroppers generally exhibit better eavesdropping performance than a single eavesdropper, leading to a higher maximum eavesdropping SINR.

Figure 8 shows the relationship between the maximum eavesdropping SINR and the sensing threshold, with the communication threshold set to $9 \mathrm{dB}$. As the sensing threshold increases, the maximum eavesdropping SINR increases monotonically for both single and multiple eavesdroppers. However, in both cases, the maximum eavesdropping SINR is always significantly lower than the communication SINR of the legitimate user.

5. Conclusions

In this paper, we propose a method for using UAVs to perform beamforming for secure communication and target sensing in the presence of multiple eavesdroppers and multiple communication users. Through the joint optimization of the UAV transmit beamforming and position, this approach minimizes the maximum eavesdropping SINR while simultaneously ensuring the required minimum SINR for user communication and the necessary beam pattern gain for target sensing. In a multi-user scenario, a SDR-based algorithm is employed to address the non-convex optimization challenge associated with transmit beamforming. The method involves using slack variables to solve the MM problem and employing the Dinkelbach algorithm to address the fractional problem in the communication SINR. For the UAV positioning problem, a SCA algorithm that utilizes a first-order Taylor expansion is employed to convert the non-convex problem into a convex one. Simulation results confirm that the proposed algorithm facilitates a versatile trade-off among communication quality, target sensing quality, and system security performance. These results also demonstrate that UAV multi-antenna beamforming significantly enhances the PLS of ISAC systems. How to extend the results to other scenarios (e.g., 1. increasing the number of users; 2. incorporating mobile users and eavesdroppers; 3. multiple UAV collaboration; and 4. complex channel models) is interesting and worth pursuing in future work.