Optimizing Supply Chain Efficiency Using Innovative Goal Programming and Advanced Metaheuristic Techniques
Abstract
1. Introduction
2. Theoretical Background of the Uncertainty Theory
2.1. Uncertainty Theory: Measure, Variable, and Distribution
2.1.1. Uncertainty Measures
- Normality:
- Duality: for any
- Sub-additivity:
- Product Measure: for independent events A and B
2.1.2. Uncertain Variables
2.1.3. Uncertainty Distribution
2.2. Dependent Chance Programming Model
Mathematical Formulation of DCP
2.3. Goal Programming and Simulation using Uncertainty (99-Method)
2.3.1. Mathematical Formulation of GP
2.3.2. Simulation under Uncertainty: 99-Method
2.4. Applications and Benefits of Uncertain Models
2.4.1. Stochastic Programming (SP)
2.4.2. Fuzzy Logic (FL)
2.4.3. Robust Optimization (RO)
Metaheuristic Algorithms
3. Supply Chain Mathematical Model
3.1. Uncertainty Theory: Measure, Variable, and Distribution
3.2. Supply Chain Network Configuration
3.2.1. Uncertain Supply Chain Network Optimization Problem
3.2.2. Key Variables and Hypothesis
- Key Variables
- Demand rates: These determine the quantity of products required by end consumers and are assumed to be uncertain random variables.
- Supply availability: This indicates the availability of raw materials and finished goods, which are also subject to uncertainty.
- Production capacity: This defines the maximum output of manufacturing facilities and can vary based on several factors.
- Transportation logistics: This encompasses the movement of goods between different nodes in the supply chain and is influenced by various uncertainties.
- Hypotheses
- All supply chain nodes are operational at time zero, and demand rates, supply availability, and transportation logistics are uncertain variables.
- Each manufacturing facility can process a limited number of products at any given time.
- Each product can only be processed on one manufacturing unit at any time.
- Production processes must be completed without interruptions or preemptions.
- Transportation routes are activated as soon as the first batch of goods is ready and cease once the last batch is delivered.
- Transportation routes remain idle between successive deliveries.
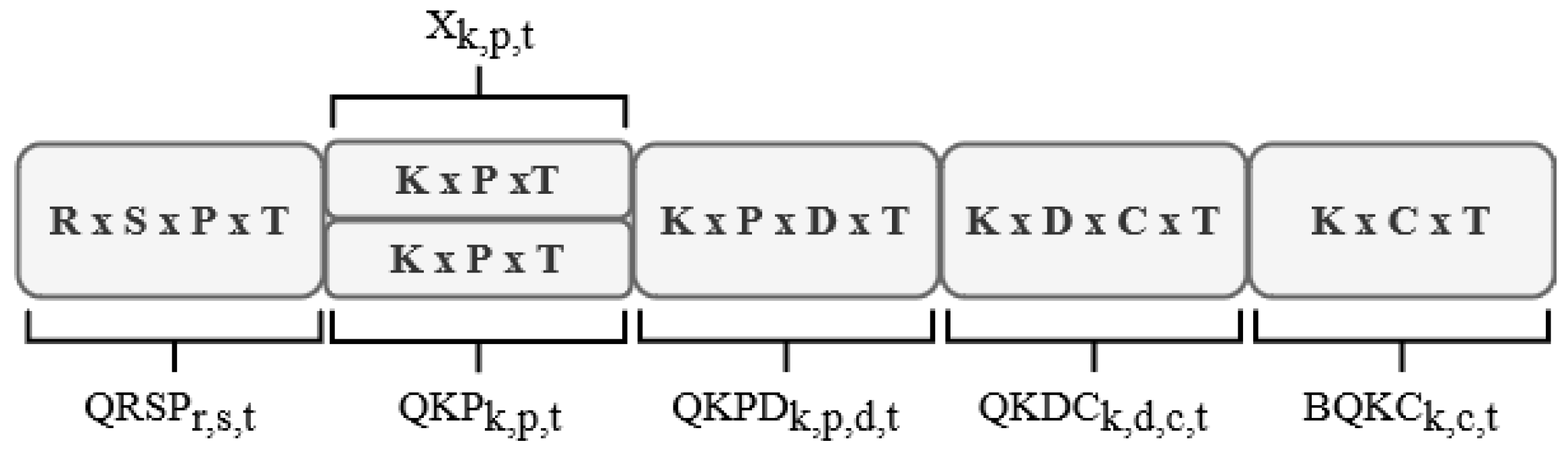
- Symbols and Formulation
- I: Number of centers.
- J: Number of products.
- : Uncertain supply availability of product j from supplier i, where are independent variables with probability distributions , and are independent uncertain variables with uncertainty distributions , respectively.
- : Uncertain vector.
- Variables and Indices
- s: Index for suppliers .
- r: Index for raw materials .
- p: Index for plants .
- k: Index for finished products .
- d: Index for distribution centers .
- c: Index for customers .
- t: Index for planning periods .
- Decision Variables
- : Binary variable, 1 if product k is produced by plant p in period t.
- : Inventory level of raw material r in plant p at the end of period t.
- : Inventory level of product k in plant p at the end of period t.
- : Inventory level of product k in distribution center d at the end of period t.
- : Quantity of raw material r dispatched from supplier s to plant p in period t.
- : Quantity of finished product k produced in plant p in period t.
- : Quantity of finished product k dispatched from plant p to distribution center d in period t.
- : Quantity of finished product k dispatched from distribution center d to customer c in period t.
- : Quantity of backorder for product k incurred by customer c in period t.
3.3. Mathematical Model Formulation
- Objective Functions
- Minimize total costs (MinOF1):
- Maximize on-time deliveries (MaxOF2):
- Constraints
- Capacity constraints:
- Demand constraints:
- Production time constraints:
- Backorder constraints:
- Balance constraints:
- Non-negativity constraints:
4. The Proposed Model on DCGP
4.1. Equivalent Model
4.2. Objective Function Uncertain Variables
- Objective function: The goal is to lexicographically minimize the values of and . This means that we first minimize , and then, among the solutions that achieve the minimal , we minimize .
- Constraints: The constraints ensure that the overall function values (denoted by and ) minus the aggregated uncertain variables (represented by various terms) do not exceed and , respectively.
- -
- The terms , , , etc., represent the inverse uncertainty distributions of the respective uncertain variables.
- -
- The variables QRSP, IRP, IKP, QKP, etc., are the corresponding uncertain parameters in the model.
- -
- The sums over r, s, p, t, k, d, c represent aggregation over different dimensions (such as regions, products, time periods, etc.).
5. Resolution Methods
5.1. Resolution of the Model Using HGS
5.1.1. Mathematical Foundation of Hunger Games Search (HGS)
- represents the range of for the search space;
- and represent random numbers uniformly distributed within the range ;
- represents a random number drawn from a normal distribution;
- t indicates the current iteration of the algorithm;
- and represent the hunger weights used in the algorithm;
- represents the location information of a random individual among all optimal individuals found so far;
- represents the location of each individual at iteration t. The value of l (related to the algorithm’s parameters) has been discussed in the parameter setting experiment.
| Algorithm 1 Pseudo-code 1 of Hunger Games Search (HGS) |
|
- represents the fitness value of each individual;
- represents the best fitness obtained in the current iteration process;
- sech represents a hyperbolic function .
- rand represents a random number in the range ;
- represents the maximum number of iterations.
- hungry represents the hunger of each individual;
- N represents the number of individuals;
- represents the sum of the hunger sensations of all individuals, i.e., ;
- and represent random numbers in the range .
- represents a parameter that preserves the fitness of each individual in the current iteration.
- represents a random number uniformly distributed within the range ;
- represents the fitness value of the i-th individual;
- represents the best fitness value obtained in the current iteration process;
- represents the worst fitness value obtained in the current iteration process;
- and represent the upper and lower bounds of the search space, respectively;
- represents the lower bound that limits the hunger sensation H.
5.1.2. Encoding Scheme
- Procurement quantity: Represents the quantity of goods procured from suppliers to plants in period tt.
- Production indicator: A binary variable indicating whether production occurs at the plant during period tt.
- Produced quantity: Represents the quantity of goods produced in period tt.
- Transported quantity (plant to DC): Indicates the quantity of goods transported from the plants to distribution centers (DCs) in period tt.
- Transported quantity (DC to customer): Indicates the quantity of goods transported from DCs to customers in period tt.
- Back-order quantity: Shows the quantity of back-orders incurred by customers in period tt.
5.2. Uncertain Simulation (99-Method)
- The first row represents the values of the uncertain distribution.
- The second row contains the associated inverse values.
- Pseudocode for Uncertain Simulation (99-Method)
| Algorithm 2 Uncertain Simulation (99-Method) |
|
- Algorithm 3 Uncertain Simulation for Chance Value
- Sampling: Generate a sample of uncertain values.
- Cost calculation: Compute the total cost (TC) for each sample.
- Threshold check: Verify if the total cost is below a predefined threshold.
- Repetition: Repeat the sampling and checking process N times.
- Proportion calculation: Determine the proportion of samples for which the total cost is below the threshold.
| Algorithm 3: Uncertain Simulation |
|
- Algorithm 4: Uncertain Simulation of
- Value iteration: Iterate over the values in the uncertainty table.
- Distribution lookup: For each value, find the corresponding distribution value in the inverse uncertainty table.
- Threshold comparison: Compare the total cost (TC) with the predefined threshold .
- Distribution value determination: Determine the appropriate distribution value based on the threshold comparison.
| Algorithm 4: Uncertain Simulation |
|
6. Results
6.1. Software and Tools
6.2. Performance Metrics of the UDCGP-HGSA Model
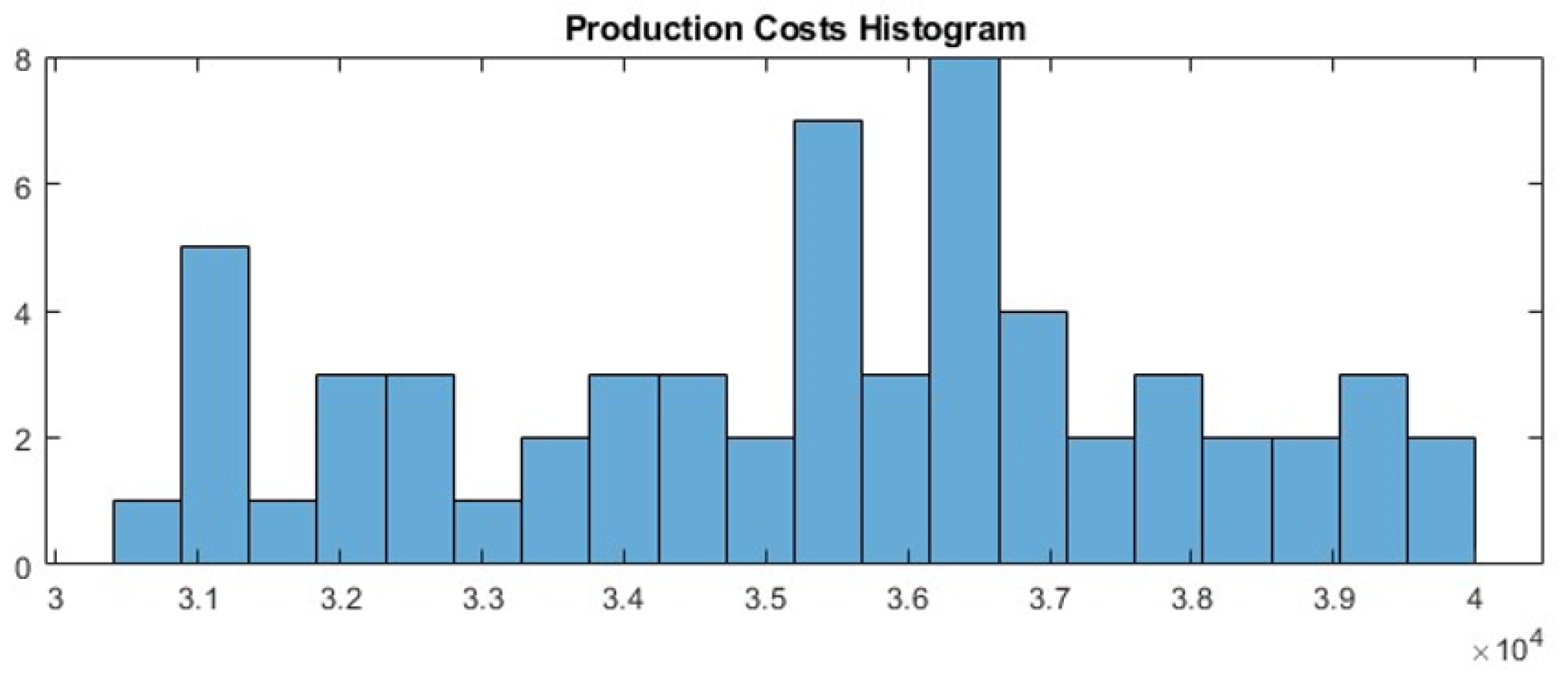
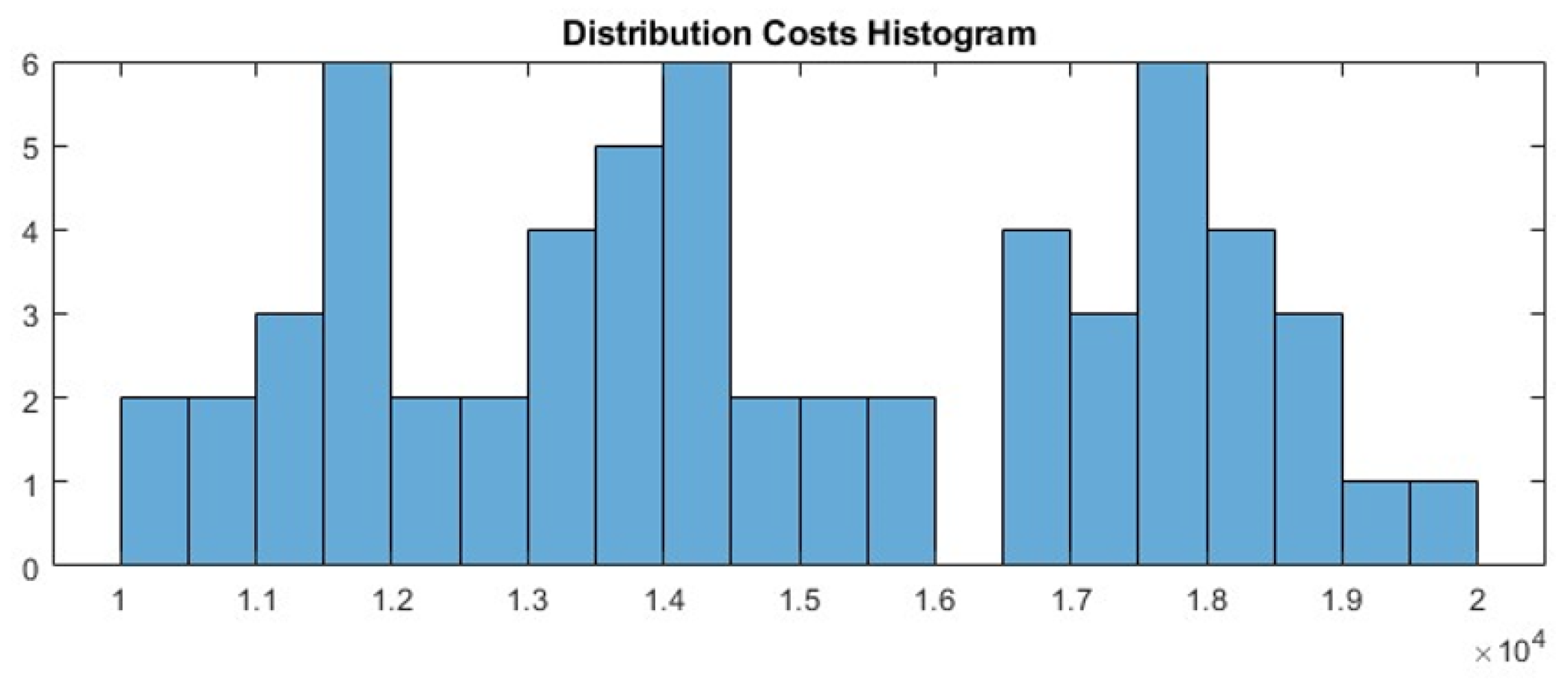
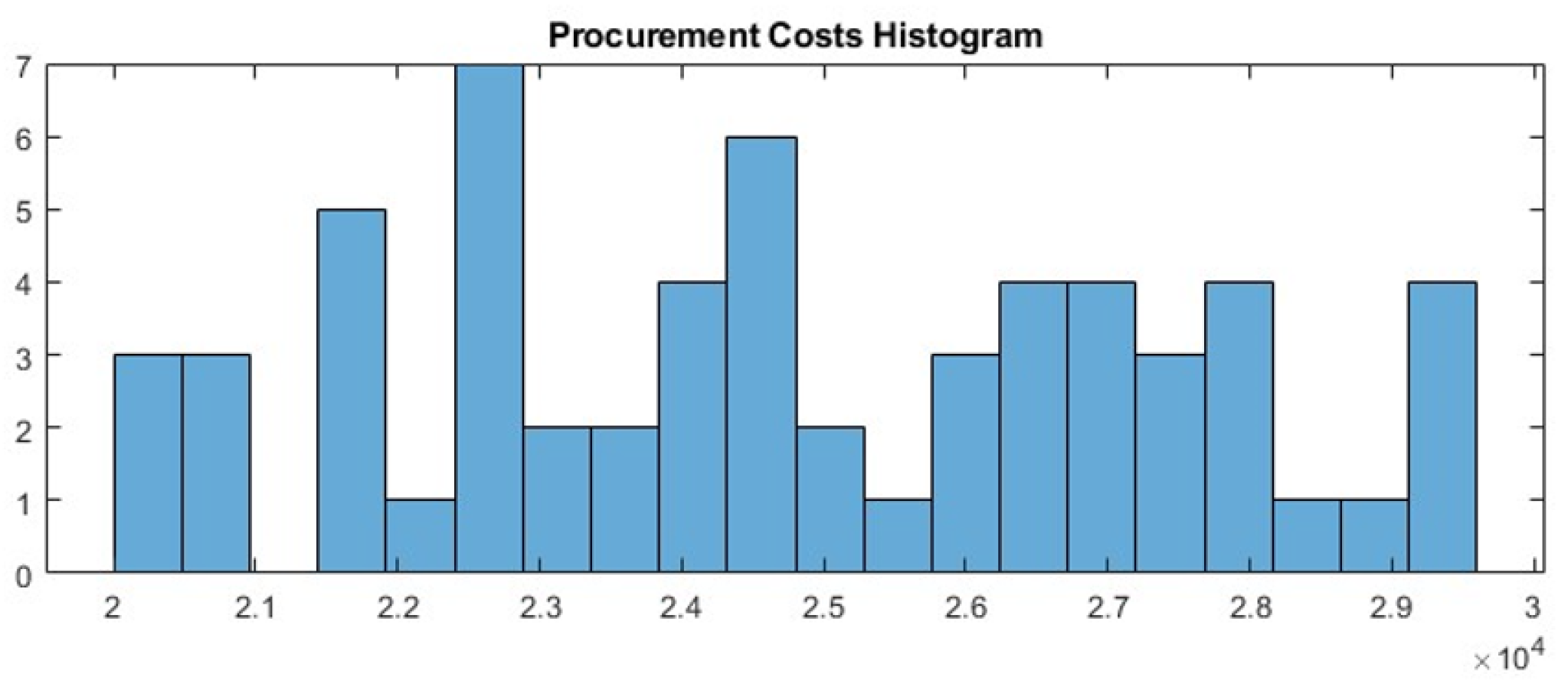
Cost Distributions
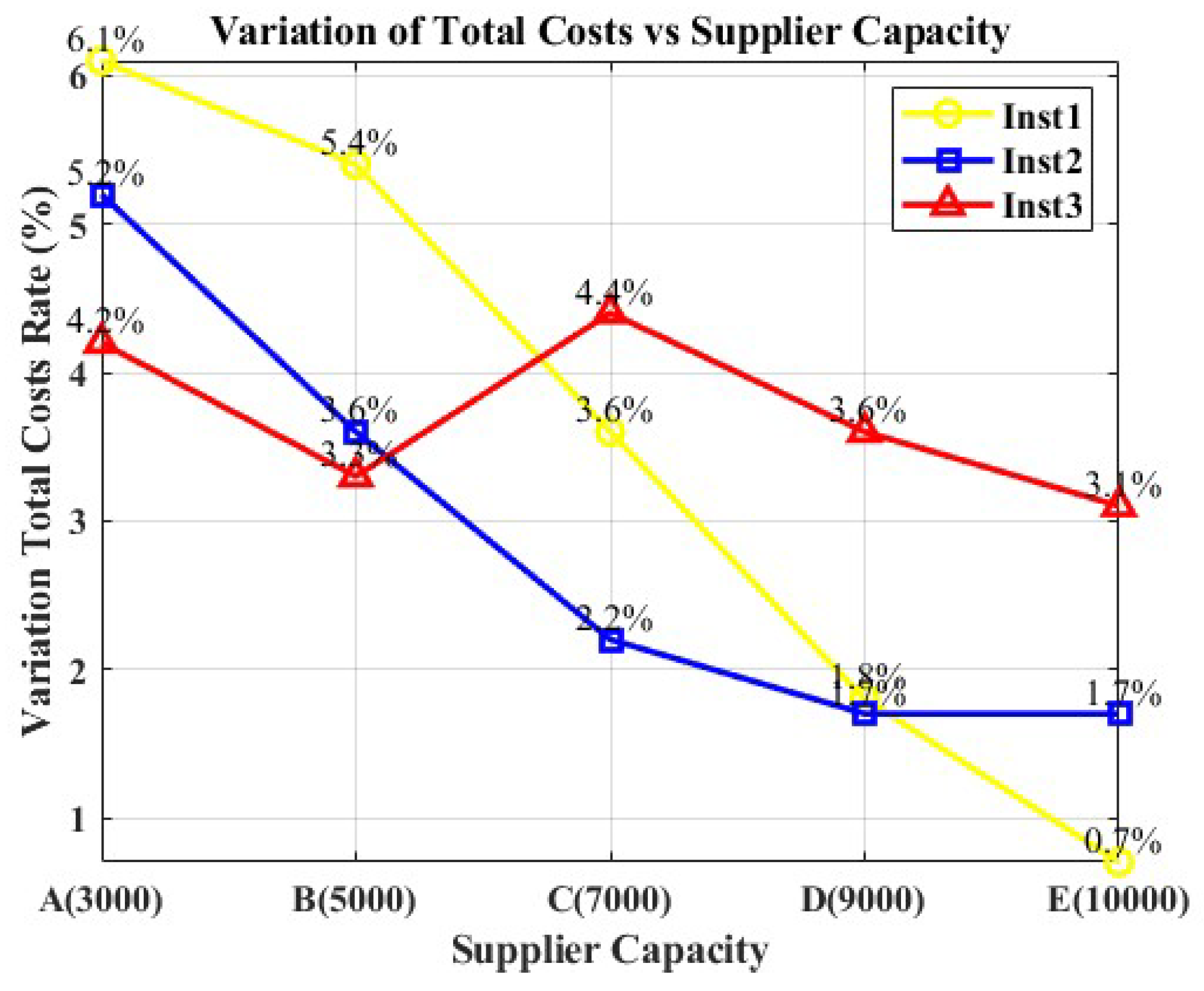
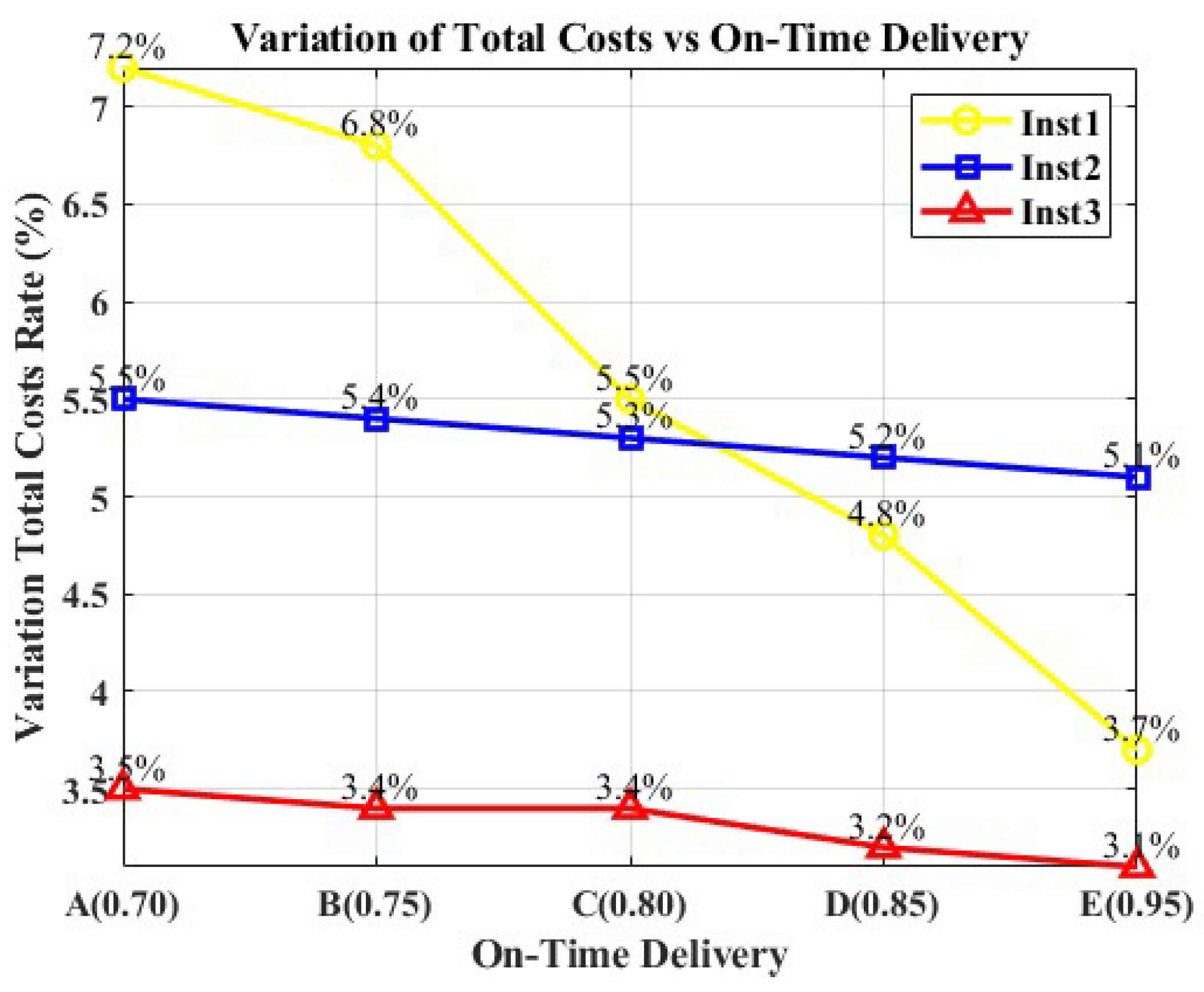
6.3. Sensitivity Analyses
6.4. Accuracy Analysis
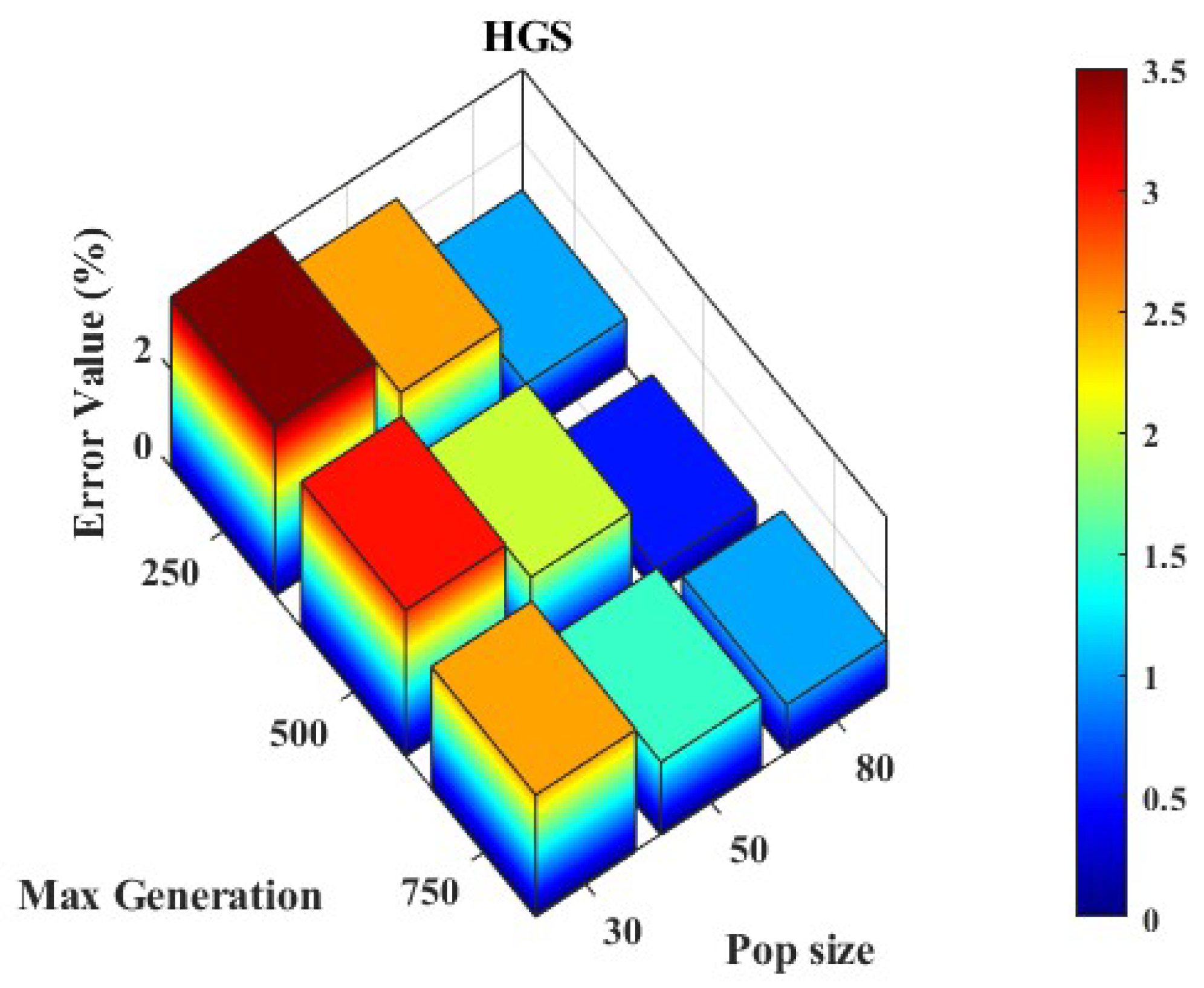
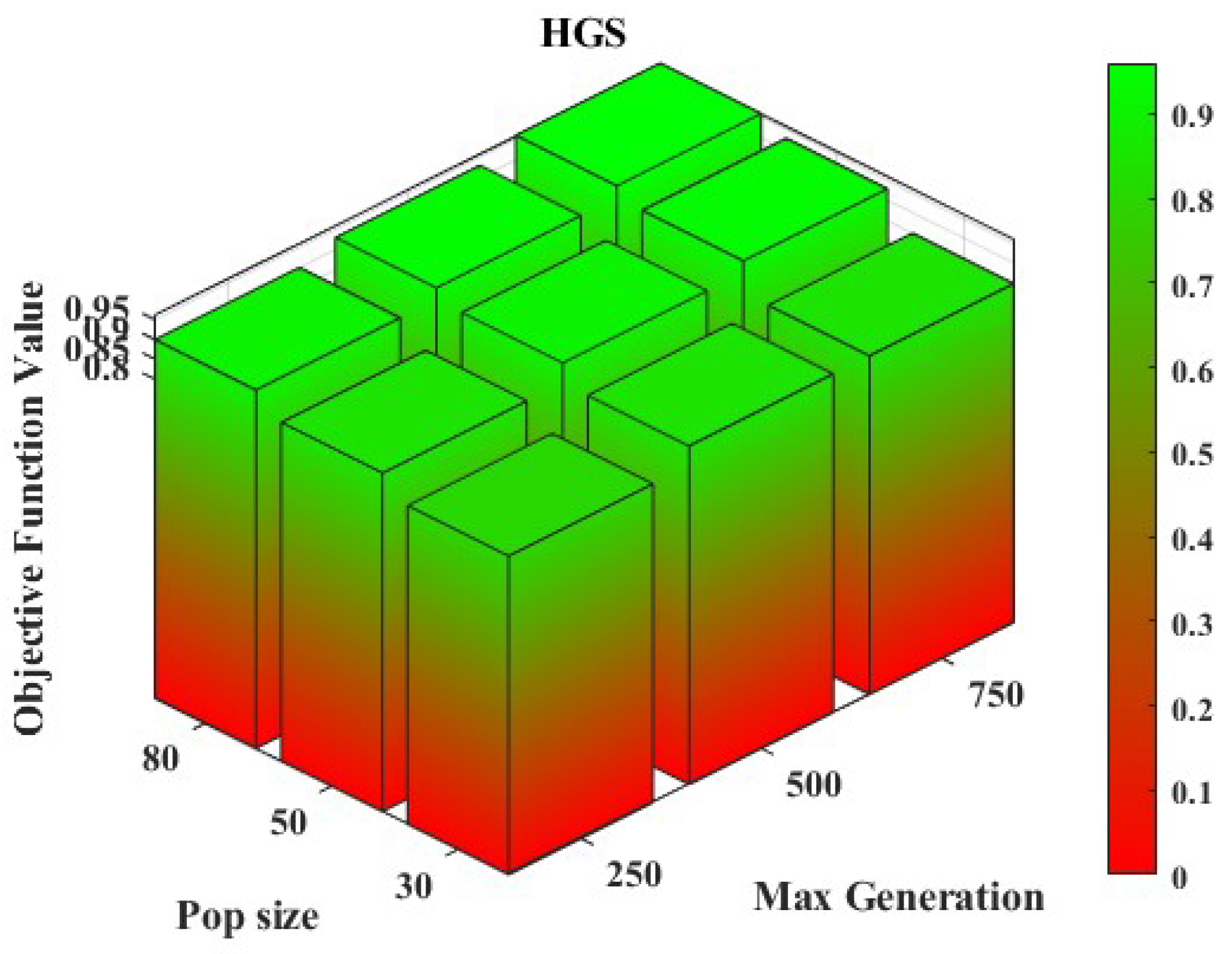
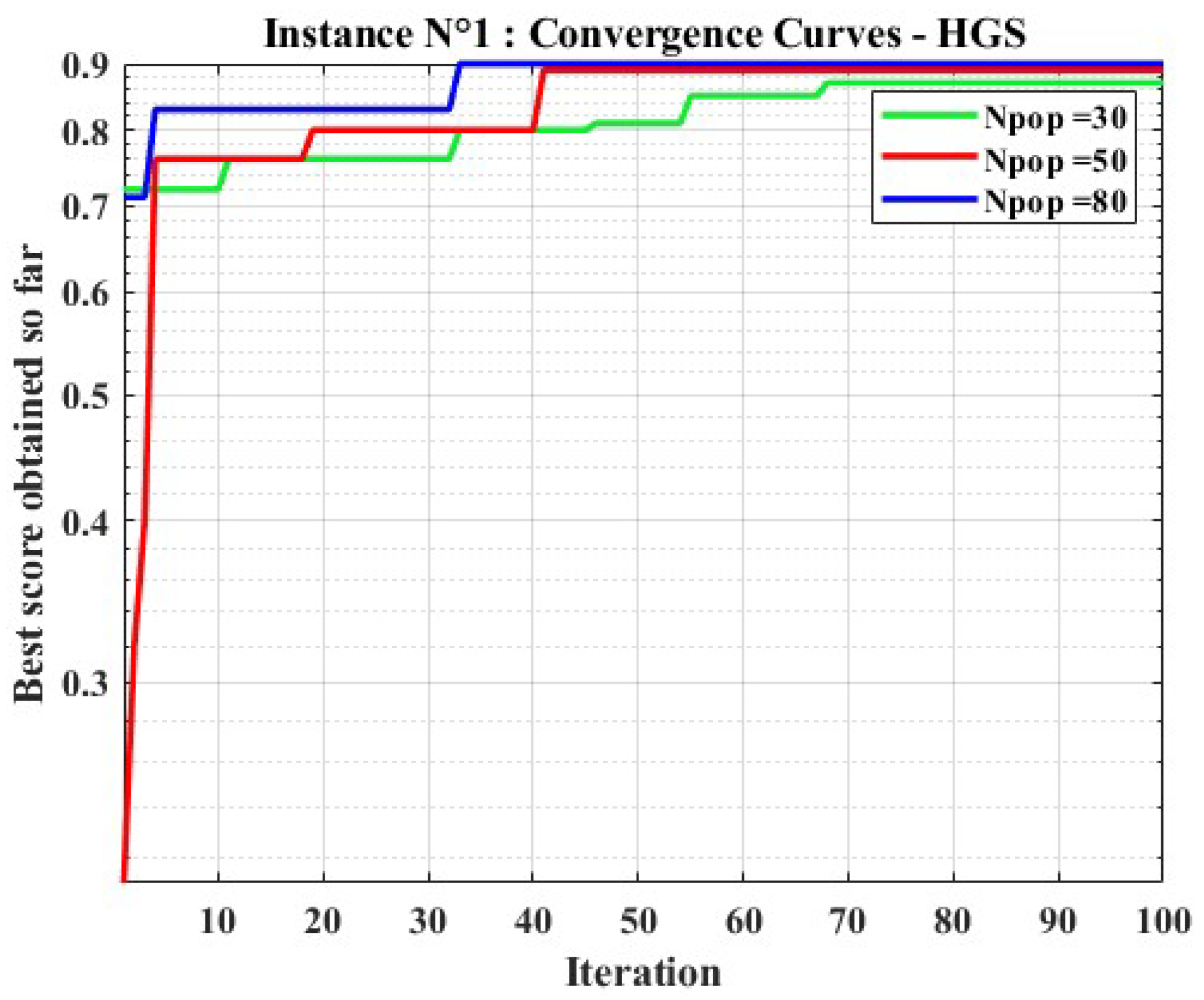
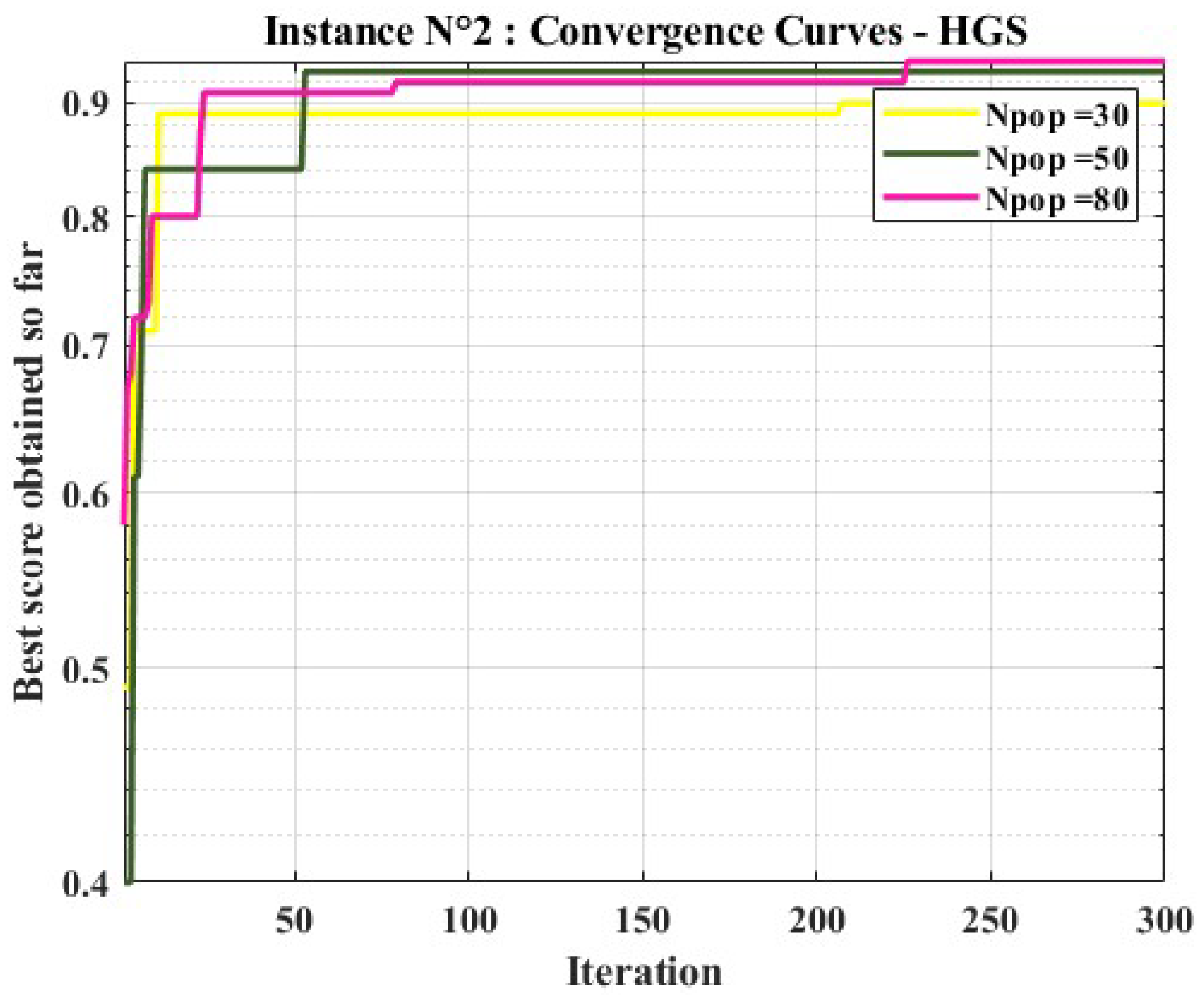
6.5. Convergence Analysis
7. Discussion
7.1. Comparison with Traditional Models
7.2. Scientific Contributions to Supply Chain Resilience
7.3. Empirical Validation
7.4. Implications for Future Research and Practice
Limitations and Future Directions
Practical Implications and Implementation Barriers
- High computational demands: Implementing GP, DCC, and HGSA together requires substantial computational resources, especially for large supply chains with numerous nodes and planning periods. This can result in long computation times and high storage costs.
- Scalability issues: As the size of the supply chain increases, the number of variables and constraints grows exponentially, potentially making the model less practical for very large applications without significant computational infrastructure.
- Real-world application constraints: Data availability, quality, and real-time processing requirements can pose additional challenges. Implementing such a complex model in a business environment may require advanced IT infrastructure and specialized skills.
Future Directions
- Algorithm optimization: Focus on optimizing the HGSA algorithm to reduce computational overhead by developing more efficient search strategies, utilizing parallel processing techniques, and leveraging high-performance computing resources.
- Model simplification: Simplify parts of the model or use approximation techniques to manage complexity. For example, breaking down the supply chain network into smaller sub-problems for easier management and optimization.
- Hybrid approaches: Combine the model with other optimization techniques, such as machine learning algorithms, to improve prediction accuracy and risk analysis. Hybrid approaches can enhance process efficiency and effectiveness.
- Incremental implementation: Introduce the model incrementally in business cases, starting with smaller, complex supply chains to identify practical issues and refine the model before full-scale implementation.
- Cloud computing: Utilize cloud computing platforms to handle large-scale optimization problems, offering necessary computational power and flexibility. Cloud computing can facilitate scaling resources and performing computationally intensive tasks more efficiently.
- Data precision: Ensure the precision of probabilistic and fuzzy parameters, as model performance is directly related to data quality. Genetic algorithm (GA) optimization requires accurate data for effective functioning in challenging environments.
- Computational resources: The complexity of the HGSA and UDCGP combination necessitates significant computational resources, which may be costly for small businesses or real-time decision-making scenarios.
- Scalability challenges: Address scalability issues to ensure the model performs satisfactorily across various supply chain networks, managing coordination and data effectively.
- Integration of real-time data analytics: Incorporate real-time data analytics to enhance the model’s responsiveness to market changes by continuously updating probabilistic and fuzzy parameters [20].
- Algorithm speed improvements: Enhance the speed of genetic algorithms to expand their use among businesses with limited infrastructure, making advanced tools accessible to more companies.
- Incorporation of social responsibility and sustainability goals: Align the model with global standards by integrating social responsibility and sustainability considerations for a holistic approach to supply chain management [36].
- Use in other complex systems: Validate the UDCGP-HGSA technique in other complex systems, such as healthcare logistics and disaster response networks, to assess its accuracy and reliability [19].
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anon, S.Y.; Amin, S.H.; Baki, F. Third-Party Reverse Logistics Selection: A Literature Review. Logistics 2024, 8, 35. [Google Scholar] [CrossRef]
- Kim, J.W.; Jeong, B.Y.; Park, M.H. A Study on the Factors Influencing Overall Fatigue and Musculoskeletal Pains in Automobile Manufacturing Production Workers. Appl. Sci. 2022, 12, 3528. [Google Scholar] [CrossRef]
- Ganesan, V.K.; Sundararaj, D.; Srinivas, A.P. Adaptive Inventory Replenishment for Dynamic Supply Chains with Uncertain Market Demand. In Industry 4.0 and Advanced Manufacturing; Lecture Notes in Mechanical Engineering; Chakrabarti, A., Arora, M., Eds.; Springer: Singapore, 2021; Available online: https://link.springer.com/chapter/10.1007/978-981-15-5689-0_28 (accessed on 26 June 2024). [CrossRef]
- McKinsey & Company. Supply Chain 4.0—The Next-Generation Digital Supply Chain. McKinsey Insights. 2021. Available online: https://www.mckinsey.com/business-functions/operations/our-insights/supply-chain-40–the-next-generation-digital-supply-chain (accessed on 26 June 2024).
- McKinsey & Company. Future Supply Chains: Resilience, Agility, Sustainability. McKinsey Insights. 2023. Available online: https://www.mckinsey.com/capabilities/operations/our-insights/future-proofing-the-supply-chain (accessed on 26 June 2024).
- Liu, B.; Chen, X. Uncertain Programming: Theory and Practice; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Lamii, N.; Fri, M.; Mabrouki, C.; Semma, E.A. Using Artificial Neural Network Model for Berth Congestion Risk Prediction. IFAC PapersOnLine 2022, 55, 592–597. [Google Scholar] [CrossRef]
- Sahin, B.; Yazir, D.; Hamid, A.A.; Rahman, N.S.F.A. Maritime Supply Chain Optimization by Using Fuzzy Goal Programming. Algorithms 2021, 14, 234. [Google Scholar] [CrossRef]
- Karimallah, K.; Drissi, H. Assessing the Impact of Digitalization on Internal Auditing Function. Int. J. Adv. Comput. Sci. Appl. IJACSA 2024, 15, 6. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W. Management Models and the Industrial Applications of Linear Programming; John Wiley: New York, NY, USA, 1961. [Google Scholar]
- Bathaee, M.; Nozari, H.; Szmelter-Jarosz, A. Designing a New Location-Allocation and Routing Model with Simultaneous Pick-Up and Delivery in a Closed-Loop Supply Chain Network under Uncertainty. Logistics 2023, 7, 3. [Google Scholar] [CrossRef]
- Douaioui, K.; Fri, M.; Mabrouki, C.; Semma, E.A. Improved Meta-Heuristic for Multi-Objective Integrated Procurement, Production and Distribution Problem of Supply Chain Network Under Fuzziness Uncertainties. J. Comput. Sci. 2021, 17, 1196–1209. [Google Scholar] [CrossRef]
- Chen, H.-W.; Liang, C.-K. Genetic Algorithm versus Discrete Particle Swarm Optimization Algorithm for Energy-Efficient Moving Object Coverage Using Mobile Sensors. Appl. Sci. 2022, 12, 3340. [Google Scholar] [CrossRef]
- Homayouni, S.; Talaei, M. Robust Optimization Techniques in Supply Chain Management. J. Logist. Manag. 2023, 42, 287–302. [Google Scholar]
- Wang, X.; Lu, Z.; Tian, X. Hunger Games Search Algorithm: A New Metaheuristic Approach for Complex Optimization Problems. Expert Syst. Appl. 2021, 177, 114864. [Google Scholar] [CrossRef]
- Nguyen, T.; Ho, D. Multi-objective Optimization in Supply Chain Management. Oper. Res. 2022, 22, 377–395. [Google Scholar]
- Zhang, Y.; Liu, X. Probabilistic Models in Supply Chain Optimization. Oper. Res. Perspect. 2020, 7, 100145. [Google Scholar]
- Goodarzian, F.; Abraham, A. Metaheuristic Algorithms in Supply Chain Optimization. Appl. Soft Comput. 2023, 110, 107598. [Google Scholar]
- Chen, Z.; Wong, P. Applications of Optimization in Healthcare Logistics. Healthc. Manag. Sci. 2023, 26, 223–239. [Google Scholar]
- Smith, J.; Garcia, M. Real-Time Data Analytics for Supply Chain Optimization. J. Big Data 2023, 10, 89–103. [Google Scholar]
- Boyd, J.E.; Sanger, B.D.; Cameron, D.H.; Protopopescu, A.; McCabe, R.E.; O’Connor, C.; Lanius, R.A.; McKinnon, M.C. A Pilot Study Assessing the Effects of Goal Management Training on Cognitive Functions among Individuals with Major Depressive Disorder and the Effect of Post-Traumatic Symptoms on Response to Intervention. Brain Sci. 2022, 12, 864. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, S.; Zhang, H.; Wu, C.; Yin, W. A Hybrid Genetic Algorithm for Two-Stage Multi-Item Inventory System with Stochastic Demand. Neural Comput. Appl. 2012, 21, 1087–1098. [Google Scholar] [CrossRef]
- Wang, Y.; Zhe, J.; Wang, X.; Sun, Y.; Wang, H. Collaborative Multidepot Vehicle Routing Problem with Dynamic Customer Demands and Time Windows. Sustainability 2022, 14, 6709. [Google Scholar] [CrossRef]
- Rasheed, K.; Saad, S.; Ammad, S.; Bilal, M. Integrating Sustainability Management and Lean Practices for Enhanced Supply Chain Performance: Exploring the Role of Process Optimization in SMEs. Eng. Proc. 2023, 56, 154. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A Review on Genetic Algorithm: Past, Present, and Future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Mahraz, M.-I.; Benabbou, L.; Berrado, A. Machine Learning in Supply Chain Management: A Systematic Literature Review. Int. J. Supply Oper. Manag. 2022, 9, 398–416. [Google Scholar] [CrossRef]
- Fri, M. Lead Time Prediction Using Advanced Deep Learning Approaches: A Case Study in the Textile Industry. Logforum 2024, 20, 2. [Google Scholar] [CrossRef]
- Gorji, S.A. Challenges and Opportunities in Green Hydrogen Supply Chain through Metaheuristic Optimization. J. Comput. Des. Eng. 2023, 10, 1143–1157. [Google Scholar] [CrossRef]
- Fri, M.; Douaioui, K.; Mabrouki, C.; Semma, E.A. Reducing Inconsistency in Performance Analysis for Container Terminals. Int. J. Supply Oper. Manag. 2021, 8, 328–346. [Google Scholar] [CrossRef]
- Fri, M.; Douaioui, K.; Lamii, N.; Mabrouki, C.; Semma, E.A. A Hybrid Framework for Evaluating the Performance of Port Container Terminal Operations: Moroccan Case Study. Pomorstvo 2020, 34, 261–269. [Google Scholar] [CrossRef]
- Liu, B. Uncertainty Theory: A Branch of Mathematics for Modeling Human Uncertainty; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Lee, S.; Moon, H. Enhancing Operational Resilience in Supply Chains. J. Bus. Res. 2022, 134, 342–355. [Google Scholar]
- Williams, T.; Patel, R. Adaptive Supply Chain Management Solutions. J. Oper. Manag. 2023, 56, 44–58. [Google Scholar]
- Thompson, R.; Lewis, S. Integrated Approaches to Supply Chain Optimization. Int. J. Logist. Manag. 2022, 33, 591–606. [Google Scholar]
- Jones, D.; Lee, S. Computational Efficiency in Metaheuristic Algorithms. J. Comput. Sci. 2023, 47, 76–89. [Google Scholar]
- Lee, B.; Kim, D. Integrating Sustainability Metrics into Supply Chain Optimization. Sustainability 2023, 15, 1932. [Google Scholar]
- Kim, Y.; Park, C. A Metaheuristic Approach to Supply Chain Network Design. Eur. J. Oper. Res. 2019, 274, 1064–1082. [Google Scholar]
- Kosaraju, N.; Sankepally, S.R.; Rao, K.M. Categorical Data: Need, Encoding, Selection of Encoding Method and Its Emergence in Machine Learning Models—A Practical Review Study on Heart Disease Prediction Dataset Using Pearson Correlation. In Proceedings of the International Conference on Data Science and Applications, Kolkata, India, 26–27 March 2022. [Google Scholar]
- Soleimani, H.; Sadeghi, A. Heuristic Approaches for Supply Chain Resilience. J. Manuf. Syst. 2022, 65, 238–252. [Google Scholar]
- Oucheikh, R.; Fri, M.; Fedouaki, F.; Hain, M. Deep Anomaly Detector Based on Spatio-Temporal Clustering for Connected Autonomous Vehicles. In Ad Hoc Networks; Foschini, L., El Kamili, M., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 201–212. [Google Scholar] [CrossRef]
- Garcia, H.; Martinez, L. Machine Learning Techniques for Supply Chain Variability Prediction. J. Artif. Intell. Res. 2023, 69, 310–324. [Google Scholar]






| 0.01 | 0.02 | 0.999 | |
|---|---|---|---|
| Best | Worst | Avg. | Std. | |
|---|---|---|---|---|
| Instance 1 | 0.800 | 0.820 | 0.800 | 0.0011 |
| Instance 2 | 0.950 | 0.970 | 0.950 | 0.0014 |
| Instance 3 | 0.870 | 0.890 | 0.870 | 0.0017 |
| Instance 4 | 0.890 | 0.910 | 0.890 | 0.0019 |
| Instance 5 | 0.910 | 0.930 | 0.910 | 0.0012 |
| Instance 6 | 0.950 | 0.970 | 0.950 | 0.0016 |
| Instance 7 | 0.890 | 0.910 | 0.890 | 0.0014 |
| Instance 8 | 0.830 | 0.850 | 0.830 | 0.0019 |
| Instance 9 | 0.900 | 0.920 | 0.900 | 0.0018 |
| Instance 10 | 0.860 | 0.880 | 0.860 | 0.0015 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Douaioui, K.; Benmoussa, O.; Ahlaqqach, M. Optimizing Supply Chain Efficiency Using Innovative Goal Programming and Advanced Metaheuristic Techniques. Appl. Sci. 2024, 14, 7151. https://doi.org/10.3390/app14167151
Douaioui K, Benmoussa O, Ahlaqqach M. Optimizing Supply Chain Efficiency Using Innovative Goal Programming and Advanced Metaheuristic Techniques. Applied Sciences. 2024; 14(16):7151. https://doi.org/10.3390/app14167151
Chicago/Turabian StyleDouaioui, Kaoutar, Othmane Benmoussa, and Mustapha Ahlaqqach. 2024. "Optimizing Supply Chain Efficiency Using Innovative Goal Programming and Advanced Metaheuristic Techniques" Applied Sciences 14, no. 16: 7151. https://doi.org/10.3390/app14167151
APA StyleDouaioui, K., Benmoussa, O., & Ahlaqqach, M. (2024). Optimizing Supply Chain Efficiency Using Innovative Goal Programming and Advanced Metaheuristic Techniques. Applied Sciences, 14(16), 7151. https://doi.org/10.3390/app14167151









