Abstract
It is a challenge for the particle swarm optimization algorithm to effectively control population diversity and select and design efficient learning models. To aid in this process, in this paper, we propose multiple learning strategies and a modified dynamic multiswarm particle swarm optimization with a master slave structure (MLDMS-PSO). First, a dynamic multiswarm strategy with a master–slave structure and a swarm reduction strategy was introduced to dynamically update the subswarm so that the population could maintain better diversity and more exploration abilities in the early stage and achieve better exploitation abilities in the later stage of the evolution. Second, three different particle updating strategies including a modified comprehensive learning (MCL) strategy, a united learning (UL) strategy, and a local dimension learning (LDL) strategy were introduced. The different learning strategies captured different swarm information and the three learning strategies cooperated with each other to obtain more abundant population information to help the particles effectively evolve. Finally, a multiple learning model selection mechanism with reward and punishment factors was designed to manage the three learning strategies so that the particles could select more advantageous evolutionary strategies for different fitness landscapes and improve their evolutionary efficiency. In addition, the results of the comparison between MLDMS-PSO and the other nine excellent PSOs on the CEC2017 test suite showed that MLDMS-PSO achieved an excellent performance on different types of functions, contributing to a higher accuracy and a better performance.
1. Introduction
Many real-world optimization problems such as classification problems, nonlinear processes, path selection, scheduling problems, structural designs, and text mining may have multimode, non-convex, nonlinear, discontinuous, and non-differentiable characteristics, which makes these problems extremely complex and difficult to solve by traditional methods [1]. To solve these problems better and more effectively, many researchers have developed population-based nature-inspired search optimization algorithms such as genetic algorithms (GAs) [2], particle swarm optimizations (PSOs) [3], ant colony optimizations (ACOs) [4], gravitation search algorithms (GSAs) [5], differential evolutions (DEs) [6], and distribution estimation algorithms (EDAs) [7], proposing various population organization patterns and learning mechanisms, cleverly utilizing individual historical knowledge to help population evolution. These population-based algorithms are capable of solving most optimization problems and are easy to implement. Due to the random initialization of the population and the introduction of random numbers into the search mechanism, their dependence on the initial scheme and gradient information is lessened to a great extent.
Among the population-based algorithms, PSO [3] was proposed by Kennedy and Eberhart in 1995 based on research on the predation behavior of birds. It finds the best solution through information sharing and cooperation among the individuals in the population. Because of its simplicity, a few parameters adjusted, and its high computational efficiency, PSO has successfully attracted the extensive attention of engineers and scholars in recent decades. The classical PSO constructs a learning mechanism in which each particle realizes its own evolution through self-cognition and social cognition. Self-cognition makes it maintain its own historical experience, and social cognition makes the individuals cooperate and share information. This learning mechanism enables particles to continuously mine better positions from the search space and guide the subsequent search behavior of particles, which gives PSO a strong ability to solve complex problems.
The learning model of PSO, that is, the information sharing mode among particles, largely determines the ability of the algorithm to solve complex problems. Generally, it is an effective way to enhance the algorithm ability to fully mine and use the effective information in the population to build an efficient learning model. In the classical PSO, particles perform the learning process by measuring the fitness and selecting the global best-so-far particles or the personal best experience as a learning model [8,9]. When optimizing the single-mode function, this learning model can help particles quickly find the global optimum. However, PSO may lose its diversity and fall into a premature convergence because the overall learning mode makes particles gradually move to one dominating candidate in the population until convergence, especially when solving nonseparable and high-dimensional optimization problems or optimization problems with many local optimizations [10].
For the population-based evolutionary algorithm, maintaining the diversity of the population gathers increasingly effective evolutionary information. According to the characteristics of population evolution, different evolutionary information is selected as a particle learning example, which balances the exploration and development and guides the population to evolve effectively. For instance, dynamic multiswarm PSO (DMS-PSO) [11] allocates all particles into multiple subswarms. The individuals in each subswarm receive different social information so that each subswarm has different evolutionary paths, and information among the subswarms is shared through population reorganization, which effectively maintains the diversity and makes it perform well on complex multimode problems. However, DMS-PSO is not conducive to the evolution of some subswarms because it adopts the same learning template for different subswarms. A heterogeneous comprehensive learning and dynamic multiswarm PSO (HCLDMS-PSO) [12] is presented, where a comprehensive learning (CL) strategy was used as the exploitation subswarm learning model and an improved DMS strategy was designed to structure the exploration subswarm learning model. The two subswarms rely on the different learning exemplars to update independently to ensure that the population does not lose its diversity.
Exploration and exploitation are two important stages for the evolution process of population-based algorithms [13,14]. In the exploration stage, to seek the global optimal solution, individuals need to reach different regional positions as much as possible, and better diversity is obtained at the population level. In the exploitation stage, particles search in a small area for the sake of obtaining a high-precision optimal solution faster, which can effectively improve the local search ability of the algorithm but sacrifices the diversity of the population and increases the risk of premature convergence. Therefore, the probability of the premature convergence can be significantly reduced by improving the diversity of the population. The multiswarm strategy divides the entire population into several subswarms. Individuals within a subswarm cooperate and share information with other subswarms to produce new offspring individuals, which makes each subswarm evolve along different paths and effectively maintains the diversity of the population during the evolution. To date, the multiswarm strategy has been widely used in population-based evolutionary algorithms because it has natural advantages in maintaining population diversity. Various population division strategies have been proposed such as stochastic division, clustering, fitness sharing, etc., in which the algorithm extends the learning beyond the dominant individuals by improving the probability of poor individuals entering the next generation. Their common starting point is to maintain the diversity of the population.
In addition, considering that the update mode of all individuals is the same for the algorithm of a single learning model, the population information cannot be fully used to guide individual evolution, which cannot intelligently deal with different complex situations. In other words, when the algorithm is in different evolutionary stages, or is used to solve different types of optimization problems, the guiding effects of the different learning models are quite different. Therefore, some scholars have begun to explore PS based on a variety of different learning models. For instance, in the triple archives PSO (TAPSO) [15], three different learning models, the Diffident Model, the Mild Model, and the Confident Model, are provided to update particles so that the particles in the population show different search behaviors, meeting the needs of the algorithm in its different evolutionary stages. In the multiswarm PSO with dynamic learning strategy (PSO-DLS) [16], particles take the local optimal position in their subswarms (focusing on exploitation) and a united local best position among subswarms (focusing on exploration), as examples. During the search process, the population can maintain diversity without being affected by the global best position of all the dominant particles.
In summary, multiple population structures can offer significant diversity at the population level, and excellent learning strategies can more extensively mine population historical knowledge, which are effective in helping find the global optimum, especially for problems with multiple local optimal solutions. However, most studies have a fixed number of populations. If the population size is large, it helps with the initial exploration of the algorithm, but limits the local development ability in the later stages of evolution, and vice versa. Meanwhile, the rational management of multiple learning strategies to match the evolutionary characteristics of the population is also an effective way to improve the overall performance of the algorithm. Motivated by this observation, we propose multiple learning strategies and a modified dynamic multiswarm PSO with a master–slave structure, called MLDMS-PSO. Specifically, the characteristics of MLDMS-PSO are as follows.
Adopting a multiswarm strategy is an effective means to improve population diversity. In this paper, a modified dynamic multiswarm (MDMS) strategy with a master–slave structure is proposed. Specifically, among the superior particles of the population, we selected the particle combinations with a more uniform spatial distribution as the master particles. With the master particles as the center, the subswarms were constructed. At the same time, the number reduction strategy of the subswarm was adopted to strengthen the local exploitation ability of the algorithm in its late evolution. Three learning strategies were adopted to update the particle positions. Respectively, a modified comprehensive learning (MCL) strategy is conducive to the diversity of the population; a local dimension learning (LDL) strategy can help better local exploitation; a united learning (UL) strategy was used to balance the MCL and LDL. In addition, to further exert the advantages of the three learning strategies, a probability function with a reward and punishment mechanism was designed to manage the three learning strategies, strengthen the competition within the subswarms and the collaboration between subswarms, and improve the search efficiency of the algorithm. Finally, a large number of experiments was carried out on 29 benchmark functions from the CEC2017 test suite. The experimental results, supported by the nonparametric Wilcoxon rank-sum test and Friedman test, consistently demonstrated the that MLDMS-PSO could effectively balance exploration and exploitation, clearly improve the convergence accuracy and reliability, and was able to provide a better and more consistent performance than all comparison algorithms on the majority of the benchmark functions.
The rest of this paper is arranged as follows. Section 2 shows the standard PSO and reviews some different types of PSOs. The proposed MLDMS-PSO is detailed in Section 3. In Section 4, extensive experiments are carried out to test the MLDMS-SSO, and its performance is analyzed and discussed in depth. Finally, the conclusions are presented in Section 5.
2. Review of the Standard PSO and Its Variants
2.1. Standard PSO
As a kind of population intelligent optimization algorithm, PSO is generally used because of its excellent performance in solving continuous optimization problems. It is assumed that the population contains M particles in the D-dimensional search space, and each particle is composed of two kinds of information, the particle position, and velocity, in which the particle position vector, , represents a solution in the search space, and the particle velocity vector, , indicates the search direction of the particle. Particle xi moves at speed vi in the search space. Due to the influence of inertia, it is more inclined to maintain its own speed and can learn from its personal best experience Pbesti and population best experience Gbest to improve the vi. In the initialization phase, each particle is given a random initial position and an initial velocity. After that, the update equations of vi and xi are as follows:
where i = 1, 2,⋯, M, j = 1, 2,⋯, D. w is an inertia weight, c1 and c2 are the acceleration coefficients, and r1,j and r2,j are two uniformly distributed random numbers independently generated within [0, 1] for the jth dimension. t is the number of iterations. The velocity and position of are updated with Equations (1) and (2) and achieve the new position of particle i. If the fitness of () is better than , is replaced by . Otherwise, will remain unchanged. Similarly, Gbest can be updated until the termination conditions are met.
2.2. Some Variants of PSO
In recent decades, the real-world problems that need to be solved have become increasingly complex. The classical PSO algorithm often shows premature convergence and a poor global search ability. To improve the performance of the classical PSO, some researchers and engineers have proposed plenty of PSO variants. Depending on the objectives to be dealt with, most PSO variants can be divided into four types: parameter tunings, domain topology adjustments, learning strategies, and hybrid strategies, which are briefly reviewed here.
- (1)
- Parameter tuning
Generally, the parameter control of a PSO mainly focuses on the inertia weight (w) and acceleration coefficients (c1 and c2). The inertia weight, used to maintain the direction of particle movement, is a critical parameter of a standard PSO. Reducing the inertia weight over time can significantly improve the performance of the PSO [17]. Now, many PSOs still use this update strategy to linearly reduce w from 0.9 to 0.4 with the progress of iteration [18,19,20,21]. It has been found through experiments that with a smaller w, the particles move at a smaller pace, which is conducive to exploitation, while with a larger w, particles can appear at a farther place each time, which is more helpful to exploration. However, considering the complexity of the PSO search process, some researchers have introduced nonlinear-varying strategies to assign inertia weights, which is able to endow particles with diverse search behaviors [22,23,24,25,26,27].
Although the above-mentioned inertia weight updating methods improve the performance of the PSO to a certain extent, they are not good enough to match between the parameter adjustments and the search process due to the lack of appropriately used evolutionary state information in the iterative process. To obtain a more satisfactory adjustment for the parameters, the inertia weight can be updated based on some feedback parameters. For instance, in [25], the success rate of the swarm was used as a feedback parameter to adaptively adjust the inertia weight, which can configure a more appropriate value of the inertia weight according to the particles’ situation in the search space. In an adaptive PSO (APSO) [28], a systematic adaptation scheme is used to control w, c1, and c2. This scheme is not only based on an evolutionary state estimation, but also considers the influence of these parameters in different evolutionary states. In the artificial multiswarm PSO (AMPSO) [29], an adaptive inertia weight strategy based on a hybrid of position diversity is matched to different subswarms to better balance exploration and exploitation and improve the performance of the algorithm. What these methods have in common is that they can deeply mine the fitness, speed, position, and other information of the particles, which can be effectively used to adjust their own parameters during the evolution process.
- (2)
- Neighborhood topology adjustments
The PSO particles with different neighborhood topologies are connected together through different structures. In these structures, the particles have different rules for communicating and sharing information, which can affect the diffusion speed of the information in the population and drive the whole population’s evolution. Therefore, neighborhood topology adjustments can also effectively improve the performance of PSO. Many neighborhood topologies have been proposed such as the star [3], ring [30], wheel [31], and Von Neumann topologies [32]. These foregoing neighborhood topologies belong to static topologies and the pattern of information acquisition is fixed, which contradicts the distinct requirements at the different evolutionary stages. Therefore, many dynamic topologies have been developed in which the neighborhood can be refreshed and regrouped depending on the particles’ parameters in the evolution process. In [33], a dynamic neighborhood that is introduced contains only a few particles during the initial stages of the optimization. With the increase in generations, the number of particles in the neighborhood gradually increases until all particles are included. This enhances the exploration abilities of the algorithm in the earlier stage and makes the algorithm focus more on exploitation at the end of the PSO run. Furthermore, in [26], the nonparametric PSO (NP-PSO) constructs two different topologies, making it perform global and local search over the search space with a fast convergence speed. In the dynamic neighborhood learning PSO (DNLPSO) [34], the exemplar particle is selected from a neighborhood dynamically updated at certain intervals, which is conducive to preserving the diversity of the population to discourage premature convergence.
The multipopulation mechanism has received extensive attention because of its advantages in maintaining population diversity. In the DMS-PSO [11] and the dynamic multiswarm global PSO (DMS-GPSO) [35], the entire population is divided into many small swarms and various regrouping schemes and information interaction methods have been designed to perform dynamic updating of these swarms. In addition, in the multiswarm ensemble PSO (MPEPSO) [36], all particles are divided into four subswarms including three indicator subswarms and one reward subswarm. AMPSO [29] contains three subswarms, namely, an exploration swarm, an artificial exploitation swarm, and an artificial convergence swarm. In the above two algorithms, the subswarms update their velocities through different strategies, with the intention of balancing exploration and exploitation.
- (3)
- Learning strategy
In PSO, the learning strategy plays a very important role because it is one of the key factors determining the particle search direction. In the global PSO (GPSO) [17], the best historical experience of the whole population is selected as an example of a particle learning. Similarly, a particle selects its local neighbors’ best positions as its learning exemplar in the local PSO (LPSO) [30]. In OLPSO [19], the method of orthogonal experimental design (OED) is used to construct the particles’ learning exemplar and the combination of the historical best experience of particles and its neighborhood’s best historical guide particles to move toward the global optimal region. In the comprehensive learning PSO (CLPSO) [21], any dimension of a particle position can learn from its historical best position or other particles with better positions through a comprehensive learning strategy, while retaining the ability to learn from the global optimal experience. Similarly, in the two-swarm learning PSO (TSLPSO) [20], a novel dimensional learning (NDL) strategy is constructed by learning from the corresponding dimensions of the population best solution through each dimension of the particle’s personal best experience to discover and integrate promising information, which focuses more on local search. In CCPSO-ISM [37], an information sharing mechanism (ISM), and a kind of competitive and cooperative operator (CC), are proposed to enhance the PSO performance. The ISM needs to keep the best information of each particle so that other particles can read the shared information, which also realizes full communication between the particles in the population and each other. The CC operation provides a more efficient way to utilize this shared information. In PSO-DLS [16], a learning strategy focusing on exploration is proposed in which particles can learn from a united local best position and can also obtain information from other subswarms to improve themselves. In [8,28], an elite learning strategy guides the best knowledge of each particle to the global optimum by effectively sharing the best experience of the dominant particles when the evolution process is in a convergent state. However, in many cases, researchers have preferred to integrate multiple learning strategies to effectively guide particles toward a global optimization to meet the needs of distinct information at the different evolutionary stages.
- (4)
- Hybridization of PSO with other algorithms
Some scholars have improved the performance of PSO by hybridizing the evolutionary mechanisms of other meta heuristic algorithms such as ACO, GA, DE, and GSA. In the genetic learning PSO (GL-PSO) [38], genetic operators are used to generate exemplars with high quality and rich diversity by performing crossover, mutation, and selection on the historical information of the particles. One of the advantages of DE is that it maintains population diversity. In [9,39,40], the differential evolution strategy was introduced into the particle swarm optimization algorithm, which could effectively improve the global optimization ability of a PSO. A novel hybrid PSO and GSA (HPSO-GSA) [41] uses coevolutionary technology, which updates particle positions simultaneously with PSO velocity and GSA acceleration, to seek an effective balance between exploration and exploitation. In the ant particle optimization algorithm (HAP) [42], the PSO and ACO work and generate the best solution, taken as the global best solution, which is used as an important basis for selecting the position of next generation particles and ants. In addition, various other algorithms are hybridized with PSO to improve the overall performance such as HPPSO [43] (PSO and POA), HFPSO [44] (Firefly and PSO), PSO-BOA [45], PSOGWO [46], and so on.
3. The Proposed Method
Based on the excellent research results of previous researchers, we proposed the MLDMS-PSO algorithm to improve the performance of the particle swarm optimization algorithm, especially in dealing with more complex multimodal function problems. An MDMS strategy with a master–slave structure helps the population maintain better diversity, and multimodel learning strategies can better utilize historical knowledge in evolution. In addition, an efficient learning strategy management mechanism was established to schedule learning strategies more reasonably based on the evolutionary stage of the population, thereby significantly enhancing the overall performance of the algorithm. The steps are shown as a flowchart of the MLDMS-PSO in Figure 1.
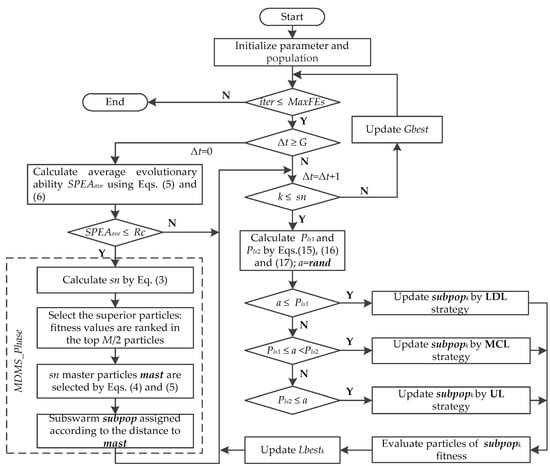
Figure 1.
MLDMS-PSO flowchart.
3.1. The Proposed MDMS Strategy
In the process of iteration, PSO continuously discards the particles with poor positions and retains the particles with better positions to achieve the goal of the population’s evolution toward a better position and the search for an optimal position. Therefore, the superior particles lead each subswarm in a dynamic multiswarm strategy that can effectively avoid the population falling into a local optimum and improve the search efficiency of the population. Based on this, we propose a modified dynamic multiswarm strategy with a master–slave structure in which the subswarm is constructed with the superior particle as the center.
- (1)
- A multiswarm segmentation scheme with a master–slave structure
Assuming that the population is composed of M particles, it is divided into sn subswarms , and each subswarm contains sm particles, , including a master particle and (smsi − 1) slave particles. The number of subswarms sn decreases linearly with the iteration of the algorithm; at the iter generation, it can be calculated by Equation (3).
where MaxGen represents the maximum number of iterations of the algorithm. Figure 2 clearly explains the proposed multiswarm segmentation scheme with a master–slave structure, which is divided into three steps.
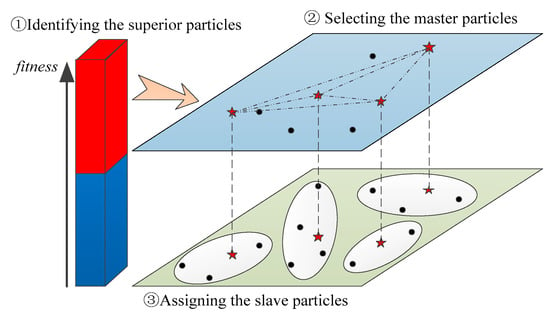
Figure 2.
The multiswarm segmentation scheme with a master–slave structure. The red stars represent master particles and the black dots represent slave particles.
First, the superior particles are identified. The individuals are sorted according to the fitness value of the particles, and the top of the M/2 particles are selected as the superior particle set , from which the master particles will be selected.
Second, the master particles are selected. The distribution of the subswarms is closely related to the leader particle, and a more balanced distribution is conducive to the particle exploring a wider area. Therefore, to ensure a more balanced distribution of each subswarm, we took the Euclidian distance between particles as a measure and selected the combination that contained sn particles with the largest sum of distances in the superior particle set ST as the set of master particles, ,. The distance sum of possible combinations, and can be calculated by Equations (4) and (5).
where disti,j denotes the distance between two different D-dimensional individuals, csi and csj, and Sum_d represents the distance sum between all individuals in the Cs. Then, the combination of Cs with the largest Sum_d can be selected as the Master by traversing all possible combinations.
Finally, the slave particles are assigned. An individual master particle, mastsi, in Master leads to a subswarm, subpopsi, and all other individuals, except those who have been selected as leader particles, should be assigned to subswarms. When assigning slave particles, the master particle is taken as the center of the subswarm, and the particle closest to itself is selected as its slave particle. Each subswarm competes for its own slave particles until the number of its slave particles reaches the upper limit. In detail, a particle xi is randomly selected from all of the particles except the master particle. If xi has the smallest Euclidean distance to mastk, it will be assigned to subpopk. Different particle numbers are allowed in each subswarm.
- (2)
- The multiswarm dynamic adjustment strategy
In the process of evolution, due to the small scale, the global exploration ability of the subswarm is limited, which makes it easy to lose diversity and fall into the local optimal region. To solve this problem, a multiswarm dynamic adjustment strategy was designed in which the evolutionary ability of each subswarm is evaluated to determine when to update and restructure all the subswarms. When the evolutionary ability of the subswarm is weakened and its advantage cannot be effectively brought into play, the population is reorganized so that the subswarms can exchange information and maintain good diversity. In detail, the evolutionary ability of the population is measured for each interval iteration parameter G. If the subswarm finds a better position after generation G, it means that it still has evolutionary abilities. In contrast, this means that the subswarm has lost its evolution abilities. Finally, the average evolutionary ability of the subswarm (SPEAave) is used as a measure of the evolutionary ability of the population and can be calculated by Equations (6) and (7).
where SPEAk is the evolutionary ability of the k-th subswarm, . and represent the fitness values of the k-th subswarm at the local neighbors’ best positions in the iter and iter + G generation, respectively. At the same time, a recombination parameter, Rc, is defined. When condition is satisfied, the subswarm will be redivided. The values of the interval iteration parameter, G, and recombination parameter, Rc, are investigated in Section 4.1. In summary, the detailed process of the MDMS strategy is shown in Algorithm 1.
| Algorithm 1. MDMS_Phase | |
| 1: | Calculate sn using Equation (3); |
| 2: | [~,index_f] = sort(fitness); |
| 3: | Index of superior particles: ST_temp = index_f (1:M/2); |
| 4: | Index of all potential combinations of master particles Comb = nchoosek(ST_temp, sn); |
| 5: | Calculate all combinations of distance sum Sum_d(Pos(Comb)) using Equations (4) and (5); |
| 6: | Index of the combination Cs: [~, index_m] = max (Sum_d); |
| 7: | The index of master particles Master = Comb(index_m,:); |
| 8: | for k = 1: sn |
| 9: | subx(1,:) = Pos(Master(k),:), subp(1,:) = Pbest(Master(k),:); |
| 10: | end for |
| 11: | for l = 1:M |
| 12: | if ~ismember(l,Master) |
| 13: | ms_d = pdist2(Pos(l), Pos(Master,:)); |
| 14: | [~,index_s] = min(ms_d); |
| 15: | subx{index_s}(end + 1,:) = Pos(l,:), subp{index_s}(end + 1,:) = Pbest(l,:); |
| 16: | end if |
| 17: | end for |
3.2. A Multimodel Learning Strategy with Reward and Punishment Mechanisms
In the evolution process of the PSO algorithm, particles find better positions by constantly learning from their own historical experience and the historical experience of their neighbors. The learning characteristics are mainly reflected in the update of particle velocity v. A good learning example should be able to adapt to the different needs of the algorithm evolution process; that is, in the initial stage, it should be able to maintain better diversity to explore a wider area in the search space, and in the final stage, it should make the algorithm have better local search abilities to improve the solution accuracy of the algorithm and save the number of evaluations. However, it is difficult for a single learning strategy to satisfy all the needs of the algorithm in the different stages. Based on this, this paper used the reward and punishment mechanism to manage three learning strategies, the MCL, LDL, and UL strategies, so that the different subswarms can dynamically choose learning strategies conducive to their own evolution.
- (1)
- MCL strategy
The CL strategy can obtain more abundant information from the entire population in the process of algorithm evolution to help particles evolve and keep the population exploring a wider area in the search space. In the multiswarm PSO, different subswarms may contain different information elements. Therefore, sufficient information sharing among the different subswarms is conducive to the evolution of the population. Based on this, this paper adjusted the CL strategy and proposed an MCL strategy. When selecting the learning template, individuals from different subswarms are selected as learning objects to promote the information interaction between subswarms in the process of evolution. The update of speed v is shown in Equations (8) and (9).
where Mpbesti is the particle xi of the learning example. The particle from each subswarm is randomly selected to form a learning set, in which Mpbesti,j is consistent with the dimension corresponding to the pbest of the winner in the learning set. Different particles adopt different learning probabilities, Pc, which are related to the number of particles in the subswarms where the particle is located sm.
- (2)
- LDL strategy
In the process of population evolution, the effective local exploitation of subswarms can better improve the overall performance of the algorithm. However, making full use of the local optimal information can speed up the development of the local areas. Using the idea of dimension learning for reference, this paper constructed an update template through the historical optimal dimension information of the particles and the global optimal dimension information of the population to update the particle speed and position, as shown in Equations (11) and (12):
The selection probability Pl is used to manage the probability that the dimension information of the xi historical optimal position Pbesti and its subswarm historical optimal position Lbestk are selected. In this paper, when updating the particle speed, we put Pbesti and Lbestk in the same important position, so we assigned Pl = 0.5. In detail, for each dimension of xi, if the generated random number rand is greater than the selection probability Pl, the information of the corresponding dimension in LDPbesti is selected from Pbesti; otherwise, the Lbestk where particle xi belongs is selected.
- (3)
- UL strategy
The MCL strategy can extract more individual information, maintain better diversity of the population, and promote particle exploration but it also limits the exploitation ability. The LDL strategy strengthens the particle exploitation ability through the information of the particle’s pbest and Lbest of the subpopulation where the particle belongs, however, it is also easier to fall into a local optimization. To balance the advantages and disadvantages of the MCL strategy and LDL strategy, the UL strategy was proposed. Randomly select subswarms, and use the Lbest of the selected subswarms to construct a unit learning example Ubest, that is, the center of the historical optimal position of all the selected subswarms is used to guide the evolution of the target particles. The particle’s speed update is affected by the combination of the particle’s pbest and Ubest, the best location in the history of the individual, and the update formulas are Equations (13) and (14):
At different evolutionary stages, learning examples have different effects on the population evolution. For example, at the initial stage of the evolution, selecting the MCL learning model can meet the needs of the algorithm to fully explore the search space at the initial stage. At the end of evolution, the LDL strategy was adopted to accelerate the convergence of the algorithm. Therefore, to meet the needs of different evolutionary stages of the algorithm and give better play to the advantages of the multiple learning templates, this paper proposed a learning model selection mechanism with reward and punishment mechanisms. By selecting the benchmark function and the reward and punishment factors, the benchmark function ensures the overall selection probability change trend of the different templates in the evolution, and the reward and punishment factors fine tune the selected probability of the templates according to the evolutionary stage. There is more effective control of the probability that different learning templates are selected in the iteration to affect the evolution process of the population to improve the performance of the algorithm. Therefore, we built two strategy selection functions, Pls1 and Pls2, to manage three different learning strategies, which can be calculated by Equation (15). As shown in Figure 3, Pls1 is used to divide the selection probability of the LDL and MCL strategies, and Pls2 is the selection probability of the MCL and UL strategies. is a random parameter that conforms to a uniform distribution. If , the subswarm selects the LDL strategy to update the individual. If , the subswarm selects the MCL strategy to update the individual. If , the subswarm selects the UL strategy to update the individual. MaxFEs is the maximum number of fitness evaluations.
where rp1 is the reward and punishment factor of the LDL strategy relative to the MCL strategy, and rp2 is the reward and punishment factor of the UL strategy relative to the MCL strategy, which was used to better balance the strategy selection at the different evolutionary stages. The reward and punishment factor was constructed based on the promotion abilities of the learning strategies in different stages for the individual evolution, that is, the improvement rate (Ir) of the fitness. In this paper, considering that the objective f is the minimum, that is, the smaller the value f(x), the better the performance of x. Therefore, the Ir of the learning strategy on the selected particles in generation t is defined as Equation (16).
where ln is the number of particles that choose a learning strategy, indicates the Euclidean distance between and , and is the fitness of . Therefore, the improvement rates of the three learning strategies LDL, MCL, and UL are IrLD, IrCL, and IrUL, respectively.
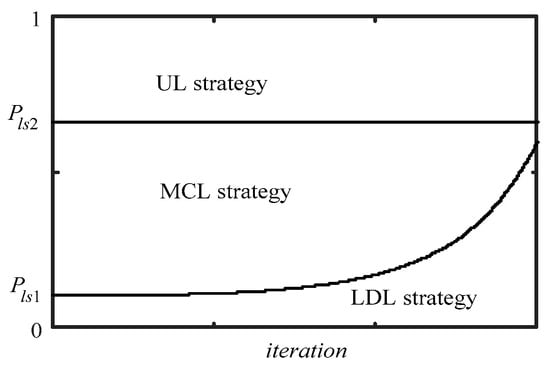
Figure 3.
The schematic diagram of the strategy selection functions.
It should be noted that in an independent iteration, the influence rate of each learning strategy on the individual evolution is random. Therefore, rp1 and rp2 cannot be directly used to observe the promotion effect of the learning model on the individual evolution at this stage. In this article, we used the technique to smooth it to reduce the influence of randomness in a single generation and obtained the performance change trend of the different learning templates at the different evolution stages. The reward and punishment factors rp1 and rp2 for learning strategy selection can be calculated by Equation (17).
where is a Savitzky–Golay smooth function and is a minimum value, which ensures that the denominator is not equal to 0.
The change in the strategy selection function with the reward and punishment factors on benchmark function f1 is shown in Figure 4. The MCL strategy has a better ability to promote the evolution of the individuals in the middle of evolution. Therefore, at this stage, the probability of the strategy being selected is increased.
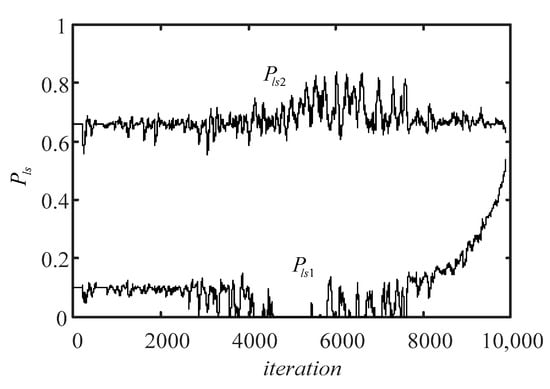
Figure 4.
The result of the strategy selection function with the reward and punishment factors on benchmark function f1.
In MLDMS-PSO, the three learning strategies are properly implemented to enable the different strategies to cooperate with each other, which is conducive to mining potential promising information to help the particles evolve. For the different evolution stages, the strategy selection function is used to effectively control the selection of advantageous particle update strategies, which balances exploration and exploitation and improves the overall performance. The process of MLDMS-PSO is shown in Algorithm 2.
| Algorithm 2. MLDMS-PSO_Phase | |
| 1: | Set parameter M,G,Rc;SPEAave = 0;delta_t = G; |
| 2: | Initialize the position and velocity of all particles x and v, respectively; |
| 3: | Evaluate x: fitness = fit(x); |
| 4: | Pbest = x, Gbest = [Pbesti | min(fit(Pbesti)]; |
| 5: | MDMS_Phase; |
| 6: | Lbestk = [subp(i,:) | min(fit(subp{k}(i,:)))]; |
| 7: | While (iter ≤ MaxFEs) |
| 8: | if delta_t ≥ G |
| 9: | Calculate average evolutionary ability SPEAave using Equations (5) and (6); |
| 10: | if SPEAave < Rc |
| 11: | MDMS_Phase; |
| 12: | end if |
| 13: | end if |
| 14: | for k = 1,2, …, sn do |
| 15: | Calculate Pls1 and Pls2 using Equations (15)–(17); |
| 16: | if a < Pls1 |
| 17: | Update particles of subpop{k} using Equations (11), (12) and (2); |
| 18: | end if |
| 19: | if Pls1 ≤ a < Pls2 |
| 20: | Update particles of subpop{k} using Equations (8), (9) and (2); |
| 21: | end if |
| 22: | if Pls2 ≤ a |
| 23: | Update particles of subpop{k} using Equations (13), (14) and (2); |
| 24: | end if |
| 25: | Evaluate particles of subpop{k} fitness |
| 26: | Update Lbestk; |
| 27: | end for |
| 28: | Update Gbest; |
| 29: | end while |
4. Experimental Studies
To calibrate the parameters and test the performance of the proposed algorithm, we conducted a series of experiments based on 29 benchmark functions from the CEC2017 test suite. These benchmark functions were divided into four different categories, that is, two unimodal functions (f1 and f3. f2 was removed because it is unstable on issues of higher dimensions), seven multimodal functions (f4–f10), ten hybrid functions (f11–f20), and ten composition functions (f21–f30), which are shown in Table 1. All the experiments were implemented in MATLAB R2021a on a computer with an Intel Core i7-10700 CPU @2.90 GHz (Intel Corporation, Santa Clara, CA, USA) and 32 GB RAM running Windows 10x64 Edition.

Table 1.
The information of the benchmark function used in this paper.
4.1. Parameter Tuning
The value of some parameters may greatly affect the performance of the algorithm. In the proposed MLDMSPSO, two important parameters, the interval iteration parameter G and the recombination parameter Rc, need to be calibrated. The parameter tuning used the same population size of 40, maximum number of fitness evaluations (MaxFEs) of 1.00 × 105, run time of 51, and 10 dimensions.
A smaller value for parameter G and a larger value for Rc may lead to frequent reorganization of the subswarms in the iterative process, which makes the subpopulation unable to make full use of the internal information to improve itself and fully exploit the local area where it is located. In contrast, for a larger parameter G and a smaller Rc, the population may have the risk of a stagnant evolution and a waste of the evaluation times. Therefore, to obtain an insightful view of how the interval iteration parameter G and recombination parameter Rc affect the performance of MLDMS-PSO, this paper tested 48 different combinations of G values, from 5 to 20, when Rc was 0.1, 0.2, and 0.3. The experimental results were ranked by the average rank with the mean of 29 benchmark functions as the measurement standards. When the average rank value corresponding to a combination of G and Rc is smaller, it indicates that the combination performs better in terms of overall performance and can exhibit better performance on more functions; on in contrast, the larger the average rank value, the weaker its comprehensiveness.
The average rank value of the 29 benchmark functions was counted when MLDMS-PSO, using different G and Rc, plotted these, as shown in Figure 5. It can be clearly seen that the algorithm exhibited a similar performance at different Rc values. The average rank value first decreased and then increased with the increase in G, indicating that larger or smaller G values could not help the MLDMS-PSO achieve better performance; on the other hand, when the value of G was close to the middle region of the value range, it was beneficial for MLDMS-PSO to obtain a better ranking on more functions and had better overall performance. When the iteration parameter G = 12 and recombination parameter Rc = 0.1, the average rank was 19.34, which was lower than all of the other combinations of G and Rc for all test functions and could bring the best performance to MLDMS-PSO. Therefore, the iteration parameter G = 12 and recombination parameter Rc = 0.1 were selected for a further performance evaluation of the proposed MLDMS-PSO.
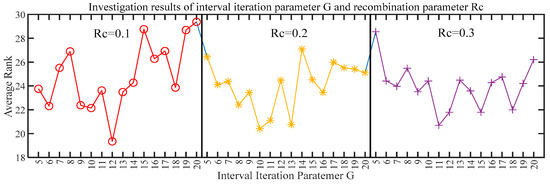
Figure 5.
Parameter investigation result in MLDMS-PSO.
4.2. Comparison with Other PSO Variants
To compare and analyze the performance of the proposed MLDMS-PSO, nine other state-of-the-art PSO variations were selected and divided into three types.
There are four PSO variants with different learning strategies, as follows:
- ➢
- Traditional global PSO algorithms with inertia weight (GPSO) [17].
- ➢
- Full information PSO (FIPS) [47]. The FIPS implements the ring topology.
- ➢
- Comprehensive learning PSO (CLPSO) [21]. All particles update the dimension information of their velocity using pbest and learn from the pbest of different particles.
- ➢
- Competitive and cooperative (CC) PSO with ISM (CCPSO-ISM) [37]. The CC operator based on the ISM is designed to use the shared information properly and efficiently.
Two PSOs adopt multiple learning strategies, as follows:
- ➢
- A PSO with the multi-exemplar and forgetting ability (XPSO) [48]. XPSO uses two exemplars to update the velocity and configures distinct forgetting abilities to different particles.
- ➢
- Two-swarm learning PSO (TSLPSO) [20]. In TSLPSO, the dimensional learning strategy and CL strategy are used to guide the local and global search of the particles, respectively.
Three PSOs divide the whole population into multiple swarms.
- ➢
- Dynamic multiple-swarm PSO (DMS-PSO) [11]. DMS-PSO adopts the multiple-swarm strategy and these swarms can be regrouped frequently.
- ➢
- Multiswarm PSO with a dynamic learning strategy (PSO-DLS) [16]. In PSO-DLS, the particle classification mechanism and the dynamic control mechanism of the strategy promote an information exchange among the subswarms.
- ➢
- Heterogeneous comprehensive learning and dynamic multiswarm PSO with two mutation operators (HCLDMS-PSO) [49]. In HCLDMS-PSO, a CL strategy and a modified DMS strategy are used to construct the exploitation subpopulation exemplar and the exploration subpopulation exemplar, respectively.
The parameter settings of the PSO variants above-mentioned and the proposed MLDMS-PSO are listed in Table 2. To make a fair comparison between the proposed MLDMS-PSO and the other state-of-the-art PSO algorithms, the mean error (mean), standard deviation (std), and rank mean value (rank) of 10 PSOs solution were calculated as a basic performance measure to evaluate the accuracy of the algorithm. The experiments were conducted on dimensions of D = 10, 30, and 50. Each algorithm was run 51 times independently on 10-D, 30-D, and 50-D problems for the 29 benchmark functions, and the termination condition was set to MaxFEs = 10,000 × D. The results of 10-D, 30-D, and 50-D are shown in Appendix A, Appendix B, and Appendix C, respectively, where the best experimental result among all of the test functions is shown in bold. Based on this result, all algorithms were sorted according to the average rank (Ave rank) of the 29 functions as the final rank (Final rank). The Ave rank is the average value of the algorithm’s experimental results ranking on each benchmark function. The Final rank is the result of sorting all algorithms by Ave rank. To compare the comprehensive performance of MLDMS-PSO and nine other state-of-the-art PSO variations in different dimensions, as shown in Table 3, we calculated the mean of each algorithm’s Ave rank in different dimensions as the comprehensive mean rank (CMean rank). Based on this CMean rank, the comprehensive ranking (Crank) of each algorithm was obtained.

Table 2.
Parameter settings of the ten PSOs.

Table 3.
The comprehensive rank of MLDMS-PSO and other PSO variations for 10-D, 30-D, and 50-D problems.
4.3. Results Analysis and Discussion
4.3.1. Solutions Accuracy
The comparison of the experimental results for the 10-D problems is shown in Appendix A. The proposed MLDMS-PSO achieved the best results on f6, f9, f11, f13, f14, f16, f18, f20, f23, and f29. The second-best solution was obtained on f12, f27, and f30. The result ranked third on f1, f4, f5, f8, f15, f17, f19, f21, f22, f24, f26, and f28, and the result ranked fourth on f7 and f10, which was better than most comparison algorithms. On f3, although the mean value of its solution ranked lower, the accuracy of the solution was satisfactory, which was 6.96 × 10−12. In addition, MLDMS-PSO achieved the minimum average rank. Therefore, MLDMS-PSO outperformed the other comparison algorithms on 10-D problems.
The comparison of the experimental results for the 30-D problems is shown in Appendix B. TSLPSO and XPSO had the best performance on unimodal functions f1 and f3, respectively. The proposed MLDMS-PSO ranked third and fifth on f1 and f3, respectively. In the simple multimodal functions, hybrid function, and composition function, the proposed MLDMS-PSO achieved the best solution on f6, f9, f11, f12, f17, f18, f20, f22, f28, and f29 and the second-best solution on f16, f25, and f30. CCPSO-ISM obtained the best performance on f6, f13, f15, f19, and f26. PSO-DLS obtained the best solution on f5, f7, f8, f21, f23, and f24. DMS-PSO found the smallest mean value of all solutions on f4, f14, f16, f25, f27, and f30. HCLDMS-PSO showed the best results on f10. In total, depending on the final rank, the MLDMS-PSO algorithm was the first. Hence, MLDMS-PSO consistently performed well and achieved the best overall performance on the 30-D problems.
As shown in Appendix C, for the 50-D problems, it can be seen that the proposed MLDMS-PSO had the highest performance on the whole test suite. Compared with other comparison algorithms, it achieved the best results on f6, f11, f13, f14, f16, f17, f20, and f29. Depending on the final rank, the MLDMS-PSO achieved the optimal performance, ranking first on eight problems, second on two problems, and third on eleven problems out of the twenty-nine benchmark problems. In addition, it is worth noting that the average ranking of the four algorithms with dynamic multiswarm DMS-PSO, PSO-DLS, HCLDMS-PSO, and MLDMS-PSO, was to a large extent, ahead of the other comparison algorithms, which also proves that a dynamic multiswarm algorithm can better implement a full exploration of the search space, effectively avoiding the population from falling into a local optimization, which can play a positive role in solving larger-scale problems.
Table 3 clearly shows that the CMean rank value of the MLDMS-PSO was the smallest among all of the compared algorithms, at 2.80. This result placed the MLDMS-PSO at the top of Crank, which is consistent with our previous discussion and further confirms the advantages of the MLDMS-PSO.
4.3.2. Convergence Process Analysis
The convergence speed is also an important indicator of the performance of evolutionary algorithms. In this part, we took the experimental results of the 30-D problems as an example to analyze the differences in the convergence process of the 10 algorithms. The results of the convergence process were classified according to the type of benchmark functions in the test set. Due to space limitations, the convergence of some functions was reduced, as shown in Figure 6, Figure 7, Figure 8 and Figure 9. The shaded area in the figures has been enlarged to more clearly illustrate the convergence process of the algorithms. It should be noted that in this experiment, the convergence curve showed the average results of 51 independent runs.
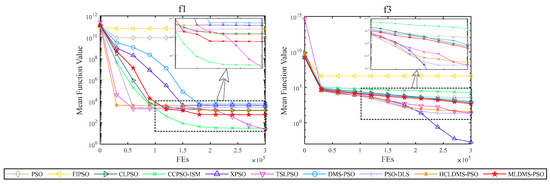
Figure 6.
Convergence progress on the unimodal functions (f1 and f3).
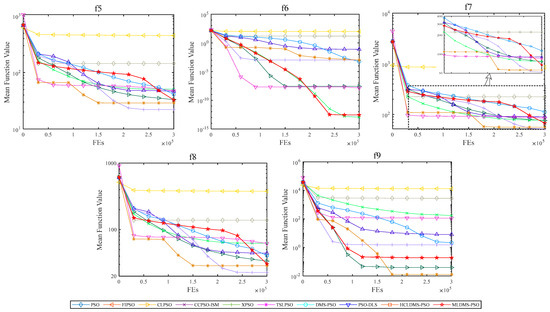
Figure 7.
Convergence progress on the simple multimodal functions (f4–f10).
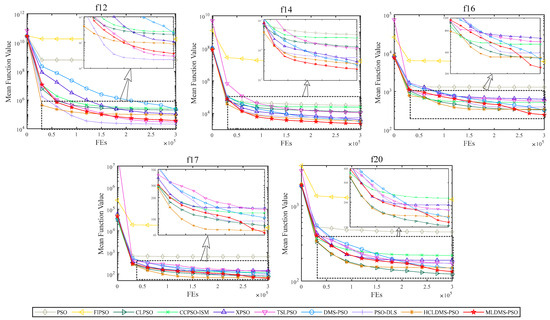
Figure 8.
Convergence progress on the hybrid functions (f11–f20).
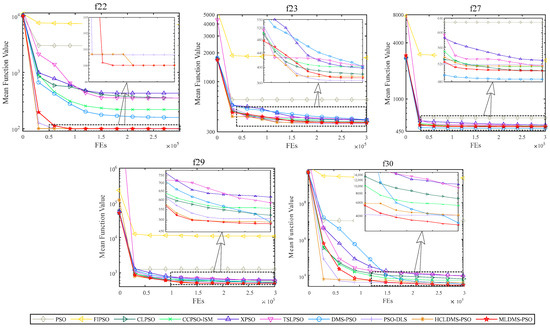
Figure 9.
Convergence progress on the hybrid functions (f21–f30).
For the unimodal functions, the convergence process of the algorithms is shown in Figure 6. TSLPSO and XPSO achieved faster convergence speeds and superior performances on f1 and f3, respectively. However, MLDMS-PSO was limited by the population dynamic reorganization scheme, which weakened its exploitation ability and made it show more stable results on two single-mode functions.
For the multimodal functions, the convergence process of the algorithms is shown in Figure 7. The classic PSO algorithm had a sharp convergence on f5, f7, and f8 but its performance was poor. MLDMS-PSO, HCLDMS-PSO, and PSO-DLS had similar features in f5, f6, f7, f8, and f9, that is, they could accelerate the convergence when approaching the late evolutionary stage, which shows that the dynamic multiswarm strategy has a stronger ability to jump out of the local optimum.
For the hybrid functions, the convergence process of the algorithms is shown in Figure 8. MLDMS-PSO achieved the best performance in f14, f16, and f17. In most hybrid functions, the convergence process was slow. The reason for this is that the effective management of multiple learning strategies can continuously obtain more favorable information, making the population continue to evolve. MLDMS-PSO also demonstrated good exploratory ability in f16 and f20 during the later stages of evolution.
For the composition functions, the convergence process of the algorithms is shown in Figure 9. MLDMS-PSO obtained competitive results in f22, f23, f27, f29, and f30, but its advantages were not obvious. By further improving the algorithm, we could make it more accurate in solving the composite function and improving the practicability of the algorithm, which is a direction that needs to be constantly explored.
In summary, MLDMS-PSO adopts a multiswarm architecture, allowing various subswarms to fully explore the solution space and demonstrate strong exploration ability in multimodal, hybrid, and composition functions. However, the cost of powerful global search capability is the loss of some local development ability, which slows down its local development speed. Compared to the improvement in solution accuracy, the slight loss in convergence speed can be accepted.
4.3.3. Statistical Results of Solutions
(1) Wilcoxon rank sum test: A Wilcoxon rank sum test [50] is a nonparametric sample test that is based on the rank order of samples and not the average value, which is used to compare the difference between the distribution positions of two populations to which two independent samples belong. In this paper, the nonparametric Wilcoxon rank sum test was used to measure the statistical significance difference between the proposed MLDMS-PSO and the other comparison algorithms. In this experiment, the distribution of the results obtained by the MLDMS-PSO algorithm and the other PSO variants on all the benchmark functions through 51 simulation runs on the 10-D, 30-D, and 50-D problems were compared, in which its significance level was 0.05. The statistical results are recorded in Table 4. The symbols “N+”, “N−”, and “N=” indicate the number that MLDMS-PSO was significantly better than, significantly worse than, and almost the same as the corresponding competitor algorithm, respectively. The comprehensive performance (CP) was equal to the sum of “N+” minus the sum of “N−”.

Table 4.
Statistical results of the Wilcoxon rank sum test for 10-D, 30-D, and 50-D problems.
Table 4 shows that MLDMS-PSO was significantly better than the other PSO variants on most 10-D, 30-D, and 50-D problems. This view is also supported by the fact that all values of “N+” were greater than “N−”. In addition, the CP of all the comparison algorithms was positive, which also showed that the new proposed MLDMS-PSO had the best comprehensive performance. HCLDMS-PSO performed well on the 30-D and 50-D test functions with CP values of 3 and 2, respectively, and its performance was close to that of MLDMS-PSO. However, in the 10-D problems, its performance was significantly weaker than MLDMS-PSO.
(2) Friedman Test: In this paper, the Friedman test of the mean was used to compare the overall performance of MLDMS-PSO and the other comparison algorithms on different benchmark functions. The Friedman test results of the 10-D, 30-D, and 50-D problems are given in Table 5, listing each algorithm and its ranking (ascending order). Finally, a comprehensive ranking based on the mean of the results was used to measure the overall performance of all of the algorithms.

Table 5.
Statistical rank of the Friedman test.
From Table 5, we can see that the proposed MLDMS-PSO algorithm in this paper ranked first in the 10-D, 30-D, and 50-D problems and obtained a better overall performance than the other comparison algorithms, which was the same as the results obtained by the Wilcoxon rank sum test. In detail, TSLPSO and CCPSO-ISM ranked behind MLDMS-PSO in the 10-D problems, and HCLDMS-PSO and PSO-DLS ranked second and third in the 30- and 50-dimensional problems, respectively. This is because the HCLDMS-PSO and PSO-DLS could obtain better population diversity during the evolution than TSLPSO and CCPSO-ISM, strengthening the exploration ability of the algorithm but also weakening the exploitation ability of the algorithm to a certain extent. The MLDMS-PSO made the algorithm more compatible with exploration and exploitation through population contraction and an adaptive learning strategy adjustment, so it had a better performance on the 10-D, 30-D, and 50-D problems.
5. Conclusions
A multipopulation metaheuristic algorithm can effectively alleviate the loss of population diversity and the risk of falling into the local optima, especially for multimode optimization problems. Based on this and the distance measurement, the MLDMS-PSO algorithm adopted a master–slave structure to divide the entire population into multiple subswarms, and through linear population reduction, it could better meet the needs of the population diversity in the different evolutionary stages. Inspired by this phenomenon, the MLDMS-PSO algorithm introduces three learning strategies, the LDL strategy, the MCL strategy and the UL strategy, to guide particle updating. At the same time, two probability selection functions are used to manage the three learning strategies, and the reward and punishment factor constructed based on the change of fitness (i.e., the improvement rate) is regarded as an additional standard. In the different stages, the probability of the selected learning strategy can be dynamically adjusted according to the change in fitness so that particles can choose more advantageous evolution strategies for different fitness terrains and improve the efficiency of the evolution. In addition, the choice of multiple learning models can better balance exploration and development. To verify the effectiveness of the MLDMS-PSO, the CEC2017 test suite was used for the performance comparisons. The results show that compared with the other existing advanced particle swarm optimization algorithms, the proposed MLDMS-PSO algorithm had better performance in multimodal, hybrid, and composition problems. During the evolution process, it could better maintain population diversity, drive continuous population evolution, strengthen the algorithm’s exploration ability, and obtain more accurate solutions. To simplify the algorithm, a linear reduction was adopted to control the number of subswarms without considering the impact of population number on the evolutionary efficiency at different stages of evolution. This sacrificed its exploitation ability to some extent, slowed down the convergence speed, and also made its performance on single-mode problems less accurate, which are not ideal.
A good population diversity can enhance the exploration ability of algorithms, but it also weakens their local exploitation ability, and vice versa. Therefore, based on the characteristics of the problem and the different stages of algorithm evolution, exploring an efficient control strategy for the number and distribution of subswarms to ensure appropriate diversity in the overall population is worth further research. In addition, the advantages and disadvantages of these three learning strategies and their management modes for different fitness landscapes are also a promising research direction, which helps to design algorithms with better reliability and robustness for different problems.
Author Contributions
Conceptualization, L.C. (Ligang Cheng); Methodology, L.C. (Ligang Cheng) and J.C.; Software, L.C. (Ligang Cheng); Validation, L.C. (Linna Cheng); Investigation, W.W.; Data curation, W.W.; Writing—original draft, L.C. (Ligang Cheng); Writing—review & editing, L.C. (Ligang Cheng); Supervision, J.C.; Funding acquisition, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the National Key Research and Development Plan under grant number 2020YFB1713600 and the National Natural Science Foundation of China under grant number 62063021. It was also supported by the Key Talent Project of Gansu Province (ZZ2021G50700016) and the Jiangmen Basic and Theoretical Science Research Project, 2023 (2023JC01001), respectively.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Comparison of experimental results for 10-dimensional problems.
Table A1.
Comparison of experimental results for 10-dimensional problems.
| GPSO | FIPS | CLPSO | CCPSO-ISM | XPSO | TSLPSO | DMS-PSO | PSO-DLS | HCLDMS-PSO | MLDMS-PSO | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| f1 | mean | 4.86 × 108 | 1.35 × 1010 | 1.01 × 103 | 5.22 × 101 | 6.11 × 102 | 1.85 × 103 | 1.49 × 102 | 2.25 × 103 | 5.25 × 102 | 3.04 × 102 |
| std | 6.59 × 108 | 3.43 × 109 | 1.12 × 103 | 5.61 × 101 | 9.71 × 102 | 2.01 × 103 | 1.88 × 102 | 2.80 × 103 | 7.22 × 102 | 5.60 × 102 | |
| rank | 9 | 10 | 6 | 1 | 5 | 7 | 2 | 8 | 4 | 3 | |
| f3 | mean | 1.11× 10−15 | 1.33 × 104 | 2.90 × 10−14 | 5.85 × 102 | 4.24 × 10−14 | 3.01 × 10−14 | 1.80 × 10−12 | 2.90 × 10−14 | 1.54 × 10−13 | 6.96 × 10−12 |
| std | 7.88 × 10−15 | 4.00 × 103 | 3.06 × 10−14 | 3.42 × 102 | 3.87 × 10−14 | 2.84 × 10−14 | 5.56 × 10−12 | 2.84 × 10−14 | 1.01 × 10−13 | 2.20 × 10−11 | |
| rank | 1 | 10 | 2 | 9 | 5 | 4 | 7 | 3 | 6 | 8 | |
| f4 | mean | 2.01 × 101 | 1.47 × 103 | 3.53 × 100 | 6.80 × 10−1 | 1.64 × 100 | 2.63 × 10−1 | 1.33 × 100 | 3.68 × 100 | 2.33 × 100 | 1.32 × 100 |
| std | 2.62 × 101 | 8.12 × 102 | 9.05 × 10−1 | 8.04 × 10−1 | 3.11 × 10−1 | 2.13 × 10−1 | 9.61 × 10−1 | 3.21 × 10−1 | 4.82 × 10−1 | 5.99 × 10−1 | |
| rank | 9 | 10 | 7 | 2 | 5 | 1 | 4 | 8 | 6 | 3 | |
| f5 | mean | 2.19 × 101 | 1.28 × 102 | 3.29 × 100 | 5.75 × 100 | 2.52 × 100 | 6.98 × 100 | 4.48 × 100 | 4.95 × 100 | 4.19 × 100 | 3.71 × 100 |
| std | 9.03 × 100 | 1.77 × 101 | 1.61 × 100 | 2.00 × 100 | 1.27 × 100 | 2.90 × 100 | 1.18 × 100 | 1.65 × 100 | 1.53 × 100 | 1.06 × 100 | |
| rank | 9 | 10 | 2 | 7 | 1 | 8 | 5 | 6 | 4 | 3 | |
| f6 | mean | 1.41 × 100 | 6.22 × 101 | 2.79 × 10−8 | 2.76 × 10−9 | 2.79 × 10−8 | 1.43 × 10−6 | 3.21 × 10−10 | 2.67 × 10−14 | 1.23 × 10−8 | 2.23 × 10−14 |
| std | 2.04 × 100 | 1.00 × 101 | 1.97 × 10−7 | 3.49 × 10−9 | 1.97 × 10−7 | 6.89 × 10−6 | 2.27 × 10−9 | 4.82 × 10−14 | 5.85 × 10−8 | 4.51 × 10−14 | |
| rank | 9 | 10 | 6 | 4 | 7 | 8 | 3 | 2 | 5 | 1 | |
| f7 | mean | 2.20 × 101 | 1.57 × 102 | 1.31 × 101 | 1.66 × 101 | 1.22 × 101 | 1.76 × 101 | 1.54 × 101 | 1.94 × 101 | 1.40 × 101 | 1.50 × 101 |
| std | 5.81 × 100 | 1.95 × 101 | 2.61 × 100 | 2.01 × 100 | 8.73 × 10−1 | 4.11 × 100 | 1.85 × 100 | 3.39 × 100 | 1.45 × 100 | 2.13 × 100 | |
| rank | 9 | 10 | 2 | 6 | 1 | 7 | 5 | 8 | 3 | 4 | |
| f8 | mean | 1.73 × 101 | 7.35 × 101 | 3.51 × 100 | 7.28 × 100 | 2.34 × 100 | 6.42 × 100 | 5.31 × 100 | 4.50 × 100 | 4.02 × 100 | 3.75 × 100 |
| std | 7.18 × 100 | 8.81 × 100 | 1.20 × 100 | 2.07 × 100 | 1.24 × 100 | 2.77 × 100 | 1.57 × 100 | 1.64 × 100 | 1.86 × 100 | 1.55 × 100 | |
| rank | 9 | 10 | 2 | 8 | 1 | 7 | 6 | 5 | 4 | 3 | |
| f9 | mean | 1.35 × 10−1 | 1.15 × 103 | 0.00 × 100 | 8.71 × 10−5 | 1.56 × 10−14 | 1.34 × 10−14 | 1.05 × 10−13 | 0.00 × 100 | 1.11 × 10−14 | 0.00 × 100 |
| std | 3.08 × 10−1 | 3.10 × 102 | 0.00 × 100 | 1.90 × 10−4 | 4.51 × 10−14 | 3.66 × 10−14 | 6.30 × 10−14 | 0.00 × 100 | 3.38 × 10−14 | 0.00 × 100 | |
| rank | 7 | 8 | 1 | 6 | 4 | 3 | 5 | 1 | 2 | 1 | |
| f10 | mean | 5.85 × 102 | 2.06 × 103 | 1.25 × 102 | 2.42 × 102 | 1.71 × 102 | 3.49 × 102 | 1.44 × 102 | 1.20 × 102 | 1.73 × 102 | 1.56 × 102 |
| std | 1.98 × 102 | 2.31 × 102 | 9.88 × 101 | 1.19 × 102 | 1.36 × 102 | 2.19 × 102 | 1.15 × 102 | 1.29 × 102 | 1.13 × 102 | 1.00 × 102 | |
| rank | 9 | 10 | 2 | 7 | 5 | 8 | 3 | 1 | 6 | 4 | |
| f11 | mean | 2.81 × 101 | 2.23 × 104 | 2.02 × 100 | 2.95 × 100 | 2.75 × 100 | 3.46 × 100 | 2.54 × 100 | 2.47 × 100 | 1.40 × 100 | 8.94 × 10−1 |
| std | 4.55 × 101 | 7.29 × 104 | 1.21 × 100 | 1.08 × 100 | 1.15 × 100 | 2.03 × 100 | 1.29 × 100 | 1.39 × 100 | 9.57 × 10−1 | 8.03 × 10−1 | |
| rank | 9 | 10 | 3 | 7 | 6 | 8 | 5 | 4 | 2 | 1 | |
| f12 | mean | 2.25 × 106 | 4.23 × 108 | 1.20 × 104 | 8.03 × 103 | 8.20 × 103 | 1.20 × 104 | 9.47 × 103 | 1.37 × 104 | 6.29 × 103 | 7.85 × 103 |
| std | 5.15 × 106 | 3.83 × 108 | 1.04 × 104 | 6.94 × 103 | 5.05 × 103 | 1.13 × 104 | 8.48 × 103 | 1.37 × 104 | 5.21 × 103 | 5.73 × 103 | |
| rank | 9 | 10 | 6 | 3 | 4 | 7 | 5 | 8 | 1 | 2 | |
| f13 | mean | 9.06 × 103 | 9.79 × 107 | 1.02 × 103 | 6.32 × 101 | 5.96 × 103 | 5.18 × 103 | 6.03 × 101 | 3.63 × 103 | 2.37 × 103 | 4.07 × 101 |
| std | 1.06 × 104 | 2.37 × 108 | 2.59 × 103 | 9.82 × 101 | 3.92 × 103 | 4.32 × 103 | 1.05 × 102 | 2.96 × 103 | 3.14 × 103 | 3.04 × 101 | |
| rank | 9 | 10 | 4 | 3 | 8 | 7 | 2 | 6 | 5 | 1 | |
| f14 | mean | 6.66 × 101 | 9.52 × 105 | 1.99 × 101 | 5.31 × 101 | 6.32 × 101 | 4.15 × 101 | 1.93 × 101 | 3.23 × 101 | 2.44 × 101 | 1.59 × 101 |
| std | 3.10 × 101 | 6.48 × 106 | 1.19 × 101 | 6.64 × 101 | 4.62 × 101 | 1.50 × 101 | 3.55 × 101 | 9.67 × 100 | 1.30 × 101 | 1.28 × 101 | |
| rank | 9 | 10 | 3 | 7 | 8 | 6 | 2 | 5 | 4 | 1 | |
| f15 | mean | 2.21 × 102 | 5.23 × 104 | 8.22 × 100 | 2.82 × 101 | 1.87 × 102 | 3.53 × 101 | 9.27 × 100 | 3.87 × 101 | 8.10 × 101 | 1.04 × 101 |
| std | 1.10 × 103 | 9.51 × 104 | 8.21 × 100 | 3.01 × 101 | 2.83 × 102 | 2.64 × 101 | 8.76 × 100 | 3.68 × 101 | 2.45 × 102 | 6.64 × 100 | |
| rank | 9 | 10 | 1 | 4 | 8 | 5 | 2 | 6 | 7 | 3 | |
| f16 | mean | 1.08 × 102 | 7.13 × 102 | 8.31 × 100 | 1.79 × 100 | 2.68 × 100 | 7.49 × 101 | 7.06 × 10−1 | 8.95 × 100 | 7.02 × 10−1 | 5.87 × 10−1 |
| std | 1.23 × 102 | 1.45 × 102 | 3.84 × 101 | 9.90 × 10−1 | 1.36 × 100 | 9.94 × 101 | 4.64 × 10−1 | 2.80 × 101 | 2.44 × 10−1 | 2.39 × 10−1 | |
| rank | 9 | 10 | 6 | 4 | 5 | 8 | 3 | 7 | 2 | 1 | |
| f17 | mean | 5.91 × 101 | 2.36 × 102 | 6.34 × 100 | 2.09 × 100 | 1.84 × 101 | 2.52 × 101 | 2.34 × 100 | 1.38 × 101 | 1.14 × 101 | 2.72 × 100 |
| std | 4.72 × 101 | 8.54 × 101 | 8.85 × 100 | 2.81 × 100 | 8.05 × 100 | 1.89 × 101 | 1.48 × 100 | 1.12 × 101 | 9.41 × 100 | 2.38 × 100 | |
| rank | 9 | 10 | 4 | 1 | 7 | 8 | 2 | 6 | 5 | 3 | |
| f18 | mean | 2.14 × 104 | 7.31 × 108 | 1.41 × 103 | 6.82 × 102 | 2.55 × 103 | 7.93 × 103 | 5.95 × 102 | 3.80 × 103 | 1.95 × 103 | 3.78 × 102 |
| std | 1.78 × 104 | 1.36 × 109 | 2.69 × 103 | 5.84 × 102 | 2.24 × 103 | 6.37 × 103 | 5.40 × 102 | 4.12 × 103 | 2.40 × 103 | 3.77 × 102 | |
| rank | 9 | 10 | 4 | 3 | 6 | 8 | 2 | 7 | 5 | 1 | |
| f19 | mean | 3.26 × 103 | 4.13 × 107 | 3.43 × 100 | 2.44 × 101 | 2.07 × 102 | 5.24 × 101 | 3.47 × 100 | 3.65 × 101 | 6.31 × 101 | 5.89 × 100 |
| std | 9.18 × 103 | 1.10 × 108 | 3.47 × 100 | 3.79 × 101 | 2.95 × 102 | 1.33 × 102 | 6.49 × 100 | 3.89 × 101 | 1.51 × 102 | 6.64 × 100 | |
| rank | 9 | 10 | 1 | 4 | 8 | 6 | 2 | 5 | 7 | 3 | |
| f20 | mean | 5.06 × 101 | 3.26 × 102 | 3.39 × 100 | 1.82 × 10−1 | 4.15 × 100 | 7.07 × 101 | 3.52 × 10−2 | 1.75 × 101 | 2.12 × 100 | 3.06 × 10−2 |
| std | 4.87 × 101 | 6.62 × 101 | 6.83 × 100 | 2.79 × 10−1 | 6.85 × 100 | 6.09 × 101 | 9.63 × 10−2 | 3.21 × 101 | 4.03 × 100 | 9.28 × 10−2 | |
| rank | 8 | 10 | 5 | 3 | 6 | 9 | 2 | 7 | 4 | 1 | |
| f21 | mean | 2.10 × 102 | 3.09 × 102 | 1.59 × 102 | 1.07 × 102 | 1.87 × 102 | 1.85 × 102 | 9.83 × 101 | 1.60 × 102 | 1.23 × 102 | 1.17 × 102 |
| std | 4.01 × 101 | 1.83 × 101 | 5.28 × 101 | 2.07 × 101 | 3.59 × 101 | 4.45 × 101 | 1.39 × 101 | 5.26 × 101 | 4.36 × 101 | 3.83 × 101 | |
| rank | 9 | 10 | 5 | 2 | 8 | 7 | 1 | 6 | 4 | 3 | |
| f22 | mean | 1.79 × 102 | 1.11 × 103 | 9.00 × 101 | 6.59 × 101 | 1.00 × 102 | 9.94 × 101 | 6.63 × 101 | 9.70 × 101 | 9.76 × 101 | 6.93 × 101 |
| std | 2.01 × 102 | 4.48 × 102 | 3.04 × 101 | 3.08 × 101 | 3.20 × 10−1 | 1.41 × 101 | 3.33 × 101 | 1.96 × 101 | 1.50 × 101 | 3.71 × 101 | |
| rank | 9 | 10 | 4 | 1 | 8 | 7 | 2 | 5 | 6 | 3 | |
| f23 | mean | 3.33 × 102 | 4.79 × 102 | 3.07 × 102 | 3.10 × 102 | 3.03 × 102 | 3.04 × 102 | 3.01 × 102 | 3.08 × 102 | 3.05 × 102 | 2.99 × 102 |
| std | 1.17 × 101 | 4.75 × 101 | 2.74 × 100 | 2.82 × 100 | 2.09 × 100 | 4.31 × 101 | 4.27 × 101 | 2.01 × 100 | 1.85 × 100 | 4.23 × 101 | |
| rank | 9 | 10 | 6 | 8 | 3 | 4 | 2 | 7 | 5 | 1 | |
| f24 | mean | 3.57 × 102 | 5.03 × 102 | 3.07 × 102 | 1.01 × 102 | 3.07 × 102 | 3.02 × 102 | 1.03 × 102 | 2.72 × 102 | 2.64 × 102 | 1.61 × 102 |
| std | 5.42 × 101 | 9.03 × 101 | 7.88 × 101 | 2.57 × 101 | 6.32 × 101 | 8.28 × 101 | 3.61 × 101 | 1.02 × 102 | 1.06 × 102 | 1.03 × 102 | |
| rank | 9 | 10 | 8 | 1 | 7 | 6 | 2 | 5 | 4 | 3 | |
| f25 | mean | 4.57 × 102 | 1.28 × 103 | 4.30 × 102 | 1.98 × 102 | 4.35 × 102 | 4.26 × 102 | 3.67 × 102 | 4.12 × 102 | 4.15 × 102 | 3.99 × 102 |
| std | 4.53 × 101 | 3.22 × 102 | 2.21 × 101 | 9.96 × 101 | 1.92 × 101 | 2.28 × 101 | 8.76 × 101 | 2.09 × 101 | 2.22 × 101 | 6.29 × 100 | |
| rank | 9 | 10 | 7 | 1 | 8 | 6 | 2 | 4 | 5 | 3 | |
| f26 | mean | 6.07 × 102 | 1.83 × 103 | 3.15 × 102 | 1.29 × 102 | 2.88 × 102 | 3.15 × 102 | 1.25 × 102 | 3.00 × 102 | 3.00 × 102 | 2.41 × 102 |
| std | 3.18 × 102 | 3.53 × 102 | 1.26 × 102 | 9.78 × 101 | 3.22 × 101 | 1.26 × 102 | 1.23 × 102 | 0.00 × 100 | 3.58 × 10−13 | 1.19 × 102 | |
| rank | 9 | 10 | 7 | 2 | 4 | 8 | 1 | 5 | 6 | 3 | |
| f27 | mean | 4.16 × 102 | 7.74 × 102 | 3.93 × 102 | 3.93 × 102 | 3.94 × 102 | 3.98 × 102 | 3.92 × 102 | 3.71 × 102 | 3.93 × 102 | 3.91 × 102 |
| std | 2.87 × 101 | 2.50 × 102 | 6.14 × 100 | 6.60 × 100 | 2.21 × 100 | 1.20 × 101 | 2.02 × 100 | 4.26 × 10−1 | 2.66 × 100 | 2.26 × 100 | |
| rank | 9 | 10 | 6 | 4 | 7 | 8 | 3 | 1 | 5 | 2 | |
| f28 | mean | 5.69 × 102 | 1.06 × 103 | 3.48 × 102 | 2.63 × 102 | 4.62 × 102 | 4.97 × 102 | 2.77 × 102 | 4.37 × 102 | 3.00 × 102 | 2.88 × 102 |
| std | 1.35 × 102 | 5.91 × 101 | 1.23 × 102 | 9.49 × 101 | 1.44 × 102 | 1.42 × 102 | 8.63 × 101 | 5.83 × 101 | 4.02 × 10−13 | 5.82 × 101 | |
| rank | 9 | 10 | 5 | 1 | 7 | 8 | 2 | 6 | 4 | 3 | |
| f29 | mean | 3.31 × 102 | 6.90 × 102 | 2.53 × 102 | 2.62 × 102 | 2.56 × 102 | 2.65 × 102 | 2.54 × 102 | 2.55 × 102 | 2.47 × 102 | 2.44 × 102 |
| std | 7.20 × 101 | 1.15 × 102 | 1.68 × 101 | 1.31 × 101 | 9.81 × 100 | 2.06 × 101 | 8.87 × 100 | 1.42 × 101 | 6.90 × 100 | 6.13 × 100 | |
| rank | 9 | 10 | 3 | 7 | 6 | 8 | 4 | 5 | 2 | 1 | |
| f30 | mean | 8.15 × 105 | 3.15 × 107 | 5.36 × 104 | 7.29 × 103 | 9.08 × 104 | 5.66 × 105 | 4.93 × 103 | 2.38 × 103 | 1.90 × 104 | 2.29 × 103 |
| std | 9.41 × 105 | 3.27 × 107 | 1.92 × 105 | 9.81 × 103 | 2.64 × 105 | 8.65 × 105 | 4.08 × 103 | 3.52 × 103 | 1.15 × 105 | 1.25 × 103 | |
| rank | 9 | 10 | 6 | 4 | 7 | 8 | 3 | 1 | 5 | 1 | |
| Ave rank | 8.62 | 8.62 | 9.93 | 4.28 | 4.14 | 5.69 | 6.72 | 3.07 | 5.12 | 4.41 | |
| Final rank | 8 | 8 | 10 | 4 | 3 | 7 | 9 | 2 | 6 | 5 | |
The best experimental result is shown in bold.
Appendix B

Table A2.
Comparison of experimental results for 30-dimensional problems.
Table A2.
Comparison of experimental results for 30-dimensional problems.
| GPSO | FIPS | CLPSO | CCPSO-ISM | XPSO | TSLPSO | DMS-PSO | PSO-DLS | HCLDMS-PSO | MLDMS-PSO | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| f1 | mean | 8.63 × 109 | 6.48 × 1010 | 1.56 × 103 | 3.12 × 101 | 4.13 × 103 | 2.33× 101 | 5.59 × 103 | 2.60 × 103 | 1.31 × 103 | 5.64 × 102 |
| std | 6.54 × 109 | 7.88 × 109 | 2.54 × 103 | 7.39 × 101 | 4.33 × 103 | 2.66 × 101 | 6.55 × 103 | 2.80 × 103 | 1.72 × 103 | 7.93 × 102 | |
| rank | 9 | 10 | 4 | 2 | 7 | 1 | 8 | 6 | 4 | 3 | |
| f3 | mean | 2.58 × 103 | 3.91 × 106 | 2.44 × 103 | 1.82 × 104 | 1.94 × 10−3 | 2.39 × 101 | 9.26 × 102 | 2.26 × 101 | 3.89 × 101 | 4.86 × 102 |
| std | 9.73 × 103 | 1.98 × 107 | 1.13 × 103 | 4.66 × 103 | 9.62 × 10−3 | 1.02 × 102 | 3.06 × 102 | 2.93 × 101 | 6.68 × 101 | 2.03 × 102 | |
| rank | 8 | 10 | 7 | 9 | 1 | 3 | 6 | 2 | 4 | 5 | |
| f4 | mean | 1.19 × 103 | 1.66 × 104 | 9.37 × 101 | 4.75 × 101 | 1.20 × 102 | 4.60 × 101 | 2.66 × 101 | 5.43 × 101 | 7.65 × 101 | 9.34 × 101 |
| std | 1.30 × 103 | 3.77 × 103 | 1.78 × 101 | 2.92 × 101 | 3.25 × 101 | 3.51 × 101 | 7.86 × 100 | 2.98 × 101 | 2.76 × 101 | 2.02 × 101 | |
| rank | 9 | 10 | 7 | 3 | 8 | 2 | 1 | 4 | 5 | 6 | |
| f5 | mean | 1.45 × 102 | 4.53 × 102 | 3.79 × 101 | 5.09 × 101 | 4.67 × 101 | 4.74 × 101 | 4.13 × 101 | 2.21 × 101 | 2.88 × 101 | 3.28 × 101 |
| std | 3.99 × 101 | 2.50 × 101 | 1.00 × 101 | 8.18 × 100 | 1.29 × 101 | 1.15 × 101 | 1.08 × 101 | 5.48 × 100 | 6.69 × 100 | 1.38 × 101 | |
| rank | 9 | 10 | 4 | 8 | 6 | 7 | 5 | 1 | 2 | 3 | |
| f6 | mean | 1.58 × 101 | 9.83 × 101 | 3.01 × 10−8 | 1.14 × 10−13 | 7.57 × 10−2 | 1.41 × 10−8 | 5.54 × 10−4 | 1.04 × 10−3 | 1.04 × 10−3 | 2.85 × 10−13 |
| std | 7.07 × 100 | 6.33 × 100 | 1.54 × 10−7 | 0.00 × 100 | 2.35 × 10−1 | 9.98 × 10−8 | 1.01 × 10−3 | 2.40 × 10−3 | 1.36 × 10−3 | 1.75 × 10−13 | |
| rank | 9 | 10 | 4 | 1 | 8 | 3 | 5 | 6 | 7 | 2 | |
| f7 | mean | 2.12 × 102 | 8.56 × 102 | 7.79 × 101 | 7.74 × 101 | 9.05 × 101 | 8.46 × 101 | 1.13 × 102 | 5.21 × 101 | 5.59 × 101 | 6.75 × 101 |
| std | 1.21 × 102 | 4.77 × 101 | 1.21 × 101 | 8.40 × 100 | 1.87 × 101 | 1.06 × 101 | 2.12 × 101 | 5.65 × 100 | 5.99 × 100 | 1.23 × 101 | |
| rank | 9 | 10 | 5 | 4 | 7 | 6 | 8 | 1 | 2 | 3 | |
| f8 | mean | 1.40 × 102 | 3.78 × 102 | 3.72 × 101 | 6.25 × 101 | 4.43 × 101 | 6.18 × 101 | 4.06 × 101 | 2.27 × 101 | 2.85 × 101 | 3.24 × 101 |
| std | 3.76 × 101 | 2.55 × 101 | 1.14 × 101 | 9.95 × 100 | 1.57 × 101 | 1.14 × 101 | 9.73 × 100 | 5.39 × 100 | 6.31 × 100 | 1.19 × 101 | |
| rank | 9 | 10 | 4 | 8 | 6 | 7 | 5 | 1 | 2 | 3 | |
| f9 | mean | 2.25 × 103 | 1.30 × 104 | 2.30 × 10−2 | 1.70 × 102 | 8.02 × 100 | 1.12 × 102 | 2.12 × 100 | 1.52 × 100 | 1.24 × 10−2 | 1.90 × 10−1 |
| std | 1.38 × 103 | 1.52 × 103 | 6.91 × 10−2 | 1.23 × 102 | 6.27 × 100 | 1.92 × 102 | 1.82 × 100 | 1.24 × 100 | 6.49 × 10−2 | 2.34 × 10−1 | |
| rank | 9 | 10 | 2 | 8 | 6 | 7 | 5 | 4 | 1 | 3 | |
| f10 | mean | 3.87 × 103 | 8.13 × 103 | 2.93 × 103 | 2.43 × 103 | 2.77 × 103 | 2.45 × 103 | 2.77 × 103 | 2.79 × 103 | 2.32 × 103 | 3.05 × 103 |
| std | 6.39 × 102 | 4.41 × 102 | 6.94 × 102 | 3.56 × 102 | 5.73 × 102 | 5.03 × 102 | 4.98 × 102 | 3.61 × 102 | 3.77 × 102 | 6.07 × 102 | |
| rank | 9 | 10 | 7 | 2 | 4 | 3 | 5 | 6 | 1 | 8 | |
| f11 | mean | 3.28 × 102 | 8.35 × 103 | 4.72 × 101 | 3.54 × 101 | 9.19 × 101 | 4.89 × 101 | 3.04 × 101 | 3.87 × 101 | 3.80 × 101 | 3.14 × 101 |
| std | 2.71 × 102 | 3.18 × 103 | 2.70 × 101 | 1.85 × 101 | 4.35 × 101 | 2.59 × 101 | 7.92 × 100 | 2.83 × 101 | 1.57 × 101 | 2.79 × 101 | |
| rank | 9 | 10 | 6 | 3 | 8 | 7 | 1 | 5 | 4 | 2 | |
| f12 | mean | 6.41 × 108 | 1.73 × 1010 | 2.07 × 105 | 2.67 × 105 | 1.07 × 105 | 2.94 × 104 | 2.30 × 105 | 2.11 × 104 | 8.62 × 104 | 3.70 × 104 |
| std | 9.68 × 108 | 3.62 × 109 | 2.09 × 105 | 1.72 × 105 | 2.49 × 105 | 1.58 × 104 | 1.89 × 105 | 1.05 × 104 | 7.00 × 104 | 1.54 × 104 | |
| rank | 9 | 10 | 6 | 8 | 5 | 2 | 7 | 1 | 4 | 3 | |
| f13 | mean | 1.44 × 108 | 1.12 × 1010 | 1.00 × 104 | 7.23 × 102 | 1.33 × 104 | 3.23 × 103 | 1.80 × 104 | 1.34 × 104 | 4.68 × 103 | 7.81 × 103 |
| std | 4.62 × 108 | 7.69 × 109 | 9.38 × 103 | 3.61 × 102 | 1.27 × 104 | 4.61 × 103 | 1.99 × 104 | 1.01 × 104 | 4.69 × 103 | 6.37 × 103 | |
| rank | 9 | 10 | 5 | 1 | 6 | 2 | 8 | 7 | 3 | 4 | |
| f14 | mean | 5.16 × 104 | 1.65 × 107 | 1.26 × 104 | 2.44 × 104 | 4.09 × 103 | 1.10 × 104 | 3.16 × 103 | 5.44 × 103 | 3.41 × 103 | 2.33 × 103 |
| std | 8.91 × 104 | 1.69 × 107 | 1.13 × 104 | 2.08 × 104 | 4.01 × 103 | 9.77 × 103 | 2.49 × 103 | 4.85 × 103 | 4.84 × 103 | 1.81 × 103 | |
| rank | 9 | 10 | 7 | 8 | 4 | 6 | 2 | 5 | 3 | 1 | |
| f15 | mean | 5.11 × 104 | 1.89 × 109 | 4.79 × 102 | 1.47 × 102 | 6.09 × 103 | 3.03 × 102 | 5.36 × 103 | 2.63 × 103 | 1.56 × 103 | 1.91 × 103 |
| std | 5.25 × 104 | 1.23 × 109 | 3.77 × 102 | 9.05 × 101 | 8.20 × 103 | 3.54 × 102 | 7.71 × 103 | 3.48 × 103 | 2.09 × 103 | 2.24 × 103 | |
| rank | 9 | 10 | 3 | 1 | 8 | 2 | 7 | 6 | 4 | 5 | |
| f16 | mean | 1.28 × 103 | 6.03 × 103 | 3.58 × 102 | 5.17 × 102 | 6.24 × 102 | 5.57 × 102 | 3.25 × 102 | 3.91 × 102 | 3.36 × 102 | 2.45 × 102 |
| std | 3.87 × 102 | 1.58 × 103 | 1.48 × 102 | 1.65 × 102 | 1.73 × 102 | 1.33 × 102 | 1.94 × 102 | 1.55 × 102 | 1.80 × 102 | 1.36 × 102 | |
| rank | 9 | 10 | 4 | 6 | 8 | 7 | 2 | 5 | 3 | 1 | |
| f17 | mean | 6.23 × 102 | 1.42 × 104 | 9.75 × 101 | 1.23 × 102 | 1.44 × 102 | 1.37 × 102 | 1.05 × 102 | 9.34 × 101 | 7.01 × 101 | 6.43 × 101 |
| std | 2.84 × 102 | 3.13 × 104 | 4.25 × 101 | 6.74 × 101 | 7.74 × 101 | 8.21 × 101 | 5.97 × 101 | 4.70 × 101 | 3.55 × 101 | 3.03 × 101 | |
| rank | 9 | 10 | 4 | 6 | 8 | 7 | 5 | 3 | 2 | 1 | |
| f18 | mean | 5.13 × 105 | 1.30 × 108 | 1.44 × 105 | 1.30 × 105 | 1.35 × 105 | 1.09 × 105 | 1.65 × 105 | 1.65 × 105 | 1.10 × 105 | 1.32 × 105 |
| std | 1.58 × 106 | 2.88 × 108 | 7.50 × 104 | 4.87 × 104 | 8.81 × 104 | 5.82 × 104 | 9.31 × 104 | 1.36 × 105 | 6.91 × 104 | 7.51 × 104 | |
| rank | 9 | 10 | 6 | 3 | 5 | 1 | 7 | 8 | 2 | 4 | |
| f19 | mean | 1.19 × 107 | 1.73 × 109 | 2.71 × 102 | 6.98 × 101 | 6.27 × 103 | 1.71 × 102 | 6.13 × 103 | 4.39 × 103 | 3.54 × 103 | 3.45 × 103 |
| std | 3.60 × 107 | 8.62 × 108 | 4.10 × 102 | 4.58 × 101 | 7.33 × 103 | 3.08 × 102 | 6.60 × 103 | 4.22 × 103 | 5.14 × 103 | 3.86 × 103 | |
| rank | 9 | 10 | 3 | 1 | 8 | 2 | 7 | 6 | 5 | 4 | |
| f20 | mean | 5.14 × 102 | 1.21 × 103 | 1.52 × 102 | 2.19 × 102 | 1.88 × 102 | 1.70 × 102 | 1.47 × 102 | 1.72 × 102 | 1.50 × 102 | 1.33 × 102 |
| std | 1.78 × 102 | 1.52 × 102 | 6.63 × 101 | 9.08 × 101 | 7.86 × 101 | 8.09 × 101 | 6.29 × 101 | 5.92 × 101 | 7.07 × 101 | 5.62 × 101 | |
| rank | 9 | 10 | 4 | 8 | 7 | 5 | 2 | 6 | 3 | 1 | |
| f21 | mean | 3.68 × 102 | 7.08 × 102 | 2.41 × 102 | 2.37 × 102 | 2.43 × 102 | 2.31 × 102 | 2.43 × 102 | 2.23 × 102 | 2.29 × 102 | 2.29 × 102 |
| std | 5.00 × 101 | 5.24 × 101 | 9.69 × 100 | 4.63 × 101 | 1.08 × 101 | 4.84 × 101 | 1.19 × 101 | 5.16 × 100 | 5.95 × 100 | 9.38 × 100 | |
| rank | 9 | 10 | 6 | 5 | 7 | 4 | 8 | 1 | 3 | 2 | |
| f22 | mean | 3.20 × 103 | 7.09 × 103 | 1.00 × 102 | 2.19 × 102 | 4.28 × 102 | 3.50 × 102 | 1.59 × 102 | 1.01 × 102 | 1.00 × 102 | 1.00 × 102 |
| std | 1.55 × 103 | 7.41 × 102 | 1.42 × 10−6 | 5.63 × 102 | 9.96 × 102 | 7.65 × 102 | 4.14 × 102 | 1.26 × 100 | 1.71 × 10−10 | 3.12 × 10−13 | |
| rank | 9 | 10 | 3 | 6 | 8 | 7 | 5 | 4 | 2 | 1 | |
| f23 | mean | 6.40 × 102 | 1.78 × 103 | 3.86 × 102 | 4.01 × 102 | 3.98 × 102 | 4.02 × 102 | 4.01 × 102 | 3.66 × 102 | 3.76 × 102 | 3.73 × 102 |
| std | 7.11 × 101 | 2.49 × 102 | 1.17 × 101 | 1.14 × 101 | 1.54 × 101 | 1.30 × 101 | 1.37 × 101 | 9.98 × 100 | 8.36 × 100 | 1.00 × 101 | |
| rank | 9 | 10 | 4 | 7 | 5 | 8 | 6 | 1 | 3 | 2 | |
| f24 | mean | 7.64 × 102 | 2.04 × 103 | 4.73 × 102 | 4.59 × 102 | 4.76 × 102 | 4.52 × 102 | 4.73 × 102 | 4.35 × 102 | 4.44 × 102 | 4.40 × 102 |
| std | 9.78 × 101 | 3.16 × 102 | 1.42 × 101 | 9.87 × 101 | 3.65 × 101 | 1.11 × 102 | 7.24 × 100 | 7.36 × 100 | 8.23 × 100 | 7.74 × 100 | |
| rank | 9 | 10 | 6 | 5 | 8 | 4 | 7 | 1 | 3 | 2 | |
| f25 | mean | 5.76 × 102 | 3.15 × 103 | 3.87 × 102 | 3.87 × 102 | 3.94 × 102 | 3.87 × 102 | 3.79 × 102 | 3.90 × 102 | 3.87 × 102 | 3.87 × 102 |
| std | 2.63 × 102 | 7.07 × 102 | 9.06 × 10−1 | 1.14 × 100 | 1.02 × 101 | 1.18 × 100 | 2.97 × 10−1 | 8.43 × 100 | 6.39 × 10−1 | 7.65 × 10−1 | |
| rank | 9 | 10 | 6 | 2 | 8 | 4 | 1 | 7 | 3 | 5 | |
| f26 | mean | 3.93 × 103 | 9.27 × 103 | 1.27 × 103 | 4.32 × 102 | 8.78 × 102 | 7.38 × 102 | 1.26 × 103 | 8.27 × 102 | 1.17 × 103 | 1.03 × 103 |
| std | 7.99 × 102 | 9.71 × 102 | 2.79 × 102 | 3.40 × 102 | 5.91 × 102 | 6.39 × 102 | 5.10 × 102 | 4.36 × 102 | 3.00 × 102 | 3.27 × 102 | |
| rank | 9 | 10 | 8 | 1 | 4 | 2 | 7 | 3 | 6 | 5 | |
| f27 | mean | 6.44 × 102 | 2.60 × 103 | 5.05 × 102 | 5.14 × 102 | 5.28 × 102 | 5.15 × 102 | 4.85 × 102 | 5.19 × 102 | 5.15 × 102 | 5.04 × 102 |
| std | 6.72 × 101 | 4.08 × 102 | 5.33 × 100 | 4.19 × 100 | 1.51 × 101 | 8.02 × 100 | 2.76 × 101 | 6.63 × 100 | 8.26 × 100 | 5.28 × 100 | |
| rank | 9 | 10 | 3 | 4 | 8 | 6 | 1 | 7 | 5 | 2 | |
| f28 | mean | 1.15 × 103 | 5.38 × 103 | 4.06 × 102 | 4.05 × 102 | 3.78 × 102 | 3.68 × 102 | 4.37 × 102 | 3.49 × 102 | 3.66 × 102 | 3.77 × 102 |
| std | 7.55 × 102 | 8.04 × 102 | 2.06 × 101 | 3.40 × 100 | 6.86 × 101 | 6.37 × 101 | 2.54 × 101 | 4.97 × 101 | 4.62 × 101 | 4.37 × 101 | |
| rank | 9 | 10 | 7 | 6 | 5 | 3 | 8 | 1 | 2 | 4 | |
| f29 | mean | 1.21 × 103 | 1.09 × 104 | 5.42 × 102 | 5.59 × 102 | 6.18 × 102 | 5.87 × 102 | 4.91 × 102 | 5.07 × 102 | 4.92 × 102 | 4.85 × 102 |
| std | 3.44 × 102 | 1.05 × 104 | 5.84 × 101 | 5.43 × 101 | 1.32 × 102 | 8.19 × 101 | 8.08 × 101 | 5.57 × 101 | 3.16 × 101 | 3.22 × 101 | |
| rank | 9 | 10 | 5 | 6 | 8 | 7 | 2 | 4 | 3 | 1 | |
| f30 | mean | 2.65 × 107 | 2.29 × 109 | 8.56 × 103 | 5.45 × 103 | 1.04 × 104 | 9.39 × 103 | 3.22 × 103 | 4.06 × 103 | 4.11 × 103 | 3.04 × 103 |
| std | 1.53 × 108 | 1.34 × 109 | 4.43 × 103 | 1.56 × 103 | 6.84 × 103 | 9.41 × 103 | 4.62 × 103 | 9.37 × 102 | 1.32 × 103 | 8.50 × 102 | |
| rank | 9 | 10 | 6 | 5 | 8 | 7 | 2 | 3 | 4 | 1 | |
| Ave rank | 8.97 | 8.97 | 10.00 | 5.03 | 4.72 | 6.52 | 4.55 | 4.93 | 3.97 | 3.28 | |
| Final rank | 9 | 9 | 10 | 7 | 5 | 8 | 4 | 6 | 3 | 2 | |
The best experimental result is shown in bold.
Appendix C

Table A3.
Comparison of experimental results for 50-dimensional problems.
Table A3.
Comparison of experimental results for 50-dimensional problems.
| GPSO | FIPS | CLPSO | CCPSO-ISM | XPSO | TSLPSO | DMS-PSO | PSO-DLS | HCLDMS-PSO | MLDMS-PSO | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| f1 | mean | 2.39 × 1010 | 1.22 × 1011 | 3.02 × 103 | 1.24E× 102 | 4.85 × 103 | 8.21 × 102 | 6.83 × 103 | 2.35 × 103 | 2.54 × 103 | 1.74 × 103 |
| std | 1.48 × 1010 | 8.22 × 109 | 3.45 × 103 | 1.70 × 102 | 6.09 × 103 | 8.66 × 102 | 9.08 × 103 | 2.39 × 103 | 3.69 × 103 | 1.82 × 103 | |
| rank | 9 | 10 | 6 | 1 | 7 | 2 | 8 | 4 | 5 | 3 | |
| f3 | mean | 2.36 × 104 | 1.96 × 105 | 1.17 × 104 | 4.99 × 104 | 1.36 × 102 | 8.22 × 103 | 6.83 × 103 | 8.35 × 103 | 5.62 × 103 | 6.22 × 103 |
| std | 3.28 × 104 | 3.50 × 104 | 2.55 × 103 | 6.55 × 103 | 1.27 × 102 | 5.71 × 103 | 1.48 × 103 | 3.09 × 103 | 2.55 × 103 | 1.34 × 103 | |
| rank | 8 | 10 | 7 | 9 | 1 | 5 | 4 | 6 | 2 | 3 | |
| f4 | mean | 2.78 × 103 | 4.42 × 104 | 1.08 × 102 | 5.75 × 101 | 2.36 × 102 | 7.33 × 101 | 4.58 × 101 | 1.07 × 102 | 9.90 × 101 | 9.80 × 101 |
| std | 1.86 × 103 | 6.77 × 103 | 4.17 × 101 | 2.84 × 101 | 4.70 × 101 | 4.72 × 101 | 1.13 × 100 | 5.01 × 101 | 4.52 × 101 | 3.97 × 101 | |
| rank | 9 | 10 | 7 | 2 | 8 | 3 | 1 | 6 | 5 | 4 | |
| f5 | mean | 3.04 × 102 | 7.56 × 102 | 9.11 × 101 | 1.12 × 102 | 8.87 × 101 | 1.28 × 102 | 1.02 × 102 | 5.84 × 101 | 5.86 × 101 | 1.06 × 102 |
| std | 8.41 × 101 | 3.99 × 101 | 1.97 × 101 | 1.82 × 101 | 2.32 × 101 | 2.81 × 101 | 1.65 × 101 | 1.19 × 101 | 9.82 × 100 | 5.37 × 101 | |
| rank | 9 | 10 | 4 | 7 | 3 | 8 | 5 | 1 | 2 | 6 | |
| f6 | mean | 3.33 × 101 | 1.07 × 102 | 2.18 × 10−8 | 9.40 × 10−10 | 1.28 × 100 | 9.79 × 10−9 | 4.33 × 10−1 | 1.51 × 10−2 | 1.00 × 10−2 | 3.36 × 10−13 |
| std | 8.69 × 100 | 4.40 × 100 | 7.56 × 10−8 | 6.65 × 10−9 | 1.35 × 100 | 6.28 × 10−8 | 4.29 × 10−1 | 1.58 × 10−2 | 5.22 × 10−3 | 1.68 × 10−13 | |
| rank | 9 | 10 | 4 | 2 | 8 | 3 | 7 | 6 | 5 | 1 | |
| f7 | mean | 6.72 × 102 | 1.48 × 103 | 1.73 × 102 | 1.53 × 102 | 1.88 × 102 | 1.82 × 102 | 2.50 × 102 | 1.15 × 102 | 1.04 × 102 | 1.46 × 102 |
| std | 2.74 × 102 | 3.08 × 101 | 2.74 × 101 | 1.80 × 101 | 2.46 × 101 | 2.26 × 101 | 5.32 × 101 | 1.30 × 101 | 9.66 × 100 | 3.37 × 101 | |
| rank | 9 | 10 | 5 | 4 | 7 | 6 | 8 | 2 | 1 | 3 | |
| f8 | mean | 3.22 × 102 | 7.55 × 102 | 8.86 × 101 | 1.11 × 102 | 9.46 × 101 | 1.34 × 102 | 9.81 × 101 | 6.47 × 101 | 6.59 × 101 | 1.07 × 102 |
| std | 6.47 × 101 | 5.41 × 101 | 1.68 × 101 | 1.96 × 101 | 2.26 × 101 | 2.53 × 101 | 1.96 × 101 | 1.14 × 101 | 1.03 × 101 | 4.40 × 101 | |
| rank | 9 | 10 | 3 | 7 | 4 | 8 | 5 | 1 | 2 | 6 | |
| f9 | mean | 8.78 × 103 | 4.40 × 104 | 2.88 × 10−1 | 1.33 × 103 | 1.43 × 102 | 1.78 × 103 | 7.91 × 101 | 2.04 × 101 | 1.53 × 10−1 | 3.08 × 100 |
| std | 2.60 × 103 | 3.75 × 103 | 2.95 × 10−1 | 9.20 × 102 | 9.22 × 101 | 1.61 × 103 | 5.01 × 101 | 1.40 × 101 | 2.52 × 10−1 | 1.80 × 100 | |
| rank | 9 | 10 | 2 | 7 | 6 | 8 | 5 | 4 | 1 | 3 | |
| f10 | mean | 7.05 × 103 | 1.44 × 104 | 5.57 × 103 | 4.91 × 103 | 5.17 × 103 | 5.00 × 103 | 5.47 × 103 | 5.29 × 103 | 4.45 × 103 | 5.47 × 103 |
| std | 9.68 × 102 | 5.41 × 102 | 9.12 × 102 | 6.76 × 102 | 9.45 × 102 | 7.87 × 102 | 6.30 × 102 | 7.48 × 102 | 6.07 × 102 | 6.69 × 102 | |
| rank | 9 | 10 | 8 | 2 | 4 | 3 | 7 | 5 | 1 | 6 | |
| f11 | mean | 1.51 × 103 | 2.43 × 104 | 8.64 × 101 | 9.82 × 101 | 2.02 × 102 | 1.33 × 102 | 1.04 × 102 | 8.52 × 101 | 1.07 × 102 | 5.44 × 101 |
| std | 3.47 × 103 | 2.41 × 103 | 2.40 × 101 | 2.05 × 101 | 4.19 × 101 | 3.85 × 101 | 2.76 × 101 | 4.32 × 101 | 3.29 × 101 | 1.50 × 101 | |
| rank | 9 | 10 | 3 | 4 | 8 | 7 | 5 | 2 | 6 | 1 | |
| f12 | mean | 8.79 × 109 | 9.58 × 1010 | 1.49 × 106 | 1.63 × 106 | 1.71 × 106 | 4.58 × 105 | 1.69 × 106 | 3.13 × 105 | 7.95 × 105 | 6.28 × 105 |
| std | 6.23 × 109 | 1.34 × 1010 | 7.80 × 105 | 6.13 × 105 | 2.53 × 106 | 3.33 × 105 | 1.08 × 106 | 1.42 × 105 | 5.44 × 105 | 2.35 × 105 | |
| rank | 9 | 10 | 5 | 6 | 8 | 2 | 7 | 1 | 4 | 3 | |
| f13 | mean | 3.23 × 109 | 5.26 × 1010 | 3.08 × 103 | 1.63 × 103 | 6.80 × 103 | 5.87 × 103 | 5.62 × 103 | 1.40 × 103 | 1.79 × 103 | 1.08 × 103 |
| std | 4.88 × 109 | 1.46 × 1010 | 3.44 × 103 | 1.21 × 103 | 6.55 × 103 | 6.50 × 103 | 8.32 × 103 | 1.29 × 103 | 2.18 × 103 | 1.19 × 103 | |
| rank | 9 | 10 | 5 | 3 | 8 | 7 | 6 | 2 | 4 | 1 | |
| f14 | mean | 1.42 × 106 | 2.18 × 108 | 1.06 × 105 | 2.22 × 105 | 3.33 × 104 | 5.52 × 104 | 6.30 × 104 | 3.05 × 104 | 2.60 × 104 | 2.44 × 104 |
| std | 2.56 × 106 | 1.81 × 108 | 7.23 × 104 | 1.02 × 105 | 3.47 × 104 | 5.21 × 104 | 3.70 × 104 | 1.84 × 104 | 1.88 × 104 | 1.60 × 104 | |
| rank | 9 | 10 | 7 | 8 | 4 | 5 | 6 | 3 | 2 | 1 | |
| f15 | mean | 4.95 × 107 | 1.27 × 1010 | 1.62 × 103 | 4.03 × 102 | 5.22 × 103 | 1.39 × 103 | 7.39 × 103 | 4.22 × 103 | 2.40 × 103 | 2.56 × 103 |
| std | 1.84 × 108 | 4.95 × 109 | 2.41 × 103 | 1.56 × 102 | 4.76 × 103 | 3.19 × 103 | 7.41 × 103 | 3.10 × 103 | 2.82 × 103 | 1.93 × 103 | |
| rank | 9 | 10 | 3 | 1 | 7 | 2 | 8 | 6 | 4 | 5 | |
| f16 | mean | 2.39 × 103 | 1.01 × 104 | 9.52 × 102 | 1.06 × 103 | 1.06 × 103 | 1.19 × 103 | 5.98 × 102 | 6.64 × 102 | 7.10 × 102 | 5.72 × 102 |
| std | 5.33 × 102 | 1.58 × 103 | 2.12 × 102 | 2.15 × 102 | 3.30 × 102 | 2.48 × 102 | 2.74 × 102 | 1.96 × 102 | 2.18 × 102 | 1.81 × 102 | |
| rank | 9 | 10 | 5 | 6 | 7 | 8 | 2 | 3 | 4 | 1 | |
| f17 | mean | 1.96 × 103 | 2.61 × 104 | 6.40 × 102 | 7.62 × 102 | 9.14 × 102 | 7.46 × 102 | 6.69 × 102 | 5.79 × 102 | 5.74 × 102 | 4.62 × 102 |
| std | 4.27 × 102 | 2.38 × 104 | 1.51 × 102 | 1.44 × 102 | 2.56 × 102 | 1.66 × 102 | 1.79 × 102 | 1.65 × 102 | 1.75 × 102 | 1.24 × 102 | |
| rank | 9 | 10 | 4 | 7 | 8 | 6 | 5 | 3 | 2 | 1 | |
| f18 | mean | 4.74 × 106 | 3.16 × 108 | 6.96 × 105 | 5.87 × 105 | 3.45 × 105 | 2.33 × 105 | 5.72 × 105 | 2.60 × 105 | 4.61 × 105 | 5.83 × 105 |
| std | 1.68 × 107 | 2.10 × 108 | 4.36 × 105 | 3.64 × 105 | 6.40 × 105 | 2.41 × 105 | 3.08 × 105 | 2.43 × 105 | 9.77 × 105 | 2.73 × 105 | |
| rank | 9 | 10 | 8 | 7 | 3 | 1 | 5 | 2 | 4 | 6 | |
| f19 | mean | 1.21 × 108 | 5.79 × 109 | 2.10 × 103 | 5.52 × 102 | 1.79 × 104 | 1.25 × 103 | 1.48 × 104 | 1.31 × 104 | 6.59 × 103 | 1.24 × 104 |
| std | 3.54 × 108 | 2.15 × 109 | 2.28 × 103 | 7.02 × 102 | 1.04 × 104 | 2.31 × 103 | 1.07 × 104 | 6.13 × 103 | 6.25 × 103 | 4.97 × 103 | |
| rank | 9 | 10 | 3 | 1 | 8 | 2 | 7 | 6 | 4 | 5 | |
| f20 | mean | 1.20 × 103 | 2.32 × 103 | 4.52 × 102 | 5.96 × 102 | 4.32 × 102 | 6.20 × 102 | 3.37 × 102 | 3.77 × 102 | 3.67 × 102 | 1.94 × 102 |
| std | 3.71 × 102 | 2.15 × 102 | 1.46 × 102 | 1.51 × 102 | 2.32 × 102 | 1.50 × 102 | 1.39 × 102 | 1.60 × 102 | 1.35 × 102 | 7.78 × 101 | |
| rank | 9 | 10 | 6 | 7 | 5 | 8 | 2 | 4 | 3 | 1 | |
| f21 | mean | 5.48 × 102 | 1.22 × 103 | 2.91 × 102 | 3.07 × 102 | 2.90 × 102 | 3.29 × 102 | 3.04 × 102 | 2.61 × 102 | 2.62 × 102 | 2.81 × 102 |
| std | 7.64 × 101 | 1.14 × 102 | 2.00 × 101 | 2.59 × 101 | 1.88 × 101 | 2.65 × 101 | 1.82 × 101 | 1.29 × 101 | 9.47 × 100 | 2.98 × 101 | |
| rank | 9 | 10 | 5 | 7 | 4 | 8 | 6 | 1 | 2 | 3 | |
| f22 | mean | 7.73 × 103 | 1.49 × 104 | 5.66 × 103 | 4.77 × 103 | 3.80 × 103 | 4.71 × 103 | 4.08 × 103 | 3.27 × 103 | 3.33 × 103 | 3.78 × 103 |
| std | 1.36 × 103 | 4.89 × 102 | 1.57 × 103 | 2.23 × 103 | 2.70 × 103 | 2.20 × 103 | 2.64 × 103 | 2.65 × 103 | 2.35 × 103 | 3.12 × 103 | |
| rank | 9 | 10 | 8 | 7 | 4 | 6 | 5 | 1 | 2 | 3 | |
| f23 | mean | 1.21 × 103 | 2.51 × 103 | 5.24 × 102 | 5.49 × 102 | 5.34 × 102 | 5.69 × 102 | 5.40 × 102 | 4.84 × 102 | 4.98 × 102 | 5.07 × 102 |
| std | 1.76 × 102 | 2.07 × 102 | 1.89 × 101 | 1.93 × 101 | 2.98 × 101 | 3.69 × 101 | 2.51 × 101 | 1.84 × 101 | 1.92 × 101 | 2.71 × 101 | |
| rank | 9 | 10 | 4 | 7 | 5 | 8 | 6 | 1 | 2 | 3 | |
| f24 | mean | 1.24 × 103 | 3.52 × 103 | 6.11 × 102 | 6.81 × 102 | 6.47 × 102 | 6.94 × 102 | 6.14 × 102 | 5.41 × 102 | 5.63 × 102 | 5.51 × 102 |
| std | 1.50 × 102 | 5.02 × 102 | 2.40 × 101 | 2.45 × 101 | 8.87 × 101 | 3.67 × 101 | 1.31 × 101 | 1.39 × 101 | 1.38 × 101 | 1.57 × 101 | |
| rank | 9 | 10 | 4 | 7 | 6 | 8 | 5 | 1 | 3 | 2 | |
| f25 | mean | 1.63 × 103 | 1.48 × 104 | 5.26 × 102 | 5.41 × 102 | 5.98 × 102 | 5.36 × 102 | 4.31 × 102 | 5.54 × 102 | 5.04 × 102 | 5.22 × 102 |
| std | 1.22 × 103 | 1.59 × 103 | 3.37 × 101 | 1.84 × 101 | 3.17 × 101 | 3.45 × 101 | 1.34 × 10−1 | 3.64 × 101 | 2.99 × 101 | 3.38 × 101 | |
| rank | 9 | 10 | 4 | 6 | 8 | 5 | 1 | 7 | 2 | 3 | |
| f26 | mean | 8.51 × 103 | 1.61 × 104 | 2.06 × 103 | 2.03 × 103 | 1.41 × 103 | 2.34 × 103 | 2.32 × 103 | 1.57 × 103 | 1.69 × 103 | 1.70 × 103 |
| std | 1.68 × 103 | 8.30 × 102 | 2.20 × 102 | 6.03 × 102 | 9.26 × 102 | 5.46 × 102 | 3.67 × 102 | 3.01 × 102 | 3.77 × 102 | 4.40 × 102 | |
| rank | 9 | 10 | 6 | 5 | 1 | 8 | 7 | 2 | 3 | 4 | |
| f27 | mean | 1.22 × 103 | 6.61 × 103 | 5.63 × 102 | 6.02 × 102 | 7.08 × 102 | 7.85 × 102 | 4.98 × 102 | 6.38 × 102 | 6.03 × 102 | 5.49 × 102 |
| std | 2.42 × 102 | 1.18 × 103 | 2.29 × 101 | 2.33 × 101 | 8.03 × 101 | 8.27 × 101 | 1.03 × 101 | 3.75 × 101 | 3.32 × 101 | 1.76 × 101 | |
| rank | 9 | 10 | 3 | 4 | 7 | 8 | 1 | 6 | 5 | 2 | |
| f28 | mean | 3.95 × 103 | 1.12 × 104 | 4.89 × 102 | 5.05 × 102 | 5.36 × 102 | 5.06 × 102 | 4.44 × 102 | 4.93 × 102 | 4.78 × 102 | 4.86 × 102 |
| std | 1.92 × 103 | 1.26 × 103 | 2.23 × 101 | 1.71 × 101 | 3.42 × 101 | 1.48 × 101 | 3.08 × 100 | 1.87 × 101 | 2.35 × 101 | 2.38 × 101 | |
| rank | 9 | 10 | 4 | 6 | 8 | 7 | 1 | 5 | 2 | 3 | |
| f29 | mean | 2.79 × 103 | 2.05 × 105 | 5.91 × 102 | 6.79 × 102 | 9.61 × 102 | 1.00 × 103 | 6.72 × 102 | 6.35 × 102 | 5.83 × 102 | 4.83 × 102 |
| std | 7.84 × 102 | 2.22 × 105 | 1.12 × 102 | 1.22 × 102 | 2.90 × 102 | 2.60 × 102 | 1.60 × 102 | 1.46 × 102 | 1.30 × 102 | 5.95 × 101 | |
| rank | 9 | 10 | 3 | 6 | 7 | 8 | 5 | 4 | 2 | 1 | |
| f30 | mean | 1.89 × 108 | 9.72 × 109 | 8.87 × 105 | 7.95 × 105 | 1.96 × 106 | 2.37 × 106 | 1.76 × 103 | 8.31 × 105 | 8.49 × 105 | 8.04 × 105 |
| std | 4.32 × 108 | 3.20 × 109 | 1.40 × 105 | 6.55 × 104 | 5.10 × 105 | 2.74 × 106 | 1.73 × 103 | 1.05 × 105 | 9.43 × 104 | 5.71 × 104 | |
| rank | 9 | 10 | 6 | 2 | 7 | 8 | 1 | 4 | 5 | 3 | |
| Ave rank | 8.97 | 8.97 | 10.00 | 4.90 | 5.10 | 5.90 | 5.79 | 4.86 | 3.41 | 3.07 | |
| Final rank | 9 | 9 | 10 | 5 | 6 | 8 | 7 | 4 | 3 | 2 | |
The best experimental result is shown in bold.
References
- Tanweer, M.R.; Suresh, S.; Sundararajan, N. Self regulating particle swarm optimization algorithm. Inf. Sci. 2015, 294, 182–202. [Google Scholar] [CrossRef]
- Carson, J. Genetic Algorithms: Advances in Research and Applications; Nova Science Publishers, Inc.: New York, NY, USA, 2017. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, G.; Rui, L.; Liu, D.; Liu, H.; Yuan, J. A failure remember-driven self-adaptive differential evolution with top-bottom strategy. Swarm Evol. Comput. 2019, 45, 1–14. [Google Scholar] [CrossRef]
- Pedro, L.; José, A.L. Estimation of Distribution Algorithms: A New Tool for Evolutionary Computation; Springer: New York, NY, USA, 2012; Volume 2002. [Google Scholar]
- Lim, W.H.; Mat Isa, N.A. An adaptive two-layer particle swarm optimization with elitist learning strategy. Inf. Sci. 2014, 273, 49–72. [Google Scholar] [CrossRef]
- Buba, A.T.; Lee, L.S. Hybrid Differential Evolution-Particle Swarm Optimization Algorithm for Multiobjective Urban Transit Network Design Problem with Homogeneous Buses. Math. Probl. Eng. 2019, 2019, 5963240. [Google Scholar] [CrossRef]
- Qin, Z.; Pan, D. Improved Dual-Center Particle Swarm Optimization Algorithm. Mathematics 2024, 12, 1698. [Google Scholar] [CrossRef]
- Liang, J.J.; Suganthan, P.N. Dynamic multi-swarm particle swarm optimizer. In Proceedings of the 2005 IEEE Swarm Intelligence Symposium, Pasadena, CA, USA, 8–10 June 2005; pp. 124–129. [Google Scholar] [CrossRef]
- Wang, S.; Liu, G.; Gao, M.; Cao, S.; Guo, A.; Wang, J. Heterogeneous comprehensive learning and dynamic multi-swarm particle swarm optimizer with two mutation operators. Inf. Sci. 2020, 540, 175–201. [Google Scholar] [CrossRef]
- Angelini, M.; Zagaglia, L.; Marabelli, F.; Floris, F. Convergence and Performance Analysis of a Particle Swarm Optimization Algorithm for Optical Tuning of Gold Nanohole Arrays. Materials 2024, 17, 807. [Google Scholar] [CrossRef]
- Gao, W.; Peng, X.; Guo, W.; Li, D. A Dual-Competition-Based Particle Swarm Optimizer for Large-Scale Optimization. Mathematics 2024, 12, 1738. [Google Scholar] [CrossRef]
- Xia, X.; Gui, L.; Yu, F.; Wu, H.; Wei, B.; Zhang, Y.L.; Zhan, Z.H. Triple Archives Particle Swarm Optimization. IEEE Trans Cybern 2020, 50, 4862–4875. [Google Scholar] [CrossRef]
- Ye, W.; Feng, W.; Fan, S. A novel multi-swarm particle swarm optimization with dynamic learning strategy. Appl. Soft Comput. 2017, 61, 832–843. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, Washington, DC, USA, 6–9 July 1999; Volume 3, p. 1945. [Google Scholar] [CrossRef]
- Zhan, Z.-H.; Zhang, J.; Li, Y.; Shi, Y.-H. Orthogonal Learning Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2011, 15, 832–847. [Google Scholar] [CrossRef]
- Xu, G.; Cui, Q.; Shi, X.; Ge, H.; Zhan, Z.-H.; Lee, H.P.; Liang, Y.; Tai, R.; Wu, C. Particle swarm optimization based on dimensional learning strategy. Swarm Evol. Comput. 2019, 45, 33–51. [Google Scholar] [CrossRef]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Jiao, B.; Lian, Z.; Gu, X. A dynamic inertia weight particle swarm optimization algorithm. Chaos Solitons Fractals 2008, 37, 698–705. [Google Scholar] [CrossRef]
- Chatterjee, A.; Siarry, P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization. Comput. Oper. Res. 2006, 33, 859–871. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.-W.; Tu, L.-P. A modified particle swarm optimization using adaptive strategy. Expert Syst. Appl. 2020, 152, 113353. [Google Scholar] [CrossRef]
- Nickabadi, A.; Ebadzadeh, M.M.; Safabakhsh, R. A novel particle swarm optimization algorithm with adaptive inertia weight. Appl. Soft Comput. 2011, 11, 3658–3670. [Google Scholar] [CrossRef]
- Beheshti, Z.; Shamsuddin, S.M. Non-parametric particle swarm optimization for global optimization. Appl. Soft Comput. 2015, 28, 345–359. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, H.; Zhang, T.; Wang, Q.; Wang, Y.; Tu, L. Terminal crossover and steering-based particle swarm optimization algorithm with disturbance. Appl. Soft Comput. 2019, 85, 105841. [Google Scholar] [CrossRef]
- Zhan, Z.H.; Zhang, J.; Li, Y.; Chung, H.S. Adaptive particle swarm optimization. IEEE Trans Syst Man Cybern B Cybern 2009, 39, 1362–1381. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Zhan, Z.-H.; Yang, Z.-X.; Wei, X. AMPSO: Artificial Multi-Swarm Particle Swarm Optimization. arXiv Prepr. 2020, arXiv:2004.07561. [Google Scholar]
- Kennedy, J. Small worlds and mega-minds: Effects of neighborhood topology on particle swarm performance. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, Washington, DC, USA, 6–9 July 1999; Volume 3, p. 1931. [Google Scholar] [CrossRef]
- Kennedy, J.; Mendes, R. Population structure and particle swarm performance. In Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02, Honolulu, HI, USA, 12–17 May 2002; Volume 2, p. 1671. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle Swarm Optimization: A Comprehensive Survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Suganthan, P.N. Particle swarm optimiser with neighbourhood operator. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, Washington, DC, USA, 6–9 July 1999; Volume 3, p. 1958. [Google Scholar] [CrossRef]
- Nasir, M.; Das, S.; Maity, D.; Sengupta, S.; Halder, U.; Suganthan, P.N. A dynamic neighborhood learning based particle swarm optimizer for global numerical optimization. Inf. Sci. 2012, 209, 16–36. [Google Scholar] [CrossRef]
- Xia, X.; Tang, Y.; Wei, B.; Zhang, Y.; Gui, L.; Li, X. Dynamic multi-swarm global particle swarm optimization. Computing 2020, 102, 1587–1626. [Google Scholar] [CrossRef]
- Liu, Z.; Nishi, T.; Dabnichki, P. Multipopulation Ensemble Particle Swarm Optimizer for Engineering Design Problems. Math. Probl. Eng. 2020, 2020, 1450985. [Google Scholar] [CrossRef]
- Li, Y.; Zhan, Z.-H.; Lin, S.; Zhang, J.; Luo, X. Competitive and cooperative particle swarm optimization with information sharing mechanism for global optimization problems. Inf. Sci. 2015, 293, 370–382. [Google Scholar] [CrossRef]
- Gong, Y.J.; Li, J.J.; Zhou, Y.; Li, Y.; Chung, H.S.; Shi, Y.H.; Zhang, J. Genetic Learning Particle Swarm Optimization. IEEE Trans Cybern 2016, 46, 2277–2290. [Google Scholar] [CrossRef]
- Pant, M.; Thangaraj, R.; Grosan, C.; Abraham, A. Hybrid differential evolution—Particle Swarm Optimization algorithm for solving global optimization problems. In Proceedings of the 2008 Third International Conference on Digital Information Management, London, UK, 13–16 November 2008; pp. 18–24. [Google Scholar] [CrossRef]
- Tang, B.; Zhu, Z.; Luo, J. Hybridizing particle swarm optimization and differential evolution for the mobile robot global path planning. Int. J. Adv. Robot. Syst. 2016, 13, 86. [Google Scholar] [CrossRef]
- Jiang, S.; Ji, Z.; Shen, Y. A novel hybrid particle swarm optimization and gravitational search algorithm for solving economic emission load dispatch problems with various practical constraints. Int. J. Electr. Power Energy Syst. 2014, 55, 628–644. [Google Scholar] [CrossRef]
- Kıran, M.S.; Gündüz, M.; Baykan, Ö.K. A novel hybrid algorithm based on particle swarm and ant colony optimization for finding the global minimum. Appl. Math. Comput. 2012, 219, 1515–1521. [Google Scholar] [CrossRef]
- Raj, A.; Punia, P.; Kumar, P. A novel hybrid pelican-particle swarm optimization algorithm (HPPSO) for global optimization problem. Int. J. Syst. Assur. Eng. Manag. 2024. [Google Scholar] [CrossRef]
- Pawar, A.; Tiwari, N. A Novel Approach of DDOS Attack Classification with Optimizing the Ensemble Classifier Using A Hybrid Firefly and Particle Swarm Optimization (HFPSO). Int. J. Intell. Eng. Syst. 2023, 16, 201–214. [Google Scholar] [CrossRef]
- Zhang, M.; Long, D.; Qin, T.; Yang, J. A Chaotic Hybrid Butterfly Optimization Algorithm with Particle Swarm Optimization for High-Dimensional Optimization Problems. Symmetry 2020, 12, 1800. [Google Scholar] [CrossRef]
- Rezk, H.; Arfaoui, J.; Gomaa, M.R. Optimal Parameter Estimation of Solar PV Panel Based on Hybrid Particle Swarm and Grey Wolf Optimization Algorithms. Int. J. Interact. Multimed. Artif. Intell. 2021, 6, 145–155. [Google Scholar] [CrossRef]
- Mendes, R.; Kennedy, J.; Neves, J. The fully informed particle swarm: Simpler, maybe better. IEEE Trans. Evol. Comput. 2004, 8, 204–210. [Google Scholar] [CrossRef]
- Xia, X.; Gui, L.; He, G.; Wei, B.; Zhang, Y.; Yu, F.; Wu, H.; Zhan, Z.-H. An expanded particle swarm optimization based on multi-exemplar and forgetting ability. Inf. Sci. 2020, 508, 105–120. [Google Scholar] [CrossRef]
- Lynn, N.; Suganthan, P.N. Heterogeneous comprehensive learning particle swarm optimization with enhanced exploration and exploitation. Swarm Evol. Comput. 2015, 24, 11–24. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).