Time-Delay Following Model for Connected and Automated Vehicles Considering Multiple Vehicle Safety Potential Fields
Abstract
1. Introduction
2. Literature Review
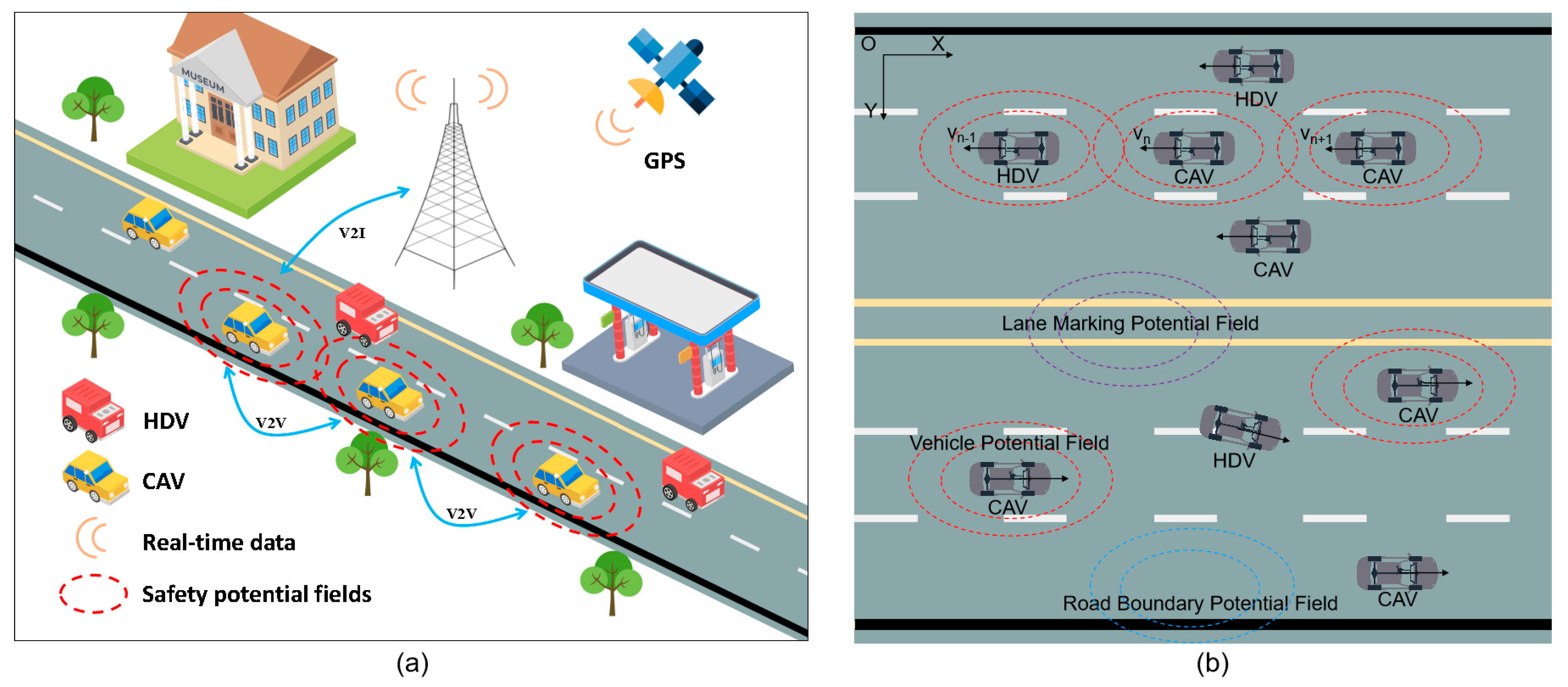
2.1. Safety Potential Fields
2.2. Car-Following Behaviour Modelling of SPF
3. Methodology
3.1. Car-Following Model Based on Safety Potential Field
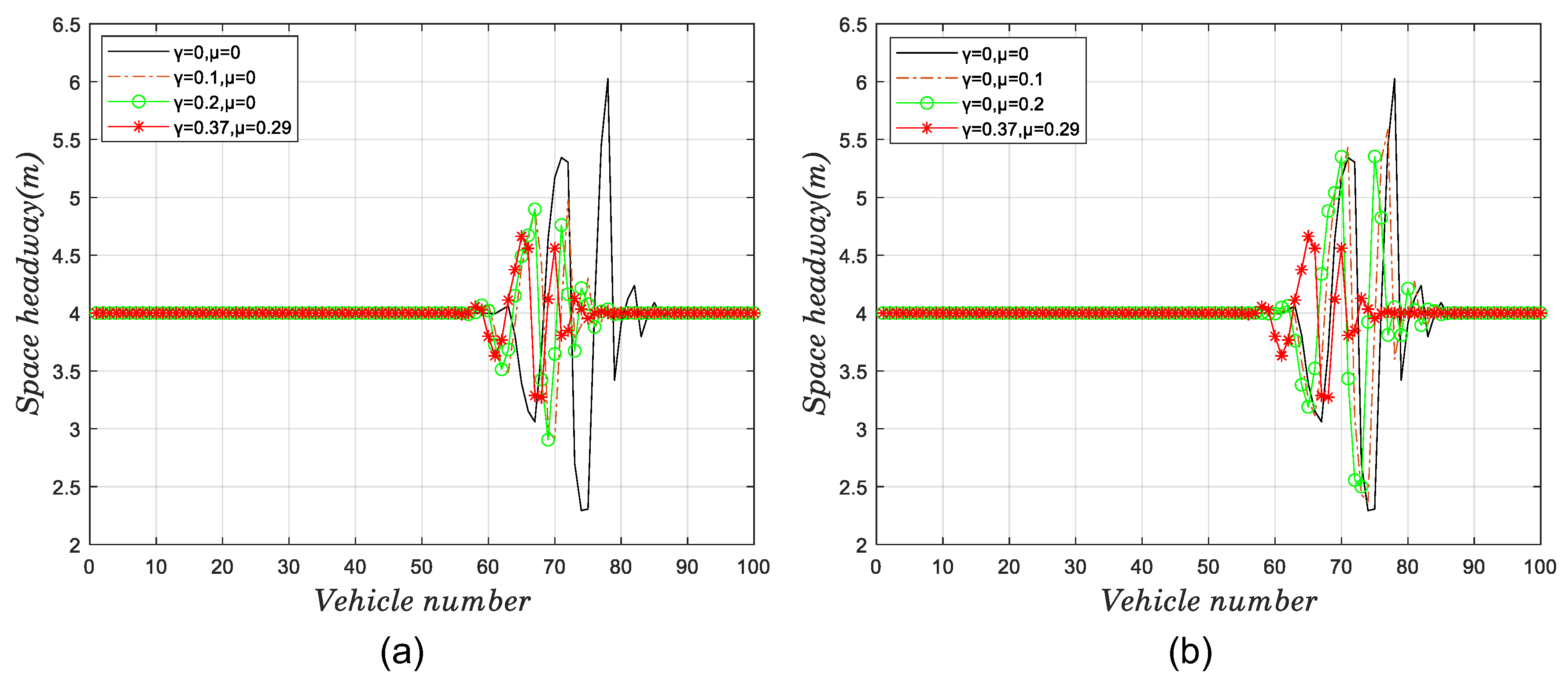
3.2. Stability Analysis
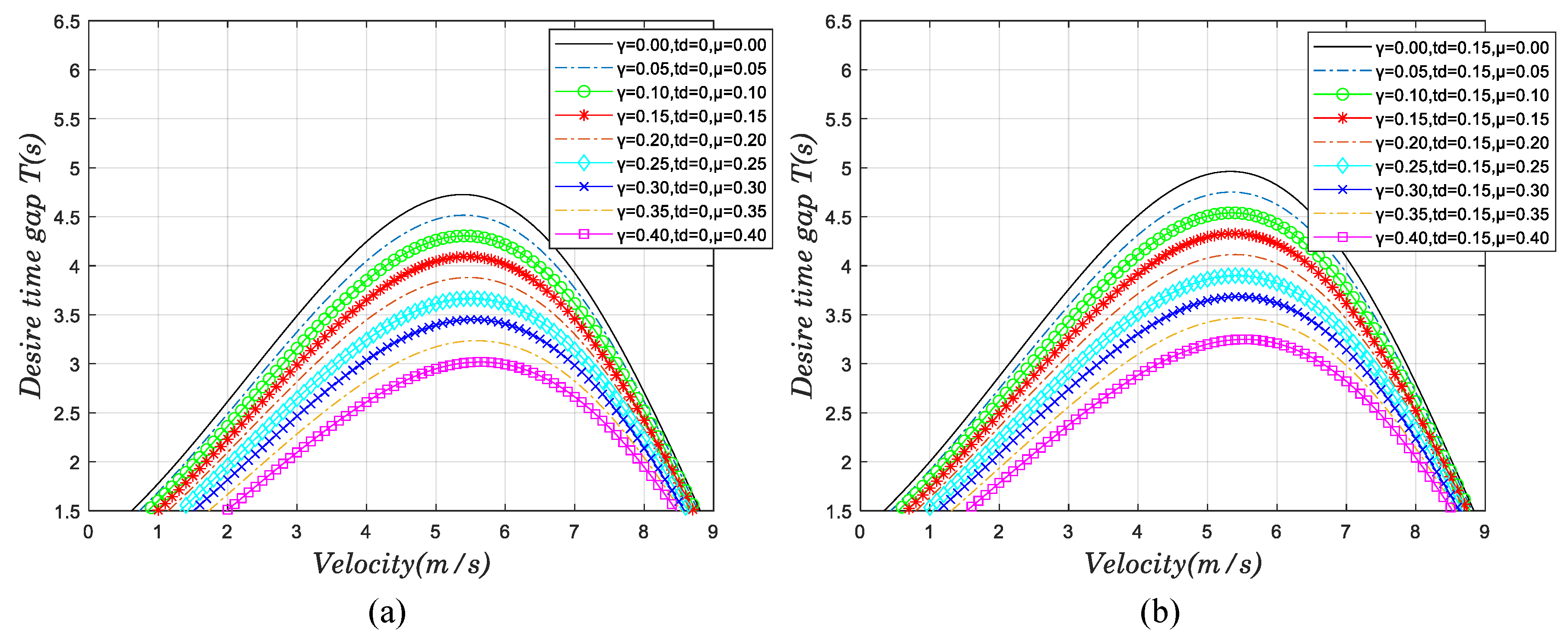
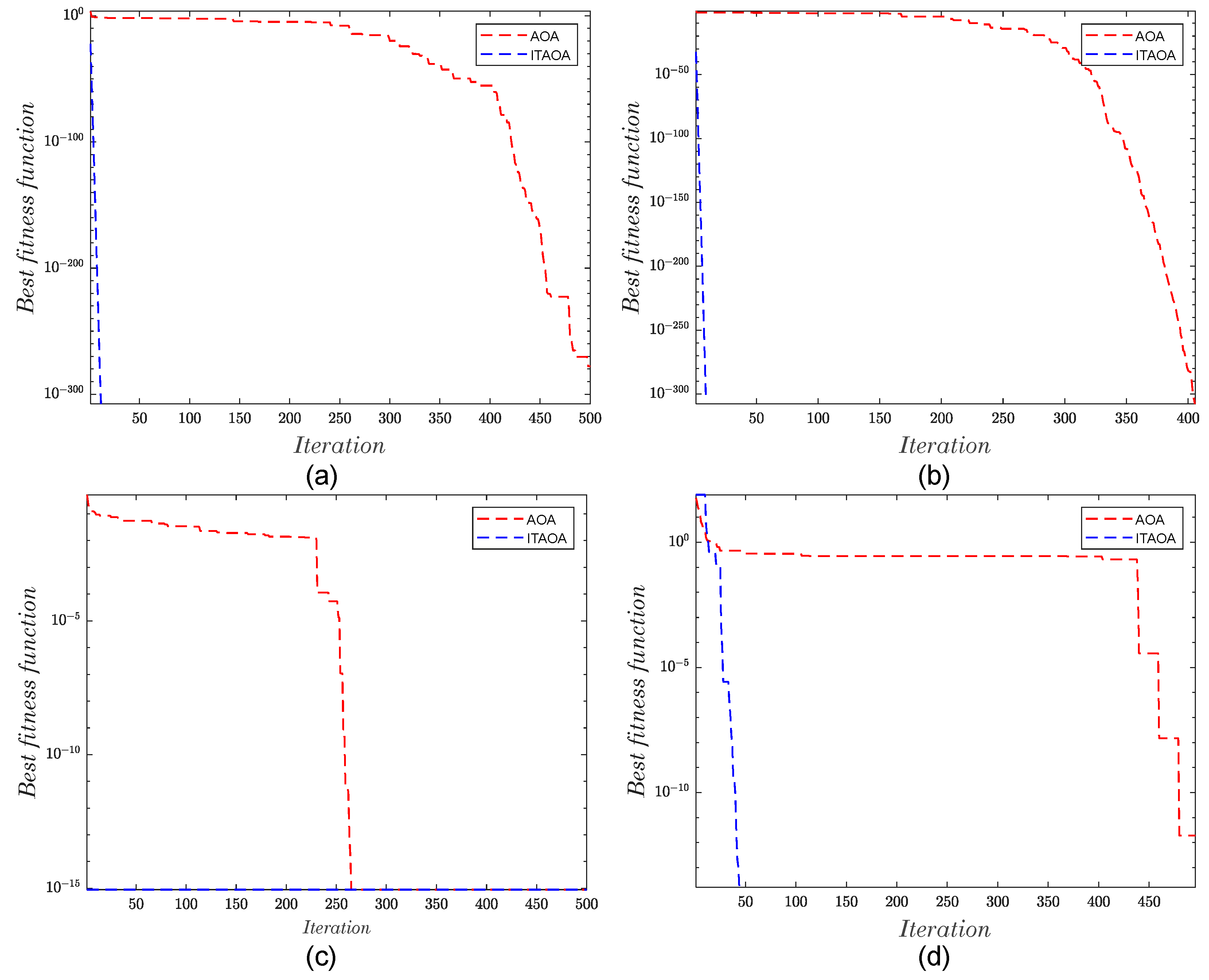
3.3. Calibration of the Model Parameter
4. Results
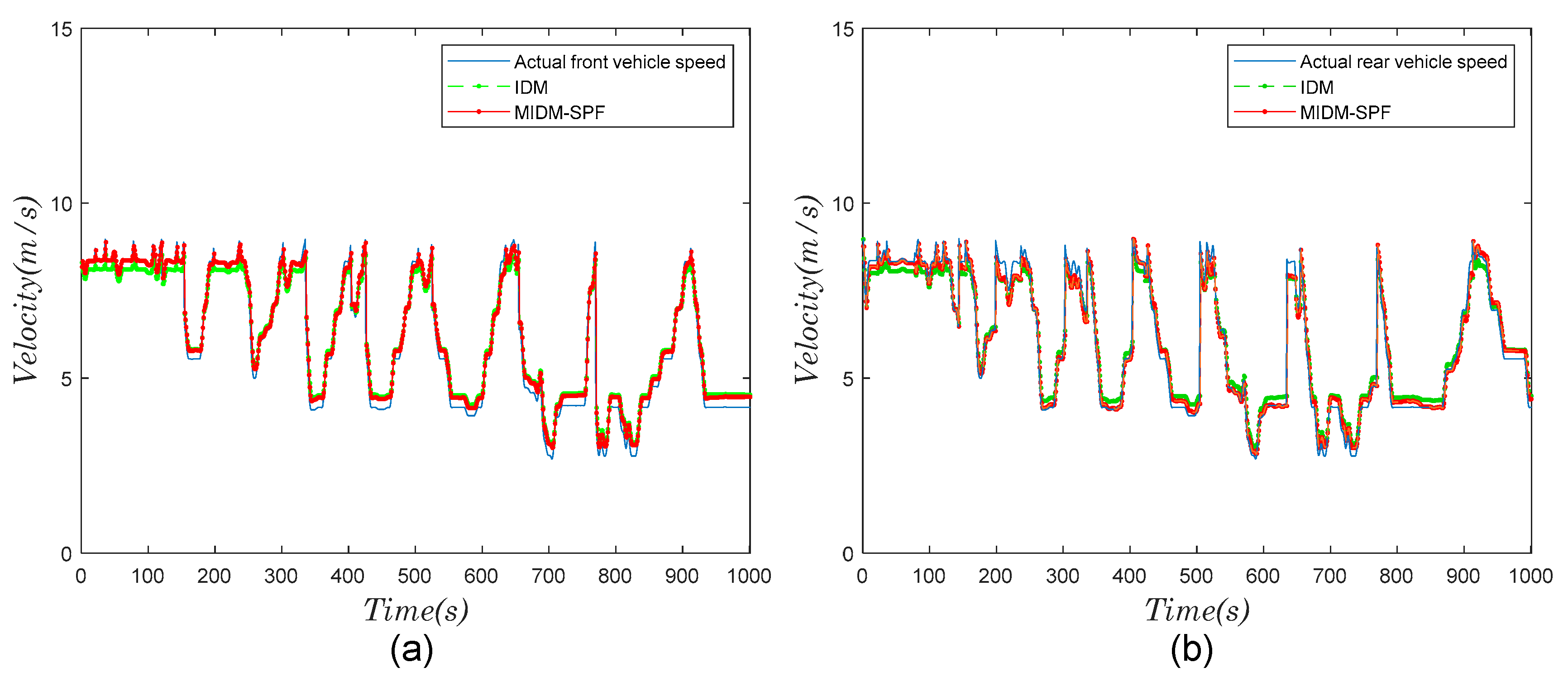
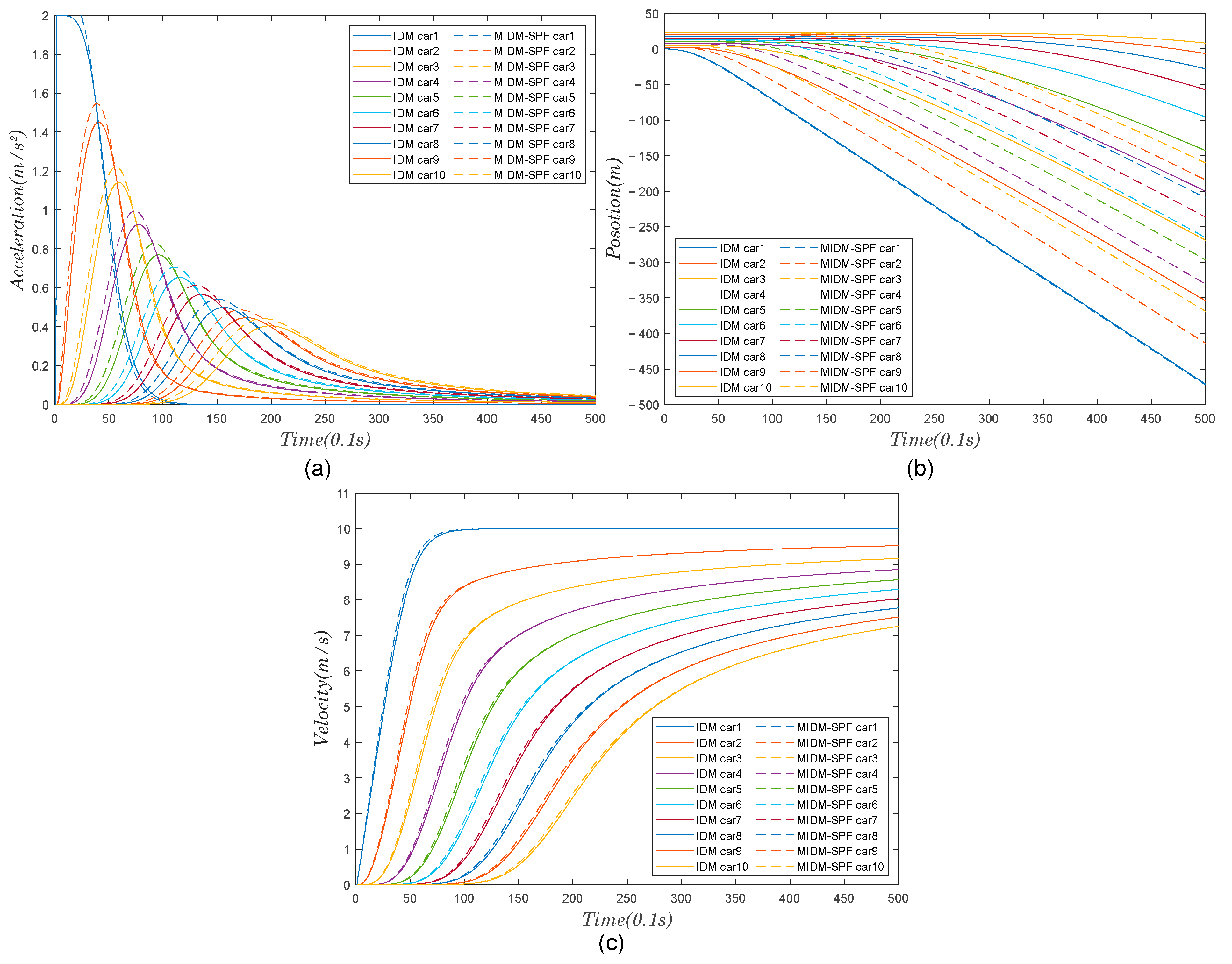
4.1. Model Calibration and Validation
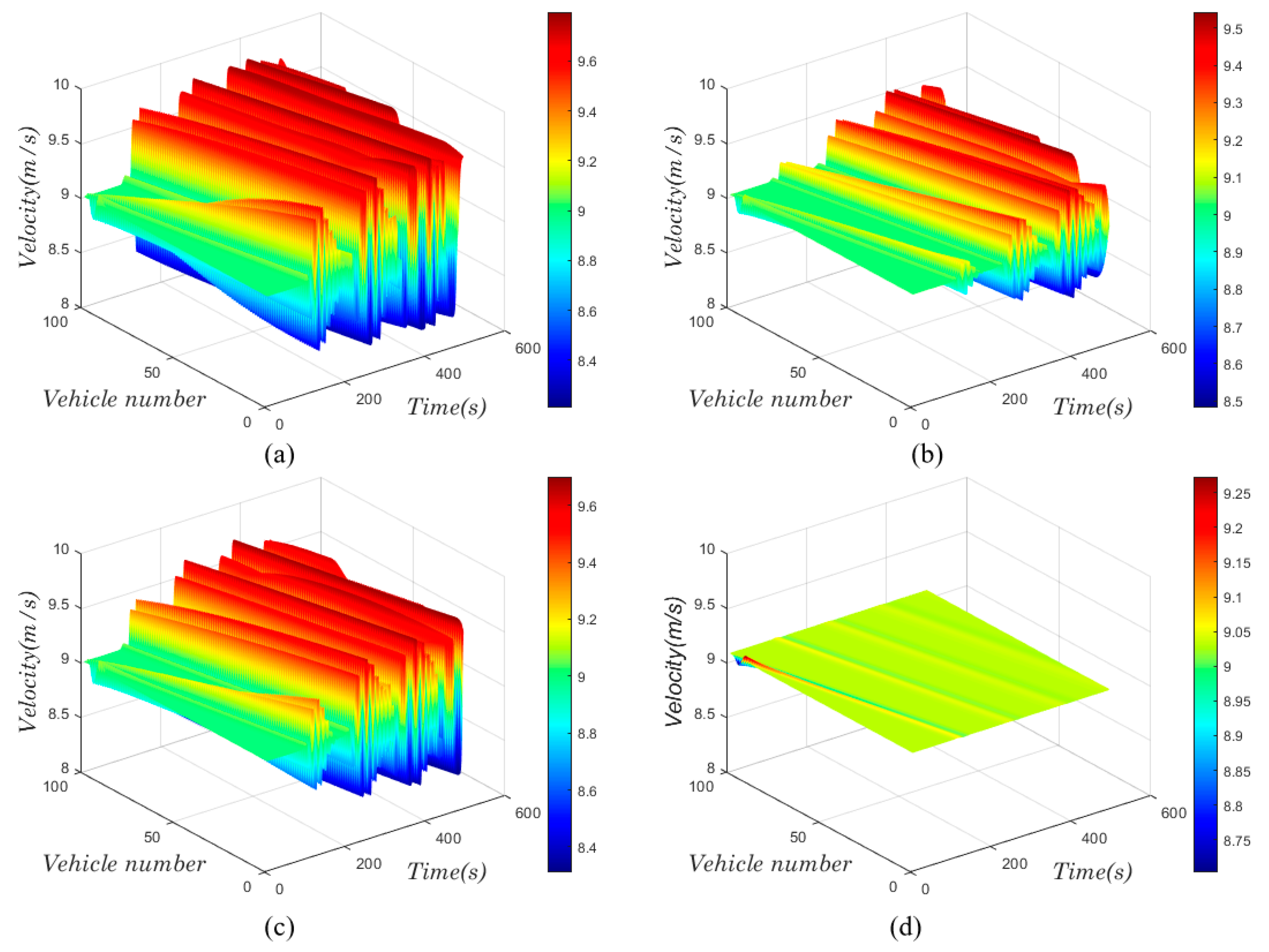
4.2. Dynamic Performance Study of the Model
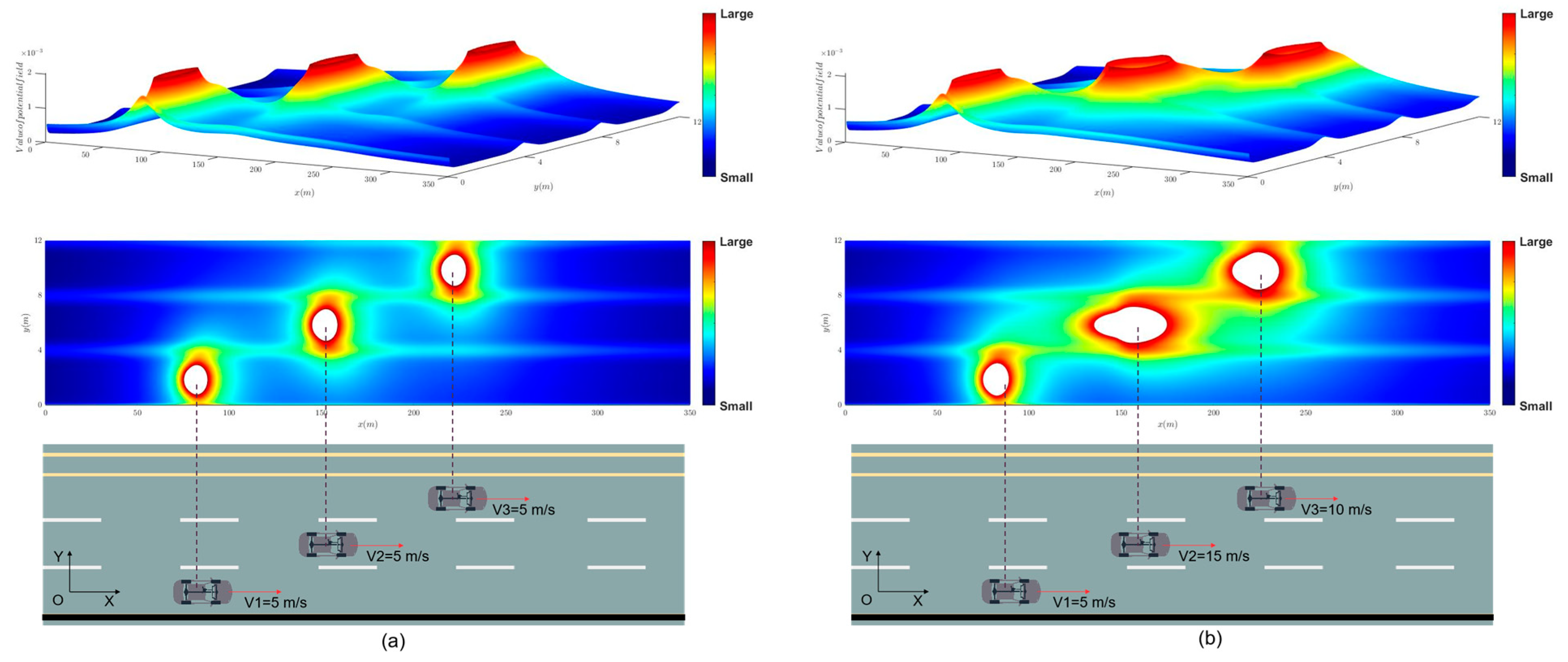
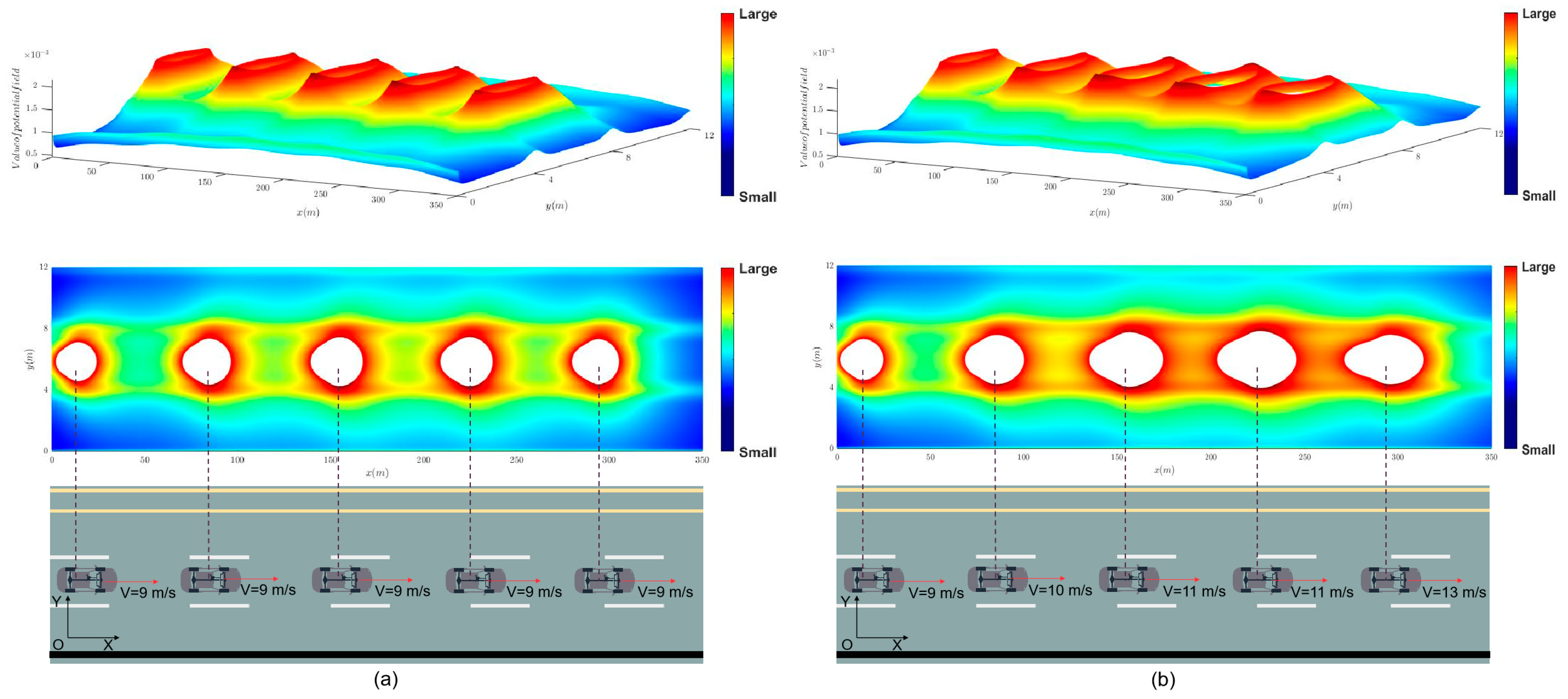
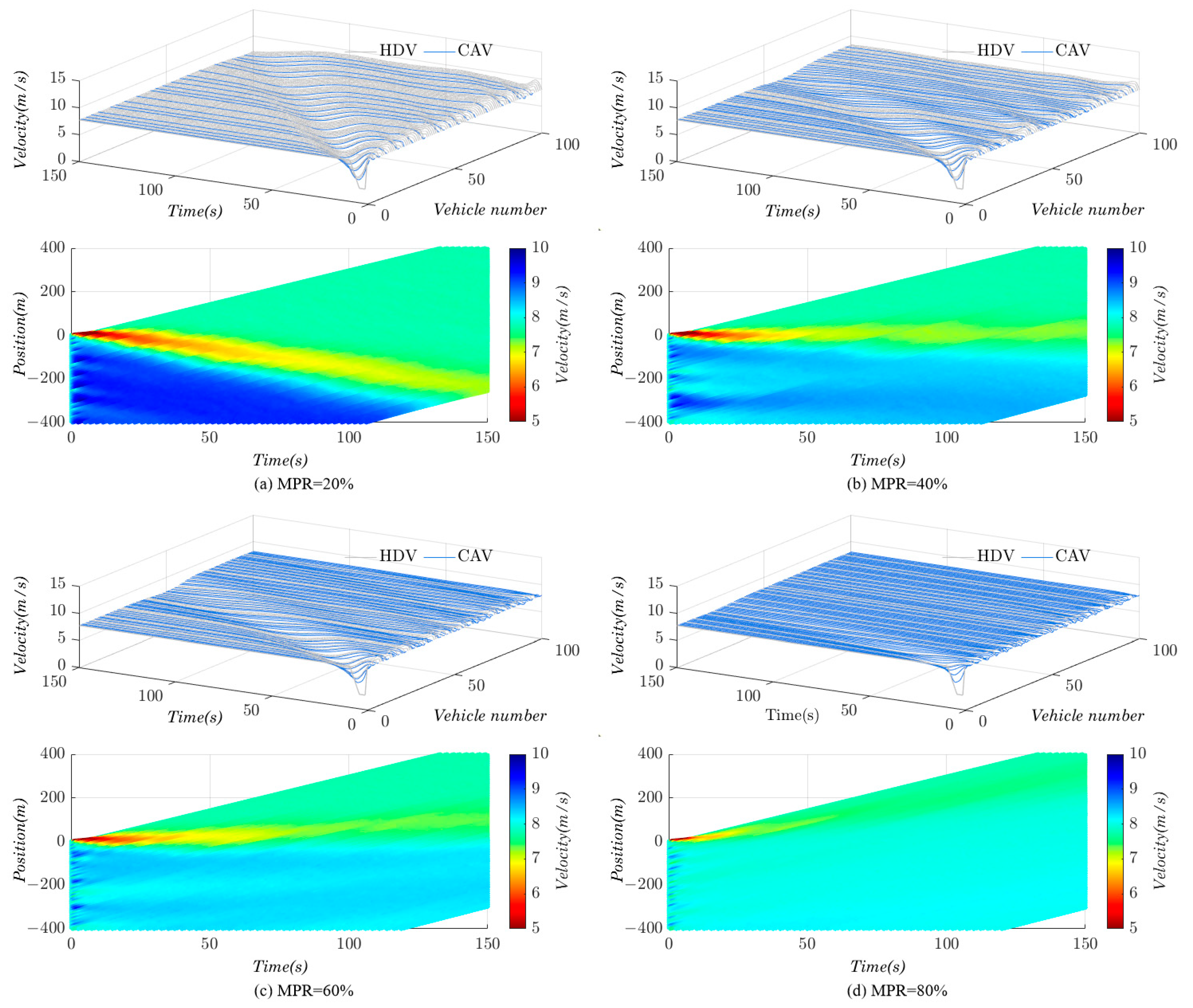
4.3. Simulation Analysis at Different Market Penetration Rates
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
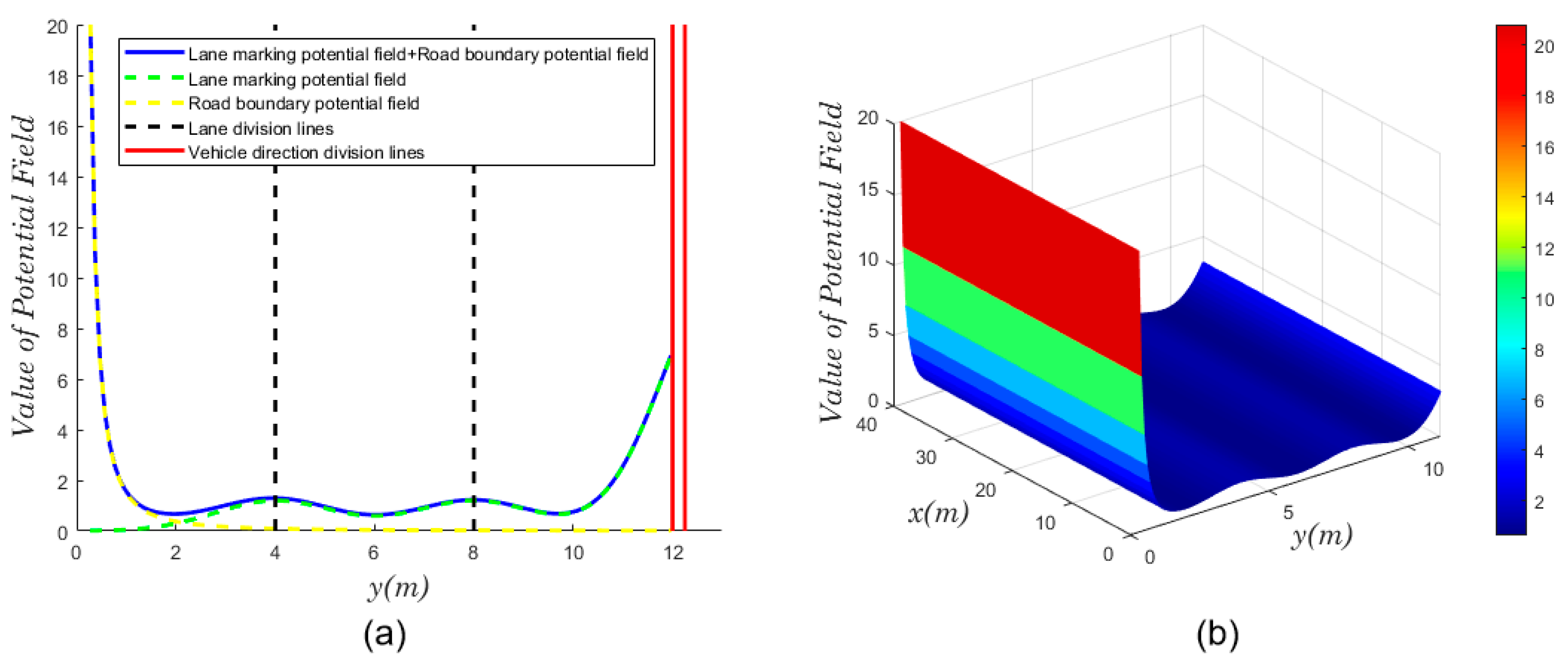
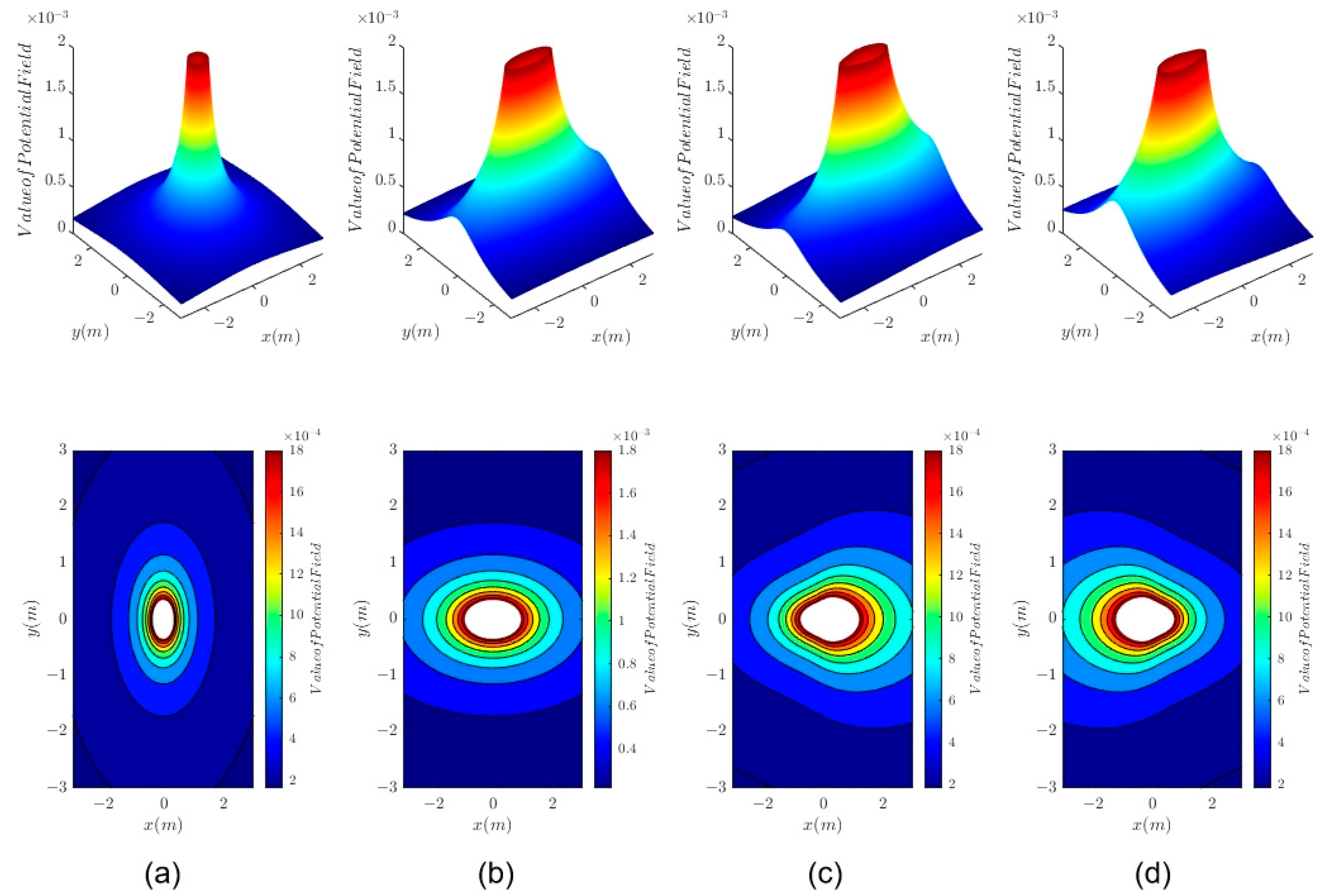
Appendix A.1. Modelling of Safety Potential Field
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| 1.2 | 12 | ||
| 10 | 12.25 | ||
| 1.22 | 0 | ||
| 4 | 3 | ||
| 8 | 3 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| 1521 | 2.6 | ||
| 0.05 | 0 | ||
| 0 | 0 |
Appendix A.2. Stability Analysis of the Proposed Model
References
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Yi, Z.; Li, L.; Qu, X.; Hong, Y.; Mao, P.; Ran, B. Using artificial potential field theory for a cooperative control model in a connected and automated vehicles environment. Transp. Res. Rec. 2020, 2674, 1005–1018. [Google Scholar] [CrossRef]
- Wang, R.; Guo, J.; Guo, S.; Fu, Q.; Xu, J. Cooperative hunting of spherical multi-robots based on improved artificial potential field method. In Proceedings of the 2022 IEEE International Conference on Mechatronics and Automation (ICMA), Guilin, China, 7–10 August 2022; pp. 575–580. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, K.; Qu, J. Research on multi-robot local path planning based on improved artificial potential field method. In Proceedings of the Fifth Euro-China Conference on Intelligent Data Analysis and Applications 5, Xi’an, China, 12–14 October 2018; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 684–690. [Google Scholar]
- Shi, M.; Nie, J. Improvement of Path Planning Algorithm based on Small Step Artificial Potential Field Method. In Proceedings of the 2022 9th International Conference on Dependable Systems and Their Applications (DSA), Ürümqi, China, 4–5 August 2022; pp. 827–831. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, T.; Xu, H. PE-A* Algorithm for Ship Route Planning Based on Field Theory. IEEE Access 2022, 10, 36490–36504. [Google Scholar] [CrossRef]
- Zhai, L.; Feng, S. An improved ant colony algorithm based on artificial potential field and quantum evolution theory. J. Intell. Fuzzy Syst. 2022, 42, 5773–5788. [Google Scholar] [CrossRef]
- Li, Y.; Yu, B.; Chen, Y.; Hu, Z. A new theory of driver vision pressure energy field and its application in driver behaviour decision-making model. IET Intell. Transp. Syst. 2022, 16, 1–12. [Google Scholar] [CrossRef]
- Semsar-Kazerooni, E.; Verhaegh, J.; Ploeg, J.; Alirezaei, M. Cooperative adaptive cruise control: An artificial potential field approach. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016; pp. 361–367. [Google Scholar] [CrossRef]
- Liu, W.; Li, Z. Comprehensive predictive control method for automated vehicles in dynamic traffic circumstances. IET Intell. Transp. Syst. 2018, 12, 1455–1463. [Google Scholar] [CrossRef]
- Xu, Y.; Ma, Z.; Sun, J. Simulation of turning vehicles’ behaviors at mixed-flow intersections based on potential field theory. Transp. B Transp. Dyn. 2018, 7, 498–518. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, P.; Hu, B. Active lane-changing model of vehicle in B-type weaving region based on potential energy field theory. Phys. A Stat. Mech. Its Appl. 2019, 535, 122291. [Google Scholar] [CrossRef]
- Joo, Y.J.; Kim, E.J.; Kim, D.K.; Park, P.Y. A generalized driving risk assessment on high-speed highways using field theory. Anal. Methods Accid. Res. 2023, 40, 100303. [Google Scholar] [CrossRef]
- Cheng, Y.; Liu, Z.; Gao, L.; Zhao, Y.; Gao, T. Traffic risk environment impact analysis and complexity assessment of autonomous vehicles based on the potential field method. Int. J. Environ. Res. Public Health 2022, 19, 10337. [Google Scholar] [CrossRef]
- Zhao, H.; He, R.; Ma, C. An extended car-following model at signalised intersections. J. Adv. Transp. 2018, 2018, 5427507. [Google Scholar] [CrossRef]
- Gazis, D.C.; Herman, R.; Rothery, R.W. Nonlinear follow-the-leader models of traffic flow. Oper. Res. 1961, 9, 545–567. [Google Scholar] [CrossRef]
- Kometani, E. Dynamic behavior of traffic with a nonlinear spacing-speed relationship. Theory Traffic Flow (Proc. Sym. TTF (GM)) 1959, 105–119. [Google Scholar]
- Michaels, R.M. Perceptual Factors in Car Following. In Proceedings of the Second International Symposium on the Theory of Traffic Flow, London, UK, 25–27 June 1963; pp. 44–59. [Google Scholar]
- Kikuchi, S.; Chakroborty, P. Car-following model based on fuzzy inference system. Transp. Res. Rec. 1992, 1194, 82. [Google Scholar]
- Bando, M.; Hasebe, K.; Nakayama, A.; Shibata, A.; Sugiyama, Y. Dynamical model of traffic congestion and numerical simulation. Phys. Rev. E 1995, 51, 1035. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wang, B.H.; Hu, B. Cellular automaton traffic flow model between the Fukui-Ishibashi and Nagel-Schreckenberg models. Phys. Rev. E 2001, 63, 056117. [Google Scholar] [CrossRef]
- Yang, Z.S.; Yu, Y.; Yu, D.X.; Zhou, H.X.; Mo, X.L. APF-based car following behavior considering lateral distance. Adv. Mech. Eng. 2013, 5, 207104. [Google Scholar] [CrossRef]
- Li, C.; Jiang, X.; Wang, W.; Cheng, Q.; Shen, Y. A simplified car-following model based on the artificial potential field. Procedia Eng. 2016, 137, 13–20. [Google Scholar] [CrossRef]
- Jia, Y.; Qu, D.; Han, L.; Lin, L.; Hong, J. Research on car-following model based on molecular dynamics. Adv. Mech. Eng. 2021, 13, 1687814021993003. [Google Scholar] [CrossRef]
- Zhang, G.; Yin, S.; Huang, C.; Zhang, W. Intervehicle Security-Based Robust Neural Formation Control for Multiple USVs via APS Guidance. J. Mar. Sci. Eng. 2023, 11, 1020. [Google Scholar] [CrossRef]
- Shen, C.; Xiao, X.; Su, W.; Tong, Y.; Hu, H. Research on V2V time headway strategy considering multi-front vehicles based on artificial potential field. Electronics 2023, 12, 3602. [Google Scholar] [CrossRef]
- Wang, J.; Wu, J.; Li, Y.; Li, K. The concept and modeling of driving safety field based on driver-vehicle-road interactions. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 974–981. [Google Scholar] [CrossRef]
- Wang, J.; Wu, J.; Li, Y. The driving safety field based on driver–vehicle–road interactions. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2203–2214. [Google Scholar] [CrossRef]
- Wang, J.; Wu, J.; Zheng, X.; Ni, D.; Li, K. Driving safety field theory modeling and its application in pre-collision warning system. Transp. Res. Part C Emerg. Technol. 2016, 72, 306–324. [Google Scholar] [CrossRef]
- Li, M.; Song, X.; Cao, H.; Wang, J.; Huang, Y.; Hu, C.; Wang, H. Shared control with a novel dynamic authority allocation strategy based on game theory and driving safety field. Mech. Syst. Signal Process. 2019, 124, 199–216. [Google Scholar] [CrossRef]
- Li, L.; Gan, J.; Yi, Z.; Qu, X.; Ran, B. Risk perception and the warning strategy based on safety potential field theory. Accid. Anal. Prev. 2020, 148, 105805. [Google Scholar] [CrossRef]
- Li, L.; Gan, J.; Zhou, K.; Qu, X.; Ran, B. A novel lane-changing model of connected and automated vehicles: Using the safety potential field theory. Phys. A Stat. Mech. Its Appl. 2020, 559, 125039. [Google Scholar] [CrossRef]
- Li, L.; Ji, X.; Gan, J.; Qu, X.; Ran, B. A macroscopic model of heterogeneous traffic flow based on the safety potential field theory. IEEE Access 2021, 9, 7460–7470. [Google Scholar] [CrossRef]
- Talal, M.; Ramli, K.N.; Zaidan, A.A.; Zaidan, B.B.; Jumaa, F. Review on car-following sensor based and data-generation mapping for safety and traffic management and road map toward ITS. Veh. Commun. 2020, 25, 100280. [Google Scholar] [CrossRef]
- Li, L.; Gan, J.; Ji, X.; Qu, X.; Ran, B. Dynamic driving risk potential field model under the connected and automated vehicles environment and its application in car-following modeling. IEEE Trans. Intell. Transp. Syst. 2020, 23, 122–141. [Google Scholar] [CrossRef]
- Li, L.; Gan, J.; Qu, X.; Mao, P.; Yi, Z.; Ran, B. A novel graph and safety potential field theory-based vehicle platoon formation and optimization method. Appl. Sci. 2021, 11, 958. [Google Scholar] [CrossRef]
- Wu, R.; Li, L.; Shi, H.; Rui, Y.; Ngoduy, D.; Ran, B. A Driving Risk Surrogate and Its Application in Car-Following Scenario at Expressway. arXiv 2022, arXiv:2211.03304. [Google Scholar]
- Jia, Y.; Qu, D.; Song, H.; Wang, T.; Zhao, Z. Car-following characteristics and model of connected autonomous vehicles based on safe potential field. Phys. A Stat. Mech. Its Appl. 2022, 586, 126502. [Google Scholar] [CrossRef]
- Li, L.; Wang, C.; Zhang, Y.; Qu, X.; Li, R.; Chen, Z.; Ran, B. Microscopic state evolution model of mixed traffic flow based on potential field theory. Phys. A Stat. Mech. Its Appl. 2022, 607, 128185. [Google Scholar] [CrossRef]
- Ma, Y.; Dong, F.; Yin, B.; Lou, Y. Real-time risk assessment model for multi-vehicle interaction of connected and autonomous vehicles in weaving area based on risk potential field. Phys. A Stat. Mech. Its Appl. 2023, 620, 128725. [Google Scholar] [CrossRef]
- Menzel, T.; Bagschik, G.; Isensee, L.; Schomburg, A.; Maurer, M. From functional to logical scenarios: Detailing a keyword-based scenario description for execution in a simulation environment. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 2383–2390. [Google Scholar] [CrossRef]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E 2020, 62, 1805. [Google Scholar] [CrossRef] [PubMed]
- Treiber, M.; Kesting, A. The intelligent driver model with stochasticity-new insights into traffic flow oscillations. Transp. Res. Procedia 2017, 23, 174–187. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, Q.; Shi, W.; Gu, T.; Li, W. Stability analysis of an improved car-following model accounting for the driver’s characteristics and automation. Phys. A Stat. Mech. Its Appl. 2019, 526, 120990. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Tian, J.; Jiang, R. Stability analysis of stochastic linear car-following models. Transp. Sci. 2020, 54, 274–297. [Google Scholar] [CrossRef]
- Wang, X.; Liu, M.; Ci, Y.; Wu, L. Effect of front two adjacent vehicles’ velocity information on car-following model construction and stability analysis. Phys. A Stat. Mech. Its Appl. 2022, 607, 128196. [Google Scholar] [CrossRef]
- Li, Y.; Chen, B.; Zhao, H.; Peeta, S.; Hu, S.; Wang, Y.; Zheng, Z. A car-following model for connected and automated vehicles with heterogeneous time delays under fixed and switching communication topologies. IEEE Trans. Intell. Transp. Syst. 2021, 23, 14846–14858. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Gölcük, İ.; Ozsoydan, F.B.; Durmaz, E.D. An improved arithmetic optimization algorithm for training feedforward neural networks under dynamic environments. Knowl.-Based Syst. 2023, 263, 110274. [Google Scholar] [CrossRef]
- Kathiravan, K.; Rajnarayanan, P.N. Application of AOA algorithm for optimal placement of electric vehicle charging station to minimize line losses. Electr. Power Syst. Res. 2023, 214, 108868. [Google Scholar] [CrossRef]
- Çelik, E. IEGQO-AOA: Information-exchanged gaussian arithmetic optimization algorithm with quasi-opposition learning. Knowl.-Based Syst. 2023, 260, 110169. [Google Scholar] [CrossRef]

| Authors | Information from Multiple Vehicles | Time Delay | Stability Analysis | Calibration of Relevant Parameters | Mixed Traffic |
|---|---|---|---|---|---|
| Li et al. [35] | X | X | X | X | |
| Li et al. [36] | X | X | X | X | |
| Wu et al. [37] | X | X | X | X | |
| Jia et al. [38] | X | X | X | ||
| Li et al. [39] | X | X | X | X | |
| Ma et al. [40] | X | X | |||
| This study |
| Name | Function | Range | Dimension |
|---|---|---|---|
| F1 | [−100, 100] | 30 | |
| F2 | [−10, 10] | 30 | |
| F10 | [−32, 32] | 30 | |
| F11 | [−600, 600] | 30 |
| Parameters | Description | Boundaries | Value |
|---|---|---|---|
| a0 | Maximum acceleration | [0.1,5] | 2.2 |
| b | Comfortable deceleration | [0.1,5] | 1.4 |
| s0 | Minimum headway | [0.1,10] | 3.6 |
| T | Safe time headway | [0.1,5] | 1.5 |
| λ | vehicle potential field strength coefficient | [0.1,1] | 0.11 |
| The coefficient of the safety potential field for the leading vehicle | [0.1,1] | 0.37 | |
| The coefficient of the safety potential field for the following vehicle | [0.1,1] | 0.29 |
| Model | ME | MAE | RMSE | R2 |
|---|---|---|---|---|
| IDM | 0.192 | 0.279 | 0.383 | 95.6% |
| MIDM-SPF | 0.103 | 0.249 | 0.351 | 97.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wang, W.; Mu, K.; Fan, S. Time-Delay Following Model for Connected and Automated Vehicles Considering Multiple Vehicle Safety Potential Fields. Appl. Sci. 2024, 14, 6735. https://doi.org/10.3390/app14156735
Wang Z, Wang W, Mu K, Fan S. Time-Delay Following Model for Connected and Automated Vehicles Considering Multiple Vehicle Safety Potential Fields. Applied Sciences. 2024; 14(15):6735. https://doi.org/10.3390/app14156735
Chicago/Turabian StyleWang, Zijian, Wenbo Wang, Kenan Mu, and Songhua Fan. 2024. "Time-Delay Following Model for Connected and Automated Vehicles Considering Multiple Vehicle Safety Potential Fields" Applied Sciences 14, no. 15: 6735. https://doi.org/10.3390/app14156735
APA StyleWang, Z., Wang, W., Mu, K., & Fan, S. (2024). Time-Delay Following Model for Connected and Automated Vehicles Considering Multiple Vehicle Safety Potential Fields. Applied Sciences, 14(15), 6735. https://doi.org/10.3390/app14156735







