Simulation Study on Ground Vibration Reduction Measures of the Elevated Subway Line
Abstract
1. Introduction
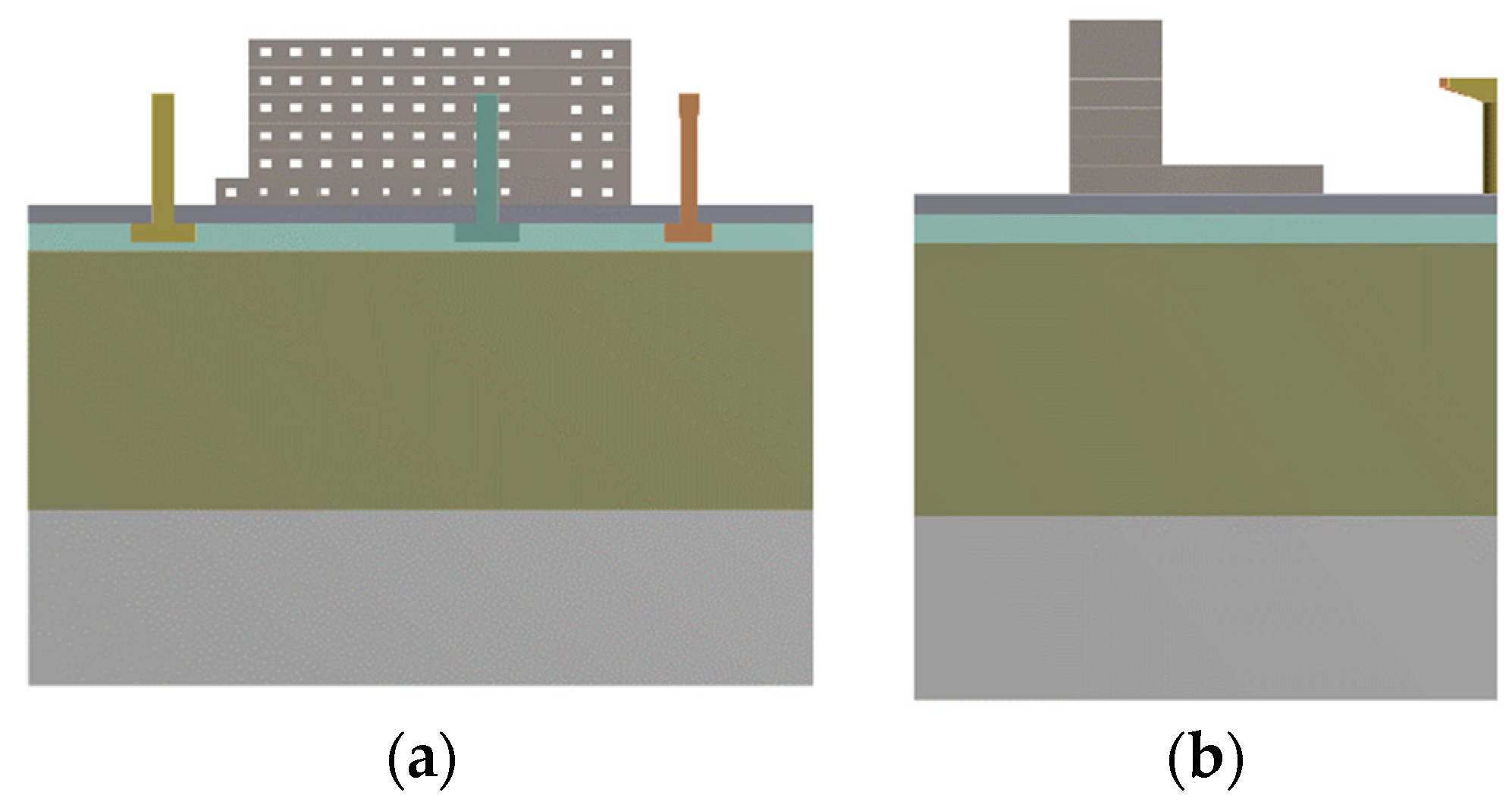
2. Numerical Model
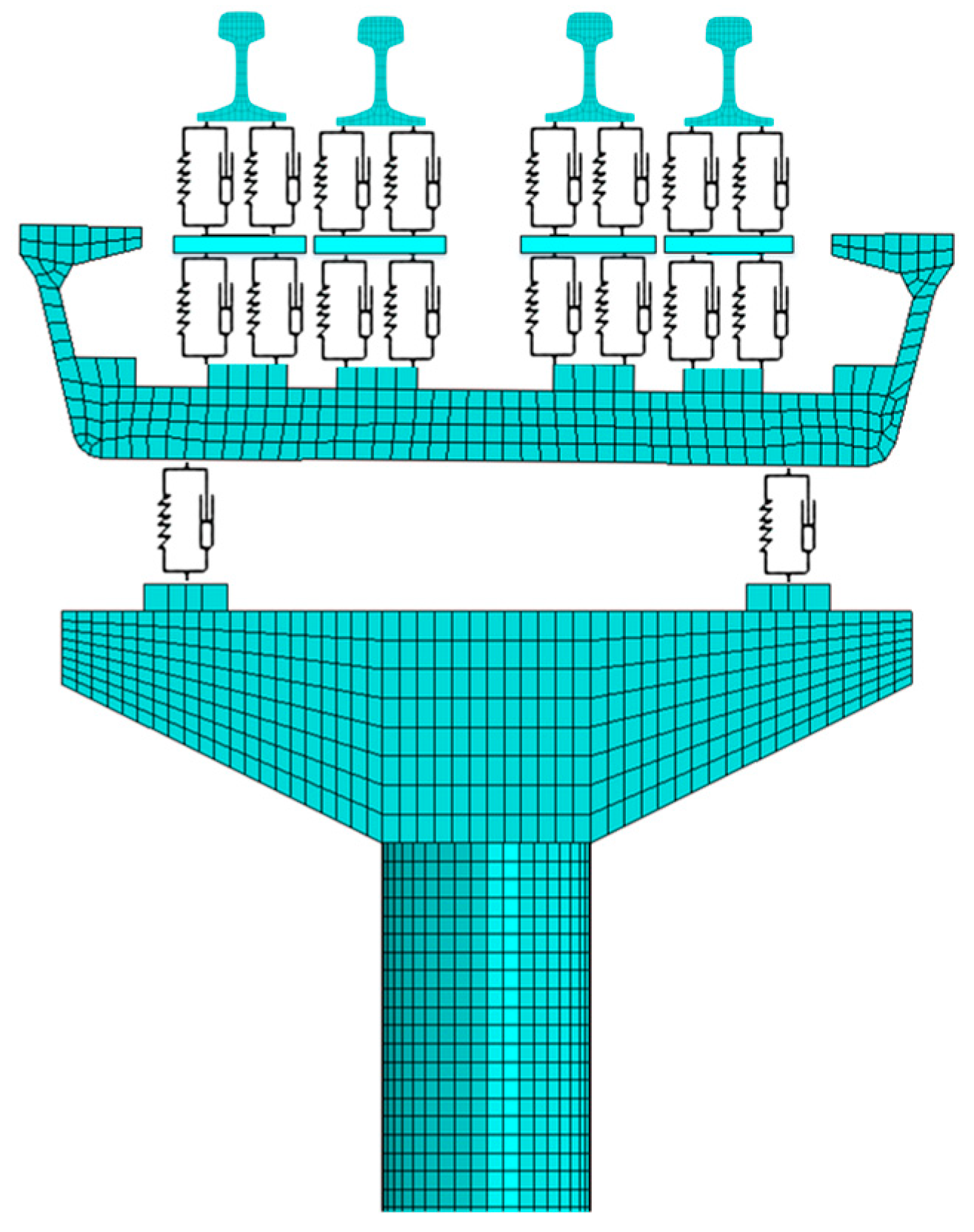
2.1. Vibration Source Model
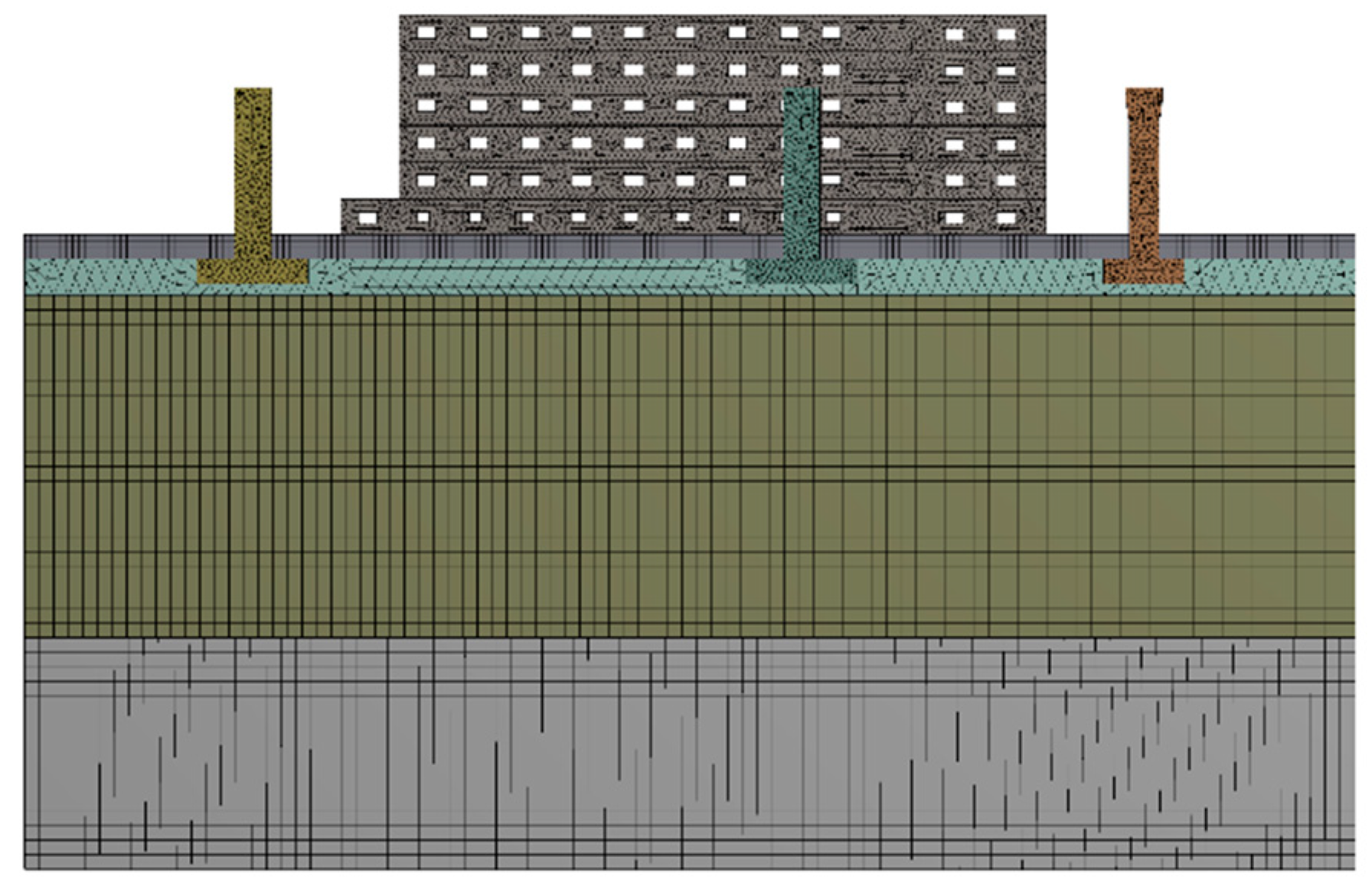
2.2. Transmission Path Model
3. Numerical Results and Discussion
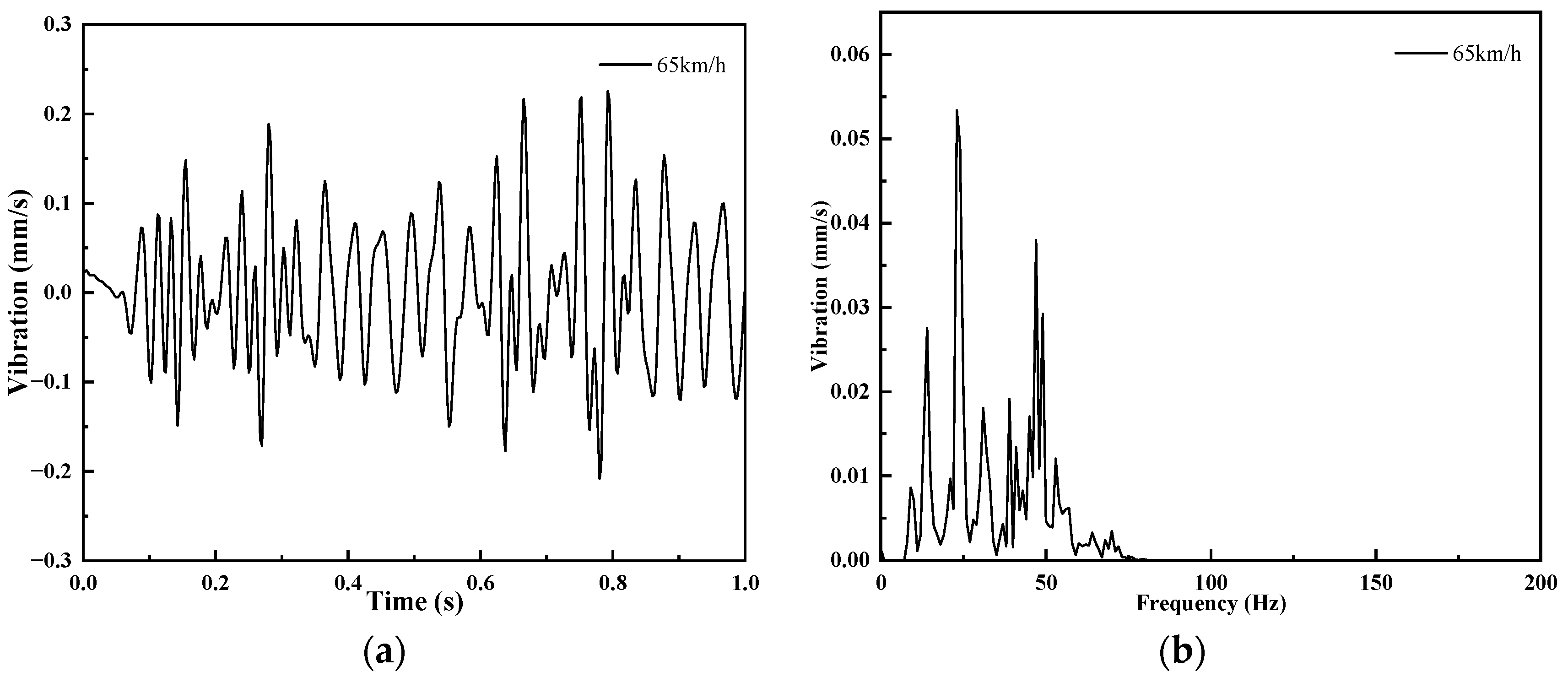
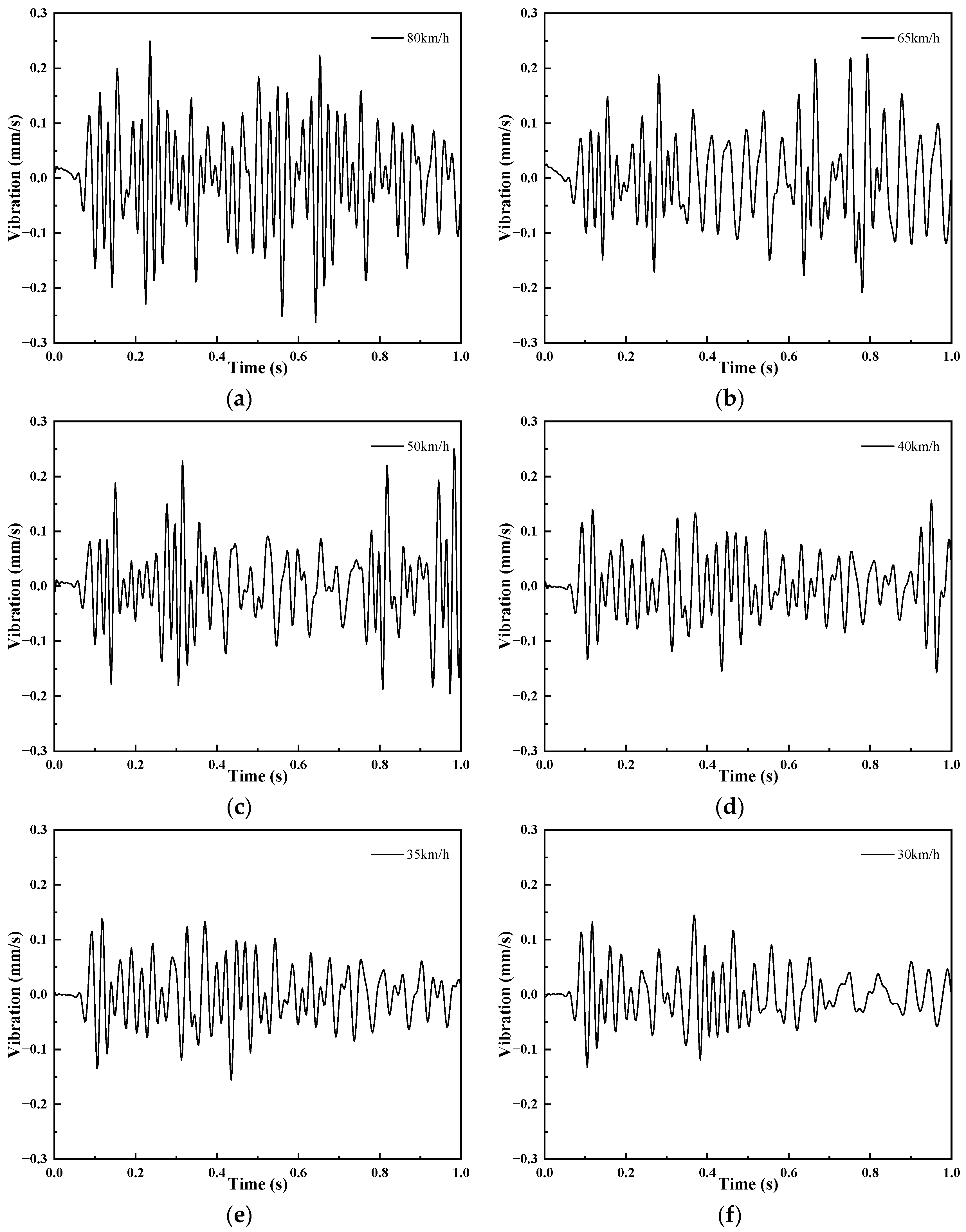
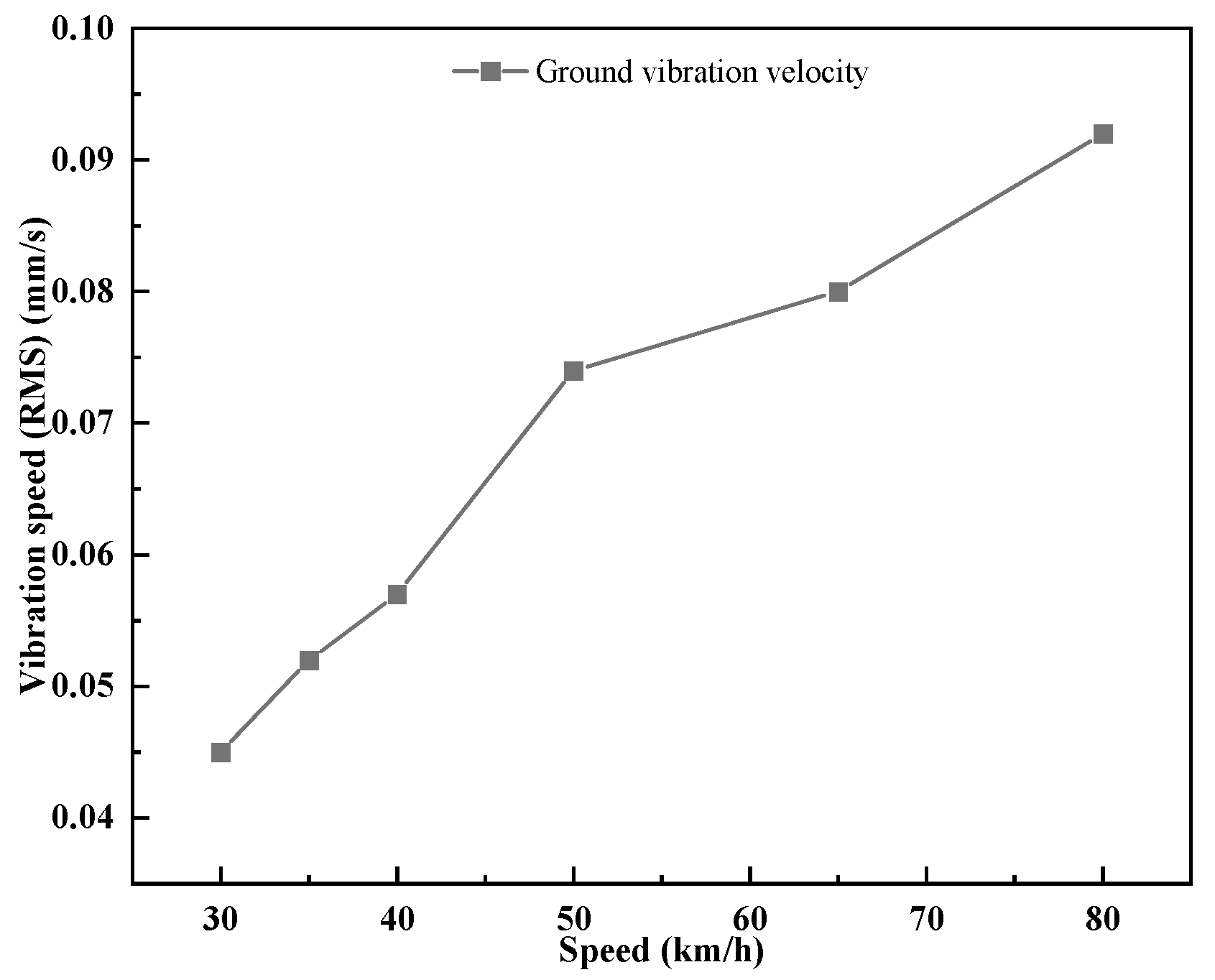
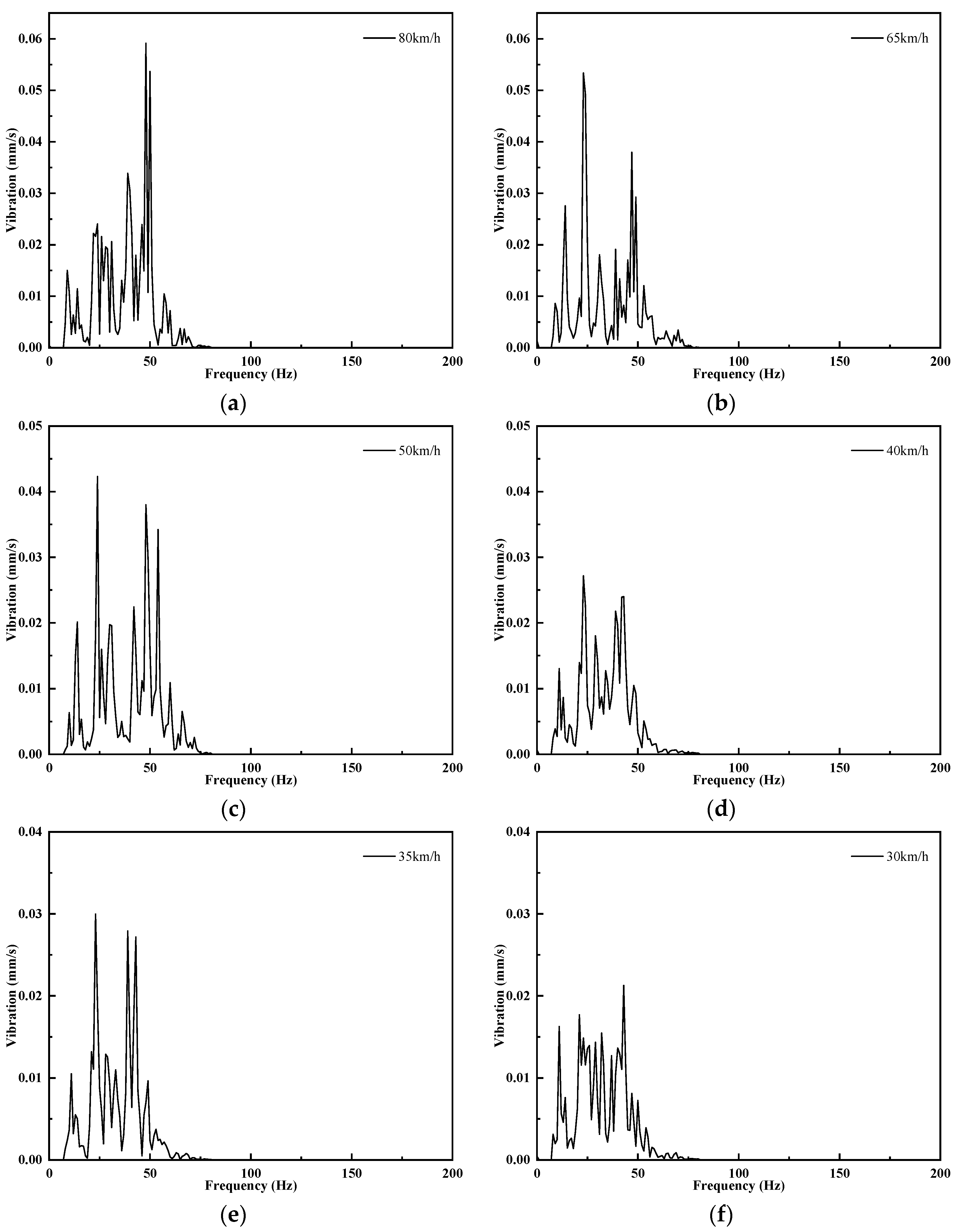
3.1. Effect of Vehicle Speed on Ground Vibration
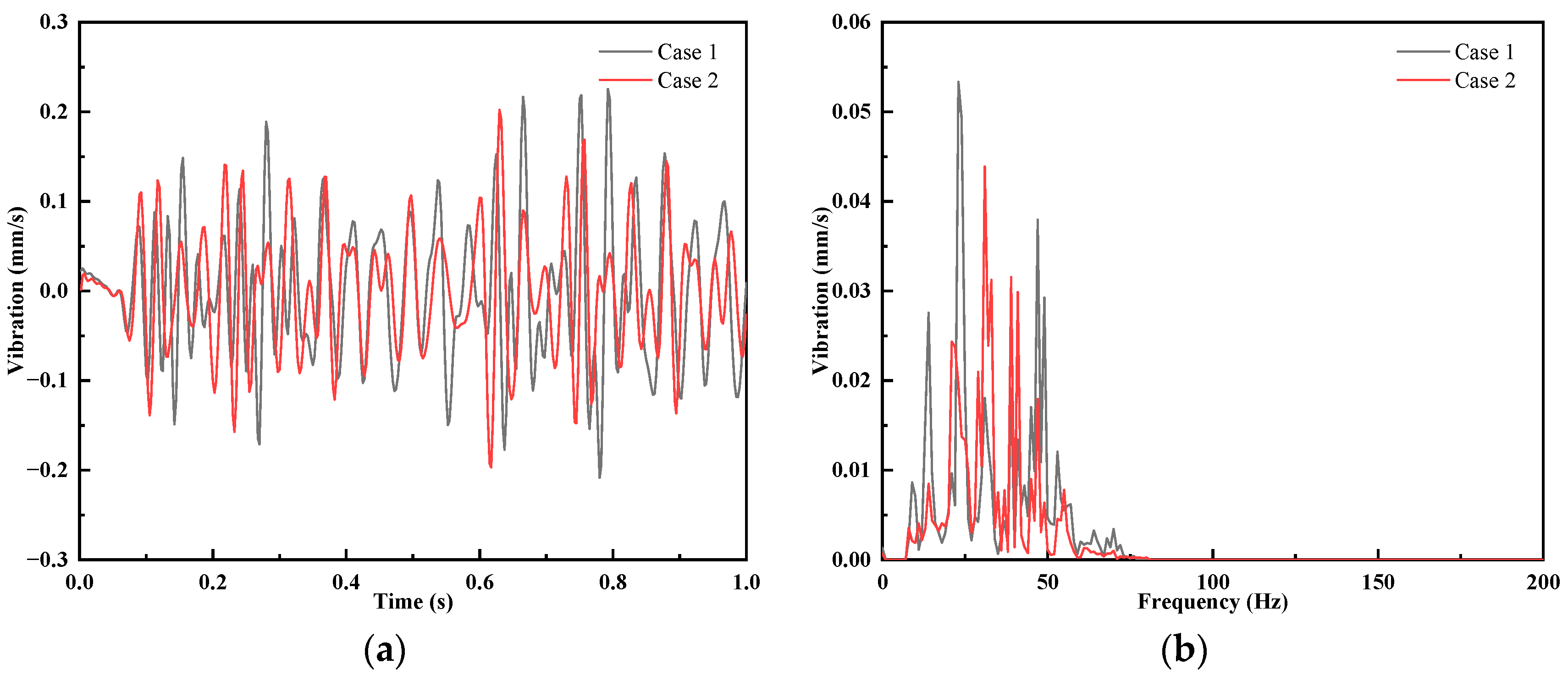
3.2. Effect of Fastener Stiffness on Ground Vibration
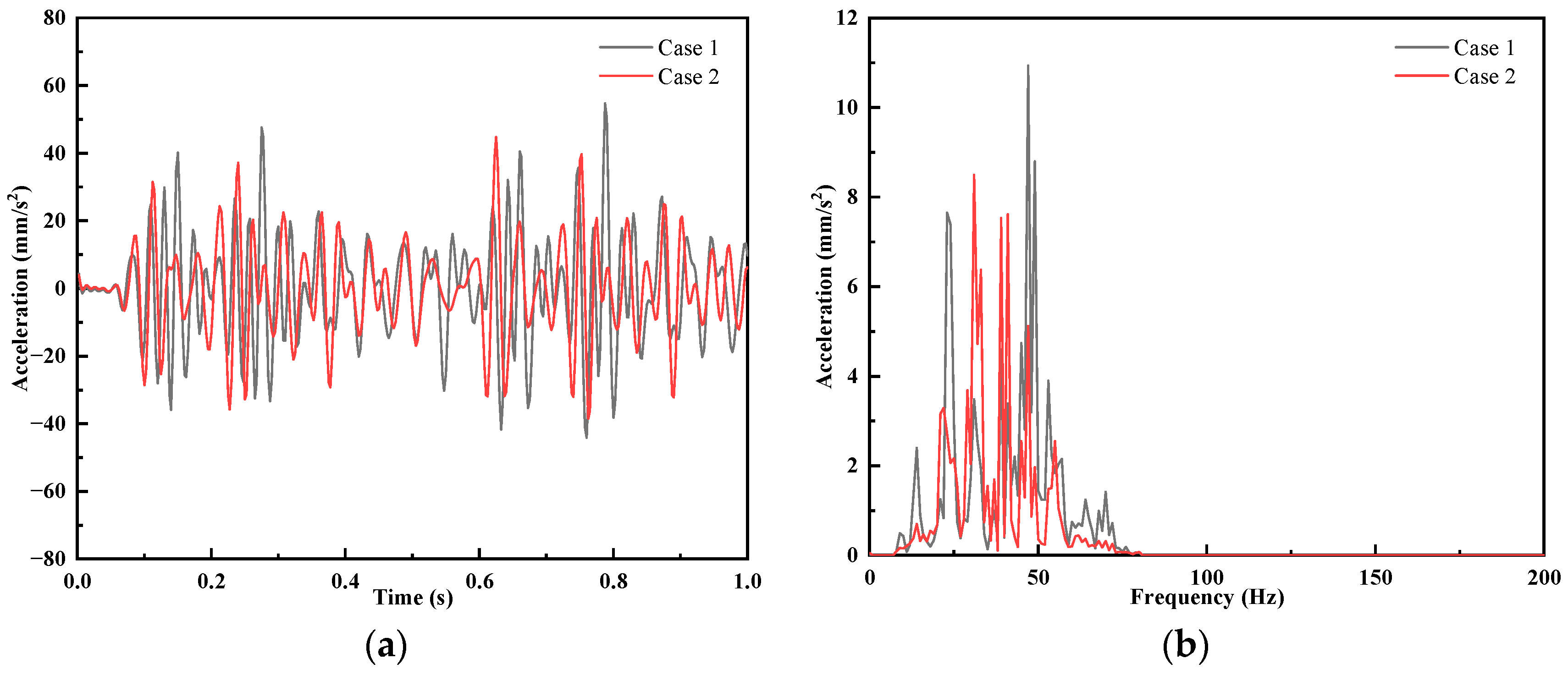
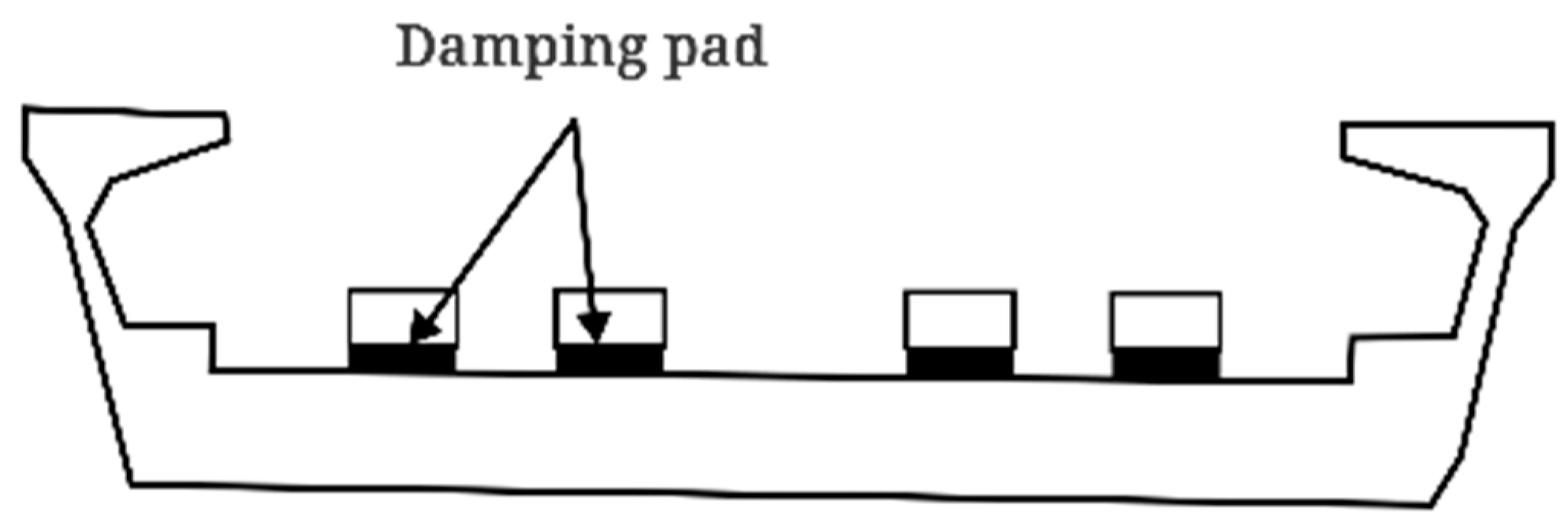
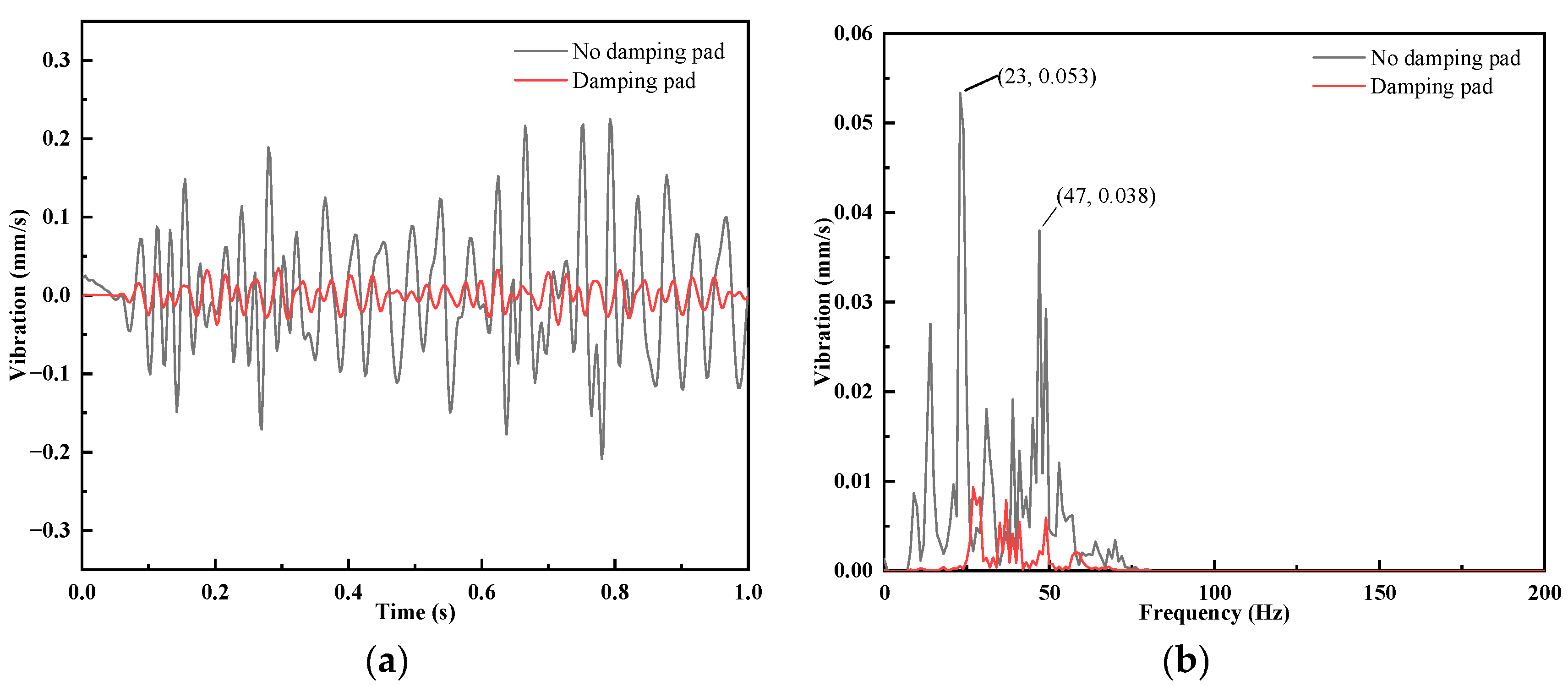
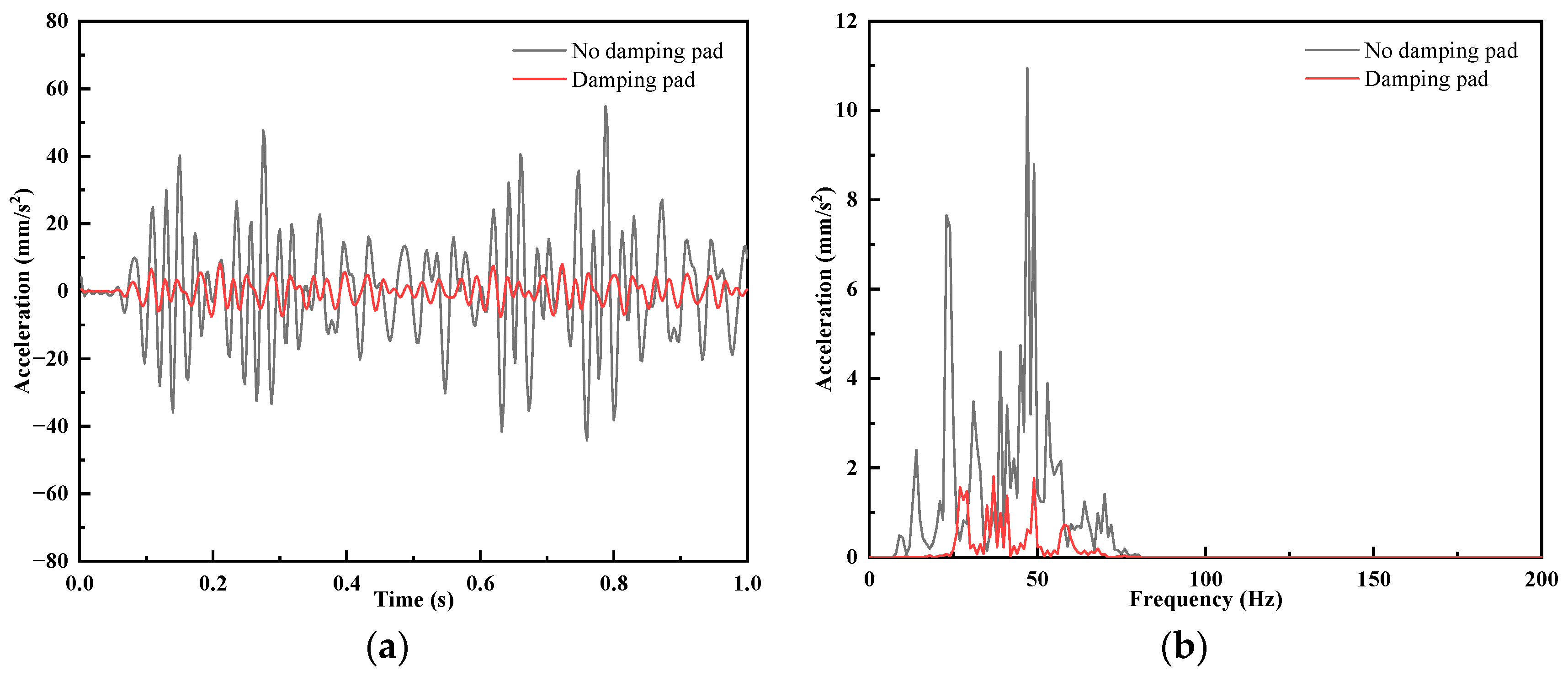
3.3. Effect of Installing Vibration Damping Pad on Ground Vibration
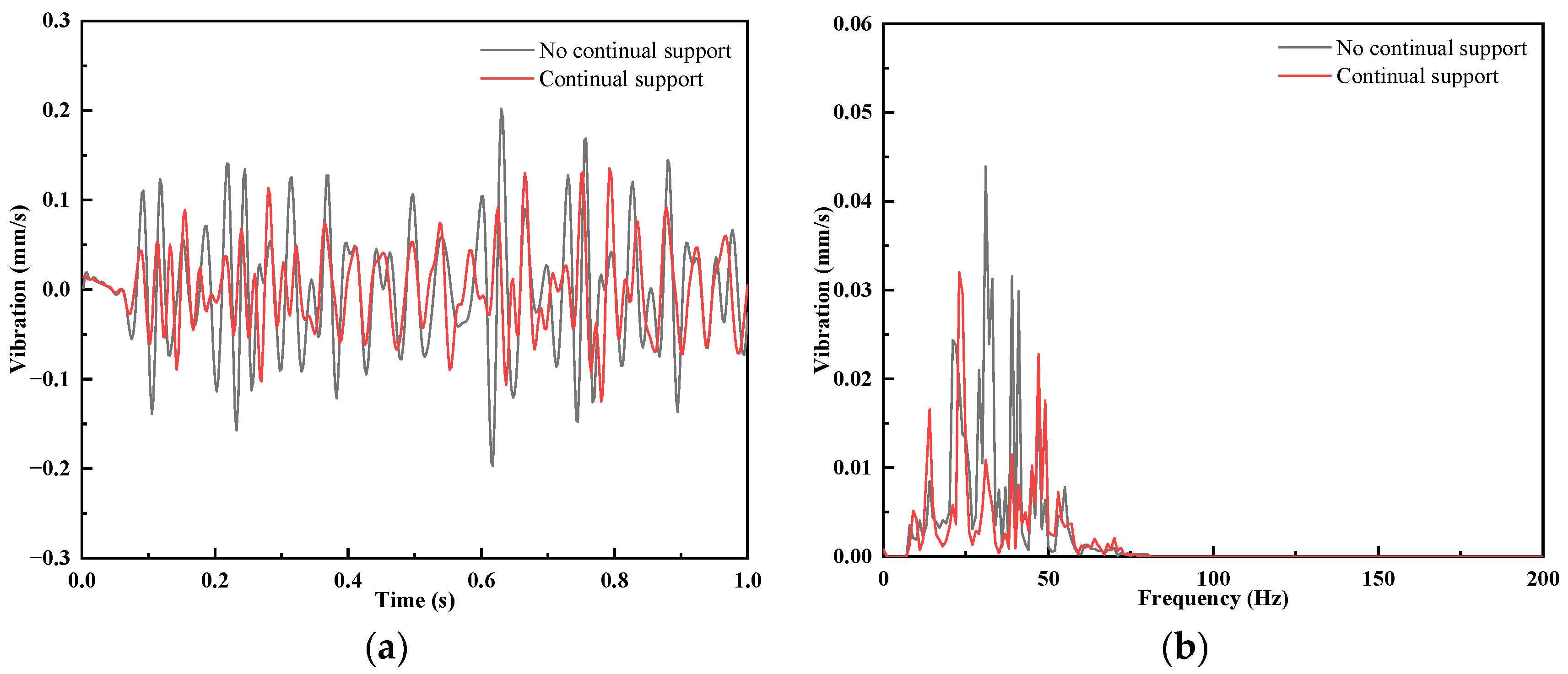
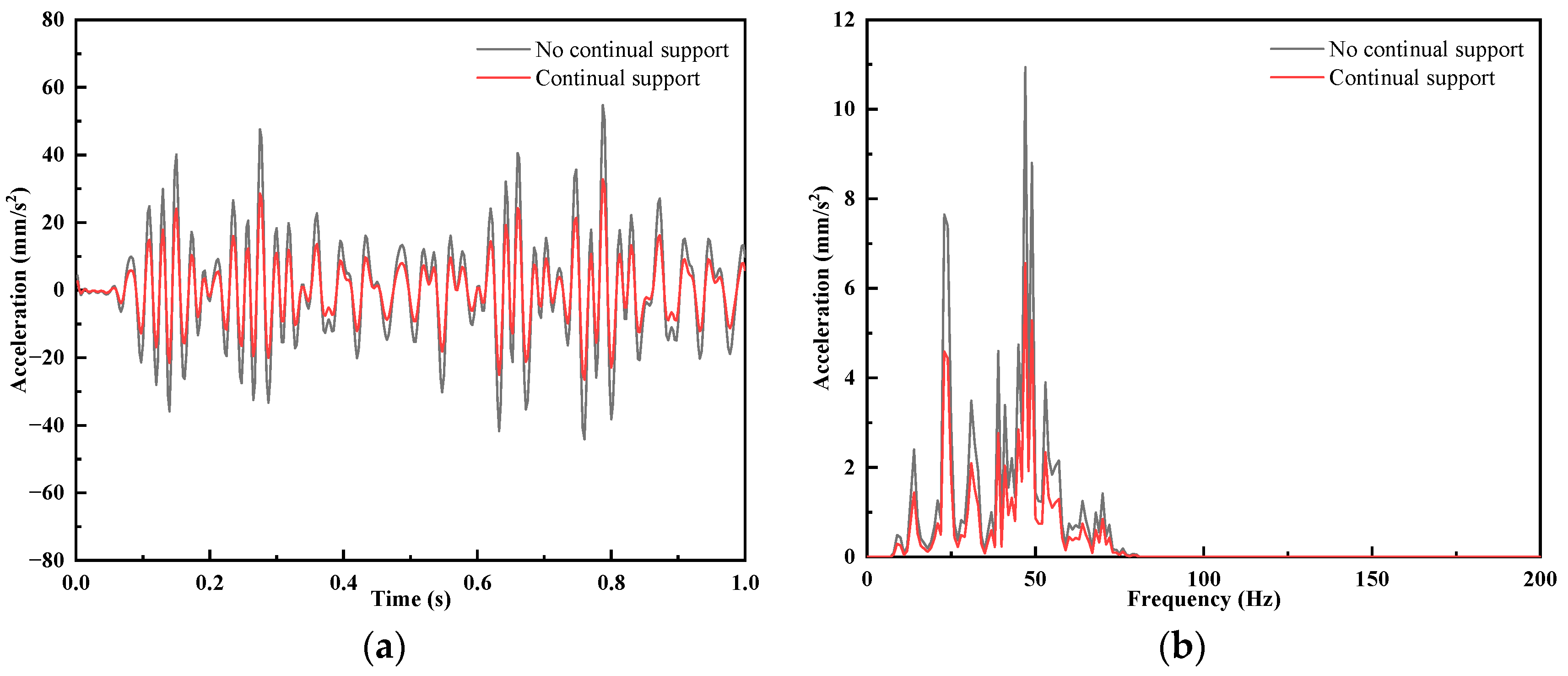
3.4. Effect of Continuous Support on Ground Vibration
4. Conclusions
- Because the building is close to the line, the ground vibration requirements near the building are high, and the existing line vibration reduction design cannot meet the environmental requirements.
- When the train running speed is reduced to 30 km/h, the ground vibration can meet the environmental limit value requirements, but the actual operating speed of the train has a greater impact. When applying vibration-damping fasteners alone, the system has the best vibration-reducing performance when the vertical stiffness of fasteners is 10 kN/mm, but it still cannot meet the requirements of ground environmental limits.
- A simulation study on the vibration reduction effect of track vibration reduction pads and a continuous support vibration reduction structure was carried out. The results show that when the vehicle running speed is 65 km/h, the vibration reduction effect of the track vibration reduction pad is outstanding, and the margin to meet the vibration limit value is larger; the vibration reduction effect of the continuous support vibration reduction structure is obvious, and the vibration reduction effect of the joint application of the fasteners and the continuous support vibration reduction structure can satisfy the vibration limit value requirement and have a reasonable margin.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Connolly, D.P.; Marecki, G.P.; Kouroussis, G.; Thalassinakis, I.; Woodward, P.K. The growth of railway ground vibration problems—A review. Sci. Total Environ. 2016, 568, 1276–1282. [Google Scholar] [CrossRef] [PubMed]
- Tao, Z.; Wang, Y.; Zou, C.; Li, Q.; Luo, Y. Assessment of ventilation noise impact from metro depot with over-track platform structure on workers and nearby inhabitants. Environ. Sci. Pollut. Res. Int. 2019, 26, 9203–9218. [Google Scholar] [CrossRef] [PubMed]
- Lopes, P.; Ruiz, J.F.; Alves Costa, P.; Medina Rodriguez, L.; Cardoso, A.S. Vibrations inside buildings due to subway railway traffic. Experimental validation of a comprehensive prediction model. Sci. Total Environ. 2016, 568, 1333–1343. [Google Scholar] [CrossRef] [PubMed]
- Xia, H.; Zhang, N. Vibration effects of light-rail train-viaduct system on surrounding environments. In Proceedings of the 4th Conference of the Eastern-Asia-Society-for-Transportation-Studies, Hanoi, Vietnam, 24–27 October 2001. [Google Scholar]
- Vogiatzis, K.; Zafiropoulou, V.; Mouzakis, H. Monitoring and assessing the effects from Metro networks construction on the urban acoustic environment: The Athens Metro Line 3 Extension. Sci. Total Environ. 2018, 639, 1360–1380. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, J.; Esmaeili, M.H.; Akbari, M. Reliability of FTA general vibration assessment model in prediction of subway induced ground borne vibrations. Soil Dyn. Earthq. Eng. 2019, 117, 300–311. [Google Scholar] [CrossRef]
- Zou, C.; Wang, Y.; Wang, P.; Guo, J. Measurement of ground and nearby building vibration and noise induced by trains in a metro depot. Sci. Total Environ. 2015, 536, 761–773. [Google Scholar] [CrossRef] [PubMed]
- Paneiro, G.; Durão, F.O.; Costa e Silva, M.; Falcão Neves, P. Prediction of ground vibration amplitudes due to urban railway traffic using quantitative and qualitative field data. Transp. Res. Part D Transp. Environ. 2015, 40, 1–13. [Google Scholar] [CrossRef]
- Sheng, X. A review on modelling ground vibrations generated by underground trains. Int. J. Rail Transp. 2019, 7, 241–261. [Google Scholar] [CrossRef]
- Xing, M.; Zhao, C.; Wang, P.; Lu, J.; Yi, Q. A Numerical Analysis of Ground Vibration Induced by Typical Rail Corrugation of Underground Subway. Shock Vib. 2019, 2019, 8406813. [Google Scholar] [CrossRef]
- Kedia, N.K.; Kumar, A.; Singh, Y. Development of Empirical Relations to Predict Ground Vibrations due to Underground Metro Trains. KSCE J. Civ. Eng. 2023, 27, 251–260. [Google Scholar] [CrossRef]
- Xu, L.; Ma, M. Vibration amplification zone phenomenon on the ground surface under various types of buried dynamic loads within metro tunnel. Soil Dyn. Earthq. Eng. 2024, 182, 108713. [Google Scholar] [CrossRef]
- Li, Z.; Yang, X.; Zhang, S.; Yu, Y.; Lin, Y.; Wu, J. Analysis of Soil Differences in Subway Vibration Transmission Paths. Buildings 2024, 14, 1338. [Google Scholar] [CrossRef]
- Ma, L.X.; Yu, Y.X.; Li, H.Y.; Yang, H. Investigation of Metro Train-Induced Environmental Vibration Using a Coupled Sliced Finite Element-Infinite Element Model. KSCE J. Civ. Eng. 2024, 28, 2380–2398. [Google Scholar] [CrossRef]
- Deng, E.; Liu, X.-Y.; Ni, Y.-Q.; Wang, Y.-W.; Zhao, C.-Y. A coupling analysis method of foundation soil dynamic responses induced by metro train based on PDEM and stochastic field theory. Comput. Geotech. 2023, 154, 105180. [Google Scholar] [CrossRef]
- Ma, M.; Xu, L.; Liu, W.; Tan, X. Semi-analytical solution of a coupled tunnel-soil periodic model with a track slab under a moving train load. Appl. Math. Model. 2024, 128, 588–608. [Google Scholar] [CrossRef]
- He, Y.; Zhang, Y.; Yao, Y.; He, Y.; Sheng, X. Review on the Prediction and Control of Structural Vibration and Noise in Buildings Caused by Rail Transit. Buildings 2023, 13, 2310. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, S. Impact source localization and vibration intensity prediction on construction sites. Measurement 2021, 175, 109148. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, Q.; Shi, Z. Floating slab track with inerter enhanced dynamic vibration absorbers. Veh. Syst. Dyn. 2023, 61, 589–615. [Google Scholar] [CrossRef]
- Sheng, T.; Bian, X.-c.; Xiao, C.; Chen, Y.; Liu, G.-b.; Li, Y. Experimental study on a geosynthetics isolator for the base vibration isolation of buildings neighboring metro transportation. Geotext. Geomembr. 2021, 49, 1066–1078. [Google Scholar] [CrossRef]
- Sun, X.; Ma, M.; Jiang, B.; Cao, R. Ground vibration from freight railway: Environmental impact and potential mitigation measure at propagation path. Environ. Sci. Pollut. Res. 2022, 29, 44364–44377. [Google Scholar] [CrossRef]
- He, W.; Zou, C.; Pang, Y.T.; Wang, X.M. Environmental noise and vibration characteristics of rubber-spring floating slab track. Environ. Sci. Pollut. Res. 2021, 28, 13671–13689. [Google Scholar] [CrossRef]
- Thompson, D.; Jones, C. Reply to Comments on Chapter 12 of “Railway Noise and Vibration: Mechanisms, Modelling and Means of Control”, by D. Thompson (with contributions from C. Jones and P.-E. Gautier), Elsevier, 2009. Appl. Acoust. 2011, 72, 787–788. [Google Scholar] [CrossRef]
- Alves Costa, P.; Calçada, R.; Silva Cardoso, A. Ballast mats for the reduction of railway traffic vibrations. Numerical study. Soil Dyn. Earthq. Eng. 2012, 42, 137–150. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, S.; Zhai, W.; Kouroussis, G.; Wang, Y.; Wang, K.; Lan, K.; Xu, F. Prediction and mitigation of train-induced vibrations of large-scale building constructed on subway tunnel. Sci. Total Environ. 2019, 668, 485–499. [Google Scholar] [CrossRef] [PubMed]
- Hou, B.W.; Gao, L.; Xin, T.; Cai, X.P. Prediction of structural vibrations using a coupled vehicle-track-building model. Proc. Inst. Mech. Eng. Part F-J. Rail Rapid Transit 2016, 230, 510–530. [Google Scholar] [CrossRef]
- Guo, T.; Cao, Z.; Zhang, Z.; Li, A. Numerical simulation of floor vibrations of a metro depot under moving subway trains. J. Vib. Control 2017, 24, 4353–4366. [Google Scholar] [CrossRef]
- Zhao, C.; Shi, D.; Zheng, J.; Niu, Y.; Wang, P. New floating slab track isolator for vibration reduction using particle damping vibration absorption and bandgap vibration resistance. Constr. Build. Mater. 2022, 336, 127561. [Google Scholar] [CrossRef]
- Li, Z.; Ma, M.; Liu, K.; Jiang, B. Performance of rubber-concrete composite periodic barriers applied in attenuating ground vibrations induced by metro trains. Eng. Struct. 2023, 285, 116027. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J.; Chen, H.; Ou, J. Mitigating train-induced building vibrations with rubber bearings designed for horizontal earthquake isolation. J. Build. Eng. 2024, 89, 109251. [Google Scholar] [CrossRef]
- Wang, T.; Jiang, B.; Sun, X. Train-Induced Vibration Prediction and Control of a Metro Depot and Over-Track Buildings. Buildings 2023, 13, 1995. [Google Scholar] [CrossRef]
- ISO 2631-1:1997; Mechanical Vibration and Shock e Evaluation of Human Exposure to Whole-body Vibration e Part 1: General Requirements. WHO: Geneva, Switzerland, 1997.




| Parameter Name | Numerical Value | Unit |
|---|---|---|
| Mass of car body | 49.52 | t |
| Mass moment of inertia of car body roll | 80 | t·m2 |
| Mass moment of inertia of car body pitch | 1836 | t·m2 |
| Mass moment of inertia of car body yaw | 1835 | t·m2 |
| Car body center of gravity coordinates | 2.056 | m |
| Mass of bogie | 4387 | kg |
| Mass moment of inertia of car body yaw | 1847.4 | kg·m2 |
| Mass moment of inertia of car body yaw | 3903.8 | kg·m2 |
| Mass moment of inertia of car body yaw | 5583.4 | kg·m2 |
| Mass of wheelset | 1443 | kg |
| Longitudinal stiffness of primary suspension | 5.2 | MN/m |
| Lateral stiffness of primary suspension | 5.2 | MN/m |
| Vertical stiffness of primary suspension | 0.95 | MN/m |
| Longitudinal damping of primary suspension | 15 | kN·s/m |
| Lateral damping of primary suspension | 2 | kN·s/m |
| Vertical damping of primary suspension | 20 | kN·s/m |
| Longitudinal stiffness of secondary suspension | 0.148 | MN/m |
| Lateral stiffness of secondary suspension | 0.148 | MN/m |
| Vertical stiffness of secondary suspension | 0.452 | MN/m |
| Longitudinal damping of secondary suspension | 50 | kN·s/m |
| Lateral damping of secondary suspension | 32 | kN·s/m |
| Vertical damping of secondary suspension | 32 | kN·s/m |
| Component | Density (kgm−3) | Elastic Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|
| Wheelset | 7800 | 206 | 0.3 |
| Steel rail | 7800 | 206 | 0.3 |
| U-shaped bridge | 2450 | 37 | 0.2 |
| Pier | 2450 | 37 | 0.2 |
| Soil Layer | Density (kgm−3) | Poisson’s Ratio | Shear Wave Velocity (m/s) | Shear Modulus (GPa) | Elastic Modulus (GPa) |
|---|---|---|---|---|---|
| First layer | 1930 | 0.35 | 130 | 0.102 | 0.276 |
| Second layer | 1850 | 0.35 | 260 | 0.134 | 0.363 |
| Third layer | 1841 | 0.36 | 270 | 0.134 | 0.365 |
| Fourth layer | 1839 | 0.35 | 201 | 0.072 | 0.200 |
| Scheme | Speed (km/h) | Distance (m) | Vibration Velocity (mm/s) | Vibration Velocity Limits (mm/s) |
|---|---|---|---|---|
| 1 | 80 | 18.5 | 0.092 | 0.05 |
| 2 | 65 | 18.5 | 0.08 | 0.05 |
| 3 | 50 | 18.5 | 0.074 | 0.05 |
| 4 | 40 | 18.5 | 0.057 | 0.05 |
| 5 | 35 | 18.5 | 0.052 | 0.05 |
| 6 | 30 | 18.5 | 0.045 | 0.05 |
| Scheme | Speed (km/h) | Fastener parameters | Vibration Velocity (mm/s) | |||
|---|---|---|---|---|---|---|
| Vertical Stiffness (N/m) | Lateral Stiffness (N/m) | Vertical Damping (Ns/m) | Lateral Damping (Ns/m) | |||
| Case 1 | 65 | 12.07 × 106 | 13.5 × 106 | 1361.12 | 947.27 | 0.08 |
| Case 2 | 65 | 10 × 106 | 32 × 106 | 1861.12 | 1474.27 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Tang, Z.; Song, L.; Li, L.; Lin, H.; Hu, X. Simulation Study on Ground Vibration Reduction Measures of the Elevated Subway Line. Appl. Sci. 2024, 14, 6706. https://doi.org/10.3390/app14156706
Wang H, Tang Z, Song L, Li L, Lin H, Hu X. Simulation Study on Ground Vibration Reduction Measures of the Elevated Subway Line. Applied Sciences. 2024; 14(15):6706. https://doi.org/10.3390/app14156706
Chicago/Turabian StyleWang, Hao, Ziqi Tang, Leiming Song, Ling Li, Hao Lin, and Xiaojun Hu. 2024. "Simulation Study on Ground Vibration Reduction Measures of the Elevated Subway Line" Applied Sciences 14, no. 15: 6706. https://doi.org/10.3390/app14156706
APA StyleWang, H., Tang, Z., Song, L., Li, L., Lin, H., & Hu, X. (2024). Simulation Study on Ground Vibration Reduction Measures of the Elevated Subway Line. Applied Sciences, 14(15), 6706. https://doi.org/10.3390/app14156706






