Aerodynamic Optimization and Characterization of a Ducted Tail for a Box-Launched Aircraft
Abstract
1. Introduction
2. Research Object and Problem Description
3. Parametric Modeling and Numerical Simulation Methods
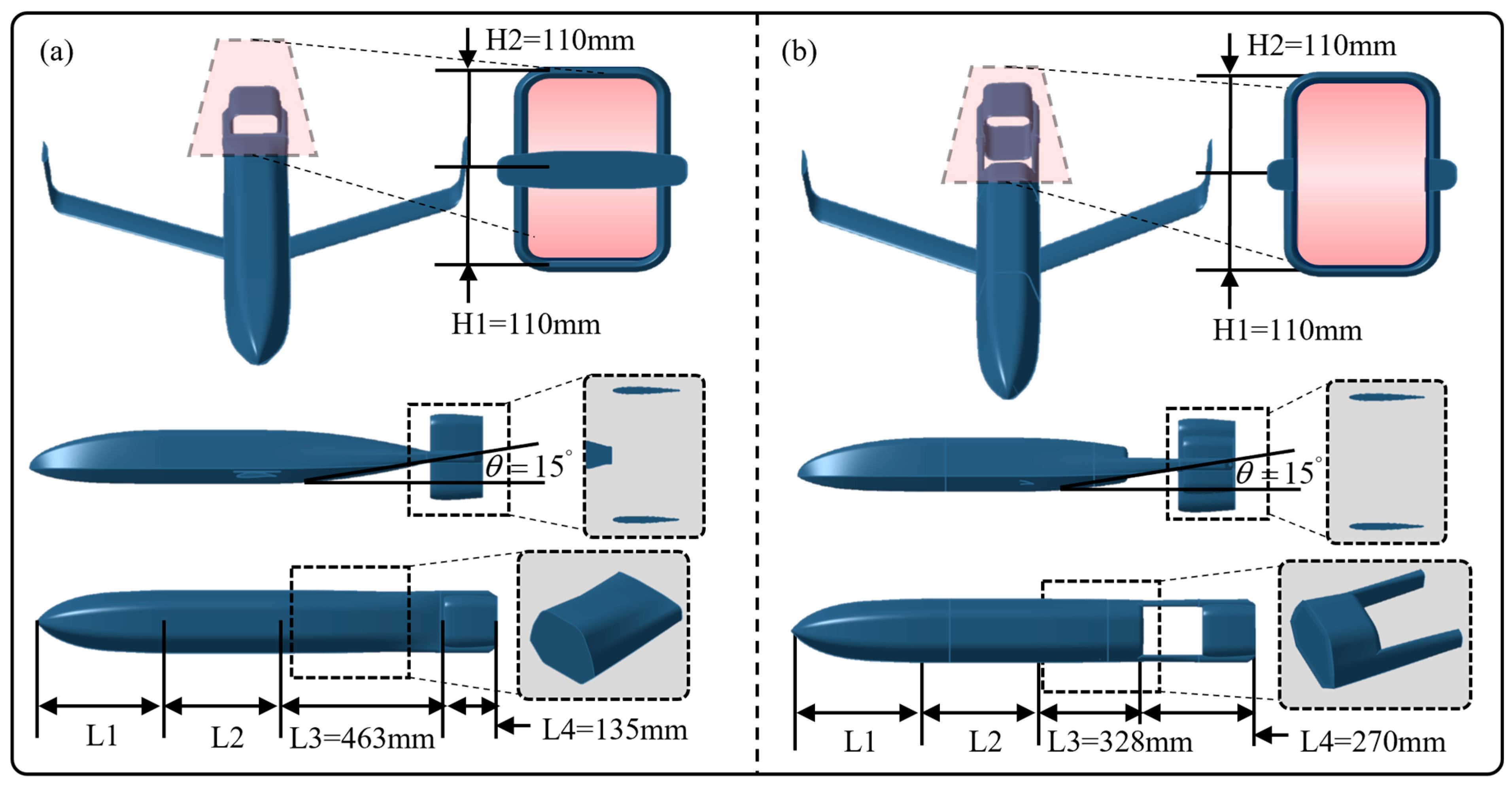
3.1. Parametric Modeling
3.2. Numerical Simulation and Mesh-Independent Analysis
3.2.1. CFD Method Validation
3.2.2. Mesh-Independent Analysis
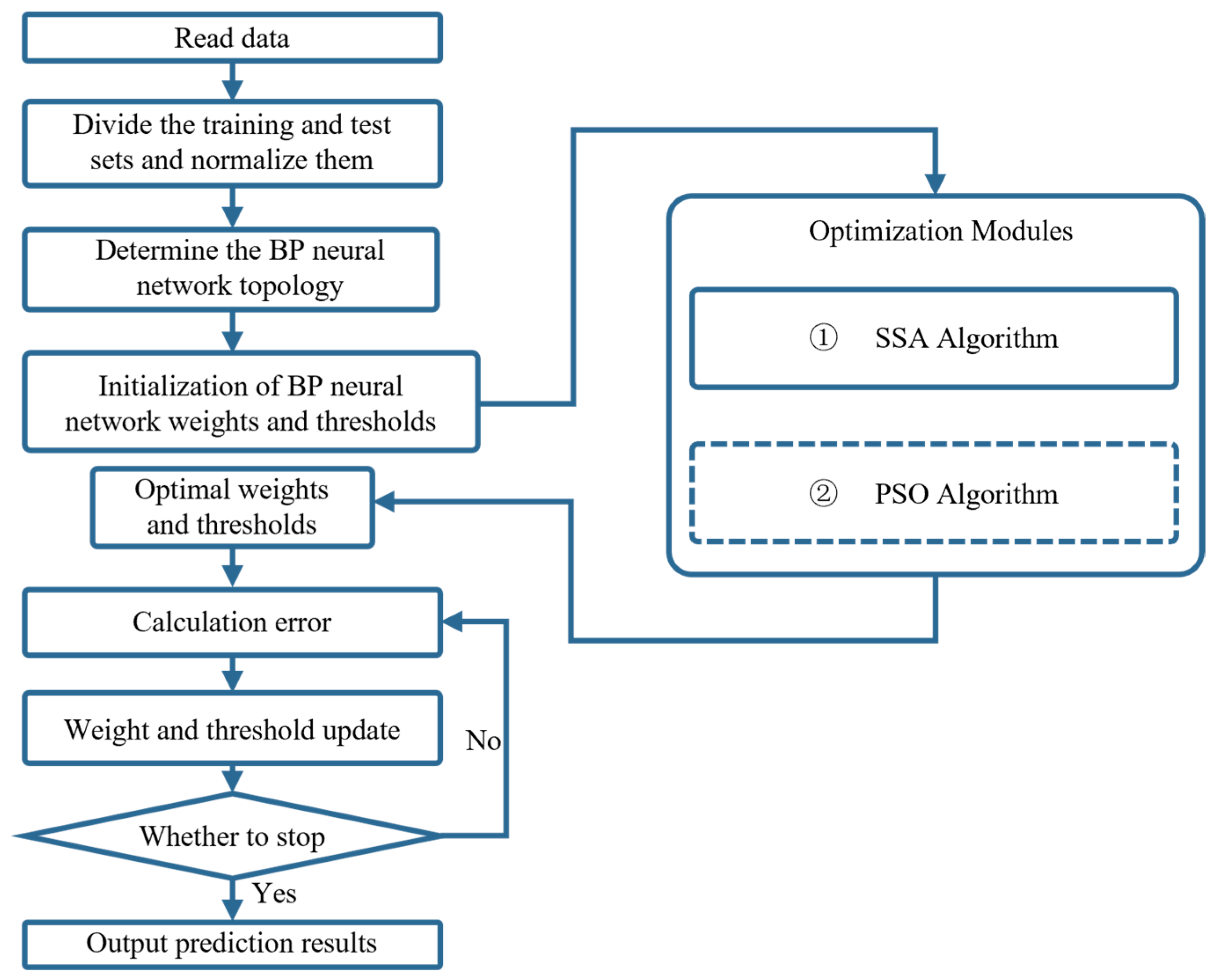
4. Aerodynamic Optimization
4.1. General Optimization Framework
4.2. Design of the Experiment
4.3. Approximate Model Selection
4.4. Optimization Design Method Based on Multi-Objective Genetic Algorithm
5. Optimization Result Analysis
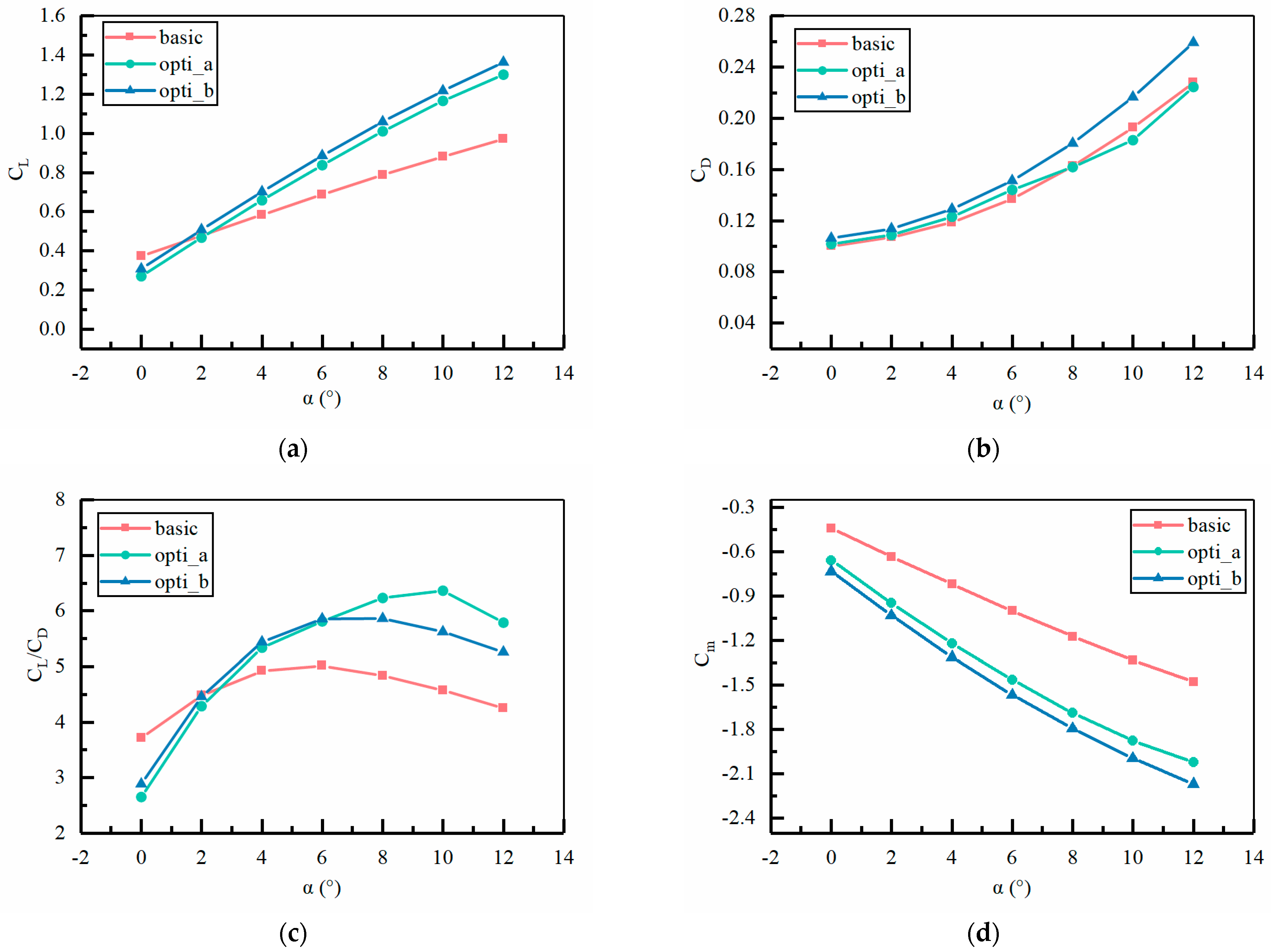
5.1. Discussion of Optimization Results for Ducted Tail Position
5.1.1. Effect of L4 on Tail Aerodynamic Performance
5.1.2. Effect of H1 on Tail Aerodynamic Performance
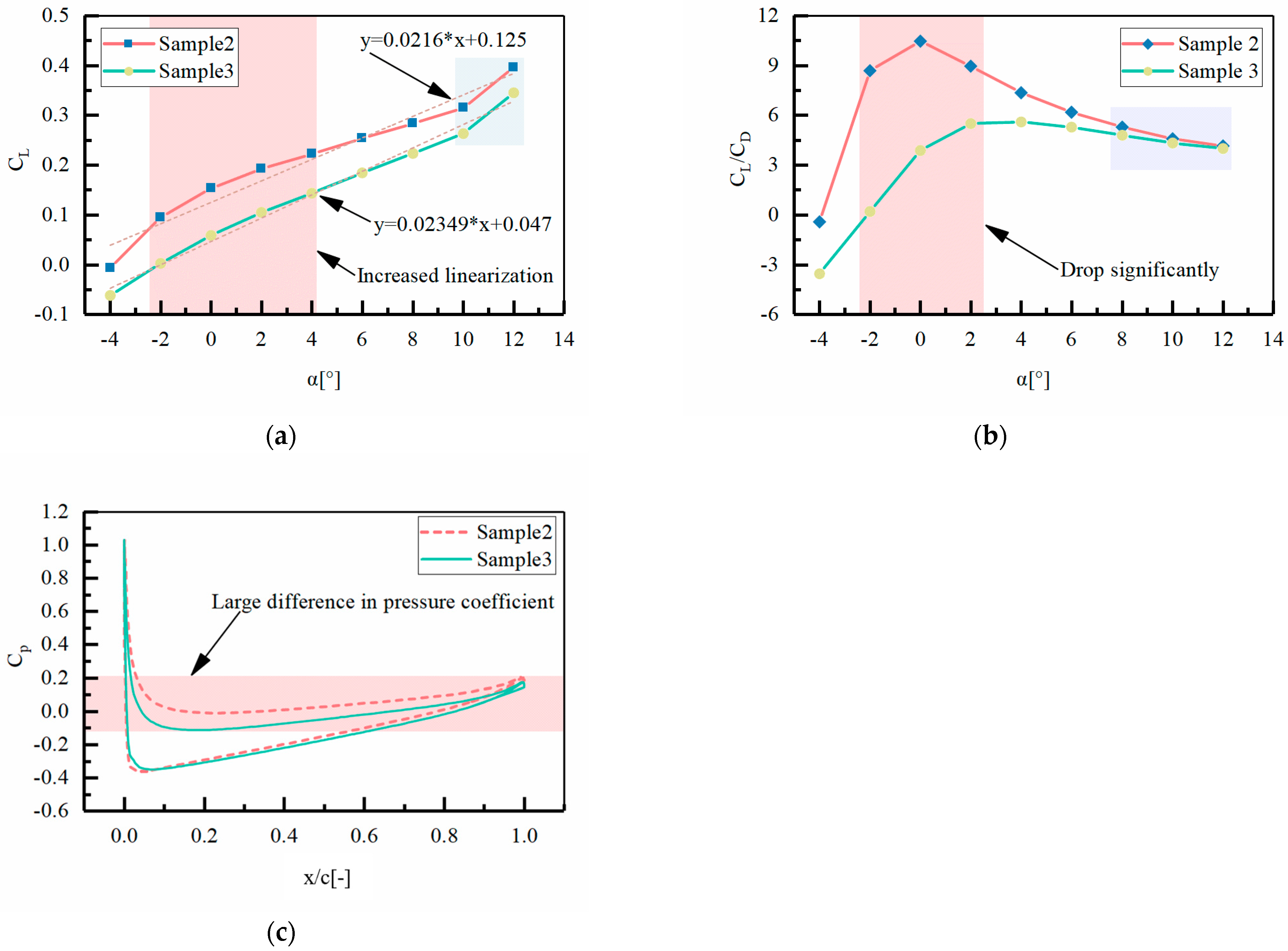
5.1.3. Effect of L4 and H1 on Tail Aerodynamic Performance
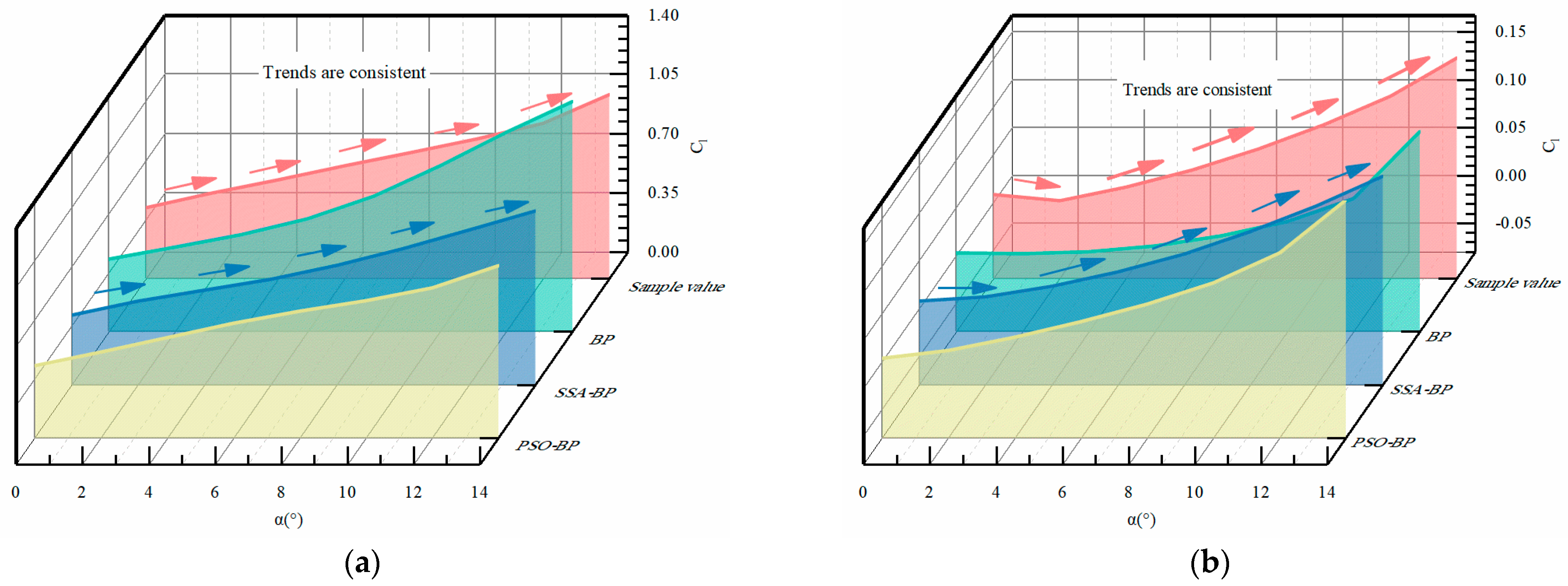
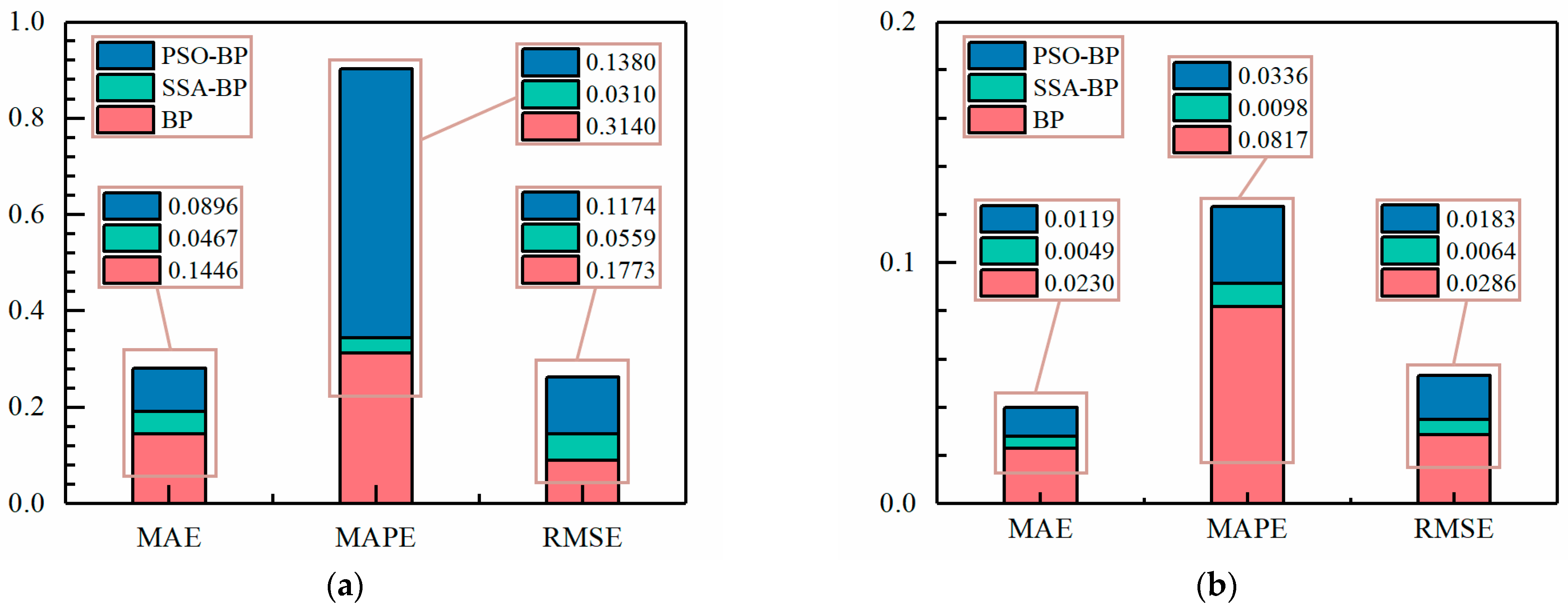
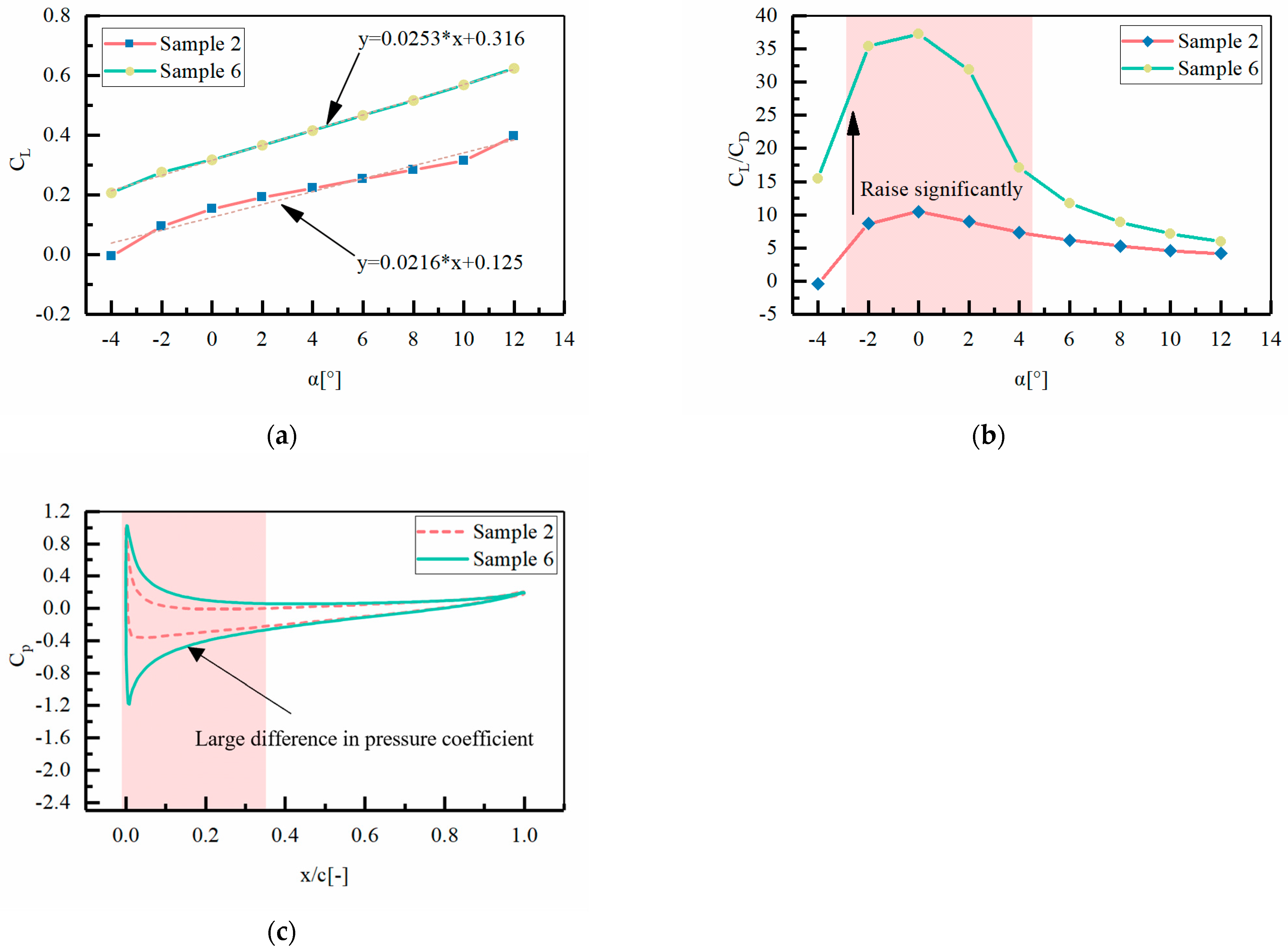
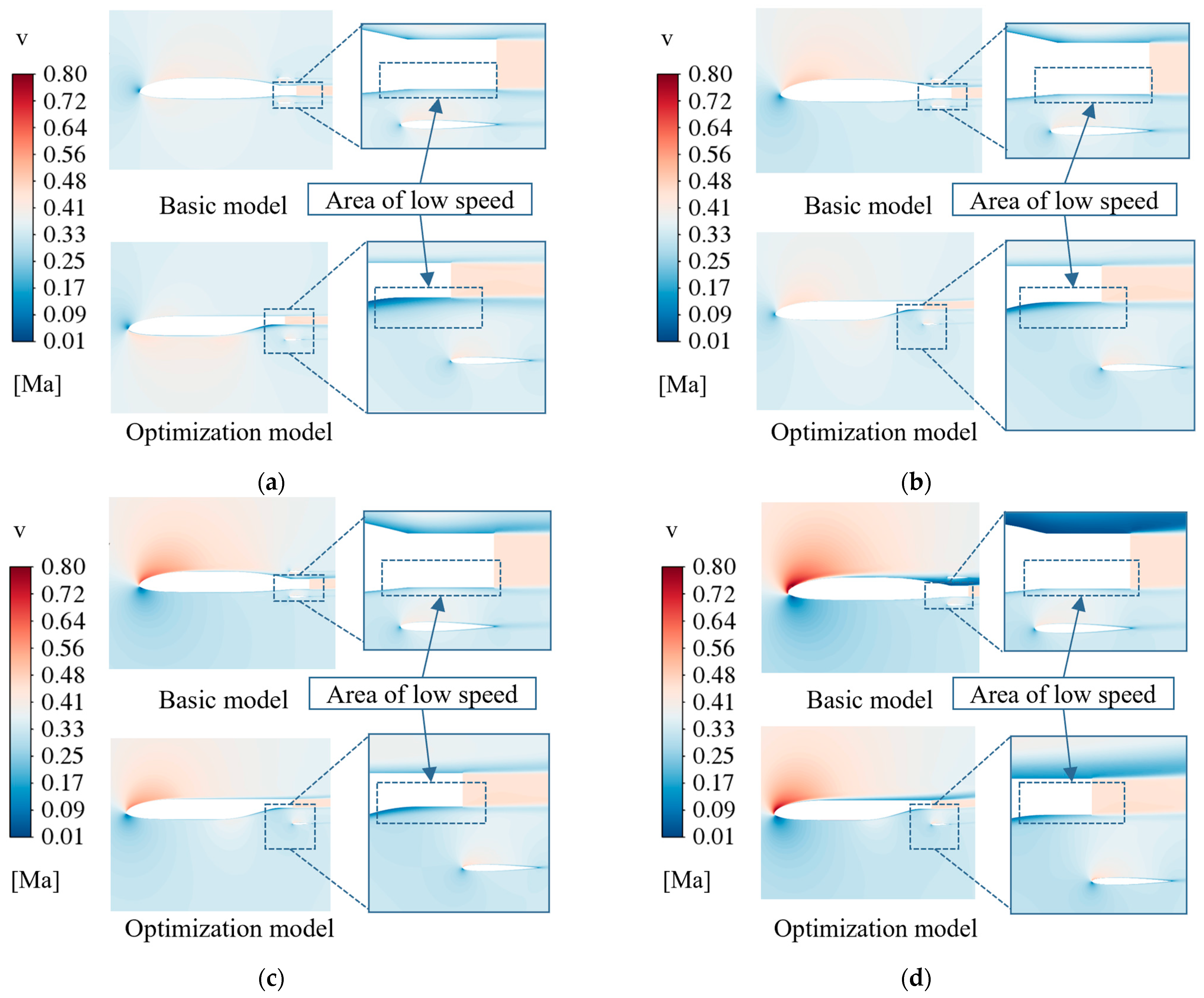
5.2. Discussion of Aerodynamic Optimization Results for Tail Trimming
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chang, M.; Sun, Y.; Bai, J. Aerodynamic Design Optimization of Twice Folding Wing for Tube-Launched UAV Constrained by Flat-Angle Rotation Mechanism. ACTA Aeronaut. Astronaut. Sin. 2022, 43, 526331. [Google Scholar] [CrossRef]
- UAVs: Launch and Recovery. Air Space Eur. 1999, 1, 59–62. [CrossRef]
- Devi, P.A.; Priyadarsini, C.I.; Avvari, C. Design of Folded Wing Mechanism for Unmanned Aerial Vehicle (UAV). Mater. Today Proc. 2022, 62, 4117–4125. [Google Scholar] [CrossRef]
- Zhao, J.; Zeng, L.; Shao, X. A Novel Prediction Method for Unsteady Aerodynamic Force on Three-Dimensional Folding Wing Aircraft. Aerosp. Sci. Technol. 2023, 137, 108287. [Google Scholar] [CrossRef]
- Zhu, Z.; Guo, H.; Ma, J. Aerodynamic Layout Optimization Design of a Barrel-Launched UAV Wing Considering Control Capability of Multiple Control Surfaces. Aerosp. Sci. Technol. 2019, 93, 105297. [Google Scholar] [CrossRef]
- Quintana, A.; Graves, G.; Hassanalian, M.; Abdelkefi, A. Aerodynamic Analysis and Structural Integrity for Optimal Performance of Sweeping and Spanning Morphing Unmanned Air Vehicles. Aerosp. Sci. Technol. 2021, 110, 106458. [Google Scholar] [CrossRef]
- Zhang, B.; Guo, J.; Wang, H.; Tang, S. Autonomous Morphing Strategy for a Long-Range Aircraft Using Reinforcement Learning. Aerosp. Sci. Technol. 2024, 148, 109087. [Google Scholar] [CrossRef]
- Xu, W.; Li, Y.; Pei, B.; Yu, Z. Coordinated Intelligent Control of the Flight Control System and Shape Change of Variable Sweep Morphing Aircraft Based on Dueling-DQN. Aerosp. Sci. Technol. 2022, 130, 107898. [Google Scholar] [CrossRef]
- Chen, X.; Li, C.; Gong, C.; Gu, L.; RONCH, A.D. A Study of Morphing Aircraft on Morphing Rules along Trajectory. Chin. J. Aeronaut. 2021, 34, 232–243. [Google Scholar] [CrossRef]
- Wang, E.; Lu, H.; Zhang, J.; Wang, C.; Qiao, J. A Novel Adaptive Coordinated Tracking Control Scheme for a Morphing Aircraft with Telescopic Wings. Chin. J. Aeronaut. 2024, 37, 148–162. [Google Scholar] [CrossRef]
- Yan, B.; Dai, P.; Liu, R.; Xing, M.; Liu, S. Adaptive Super-Twisting Sliding Mode Control of Variable Sweep Morphing Aircraft. Aerosp. Sci. Technol. 2019, 92, 198–210. [Google Scholar] [CrossRef]
- Qiao, F.; Shi, J.; Qu, X.; Lyu, Y. Hardware-in-Loop Adaptive Neural Control for a Tiltable V-Tail Morphing Aircraft. Def. Technol. 2023, 22, 197–211. [Google Scholar] [CrossRef]
- Xu, H.; Han, J.; Yun, H.; Chen, X. Correction Method of Airfoil Thickness Effect in Hinge Moment Calculation of a Folding Wing. Chin. J. Aeronaut. 2020, 33, 922–932. [Google Scholar] [CrossRef]
- Guo, X.; Wang, S.; Qu, Y.; Cao, D. Nonlinear Dynamics of Z-Shaped Morphing Wings in Subsonic Flow. Aerosp. Sci. Technol. 2021, 119, 107145. [Google Scholar] [CrossRef]
- Mardanpour, P.; Hodges, D.H. Passive Morphing of Flying Wing Aircraft: Z-Shaped Configuration. J. Fluids Struct. 2014, 44, 17–30. [Google Scholar] [CrossRef]
- Balatti, D.; Khodaparast, H.H.; Friswell, M.I.; Manolesos, M.; Castrichini, A. Experimental and Numerical Investigation of an Aircraft Wing with Hinged Wingtip for Gust Load Alleviation. J. Fluids Struct. 2023, 119, 103892. [Google Scholar] [CrossRef]
- Tian, K.; Wang, Y.; Cao, D.; Yu, K. Approximate Global Mode Method for Flutter Analysis of Folding Wings. Int. J. Mech. Sci. 2024, 265, 108902. [Google Scholar] [CrossRef]
- Gu, H.; Healy, F.; Jayatilake, S.; Rezgui, D.; Lowenberg, M.; Cooper, J.; Wilson, T.; Castrichini, A. Flight Dynamics of Aircraft Incorporating the Semi-Aeroelastic Hinge. Aerosp. Sci. Technol. 2024, 147, 109026. [Google Scholar] [CrossRef]
- Ma, N.; Liu, L.; Meng, F.; Meng, J. Structural Design and Modal Behaviors Analysis of a New Swept Baffled Inflatable Wing. Def. Technol. 2023, 24, 382–398. [Google Scholar] [CrossRef]
- Beguin, B.; Breitsamter, C.; Adams, N. Wake Measurements to Assess the Flow-Structure Interaction of an Elasto-Flexible Morphing Wing Configuration. In New Results in Numerical and Experimental Fluid Mechanics VIII: Contributions to the 17th STAB/DGLR Symposium Berlin, Germany 2010; Dillmann, A., Heller, G., Kreplin, H.-P., Nitsche, W., Peltzer, I., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2013; pp. 43–50. [Google Scholar] [CrossRef]
- Chen, L.; Hu, Q.; Zhang, H.; Tong, B.; Shi, X.; Jiang, C.; Sun, L. Research on Underwater Motion Modeling and Closed-Loop Control of Bionic Undulating Fin Robot. Ocean Eng. 2024, 299, 117400. [Google Scholar] [CrossRef]
- Li, M.; Bai, J.; Li, L.; Meng, X.; Liu, Q.; Chen, B. A Gradient-Based Aero-Stealth Optimization Design Method for Flying Wing Aircraft. Aerosp. Sci. Technol. 2019, 92, 156–169. [Google Scholar] [CrossRef]
- Song, L.; Yang, H.; Zhang, Y.; Zhang, H.; Huang, J. Dihedral Influence on Lateral–Directional Dynamic Stability on Large Aspect Ratio Tailless Flying Wing Aircraft. Chin. J. Aeronaut. 2014, 27, 1149–1155. [Google Scholar] [CrossRef]
- Li, P.; Zhang, B.; Chen, Y.; Yuan, C.; Lin, Y. Aerodynamic Design Methodology for Blended Wing Body Transport. Chin. J. Aeronaut. 2012, 25, 508–516. [Google Scholar] [CrossRef][Green Version]
- Tianyuan, H.; Xiongqing, Y. Aerodynamic/Stealthy/Structural Multidisciplinary Design Optimization of Unmanned Combat Air Vehicle. Chin. J. Aeronaut. 2009, 22, 380–386. [Google Scholar] [CrossRef]
- Benaouali, A.; Kachel, S. Multidisciplinary Design Optimization of Aircraft Wing Using Commercial Software Integration. Aerosp. Sci. Technol. 2019, 92, 766–776. [Google Scholar] [CrossRef]
- Wu, Y.C.; Sun, G.; Tao, J. Optimization design on the wig of a general aviation airplane based on deep belief network and multi-objective particle swarm optimization algorithm. Acta Aerodyn. Sin. 2023, 41, 16–27. [Google Scholar]
- Panagiotou, P.; Yakinthos, K. Aerodynamic Efficiency and Performance Enhancement of Fixed-Wing UAVs. Aerosp. Sci. Technol. 2020, 99, 105575. [Google Scholar] [CrossRef]
- Altunkaya, E.C.; Ozkol, I. Multi-Parameter Aerodynamic Design of a Horizontal Tail Using an Optimization Approach. Aerosp. Sci. Technol. 2022, 121, 107310. [Google Scholar] [CrossRef]
- Davari, A.R. A Simple Analytical Model to Describe the Impact of Wing on the Flowfield over the Tail in Subsonic Flow. Aerosp. Sci. Technol. 2018, 75, 88–98. [Google Scholar] [CrossRef]
- Davari, A.R.; Soltani, M.R.; Askari, F.; Pajuhande, H.R. Effects of Wing Geometry on Wing-Body-Tail Interference in Subsonic Flow. Sci. Iran. 2011, 18, 407–415. [Google Scholar] [CrossRef][Green Version]
- Zhou, Z.; Huang, J. Facilitating Learning Adaptive V-Tail of a Supersonic Missile for Radar Cross-Section Reduction during Interval Flight. Heliyon 2023, 9, e20984. [Google Scholar] [CrossRef]
- Kim, H.D.; Brown, G.V.; Felder, J.L. Distributed Turboelectric Propulsion for Hybrid Wing Body Aircraft. In Proceedings of the 2008 International Powered Lift Conference Royal Aeronautical Society, London, UK, 22–24 July 2008. [Google Scholar]
- Sun, P.B.; Zhou, Z.; Li, X. Influence analysis and optimization of distribution-propulsion-wing parameters with target aerodynamic characteristics. Acta Aeronaut. Et Astronaut. Sin. 2024, 45, 204–221. [Google Scholar]
- Wang, K.; Zhou, Z.; Fan, Z.; Guo, J. Aerodynamic Design of Tractor Propeller for High-Performance Distributed Electric Propulsion Aircraft. Chin. J. Aeronaut. 2021, 34, 20–35. [Google Scholar] [CrossRef]
- Schetz, J.A.; Hosder, S.; Dippold, V.; Walker, J. Propulsion and Aerodynamic Performance Evaluation of Jet-Wing Distributed Propulsion. Aerosp. Sci. Technol. 2010, 14, 1–10. [Google Scholar] [CrossRef]
- Blackwell, J.A. Aerodynamic Characteristics of an 11-Percent-Thick Symmetrical Supercritical Airfoil at Mach Numbers between 0.30 and 0.85; NASA: Washington, DC, USA, 1969. [Google Scholar]
- Hu, J.; Zhou, Q.; Jiang, P.; Xie, T. An Improved Hierarchical Kriging for Variable-Fidelity Surrogate Modeling. In Proceedings of the 2016 International Conference on Cybernetics, Robotics and Control (CRC), Hong Kong, China, 19–21 August 2016; pp. 86–90. [Google Scholar]
- Lam, X.; Kim, Y.; Hoang, A.; Park, C. Coupled Aerostructural Design Optimization Using the Kriging Model and Integrated Multiobjective Optimization Algorithm. J. Optim. Theory Appl. 2009, 142, 533–556. [Google Scholar] [CrossRef]
- Xue, J.-K.; Shen, B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J.; Hou, T.; Pan, C. The SSA-BP-Based Potential Threat Prediction for Aerialtarget Considering Commander Emotion. Def. Technol. 2021, 18, 2097–2106. [Google Scholar] [CrossRef]
- Xin, J.; Chen, J.; Li, C.; Lu, R.; Li, X.; Wang, C.; Zhu, H.; He, R. Deformation Characterization of Oil and Gas Pipeline by ACM Technique Based on SSA-BP Neural Network Model. Measurement 2022, 189, 110654. [Google Scholar] [CrossRef]
- Wang, J.; Sheng, Z.; Zhou, B.; Zhou, S. Lightning Potential Forecast over Nanjing with Denoised Sounding-Derived Indices Based on SSA and CS-BP Neural Network. Atmospheric Res. 2014, 137, 245–256. [Google Scholar] [CrossRef]
- Ghorani, M.M.; Haghighi, M.H.S.; Riasi, A. Entropy Generation Minimization of a Pump Running in Reverse Mode Based on Surrogate Models and NSGA-II. Int. Commun. Heat Mass Transf. 2020, 118, 104898. [Google Scholar] [CrossRef]







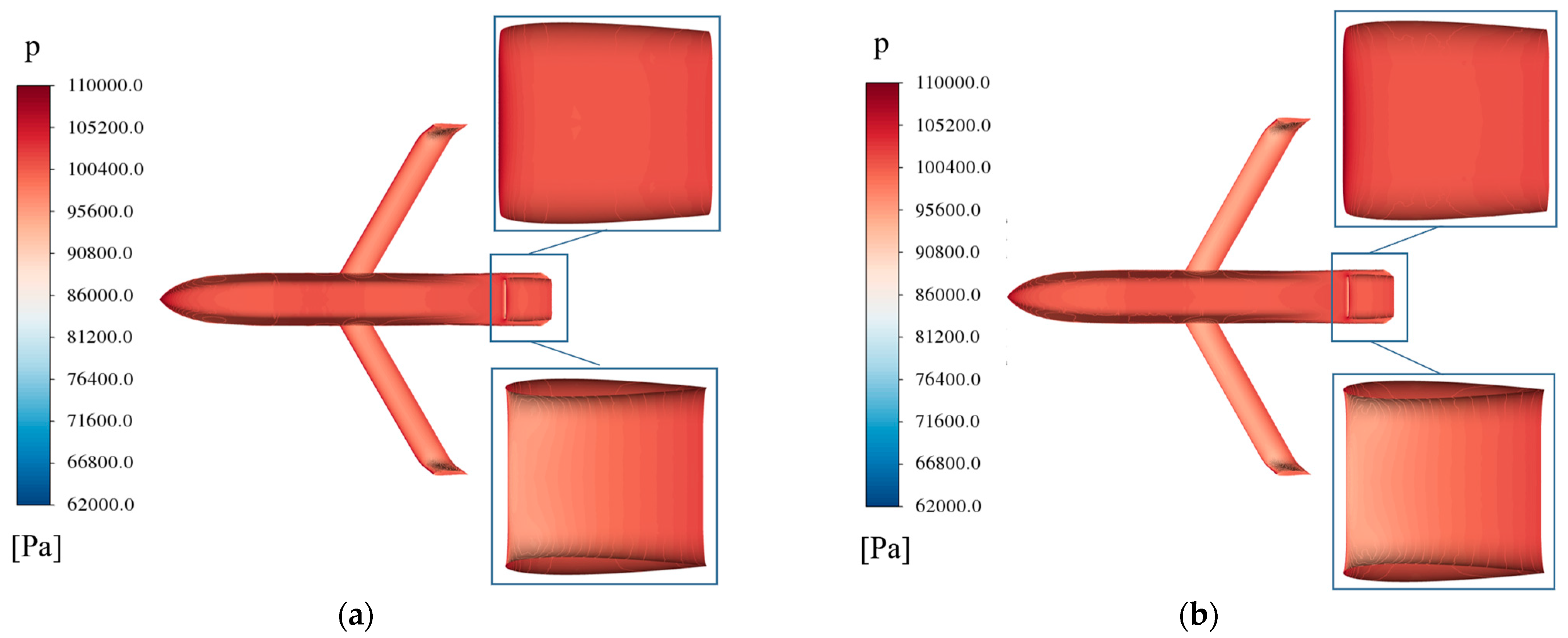

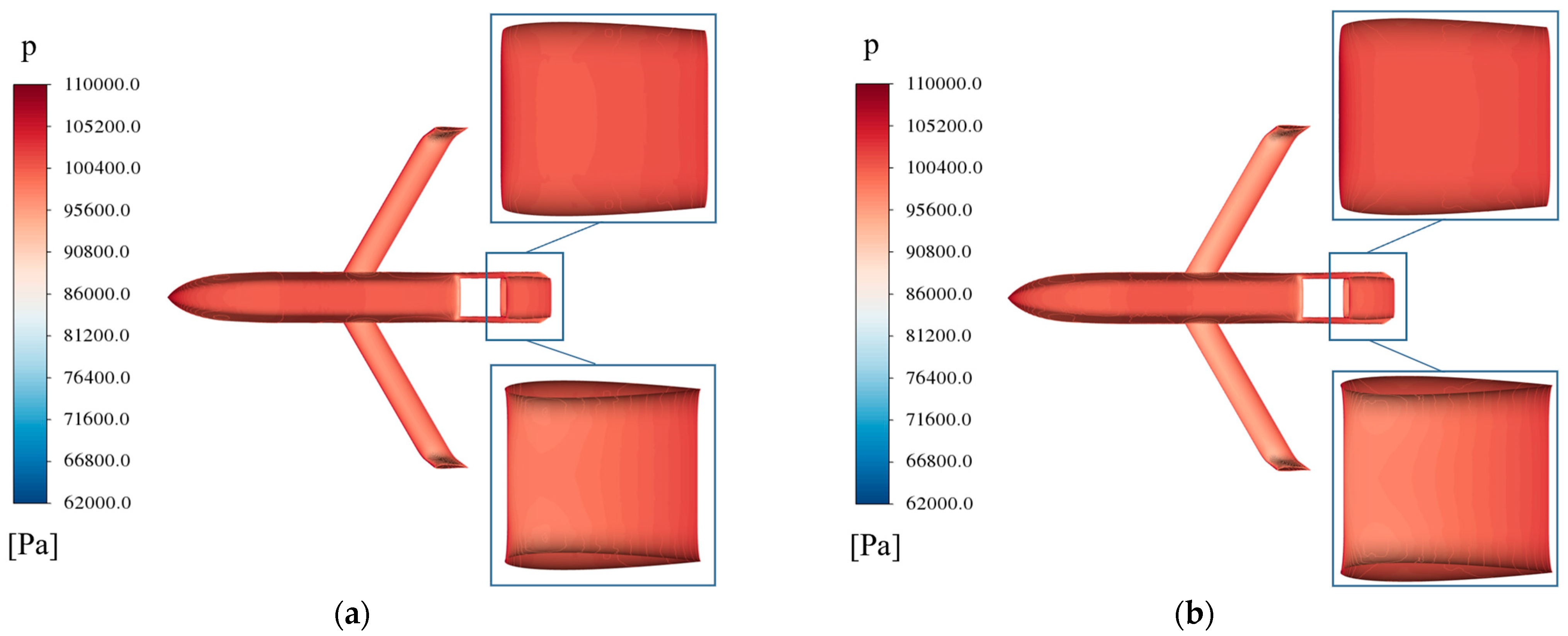

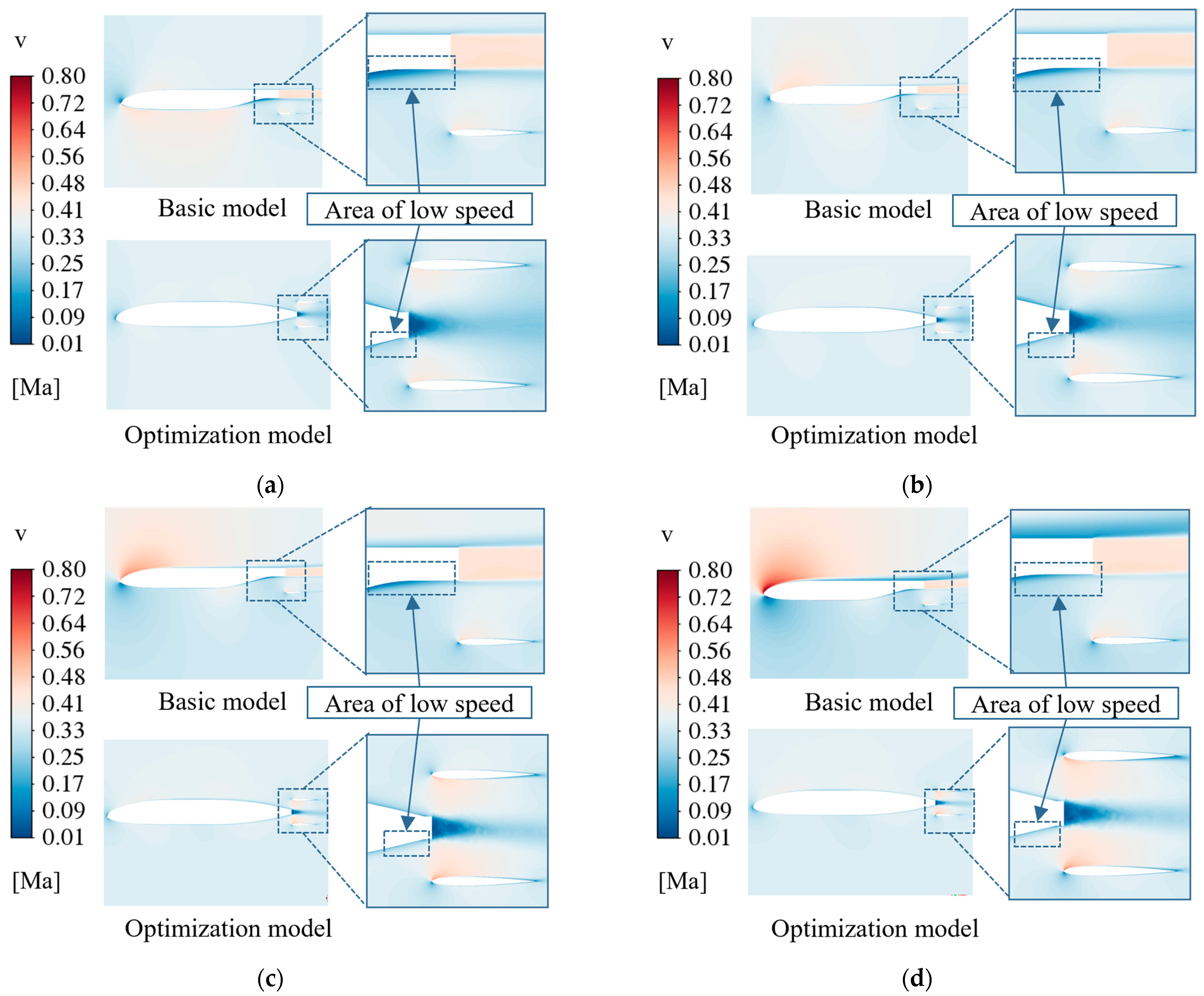
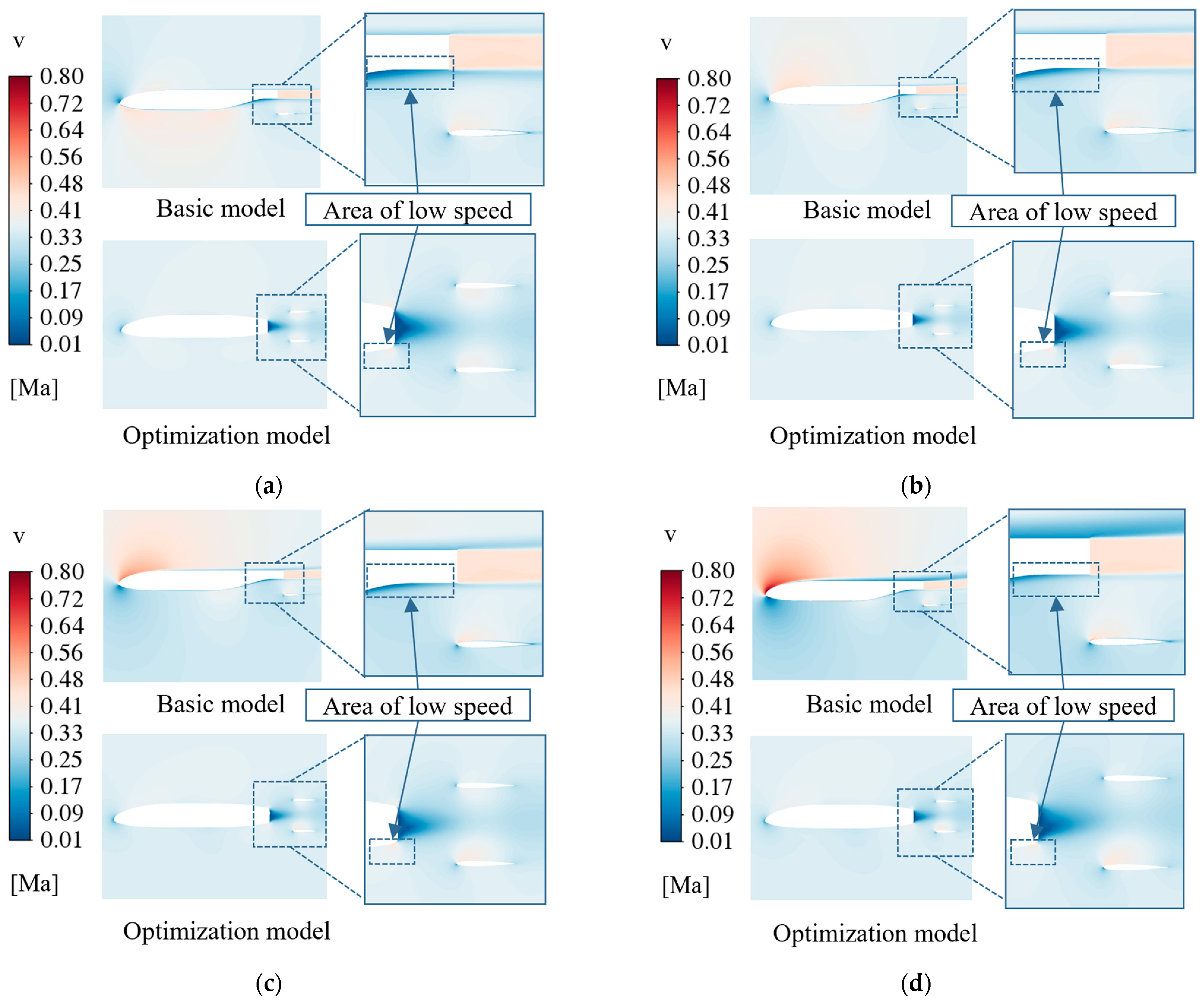
| Number | Parameters | Value Range (mm) |
|---|---|---|
| 1 | H1 | 50~140 |
| 2 | H2 | 50~140 |
| 3 | L | 1200 |
| 4 | L1 | 350 |
| 5 | L2 | 250 |
| 6 | L3 | 400~600 |
| 7 | L4 | 0~363 |
| 8 | 0°~20° |
| Parameters | Number of Coarse Meshes | Number of Medium Meshes | Number of Refined Meshes |
|---|---|---|---|
| NACA0012 | 140,000/210,000 | 50,000/470,000 | 680,000 |
| Ducted tail model | 340,000 | 690,000 | 1,500,000 |
| Parameters | Number of Coarse Meshes | Number of Medium Meshes | Number of Refined Meshes |
|---|---|---|---|
| Lift coefficient of the ducted tail | 0.1885 | 0.1958 | 0.1975 |
| Drag coefficient of the ducted tail | 0.0109 | 0.0113 | 0.0148 |
| Number | Parameters | Lift Coefficient | Drag Coefficient |
|---|---|---|---|
| 1 | H1 = 50 mm H2 = 50 mm L3 = 300 mm L4 = 27 mm | 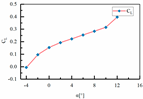 | 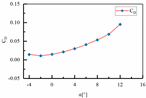 |
| 2 | H1 = 67.5 mm H2 = 50 mm L3 = 350 mm L4 = 135 mm | 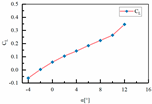 | 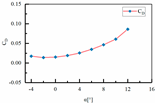 |
| 3 | H1 = 80 mm H2 = 50 mm L3 = 420 mm L4 = 216 mm | 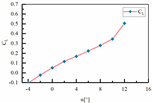 | 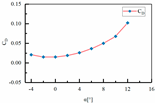 |
| 4 | H1 = 100 mm H2 = 00 mm L3 = 465 mm L4 = 00 mm |  | 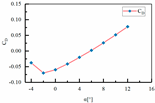 |
| 5 | H1 = 110 mm H2 = 00 mm L3 = 460 mm L4 = 243 mm | 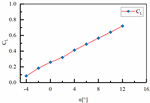 | 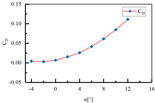 |
| 6 | H1 = 110 mm H2 = 00 mm L3 = 400 mm L4 = 270 mm |  |  |
| 7 | H1 = 120 mm H2 = 00 mm L3 = 380 mm L4 = 135 mm | 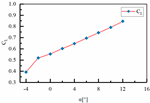 | 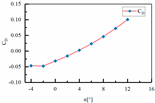 |
| 8 | H1 = 140 mm H2 = 00 mm L3 = 410 mm L4 = 270 mm |  | 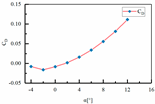 |
| Number | Parameters | Value |
|---|---|---|
| SSA-BP | Initial sparrow population | 60 |
| Number of iterations | 100 | |
| Warning value | 0.8 | |
| Percentage of discoverers | 0.4 | |
| Percentage of anti-predatory sparrows | 0.3 | |
| PSO-BP | Initial population size | 60 |
| Number of iterations | 100 | |
| Acceleration constant C1 | 1.5 | |
| Acceleration constant C2 | 1.5 | |
| Inertial weighting | 0.8 |
| Number | Parameters | Lift Coefficient | Lift-Drag Ratio |
|---|---|---|---|
| Sample 1 | H1 = 67.5 mm L3 = 460 mm L4 = 0 mm |  | 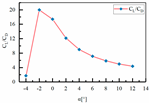 |
| Sample 2 | H1 = 67.5 mm L3 = 457 mm L4 = 27 mm |  | 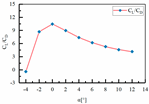 |
| Sample 3 | H1 = 67.5 mm L3 = 455 mm L4 = 135 mm | 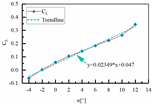 | 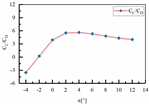 |
| Sample 4 | H1 = 67.5 mm L3 = 470 mm L4 = 216 mm | 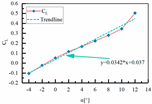 |  |
| Sample 5 | H1 = 140 mm L3 = 460 mm L4 = 27 mm | 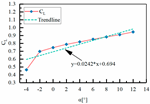 | 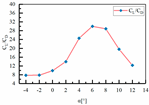 |
| Sample 6 | H1 = 110 mm L3 = 463 mm L4 = 135 mm | 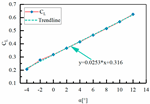 | 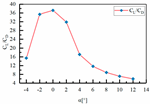 |
| Sample 7 | H1 = 110 mm L3 = 455 mm L4 = 162 mm |  | 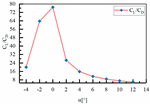 |
| Sample 8 | H1 = 110 mm L3 = 465 mm L4 = 189 mm | 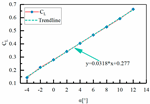 | 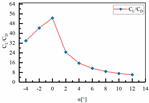 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, H.; Zheng, H.; Zhou, H.; Zhang, Q. Aerodynamic Optimization and Characterization of a Ducted Tail for a Box-Launched Aircraft. Appl. Sci. 2024, 14, 6496. https://doi.org/10.3390/app14156496
Jia H, Zheng H, Zhou H, Zhang Q. Aerodynamic Optimization and Characterization of a Ducted Tail for a Box-Launched Aircraft. Applied Sciences. 2024; 14(15):6496. https://doi.org/10.3390/app14156496
Chicago/Turabian StyleJia, Huayu, Huilong Zheng, Hong Zhou, and Qian Zhang. 2024. "Aerodynamic Optimization and Characterization of a Ducted Tail for a Box-Launched Aircraft" Applied Sciences 14, no. 15: 6496. https://doi.org/10.3390/app14156496
APA StyleJia, H., Zheng, H., Zhou, H., & Zhang, Q. (2024). Aerodynamic Optimization and Characterization of a Ducted Tail for a Box-Launched Aircraft. Applied Sciences, 14(15), 6496. https://doi.org/10.3390/app14156496





