A New Reversible Data Hiding Method Using a Proportional Relation between Peak Signal-to-Noise Ratio and Embedding Capacity on Convolutional Neural Network

Abstract

In the rapidly evolving fields of artificial intelligence and various industries, the secure processing and management of massive data have become paramount. This paper introduces an innovative reversible data hiding (RDH) method that leverages a Convolutional Neural Network (CNN)-based predictor to generate a predicted image from a given cover image. The secret data are ingeniously embedded within the differences in pixel values between the cover and predicted images. Our experimental analysis reveals a notable reduction in image distortion with increasing secret data size, showcasing the method’s potential for diverse applications. The unique aspect of our approach lies in the proportional relation between the Peak Signal-to-Noise Ratio (PSNR) and Embedding Capacity, highlighting its efficacy and efficiency in reversible data hiding.

1. Introduction

With recent advancements in information technology, there has been a rapid increase in the volume of data. Consequently, the importance of data protection and the security of personal information have become increasingly significant. In light of these developments, reversible data hiding has garnered attention.

Reversible data hiding (RDH) is one of the techniques used to hide data, primarily applied to images or videos. This technique not only hides the secret data but also has the ability to extract and restore the hidden data on the receiver side. The main goal of reversible data hiding is to perfectly restore the original data when extracting the hidden data. This means preserving the original data without making any changes when hiding the data. Due to these characteristics, reversible data hiding is currently being used in various fields such as healthcare, military, and so on.

Reversible data hiding has been explored through various approaches. One approach focuses on developing embedding methods that reduce data distortion. Another approach involves developing predictors to enhance prediction accuracy [1]. Embedding methods that reduce data distortion include techniques such as difference expansion (DE), where pixel value differences are increased to hide data and the original data are recovered using these differences [2,3]. Histogram shifting (HS) is another technique that analyzes the histogram of the original data to find available space for hiding data and performs data embedding in that space [4,5,6,7]. Prediction error expansion (PEE) is a technique where pixel values are predicted, and the difference between the predicted and actual values is used to embed data. During extraction, the prediction error values are used to recover the original data [8,9,10,11].

The development of predictors includes the difference predictor (DP) (which predicts the difference between pixels to hide data [2]), the median edge direction predictor (MEDP) (which predicts the edge direction around pixels as the median value to hide data [11]), the gradient adaptive predictor (GAP) (which predicts the gradient values around pixels to hide data [12]), and pixel-value-ordering (PVO) (which is the method of arranging image pixel values in ascending order and hiding data afterwards [12,13,14]).

However, the previous predictors have limitations in that they only refer to a few adjacent pixels to predict the target pixel. To overcome this limitation, predictors using CNN (Convolutional Neural Network) have recently been attracting attention [1,15,16,17,18,19,20].

A CNN-based method in [15], image scrambling, was performed on encrypted images using Arnold transform, and CNN was applied to extract the secret data.

Hu et al.’s method in [1], a predictor CNNP based on CNN, was proposed, and it showed better performance in terms of accuracy and prediction error compared to various existing predictors.

Subsequently, ICNNP was developed in [16], which takes into account the complexity of pixels in the original CNNP, showing further improved performance.

In the field of data hiding, predictor development and data embedding using CNN have been actively researched, showing superior performance compared to existing methods. However, there is a trade-off between the performance metrics of data hiding, such as PSNR (Peak Signal-to-Noise Ratio) and EC (Embedding Capacity). As the amount of data to be hidden increases, the distortion of the cover image becomes severe.

To overcome these limitations, this paper proposes a new embedding algorithm utilizing predictors developed using CNN. In the proposed method, the cover image is predicted using the CNN predictor, and the gap between the generated predicted image and the cover image is calculated. Then, the secret data are embedded into the predicted image to the direction closer to the pixels of the cover image. This approach reduces the distortion of the cover image as the amount of data to be hidden increases, forming a proportional relation between PSNR and EC. The proposed embedding algorithm can contribute significantly to the advancement of the data hiding field.

The rest of this paper is organized as follows. The related work is described in Section 2, and the proposed method is provided in detail in Section 3. The experimental results and conclusions are described in Section 4 and Section 5, respectively.

2. Related Work

2.1. Embedding Algorithm

In this subsection, traditional embedding methods such as DE (difference expansion), HS (histogram shifting), and PEE (prediction-error expansion) are explained.

2.1.1. Difference Expansion

In 2003, Tian et al. [2] proposed a method called difference expansion (DE) for hiding secret data in an image. They defined blocks by grouping two consecutive pixels in an image and transformed the pixel values within the block so that the difference between them doubled. The formula for calculating the difference $d_i$ between two pixels $\left(a_i,b_i\right)$ in an 8-bit grayscale image is represented by Equation (1):

$$d_i=a_i-b_i$$

(1)

After generating $d_i$ through Equation (1), the value of $d_i$ is doubled, and the secret data $S_i$ are added to the expanded space to generate ${\overline{d}}_{𝚤}$. This formula is defined by Equation (2):

$$\overline{d_{𝚤}}=2\times d_i+S_i$$

(2)

Calculating the pixel block with the inserted secret data ($\overline{a_{𝚤}}, \overline{b_{𝚤}}$) using the generated $\overline{d_{𝚤}}$ is defined by Equation (3):

$$\overline{a_{𝚤}}=S_i+⌊\left(\overline{d_{𝚤}}+1\right)/2⌋, \overline{b_{𝚤}}=S_i-⌊\overline{d_{𝚤}}/2⌋$$

(3)

By repeating the above Equations (1)–(3), a stego-image is generated, which contains the secret data.

2.1.2. Histogram Shifting

In 2006, Ni et al. [17] proposed the method of histogram shifting (HS) using the histogram of image pixels. This technique involves assigning the pixel value with the highest frequency as the peak point and the pixel value with the lowest frequency as the zero point. Secret data are then inserted at the peak point within the histogram.

First, peak and zero points are identified, and then the pixel values shift between them by one position towards the zero point. The secret data are subsequently inserted at the peak point. By employing this method, the frequency of the peak point decreases while the frequency of the zero point increases, effectively reducing distortion in the image.

2.1.3. Prediction Error Expansion

Prediction-error expansion (PEE) is a data hiding method proposed by Thodi et al. in 2004 [5]. The concept of PEE involves expanding the difference, $P_e$, between the cover image pixel χ and the predicted pixel ${\mathsf{\chi }}_p$ for a given pixels block, $\left(\begin{array}{cc}x& b\\ a& c\end{array}\right)$, and then hiding the secret data within that difference. The method of calculating the predicted pixel ${\mathsf{\chi }}_p$ using the cover image pixel χ and surrounding pixels is defined by Equation (4):

$${\mathsf{\chi }}_p=\left\{\begin{array}{c}\max \left(a,b\right) if c\le \min \left(a,b\right)\\ \min \left(a,b\right) if c\ge \max \left(a,b\right)\\ a+b-c if otherwise\end{array}\right.$$

(4)

Once ${\mathsf{\chi }}_p$ is calculated, the prediction error is calculated by determining the difference P_e between χ and ${\mathsf{\chi }}_p$, as described in Equation (5):

$$P_e= \mathsf{\chi }-{ \mathsf{\chi }}_p$$

(5)

Subsequently, the generated $P_e$ is expanded and the binary secret bit-stream, $b_i$, is added. As a result, ${\overline{P}}_e$ is generated, and the entire process is described by Equation (6):

$$\overline{P_e}=2\times P_e+b_i$$

(6)

Finally, the conclusive pixel $\overline{\mathsf{\chi }}$ with hidden secret data is defined by adding ${\overline{P}}_e$ to the prediction pixel as described in Equation (7):

$$\overline{\mathsf{\chi }}={\mathsf{\chi }}_p+{\overline{P}}_e$$

(7)

By repeating the above process, it is possible to generate a stego-image with the inserted secret data.

2.2. CNN-Based Predictor

In this paper, a predictor utilizing CNN is employed to generate predicted images. Therefore, predictors applying CNN instead of traditional methods are described in this subsection.

2.2.1. CNNP

In 2021, Hu et al. [1] proposed a new approach for image prediction in RDH by incorporating CNN, which is widely used in image classification and prediction in deep learning, to achieve higher performance than traditional predictor algorithms. In [1], the cover image is divided into cross set and dot set, designed for each set to predict each other.

The CNNP model is designed to generate predict images by utilizing them as input data by using the dot set image and cross set image divided as described in Figure 1. Then, the generated predict images are used to hide secret data using embedding algorithms such as error expansion and histogram shifting.

2.2.2. ICNNP

In 2023, Qiu et al. [16] proposed an improved CNNP (ICNNP) by adding a complexity prediction part to the existing CNN predictors to consider the complexity of each pixel. This enhancement further improved the performance of CNN predictors.

In the embedding step similar to [1], the cover image is divided into the dot set image and the cross set image, and each image predicts the other using ICNNP.

Afterwards, the prediction errors of predicted pixels are sorted according to the complexities of the pixels, and histogram shifting is used to embed them into prediction errors with lower complexity. Thus, the ICNNP model, which considers complexity, demonstrates higher performance compared to the previously published CNNP model [1].

3. The Proposed Method

The proposed methods can be divided into three main categories: CNN predictor development, data embedding, and data extraction and recovery. In CNN predictor development, the structure and training methods of the CNN predictor are introduced. For data embedding, the method of hiding secret data using predicted images is explained. In data extraction and recovery, we introduce the methods of extracting secret data from stego-images and the recovery process.

3.1. CNN Predictor

In the proposed method, the CNN predictor is divided into three main parts: pre-processing image, network architecture, and training, and each part is explained separately.

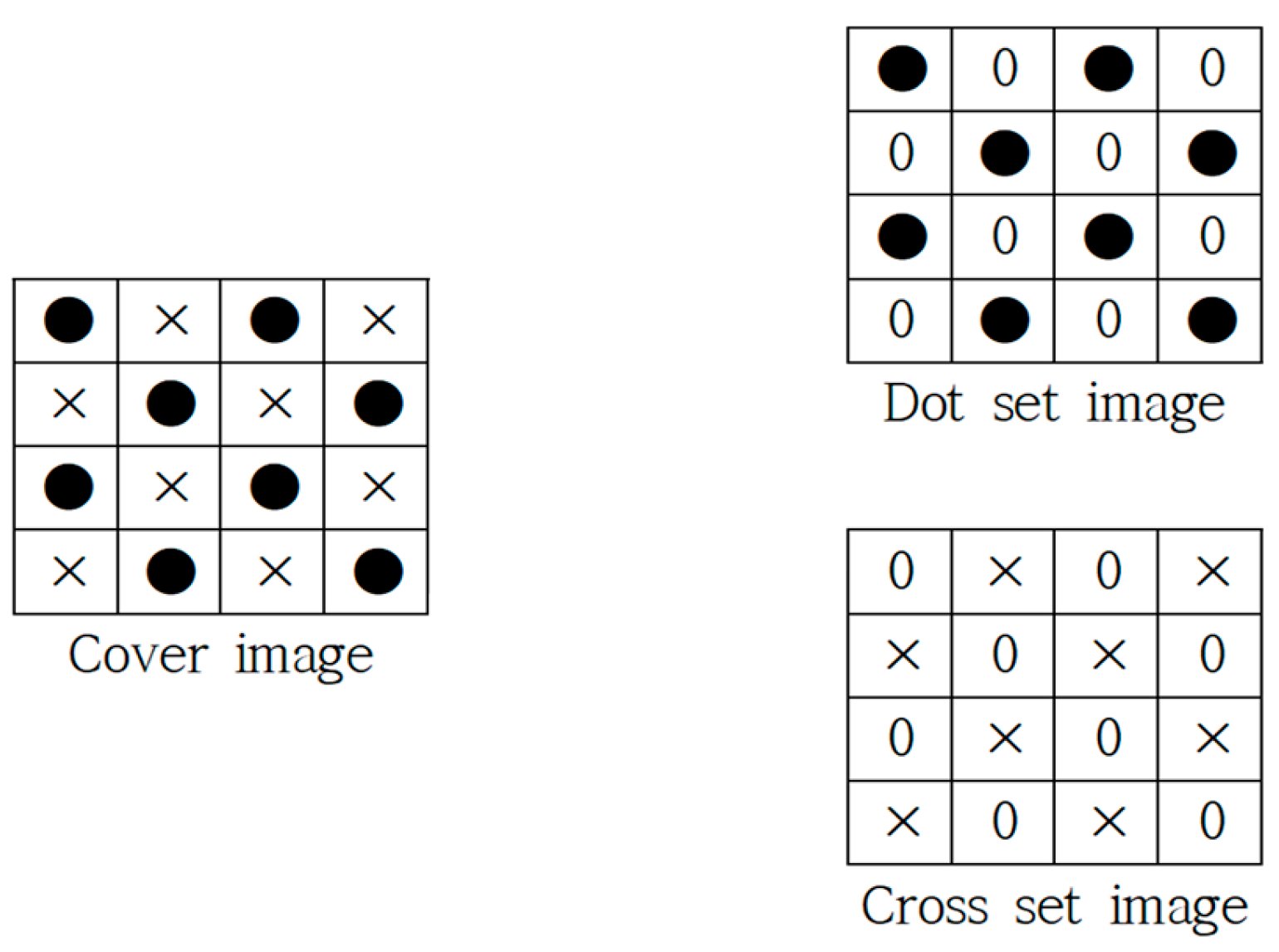
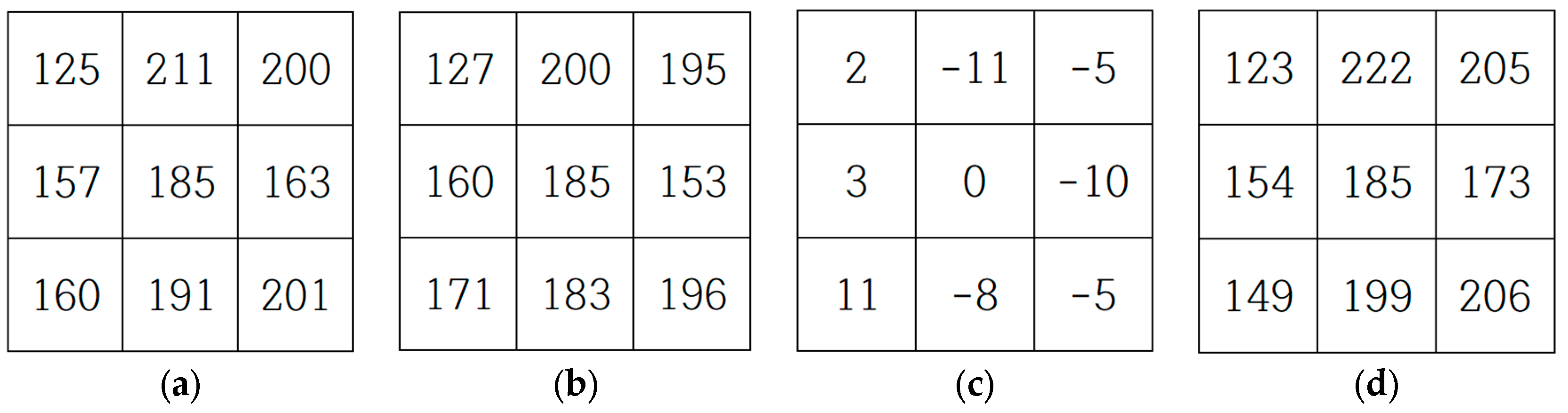
3.1.1. Preparation for Image Prediction

The proper construction of the training set and target set is a crucial task for increasing the predictor’s accuracy. In [1,18], the cover image is divided into cross set and dot set, and each set is designed to predict each other. In [12], the cover image is divided into 2 × 2 blocks, and the pixels within each block are numbered in order as 1, 2, 3, and 4, and then grouped into four sets.

In this paper, the general structure of the image is analyzed to divide the image into training set and target set according to the image structure. Although not all images follow this pattern, generally, the most important part in the image is located in the center of the image, while less important background elements are located towards the edges. Figure 2 presents GBVS saliency maps and GC saliency maps for 1000 photos, which is respecting the “rule of thirds” (GBVS and GC are algorithms for estimating saliency) in [19].

The “rule of thirds” is one of the important compositional principles used in photography and art. According to this principle, a virtual grid can be imagined by dividing the image into thirds horizontally and vertically, and position important elements or subjects at the intersections of the grid. This method is a way to obtain aesthetically attractive photos.

The saliency map is a heat-map that visually represents the important areas in an image. It is widely used in various fields such as computer vision, image processing, and computer graphics. It is useful for tasks like object detection, image segmentation, and attention analysis.

Based on this result, the cover image is divided into two sets: the inner square and the outer square. Assuming an image size of 512 by 512, the inner square set starts from the 4 pixels in the center of the image, (255, 255), (255, 256), (256, 255), and (256, 256), while the outer square starts from the 12 pixels surrounding the inner square. Furthermore, the 20 pixels surrounding the outer square are included in the inner square, and the 28 pixels surrounding the inner square are included in the outer square. This process is repeated until the pixels at the edges of the image are included in the outer square, completing the set composition as shown in Figure 3.

In the divided image in Figure 3, the inner square is used as training data and the outer square is used as target data.

3.1.2. Network Architecture

As shown in Figure 4a, the CNN-based predictor can be divided into two main parts: feature extraction and image prediction. The feature extraction consists of multiple parallel conv blocks, where the channel is 32, the kernel is greater than 4, and the image size is 512 by 512. The input image of the CNN is the “inner square” image, denoted as $I_{inner}$, and the output image is the “outer square” image, denoted as $I_{outer}$. The structure of the conv block in the feature extraction part and the conv block in the image prediction part is shown in Figure 4b.

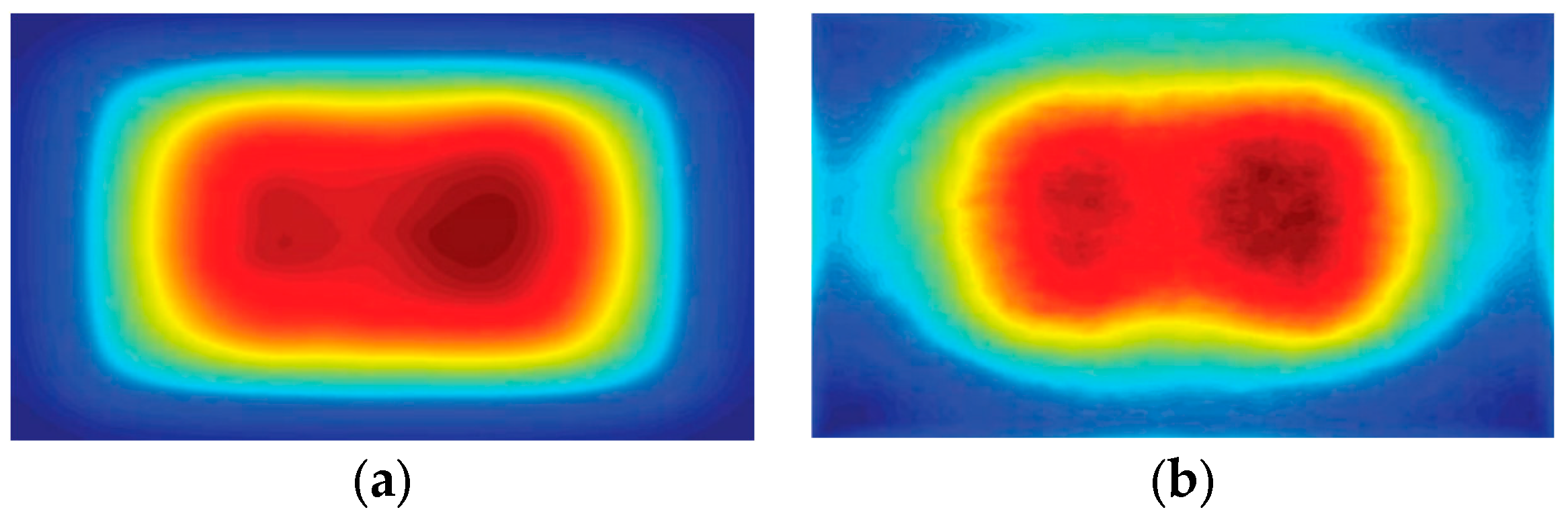
3.1.3. Training

The proposed CNN-based predictor is trained using 10,000 randomly selected images from Kaggle. And all images were converted to 8-bits grayscale with a size of 512 × 512 for training. The input and target are used, respectively, as the “inner square” and “outer square”. For optimization, the Adam parameter is used for back-propagation and optimizer. Batch size is 4 and training loss function is defined by Equation (8):

$$loss={\displaystyle \frac{1}{n}}{{\displaystyle \sum }}_{i=1}^n{\left(\overline{I_o}-I_o\right)}^2+\lambda {||\omega ||}_2^2$$

(8)

where $n$ is number of training data, ${\overline{I}}_o$ is the output image, I_o is the target image, λ is weight decay, and $\omega$ denotes all the weight in the network.

In this paper, the proposed predictor was tested on Google Colab pro T4 GPU with 51 GB RAM. To apply this algorithm, a predictor model (.h5 file) generated from the training process is required, and the size of this model is 940 KB. When performing the entire embedding and extraction process, the memory usage is approximately 3900 MiB. This relatively high memory consumption is due to the use of a deep learning model.

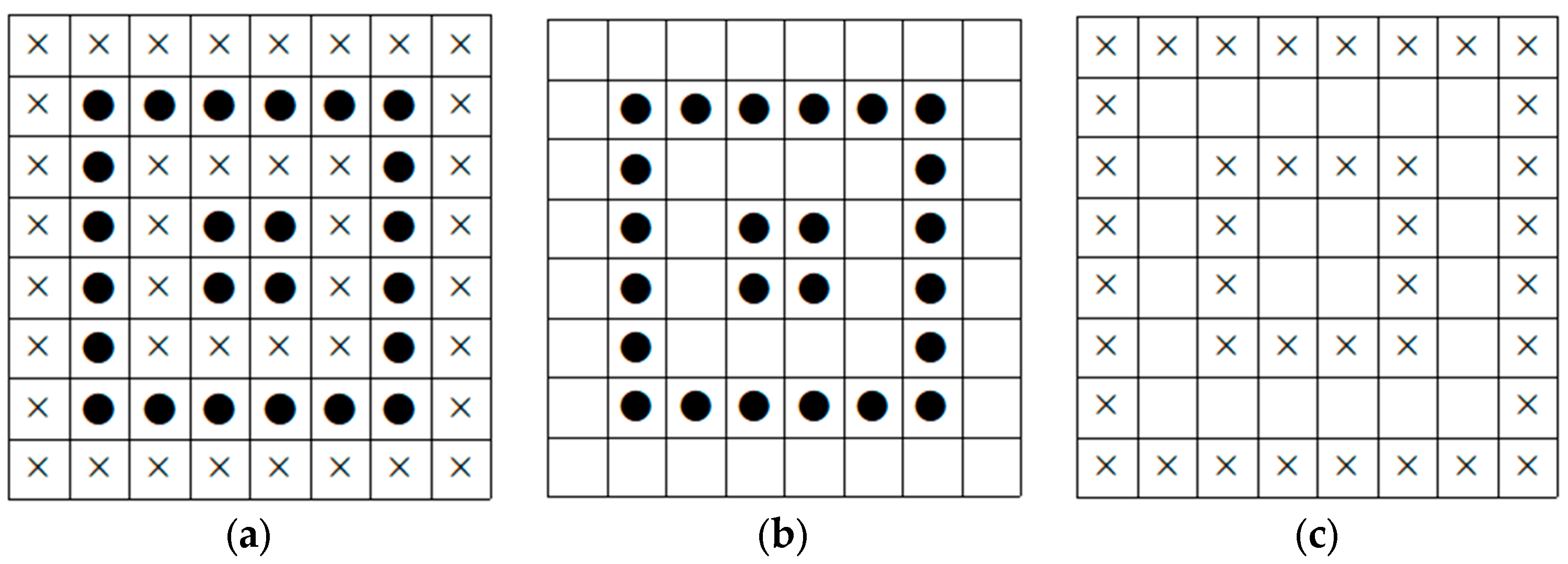
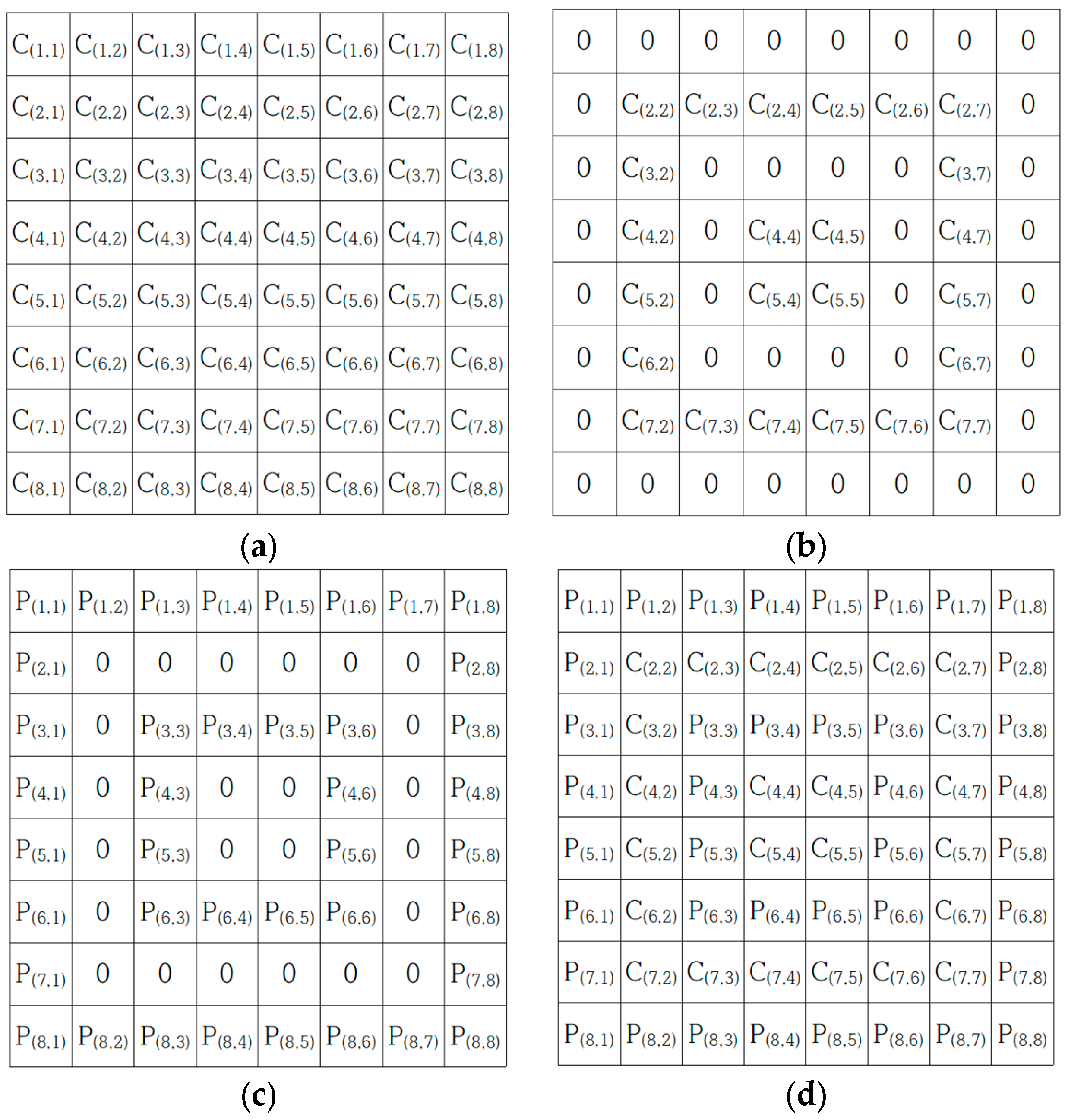
3.2. Pre-Processing

Before initiating the embedding process, it is essential to address potential overflow/underflow issues that may arise during the embedding procedure. Upon analysis of this procedure, it is necessary to ensure that the pixel values do not exceed the range of [0, 255] when computing the difference between the pixel values of the cover image multiplied by 2 and the predicted image. Consequently, pre-processing is conducted to ensure whether each cover image’s pixel values satisfy Equation (9) before proceeding with the embedding.

$$0\le 2\times C_{\left(x,y\right)}-P_{\left(x,y\right)}<255$$

(9)

In Equation (9), $C_{\left(x,y\right)}$ represents the pixel value at coordinates (x, y) in the cover image, and $P_{\left(x,y\right)}$ signifies the pixel value at coordinates (x, y) in the predicted image. By pre-processing the pixel values of the cover image to satisfy Equation (9), overflow/underflow issues are effectively managed during experimentation. For accurate experiments, pre-processing according to Equation (9) was applied not only to the proposed method but also to other embedding algorithms conducted for performance comparison in Section 4.

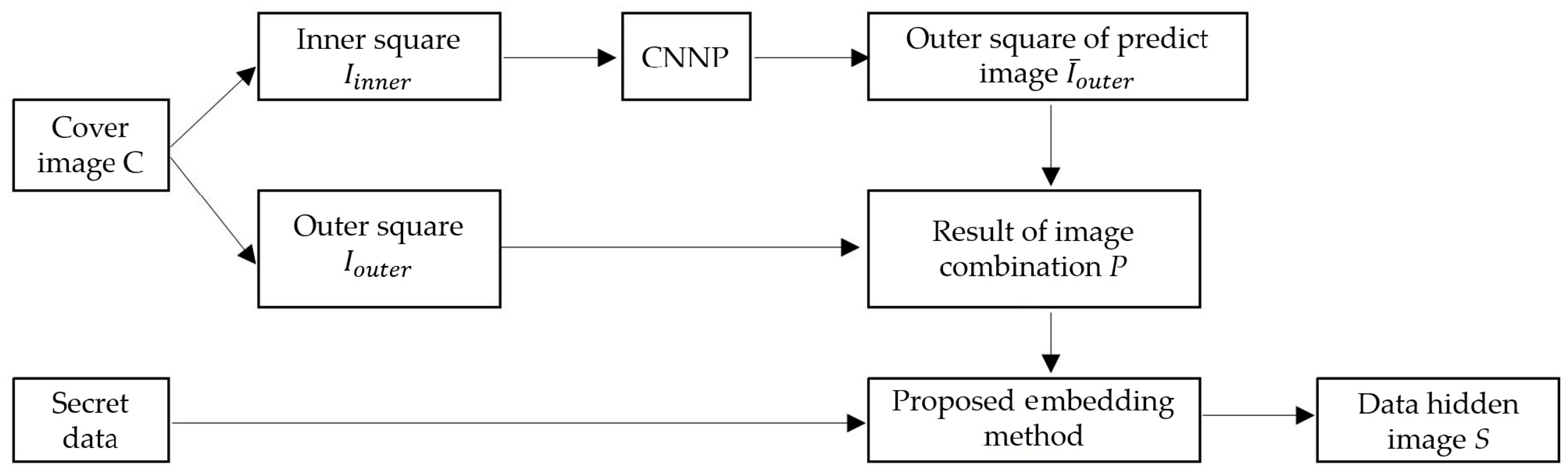
3.3. Embedding

In the embedding phase, we utilize the previously described CNN-based predictor to generate the predict image and hide the secret data by prioritizing the pixels with the largest differences between the generated predict image and the cover image. Therefore, before performing embedding, a trained CNN-based predictor model is required. The detailed embedding process follows the steps below.

Step 1: As shown in Figure 5b, to create the inner square corresponding to the input data of the CNN-based predictor model, leave only the pixels that will be used as input from the cover image, while setting the remaining pixels to 0.

The generated input data are inserted into the previously created CNN-based predictor model, resulting in the prediction of outer square pixel values as illustrated in Figure 5c, $I_{outer}$. The inner square used as input values in the CNN-based predictor is combined with the outer square from Figure 5c, $I_{outer}$, resulting in the generation of the predicted image as illustrated in Figure 5d.

Step 2: The proposed embedding method hides secret data in the difference between P and C, so we calculate the difference between P and C as described in Equation (10) and designate it as G.

$$G_{\left(i,j\right)}=P_{\left(i,j\right)}-C_{\left(i,j\right)}$$

(10)

For each pixel where the value of $G_{\left(i,j\right)}$ is not 0, indicating the presence of a difference between the cover image and the predicted image, hide 1 bit of secret data per pixel. To determine the locations where the data are hidden, we multiply the value of $G_{\left(i,j\right)}$ by 2 to make it even.

Step 3: The new image pixel $S$ is generated by subtracting twice the difference of $P$ and $C$, denoted as $G$ from $P$. In this way, the generated $S$ hides the secret data. The formula for calculating this is Equation (11):

$$S_{\left(i,j\right)}=P_{\left(i,j\right)}-G_{\left(i,j\right)}\times 2$$

(11)

For example, given an image of size 3 × 3 and pixel values as shown in Figure 6a, the difference between the predicted image, Figure 6b, is represented by Figure 6c. The generated $S_{\left(i,j\right)}$ resulting from the difference between $P_{\left(i,j\right)}$ and two times the results in $G_{\left(i,j\right)}$ is shown in Figure 6d.

Step 4: Use the G generated in Step 3 to determine the locations of the pixels where the secret data will be hidden. Since G contains both negative and positive values, apply the absolute value of G to calculate $G_{abs}$, which is described in Equation (12). Then, sort the coordinates of the pixels in descending order based on the magnitude of $G_{abs}$. If multiple pixels have the same value of $G_{abs}$, prioritize the coordinates of the top-left pixel to obtain the absolute value.

$$G_{abs}=\left|G\right|$$

(12)

Step 5: Once the coordinates with the largest $G_{abs}$ values are sorted, hide the secret data in descending order of $G_{abs}$ values. The hidden data consist of binary data composed of 1 and 0, and based on the magnitude of the $G_{abs}$ values, add the secret data to the corresponding $S_{\left(i,j\right)}$ pixel. If the secret data are 0, no data are hidden in the corresponding pixel. If the secret data are 1, then 3 is added to or subtracted from the corresponding pixel. As explained in Equation (13), add 3 to $S_{\left(i,j\right)}$ if the $G_{\left(i,j\right)}$ value is greater than 0. If the $G_{\left(i,j\right)}$ value is less than 0, a new value of $S_{\left(i,j\right)}$ is subtracted by 3. The hiding secret data are 1 bit per pixel, but in reality, 3 is added to the corresponding pixel, which is greater than 1 and an odd number. The reason for adding a value greater than 1 is that $S$ becomes closer to C as the added value increases, ultimately resulting in an increase in the PSNR of the stego-image.

$$S_{\left(i,j\right)}=\left\{\begin{array}{c}{S}_{\left(i,j\right)}+\left(3\times SecretData\right) if G_{\left(i,j\right)}>0\\ S_{\left(i,j\right)}-\left(3\times SecretData\right) if G_{\left(i,j\right)}<0\end{array}\right.$$

(13)

Step 6: Once all the secret data are hidden in $S_{\left(i,j\right)}$, generate an end token to mark the end point of the secret data. The end token is placed at the coordinates following the last location where secret data are hidden. To determine the placement of the end token, add or subtract 5 to the coordinates with higher $G_{\left(i,j\right)}$ values. If $G_{\left(i,j\right)}$ is greater than 0, add 5 or subtract 5 if it is less than 0. The reason for using 5 instead of 3 is to prevent the $G_{\left(i,j\right)}$ value of the last hidden secret data from becoming the same as the end token’s coordinates. The overall structure of the embedding process is illustrated in Figure 7.

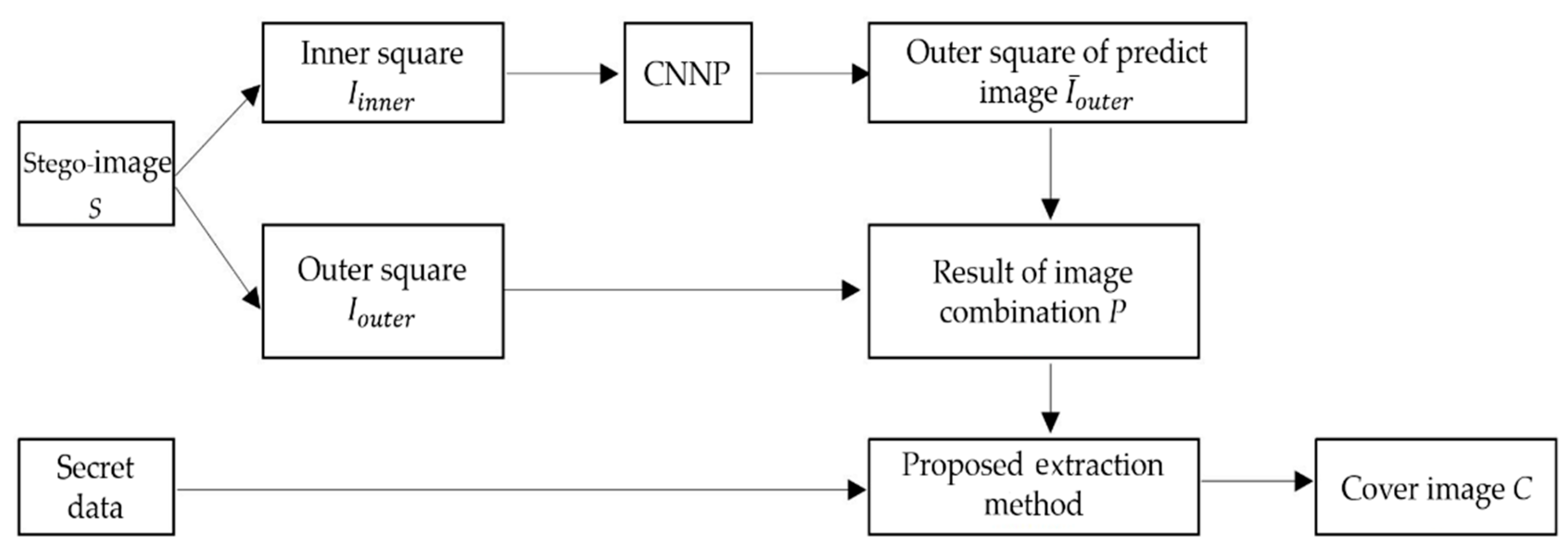
3.4. Extraction and Recovery

In this section, the method of extracting hidden data and restoring the stego-image to the cover image is explained.

Step 1: To begin with extraction, a stego-image is needed, denoted as S, which contains hidden information, as well as the predicted image, denoted as P. To generate P, you need to utilize a CNN-based predictor model. Extract the inner square portion from S and use it as the input data for the CNN-based predictor. The CNN model predicts the outer square, and P is generated by combining the inner and outer squares. By using the P and S generated in this step, an extraction can be performed.

Step 2: Consistent with Equation (14), calculate the difference between S and P generated in Step 1, and assign it as $\tilde{G}$. $\tilde{G}$ contains a hidden secret datum in the difference between P and C in the embedding.

$${\tilde{G}}_{\left(i,j\right)}=P_{\left(i,j\right)}-S_{\left(i,j\right)}$$

(14)

Step 3: To find the end token in the generated $\tilde{G}$, we look for the smallest odd value and its corresponding coordinates. The end token is a datum generated during the embedding phase to indicate the point where the entire secret datum ends. It corresponds to the position that is the secret datum’s length +1 when the $G_{abs}$ is sorted in descending order. It is derived by adding or subtracting 5 from the original size. Therefore, the coordinates with values greater than or equal to the data corresponding to the end token contain hidden secret data of 1 or 0, and the actual $\tilde{G}$ value has increased or decreased by 3 or 0 in $\tilde{G}$. Therefore, the size and coordinates of the end token are determined to identify the last coordinates where secret data are hidden. The pixel values, incremented or decremented by 5 in the end-token-generation step, are then reverted to their original sizes. As a result, we apply −5 if $G_{\left(i,j\right)}$ is positive, and +5 if it is negative when considering Equation (15).

$$\begin{array}{c}K=\min \left(G_{\left(i,j\right)} mod 2=1\right)\\ {\tilde{G}}_{\left(i,j\right)}=\left\{\begin{array}{c}K-5 if K>0\\ K+5 if K<0\end{array}\right.\end{array}$$

(15)

Step 4: Extract the secret data from the hidden coordinates identified in Step 3. Apply the absolute value to $\tilde{G}$ and sort them in descending order. And following Equation (16), where the absolute value of ${\tilde{G}}_{\left(i,j\right)}$ is odd, apply −3 if ${\tilde{G}}_{\left(i,j\right)}$ is positive or +3 if ${\tilde{G}}_{\left(i,j\right)}$ is negative, and sort them in descending order. During this process, $\tilde{G}$ becomes the same as the G generated in the embedding phase. The coordinates where the absolute value of $\tilde{G}$ is greater than the end token are sorted in order. At locations where $\tilde{G}$ values are odd, 1 is assigned, while 0 is assigned as secret data at even locations. By arranging Step 4, all of the hidden data can be generated.

$${\tilde{G}}_{\left(i,j\right)}=\left\{\begin{array}{c}{\tilde{G}}_{\left(i,j\right)}-3 if {\tilde{G}}_{\left(i,j\right)} mod 2=1 and {\tilde{G}}_{\left(i,j\right)}>0\\ {\tilde{G}}_{\left(i,j\right)}+3 if {\tilde{G}}_{\left(i,j\right)} mod 2=1 and {\tilde{G}}_{\left(i,j\right)}<0\end{array}\right.$$

(16)

Step 5: Once the process of extracting, which is finding secret data, is complete, we move on to the recovery phase, which is the process of converting S back to C. In the previous step, ${\tilde{G}}_{\left(i,j\right)}$ is adjusted by adding or subtracting 3 or 5 to the odd data, so that they match with G generated by Equation (10) during the embedding phase. Therefore, the method of generating C using Equations (10) and (11) is defined in Equation (17) by reversing the process.

$$C_{\left(i,j\right)}=P_{\left(i,j\right)}-{\displaystyle \frac{{\tilde{G}}_{\left(i,j\right)}}{2}}$$

(17)

By using Equation (17), the proposed method can generate the cover image C, and the recovery process can be complete. The overall structure of the embedding process is illustrated in Figure 8.

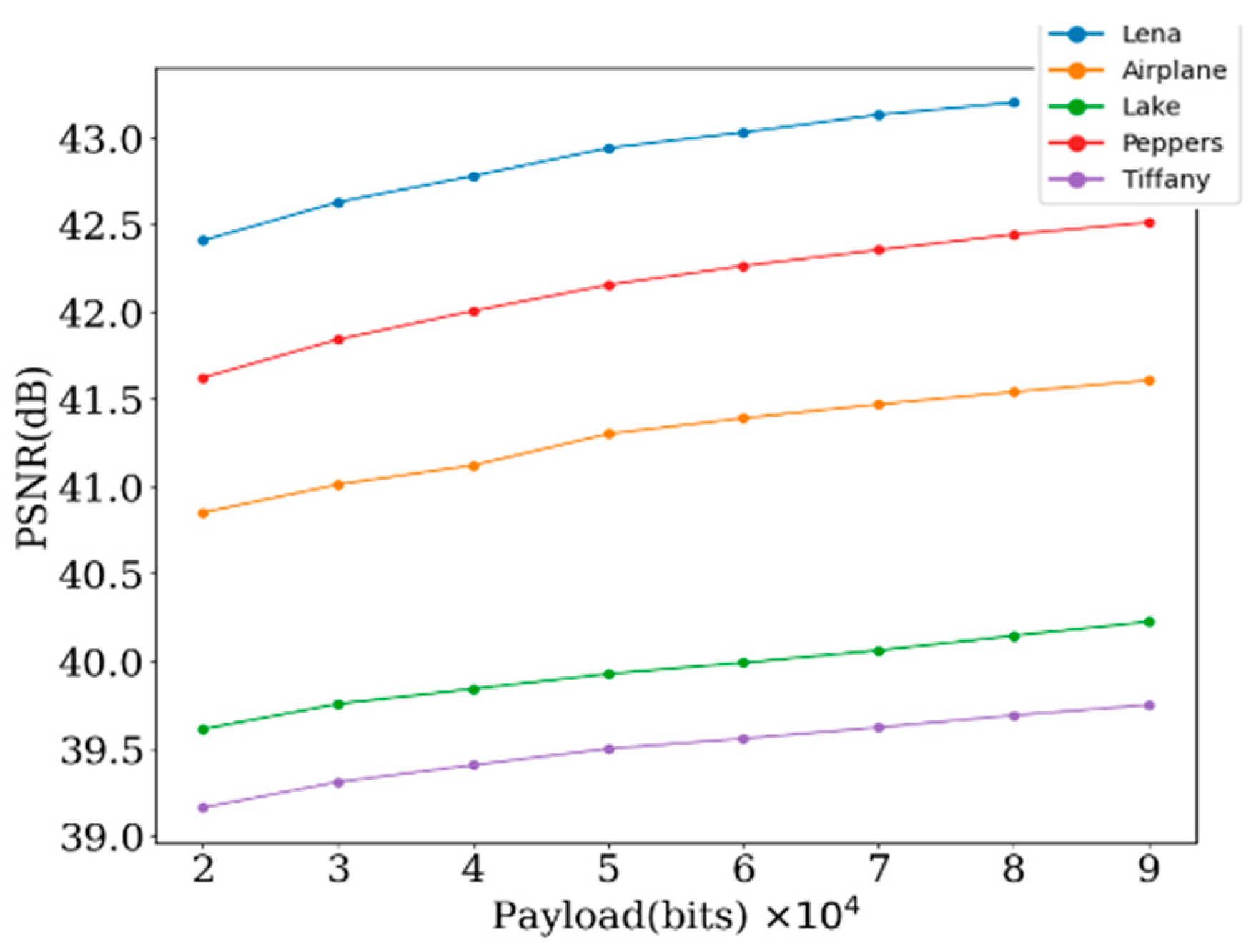
4. Experimental Results

To evaluate the proposed embedding algorithm, experiments were conducted by comparing it with classical RDH embedding algorithms such as DE, Skewed HS [20], and PEE. The performance evaluation was based on PSNR (Peak Signal-to-Noise Ratio) with respect to EC (Embedding Capacity) and the rate of change in PSNR, specifically, the slope of the graph for each interval. The rate of change in PSNR was used to assess the magnitude of image distortion based on the size of the embedded data and to understand the variation in image distortion with respect to the size of the embedded data. For experiments, wide and recognized standard images in the field of steganography including Lena, Airplane, Lake, Peppers, Tiffany, and 100 randomly selected images from Kaggle were used.

Firstly, when embedding secret data into the 5 standard images in the proposed method, the relation between Embedding Capacity and PSNR is illustrated by Figure 9.

Figure 9 illustrates the relation between PSNR and EC after embedding secret data into the five standard images using the proposed method. As observed in Figure 9, when utilizing the proposed method, an increase in the size of secret data corresponds to an increase in PSNR. This proportional relation between PSNR and EC is a key characteristic of the proposed method. Figure 10 illustrates the comparison between the proposed method and the conventional embedding algorithm widely used in traditional embedding method.

Figure 10 illustrates the results of embedding using four different embedding algorithms, including the proposed method, on four standard images. As observed in Figure 10, traditional embedding algorithms exhibit a downward-sloping graph, indicating that as the size of secret data increases, the PSNR decreases, and image distortion rises. In other words, larger hidden data lead to higher image distortion in traditional methods. However, the embedding algorithm proposed in this paper, among the four algorithms utilized, uniquely presents an upward-sloping graph in Figure 10. This implies that as the size of hidden data increases, image distortion decreases, showcasing a distinctive characteristic of the proposed embedding method.

The comparison results with the previous four algorithms based on numerical values are shown in

Table 1. The rate of change in PSNR according to the payload segment of 10,000 bits.

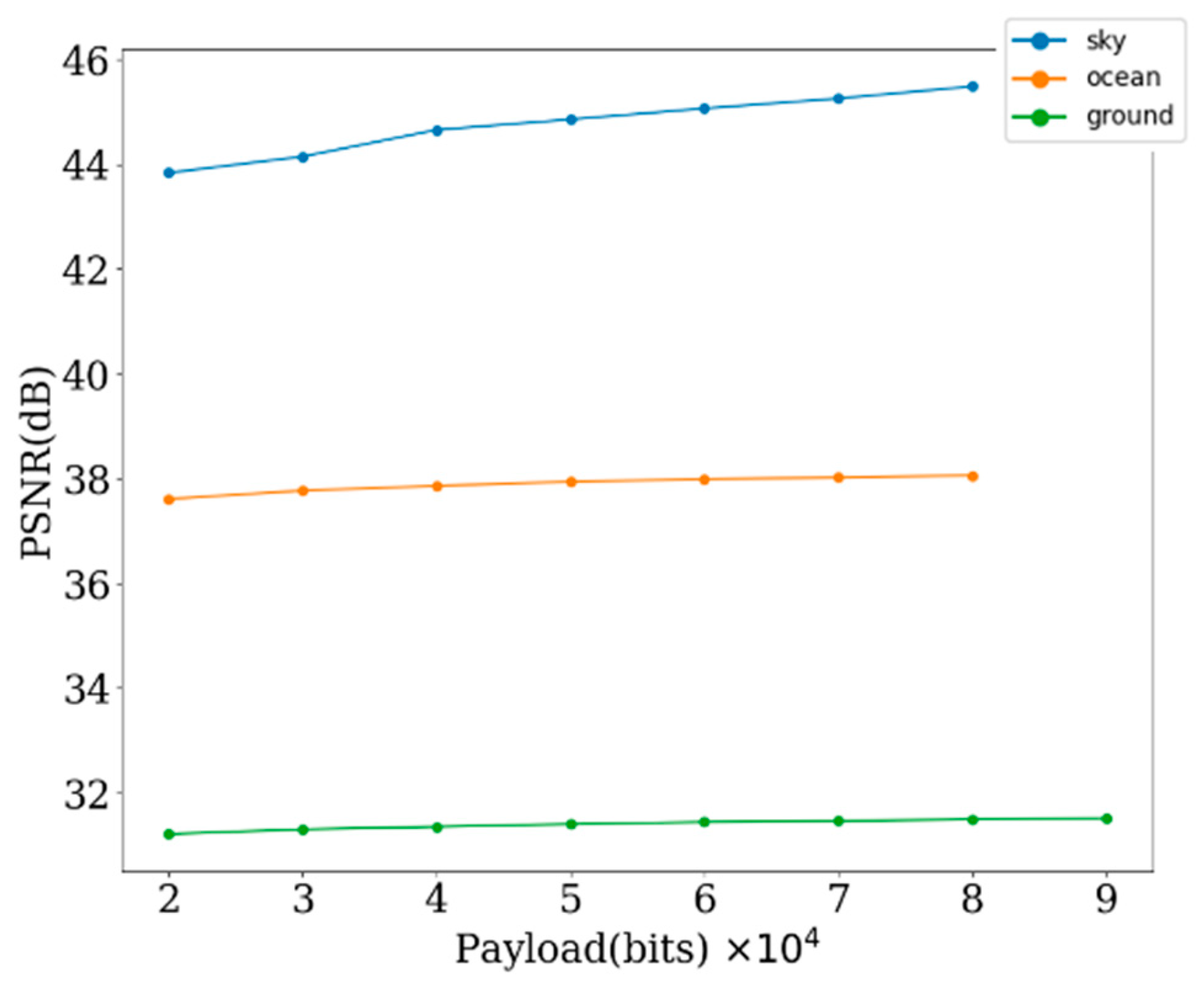
(a) Lena Image
Bits	DE	Skewed HS	PEE	Proposed
20,000~30,000	−0.19	−0.19	−0.02	0.02
30,000~40,000	−0.13	−0.13	−0.12	0.02
40,000~50,000	−0.09	−0.09	−0.08	0.02
50,000~60,000	−0.07	−0.07	−0.06	0.01
60,000~70,000	−0.06	−0.06	−0.05	0.01
70,000~80,000	−0.06	−0.06	−0.05	0.01
80,000~90,000	−0.06	−0.06	−0.05	0.01
(b) Airplane Image
Bits	DE	Skewed HS	PEE	Proposed
20,000~30,000	−0.22	−0.09	−0.17	0.02
30,000~40,000	−0.13	−0.14	−0.11	0.01
40,000~50,000	−0.09	−0.23	−0.08	0.02
50,000~60,000	−0.06	−0.25	−0.06	0.01
60,000~70,000	−0.06	−0.14	−0.06	0.01
70,000~80,000	−0.05	−0.2	−0.07	0.01
80,000~90,000	−0.06	−0.21	−0.08	0.01
(c) Lake Image
Bits	DE	Skewed HS	PEE	Proposed
20,000~30,000	−0.21	−0.21	−0.2	0.01
30,000~40,000	−0.12	−0.14	−0.13	0.01
40,000~50,000	−0.09	−0.08	−0.09	0.01
50,000~60,000	−0.07	−0.05	−0.06	0.01
60,000~70,000	−0.06	−0.07	−0.07	0.01
70,000~80,000	−0.05	−0.05	−0.06	0.01
80,000~90,000	−0.04	−0.05	−0.07	0.01

.

In Table 1, the rate of change in PSNR across intervals for different payload sizes is illustrated using four different embedding methods. The formula for calculating the rate of change in PSNR is defined Equation (18):

$$R=\left(D_{n+1}-D_n\right)/2$$

(18)

R is the rate of change of PSNR and D represents the PSNR for each interval. $n$ is represented as the payload size interval, such as 20,000 and 30,000 and so on.

Table 1 illustrates that the proposed method is the only one with a positive value, while all other embedding methods show a negative rate of change in PSNR across intervals based on payload size. In other words, the PSNR value increases as the payload size grows when the proposed method is employed for embedding. In contrast, experimental results show that PSNR values decrease as the payload size increases for previous embedding methods.

As evident from

Table 2. The average PSNR and rate of change across payload intervals for 100 random images.

	20,000		30,000		40,000		50,000		60,000		70,000		80,000		90,000
PSNR	39.93		40.1		40.21		40.32		40.34		40.41		40.47		40.53
Rate		0.08		0.06		0.06		0.01		0.03		0.03		0.03

, it can be observed that the average PSNR also increases as the payload size increases. Additionally, the PSNR rate of change indicates positive values.

The proposed method assumes that most of images follow the saliency map, and based on this, the cover image is divided into two images as shown in Figure 3. However, the proposed method works correctly even if the images do not follow the saliency map as seen in Figure 11 and Figure 12.

Figure 13 shows the cover image of the Lena image before hiding the secret data, the predicted image by the CNN-based predictor, and the stego-image after hiding the secret data shown in Figure 13d. As seen in Figure 13, there is no significant visual difference between the cover image and the stego-image.

5. Conclusions

In this paper, a new embedding method utilizing a CNN-based predictor was proposed. The fundamental idea was to generate a predicted image using the CNN-based predictor and expand the pixel value difference between the cover image and the predicted image to embed secret data in the extended space. The main difference from conventional embedding methods was the strategy of concealing secret data in the stego-image in a manner that closely aligned with the pixel values of the cover image. As a result, the pixel values of the cover image became closer, leading to a reduction in image distortion as more secret data were embedded in the proposed method. Unlike most of previous embedding methods, a new idea was suggested in the field of reversible data hiding methods. The experimental results demonstrated that image distortion decreased as the size of secret data increased.

This study has a limitation in that the amount of data that can be concealed varies depending on the performance of the CNN-based predictor. If the predictor’s performance is exceptionally high, resulting in the pixel values of the cover image and the predicted image being nearly identical, there is less space available for hiding secret data, making it difficult to conceal large amounts of data. Therefore, it is necessary to experiment with the relationship between PSNR (Peak Signal-to-Noise Ratio) and EC (Embedding Capacity) according to the predictor’s accuracy in this algorithm and identify improvements to address this limitation.